An Adaptive Fictitious Domain Method for Elliptic Problems

Abstract

In the Fictitious Domain Method with Lagrange multiplier (FDM ) the physical domain is embedded into a simpler but larger domain called the fictitious domain. The partial differential equation is extended to the fictitious domain using a Lagrange multiplier to enforce the prescribed boundary conditions on the physical domain while all the other data are extended to the fictitious domain. This lead to a saddle point system coupling the Lagrange multiplier and the extended solution of the original problem. At the discrete level, the Lagrange multiplier is approximated on subdivisions of the physical boundary while the extended solution is approximated on partitions of the fictitious domain. A significant advantage of the FDM is that no conformity between these two meshes is required. However, a restrictive compatibility conditions between the mesh-sizes must be enforced to ensure that the discrete saddle point system is well-posed. In this paper, we present an adaptive fictitious domain method (AFDM ) for the solution of elliptic problems in two dimensions. The method hinges upon two modules ELLIPTIC and ENRICH which iteratively increase the resolutions of the approximation of the extended solution and the multiplier, respectively. The adaptive algorithm AFDM is convergent without any compatibility condition between the two discrete spaces. We provide numerical experiments illustrating the performances of the proposed algorithm.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

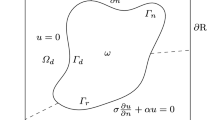
In many engineering applications the efficient numerical solution of partial differential equations on deformable or complex geometries is of paramount importance. In this respect, one crucial issue is the construction of the computational grid. To face this problem, one can basically resort to two different types of approaches. In the first approach, a mesh is constructed on a sufficiently accurate approximation of the exact physical domain (see, e.g., isoparametric finite elements [8], or isogeometric analysis [9]), while in the second approach one embeds the physical domain into a simpler computational mesh whose elements can intersect the boundary of the given domain. Clearly, the mesh generation process is extremely simplified in the second approach, while the imposition of boundary conditions requires extra work. Among the huge variety of methods sharing the philosophy of the second approach, let us mention here the Immersed Boundary methods (see, e.g., [16] and the references therein), the Penalty Methods (see, e.g., the seminal work [2]), the Fictitious Domain/Embedding Domain Methods (see, e.g., [7] and the references therein). In this paper, we focus on the Fictitious Domain Method with Lagrange multiplier (FDM) introduced in [11, 12] (see also [1] for the pioneering work inspiring this approach). In this approach, the physical domain ω is embedded into a simpler and larger domain Ω (the fictitious domain), the right-hand side is extended to the fictitious domain and the boundary conditions on the boundary of the physical domain are appended through the use of a Lagrange multiplier. The FDM gives rise to a saddle point problem whose exact solution restricted to ω corresponds to the solution of the original problem. At the discrete level, the FDM allows the use of structured and uniform meshes in the fictitious domain, without requiring any conformity between the bulk mesh and the boundary of the physical domain. This represents a relevant computational advantage. However, there are two important issues to be taken into account to build numerical techniques that are able to take advantage of the crucial features of FDM: the choice of the discrete spaces for the approximation of the solution and the multiplier, and the construction of the extension of the right-hand side from the physical domain to the fictitious one. As pointed out in the analysis performed in [11] in the context of finite element approximation for the solution of elliptic problems with Dirichlet boundary conditions, the first condition (inf-sup condition) is essential to ensure existence and uniqueness of the discrete solution, while the second one influences the regularity of the extended continuous solution, thus impacting on the approximation properties of the discrete spaces (on this latter topic, see, e.g., [14]). The first condition turns out to introduce some restrictive compatibility conditions between the mesh-sizes of the fictitious domain grid and the subdivision of boundary of the physical domain (needed to approximate the Lagrange multiplier). The second issue can spoil, for example, the performance of the linear finite element method on uniform meshes whenever the original solution is sufficiently regular, e.g. H ² regular, while the extended solution is less regular.

In view of the above discussion, the computational effectivity of FDM seems to be a non trivial issue. However, as shown in the present paper, a judicious use of adaptivity can allow to overcome the above two obstructions and recover the full potentiality of FDM, i.e. working with discrete spaces (and meshes) violating the compatibility conditions and recover even in presence of less regular extended solutions, the optimal performance of finite elements on uniform grids in presence of regular solutions. In particular, in this work we present an adaptive fictitious domain method, named AFDM, based on the use of linear finite elements for the approximation of the solution and piecewise constants for the approximation of the Lagrange multiplier. In the spirit of the algorithm provided in [6], the method hinges upon two modules, ELLIPTIC and ENRICH that iteratively modify the discrete spaces for the approximation of the extended solution and the multiplier. Our method is proved to be convergent regardless of the imposition of any compatibility condition between the two discrete spaces. Similar remarks has been already pointed out in different contexts by Dahlke et al. [10] and Bänsch et al. [4] (see also [3] for an abstract discussion of inexact Uzawa methods) and we refer to [13] for the mathematical study of an adaptive algorithm for the Stokes system, which serves as a benchmark for saddle point problems. Moreover, preliminary numerical results show that AFDM is optimal with respect to the number of degrees of freedom employed to approximate the extended solution and the Lagrange multiplier. In two dimension, the optimality of the adaptive refinement strategy seems to require an adaptive strategy to generate the successive subdivision of the fictitious domain, while uniform or quasi-uniform subdivisions can be used for the boundary mesh.

The outline of the paper is as follows. In Sect. 2 we introduce the fictitious domain method, while in Sect. 3 we introduce the adaptive fictitious domain method. Finally, in Sect. 4 we numerically explore the convergence (and optimality) properties of our algorithm.

2 Fictitious Domains Method

Let ω be a bounded domain of $\mathbb{R}^{2}$ with boundary γ. To make the presentation simpler, we assume that ω is a polygon. We are interested in employing the fictitious domain method to solve the following model problem: let f ∈ L ²(ω), find u ∈ H ₀ ¹(ω) such that

$$\displaystyle\begin{array}{rcl} -\varDelta \ u = f\qquad \text{in}\ \omega \,& &{}\end{array}$$

(1)

$$\displaystyle\begin{array}{rcl} u = 0\qquad \text{on}\ \gamma .& &{}\end{array}$$

(2)

The fictitious domain formulation of problem (1)–(2) hinges on a square or rectangular domain Ω with boundary Γ: = ∂ Ω and such that ω ⊂ ⊂ Ω. It reads: for any L ²-extension $\tilde{f}$ of f to Ω, find $(\tilde{u},\lambda ) \in H_{0}^{1}(\varOmega ) \times H^{-\frac{1} {2} }(\gamma )$ such that

$$\displaystyle\begin{array}{rcl} \int _{\varOmega }\nabla \tilde{u} \cdot \nabla v-\langle \lambda,v\rangle _{\gamma }& =& \int _{\varOmega }\tilde{f} v\ dx\qquad \forall v \in H_{0}^{1}(\varOmega )\,{}\end{array}$$

(3)

$$\displaystyle\begin{array}{rcl} \langle \mu,\tilde{u}\rangle _{\gamma }& =& 0\qquad \forall \mu \in H^{-\frac{1} {2} }(\gamma )\,{}\end{array}$$

(4)

where for v ∈ H ₀ ¹(Ω), its restriction to γ is understood in the sense of traces, and 〈⋅ , ⋅ 〉 _γ denotes the duality pairing between $H^{-\frac{1} {2} }(\gamma )$ and $H^{\frac{1} {2} }(\gamma )$ (recall that γ is a closed curve). Using an integration by parts formula, it is immediate to verify (see, e.g., [12]), that the fictitious domain formulation (3)–(4) is equivalent to original formulation (1)–(2) where

$$\displaystyle{ \lambda =\Big [\frac{\partial \tilde{u}} {\partial n}\Big]_{\gamma } }$$

(5)

is the jump of $\frac{\partial \tilde{u}} {\partial n}$ across γ and n denotes the unit normal exterior to ω.

The regularity of $\tilde{u}$ and λ depends on the extension chosen for f and the domain ω. In the worst case, $\tilde{u} \in H^{\frac{3} {2} -\epsilon }(\varOmega )$ for any ε > 0 and λ ∈ L ²(γ) satisfies $\lambda \in H^{\frac{1} {2} }(\gamma _{i})$, for every straight line γ _i composing γ (see [11]). In what follows we will drop the symbol $\ \tilde{}\$ if no confusion arises.

In [11], the Babuska-Brezzi’s theory is used to guarantee that problem (3)–(4) is well posed. In particular, the bilinear form (u, v) ↦ ∫ _Ω ∇u ⋅ ∇v is coercive on the set $\{v \in H_{0}^{1}(\varOmega ):\langle \mu,v\rangle _{\gamma } = 0\ \forall \mu \in H^{-1/2}(\gamma )\}$ and that the following inf-sup condition holds: there exists a constant κ > 0 such that

$$\displaystyle{ \inf _{\mu \in H^{-\frac{1} {2} }(\gamma )}\sup _{v\in H_{0}^{1}(\varOmega )} \frac{\langle v,\mu \rangle _{\gamma }} {\|\mu \|_{ H^{-\frac{1} {2} }(\gamma )}\|v\|_{H^{1}(\varOmega )}} \geq \kappa . }$$

(6)

3 Adaptive Fictitious Domain Method

In this section we present our adaptive fictitious domain method (AFDM ) based on Uzawa iterations. In Sect. 3.1, we describe the infinite dimensional version of the algorithm, whereas in Sect. 3.2 we introduce its adaptive finite dimensional counterpart.

3.1 Infinite Dimensional Fictitious Domain Algorithm

We start this section by describing the infinite dimensional fictitious domain algorithm for solving (3)–(4). It consists of Uzawa-type successive iterations: Given α > 0 and $\lambda _{0} \in H^{-\frac{1} {2} }(\gamma )$ we seek, for j ≥ 1,

$$\displaystyle\begin{array}{rcl} & & u_{j} \in H_{0}^{1}(\varOmega ): \qquad \int _{\varOmega }\nabla u_{ j} \cdot \nabla v =\int _{\varOmega }fv +\langle \lambda _{j-1},v\rangle _{\gamma }\quad \forall v \in H_{0}^{1}(\varOmega )\,{}\end{array}$$

(7)

$$\displaystyle\begin{array}{rcl} & & \lambda _{j} \in H^{-\frac{1} {2} }(\gamma ): \qquad (\lambda _{j},\mu )_{\gamma } = (\lambda _{j-1},\mu )_{\gamma } -\alpha \ (u_{j},\mu )_{\gamma }\quad \forall \mu \in H^{-\frac{1} {2} }(\gamma ){}\end{array}$$

(8)

where we denote by (⋅ , ⋅ ) _γ the scalar product in $H^{-\frac{1} {2} }(\gamma )$ and where we used the identification of L ²(γ) and have with a slight abuse of notation $H^{\frac{1} {2} }(\gamma ) \subset H^{-\frac{1} {2} }(\gamma )$.

The Schur complement operator $S: H^{-\frac{1} {2} }(\gamma ) \rightarrow H^{\frac{1} {2} }(\gamma ) \subset H^{-\frac{1} {2} }(\gamma )$ defined as

$$\displaystyle{ S\lambda = u_{\lambda }\, }$$

(9)

where u _λ  ∈ H ₀ ¹(Ω) is the solution to

$$\displaystyle{ \int _{\varOmega }\nabla u_{\lambda } \cdot \nabla v =\langle \lambda,v\rangle _{\gamma }\quad \forall v \in H_{0}^{1}(\varOmega ). }$$

The operator S is symmetric and positive definite [12] and is instrumental in the analysis of the Uzawa iterations. In fact, (7)–(8) can be written using S as

$$\displaystyle{ \lambda _{j} = (I -\alpha S)\lambda _{j-1} +\alpha u_{f}\ \qquad \text{in }H^{-\frac{1} {2} }(\gamma ), }$$

(10)

where u _f  ∈ H ₀ ¹(Ω) is given by

$$\displaystyle{ \int _{\varOmega }\nabla u_{f} \cdot \nabla v =\int _{\varOmega }f\ v\qquad \forall v \in H_{0}^{1}(\varOmega ). }$$

It is immediate to verify that if $0 <\alpha <2/\|S\|_{ \mathcal{L}(H^{-\frac{1} {2} }(\gamma ),H^{-\frac{1} {2} }(\gamma ))}$, then

$$\displaystyle{ \beta:=\| I -\alpha S\|_{ \mathcal{L}(H^{-\frac{1} {2} },H^{-\frac{1} {2} })} <1 }$$

(11)

and thus the infinite dimensional fictitious domain algorithm is convergent.

3.2 Adaptive Finite Dimensional Fictitious Domain Method

We now introduce our adaptive finite dimensional fictitious domain algorithm (AFDM ) which iteratively builds a sequence of nested finite dimensional spaces to achieve a reduction of the approximation error between each iterative step. We start with an initial conforming subdivision $\mathcal{T}_{0}$ of Ω made of triangles and an initial subdivision of γ (made of segments). We assume that

$$\displaystyle{ \text{for each }T \in \mathcal{T}_{0},\mathring{T} \cap \gamma \text{ is connected,} }$$

(12)

which is automatically satisfied upon assuming that the initial subdivision $\mathcal{T}_{0}$ is sufficiently fine to capture the interface and could be enforced via uniform refinements without affecting the asymptotic performances of the algorithm. From now on, j ≥ 0 will always denote the AFDM iteration counter. We denote by $\mathcal{T}_{j}$ and $\mathcal{S}_{j}$ the j-th conforming partitions of Ω and γ made of triangles and segments, respectively. The diameters of the elements $T \in \mathcal{T}_{j}$ and $\ell\in \mathcal{S}_{j}$ are denoted h _T : = diam(T) and h _ℓ : = diam(ℓ), respectively. We emphasize that the two partitions built by the adaptive algorithm described below are mutually independent and in particular no compatibility conditions between the two partitions is required. This is a crucial difference from the results in [11] (see Remark 2 below). The shape regularity constant of a generic subdivision $\mathcal{T}$ is $\max _{T\in \mathcal{T}}\frac{h_{T}} {\rho _{T}}$, where ρ _T is the diameter of the largest ball inside T. The shape regularity constant of a sequence of subdivision $\{\mathcal{T}_{i}\}_{i\geq 0}$ is

$$\displaystyle{\sup _{i\geq 0}\max _{T\in \mathcal{T}_{i}}\frac{h_{T}} {\rho _{T}}.}$$

Associated with conforming partitions $\mathcal{T}$ of Ω and $\mathcal{S}$ of γ, we introduce the finite dimensional spaces

$$\displaystyle{\mathbb{V}_{\mathcal{T}}:= \left \{v \in C^{0}(\overline{\varOmega }): v\vert _{ T} \in \mathcal{P}^{1}(T)\ \forall T \in \mathcal{T}_{ j}\right \} \cap H_{0}^{1}(\varOmega )}$$

and

$$\displaystyle{\mathbb{M}_{\mathcal{S}}:=\{ w \in L^{2}(\gamma ): w\vert _{\ell} \in \mathcal{P}^{0}(\ell)\ \forall \ell \in \mathcal{S}\},}$$

where for $k \in \mathbb{N}$, $\mathcal{P}^{k}(D)$ is the set of polynomials of degree k in D. In the following, we set $\mathbb{V}_{j}:= \mathbb{V}_{\mathcal{T}_{j}}$ and $\mathbb{M}_{j}:= \mathbb{M}_{\mathcal{S}_{j}}$.

The finite dimensional adaptive fictitious domain algorithm relies on two sub-routines described now.

3.2.1 The Module ELLIPTIC

The module ELLIPTIC adaptively constructs approximations U _j of the exact solution u _j to (7). To describe this procedure, we let u _j  ∈ H ₀ ¹(Ω) satisfying

$$\displaystyle{ \int _{\varOmega }\nabla u_{j} \cdot \nabla v =\int _{\varOmega }f\ v +\int _{\gamma }\varLambda _{j-1}\ v\qquad \forall v \in H_{0}^{1}(\varOmega )\, }$$

(13)

for a given $\varLambda _{j-1} \in \mathbb{M}_{j-1}$.

In contrast to (7) where $\lambda _{j-1} \in H^{-\frac{1} {2} }(\gamma )$, we note that Λ _j−1 belongs to a finite dimensional subspace of L ²(γ). Moreover, we observe that (13) is a weak formulation of

$$\displaystyle\begin{array}{rcl} & -\varDelta u_{j} = f& \ \text{in }\omega,\quad -\varDelta u_{j} = f\quad \text{in }\varOmega \setminus \overline{\omega }, \\ & [u_{j}] = 0& \ \text{on}\gamma,\quad \left [\frac{\partial u_{j}} {\partial n} \right ]_{\gamma } =\varLambda _{j-1}\quad \text{on }\gamma, \\ & u_{j} = 0 & \ \text{on }\partial \varOmega. {}\end{array}$$

(14)

If ɛ _j stands for an adjustable error tolerance, then the module ELLIPTIC,

$$\displaystyle{ (\mathcal{T}_{j},U_{j}) = \mathbf{\mathtt{ELLIPTIC}}(\mathcal{T}_{j-1},\varLambda _{j-1},\varepsilon _{j}), }$$

constructs adaptively a refined mesh $\mathcal{T}_{j}$ of $\mathcal{T}_{j-1}$ such that the solution of the discrete elliptic problem

$$\displaystyle{ U_{j} \in \mathbb{V}_{j}: \qquad \int _{\varOmega }\nabla U_{j} \cdot \nabla V =\int _{\varOmega }f\ V +\int _{\gamma }\varLambda _{j-1}\ V \qquad \forall V \in \mathbb{V}_{j}\, }$$

(15)

approximate u _j within in the prescribed tolerance ɛ _j , i.e.

$$\displaystyle{ \|\nabla (u_{j} - U_{j})\|_{L^{2}(\varOmega )} \leq \varepsilon _{j}. }$$

(16)

The adaptive ELLIPTIC module iterates a classical strategy of the type

$$\displaystyle{\mathbf{\mathtt{SOLVE}}-\mathbf{\mathtt{ESTIMATE}}-\mathbf{\mathtt{MARK}}-\mathbf{\mathtt{REFINE}}}$$

until condition (16) is satisfied (see, e.g., [15]).

The following upper bound for the error of any inner-iterate is instrumental in ESTIMATE. A corresponding lower bound is also valid and we refer to [5] for their proofs.

Proposition 3.1 (Upper Bound for ELLIPTIC )

Let u _j ∈ H ₀ ¹ (Ω) be the solution to (13) and $U_{j}^{i} \in \mathbb{V}_{i}$ be the discrete Galerkin solution to (15) associated with any refinement $\mathcal{T}^{i}$ of $\mathcal{T}_{j-1}$ . Assume that the initial subdivision satisfy (12) . Then, there exists a positive constant K ^∗ only depending on $\mathcal{T}^{i}$ through its shape-regularity constant such that the following a posteriori error estimate holds

$$\displaystyle{ \|\nabla (u_{j} - U_{j}^{i})\|_{ L^{2}(\varOmega )}^{2} \leq K^{{\ast}}\sum _{ T\in \mathcal{T}^{i}}\eta ^{i}(T)^{2} }$$

(17)

where

$$\displaystyle\begin{array}{rcl} & & \eta ^{i}(T)^{2}:= h_{ T}^{2}\|R_{ T}^{i}\|_{ L^{2}(T)}^{2} + h_{ T}\sum _{e\ \text{edge of }T}\|J_{e}^{i}\|_{ L^{2}(e)}^{2} + h_{ T}\|\varLambda _{j-1}\|_{L^{2}(\mathring{T} \cap \gamma )}^{2}\, {}\\ \end{array}$$

with

$$\displaystyle{ R_{T}^{i}:= (\,f+\varDelta U_{ j}^{i})\vert _{ T},\qquad J_{e}^{i}:= \left \{\begin{array}{ll} [\frac{\partial U_{j}^{i}} {\partial n} ]_{e} -\varLambda _{j-1} & \quad \text{on }e\cap \gamma, \\{} [\frac{\partial U_{j}^{i}} {\partial n} ]_{e} &\quad \text{on }e\setminus \gamma. \end{array} \right. }$$

(18)

Here $\left [.\right ]_{e}$ is the jump across the edge e and $\mathring{T}$ is the topological interior of T.

Remark 1 (Elliptic Estimator)

We note that the non-standard terms containing Λ _j−1 in the estimator η ⁱ(T) above both measure the discrepancy from the exact relation $\lambda = [\frac{\partial u} {\partial n}]_{\gamma }$, see (5). In particular, within an element T, ∇U _j ⁱ is continuous so that

$$\displaystyle{\|\varLambda _{j-1}\|_{L^{2}(\mathring{T}\cap \gamma )} =\| \left [\frac{\partial U_{j}^{i}} {\partial m} \right ]_{\mathring{T}\cap \gamma }-\varLambda _{j-1}\|_{L^{2}(\mathring{T}\cap \gamma )},}$$

where $[\frac{\partial U_{j}^{i}} {\partial m} ]_{\mathring{T}\cap \gamma }$ denotes the jump of $\frac{\partial U_{j}^{i}} {\partial m}$ across $\mathring{T}\cap \gamma$ and m denotes one of the normal to $\mathring{T}\cap \gamma$.

3.3 The Module ENRICH

Let $\mathbb{V}_{j}^{\gamma }$ be the restriction of functions in $\mathbb{V}_{j}$. We denote by $\varPi _{j}: \mathbb{V}_{j}^{\gamma } \rightarrow \mathbb{M}_{j}$ the orthogonal L ²-projection onto $\mathbb{M}_{j}$. The module

$$\displaystyle{ \mathcal{S}_{j} = \mathbf{\mathtt{ENRICH}}(\mathcal{S}_{j-1},U_{j},\varepsilon _{j})\, }$$

(19)

constructs a refinement $\mathcal{S}_{j}$ of $\mathcal{S}_{j-1}$ such that

$$\displaystyle{ \|(I -\varPi _{j})U_{j}\|_{ H^{-\frac{1} {2} }(\gamma )} \leq C\varepsilon _{j} }$$

(20)

for a given C independent of j.

The quantity $\|(I -\varPi _{j})U_{j}\|_{ H^{-\frac{1} {2} }(\gamma )}$ is not computed exactly but estimated as follows. Standard interpolation error estimates together with a trace estimate and the stability of the L ²-projection yield

$$\displaystyle\begin{array}{rcl} \|(I -\varPi _{j})U_{j}\|_{H^{-1/2}(\gamma )}& =& \sup _{\phi \in H^{1/2}(\gamma )}\frac{\int _{\gamma }(I -\varPi _{j})U_{j}\phi } {\|\phi \|_{H^{1/2}(\gamma )}} =\sup _{\phi \in H^{1/2}(\gamma )}\frac{\int _{\gamma }(I -\varPi _{j})U_{j}(\phi -\varPhi )} {\|\phi \|_{H^{1/2}(\gamma )}} {}\\ & \leq & \sup _{\phi \in H^{1/2}(\gamma )}\frac{\|h_{\ell}^{1/2}(I -\varPi _{j})U_{j}\|_{L^{2}(\gamma )}\|h_{\ell}^{-1/2}(\phi -\varPhi )\|_{L^{2}(\gamma )}} {\|\phi \|_{H^{1/2}(\gamma )}} {}\\ & \leq & C\|h_{\ell}^{1/2}(I -\varPi _{ j})U_{j}\|_{L^{2}(\gamma )} \leq C(\max _{\ell\in \mathcal{S}_{j}}h_{\ell})^{1/2}\|(I -\varPi _{ j})U_{j}\|_{L^{2}(\gamma )} {}\\ & \leq & C(\max _{\ell\in \mathcal{S}_{j}}h_{\ell})\|U_{j}\|_{H^{1/2}(\gamma )} \leq C(\max _{\ell}h_{\ell})\|U_{j}\|_{H^{1}(\varOmega )}, {}\\ \end{array}$$

where $\varPhi \in \mathbb{M}_{j}$ and C is a generic constant independent of j. Now the stability estimate $\|U_{j}\|_{H^{1}(\varOmega )} \leq C\|\,f\|_{L^{2}(\varOmega )}$ imply

$$\displaystyle{ \|(I -\varPi _{j})U_{j}\|_{H^{-1/2}(\gamma )} \leq C(\max _{\ell}h_{\ell})\|\,f\|_{L^{2}(\varOmega )}. }$$

(21)

Based on this, the ENRICH routine refines recursively all the elements of $\mathcal{S}_{j-1}$ until they all have a mesh-size smaller than $\frac{\varepsilon _{j}} {\|\,f\|_{L^{2}(\varOmega )}}$. The resulting mesh is output of ENRICH since it satisfies (20).

3.4 The Module UPDATE

The discrete Lagrange multiplier is updated by the module UPDATE

$$\displaystyle{ \varLambda _{j} = \mathbf{\mathtt{UPDATE}}(\mathcal{T}_{j},\mathcal{S}_{j},\varLambda _{j-1},U_{j},\alpha )\, }$$

(22)

which computes according to (8)

$$\displaystyle{ \varLambda _{j} \in \mathbb{M}_{j}: \qquad \varLambda _{j} =\varLambda _{j-1} -\alpha \varPi _{j}U_{j}. }$$

(23)

We note that as $U_{j} \in \mathbb{V}_{j}$ its restriction to γ is an element of $\mathbb{V}_{j}^{\gamma }$ (by construction).

3.5 The AFDM Algorithm

We are now in a position to detail the iterative structure of AFDM. Each iteration of the algorithm consists of an inner solver employing ELLIPTIC in place of (7), followed by an application of the module ENRICH and by an update of the multiplier performed by the module UPDATE.

Adaptive Fictitious Domain Method (AFDM )

Given the initial triangulations $\mathcal{T}_{0}$ and $\mathcal{S}_{0}$ , and the parameters α, ɛ ₀ > 0, 0 < ζ < 1 set j  = 1 and iterate:

• 1. Select any function $\varLambda _{0} \in \mathbb{M}_{0}$ .

• 2. Update $\varepsilon _{j} \leftarrow \zeta \varepsilon _{j-1}$.

• 3. Compute $(\mathcal{T}_{j},U_{j}) = \mathbf{\mathtt{ELLIPTIC}}(\mathcal{T}_{j-1},\varLambda _{j-1},\varepsilon _{j})$.

• 4. Enrich $\mathcal{S}_{j} = \mathbf{\mathtt{ENRICH}}(\mathcal{S}_{j-1},U_{j},\varepsilon _{j})$.

• 5. Compute $\varLambda _{j} = \mathbf{\mathtt{UPDATE}}(\mathcal{T}_{j},\mathcal{S}_{j},\varLambda _{j-1},U_{j},\alpha )$.

• 6. Update j ← j + 1.

• 7. Go to step (2).

The algorithm AFDM is convergent [5] as reported in the theorem below.

Theorem 1 (Convergence)

Let α > 0 be such that (11) holds and assume that the initial subdivision satisfy (12) . Let $(\mathcal{T}_{j},\mathcal{S}_{j},U_{j},\varLambda _{j})$ be the sequence of meshes and subdivision produced by AFDM  . There exist positive constants C ₁ and δ < 1 depending on the shape regularity constant of $\{\mathcal{T}_{j}\}_{j\geq 0}$ such that

$$\displaystyle{ \|\nabla (u - U_{j})\|_{L^{2}(\varOmega )} +\|\lambda -\varLambda _{j}\|_{ H^{-\frac{1} {2} }(\gamma )} \leq C_{1}\delta ^{j}. }$$

(24)

Remark 2 (Compatibility Condition)

In [11] the authors obtain a priori error estimates for the finite element approximation of (3)–(4) under the assumption that the mesh size of the bulk triangulation is sufficiently large compared to the mesh size of the boundary triangulation, i.e. there holds a compatibility condition between the discrete spaces. This latter is a crucial requirement to prove the validity of a discrete inf-sup condition and thus the existence of the discrete solution. We emphasize that the convergence of our adaptive algorithm holds without enforcing any compatibility condition, thus possibly violating, the discrete inf-sup condition (see [4, 10] for similar results in different contexts).

The algorithm AFDM described above never ends until a stopping criterion is appended. In principle, we can resort to (24) to obtain an a priori estimate for the necessary number of iterations to reach a prescribed tolerance. However, this strategy is not implementable as the constant δ appearing in (24) is not accessible in practice. For this reason, we now provide an a-posteriori error estimate for the quantity $\|\nabla (u - U_{j})\|_{L^{2}(\varOmega )} +\|\lambda -\varLambda _{j-1}\|_{ H^{-\frac{1} {2} }(\gamma )}$ which can be employed to stop AFDM while guarantying a prescribed approximation error.

Proposition 3.2 (Upper Bound for AFDM )

Let $(u,\lambda ) \in H_{0}^{1}(\varOmega ) \times H^{-\frac{1} {2} }(\gamma )$ be the solution to (3)–(4) and $\{(U_{j},\varLambda _{j-1})\}$ be the sequence of approximations produced by AFDM . Assume that the initial subdivision satisfy (12) . Then there exists a constant C ₂ depending on the shape regularity constant of $\mathcal{T}_{j}$ such that

$$\displaystyle\begin{array}{rcl} \|\nabla (u - U_{j})\|_{L^{2}(\varOmega )} +\|\lambda -\varLambda _{j-1}\|_{ H^{-\frac{1} {2} }(\gamma )}& \leq & C_{2}\left (\eta _{\mathcal{T}_{j}} +\eta _{\mathcal{S}_{j-1}}\right )\,{}\end{array}$$

(25)

where

$$\displaystyle\begin{array}{rcl} \eta _{\mathcal{T}_{j}}&:=& \Big(\sum _{T\in \mathcal{T}_{j}}\eta _{j}(T)^{2}\Big)^{1/2}{}\end{array}$$

(26)

$$\displaystyle\begin{array}{rcl} \eta _{\mathcal{S}_{j-1}}&:=& \Big(\sum _{\ell\in \mathcal{S}_{j-1}}h_{\ell}\|\nabla _{\gamma }U_{j}\|_{L^{2}(\ell)}^{2}\Big)^{1/2}{}\end{array}$$

(27)

and

$$\displaystyle\begin{array}{rcl} \eta _{j}(T)^{2}&:=& h_{ T}^{2}\|R_{ T,j}\|_{L^{2}(T)}^{2} + h_{ T}\sum _{e\text{ edge in }T}\|J_{e,j}\|_{L^{2}(e)}^{2} + h_{ T}\|\varLambda _{j-1}\|_{L^{2}(\mathring{T}\cap \gamma )}^{2},{}\\ \end{array}$$

with

$$\displaystyle{ R_{T,j}:= (\,f+\varDelta U_{j})\vert _{T},\qquad J_{e,j}:= \left \{\begin{array}{ll} [\frac{\partial U_{j}} {\partial n} ]_{e} -\varLambda _{j-1} & \quad \text{on }e\cap \gamma, \\{} [\frac{\partial U_{j}} {\partial n} ]_{e} &\quad \text{on }e\setminus \gamma. \end{array} \right. }$$

(28)

Remark 3 (Boundary Indicator)

In view of the results contained in [17], the indicator $\eta _{\mathcal{S}_{j-1}}$ measures the mismatch between the trace of U _j on γ and the exact homogeneous Dirichlet boundary condition (2).

4 Numerical Results

In this section we illustrate numerically the convergence properties of the AFDM algorithm and investigate numerically its optimality studied in [5]. Before presenting the numerical results we discuss some details regarding the implementation of AFDM.

4.1 Implementation Issues

Data structures for representing the (two dimensional) triangular bulk mesh of the fictitious domain Ω and the (one dimensional) boundary mesh of γ are organized as binary trees starting from the 0-th level meshes $\mathcal{T}_{0}$ and $\mathcal{S}_{0}$, respectively. The initial bulk mesh $\mathcal{T}_{0}$ is a regular mesh of the domain Ω constructed ignoring the conformity with γ. The initial boundary mesh $\mathcal{S}_{0}$ is made of the edges of γ, which is assumed to be a polygonal curve, see Fig. 4.1(left). The refinement of the triangular bulk mesh is performed by employing the longest edge splitting. The refined elements are labeled as non-active and the newly created elements become active. Notice that additional refinements of neighboring elements may be needed in order to ensure conformity.

The refinement strategy advocated for the boundary mesh is more involved. On each boundary edge, we consider the points given by the intersection between the edge itself and the triangular mesh elements. We refer to these points as to boundary points. Whenever a refinement of a boundary edge is needed, we split the edge at the closest boundary point to the edge mid-point, see Fig. 4.1(right). In Fig. 4.1(bottom-left) we sketch three successive refinement of the horizontal portion of γ. In Fig. 4.1(top-left), we report the meshes resulting from the first four steps of a uniform refinement of the boundary elements. In case no boundary nodes are available, we perform successive refinements of the triangle containing the edge until one boundary nodes becomes available. However the two children produced by refinement of the triangle are labeled as non-active unless needed by the bulk mesh refinement procedure.

In our implementation the elements of the mesh $\mathcal{S}$ are always determined by the intersection between the boundary γ and a triangle (not necessarily active) belonging to the infinite binary tree with root $\mathcal{T}_{0}$. In view of this construction, the levels of refinement to which the elements in $\mathcal{S}$ and in $\mathcal{T}$ belong to are completely independent. Clearly, the above construction of $\mathcal{S}$ adds some geometric restrictions on the set of meshes we can deal with. However, the advantage at the computational level is quite remarkable because all the computer operations required by the refining process, as well as all the numerical computation of integrals involving the interaction between bulk and boundary objects (mesh elements or functions) can be always performed at the level of the single element (or of the binary tree stemming from it) without affecting the binary data structure of the neighboring elements.

Fig. 1

Example of boundary refinement: (top-left) four different levels of refinement of the boundary mesh and (bottom-left) associated bulk mesh with local refinement (dotted line); (right) boundary points produced by the refinement of the bulk elements

For the sake of presentation in the rest of this section we employ the following notation. We set e _j ^u = u − U _j and e _j ^λ = λ −Λ _j . Moreover, we denote by ∥ ⋅ ∥ ₀ the L ²(Ω) or L ²(γ)-norm depending on the context and by | ⋅ | ₁ the H ¹(Ω)-seminorm.

4.2 Test Case: L-Shape Domain

We consider the L-shaped domain ω = (−1 1)² ∖(−1 0)² with boundary γ. We are interested in the following model problem: we choose f ∈ L ²(ω) such that, after introducing polar coordinates (r, ϕ), the solution to (1)–(2) is

$$\displaystyle{u(r,\phi ) = h(r)r^{2/3}\sin (2/3(\phi +\pi /2))}$$

where

$$\displaystyle{h(r) = \frac{w(3/4 - r)} {w(r - 1/4) + w(3/4 - r)},\quad w(r) = \left \{\begin{array}{ll} r^{2} & \mbox{ if}\ r> 0 \\ 0 &\mbox{ else.} \end{array} \right.}$$

The fictitious domain formulation of problem (3)–(4) is obtained by embedding ω in the square domain Ω = (−1 1)² with boundary Γ = ∂ Ω, see Fig. 2, and extend f by zero outside ω. It is not difficult to see that $u \in H^{\frac{5} {3} -\epsilon }(\omega )$, for any ε > 0 and the exact Lagrange multiplier is

$$\displaystyle{\lambda = \frac{2} {3}h(r)\ r^{-1/3}.}$$

In the following, we explore the convergence and optimality properties of AFDM algorithm. The AFDM algorithm is applied with the following parameters: α = 0. 5, ζ = 0. 95 and different values of ɛ ₀, namely ɛ ₀ = 1. 0,  0. 5,  0. 25,  0. 1 (see Sect. 3 for the precise meaning of the parameters). In the sequel, we report the results obtained by AFDM. The outer iteration of AFDM is stopped when

$$\displaystyle{\eta _{\mathcal{T}_{j}} +\eta _{\mathcal{S}_{j-1}} <\zeta ^{45}\varepsilon _{ 0}.}$$

Fig. 2

Adaptive meshes produced by AFDM. (a ) Initial mesh $\mathcal{T}_{0}$ (left) and mesh at iteration 12 (right), (b ) mesh at iteration 18 (left) and final mesh (right)

Fig. 3

Left: discrete solution U in the fictitious domain. Right: zoom on γ at the reentrant corner of the discrete solutions U (red), Λ (blue) and exact multiplier λ (green)

In Fig. 2 we display the initial and the final mesh together with two intermediate adaptively refined meshes, while in Fig. 3 (left) we report the final discrete solution U plotted on the fictitious domain and in Fig. 3 (right) we collect the graphs of final discrete Lagrange multiplier Λ together with the exact multiplier λ and the restriction of U on the boundary γ. A close inspection of the figures reveals that the algorithm AFDM correctly approximates the exact pair (u, λ). As the value of β is unknown, an a priori choice for ξ is impossible. However, as already observed in [4], a practical choice for ξ seems to be ξ = 0. 95. Indeed, larger values of ξ clearly guarantee the boundedness of the inner iterations of ELLIPTIC, but at the expense of an increased number of outer iterations. Values of ξ close to 0. 95 ensure an optimal decay rate of the H ¹-error. This motivates the initial choice of setting ξ = 0. 95 for running the numerical tests.

Table 1 Computed rates of convergence of the true errors and of the error estimators $\eta _{\mathcal{T}_{j}}$ and $\eta _{\mathcal{S}_{j-1}}$ with respect to the total number of dofs $\#\mathcal{T}_{j} + \#\mathcal{S}_{j-1}$ for different values of ɛ ₀

Table 2 Growing rate r of the total number of dofs (second column), bulk dofs (third) and boundary dofs (fourth) with respect to ɛ _j , i.e. r such that $\#(\cdot )_{j} \in \mathcal{O}(\varepsilon _{j}^{r})$

In the following, we further explore the optimality properties of AFDM and see their dependency on the parameter ɛ ₀. In particular, in Table 1 we report the rates of convergence with respect to the total number of degrees of freedom, of the true errors for e _j ^u in L ²(Ω), H ¹(Ω), the error for e _j−1 ^λ in an approximate $H^{-\frac{1} {2} }(\gamma )$ computed as a weighted L ² norm

$$\displaystyle{\|e_{j-1}^{\lambda }\|_{ -\frac{1} {2} } \approx \| e_{j-1}^{\lambda }\|_{ -\frac{1} {2},j-1}:=\Big (\sum _{\ell\in \mathcal{S}_{j-1}}h_{\ell}\|\lambda -\varLambda _{j-1}\|_{L^{2}(\ell)}^{2}\Big)^{1/2},}$$

and the error estimators $\eta _{\mathcal{T}_{j}}$ and $\eta _{\mathcal{S}_{j-1}}$.

From the third and fourth columns we infer that the total error $\|\nabla (u - U_{j})\|_{L^{2}(\varOmega )} +\|\lambda -\varLambda _{j-1}\|_{ H^{-\frac{1} {2} }(\gamma )}$ decreases to zero roughly as $(\#\mathcal{T}_{j} + \#\mathcal{S}_{j-1})^{-0.5}$, the optimal decay for piecewise approximations of u. This is corroborated by the results in columns five and six which are thus in agreement with Proposition 3.2.

In Table 2 we collect the growing rates of the total number of dofs $\#\mathcal{T}_{j} + \#\mathcal{S}_{j-1}$, of the bulk dofs $\#\mathcal{T}_{j}$ and of the boundary dofs $\#\mathcal{S}_{j-1}$. The results shows that optimal convergence is dictated by the regularity of the original non-extended solution u. Finally, collecting the results of Tables 1–2, we realize that both the total error and the error indicator $\eta _{\mathcal{T}_{j}} +\eta _{\mathcal{S}_{j-1}}$ decay as ɛ _j .

5 Conclusions

We introduced an Adaptive Fictitious Domain Method (AFDM ). The core of the method is based on two modules, ELLIPTIC and ENRICH that iteratively modify the discrete spaces for the approximation of the extended solution and the multiplier, respectively. Numerical results show that AFDM is convergent, regardless of the imposition of any compatibility condition between the two discrete space. Moreover, preliminary tests seem to suggest the optimal behaviour of AFDM. This last topic requires further investigations, which is the topic of [5].