Dynamic Hyper Elastic Behavior of Compression Shock Loaded Vibration Dampers

Abstract

A variety of rubber dampers are available, these having been designed over the years through approximate methods of analyses and based on the experience drawn from their operation over the years. Behavior of rubbers, polymers and elastomers is highly non-linear posing difficulties in the analyses. Although the behavior of rubber blends have been researched in the past decades, its behavior in high strain range has attracted the attention of researchers only in the recent past. In the present work, the characterization of natural rubber and high performance SB rubber under severe dynamic compression loading is carried out based on the material response curves provided by recent researchers using material models. With a view to examining the feasibility of using these rubber formulations, these material models are then applied to the case of dynamically compression-loaded dampers in the high strain rate regimes. The discrepancies in the results obtained by utilizing the different material models are discussed in detail.

33.1 Introduction

Elastomers, more precisely Rubber like materials usually have long molecular chains, which can with stand high strains and does not undergo permanent deformation or fail due to fracture. Rubbers have typical physical properties like extensibility, resilience and durability, which generally are not found in other materials. These materials generally have a complicated behavior that generally exceed linear elastic theory and contain large deformations, plastic and visco—elastic properties and softening due to stresses.

The paper utilizes the results of experimental characterization of SB rubber utilizing expensive and controlled experiments on rectangular specimens under high strain rates.

The behavior of rubber exhibits three states of behavior vizz. Elastic behavior at small strains and deformations, visco-elastic behavior during transition and finally hyper-elastic behavior at large strain rates and large deformations.

Various mathematical models have been proposed and used earlier in the analysis of hyper-elastic material and for the design of vibration dampers. Hyper elastic models are based on phenomological aspects (i.e. only the physical behavior is represented by the relationship and not the microscopic aspects).

This General behavior of rubber is reflected in Rivlin’s theory, it exhibits a isotropic behavior in elastic behavior and is nearly incompressible.

Elastic properties of Rubber can be expressed in the form of stress invariants I _1, I ₂ ,I ₃ and this will enable solving the problem as independent of microscopic properties.

The general consideration for Strain energy density and I₁ I₂ I₃ can be given as ${\displaystyle \sum }{C}_{\mathrm{ijkl}}{\left({\mathrm{I}}_1-3\right)}^{\mathrm{I}}\ {\mathrm{I}}_2-3\Big){}^{\mathrm{j}}.\ {\left({\mathrm{I}}_3-1\right)}^{\mathrm{k}}$ where i + j + k = 1 and when the volume is considered to be unchanged during this behavior the third term will become unity and the expression reduces to ${\displaystyle \sum }{C}_{\mathrm{ijkl}}{\left({\mathrm{I}}_1-3\right)}^{\mathrm{I}}{\left({\mathrm{I}}_2-3\right)}^{\mathrm{j}}$.

33.1.1 Features of the Behavior of a Solid Rubber

The material is close to ideally elastic. i.e. (i) when deformed at constant temperature or adiabatically, stress is a function only of current strain and independent of history or rate of loading, (ii) the behavior is reversible, no net work is done on the solid when subjected to a closed cycle of strain under adiabatic or isothermal conditions. The material strongly resists volume changes. The bulk modulus (the ratio of volume change to hydrostatic component of stress) is comparable to that of metals or covalently bonded solids; the material is very compliant in shear and shear modulus is of the order of 10⁻⁵ times that of most metals; the material is isotropic, its stress-strain response is independent of material orientation. The shear modulus is temperature dependent: the material becomes stiffer as it is heated, in sharp contrast to metals; when stretched, the material gives off heat.

Different hyper elastic models [7] of different series of elements will be used to predict the hyper elastic behavior, however the choice of the model depends on its application, and only the few described below can be better used to describe the complete behavior of these materials, for different loading conditions, they are: Mooney, Arruda–Boyce, Polynomial, Yeoh, Neo Hookean, Gent and Ogden.

33.1.1.1 Generalized Neo-Hookean Solid

$$ \overline{U}=\frac{\mu_1}{2}\left({\overline{I}}_1-3\right)+\frac{K_1}{2}\left(J-{1}^2\right) $$

where μ ₁ and K ₁ are material properties (for small deformations, μ ₁ and K ₁ are the shear modulus and bulk modulus of the solid, respectively). Elementary statistical mechanics treatments predict that ${\mu}_1=NKT$, where N is the number of polymer chains per unit volume, k is the Boltzmann constant, and T is temperature. This is a rubber elasticity model, for rubbers with very limited compressibility, and should be used with ${K}_1>>{\mu}_1$. The stress-strain relation follows as

$$ {\sigma}_{ij=\frac{\mu_i}{J^{\frac{5}{3}}}\left({B}_{ij}-\frac{1}{3}{B}_{ij{\delta}_{ij}}\right)+{k}_1\left(j-1\right){\delta}_{ij}} $$

The fully incompressible limit can be obtained by setting ${K}_1\left(J-1\right)=\frac{P}{3}$ in the stress-strain law.

33.1.1.2 Generalized Mooney-Rivlin Solid

Deformations, the shear modulus and bulk modulus of the solid are $\mu ={\mu}_1+{\mu}_2$ and $K={K}_1$ _. This is a rubber elasticity model, and should be used with ${K}_1>>{\mu}_1.$ The stress strain relation follows as:

$$ \overline{U}=\frac{\mu_1}{2}\left({\overline{I}}_1-3\right)+\frac{\mu_2}{2}\left({\overline{I}}_2-3\right)+\frac{K_1}{2}{\left(J-1\right)}^2 $$

33.1.1.3 Generalized Polynomial Rubber Elasticity Potential

$$ \overline{U}={\displaystyle \sum_{i+j=1}^N}{C}_{ij}{\left({\overline{I}}_1-3\right)}^i{\left({\overline{I}}_2-3\right)}^j+{\displaystyle \sum_{i=1}^N}\frac{k_i}{2}{\left(J-1\right)}^{2i} $$

where C _ij and k _i are material properties. For small strains the shear modulus and bulk modulus follow as $\mu =2\left({c}_{01}+{c}_{10}\right)$ _, $K=2{K}_1$,This model is implemented in many finite element codes. Both the neo-Hookean solid and the Mooney-Rivlin solid are special cases of the law (with N = 1 and appropriate choices of C _ij ). Values $N>2$ are rarely used, because it is difficult to fit such a large number of material properties to experimental data.

33.1.1.4 Ogden Model

$$ {\displaystyle \sum_{i=1}^N}\frac{2{\mu}_i}{\alpha_i^2}\ \left({\overline{\lambda}}_1^{\alpha_i}+{\overline{\lambda}}_2^{\alpha_i}+{\overline{\lambda}}_3^{\alpha_i}-3\right)+\frac{K_1}{2}{\left(J-1\right)}^2 $$

where, ${\overline{\lambda}}_i=\frac{\lambda_i}{J^{1/3}}$ and μ _i, α _i, K are material properties. For small strains the shear modulus and bulk modulus follow as $\mu ={\displaystyle \sum_{i=1}^N}{\mu}_i,K={K}_1$ _. This is a rubber elasticity model, and is intended to be used with The stress can be computed using the formulas but are too lengthy to write out in full here.

33.1.1.5 Arruda–Boyce Model

$$ \overline{U}=\mu \left\{\frac{1}{2}\ \left({\overline{I}}_1-3\right)-\frac{1}{20{\beta}^2}\left({\overline{I}}_1^2-9\right)+\frac{11}{1050{\beta}^4}\ \left({\overline{I}}_1^3-27\right)+\dots \right\}+\frac{K{\left(J-1\right)}^2}{2} $$

where μ, β, K are material properties. For small deformations μ, K are the shear and bulk modulus, respectively. This is a rubber elasticity model, so $K>>\mu$ The potential was derived by calculating the entropy of a simple network of long-chain molecules, and the series is the result of a Taylor expansion of an inverse Langevin function. The reference provided lists more terms if you need them. The stress-strain law is

$$ {\sigma}_{ij}=\frac{\mu }{J^{\frac{5}{3}}}\ \left(1+\frac{B_{kk}}{5{J}^{\frac{2}{3}}{\beta}^2}+\frac{33{\left({B}_{kk}\right)}^2}{525{\beta}^4{J}^{\frac{4}{3}}}+\dots \right)\left({B}_{ij}-\frac{B_{kk}}{3}{\delta}_{ij}\right) + K\left(J-1\right){\delta}_{ij} $$

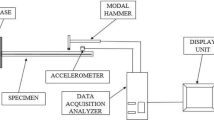
33.1.2 Experimentation

A rectangular speicmen [3] of styrene butadiene rubber is considered in the experiment, with one end fixed and the other end is loaded, so the specimen will remain in uni-axial Tension and compression. The experimental values of the stress—strain behavior of the same material given in the references is utilized for a relative comparison of the experimental data with different models available to access the hyper-elastic behavior. The general comparison is done for all the models individually. The cumulative results of comparison of the graphs and their matching positions with the experimental behavior are tabulated and the best fit criteria is taken for the analysis in static and transient conditions of model as shown in Table 33.1.

Table 33.1 Comparison of graphs

33.1.3 Finite Element Modeling

Utilizing the same experimental results [1] on SB rubber provided by earlier investigators referred to above, finite element analysis is carried out to characterize the rubber in order to choose the best fit mathematical model to the experimental data. For this purpose, finite element code in ANSYS 14.5 has these models incorporated. It must be noted that the results provided are for high rates of strain, which implies sudden loading.

33.2 Results and Discussions

The experimental data for the stress-strain behaviour of the SB rubber is obtained from the earlier works done and quoted in the reference [3]. The comparison of the work is done by the available models for characterization of Hyper-elastic behaviour, which are provided in the Ansys 14.5 version.

A detailed comparison of the available data is done with various models like, Mooney-Rivlin, Ogden, Polynomial, Neo-hookean, Arruda–Boyce, Yeoh, Gent .etc, comparison of the experimental stress- strain behaviour and the models shown in the Table 33.1 and the better fit models are identified based upon the curve-fitting details as listed. Amongst the total 16 iterations considered the picked are Mooney 3 parameter with 11 points coinciding with the actual curve, Ogden first order with 12 points coinciding, polynomial second order 12. Upon considering the deviations from the actual curve, Arruda–Boyce model was picked as the deviation obtained is minimum, 6 Mpa. The variations of the presented models with the actual stress-strain behaviour shown in Fig. 33.1, Mooney-Rivlin, Fig. 33.2 for Ogden, and Fig.33.3 Polynomial and Fig.33.4 for Arruda–Boyce.

Fig. 33.1

Experimental vs. Ogden

Fig. 33.2

Experimental. vs. Mooney

Fig. 33.3

Experimental vs. polynomial order 3

Fig. 33.4

Experimental. vs. Arruda–Boyce

The deflection in static behavior for the selected models were listed in Table 33.2 for 2 N load, and in Table 33.3 for 4 N load, in Table 33.4 for 6 N load, Table 33.5 for 8 N load and Table 33.6 for 10 N load. The deflections are noted down for node number 35, 78 and 168, which were picked at salient positions on the FE model of the sample analyzed. The relative comparison of the load and displacement characteristics were shown in figures from Figs. 33.5, 33.6, 33.7 and to 33.8.

Table 33.2 Deflection at 2 N load

Table 33.3 Deflection at 4 N load

Table 33.4 Deflection at 6 N load

Table 33.5 Deflection at 8 N load

Table 33.6 Deflection at 10 N load

Fig. 33.5

Mooney static—deflection in (mm) on YY axis

Fig. 33.6

Ogden—static—deflection. (mm) on YY axis

Fig. 33.7

Polynomial second order static—deflection (mm) on YY axis

Fig. 33.8

Arruda–Boyce staic—deflection (mm) on YY axis

Transient analysis for the model was done to predict the response of the test sample after the release of the load which is acting for a very brief period. Initially a loading of 2 N to 10 N is considered in steps of 2 N to obtain the response in transient and the corresponding deflections are considered for the various models at the nodes mentioned earlier and were tabulated in the Table 33.7. The stress and strains for various loadings in static behaviour were tabulated in Tables 33.8, 33.9 and 33.10, the max. stress experienced and min. stress experienced is observed. However in the present paper the data for load set of 10 N is only presented. The velocity and acceleration of the transient response were also plotted in Figs. 33.9 and 33.10 through which the variation in the velocity and acceleration over the time step can be observed.

Table 7 Table 33.7

Table 8 Table 33.8

Table 9 Table 33.9

Table 10 Table 33.10

Fig. 33.9

Arruda–Boyce transient analysis—velocity

Fig. 33.10

Arruda–Boyce transient analysis—acceleration

33.3 Curve Fits

33.3.1 Static Behavior of Rubber Under Varying Loads

• All deflections can be considered in mm.

33.4 Transient Analysis

Dampers for reducing vibration of mechanical systems have been based on springs, dashpots, a combination of these and hydraulic device. The advantages of rubber dampers are that they do not require may maintenance, less expensive and less messy due to no oil being present. In some of the situations, they are preferred like in automobiles, aircraft and civil bridges etc. The same tensile specimen is subjected to transient loading at high strain rates as per the loading diagram given below (Tables 33.11, 33.12 and 33.13; Figs.33.11, 33.12, 33.13 and 33.14).

Table 11 Table 33.11

Table 12 Table 33.12

Table 13 Table 33.13

Fig. 33.11

General model with mesh and deformation, under static loading

Fig. 33.12

Arruda–Boyce static-FE model

Fig. 33.13

Mooney static—deflection in (mm) on YY axis

Fig. 33.14

Polynomial static—deflection in (mm) on YY axis

33.5 Transient Analysis for Compression

33.5.1 2 Newtons

Table 33.14

Table 33.14 Deflection at 2 N load

33.5.2 4 Newtons

Table 33.15

Table 33.15 Deflection at 4 N load

33.5.3 6 Newtons

Table 33.16

Table 33.16 Deflection at 6 N load

33.5.4 8 Newtons

Table 33.17

Table 33.17 Deflection at 8 N load

33.6 Stresses and Strain of Nodes

33.6.1 2 Newtons

Tables 33.18, 33.19 and 33.20

Table 33.18 Stresses and strain of node 35

Table 33.19 Stresses and strain of node 78

Table 33.20 Stresses and strain of node 168

33.6.2 4 Newton

Tables 33.21, 33.22 and 33.23

Table 33.21 Stresses and strain of node 35

Table 33.22 Stresses and strain of node 78

Table 33.23 Stresses and strain of node 168

33.6.3 6 Newtons

Tables 33.24, 33.25 and 33.26

Table 33.24 Stresses and strain of node 35

Table 33.25 Stresses and strain of node 78

Table 33.26 Stresses and strain of node 168

33.6.4 8 Newtons

Tables 33.27, 33.28 and 33.29

Table 33.27 Stresses and strain of node 35

Table 33.28 Stresses and strain of node 78

Table 33.29 Stresses and strain of node 168

33.7 Conclusions

The best suited model to model the SBR is Arruda–Boyce when max, deflection is the criteria under static analysis based on the results obtained and tabulated from Tables 33.2 to 33.6 shown above, and for the Transient analysis Polynomial of second order is preferred, based on the tabulated results in the Tables 33.13, 33.14, 33.15 and 33.16 for deflection and stresses and strains considering various intensities of loading in both tension and compression. The same data and procedure can be applied for studying the dynamic characteristics of rubber dampers.