Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Aorta is the main artery of our circulatory system; the investigation of its hemodynamics in physiological and pathological conditions is still one of the major topic of vascular biomechanics because it represents a driving factor in the evaluation of mechanisms underlying the aortic diseases, such as dissection or aneurysm, which are characterized by high mortality if untreated [6]. In particular, thanks to the developments of new endovascular technologies such as thoracic endovascular repair (TEVAR), which is rapidly replacing the classical open-surgery, a lot of attention is paid to the hemodynamics analysis of thoracic aorta, (see, e.g., [1, 11]), i.e., the aortic region from the sino-tubular junction to the celiac bifurcation. Such an analysis accounts also for aortic arch embedding the supra-aortic branches, which is considered the new frontier for further developments of endovascular approaches aimed at treating challenging clinical situations located in the region close to the heart (see, e.g., [18]). Furthermore, there are several aspects that make aortic hemodynamics very peculiar from patient to patient. First of all, the morphology of the arch triggers special features (see, e.g., [3]) that generally have a major impact on the fluid dynamics. Other aspects refer to the flow regime and the disturbances of the flow that in dependence on the patient’s conditions require special numerical treatments.In this work we aim at performing a sensitivity analysis of morphological aspects by comparing numerical results about three cases: (i) an idealized aortic arch with a candy cane shape; (ii) a patient-specific healthy arch; (iii) a patient-specific dissected aorta. For the idealized aortic arch case we also compare the obtained results with respect to the theoretical and experimental literature dedicated to curved pipes.

2 Fluid Model and Numerical Method

The fluid problem is modeled by the incompressible Navier–Stokes equations (that is, a Newtonian isothermal fluid with a homogeneous density and viscosity distribution). Such an approximation is known to be acceptable in the aorta (see, e.g., [7]). In particular, we solve

$$\displaystyle\begin{array}{rcl} \rho \left (\frac{\partial \mathbf{u}} {\partial t} + \mathbf{u} \cdot \nabla \mathbf{u}\right ) + \nabla p -\nabla \cdot \mu \left (\nabla \mathbf{u} + \nabla \mathbf{u}^{T}\right ) = \mathbf{f},& &{}\end{array}$$
(1)
$$\displaystyle\begin{array}{rcl} \nabla \cdot \mathbf{u} = 0,& &{}\end{array}$$
(2)

where ρ is the density (1. 06 g∕cm3), μ is the dynamic viscosity (4 cP), u is the velocity, p is the pressure, and f a possible load.

For the geometries of interest, the analytical solutions of equations (1–2) are not available and we need to resort to numerical approximations. As for a consolidated practice, computational tools provide reliable quantitative results to investigate physiopathological conditions (see, e.g., [7]).

In particular, we consider a classical finite element approximation applied to the primitive variable formulation of the incompressible fluid equations given in  (1–2). The special nature of the problem requires care in the selection of the piecewise polynomial approximation of the discrete velocity and pressure fields. In our case, we use piecewise linear pressures while velocities are approximated by piecewise linear functions added by a cubic correction (called “bubble”). We use unstructured tetrahedral meshes within the LifeV Library (https://www.lifev.org). Time advancing is obtained by a second order BDF scheme with an algebraic splitting of velocity and pressure computation—Yosida scheme, see [16]. Initial conditions are set to zero, their impact on the solution is negligible after simulating a judicious number of heart beats [17]. Boundary conditions are specified later on (see section 4.1).

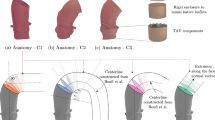
3 Considered Geometries

In the present work, we consider three vascular geometries.

  • A simplified candy cane geometry, depicted in Fig. 1, basically represented by four parameters: pipe diameter a (3. 2 cm), curvature radius R (2. 9 cm), proximal L 1 (5 cm), and distal extension L 2 (14 cm) of the pipe.

    Fig. 1
    figure 1

    Considered geometries, from left to right: the candy cane, the healthy and pathological aortas

    Full size image

  • A healthy patient-specific aorta: a dataset of medical images has been acquired at Ospedale Maggiore in Milano (Italy), using a Siemens SOMATOM Definition Flash Dual-Source CT Scanner, able to capture 10 time frames per cardiac cycle. The original computed tomography angiography set refers to a 72-year-old male patient and covers the entire length of the thoracic and abdominal aorta from the aortic root to the bifurcation into the iliac arteries. From this set, the region including the aortic arch has been selected and a level set segmentation has been performed.

  • A pathological patient-specific aorta: this anatomy is obtained by the segmentation of pre-operative multislice computed tomography regarding a 51-year-old male patient suffering hypertension and having an asymptomatic post-dissecting thoracic aortic aneurysm. It is worth noting that in this case we do not include the distal tract of the descending aorta. As a matter of fact, the presence of the false lumen and of one entry tear complicates the simulation and are, however, out of our region of interest, i.e., ascending, arch, and proximal descending aorta.

    Both healthy and pathological aortas have an average diameter of 2.8cm.

4 Boundary Conditions

We assumed different boundary conditions when performing the different test cases as detailed in the following. The prescription of boundary conditions in computational hemodynamics is critical. In patient specific cases, we typically experience a lack of measures that prevents a completely data-driven analysis. Simplifying assumptions and surrogate models are necessary to have mathematically consistent problems to simulate. Here we present some possible choices aiming at being reliable for the aortic problems and at having significantly comparable cases.

4.1 Inflow Conditions

  1. 1.

    Steady inflow: we choose as an almost flat profile given by the equation:

    $$\displaystyle{ f(r) = \left \{\begin{array}{@{}l@{\quad }l@{}} 1 \quad &r \leq \alpha a, \\ \frac{(r-a)} {(\alpha -1)a}\quad &r>\alpha a,\end{array} \right. }$$
    (3)

    where r is the radial coordinate, α is an adimensional smoothing factor, set to 0. 8 in our simulations.

    This choice is motivated by the fact that at the entrance of the arch flow is not fully developed. Actually, flow patterns are the result of the complex interaction with the leaflets of the valves. In absence of a complete modeling of this interaction, flat profile is a choice more reliable than fully developed flow [3].

    As a matter of fact, the inlet flow in our simulations is not yet fully developed. We believe that this is not an analysis drawback because, at the inlet of the arch, the flow is mainly driven by the heart during systolic phase with a profile close to a flat shape more than to a fully developed paraboloid (see [3]).

  2. 2.

    Unsteady inflow: For the unsteady test cases, on the inflow section, we modulate the flat profile in eq. (3) by a time waveform retrieved from [10] and displayed in Fig. 2.

    Fig. 2
    figure 2

    Considered pulsatile physiological entry-flow rate (see [10])

    Full size image

4.2 Outflow Conditions

Outlet conditions are critical for the reliability of the simulations. A popular approach is to incorporate the presence of distal districts by means of surrogate low fidelity and low dimensional models like lumped parameter systems. In simple idealized cases we can simply prescribe homogeneous Neumann conditions when no peripheral circulation needs to be included. This motivates the following choices.

  • 3-elements Windkessel outflow: For the patient-specific aortas, we prescribed a classical 3-elements Windkessel modeling of the distal circulation. This means that the peripheral impedance at each outflow section is represented by two resistances R 1 and R 2 and one compliance C (RCR model). The specific values of those parameters are taken from [8].

  • Traction free outflow: For the candy cane geometries, we impose the free-stress boundary condition. As there is only one outflow boundary and this choice basically shifts the pressure only up to a hydrostatic constant.

  • Wall boundary condition: we prescribe null velocity on the lumen walls. Despite such an approach is commonly adopted in literature, a more accurate model would include the interaction of fluid and structure, but the computational costs would be significantly higher and the accuracy advantage questionable because the structural model for the arterial wall (differently from the blood model given by the Navier–Stokes equations) is affected by several uncertainties.

5 Numerical Tests

As mentioned before we consider three geometries and four numerical tests.

  1. 1.

    Candy cane geometry with constant entry-flow rate, whose value is the maximal flow rate at the systolic peak of the pulsatile physiological entry flow (347 cm3∕s), see Fig. 2, and free-stress outflow.

  2. 2.

    Candy cane geometry with a pulsatile physiological entry-flow rate (see Fig. 2) and free-stress outflow.

  3. 3.

    Healthy aorta geometry with a pulsatile physiological entry-flow rate (see Fig. 2) and 3-Windkessel outflows (see section 4).

  4. 4.

    Pathological aorta geometry with a pulsatile physiological entry-flow rate (see Fig. 2) and 3-Windkessel outflows (see section 4).

In what follows, we first present a discussion on the flow and wall shear stress in curved pipes for steady and pulsatile flows; however we do not review extensively previous contributions, since our main objective is to discuss trends observed in simplified geometries with respect to the two patient-specific geometries at hand. Nevertheless, we provide many important references on the subject for the interested reader. We conclude by comparing the flows and wall shear stresses in the patient specific aortas with respect to the results obtained with the candy cane geometry. Simulations are carried out with the C + + Object Oriented library LifeV (www.lifev.org), in particular with the solvers developed in the Emory-Pavia branch described in [16].

5.1 Curved Pipes

Steady flows in curved pipes with a constant curvature are characterized by the following adimensional group, known as the Dean number (see [12]):

$$\displaystyle{ D:=\mathrm{ Re}\sqrt{ \frac{a} {R}} = \frac{2\rho Q} {\mu \pi } \sqrt{ \frac{1} {aR}}, }$$

where Q is the flux, a is the radius of the pipe, R the radius of curvature, and Re is the Reynolds number, i.e., (Re = 2ρ U a∕μ) with U the inflow mean velocity.

The maximum Dean number for our application is about 2717 with the maximal entry flux-rate being of 347 cm3∕s at the systolic peak (see Fig. 2) and, as a consequence, our application belongs to the category of large Dean numbers for which no analytical solutions exist (see [12]). It is worth pointing out that not all the definitions of the Dean numbers are consistent, which renders cumbersome the comparisons of the results with the literature (see [2] for a discussion on the subject).

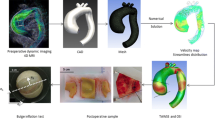
Major results from the analysis of Dean’s equations are, firstly, that symmetric secondary flows are introduced since the curvature of the pipe induces a gradient of pressure from the inner bend to the outer one and, secondly, that the fastest flow tends to be pushed toward the outer bend as the Dean number grows (see [12]). These analytical and numerical results assume that the flow is fully developed. For such a high Dean number used in our application, we would therefore expect the fastest flow to be much closer to the outward part of the bend than the one we obtain (see Figs. 3 and 4). The discrepancy comes from the fact that we do not employ a fully developed but a flat profile in inflow (see Sec. 4). Instead, we observe two vortexes on the inner part of the arch; a similar result is obtained in [13] with an experimental setting and a flat inflow profile (see also [3]). A major implication is that with fully developed flows we would expect the wall shear stress to be much higher on the outward part of the arch. Instead, it clearly appears in Fig. 5 that a high wall shear stress occurs near the two vortexes as observed in Fig 3. We may also observe in Fig. 5(b) a very low wall shear stress on the inner part of the arch.

Fig. 3
figure 3

Streamlines (top) and velocity contour plots (bottom) for the four cases considered. From left to right: candy cane steady, candy cane pulsatile, healthy patient, pathological case. The cross sections displayed are taken in the center of the aortic arch. Bottom side corresponds to the internal bend. Results refer to the systolic peak for the three rightmost (unsteady) simulations

Full size image
Fig. 4
figure 4

Streamlines and speed at systolic peak. From left to right, we have: steady and unsteady flows in candy cane, unsteady flows in the healthy and pathological aorta

Full size image
Fig. 5
figure 5

Wall shear stresses for the different cases under investigation

Full size image

Oscillatory flows in curved pipes were first studied in [9] (see again, e.g., [2, 3, 12] for an extensive review) and a major result is the possible presence of a Stokes boundary layer (or oscillatory boundary layers), as it can clearly be observed in Fig. 3 by the presence of reversed eddies. More complex flow patterns with multiple vortexes are also observed since we employ a physiological pulsatile entry flow, as in [5]. As opposed to [5] in which symmetry of the secondary flows is assumed, we can see in Fig. 3 that the secondary flows are not symmetric, as shown in, e.g., [15], while the symmetry is always present in the steady entry flow case with finite curvature, as shown in [14].

Another major difference between steady and pulsatile flows in curved pipes is that, in the case of pulsatile flows, the maximal axial speed is pushed toward the inner bend, as clearly observed in Fig. 4. As a consequence, the wall shear stress is higher in the inner part of the pipe, as it can be seen in Fig. 5, and as opposed to the steady flow case, in particular with fully developed entry flows, as shown experimentally in [4] and theoretically in [9].

5.2 Patient-Specific Aortas

Two important shared trends are observed from the pulsatile entry flow analysis between the simplified geometry and the patient-specific ones:

  1. 1.

    the highest axial speed is bended toward the inner part of the bend (see Fig. 4);

  2. 2.

    high wall shear stress remains on the lower part of the aorta (see Fig. 5).

Furthermore, for the healthy aorta, the flow boundary layer appears to be of the same size as the candy cane with a pulsatile entry flow and the speed is of the same order of magnitude. On the contrary, due to a strong bending in the pathological aorta much faster flow is observed at the inner part of the arch, as well as a much thinner boundary layer. Also, results in Fig.3 suggest completely different and irregular flow patterns from the idealized and patient-specific aortas; meaning that irregular diseased conditions may even accelerate and drive the evolution of the pathology.

However, it clearly appears that only a patient-specific analysis can provide a precise distribution of the wall shear stress which is severely impacted from the changes of topology of the aorta wall. Also, the pathological aorta bluff induces a boundary-layer flow separations, resulting in a disturbed flow in the upper part of the descending aorta, leading thus to a much greater Reynolds number in this part of the aorta.

6 Conclusion

As well known, numerical results in computational hemodynamics are majorly influenced by the vascular geometry and the prescription of the boundary conditions. Image and geometrical processing techniques enable an accurate reconstruction of patient-specific cases, while for the boundary conditions the gap between available measures and needed data for the mathematical consistency of the problems to solve is still challenging. In this paper, we tested our numerical solver on nontrivial cases for the aortic flow. Aorta has a complex fully 3D morphology that triggers specific flow patterns and simplifying assumptions in the numerical process may prevent a correct capturing of the relevant features. In cross-checking our results and comparing available experimental data, we assess the reliability of our specific numerical solver while pointing out the importance of an accurate reconstruction of the patient-specific geometry and of the selection of boundary data.