Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The supercomputer architecture landscape has encountered dramatic changes in the past decade. Heterogeneous architectures hosting different compute devices (CPU, GPGPU, and Intel Xeon Phi) and systems running 105 cores or more are dominating the Top500 top ten [33] since the year 2013. Since then, however, turnover in the top ten has slowed down considerably. A new impetus is expected by the “Collaboration of Oak Ridge, Argonne, and Livermore” (CORAL)Footnote 1 with multi-100 Pflop/s systems to be installed around 2018. These systems may feature high levels of thread parallelism and multiple compute devices at the node-level, and will exploit massive data parallelism through SIMD/SIMT features at the core level. The SUMMITFootnote 2 and AuroraFootnote 3 architectures are instructive examples. State-of-the-art interconnect technologies will be used to build clusters comprising 103 to 105 compute nodes. While the former will be of heterogeneous nature with IBM Power9 CPUs and Nvidia Volta GPUs in each node, the latter is projected to be built of homogeneous Intel Xeon Phi manycore processors. Although two different approaches towards exascale computing are pursued here, commonalities like increasing SIMD parallelism and deep memory hierarchies can be determined and should be regarded when it comes to software development for the exascale era.

The hardware architecture of the CORAL systems, which are part of the DOE Exascale Computing Project, can be considered blueprints for the systems to be deployed on the way to exascale computing and thus define the landscape for the development of hardware-/energy-efficient, scalable, and sustainable software as well as numerical algorithms. Additional constraints are set by the continuously increasing power consumption and the expectation that mean-time-to-failure (MTTF) will steadily decrease. It is obvious that long-standing simulation software needs to be completely re-designed or new codes need to be written from scratch. The project “Equipping Sparse Solvers for Exascale” (ESSEX),Footnote 4 funded by the Priority Program “Software for Exascale Computing” (SPPEXA) of the German Research Foundation (DFG) is such an endeavor in the field of sparse eigenvalue solvers.

The ESSEX project addresses the above challenges in a joint software co-design effort involving all three fundamental layers of software development in computational science and engineering: basic building blocks, algorithms, and applications. Energy efficiency and fault tolerance (FT) form vertical pillars forcing a strong interaction between the horizontal activities (see Fig. 1 for overall project organization). The overarching goal of all activities is minimal time-to-solution. Thus, the project is embedded in a structured holistic Performance Engineering (PE) process that detects performance bottlenecks and guides optimization and parallelization strategies across all activities.

Fig. 1
figure 1

Basic ESSEX project organization: the classic boundaries of application, algorithms, and basic building blocks tightly interact via a holistic performance engineering process

Full size image

In the first funding period (2013–2015) the ESSEX project has developed the “Exascale enabled Sparse Solver Repository” (ESSR), which is accessible under a BSD open source license.Footnote 5

The application layer has contributed various scalable matrix generation routines for relevant quantum physics problems and has used the ESSR components to advance research in the fields of graphene structures [8, 22, 23, 25] and topological materials [26].

In the algorithms layer various classic, application-specific and novel eigensolvers have been implemented and reformulated in view of the holistic PE process. A comprehensive survey on the activities in the algorithms layer (including FT) is presented in [32]. There we also report on the software engineering process to allow for concurrent development of software in all three layers.

Work performed in the basic building block layer, which drives the holistic PE process, is presented in this report.

2 Contribution

The building block layer in ESSEX is responsible for providing an easy to use but still efficient infrastructure library (GHOST), which allows exploiting optimization potential throughout all software layers. GHOST is an elaborate parallelization framework based on the “MPI+X”Footnote 6 model, capable of mastering the challenges of complex node topologies (including ccNUMA awareness and node-level resource management) and providing efficient data structures and tailored kernels. In particular the impact of data structures on heterogeneous performance is still underrated in many projects. On top of GHOST we have defined an interface layer that can be used by algorithms and application developers for flexible software development (see [32]).

In this work we illustrate selected accomplishments, which are representative for the full project. We briefly present a SIMD/SIMT-friendly sparse matrix data layout, which has been proposed by ESSEX and gives high performance across all available HPC compute devices. As a sample application we choose the Kernel Polynomial Method (KPM), which will first be used to revisit our model-driven PE process. Then we demonstrate for the first time the impact of PE on improving the energy efficiency on the single socket level for the KPM. Using a coupled performance and energy model, we validate these findings qualitatively and can conclude that the achieved performance improvements for KPM directly correlate with energy savings.

Then we present a brief overview of the GHOST library and give an overview of selected solvers that use GHOST in ESSEX. We finally demonstrate that sustained petascale performance on a large CPU-GPGPU cluster is accessible for our very challenging problem class of sparse linear algebra.

3 Holistic Performance Engineering Driving Energy Efficiency on the Example of the Kernel Polynomial Method (KPM)

Algorithm 1 Naive version of the KPM-DOS algorithm with corresponding BLAS level 1 function calls

The KPM [36] is well established in quantum physics and chemistry. It is used for determining the eigenvalue density (KPM-DOS) and spectral properties of sparse matrices, exposing high optimization potential and the feasibility of petascale implementations. In the following study the KPM is applied to a relevant problem of quantum physics: the determination of electronic structure properties of a three-dimensional topological insulator.

3.1 Performance Engineering for KPM

The naive version of the KPM as depicted in Algorithm 1 builds on several BLAS [17] level 1 routines and the Sparse BLAS [7] level 2 spmv (Sparse matrix–vector multiplication) kernel.

The computational intensities of all involved kernels for the topological insulator application are summarized in Table 1. To classify the behavior of a kernel on a compute architecture it is useful to correlate the computational intensity with the machine balance which is the flops/byte ratio of a machine for data from main memory or, in other words, the ratio between peak performance and peak memory bandwidth. It turns out that for each kernel in Table 1 the computational intensity is smaller than the machine balance of any relevant HPC architecture. Even very bandwidth-oriented vector architectures like the NEC SX-ACE with a theoretical machine balance of 1 byte/flop, fail to deliver enough data per cycle from main memory to keep the floating point units busy. This discrepancy only gets more severe on standard multicore CPUs or GPGPUs.

Table 1 Maximum computational intensities I max in flops/byte and approximate minimum relative share of overall data volume in the solver for each kernel and the full naive KPM-DOS implementation (Algorithm 1) for the topological insulators application
Full size table

The relative share of data volume assuming minimum data traffic for each kernel can also be seen in Table 1. As all kernels are strongly bound to main memory bandwidth, we can directly translate the relative data volume shares to relative runtime shares if we assume optimal implementations of all kernels and no excess data transfers. Hence, the spmv is the dominating operation in the naive KPM-DOS solver. This, together with the fact that BLAS level 1 routines offer only very limited performance optimization potential, necessitates a detailed examination of this kernel.

3.1.1 Sparse Matrix Data Format

Not only KPM-DOS but also many other sparse linear algebra algorithms are dominated by SpMV. This gave rise to intense research dealing with the performance of this operation. A common finding is that SpMV performance strongly depends on the sparse matrix data format. In the past there was an implicit agreement that an optimal choice of sparse matrix data format strongly depends on the compute architecture used. Obviously, this poses obstacles especially in the advent of heterogeneous machines we are facing today. This led to several efforts trying to either identify data formats that yield good performance on all relevant architectures or to alter the de facto standard format on CPUs (Compressed Sparse Row, or CSR) to enable high performance CSR SpMV kernels also on throughput-oriented architectures. The latter approach resulted in the development of ACSR [1], CSR-Adaptive [5, 9], and CSR5 [19]. The former approach was pursued by ESSEX, e.g., in [13] and led to the proposition of SELL-C-σ as a “catch-all” sparse matrix storage format for the heterogeneous computing era. Although re-balancing the sparse matrix between heterogeneous devices at runtime is not in the scope of this work, it probably is a wise decision in view of the future to choose an architecture-independent storage format if it does not diminish the performance of CPU-only runs. In ESSEX we decided for the SELL-C-σ storage format, which we will explain briefly in the following. Moreover, our preference of SELL-C-σ over CSR will be justified.

SELL-C-σ is a generalization of the Sliced ELLPACK [21] format. The sparse matrix is cut into chunks where each chunk contains C matrix rows, with C being a multiple of the architecture’s SIMD width. Within a chunk, all rows are padded with zeros up to the length of the longest row. Matrix values and according column indices are stored along jagged diagonals and chunk after chunk. To avoid excessive zero padding, it may be helpful to sort σ successive matrix rows (σ > C) by their number of non-zeros before chunk assembly. In this case, also the column indices of matrix entries have to be permuted accordingly. Figure 2 demonstrates the assembly of a SELL-C-σ matrix from an example matrix. In contrast to CSR, SIMD processing is achieved along jagged diagonals of the matrix instead of rows. This enables effective vectorized processing for short rows (comparable to or shorter than the SIMD width), and it enhances the vectorization efficiency of longer rows compared to CSR due to the absence of a reduction operation.

Fig. 2
figure 2

SELL-C-σ matrix construction where the SELL-2-4 matrix (b ) is created from the source matrix (a ), which includes row permutation according to (c ), and yields the final SELL-C-σ data structure for this matrix as shown in (d )

Full size image

Typically, even non-vectorized code yields optimal performance for bandwidth-bound kernels on a full multi-core CPU socket. However, a higher degree of vectorization usually comes with higher energy efficiency. Hence, we used SELL-C-σ for our experiments. Even if no performance gain over CSR can be expected on a full socket, we will demonstrate in Sect. 3.2 that SELL-C-σ turns out to be beneficial in terms of energy consumption. Due to the regular structure of the topological insulator system matrix, no row sorting has to be applied, i.e., σ = 1. The chunk height C was set to 32. While it is usually a good practice to choose C as small as possible (which would be C=4 in this case, cf. [13]) to avoid a loss of chunk occupancy in the SELL-C-σ matrix, we do not expect such problems for the present test case due to the regularity of the system matrix. Hence, we opted for a larger C which turned out to be slightly more efficient due to a larger degree of loop unrolling.

3.1.2 Kernel Fusion and Blocking

The naive KPM-DOS implementation is strongly memory-bound as described in the introduction to Sect. 3.1. Thus, the most obvious way to achieve higher performance is to decrease the amount of data traffic.

Algorithm 2 Enhanced version of the KPM-DOS algorithm using the augmented SpMV kernel, which covers all operations chained by ‘&’

Algorithm 3 Fully optimized version of the KPM-DOS algorithm combining kernel fusion (see Algorithm 2) and vector blocking; each η is a vector of R column-wise dot products of two block vectors

As previously described in [15], a simple and valid way to do this is to fuse all involved kernels into a single tailored KPM-DOS kernel. Algorithm 2 shows the KPM-DOS algorithm with all operations fused into a single kernel. Taking the algorithmic optimization one step further, we can eliminate the outer loop by combining all random initial states into a block of vectors and operate on vector blocks in the fused kernel. The resulting fully optimized (i.e., fused and blocked) kernel can be seen in Algorithm 3. Each of the proposed optimization steps increases the computational intensity of the KPM-DOS solver:

Eventually, the fully optimized solver is decoupled from main memory bandwidth on the Intel Ivy Bridge architecture as we have demonstrated in [15].

3.2 Single-Socket Performance and Energy Analysis

3.2.1 Multi-Core Energy Modeling

The usefulness of analytic models that describe the runtime and power dissipation of programs and the systems they run on is obvious. Even if such models are often over-simplified, they can still predict and explain many important properties of hardware–software interaction. Bandwidth-based upper performance limits on the CPU level have been successfully used for decades [4, 12], but modeling power dissipation is more intricate. In [10] we have introduced a phenomenological power and energy consumption model from which useful guidelines for the energy-optimal operating point of a code (number of active cores, clock speed) could be derived. In the following we briefly review the model and its predictions as far as they are relevant for the application case of KPM.

The model takes a high-level view of energy consumption. It is assumed that the CPU chip dissipates a constant baseline power W 0, which is defined as the power at zero (extrapolated) clock speed. W 0 also contains contributions from cores in idle or deep sleep state, and it may also comprise other system components whose power dissipation is roughly constant. Every active core, i.e., when executing instructions, contributes additional dynamic power, which depends on the clock speed f. The power dissipation at n active cores is assumed as

$$\displaystyle{ W = W_{0} + \left (W_{1}f + W_{2}\,f^{2}\right )n. }$$
(3)

There is no cubic term in f since measurements on current multi-core CPUs show that the dynamic power is at most quadratic in f. The exact dependance on f is parameterized by W 1 and W 2. This is a consequence of the automatic adaptation of supply voltage to clock speed as imposed by the processor or the OS kernel [6]. Power- and energy-to-solution are connected by the program’s runtime, which is work divided by performance. If F is the amount of work (e.g., in flops) we assume the following model for the runtime:

$$\displaystyle{ T(n,f) = \frac{F} {\min \left (nP_{0}(\,f),P_{\mathrm{max}}\right )}\, }$$
(4)

where P 0 is the single-core (i.e., sequential) performance and P max is the maximum performance as given by a bandwidth-based limit (e.g., as given by the product of arithmetic intensity and memory bandwidth if the memory interface is a potential bottleneck). Assuming linear scalability up to a saturation point is justified on current multi-core designs if no other scaling impediments apply. In general P 0 will depend strongly on the clock speed since the serial execution time is dominated by intra-cache data transfers or in-core execution on modern CPUs with deep cache hierarchies. This is clearly described by our ECM performance model [31]. The energy-to-solution is thus

$$\displaystyle{ E(n,f) = F \cdot \frac{W_{0} + \left (W_{1}f + W_{2}f^{2}\right )n} {\min \left (nP_{0}(\,f),P_{\mathrm{max}}\right )} . }$$
(5)

There are several immediate conclusions that can be drawn from this model [10]. Here we restrict ourselves to the case of a fixed clock speed f. Then,

  • if the performance saturates at some number of cores n s, this is the number of active cores to use for minimal energy-to-solution.

  • If the performance is linear in n one must use all cores for minimal energy-to-solution.

  • Energy-to-solution is inversely proportional to performance, regardless of whether the latter is saturated or not.

We consider the last of these conclusions to be the most important one, since runtime (i.e., inverse performance) is the only factor in which energy is linear. This underlines that performance optimization is the pivotal strategy in energy reduction.

3.2.2 Measurements

In order to provide maximum insight into the connections between performance and energy in a multi-core chip we use what we call a Z-plot, combining performance in Gflop/s on the x axis with energy-to-solution in J on the y axis (see Fig. 3). One set of data points represents measurements for solving a fixed problem with a varying number of active cores on the chip. In a Z-plot, horizontal lines are “energy iso-lines,” vertical lines are “performance iso-lines,” and hyperbolas are “power iso-lines” (doubling performance, i.e., cutting the runtime in half, also halves energy). If a program shows saturating performance with respect to the number of cores, the curve bends upward at the saturation point, indicating that more resources (thus more power) are used without a performance gain, leading to growing energy-to-solution. For scalable programs the curve is expected to stay flat or keep falling if the power model described in Sect. 3.2.1 holds. The Z-plot has the further advantage that lines of constant energy-delay product (energy-to-solution multiplied by program runtime, EDP) are straight lines through the origin. This is convenient when EDP is used as an alternative target metric instead of plain energy.

Fig. 3
figure 3

Single-socket performance and energy Z-plot of naive (squares), augmented (circles), and blocked (triangles) versions on IVB, comparing one thread per core (filled) vs. two threads (open) using SELL-32-1. (Inset: enlarged region of saturation for naive and blocked versions with absolute upper performance limit)

Full size image

All measurements shown in this section were performed on one node (actually a single socket with ten cores) of the “Emmy” cluster at RRZE, comprising Intel Ivy Bridge (Xeon E5-2660v2; “IVB”) CPUs with 2.2 GHz base clock speed and 32 GB of RAM per socket. The clock frequency was set to 2.2 GHz, i.e., “Turbo Mode” was disabled. Energy measurements were done via the likwid-perfctr tool from the LIKWID tool suite [18, 34], leveraging Intel’s on-chip RAPL infrastructure. No significant variation in energy or performance was observed over multiple runs on the socket.

In Figure 3 we show package-level energy and performance data for the naive implementation of KPM (Algorithm 1) and the augmented and blocked versions (Algorithms 2 and 3) on one IVB socket at a fixed baseline frequency of 2.2 GHz. As expected from their low computational intensities (see Table 1 and Sect. 3.1.2), the naive and augmented variants show strong performance saturation at about 5 and 6 cores, respectively. The augmented kernel requires more cores for saturation since it performs more work per byte transferred from main memory. In the inset we show the bandwidth-based performance limits calculated by multiplying the maximum achievable memory bandwidth on the chip (45 GB/s) with the respective computational intensity. The measured saturated performance is only 6–7 % below this limit in both cases. Note that the maximum bandwidth was obtained using a read-only benchmark (likwid-bench load [35]) but the kernels do not exhibit pure load characteristics. Depending on the fraction of stored vs. loaded data, the maximum bandwidth delivered to the IVB chip can drop by more than 10 %. The blocked variant does not suffer from a memory bandwidth bottleneck on this processor and thus profits from all cores on the chip. As opposed to the naive and blocked versions, it also shows a significant speedup of 12 % when using both hardware threads per core (SMT2).

The energy-to-solution data in the figure was measured on the CPU package level, i.e., ignoring the rest of the system such as RAM, I/O, disks, etc. On the other hand, the particular IVB processor used for the benchmarks shows a low dynamic power compared to chips with higher clock speeds. As a consequence, performance improvements by algorithmic or implementation changes translate into almost proportional energy savings. This is demonstrated by the dashed lines in Fig. 3: Comparing full sockets, the naive version is 1.5× slower and takes 1.45× more energy than the augmented version. The blocked version is 3.1× faster and takes 2.9× less energy than the augmented version. This correspondence becomes only more accurate when adding the full baseline power contributions from all system components. Note that a further 20 % of package-level energy can be saved with the naive and blocked versions by choosing the minimum number of cores that ensures saturation.

The influence of SMT is minor in the saturating cases, which is expected since SMT cannot improve performance in the presence of a strong memory bottleneck. The 12 % performance boost for the blocked version comes with negligible energy savings. We must conclude that executing code on both hardware threads increases the power dissipation, which is also seen by the slight energy increase for SMT2 in the saturated case.

A performance-energy comparison of the SELL-1-1 (a.k.a. CSR) matrix storage format with SELL-32-1 is shown in Fig. 4 for all code versions. The energy advantage of SELL-32-1 in the saturating case is mainly due to the higher single-core performance and accordingly smaller number of required cores to reach the saturation point, leading to package-level energy savings of 8 % and 13 % for the naive and augmented kernels, respectively. We attribute the slight difference in saturated performance to the different right-hand side data access patterns in the SpMV. The blocked variant shows no advantage (even a slight slowdown) for the SIMD-friendly data layout, which is expected since the access to the matrix data is negligible.

Fig. 4
figure 4

Single-socket performance and energy Z-plot for the same kernel versions as in Fig. 3 but comparing the SELL-1-1 (CSR) matrix format (filled symbols) with SELL-32-1 (open symbols) at two threads per core

Full size image

The conclusion from the socket-level performance and energy analysis is that optimization by performance engineering translates, to lowest order, into equivalent energy savings. Overall, the performance ratio between the fastest variant (blocked, with two threads per core) and the lowest (full-socket CSR-based naive implementation) is 5.1, at an energy reduction of 4.5×. At least on the Intel Ivy Bridge system studied here we expect similar findings for other algorithms investigated in the ESSEX project.

A comprehensive analysis of the power dissipation and energy behavior of the studied code variants and the changes for multi-socket and highly parallel runs is beyond the scope of this paper and will be published elsewhere.

4 An Overview of GHOST

The GHOST (General, Hybrid, and Optimized Sparse Toolkit) library summarizes the effort put into computational building blocks in the ESSEX project. A detailed description can be found in [16]. GHOST, a “physics” package containing several scalable sparse matrices, and a range of example applications are available for download.Footnote 7 GHOST features high performance building blocks for sparse linear algebra. It builds on the “MPI+X” programming paradigm where “X” can be one of either OpenMP+SIMD or CUDA. The development process of GHOST is closely accompanied by analytic performance modeling, which guarantees compute kernels with optimal performance where possible.

There are several software libraries available that offer some sort of heterogeneous execution capabilities. MAGMA [20], ViennaCL [30], PETSc [3], and Trilinos [11] are arguably the most prominent approaches, all of which have their strengths and weaknesses. PETSc and Trilinos are similar to GHOST as they also build on “MPI+X”. MAGMA and ViennaCL, on the other hand, provide shared memory building blocks for different architectures but do not expose any distributed memory capabilities themselves. The most fundamental difference between GHOST and the aforementioned libraries is the possibility of data-parallel heterogeneous execution in GHOST (see below). GHOST has been designed from scratch with heterogeneous architecture in mind. This has to be viewed in contrast to the subsequent addition of heterogeneous computing features to originally homogeneous libraries such as, e.g., PETSc, for which a disclaimer says:Footnote 8 “WARNING: Using GPUs effectively is difficult! You must be dedicated and willing to get into the guts of GPU usage if you are serious about using GPUs.”

GHOST is not intended to be a rival of the mentioned libraries, but rather a promising supplement and novel approach. Due to its young age, it certainly falls behind in terms of robustness and maturity. While other solutions focus on broad applicability, which often comes with sacrificing some performance, achieving optimal efficiency for selected applications without losing sight of possible broader applicability is clearly the main target of GHOST development. Within the ESSEX effort, we supply mechanisms to use GHOST in higher level software frameworks using the PHIST library [32]. To give an example, in [16] we have demonstrated the feasibility and performance gain of using PHIST to leverage GHOST for a Krylov-Schur algorithm as implemented in the Trilinos package Anasazi [2]. In the following we will briefly summarize the most important features of GHOST and how they influence the ESSEX effort.

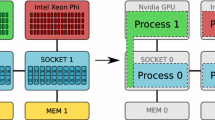
A unique feature of GHOST is the capability of data-parallel execution across heterogeneous devices. MPI ranks can be assigned to arbitrary combinations of heterogeneous compute devices, as depicted in Fig. 5. A sparse system matrix is the central data structure in GHOST, and it is distributed row-wise among MPI ranks. In order to reflect heterogeneous systems in an efficient manner, the amount of matrix rows per rank can be arbitrarily set at runtime. Section 5.1 demonstrates possible performance gains due to this feature.

Fig. 5
figure 5

Heterogeneous compute node and sensible process placement as suggested by GHOST (Figure taken from [16]). (a ) Heterogeneous node. (b ) Process placement

Full size image

On top of “MPI+X”, GHOST exposes the possibility for affinity-aware task-level parallelism. Users can create tasks, which are defined as arbitrary callback functions. OpenMP parallelism can be used inside those tasks and GHOST will take care of thread affinity and resource management. This feature can be used, e.g., for communication hiding, asynchronous I/O, or checkpointing. In future work we plan to implement asynchronous preconditioning techniques based on this mechanism.

GHOST uses the SELL-C-σ sparse matrix storage format as previously described in Sect. 3.1.1. Note that this does not imply exclusion of CSR, since CSR is just a special case of SELL-C-σ with C=1 and σ=1. Selected kernels are implemented using compiler intrinsics to ensure efficient vectorization. This turned out to be a requirement for optimal performance of rather complex, compute-intensive kernels. However, vectorization may also pay off for kernels with lower computational intensity. Figure 6 backs up the findings of Sect. 3.2.2 in this regard. Not only the superior vectorization potential of SELL-C-σ over CSR, but also a manually vectorized implementation of the SELL-C-σ SpMV kernel yields a highly energy-efficient SpMV kernel.

Fig. 6
figure 6

Intra-socket performance on a single CPU showing the impact of vectorization on SpMV performance for different storage formats (Figure taken from [16])

Full size image

Vector blocking, i.e., processing several dense vectors at once, is usually a highly appropriate optimization technique in sparse linear algebra due to the often bandwidth-limited nature of sparse matrix algorithms. GHOST addresses this by supporting efficient block vector operations for row- and column-major storage.

Block vector operations often lead to short loops due to a small number of vectors (i.e., in the order of tens) in a block. As short loops are often accompanied by performance penalties, it is possible to define a list of small dimensions at GHOST compile time. Block vector kernels will be automatically generated according to this list. This mechanism is used not only for block vectors, but also for the chunk height C in the SELL-C-σ sparse matrix format. Figure 7 illustrates the performance benefit observed due to generated block vector kernels for the sparse matrix multiple vector multiplication (SpMMV).

Fig. 7
figure 7

The impact of hard-coded loop length on the SpMMV performance with increasing block vector width on a single CPU (Figure taken from [16])

Full size image

Another way to improve the computational intensity of sparse linear algebra algorithms is kernel fusion. In this regard, specialized kernels like the KPM-DOS operator are implemented in close collaboration with experts from the application domain. The specialization grade, i.e., the number and combination of fused operations, of those kernels can be gradually increased, which makes them potentially useful for applications beyond the ESSEX scope. In this regard it should be noted that kernel fusion, while certainly being a promising optimization approach, diminishes the potential for efficient task-parallel execution. This fact promotes the use of kernel fusion together with data parallelism as used in GHOST.

Among others, the described features enable very high performance on modern, heterogeneous supercomputers as demonstrated in our previous work [14, 15, 24, 29].

5 GHOST Applications

In the course of the ESSEX project the GHOST library has been used by several numerical schemes (developed and implemented in the computational algorithms layer) to enable large-scale (heterogeneous) computations for quantum physics scenarios defined by the application layer. Here we summarize selected (already published) application scenarios to demonstrate the capability, the state, and the broad applicability of the GHOST library. We have added measurements, where appropriate, to demonstrate the performance sustainability of the GHOST framework over several processor generations. Moreover these measurements also provide an impression of the rather moderate technological improvements on the hardware level during the ESSEX project period. In particular we focus on a node-level comparison of a Cray XC30 system, which hosts one Nvidia K20X GPGPU and one Intel Xeon E5-2670 “Sandy Bridge” (SNB) processor in each node, with a recent CPU compute node comprising two Intel Xeon E5-2695v3 “Haswell” (HSW) CPUs. While the Cray XC30 system (Piz Daint at CSCS Lugano) has entered the Top500 top ten list at the start of the ESSEX project and is still ranked as #7 (November 2015), Intel Haswell-based systems showed up first in the top ten in 2015.

5.1 Density of States Computations Using KPM-DOS

The basic algorithm (KPM-DOS) used in ESSEX to compute the density of states of large sparse matrices has been introduced in Sect. 3.1. In reference [15] we have presented the PE process and implementation details to enable fully heterogeneous (CPU+GPGPU) KPM-DOS computations and could achieve high node-level performance up to 1024 nodes in weak scaling scenarios. Since then we have extended our runs to up to 4096 nodes (which is approximately 80% of Piz Daint) to achieve 0.5 Pflop/s of sustained performance when computing the DOS of a topological insulator model Hamiltonian (see Fig. 8). The corresponding matrix has a dimension of 3 × 1010 and is extremely sparse with an average of 13 non-zero entries per row.

Fig. 8
figure 8

Strong and weak scaling performance results for different geometries for the topological insulator test case on Piz Daint (measurements up to 1024 nodes have been presented in [15])

Full size image

On the node-level the optimizations described earlier have led to significant performance gains for both devices as shown in Fig. 9, and we expect similar energy efficiency improvements on the Cray XC30 system as demonstrated above. Note that during the optimization steps the performance bottleneck on the GPGPU changed from main memory saturation to the dot product. Extending the discussion to latest CPU hardware, we find the Haswell-based system being only 15% ahead of the Cray XC30 node.

Fig. 9
figure 9

Impact of optimization steps described in Sect. 3.1 on the node-level performance of Piz Daint (single device and heterogeneous) and a CPU-only node containing two HSW processors (Piz Daint numbers are taken from [15])

Full size image

5.2 Inner Eigenvalue Computation with Chebyshev Filter Diagonalization (ChebFD)

Applying Chebyshev polynomials as a filter in an iterative subspace scheme allows for the computation of inner eigenpairs of large sparse matrices. The attractive feature of this well-known procedure is the close relation between the filter polynomial and the KPM-DOS scheme. Replacing the norm computation (nrm2) and the dot product in Algorithm 1 by a vector addition (axpy) yields the polynomial filter in our ChebFD scheme. For a more detailed description of ChebFD (which is also part of our BEAST-P solver), and the relation to KPM-DOS we refer to the report on the ESSEX solver repository [32] and to [24]. In ChebFD the polynomial filter is applied to a subspace of vectors and also optimization stage 2 (see Algorithm 3) can be applied. As compared to the KPM-DOS kernel, the lower computational intensity of the filter kernel reduces performance on the CPU architectures, while the GPGPU benefits from the lack of reduction operations moving its bottleneck back to data transfer (see Fig. 10).

Fig. 10
figure 10

Performance of KPM-DOS kernel and polynomial filter for the topological insulator matrix on the Nvidia K20m GPGPU, a single SNB, and 2 HSW sockets (the latter two only for block vector width R = 32)

Full size image

It is also evident that the Cray XC30 node (K20X+SNB) outperforms the Intel Haswell node (2× HSW) on this kernel.

As a second part ChebFD requires a subspace orthogonalization step, which basically leads to matrix–matrix multiplications involving “tall and skinny” matrices. The performance of widely used BLAS level 3 multi-threaded libraries such as Intel MKL or ATLAS are often not competitive in the relevant parameter space addressed by ESSEX applications as can be seen in Fig. 11. Up to a block vector size of approximately 50 they may miss the upper performance bound imposed by the memory bandwidth and the arithmetic peak performance by a large margin. Hence, GHOST provides optimized kernels for these application scenarios achieving typically 80 % of the maximum attainable performance (see Fig. 11). Note that automatic kernel generation with compile time defined small dimensions as described in Sect. 4 also works for “tall and skinny” GEMM operations.

Fig. 11
figure 11

Performance on a single IVB socket of tall and skinny matrix–matrix multiplication X ← V × W with double complex data type, where X is R × R, V is R × D, W is D × R and D = 107

Full size image

The corresponding cuBLAS calls show similar characteristics and thus ESSEX is currently preparing hand-optimized GPGPU kernels for “tall and skinny” dense matrix operations as well.

With the current ChebFD implementation we have computed 148 innermost eigenvalues of a topological insulator matrix (matrix dimension 109) on 512 Intel Xeon nodes on the second phase of SuperMUCFootnote 9 within 10 h (see [24] for details). Using all of the 3072 nodes we will be able to compute the relevant inner eigenvalues for a topological insulator matrix dimension of 1010 at a sustained performance of approximately 250 Tflop/s on that machine.

ChebFD is similar to the recent FEAST algorithm [27]. In FEAST the acceleration is not done with a matrix polynomial but by a contour integration of the resolvent, thus involving the solution of linear systems. FEAST can be faster if a very efficient (e.g., direct) solver is available for the ill-conditioned and highly indefinite linear systems and if high-degree polynomials must be employed in ChebFD. In other situations, ChebFD may be superior due to the high-performance kernels. ChebFD is limited to standard eigenvalue problems, whereas FEAST also can address generalized problems.

5.3 Block Jacobi-Davidson QR Method

The popular Jacobi-Davidson method has been chosen in ESSEX to compute a few low eigenpairs of large sparse matrices. A block variant (BJDQR) was implemented which operates on dense blocks of vectors and thus increases the computational intensity (similar to optimization stage 2 in Fig. 3) and decreases the amount of synchronization points (see [29] and our report on the ESSEX solver repository [32] for details).

The most time consuming operations in this algorithm are the SpMMV and various tall-skinny matrix–matrix products for a limited number of block sizes (e.g. 2,4 and 8). The implementation was tuned to make the best possible use of the highly optimized GHOST kernels (see Fig. 11), and in particular block vectors in row-major storage.

As soon as all optimized CUDA “tall and skinny” GEMM kernels are implemented in GHOST, BJDQR will also be available for fully heterogeneous computations. For a more detailed analysis of performance and numerical efficiency of our BJDQR solver we refer to [28, 29], where it was shown that GHOST delivers near optimal performance on an IVB system and is clearly superior to other implementations.

6 Summary and Outlook

We have given an overview of the building block layer in the ESSEX project, specifically the GHOST library. Using several examples of applications within the project (Kernel Polynomial Method [KPM], Chebyshev filter diagonalization [ChebFD], block Jacobi-Davidson QR [BJDQR]) we have shown that GHOST can address the challenges of heterogeneous, highly parallel architectures with its consistent “MPI+X” approach. GHOST implements the highly successful SELL-C-σ sparse matrix format, which contains several other popular formats such as CSR as special cases. We have demonstrated our model-driven Performance Engineering approach using the example of a KPM-DOS application, showing that improvements in the kernel implementation (including the choice of a SIMD-friendly data layout, loop fusion, and blocking) lead not only to the expected performance improvements but also to proportional savings in energy-to-solution on the CPU level, both validated using appropriate performance and power models. For KPM we have also shown the scalability on up to 4096 nodes on the Piz Daint supercomputer, delivering a sustained performance of 0.5 Pflop/s and 87% heterogeneous parallel efficiency on the node-level (CPU+GPGPU). The algorithmically more challenging ChebFD implementation benefited from the optimized tall skinny matrix multiplications in GHOST, which reach substantially higher (in fact, near-light speed, i.e., close to the roofline limit) socket-level performance than the vendor library (MKL) for small to medium block vector sizes. Finally, guided by the same PE approach as in the other cases we could improve the performance of our BJDQR implementation to yield a 3× speedup compared with the Trilinos building block library Tpetra.

The first three years of research into sparse building blocks have already yielded effective ways of Performance Engineering, based on analytic models and insight into hardware-software interaction. Beyond the continued implementation and optimization of tailored kernels for the algorithmic and application-centric parts of the ESSEX project, we will in the future place more emphasis on optimized (problem-aware) matrix storage schemes, high-precision reduction operations with automatic error control, and on more advanced modeling and validation approaches. We have also just barely scratched the surface of the energy dissipation properties of our algorithms; more in-depth analysis is in order to develop a more detailed understanding of power dissipation on heterogeneous hardware.