Paraconsistency, Chellas’s Conditional Logics, and Association Rules

Abstract

Paraconsistency and its dual paracompleteness are now counted as key concepts in intelligent decision systems because so much inconsistent and incomplete information can be found around us. In this paper, a framework of conditional models for conditional logic and their measure-based extensions are introduced in order to represent association rules in a logical way. Then paracomplete and paraconsistent aspects of conditionals are examined in the framework. Finally we apply conditionals into the definition of association rules in data mining with confidence and consider their extension to the case of Dempster-Shaer theory of evidence serving double-indexed confidence.

Dedicated to Jair Minoro Abe for his 60th birthday

9.1 Introduction

The authors have tried to give a kind of logical foundation to data mining. Murai et al. [15–17] tried to present a logical formulation of association rules [1–3] using Chellas’s conditional models for conditional logics [7] and their measure-based extensions (cf. [12–14]). Akama and Abe [6] proposed a comprehensive idea of paraconsistent logic databases as data warehouse based on paraconsistent and annotated logics [4, 5, 8].

In our opinion, paraconsistency and its dual paracompleteness become key concepts in future development of intelligent decision systems because nowadays there are so much inconsistent and incomplete information around us. In classical logic, inconsistency means triviality in the sense that all sentences become theorems. Paraconsistency means inconsistency but non-triviality. Thus we need new kinds of logic like paraconsistent and annotated logics [4, 5, 8]. Paracompleteness is the dual concept of paraconsistency where the excluded middle is not true.

In this paper, we put association rules in a framework of conditional models [7] and their measure-based extensions (cf. [12–14]) and examine their paracomplete and paraconsistent aspects in the framework.

Then we notice that the standard confidence [1] is nothing but a conditional probability where even weights are a priori assigned to each transaction that contains the items in question at the same time. All of such transactions, however, do not necessarily give us such evidence because some co-occurrences might be contingent. For describing such cases we further introduce double-indexed confidence based on Dempster-Shafer theory [19].

9.2 Chellas’s Conditional Models and Their Measure-Based Extensions for Conditional Logics

9.2.1 Standard and Minimal Conditional Models

Given a finite set $\mathcal{P}$ of items as atomic sentences, a language $\mathcal{L}_\mathrm{CL}(\mathcal{P})$ for conditional logic is formed from $\mathcal{P}$ as the set of sentences closed under the usual propositional operators such as $\top$, $\bot$, $\lnot$, $\wedge$, $\vee$, $\rightarrow$, and $\leftrightarrow$ as well as ${{\Box }\!\rightarrow }$ and ${{\Diamond }\!\rightarrow }$ ¹ (two kinds of conditionals) in the following usual way.

• 1. If $x\in \mathcal{P}$ then ${x\in \mathcal{L}_\mathrm{CL}(\mathcal{P})}$.

• 2. $\top , \bot \in \mathcal{L}_\mathrm{CL}(\mathcal{P})$.

• 3. If ${p\in \mathcal{L}_\mathrm{CL}(\mathcal{P})}$ then ${\lnot {p} \in \mathcal{L}_\mathrm{CL}(\mathcal{P})}$.

• 4. If $p,q\in \mathcal{L}_\mathrm{CL}(\mathcal{P})$ then $p\wedge q$, $p\vee q$, $p \rightarrow q$, $p \leftrightarrow q$, $p {{\Box }\!\rightarrow }q$, $p {{\Diamond }\!\rightarrow }q \in \mathcal{L}_\mathrm{CL}(\mathcal{P})$.

Chellas [7] introduces two kind of models called standard and minimal. There relationship is similar to Kripke and Scott-Montague models for modal logics.

Definition 9.1

(Chellas [7], p. 268) A standard conditional model $\mathcal{M}_\mathrm{CL}$ for conditional logic is a structure

$$\begin{aligned} \langle {W,f,v}\rangle , \end{aligned}$$

where W is a non-empty set of possible worlds, v is a truth-assignment function

$$\begin{aligned} v:\mathcal{P}\times W\rightarrow \{0,1\}, \end{aligned}$$

and f is a function

$$\begin{aligned} f: W\times 2^{W}\rightarrow {2^{W}}.\;\;\blacksquare \end{aligned}$$

The truth conditions for ${{\Box }\!\rightarrow }$ and ${{\Diamond }\!\rightarrow }$ in standard conditional models are given by

• 1. $\mathcal{M}_\mathrm{CL},w\models p{{\Box }\!\rightarrow }q \mathop {\Longleftrightarrow }\limits ^\mathrm{def} f(w, \Vert {p}\Vert ^{\mathcal{M}_\mathrm{CL}})\subseteq \Vert {q}\Vert ^{\mathcal{M}_\mathrm{CL}}$,

• 2. $\mathcal{M}_\mathrm{CL},w\models p{{\Diamond }\!\rightarrow }q \mathop {\Longleftrightarrow }\limits ^\mathrm{def} f(w, \Vert {p}\Vert ^{\mathcal{M}_\mathrm{CL}})\cap \Vert {q}\Vert ^{\mathcal{M}_\mathrm{CL}}\ne \emptyset$,

where $\Vert {p}\Vert ^{\mathcal{M}_\mathrm{CL}}=\{w\in W\;|\;\mathcal{M}_\mathrm{CL},w\models p\}$. Thus we have the following relationship between the two kind conditionals:

$$\begin{aligned} p{{\Box }\!\rightarrow }q \leftrightarrow \lnot (p{{\Diamond }\!\rightarrow }\lnot q). \end{aligned}$$

The function f can be regarded as a kind of selection function. That is, $p{{\Box }\!\rightarrow }q$ is true at a world w when q is true at any world selected by f with respect p and w. Similarly, $p{{\Diamond }\!\rightarrow }q$ is true at a world w when q is true at least at one of the worlds selected by f with respect p and w.

A minimal conditional models is a Scott-Montague-like extension of standard conditional model [7].

Definition 9.2

(Chellas [7], p. 270) A minimal conditional model $\mathcal{M}_\mathrm{CL}$ for conditional logic is a structure

$$\begin{aligned} \langle {W,g,v}\rangle , \end{aligned}$$

where W and v are the same ones as in the standard conditional models. The difference is the second term

$$\begin{aligned} g: W\times 2^{W}\rightarrow 2^{2^{W}}.\;\;\blacksquare \end{aligned}$$

The truth conditions for ${{\Box }\!\rightarrow }$ and ${{\Diamond }\!\rightarrow }$ in a minimal conditional model are given by

• 1. $\mathcal{M}_\mathrm{CL},w\models p{{\Box }\!\rightarrow }q$ $\mathop {\Longleftrightarrow }\limits ^\mathrm{def}$ $\Vert {q}\Vert ^{\mathcal{M}_\mathrm{CL}}\in g(w, \Vert {p}\Vert ^{\mathcal{M}_\mathrm{CL}})$,

• 2. $\mathcal{M}_\mathrm{CL},w\models p{{\Diamond }\!\rightarrow }q \mathop {\Longleftrightarrow }\limits ^\mathrm{def} {(\Vert {q}\Vert ^{\mathcal{M}_\mathrm{CL}})}^\mathrm{C}\not \in g(w, \Vert {p}\Vert ^{\mathcal{M}_\mathrm{CL}})$,

Thus we have also the following relationship:

$$\begin{aligned} p{{\Box }\!\rightarrow }q \leftrightarrow \lnot (p{{\Diamond }\!\rightarrow }\lnot q). \end{aligned}$$

Note that, if the function g satisfies the following condition

$$\begin{aligned} {X}\in g(w, \Vert {p}\Vert ^{\mathcal{M}_\mathrm{CL}})\Leftrightarrow \cap g(w, \Vert {p}\Vert ^{\mathcal{M}_\mathrm{CL}})\subseteq {X} \end{aligned}$$

for every world w and every sentence p, then, by defining

$$\begin{aligned} f_g(w, \Vert {p}\Vert ^{\mathcal{M}_\mathrm{CL}})\mathop {=}\limits ^\mathrm{def}\cap g(w, \Vert {p}\Vert ^{\mathcal{M}_\mathrm{CL}}), \end{aligned}$$

we have the standard conditional model $\langle W,f_g,v \rangle$ that is equivalent to the original minimal model.

9.2.2 Measure-Based Extensions

Next we introduce measure-based extensions of the previous minimal conditional models. Such extensions are models for graded conditional logics.

Given a finite set $\mathcal{P}$ of items as atomic sentences, a language $\mathcal{L}_\mathrm{gCL}(\mathcal{P})$ for graded conditional logic is formed from $\mathcal{P}$ as the set of sentences closed under the usual propositional operators such as $\top$, $\bot$, $\lnot$, $\wedge$, $\vee$, $\rightarrow$, and $\leftrightarrow$ as well as ${{\Box }\!\rightarrow }_k$ and ${{\Diamond }\!\rightarrow }_k$ (graded conditionals) for $0 < k \le 1$ in the usual way.

• 1. If $x\in \mathcal{P}$ then ${x\in \mathcal{L}_\mathrm{gCL}(\mathcal{P})}$.

• 2. $\top , \bot \in \mathcal{L}_\mathrm{gCL}(\mathcal{P})$.

• 3. If ${p\in \mathcal{L}_\mathrm{gCL}(\mathcal{P})}$ then ${\lnot {p} \in \mathcal{L}_\mathrm{gCL}(\mathcal{P})}$.

• 4. If $p,q\in \mathcal{L}_\mathrm{gCL}(\mathcal{P})$ then $p\wedge q$, $p\vee q$, $p \rightarrow q$, $p \leftrightarrow q \in \mathcal{L}_\mathrm{gCL}(\mathcal{P})$,

• 5. If [$p,q \in \mathcal{L}_\mathrm{gCL}(\mathcal{P})$ and $0 < k \le 1$] then $p {{\Box }\!\rightarrow }_k q$, $p {{\Diamond }\!\rightarrow }_k q \in \mathcal{L}_\mathrm{gCL}(\mathcal{P})$.

A graded conditional model is defined as a family of minimal conditional model (cf. Chellas [7]):

Definition 9.3

Given a fuzzy measure

$$\begin{aligned} m: 2^{W}\times 2^{W}\rightarrow [0,1], \end{aligned}$$

a measure-based conditional model $\mathcal{M}^{m}_\mathrm{gCL}$ for graded conditional logic is a structure

$$\begin{aligned} \langle {W,\{g_k\}_{0<k\le 1},v}\rangle , \end{aligned}$$

where W and V are the same ones as in the standard conditional models. $g_k$ is defined by a fuzzy measure m as

$$\begin{aligned} g_k(t, {X})\mathop {=}\limits ^\mathrm{def} \{ {Y}\subseteq 2^{W} \; | \; m({Y},{X})\ge k\}. \;\;\blacksquare \end{aligned}$$

The model $\mathcal{M}^{m}_\mathrm{gCL}$ is called finite because so is W. Further, in this paper, we call the model $\mathcal{M}^{m}_\mathrm{gCL}$ uniform since functions $\{g_k\}$ in the model does not depend on any world in $\mathcal{M}^{m}_\mathrm{gCL}$.

The truth conditions for ${{\Box }\!\rightarrow }_k$ and ${{\Diamond }\!\rightarrow }_k$ in a measure-based conditional model are given by

$$\begin{array}{l} \mathcal{M}^{m}_\mathrm{gCL},t\models p{{\Box }\!\rightarrow }_k q\ { \mathsf{iff} }\ \Vert {q}\Vert ^{\mathcal{M}^{m}_\mathrm{gCL}}\in g_k(t, \Vert {p}\Vert ^{\mathcal{M}^{m}_\mathrm{gCL}}),\\ \mathcal{M}^{m}_\mathrm{gCL},t\models p{{\Diamond }\!\rightarrow }_k q\ { \mathsf{iff} }\ {(\Vert {q}\Vert ^{\mathcal{M}^{m}_\mathrm{gCL}})}^\mathrm{C}\not \in g_k(t, \Vert {p}\Vert ^{\mathcal{M}^{m}_\mathrm{gCL}}). \end{array}$$

The basic idea of these definitions is the same as in fuzzy-measure-based semantics for graded modal logic defined in [12–14].

When we take m as a conditional probability, the truth conditions of graded conditional becomes

$$\begin{aligned} \mathcal{M}^{\text{ Pr }}_\mathrm{gCL},t\models p{{\Box }\!\rightarrow }_k q\ { \mathsf{iff} }\ \text{ Pr }(\Vert {q}\Vert ^{\mathcal{M}^{\text{ Pr }}_\mathrm{gCL}}\;|\;\Vert {p}\Vert ^{\mathcal{M}^{\text{ Pr }}_\mathrm{gCL}})\ge k. \end{aligned}$$

We have several soundness results based on probability-measure-based semantics (cf. [12–14]) shown in Table 9.1.

Table 9.1 Soundness results of graded conditionals by probability measures

9.3 Paraconsistency and Paracompleteness in Conditionals

As Chellas pointed out in his book [7] (p. 269), conditionals $p{{\Box }\!\rightarrow }q$ (and also $p{{\Diamond }\!\rightarrow }q$) is regarded as relative modal sentences like [p]q (and also $\langle p \rangle q$). So we first see paraconsistency and paracompleteness in the usual modal setting for convenience.

9.3.1 Modal Logic Case

Let us define some standard language $\mathcal L$ for modal logic with two modal operators $\Box$ and $\Diamond$. In [18], we examined some relationship between modal logics and paraconsistency and paracompleteness. Let us assume a language $\mathcal L$ of modal logic as usual. In terms of modal logic, paracompleteness and paraconsistency have a close relation to the following axiom schemata:

$$\begin{array}{ll} \mathbf{D. } &{} \Box p \rightarrow \lnot \Box \lnot p, \\ \mathbf{{D_{C.}}} &{} \lnot \Box \lnot p \rightarrow \Box p, \end{array}$$

because they have their equivalent expressions

$$\begin{array}{l} \lnot (\Box p \wedge \Box \lnot p), \\ \Box p \vee \Box \lnot p, \end{array}$$

respectively. That is, given a system of modal logic $\varSigma$, define the following set of sentences

$$\begin{aligned} T\;\mathop {=}\limits ^\mathrm{def}\;\{p\in \mathcal{L} \;|\; \vdash _{\varSigma } \Box p\}, \end{aligned}$$

where $\vdash _{\varSigma }\Box p$ means $\Box p$ is a theorem of $\varSigma$. Then the above two schemata mean that, for any sentence p

$$\begin{array}{l} \mathsf{{not }}(p\in T\ \mathsf{{ and }}\ \lnot p\in T) \\ p\in T \ \mathsf{{ or }}\ \lnot p \in T \end{array}$$

respectively, and obviously the former describes the consistency of T and the latter the completeness of T. Thus

• T is inconsistent when $\varSigma$ does not contain D.

• T is incomplete when $\varSigma$ does not contain D $_\mathrm{C}$.

A system $\varSigma$ is regular when it contains the following rule and axiom schemata

$$\begin{array}{l} p\leftrightarrow q \Rightarrow \Box p\leftrightarrow \Box q \\ (\Box p\wedge \Box q)\leftrightarrow \Box (p\wedge q) \end{array}$$

Note that any normal system is regular.

In [18] we pointed out the followings. If $\varSigma$ is regular, then we have

$$\begin{aligned} (\Box p\wedge \Box \lnot p)\leftrightarrow \Box \lnot \top \end{aligned}$$

(9.1)

where $\bot \leftrightarrow \lnot \top$ and $\bot$ is falsity constant, which means inconsistency itself. Thus we have triviality:

$$\begin{aligned} T=\mathcal{L}. \end{aligned}$$

But if $\varSigma$ is not regular, then we have no longer (9.1), thus, in general

$$\begin{aligned} T\ne \mathcal{L}, \end{aligned}$$

which means T is paraconsistent. That is, local inconsistency does not generate triviality as global inconsistency.

9.3.2 Conditional Logic Case

Next we apply the previous idea into conditional logics. In conditional logics, the corresponding axiom schemata

$$\begin{array}{ll} \mathbf{CD. } &{} \lnot ({(p{{\Box }\!\rightarrow }q)}\wedge {(p {{\Box }\!\rightarrow }\lnot q)}) \\ \mathbf{CD_{C}.} &{} {(p{{\Box }\!\rightarrow }q)}\vee {(p{{\Box }\!\rightarrow }\lnot q)} \end{array}$$

Given a system CL of conditional logic, define the following set of conditionals (rules):

$$\begin{aligned} R\;\mathop {=}\limits ^\mathrm{def}\;\{p{{\Box }\!\rightarrow }q\in \mathcal{L}_{CD} \;|\; \vdash _{CL} p{{\Box }\!\rightarrow }q\}. \end{aligned}$$

where $\mathcal{L}_{CD}$ is a language for conditional logic and $\vdash _{CL}p{{\Box }\!\rightarrow }q$ means $p{{\Box }\!\rightarrow }q$ is a theorem of CL. Then the above two schemata mean that, for any sentence p

$$\begin{array}{l} \mathsf{{not }}(p{{\Box }\!\rightarrow }q\in R \ \mathsf{{ and }}\ p{{\Box }\!\rightarrow }\lnot q\in R) \\ p{{\Box }\!\rightarrow }q\in R \ \mathsf{{ or }}\ p{{\Box }\!\rightarrow }\lnot q \in R \end{array}$$

respectively, and obviously the former describes the consistency of R and the latter the completeness of R. Thus, for the set R of conditionals (rules)

• R is inconsistent when CL does not contain CD.

• R is incomplete when CL does not contain CD $_\mathrm{C}$.

9.4 Paraconsistency and Paracompleteness in Association Rules

9.4.1 Association Rules

Let $\mathcal I$ be a finite set of items. Any subset X in $\mathcal I$ is called an itemset in $\mathcal I$. A database is comprised of transactions, which are actually obtained or observed itemsets. Formally, we give the following definition:

Definition 9.4

A database $\mathcal D$ on $\mathcal I$ is defined as

$$\begin{aligned} \langle {T,V}\rangle , \end{aligned}$$

where

• 1. $T=\{1,2,\ldots ,n\}$ (n is the size of the database),

• 2. $V:T\rightarrow 2^\mathcal{I}$.    $\blacksquare$

Thus, for each transaction $i\in T$, V gives its corresponding set of items $V(i)\subseteq \mathcal{I}$.

For an itemset X, its degree of support s(X) is defined by

$$\begin{aligned} s(X)\mathop {=}\limits ^\mathrm{def}\frac{|\{t\in T\; | \;X\subseteq V(t)\}|}{|T|}, \end{aligned}$$

where $|\cdot |$ is a size of a finite set.

Definition 9.5

(Agrawal et al. [1]) Given a set of items $\mathcal I$ and a database $\mathcal D$ on $\mathcal I$, an association rule  is an implication of the form

$$\begin{aligned} X\Longrightarrow Y, \end{aligned}$$

where X and Y are itemsets in $\mathcal I$ with $X \cap Y = \emptyset$.   $\blacksquare$

The following two indices were introduced in [1].

Definition 9.6

(Agrawal et al. [1])

• 1. An association rule $r=(X \Longrightarrow Y)$ holds with confidence c(r) $(0\le c(r) \le 1)$ in $\mathcal D$ if and only if

  $$\begin{aligned} c(r)=\frac{s(X\cup Y)}{s(X)}. \end{aligned}$$

• 2. An association rule $r=(X \Longrightarrow Y)$ has a degree of support s(r) $(0\le s(r) \le 1)$ in $\mathcal D$ if and only if

  $$\begin{aligned} s(r)=s(X\cup Y). \;\;\blacksquare \end{aligned}$$

In this paper, we will deal with the former index.

Mining of association rules is actually performed by generating all rules that have certain minimum support (denoted minsup) and minimum confidence (denoted minconf) that a user specifies. See, e.g., [1–3] for details of such algorithms for finding association rules.

Table 9.2 Movie database

For example, consider the movie database in Table 9.2, where AH and HM means Ms. Audrey Hepburn and Mr. Henry Mancini, respectively. If you have watched several (famous) Ms. Hepburn’s movies, you might hear some wonderful music composed by Mr. Mancini. This can be represented by the association rule

$$\begin{aligned} r=\{\text{ AH }\}\;\Longrightarrow \;\{\text{ HM }\} \end{aligned}$$

with its confidence

$$\begin{aligned} c(r)=\frac{s(\{\text{ AH }\}\cup \{\text{ HM }\})}{s(\{\text{ AH }\})}=0.5 \end{aligned}$$

and its degree of support

$$\begin{aligned} s(r)=\frac{|\{T\; |\; T\subseteq \{\text{ AH }\}\cup \{\text{ HM }\}\}|}{|\mathcal{D}|}=\frac{4}{100}=0.04. \end{aligned}$$

9.4.2 Measure-Based Conditional Models for Databases

Let us regards a finite set $\mathcal{I}$ of items as atomic sentences. Then, a language $\mathcal{L}_\mathrm{gCL}(\mathcal{I})$ for graded conditional logic is formed from $\mathcal{I}$ as the set of sentences closed under the usual propositional operators such as $\top$, $\bot$, $\lnot$, $\wedge$, $\vee$, $\rightarrow$, and $\leftrightarrow$ as well as ${{\Box }\!\rightarrow }_k$ and ${{\Diamond }\!\rightarrow }_k$ (graded conditionals) for $0 < k \le 1$ in the usual way.

• 1. If $x\in \mathcal{I}$ then ${x\in \mathcal{L}_\mathrm{gCL}(\mathcal{I})}$.

• 2. $\top , \bot \in \mathcal{L}_\mathrm{gCL}(\mathcal{I})$.

• 3. If ${p\in \mathcal{L}_\mathrm{gCL}(\mathcal{I})}$ then ${\lnot {p} \in \mathcal{L}_\mathrm{gCL}(\mathcal{I})}$.

• 4. If $p,q\in \mathcal{L}_\mathrm{gCL}(\mathcal{I})$ then $p\wedge q$, $p\vee q$, $p \rightarrow q$, $p \leftrightarrow q \in \mathcal{L}_\mathrm{gCL}(\mathcal{I})$,

• 5. If [$p,q \in \mathcal{L}_\mathrm{gCL}(\mathcal{I})$ and $0 < k \le 1$] then $p {{\Box }\!\rightarrow }_k q$, $p {{\Diamond }\!\rightarrow }_{k} q \in \mathcal{L}_\mathrm{gCL}(\mathcal{I})$.

A measure-based conditional model is defined as a family of minimal conditional model (cf. Chellas [7]):

Definition 9.7

Given a database $\mathcal{D}=\langle {T,V}\rangle$ on $\mathcal I$ and a fuzzy measure m, a measure-based conditional model $\mathcal{M}^{m}_\mathrm{g\mathcal{D}}$ for $\mathcal D$ is a structure

$$\begin{aligned} \langle {W,\{g_k\}_{0<k\le 1},v}\rangle , \end{aligned}$$

where (1) $W=T$, (2) for any world (transaction) t in W and any set of itemsets X in $2^\mathcal{I}$, $g_k$ is defined by a fuzzy measure m as

$$\begin{aligned} g_k(t, {X})\mathop {=}\limits ^\mathrm{def} \{ {Y}\subseteq 2^{W} \; | \; m({Y},{X})\ge k\}, \end{aligned}$$

and (3) for any item x in $\mathcal{I}$, $v(x,t)=\mathsf{1}\ { \mathsf{iff} }\ x\in V(t)$.   $\blacksquare$

The model $\mathcal{M}^{m}_\mathrm{g\mathcal{D}}$ is called finite because so is W. Further, in this paper, we call the model $\mathcal{M}^{m}_\mathrm{g\mathcal{D}}$ uniform since functions $\{g_k\}$ in the model does not depend on any world in $\mathcal{M}^{m}_\mathrm{g\mathcal{D}}$.

The truth condition for ${{\Box }\!\rightarrow }_k$ in a grade conditional model is given by

$$\begin{aligned} \mathcal{M}^{m}_\mathrm{g\mathcal{D}},t\models p{{\Box }\!\rightarrow }_k q\ { \mathsf{iff} }\ \Vert {q}\Vert ^{\mathcal{M}^{m}_\mathrm{g\mathcal{D}}}\in g_k(t, \Vert {p}\Vert ^{\mathcal{M}^{m}_\mathrm{g\mathcal{D}}}), \end{aligned}$$

where

$$\begin{aligned} \Vert p\Vert ^{\mathcal{M}^{m}_\mathrm{g\mathcal{D}}}\mathop {=}\limits ^\mathrm{def}\{t\in W(=T)\;|\; \mathcal{M}^{m}_\mathrm{g\mathcal{D}},t\models p\}. \end{aligned}$$

The basic idea of this definition is the same as in fuzzy-measure-based semantics for graded modal logic defined in [12–14].

9.4.3 Association Rules and Graded Conditionals

For example, the usual degree of confidence [1] is nothing but the well-known conditional probability, so we define function $g_k$ by conditional probability.

Definition 9.8

For a given database $\mathcal{D}=\langle {T,V}\rangle$ on $\mathcal I$ and a conditional probability

$$\begin{aligned} \text{ Pr }({B}|{A})=\frac{|{A}\cap {B}|}{|{A}|}, \end{aligned}$$

its corresponding probability-based graded conditional model $\mathcal{M}^{\text{ Pr }}_\mathrm{g\mathcal{D}}$ is defined as a structure

$$\begin{aligned} \langle {W,\{g_k\}_{0<k\le 1},v}\rangle , \end{aligned}$$

where

$$\begin{aligned} g_k(w,{X})\mathop {=}\limits ^\mathrm{def} \{ {Y}\subseteq 2^{W} \; | \; \text{ Pr }(t(Y)\;|\;t(X))\ge k\}, \end{aligned}$$

where

$$\begin{aligned} t(X)\;\mathop {=}\limits ^\mathrm{def}\;\{w\in W\;|\;X\subseteq w\}. \;\;\blacksquare \end{aligned}$$

The truth condition of graded conditional is given by

$$\begin{aligned} \mathcal{M}^{\text{ Pr }}_\mathrm{g\mathcal{D}},t\models p{{\Box }\!\rightarrow }_k q\ { \mathsf{iff} }\ \text{ Pr }(\Vert {q}\Vert ^{\mathcal{M}^{\text{ Pr }}_\mathrm{g\mathcal{D}}}\;|\;\Vert {p}\Vert ^{\mathcal{M}^{\text{ Pr }}_\mathrm{g\mathcal{D}}})\ge k. \end{aligned}$$

Then we can have the following theorem:

Theorem 9.1

Given a database $\mathcal{D}$ on $\mathcal I$ and its corresponding probability-based graded conditional model $\mathcal{M}_{\mathrm{g}\mathcal{D}}$, for an association rule $X\Longrightarrow Y$, we have

$$\begin{aligned} c(X\Longrightarrow Y)\ge k \ { \mathsf{iff} }\ \mathcal{M}^{\text{ Pr }}_\mathrm{g\mathcal{D}}\models {p_X}{{\Box }\!\rightarrow }_{k} {p_Y}. \;\;\blacksquare \end{aligned}$$

9.4.4 Paraconsistency and Paracompleteness in Association Rules

We formulated association rules as graded conditionals based on probability. Define the following set of rules with confidence k:

$$\begin{aligned} R_k\;\mathop {=}\limits ^\mathrm{def}\;\{p{{\Box }\!\rightarrow }_k q\in \mathcal{L}_{gCD} \;|\; \vdash _{gCL} p{{\Box }\!\rightarrow }_k q\}. \end{aligned}$$

A graded conditional $p{{\Box }\!\rightarrow }_k q$ is also regarded as a relative necessary sentences $[p]_kq$ and the properties of relative modal operator $[\cdot ]_k$ are examined in Murai et al. [12–14] in the following correspondence:

$$ \begin{array}{l|l}\hline \text{ Confidence } \text{ k }&{} \text{ Systems } \\ \hline 0<k\le \frac{1}{2} &{} EMD_CNP \\ \frac{1}{2}<k< 1 &{} EMDNP \\ \hline k=1 &{} KD \\ \hline \end{array}$$

The former two systems are not regular, so $R_k$ may be paraconsistent. The last one is normal so regular.

For $0<k\le \frac{1}{2}$, $R_k$ is complete but for some p and q, the both rules $p{{\Box }\!\rightarrow }_k q$ and $p{{\Box }\!\rightarrow }_k \lnot q$ may be generated. This should be avoided.

For $\frac{1}{2}<k<1$, $R_k$ is consistent but may be paracomplete.

9.5 Dempster-Shafer-Theory-Based Confidence

9.5.1 D-S Theory and Confidence

The standard confidence [1] described in the previous section is based on the idea that co-occurrences of items in one transaction are evidence for association between the items. Since the definition of confidence is nothing but a conditional probability, even weights are a priori assigned to each transaction that contains the items in question at the same time. All of such transactions, however, do not necessarily give us such evidence because some co-occurrences might be contingent. Thus we need a framework that can differentiate proper evidence from contingent one and we introduce Dempster-Shafer theory of evidence [9, 19] to describe such a more flexible framework to compute confidence. There are a variety of ways of formalizing D-S theory and, in this paper, we adopt multivalued-mapping-based approach, which was originally used by Dempster [9]. In the approach, we need two frames, one of which has a probability defined, and a multivalued mapping between the two frames. Given a database $\mathcal{D}=\langle {T,V}\rangle$ on $\mathcal I$ and an association rule $r=(X\;\Longrightarrow \;Y)$ in $\mathcal D$, one of frames is the set T of transactions. Another one is defined by

$$\begin{aligned} R=\{r,\overline{r}\}, \end{aligned}$$

where $\overline{r}$ denotes the negation of r. The remaining tasks are (1) to define a probability distribution $\text{ Pr }$ on T: $\text{ Pr }: T\rightarrow [0,1]$, and (2) to define a multivalued mapping $\varGamma : T\rightarrow 2^{{R}}$. Given $\text{ Pr }$ and $\varGamma$, we can define the well-known two kinds of functions in Dempster-Shafer theory: for $X\subseteq 2^{{R}}$,

$$\begin{aligned} \text{ Bel }(X)\;\mathop {=}\limits ^\mathrm{def}\;\text{ Pr }(\{{t\in T}\;{|}\;{\varGamma (t)\subseteq X}\}),\\ \text{ Pl }(X)\;\mathop {=}\limits ^\mathrm{def}\;\text{ Pr }(\{{t\in T}\;{|}\;{\varGamma (t)\cap X\ne \emptyset }\}) \end{aligned}$$

which are called belief and plausibility functions, respectively. Now we have the following double-indexed confidence:

$$\begin{aligned} c(r)=\langle {\text{ Bel }(r),\text{ Pl }(r)}\rangle . \end{aligned}$$

9.5.2 Multi-graded Conditional Models for Databases

Given a finite set $\mathcal{I}$ of items as atomic sentences, a language $\mathcal{L}_\mathrm{mgCL}(\mathcal{I})$ for graded conditional logic is formed from $\mathcal{I}$ as the set of sentences closed under the usual propositional operators as well as ${{\Box }\!\rightarrow }_k$ and ${{\Diamond }\!\rightarrow }_k$ (graded conditionals) for $0 < k \le 1$ in the usual way. Note that, in particular,

$$\begin{aligned} (p,q\in \mathcal{L}_\mathrm{mgCL}(\mathcal{I}) \text{ and } 0<k\le 1) \Rightarrow p{{\Box }\!\rightarrow }_k q, p{{\Diamond }\!\rightarrow }_k q\in \mathcal{L}_\mathrm{mgCL}(\mathcal{I}). \end{aligned}$$

Definition 9.9

Given a database $\mathcal D$ on $\mathcal I$, a multi-graded conditional model $\mathcal{M}_\mathrm{mg\mathcal{D}}$ for $\mathcal D$ is a structure

$$\begin{aligned} \langle {W,\{\{\underline{g}_k,\overline{g}_k\}\}_{0<k\le 1},v}\rangle , \end{aligned}$$

where (1) $W$ $=$ $T$, (2) for any world (transaction) t in W and any set of itemsets $\mathcal{X}$ in $2^\mathcal{I}$, $g_k$ is defined by belief and plausibility functions:

$$\begin{aligned} \underline{g}_k(t, \mathcal{X})\mathop {=}\limits ^\mathrm{def} \{ \mathcal{Y}\subseteq 2^{W} |\; \text{ Bel }(\mathcal{Y},\mathcal{X})\ge k\}, \\ \overline{g}_k(t, \mathcal{X})\mathop {=}\limits ^\mathrm{def} \{ \mathcal{Y}\subseteq 2^{W} |\; \text{ Pl }(\mathcal{Y},\mathcal{X})\ge k\}, \end{aligned}$$

and (3) for any item x in $\mathcal{I}$, $v(x,t)=\mathsf{1} \ { \mathsf{iff} }\ x\in V(t)$   $\blacksquare$

The truth conditions for ${{\Box }\!\rightarrow }_k$ and ${{\Diamond }\!\rightarrow }_k$ are given by

$$\begin{aligned} \mathcal{M}_\mathrm{mg\mathcal{D}},w\models p{{\Box }\!\rightarrow }_k q \ { \mathsf{iff} }\ \Vert {q}\Vert ^{\mathcal{M}_\mathrm{mg\mathcal{D}}}\in \underline{g}_k(t, \Vert {p}\Vert ^{\mathcal{M}_\mathrm{mg\mathcal{D}}}) \\ \mathcal{M}_\mathrm{mg\mathcal{D}},w\models p{{\Diamond }\!\rightarrow }_k q \ { \mathsf{iff} }\ \Vert {q}\Vert ^{\mathcal{M}_\mathrm{mg\mathcal{D}}}\in \overline{g}_k(t, \Vert {p}\Vert ^{\mathcal{M}_\mathrm{mg\mathcal{D}}}), \end{aligned}$$

respectively. Its basic idea is also the same as in fuzzy-measure-based semantics for graded modal logic defined in [12–14]. Several soundness results based on belief- and plausibility-function-based semantics (cf. [12–14]) are shown in Table 9.3.

Table 9.3 Soundness results of graded conditionals by belief and plausibility functions

9.5.3 Two Typical Cases

First we define a probability distribution on T by

$$ \text{ Pr }(t)\;\mathop {=}\limits ^\mathrm{def}\; \left\{ \begin{array}{ll} \frac{1}{a}, &{} \text{ if } t\in \Vert {p_X}\Vert ^{{\mathcal{M}_\mathrm{mg\mathcal{D}}}}\text{, } \\ 0, &{} \text{ otherwise, } \end{array}\right. $$

where $a=|\Vert {p_X}\Vert ^{{\mathcal{M}_\mathrm{mg\mathcal{D}}}}|$. This means that each world (transaction) t in $\Vert {p_X}\Vert ^{{\mathcal{M}_\mathrm{mg\mathcal{D}}}}$ is given an even mass (weight) $\frac{\displaystyle 1}{a}$. To generalize the distribution is of course another interesting task.

Next we shall see two typical cases of definition of $\varGamma$. First we describe strongest cases. When we define a mapping $\varGamma$ by

$$ \varGamma (t)\;\mathop {=}\limits ^\mathrm{def}\; \left\{ \begin{array}{ll} \{r\}, &{} \text{ if } t\in \Vert {p_X}\Vert ^{{\mathcal{M}_\mathrm{mg\mathcal{D}}}}\text{, } \\ \{\overline{r}\}, &{} \text{ otherwise. } \end{array}\right. $$

This means that the transactions in $\Vert {p_X\wedge p_Y}\Vert ^{{\mathcal{M}_\mathrm{mg\mathcal{D}}}}$ contribute as evidence to r, while the transactions in $\Vert {p_X\wedge \lnot p_Y}\Vert ^{{\mathcal{M}_\mathrm{mg\mathcal{D}}}}$ contribute as evidence to $\overline{r}$. This is the strongest interpretation of co-occurrences. Then, we can compute $\text{ Bel }(r)=\frac{\displaystyle 1}{a}\times b$ and $\text{ Pl }(r)=\frac{\displaystyle 1}{a}\times b$, where $b=|\Vert {p_X\wedge p_Y}\Vert ^{{\mathcal{M}_\mathrm{mg\mathcal{D}}}}|$. Thus the induced belief and plausibility functions collapse to the same probability measure $\text{ Pr }$: $\text{ Bel }(r)=\text{ Pl }(r)=\text{ Pr }(r)=\frac{b}{a}$, and thus

$$\begin{aligned} c(r)=\langle {\displaystyle \frac{b}{a},\displaystyle \frac{b}{a}}\rangle . \end{aligned}$$

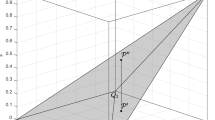
Hence this case represents the usual confidence. According to this idea, in our movie database, we can define $\text{ Pr }$ and $\varGamma$ in the way in Fig. 9.1. That is, any movie in $\Vert {\mathrm{AH}\wedge \mathrm{HM}}\Vert ^{{\mathcal{M}_\mathrm{mg\mathcal{D}}}}$ contributes as evidence to that the rule holds (r), while all movie in $\Vert {\mathrm{AH}\wedge \lnot \mathrm{HM}}\Vert ^{{\mathcal{M}_\mathrm{mg\mathcal{D}}}}$ contributes as evidence to that the rule does not hold ($\overline{r}$). Thus we have

$$\begin{aligned} c(\{AH\}\Longrightarrow \{HM\})=\langle {0.5,0.5}\rangle . \end{aligned}$$

Fig. 9.1

An example of the strongest cases

Next we describe weakest cases. In general, co-occurrences do not necessarily mean actual association. The weakest interpretation of co-occurrences is to consider transactions totally unknown as described as follows: When we define a mapping $\varGamma$ by

$$ \varGamma (t)\;\mathop {=}\limits ^\mathrm{def}\; \left\{ \begin{array}{ll} \{r,\overline{r}\}, &{} \text{ if } t\in \Vert {p_X}\Vert ^{{\mathcal{M}_\mathrm{mg\mathcal{D}}}}\text{, } \\ \{\overline{r}\}, &{} \text{ otherwise. } \end{array}\right. $$

This means that the transactions in $\Vert {p_X\wedge p_Y}\Vert ^{{\mathcal{M}_\mathrm{g\mathcal{D}}}}$ contribute as evidence to $R=\{r,\overline{r}\}$, while the transactions in $\Vert {p_X\wedge \lnot p_Y}\Vert ^{{\mathcal{M}_\mathrm{g\mathcal{D}}}}$ contribute as evidence to $\overline{r}$. Then, we can compute $\text{ Bel }(r)=0$ and $\text{ Pl }(r)=\frac{\displaystyle 1}{a}\times b$, and thus

$$\begin{aligned} c(r)=\langle {0,\displaystyle \frac{b}{a}}\rangle . \end{aligned}$$

According to this idea, in our movie database, we can define $\text{ Pr }$ and $\varGamma$ in the way in Fig. 9.2. That is, all movie in $\Vert {\mathrm{AH}\wedge \lnot \mathrm{HM}}\Vert ^{{\mathcal{M}_\mathrm{mg\mathcal{D}}}}$ contributes as evidence to that the rule does not hold ($\overline{r}$), while we cannot expect whether each movie in $\Vert {\mathrm{AH}\wedge \mathrm{HM}}\Vert ^{{\mathcal{M}_\mathrm{mg\mathcal{D}}}}$ contributes or not as evidence to that the rule holds (r). Thus we have

$$\begin{aligned} c(\{AH\}\Longrightarrow \{HM\})=\langle {0,0.5}\rangle . \end{aligned}$$

In the case, the induced belief and plausibility functions, denoted respectively $Bel_{bpa'}$ and $Pl_{bpa'}$, become necessity and possibility measures in the sense of Dubois and Prade [10]. We have several soundness results based on necessity- and possibility-measure-based semantics (cf. [12–14]) shown in Table 9.4.

Fig. 9.2

An example of the weakest cases

Table 9.4 Soundness results of graded conditionals by necessity and possibility measures

9.5.4 General Cases

In the previous two typical cases, one of which coincides to the usual confidence, any transaction in $\Vert {\mathrm{AH}\wedge \mathrm{HM}}\Vert ^{{\mathcal{M}_\mathrm{mg\mathcal{D}}}}$ (or in $\Vert {\mathrm{AH}\wedge \lnot \mathrm{HM}}\Vert ^{{\mathcal{M}_\mathrm{mg\mathcal{D}}}}$) has the same weight as evidence. It would be, however, possible that some of $\Vert {\mathrm{AH}\wedge \mathrm{HM}}\Vert ^{{\mathcal{M}_\mathrm{mg\mathcal{D}}}}$ (or $\Vert {\mathrm{AH}\wedge \lnot \mathrm{HM}}\Vert ^{{\mathcal{M}_\mathrm{mg\mathcal{D}}}}$) does work as positive evidence to r (or $\overline{r}$) but other part does not.

Thus we have a tool that allows us to introduce various kinds of ‘a posteriori’ pragmatic knowledge into the logical setting of association rules. As an example, we assume that (1) the music of the first and second movies was not composed by Mancini, but the fact does not affect the validity of $\overline{r}$ because they are not very important ones, and (2) the music of the seventh movie was composed by Mancini, but the fact does not affect the validity of r. Then we can define $\varGamma$ in the way in Fig. 9.3. Thus we have

Fig. 9.3

An example of general cases

$$\begin{aligned} c(\{AH\}\Longrightarrow \{HM\})=\langle {0.375,0.75}\rangle . \end{aligned}$$

In general, users have such kind of knowledge ‘a posteriori.’ Thus the D-S based approach allows us to introduce various kinds of ‘a posteriori’ pragmatic knowledge into association rules.

9.6 Concluding Remarks

In this paper, we examined paraconsistency and paracompleteness that appear in association rules in a framework of probability-based models for conditional logics. For lower values of confidence (less than or equal to $\frac{1}{2}$), both $p{{\Box }\!\rightarrow }_k q$ and $p{{\Box }\!\rightarrow }_k \lnot q$ may be generated so we must be careful to use such lower confidence.

Further we extended the above discussion into the case of Dempster-Shafer theory of evidence to double-indexed confidences. Users have, in general, such kind of knowledge ‘a posteriori’ describe in the previous section. Thus the D-S based approach allows a sophisticated way of calculating confidence by introducing various kinds of ‘a posteriori’ pragmatic knowledge into association rules.