Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Conservation laws are ubiquitous in science and engineering, describing a wide variety of phenomena, such as chemically reacting flow, electrical discharges in gases, transport in porous media etc. These conservation laws are often of advection-diffusion-reaction type, describing the interplay between different processes such as advection or drift, diffusion or conduction and (chemical) reactions or impact ionization. We restrict ourselves to stationary conservation laws.

Numerical simulation of these equations requires sophisticated space discretization methods and efficient (iterative) solvers for the resulting algebraic system. For space discretization of the conservation law we employ the finite volume method (FVM); see [2] for a detailed account. For the numerical fluxes in the discrete conservation law there exist many schemes. Basic schemes are the central difference and upwind schemes. The central difference scheme is prone to spurious oscillations for dominant advection while the upwind discretization is too diffusive. To remedy this, exponentially fitted schemes were introduced, see [6] and the many references therein. These schemes combine the central difference and upwind schemes in such a way that the resulting discretization reproduces the exact solution of a local one-dimensional and homogeneous boundary value problem (BVP). Exponentially fitted schemes are especially useful for singularly perturbed problems [4]. Moreover, these schemes are applied in various disciplines in computational physics, such as the numerical simulation of reactive flow or plasmas. In the field of semiconductor device simulation the exponetially fitted scheme is often referred to as the Scharfetter-Gummel scheme; see e.g. [7] for a general introduction. An ingenious generalization to nonlinear convection-diffusion problems was introduced in [3], where an (iterative) procedure is proposed to compute the numerical flux from a nonlinear, but homogeneous, BVP. Another generalization is the complete flux scheme, where the flux is derived from a local BVP for the entire equation, including the source term [8]. Consequently, the numerical flux can be written as the superposition of a homogeneous flux, which is the exponentially fitted flux corresponding to the advection-diffusion operator, and an inhomogeneous flux, taking into account the effect of the source term.

In this contribution, we extend the derivation of the complete flux scheme to conservation laws containing a linear source. We split off the linear part and incorporate this term in the homogeneous flux. To that purpose, we solve the corresponding homogeneous boundary value problem, which describes the balance between advection, diffusion and a linear source. The remaining (nonlinear) part of the source is included in the inhomogeneous flux, as usual. The modified homogeneous and inhomogeneous fluxes reduce to the classical fluxes when the linear source vanishes. On the other hand, for a dominant linear source, the solution of the underlying boundary value problem exhibits oscillatory behaviour, resulting in completely different fluxes. A similar scheme is presented in [5] for the special case that the characteristic equation of the local BVP has two distinct real roots. Our scheme also allows for double real or complex (conjugate) roots.

Thus, we consider the model advection-diffusion-reaction equation

$$\displaystyle{ \frac{\mathrm{d}} {\mathrm{d}x}\Big(u\varphi -\varepsilon \frac{\mathrm{d}\varphi } {\mathrm{d}x}\Big) = c\varphi + s(\varphi ), }$$
(1)

where, for example, u is an advection velocity, ɛ ≥ ɛ min > 0 a diffusion coefficient, c φ the linear part of the source, and s(φ) the remaining (nonlinear) source. The unknown φ might be the mass fraction of one of the constituent species in a reacting flow or plasma. Associated with (1) we introduce the flux f, which is defined by

$$\displaystyle{ f = u\varphi -\varepsilon \frac{\mathrm{d}\varphi } {\mathrm{d}x}. }$$
(2)

The conservation law (1) can be concisely written as df∕dx = c φ + s(φ) with the flux f defined in (2). In the FVM we cover the domain with a finite number of control volumes (cells) I j of size Δ x. We choose the grid points x j , where the variable φ has to be approximated, in the cell centres. Consequently, we have I j : = [x j−1∕2, x j+1∕2] with \(x_{j+1/2}:= \tfrac{1} {2}(x_{j} + x_{j+1})\). Integrating the equation over I j and applying the midpoint rule for the integral of c φ + s(φ), we obtain the discrete conservation law

$$\displaystyle{ F_{j+1/2} - F_{j-1/2} =\varDelta x\,\big(c\,\varphi _{j} + s(\varphi _{j})\big), }$$
(3)

where F j+1∕2 and φ j are the numerical approximation of the flux f at the cell edge x j+1∕2 and of the unknown φ at the grid point x = x j , respectively. The complete flux approximation F j+1∕2 is the sum of the homogeneous flux F j+1∕2 h and the inhomogeneous flux F j+1∕2 i, i.e.,

$$\displaystyle{ \begin{array}{rl} F_{j+1/2} & = F_{j+1/2}^{\mathrm{h}} + F_{j+1/2}^{\mathrm{i}} \\ & =\alpha _{j+1/2}\varphi _{j} -\beta _{j+1/2}\varphi _{j+1} +\varDelta x\big(\gamma _{j+1/2}s(\varphi _{j}) +\delta _{j+1/2}s(\varphi _{j+1})\big). \end{array} }$$
(4)

The coefficients α j+1∕2 and β j+1∕2 depend on the homogeneous differential operator, containing the advection-diffusion operator as well as the linear source, and the coefficients γ j+1∕2 and δ j+1∕2 depend on the nonlinear source s(φ).

We have organized our paper as follows. In Sect. 2 we derive expressions for the homogeneous flux, and subsequently in Sect. 3, we outline the derivation of the inhomogeneous flux. For the latter we reformulate equation (1) and relation (2) together as a first order ODE-system. In Sect. 4 we demonstrate the performance of the homogeneous flux scheme, and finally we present conclusions in Sect. 5.

2 Modification of the Homogeneous Flux

In this section we present the extension of the homogeneous flux scheme to equation (1). We assume in the sequel of this paper that u, ɛ and c are constant. The expression for the homogeneous flux F j+1∕2 h is then derived from the following local BVP

$$\displaystyle{ \varepsilon \varphi ^{{\prime\prime}}- u\varphi ^{{\prime}} + c\varphi = 0,\quad x_{ j} < x < x_{j+1}, }$$
(5a)
$$\displaystyle{ \varphi (x_{j}) =\varphi _{j},\quad \varphi (x_{j+1}) =\varphi _{j+1}, }$$
(5b)

including the linear source term c φ, where the prime (′) denotes differentiation with respect to x. Although the source term c φ is included, we refer to the resulting numerical flux as homogeneous, since equation (5a) is homogeneous. The inhomogeneous flux takes into account the effect of the nonlinear source s(φ) and will be discussed in the next section.

The characteristic equation of equation (5a) reads ɛ λ 2 − u λ + c = 0 and has discriminant D = u 2 − 4ɛ c. Let us introduce the auxiliary variables

$$\displaystyle{ d = \frac{\varepsilon c} {u^{2}},\quad P = \frac{u\varDelta x} {\varepsilon },\quad S = \sqrt{\frac{\vert c\vert } {\varepsilon }} \varDelta x. }$$
(6)

In (6), P is the well-known Péclet number and S is a dimensionless parameter measuring the reaction-diffusion ratio. Moreover, in the presentation that follows we encounter the following functions:

$$\displaystyle{ B(z) = \frac{z} {\mathrm{e}^{z} - 1},\quad \mathrm{sinhc}(z) = \frac{\sinh (z)} {z},\quad \mathrm{sinc}(z) = \frac{\sin (z)} {z}. }$$
(7)

Based on the sign of the discriminant D, we can distinguish the following three cases. First, for D > 0, or equivalently \(d < \tfrac{1} {4}\), the characteristic equation has two distinct real roots λ = u(1 ± r)∕(2ɛ) with \(r = \sqrt{1 - 4d}\). We can solve the BVP (5) and subsequently compute the numerical flux from (2). We find

$$\displaystyle{ F_{j+1/2}^{\mathrm{h}} = \frac{\varepsilon } {\varDelta x}\big(C(P;r)B(-Pr)\varphi _{j} - C(-P;r)B(Pr)\varphi _{j+1}\big), }$$
(8a)
$$\displaystyle{ C(P;r) =\mathrm{ e}^{P(1-2r)/4}\big(\cosh \big(\tfrac{1} {4}Pr\big) + \tfrac{1} {4}P\,\mathrm{sinhc}\big(\tfrac{1} {4}Pr\big)\big). }$$
(8b)

Note that the numerical flux in (8) is reminiscent of the classical homogeneous flux, and contains ‘correction factors’ C(P; r) and C(−P; r).

Second, for D = 0, and hence \(d = \tfrac{1} {4}\) and r = 0, the characteristic equation has the double real root λ = u∕(2ɛ). We find for the numerical flux

$$\displaystyle{ F_{j+1/2}^{\mathrm{h}} = \frac{\varepsilon } {\varDelta x}\big(C(P)\varphi _{j} - C(-P)\varphi _{j+1}\big), }$$
(9a)
$$\displaystyle{ C(P) =\mathrm{ e}^{P/4}\big(1 + \tfrac{1} {4}P\big). }$$
(9b)

Note that the numerical flux (8) reduces to (9) for r = 0. Finally, for D < 0, or equivalently \(d > \tfrac{1} {4}\), the characteristic equation has two complex (conjugate) roots λ = u(1 ± ir)∕(2ɛ) with \(r = \sqrt{4d - 1}\). We simply have to replace in the expressions in (8) r by ir. For the numerical flux, for example, we find

$$\displaystyle{ F_{j+1/2}^{\mathrm{h}} = \frac{\varepsilon } {\varDelta x}\big(C(P;\mathrm{i}r)B(-\mathrm{i}Pr)\varphi _{j} - C(-P;\mathrm{i}r)B(\mathrm{i}Pr)\varphi _{j+1}\big), }$$
(10)

so it seems as if the numerical flux is complex-valued! However, using Euler’s formula, we can show that the numerical flux is real and is given by

$$\displaystyle{ F_{j+1/2}^{\mathrm{h}} = \frac{\varepsilon } {\varDelta x}\big(C(P;r)\varphi _{j} - C(-P;r)\varphi _{j+1}\big), }$$
(11a)
$$\displaystyle{ C(P;r) =\mathrm{ e}^{P/4}\,\frac{\cos \big(\tfrac{1} {4}Pr\big) + \tfrac{1} {4}P\,\mathrm{sinc}\big(\tfrac{1} {4}Pr\big)} {\mathrm{sinc}\big(\tfrac{1} {2}Pr\big)}. }$$
(11b)

Note that this expression is valid provided \(\tfrac{1} {2}\vert P\vert r <\pi\).

It is interesting to investigate some limiting cases. First, for c = 0, we have D > 0, r = 1 and recover the well-known homogeneous numerical flux for the advection-diffusion equation given by

$$\displaystyle{ F_{j+1/2}^{\mathrm{h}} = \frac{\varepsilon } {\varDelta x}\big(B(-P)\varphi _{j} - B(P)\varphi _{j+1}\big), }$$
(12)

see [8]. Next, for ɛ = 0 equation (1) is an advection-reaction equation and we also have D > 0 and r = 1. The numerical flux (8) reduces to the upwind flux. Finally, for u = 0 equation (1) is a diffusion-reaction equation and we have P = 0 and D = −4ɛ c. Consequently, we have to distinguish two different cases, i.e., c < 0 and c > 0. First, for c < 0 it is obvious that D > 0 and the numerical flux (8) reduces to

$$\displaystyle{ F_{j+1/2}^{\mathrm{h}} = - \frac{\varepsilon } {\varDelta x}\, \frac{\varphi _{j+1} -\varphi _{j}} {\mathrm{sinhc}\big(\tfrac{1} {2}S\big)}. }$$
(13)

Finally, for c > 0 and D < 0 the numerical flux (11) is given by

$$\displaystyle{ F_{j+1/2}^{\mathrm{h}} = - \frac{\varepsilon } {\varDelta x}\, \frac{\varphi _{j+1} -\varphi _{j}} {\mathrm{sinc}\big(\tfrac{1} {2}S\big)}, }$$
(14)

provided \(\tfrac{1} {2}S <\pi\). Both expressions are in fact the central difference approximation of the flux divided by the correction factor \(\mathrm{sinhc}\big(\tfrac{1} {2}S\big)\) or \(\mathrm{sinc}\big(\tfrac{1} {2}S\big)\). Alternatively, we could have computed these numerical fluxes directly from the BVP (5) with u = 0.

3 Modification of the Inhomogeneous Flux

In this section we outline the modification of the inhomogeneous flux for equation (1); a more elaborate discussion will be presented elsewhere. To derive the integral representation for the inhomogeneous flux, it is convenient to reformulate equation (1) coupled with expression (2) for the flux as the first order ODE-system

$$\displaystyle{ \boldsymbol{v}^{{\prime}} =\boldsymbol{ A}\boldsymbol{v} +\boldsymbol{ b},\quad x_{ j} < x < x_{j+1}, }$$
(15a)
$$\displaystyle{ \varphi (x_{j}) =\varphi _{j},\quad \varphi (x_{j+1}) =\varphi _{j+1}, }$$
(15b)

where \(\boldsymbol{v}\), \(\boldsymbol{A}\), and \(\boldsymbol{b}\) are given by

$$\displaystyle{ \boldsymbol{v} = \left (\begin{array}{*{10}c} \varphi \\ f \end{array} \right ),\quad \boldsymbol{A} = \left (\begin{array}{*{10}c} \frac{u} {\varepsilon } &-\frac{1} {\varepsilon } \\ c & 0 \end{array} \right ),\quad \boldsymbol{b} = \left (\begin{array}{*{10}c} 0\\ s(\varphi ) \end{array} \right ). }$$
(15c)

This formulation is somewhat unusual, since the second component of \(\boldsymbol{v}\) is the flux, for obvious reasons, instead of the derivative φ ′. The fundamental matrix

$$\displaystyle{ \boldsymbol{V } = \left (\begin{array}{*{10}c} \varphi _{1}\, & \varphi _{2} \\ f_{1}\, & f_{2} \end{array} \right ) }$$
(16)

corresponding to (15) satisfies the BVP

$$\displaystyle{ \boldsymbol{V }^{{\prime}} =\boldsymbol{ A}\boldsymbol{V },\quad x_{ j} < x < x_{j+1}, }$$
(17a)
$$\displaystyle{ \varphi _{1}(x_{j}) = 1,\,\varphi _{1}(x_{j+1}) = 0,\quad \varphi _{2}(x_{j}) = 0,\,\varphi _{1}(x_{j+1}) = 1. }$$
(17b)

Note that only boundary conditions for the unknown φ are specified. A straightforward derivation shows that for D > 0 the solutions φ 1(x) and φ 2(x) are given by

$$\displaystyle{ \varphi _{1}(x) =\mathrm{ e}^{P\sigma (x)/2}\frac{\mathrm{sinh}\big(\tfrac{1} {2}Pr(1 -\sigma (x))\big)} {\mathrm{sinh}\big(\tfrac{1} {2}Pr\big)}, }$$
(18a)
$$\displaystyle{ \varphi _{2}(x) =\mathrm{ e}^{-P(1-\sigma (x))/2}\frac{\mathrm{sinh}\big(\tfrac{1} {2}Pr\sigma (x)\big)} {\mathrm{sinh}\big(\tfrac{1} {2}Pr\big)}, }$$
(18b)

where σ(x) = (x − x j )∕Δ x is the normalized coordinate on (x j , x j+1). The corresponding (homogeneous) fluxes f 1(x) and f 2(x) can be readily determined from (2). Similar expressions hold for D = 0 or D < 0.

Applying variation of constants, we can derive the following representation of the solution of (15), see also [1]:

$$\displaystyle{ \boldsymbol{v}(x) =\boldsymbol{ V }(x)\boldsymbol{r}+\int _{x_{j}}^{x_{j+1} }\boldsymbol{G}(x;y)\boldsymbol{b}(y)\,\mathrm{d}y,\quad \boldsymbol{r} = \left (\begin{array}{*{10}c} \varphi _{j} \\ \varphi _{j+1} \end{array} \right ), }$$
(19)

with \(\boldsymbol{G}(x;y)\) the Green’s function given by

$$\displaystyle{ \boldsymbol{G}(x;y) =\big (\varepsilon W(\varphi _{1},\varphi _{2})(y)\big)^{-1}\left \{\begin{array}{@{}l@{\quad }l@{}} \left (\begin{array}{*{10}c} -\varphi _{1}(x)f_{2}(y) & \varphi _{1}(x)\varphi _{2}(y) \\ -f_{1}(x)f_{2}(y)&f_{1}(x)\varphi _{2}(y) \end{array} \right )\quad \text{for}\quad x_{j} < y \leq x, \quad \\ \left (\begin{array}{*{10}c} -\varphi _{2}(x)f_{1}(y) & \varphi _{2}(x)\varphi _{1}(y) \\ -f_{2}(x)f_{1}(y)&f_{2}(x)\varphi _{1}(y) \end{array} \right )\quad \text{for}\quad x < y < x_{j+1}.\quad \end{array} \right. }$$
(20)

In (20), W(φ 1, φ 2) is the Wronskian of φ 1 and φ 2, which for D > 0 is given by

$$\displaystyle{ W(\varphi _{1},\varphi _{2}) = \left \vert \begin{array}{*{10}c} \varphi _{1}\, & \varphi _{2} \\ \varphi _{1}^{{\prime}}\,&\varphi _{2}^{{\prime}} \end{array} \right \vert = \frac{1} {\varDelta x} \frac{\mathrm{e}^{P(\sigma (x)-1/2)}} {\mathrm{sinhc}\big(\tfrac{1} {2}Pr\big)}. }$$
(21)

Note that the relations (19), (20), and (21) define the complete solution, i.e., the unknown φ and the flux f, on the entire interval [x j , x j+1]. However, we are only interested in the flux at the interface x = x j+1∕2. The second component of the term \(\boldsymbol{V }(x_{j+1/2})\boldsymbol{r}\) is the homogeneous flux F j+1∕2 h as detailed in the previous section. The inhomogeneous flux f i(x j+1∕2) is the second component of the inhomogeneous term in (19) evaluated at x j+1∕2 and reads

$$\displaystyle{ \begin{array}{rl} f^{\mathrm{i}}(x_{j+1/2})& = \frac{1} {\varepsilon } F_{1,j+1/2}^{\mathrm{h}}\int _{ x_{j}}^{x_{j+1/2} } \frac{\varphi _{2}(x)s(x)} {W(\varphi _{1},\varphi _{2})(x)}\,\mathrm{d}x \\ &\quad + \frac{1} {\varepsilon } F_{2,j+1/2}^{\mathrm{h}}\int _{ x_{j+1/2}}^{x_{j+1}} \frac{\varphi _{1}(x)s(x)} {W(\varphi _{1},\varphi _{2})(x)}\,\mathrm{d}x. \end{array} }$$
(22)

The flux values F 1, j+1∕2 h and F 2, j+1∕2 h correspond to f 1(x) and f 2(x) and follow readily from the expressions (8), (9) or (11) by substituting φ j  = 1,  φ j+1 = 0 or φ j  = 0,  φ j+1 = 1, respectively. Applying suitable quadrature rules, we can derive expressions for the numerical inhomogeneous flux F j+1∕2 i.

4 Numerical Example

As an example we apply the modified homogeneous flux scheme to the following model problem

$$\displaystyle{ \frac{\mathrm{d}} {\mathrm{d}x}\Big(u\varphi -\varepsilon \frac{\mathrm{d}\varphi } {\mathrm{d}x}\Big) = c\varphi,\quad 0 < x < L, }$$
(23a)
$$\displaystyle{ \varphi (0) =\varphi _{\mathrm{L}},\quad \varphi (L) =\varphi _{\mathrm{R}}. }$$
(23b)

We consider two cases, viz. a boundary layer solution, characterized by dominant advection, and an oscillatory solution, for which the source term is dominant. For the first solution D > 0 and we employ the numerical flux (8), whereas for the second solution we apply the numerical flux (11) since D < 0.

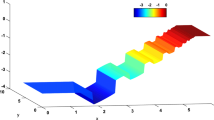
To assess the (order) of accuracy of the modified scheme, we define the average discretization error \(e(\varDelta x) =\varDelta x\vert \vert \boldsymbol{\varphi }-\boldsymbol{\varphi }^{{\ast}}\vert \vert _{1}\), with \(\boldsymbol{\varphi }^{{\ast}}\) the exact solution of (23) restricted to the grid. A representative numerical solution and the average discretization error as function of the grid size are shown in the figures above. From the Fig. 1, we conclude that for the boundary layer solution the modified homogeneous flux scheme is much more accurate than the standard scheme, although both schemes exhibit second order convergence. On the other hand, for the oscillatory solution, the modified scheme is slightly better, as is evident from Fig. 2. Further research is needed to investigate this issue further.

Fig. 1
figure 1

Boundary layer solution: numerical solutions (left) and error plots (right). Parameter values are u = −1, ɛ = 10−2, c = 2, and Δ x = 10−1

Full size image
Fig. 2
figure 2

Oscillatory solution: numerical solutions (left) and error plots (right). Parameter values are u = 1, ɛ = 0. 5, and c = 2 × 102, and Δ x = 2. 5 × 10−3

Full size image

5 Concluding Remarks

In this contribution we derived a new complete flux approximation scheme for conservation laws containing a linear source. We included the linear source in the homogeneous differential operator to determine the homogeneous flux. The inhomogeneous flux contains the effect of the remaining (nonlinear) part of the source. In the derivation of the inhomogeneous flux, we reformulated the conservation law coupled with the expression for the flux as a first order ODE-system. First numerical results are encouraging, however, more testing is needed.

To be relevant for practical applications, the scheme should be extended to (at least) two-dimensional problems. This can be achieved if we include the cross-flux term as an additional source in the one-dimensional model BVP. To close the discretization, we employ the homogeneous flux scheme for the cross flux; see [8] were this idea is elaborated for the original CF scheme.