Keywords

1 Introduction

Petri nets [7, 8, 12] have been proposed as a formalism for modeling and analysis of discrete-event systems with asynchronous, interacting components. Computer and communication networks, manufacturing systems and transportation networks are just a few examples of such systems. Popularity of net models is due to a simple and ‘natural’ representation of concurrent and asynchronous activities, typical for many discrete-event dynamical systems, that, however, cannot be modeled easily using queueing theory or other traditional modeling and evaluation techniques. Moreover, a well-developed mathematical foundations exists for the description and analysis of net models.

In order to study the performance aspects of Petri net models, the duration of activities must also be taken into account. Several types of Petri nets ‘with time’ have been proposed by assigning ‘firing times’ to transitions or ‘enabling times’ to places [1, 9, 13]. In timed Petri nets [3, 11, 14, 15], the events occur in ‘real time’, i.e., there is a (deterministic or stochastic) duration associated with each transition’s firing, and different (concurrent) firings of transitions correspond to (concurrent) activities in the modeled systems. For timed Petri nets, the concept of ‘state’ and state transitions can be formally defined, and used to derive different performance characteristics of the model [15].

For a class of Petri net models, structural analysis, based on place invariants [12], is an attractive approach because it provides an analytical characterization of the model’s performance, and also it eliminates the exhaustive analysis of the state space (which can be huge for large models). Structural analysis is based on the set of place invariants, which—for complex models—can be difficult to find. Incremental approach reduces the process of finding basic place invariants by first finding the invariants for very simple submodels of the original models, and then combining the submodels into more complex ones with invariants determined in a way that eliminates many steps of the direct approach to finding the invariants.

Section 2 recalls basic concepts of Petri nets and timed nets, their place invariants and (structural) performance analysis. Finding place invariants is discussed in Sect. 3 while Sect. 4 introduces the incremental approach and compares it with the direct approach of Sect. 3. Section 5 provides some concluding remarks.

2 Nets, Net Invariants, Timed Nets and Performance Analysis

A place/transition (ordinary, i.e., with no arc weights) net N is a triple \( {\mathbf{N}} = (P,T,A) \) where P is a finite, nonempty set of places, T is a finite, nonempty set of transitions, and A is a set of directed arcs, \( A\, \subseteq \, P \times T \cup T \times P \), such that for each transition there exists at least one place connected with it. For each place p (and each transition t) the input set, Inp(p) (or Inp(t)), is the set of transitions (or places) connected by directed arcs to p (or t). The output sets, Out(p) and Out(t), are defined similarly.

A marked Petri net M is a pair \( {\mathbf{M}} = (N,m_{0} ) \) where N is a Petri net, \( {\mathbf{N}} = (P,T,A) \), and \( m_{0} \) is an initial marking function, \( m_{0} :P \to \{ 0,1, \ldots \} \) which assigns a (nonnegative) integer number of tokens to each place of the net.

Let any function \( m:P \to \{ 0,1, \ldots \} \) be called a marking in a net \( {\mathbf{N}} = (P,T,A) \).

A transition t is enabled by a marking m iff m assigns at least one token to every input place of this transition. Every transition enabled by a marking m can fire (or occur). When a transition fires, a token is removed from each of its input places and a token is added to each of its output places. This determines a new marking in a net, new set of enabled transitions, and so on. The set of all markings that can be derived from the initial marking is called the set of reachable markings. If this set if finite, the net is bounded, otherwise it is unbounded.

A place p is shared iff it is an input place for more than one transition. A net is (structurally or statically) conflict-free if it does not contain shared places. A marked net is (dynamically) conflict-free if for any marking in the set of reachable markings, and for any shared place, at most one of transitions sharing the place is enabled. Only bounded conflict-free nets are considered in this paper.

Each place/transition net \( {\mathbf{N}} = (P,T,A) \) can be represented by a connectivity (or incidence) matrix \( {\mathbf{C}}:P \times T \to \{ - 1,0, + 1\} \) in which places correspond to rows, transitions to columns, and the entries are defined as:

$$ \forall p \in P\, \forall t \in T:{\mathbf{C}}[p,t] = \left\{ {\begin{array}{*{20}l} { - 1,} \hfill & {{\text{if }}t \in Out(p) - Inp(t),} \hfill \\ { + 1,} \hfill & {{\text{if }}t \in Inp(p) - Out(p),} \hfill \\ {0,} \hfill & {{\text{otherwise}} . } \hfill \\ \end{array} } \right. $$

If a marking \( m_{j} \) is obtained from another marking \( m_{i} \) by firing a transition \( t_{k} \) then (in vector notation) \( m_{j} = m_{i} + {\mathbf{C}}[k] \), where C[k] denotes the k-th column of C, i.e., the column representing \( t_{k} \).

Connectivity matrices disregard ‘selfloops’, that is, pairs of arcs (p, t) and (t, p); any firing of a transition t cannot change the marking of p in such a selfloop, so selfloops are neutral with respect to token count of a net. A pure net is defined as a net without selfloops [12].

A P-invariant (place invariant) of a net N is any nonnegative, nonzero integer (column) vector I which is a solution of the matrix equation

$$ {\mathbf{C}}^{T} \times I = 0, $$

where \( {\mathbf{C}}^{T} \) denotes the transpose of matrix C. It follows immediately from this definition that if \( I_{1} \) and \( I_{2} \) are P-invariants of N, then also any linear (positive) combination of \( I_{1} \) and \( I_{2} \) is a P-invariant of N.

A basic P-invariant of a net is defined as a P-invariant which does not contain simpler invariants. All basic P-invariants I of ordinary nets are binary vectors [12], \( I:P \to \{ 0,1\} \).

A net \( {\mathbf{N}}_{i} = (P_{i} ,T_{i} ,A_{i} ) \) is a P i -implied subnet of a net \( {\mathbf{N}} = (P,T,A) \), \( P_{i} \subset P \), iff:

  1. (1)

    \( A_{i} = A \cap (P_{i} \times T \cap T \times P_{i} ), \)

  2. (2)

    \( T_{i} = \{ t \in T|\exists p \in P_{i} :(p,t) \in A \vee (t,p) \in A\} . \)

It should be observed that in a (pure) net N, each P-invariant I of N determines a P I -implied (invariant) subnet of N, where \( P_{I} = \{ p \in P|I(p) > 0\} \); P I is sometimes called the support of the invariant I; all nonzero elements of I select rows of C, and each selected row i corresponds to a place p i with all its input (+1) and all output (–1) arcs associated with it.

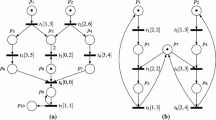
For the Petri net shown in Fig. 1, the connectivity matrix is:

Fig. 1
figure 1

Petri net

Full size image

It can be easily observed that the sum of rows 1 and 2, as well as 3 and 4 are equal to zero, so \( \{ p_{1} ,p_{2} \} \) and \( \{ p_{3} ,p_{4} \} \) are basic place invariants. Similarly, \( \{ p_{5} ,p_{6} ,p_{7} ,p_{8} ,p_{9} \} \) is also a basic place invariant. Subnets implied by these invariants are shown in Fig. 2.

Fig. 2
figure 2

Invariant implied subnets

Full size image

The net shown in Fig. 1 has two more place invariants: \( \{ p_{1} ,p_{3} ,p_{5} ,p_{6} \} \) and \( \{ p_{2} ,p_{4} ,p_{7} ,p_{8} ,p_{9} \} \).

In timed Petri nets each transition takes a ‘real time’ to fire, i.e., there is a ‘firing time’ associated with each transition of a net which determines the duration of transition’s firings.

A conflict-free timed Petri net T is a pair \( {\mathbf{T}} = ({\mathbf{M}},f) \) where:

M is a conflict-free marked Petri net, \( {\mathbf{M}} = ({\mathbf{N}},m_{0} ) \), \( {\mathbf{N}} = (P,T,A) \),

f is a firing time function which assigns the nonnegative (average) firing time \( f(t) \) to each transition t of the net, \( f:T \to {\mathbf{R}}^{ \oplus } \), and \( {\mathbf{R}}^{ \oplus } \) denotes the set of nonnegative real numbers.

The behavior of a timed Petri net can be represented by a sequence of ‘states’ and state transitions where each ‘state’ describes the distribution of tokens in places as well as firing transitions of the net; detailed definitions of states and state transitions are given in [15]. The states and state transitions can be combined into a graph of reachable states; this graph is a semi-Markov process defined by the timed net T. For cyclic conflict-free timed nets, such state graphs are simple cycles which represent the cyclic behavior of such nets. Each such timed Petri net contains a basic invariant subnet with the cycle time equal to the cycle time of the whole net. All other subnets, with smaller cycle times, will be subjected to some synchronization delays, imposed by the ‘slowest’ subnet that determines the cycle time of the whole net.

The cycle time of the net, \( \tau_{0} \), is thus equal to the maximum cycle time if its invariant subnets [13]:

$$ \tau_{0} = { \hbox{max} }(\tau_{1} ,\tau_{2} , \ldots ,\tau_{k} ) $$

where k is the number of subnets covering the original net, and each \( \tau_{i} \), \( i = 1, \ldots ,k \), is the cycle time of the subnet i, equal to the sum of occurrence times associated with the transitions divided by the total number of tokens assigned to the subnet:

$$ \tau_{i} = \frac{{\sum\nolimits_{{t \in T_{i} }} {f(t)} }}{{\sum\nolimits_{{p \in P_{i} }} {m(p)} }}. $$

In many cases, the number of basic P-invariants can be reduced by removing from the analyzed net all these elements which do not affect the performance of models. Some of such reductions are discussed in [16].

3 Finding Place Invariants

Finding place invariants can be done in several ways [5, 6]. A polynomial algorithm for finding all place invariants can be derived from the property that the sum of rows of the connectivity matrix corresponding to a place invariant is equal to zero. For each place \( p_{i} \), the algorithm starts with the i-th row of a connectivity matrix and uses other rows to eliminate nonzero elements in the original row. This is performed by a recursive procedure “Eliminate” with three parameters, “w” which is the current working vector (initialized to the i-th row of the connectivity matrix), “u” which is a set of places constituting the invariant and “r” which ia a set of columns of the connectivity matrix (i.e., transitions) used for reductions of “w”:

“Inv” is the set of invariants and “add(u,Inv)” adds the invariant “u” to the set. “Inv” if it is not there; \( n_{t} \) is the number of transitions and \( n_{p} \) is the number of places. The function “check(w, j)” returns the set of indices of nonzero elements of the sum of “w” and row “j” of “M”.

“Eliminate” is invoked for consecutive places of the net model:

The initial steps of finding place invariants for the model shown in Fig. 1 are presented in Table 1; the table shows the vector “w”, the set “u” and the set “r” for consecutive invocations of “Eliminate”).

Table 1 Finding place invariants for the net shown in Fig. 1
Full size table

The complete set of basic place invariants for the net shown in Fig. 1 is:

i

\( place\,invariant \)

\( implied\,transitions \)

1

\( \{ p_{1} ,p_{2} \} \)

\( t_{1} ,t_{2} \)

2

\( \{ p_{3} ,p_{4} \} \)

\( t_{2} ,t_{3} \)

3

\( \{ p_{5} ,p_{6} ,p_{7} ,p_{8} ,p_{9} \} \)

\( t_{1} ,t_{3} ,t_{4} ,t_{5} ,t_{6} \)

4

\( \{ p_{1} ,p_{3} ,p_{5} ,p_{6} \} \)

\( t_{1} ,t_{2} ,t_{3} ,t_{4} \)

5

\( \{ p_{2} ,p_{4} ,p_{7} ,p_{8} ,p_{9} \} \)

\( t_{1} ,t_{2} ,t_{3} ,t_{5} ,t_{6} \)

so the cycle time is:

$$ \tau_{0} = { \hbox{max} }(\tau_{1} ,\tau_{2} ,\tau_{3} ,\tau_{4} ,\tau_{5} ) $$

where:

$$ \begin{aligned} \tau_{1} & = f(t_{1} ) + f(t_{2} ), \\ \tau_{2} & = f(t_{2} ) + f(t_{3} ), \\ \tau_{3} & = f(t_{1} ) + f(t_{3} ) + f(t_{4} ) + f(t_{5} ) + f(t_{6} ), \\ \tau_{4} & = (f(t_{1} ) + f(t_{2} ) + f(t_{3} ) + f(t_{4} ))/2, \\ \tau_{5} & = f(t_{1} ) + f(t_{2} ) + f(t_{3} ) + f(t_{5} ) + f(t_{6} ). \\ \end{aligned} $$

Other performance characteristics can be derived in a similar way [4].

4 Incremental Approach

In many cases, the components of the model are known in advance and can be used for incremental approach to finding place invariants of a net model.

For the example shown in Fig. 2, place invariants of simple subnets are obvious (and even formally can be determined in a single step). Submodels (a) and (c) (i.e., subnets implied by place invariants \( \{ p_{1} ,p_{2} \} \) and \( \{ p_{5} ,p_{6} ,p_{7} ,p_{8} ,p_{9} \} \)) are combined using a single transition (\( t_{1} \)) which does not change the invariants. The combined subnet implied by \( \{ p_{1} ,p_{2} ,p_{5} ,p_{6} ,p_{7} ,p_{8} ,p_{9} \} \) is merged with the remaining subnet by transitions \( t_{2} \) and \( t_{3} \), as shown in Fig. 3. This integration can create new invariants, but all such invariants must contain places connected to \( t_{2} \) and/or \( t_{3} \), so only these places should be checked for new place invariants.

Fig. 3
figure 3

Merging subnets

Full size image

In general, if two subnets are merged by transitions in a set \( \text{T}_{shared} \), new place invariants are found by the same procedure as before but restricted to places in the set Inp(\( \text{T}_{shared} \)) and Out(\( \text{T}_{shared} \)):

Analysis of the case shown in Fig. 3 corresponds to a part of Table 1 that includes places \( p_{1} \) to \( p_{4} \), \( p_{6} \) and \( p_{7} \), which is about one half of the total Table.

It should be observed that the gains of the incremental approach actually increase with the size of the model.

5 Concluding Remarks

Invariant-based performance analysis derives analytical characterization of the model’s performance provided the model is covered by a family of conflict-free subnets. If this is the case, the subnets are implied by place invariants of the net model. Efficient method of finding place invariants uses an incremental approach of merging simple submodels into more complex ones.

It should be noted that the efficiency of the incremental approach depends upon ordering the merged models. For instance, if the first step of merging the submodels shown in Fig. 2 combines submodels (a) and (b) rather than (a) and (c), the potential advantages of the approach will be lost.

The process of finding place invariants can be simplified in several ways, for example, by model reductions. Each simple path in the model can be reduced to a single element because any place invariant must either contain the whole path or none of its elements. Similarly, parallel paths (i.e., simple paths originating and terminating in a single transition) can be merged because if a place invariant contains one of these paths then there must exist another invariant containing the other path—there is no need to repeat the steps of finding these two invariants independently.

A similar considerations in the context of deadlock analysis (and finding siphons in net models) showed that simple net reductions can significantly reduce the required computations [16].