On the Optimal Trade-Off Between Fire Power and Intelligence in a Lanchester Model

Abstract

Combat between governmental forces and insurgents is modelled in an asymmetric Lanchester-type setting. Since the authorities often have little and unreliable information about the insurgents, ‘shots in the dark’ have undesirable side-effects, and the governmental forces have to identify the location and the strength of the insurgents. In a simplified version in which the effort to gather intelligence is the only control variable and its interaction with the insurgents based on information is modelled in a non-linear way, it can be shown that persistent oscillations (stable limit cycles) may be an optimal solution. We also present a more general model in which, additionally, the recruitment of governmental troops as well as the attrition rate of the insurgents caused by the regime’s forces, i.e. the ‘fist’, are considered as control variables.

1 Introduction

In a remarkably early paper Lanchester (1916) describes the course of a battle between two adversaries by two ordinary differential equations. By modelling the attrition of the forces as result of the attacks by their opponent, the author is able to predict the outcome of the combat. There are dozens, maybe even hundreds of papers dealing with variants of Lanchester model and extending it. There is, however, a remarkable fact.

Together with A.K. Erlang’s idea to model telephone engineering problems by queueing methods, Lanchester’s approach may be seen as one of the forerunners of Operations Research. And OR is—at least to a certain extent—the science of optimization. But, strangely enough, virtually all existing Lanchester models neglect optimization aspects.

Lanchester’s model has been modified and extended in various directions. Deitchman (1962) and later Schaffer (1968) study asymmetric combat between a government and a group of insurgents. Since the regime’s forces have only limited situational awareness of their enemies, they ‘shoot in the dark’. But such tactics lead to collateral damage. Innocent civilians are killed and infrastructure is destroyed. Moreover, insurgents may escape unharmed and will continue their terroristic actions.

Collateral damage will trigger support for the insurgency and new potential terrorists will join the insurgents, as modelled, e.g., in Caulkins et al. (2009) and Kress and Szechtmann (2009); see also Caulkins et al. (2008). For a more detailed discussion on such ‘double-edged sword’ effects see also Kaplan et al. (2005), Jacobson and Kaplan (2007), and Washburn and Kress (2009, Sect. 10.4). In a recent paper Kress and MacKay (2014) generalize Deitchman’s guerrilla warfare model to account for trade-off between intelligence and firepower.

To avoid responses with these undesirable side-effects improved intelligence is required. As stressed by Kress and Szechtmann (2009):‘Efficient counter-insurgency operations require good intelligence’. These authors were first to include intelligence in a dynamic combat setting. While their model was descriptive, Kaplan et al. (2010) presented a first attempt to apply optimization methods to intelligence improvement.

The present paper uses dynamic optimization to determine an optimal intelligence gathering rate. Acting as decision maker, the government tries to minimize the damage caused by the insurgents, the cost of gathering intelligence (the ‘eye’) and militarily attacking the insurgents (the ‘fist’) as well as the costs for maintaining its forces, and, possibly, recruitment costs.

The continuous-time version in which we will formulate the model below (see Sect. 2) and the use of optimal control theory allows one to derive interesting insights into the course of the various variables of the model especially concerning the occurrence of persistent oscillations. Using Hopf bifurcation theory we will demonstrate (at least numerically) the existence of stable limit cycles for the variables of the model.

The paper is organized as follows. The model is presented in Sect. 2. In Sect. 3 a simplified model is presented and analysed leading to two results. On one hand it can be shown analytically that interior steady states can only exist iff the marginal effect of casualties on the increase of insurgents is smaller than the average effect; on the other hand the existence of periodic solutions is shown numerically by applying Hopf bifurcation theory. Moreover the qualitative structure of periodic solution paths is discussed. Finally, in Sect. 4 some conclusions are drawn and suggestions for possible extensions are given.

2 The Model

Following the model of Kress and Szechtmann (2009) we describe the interaction between governmental forces and insurgents by a variant of Lanchester’s model by

$$\displaystyle\begin{array}{rcl} \dot{G}(t)& =& -\alpha I(t) +\beta (t) -\delta G(t){}\end{array}$$

(1)

$$\displaystyle\begin{array}{rcl} \dot{I}(t)& =& -\gamma (t)G(t)\left [\mu (\epsilon (t),I(t)) + (1 -\mu (\epsilon (t),I(t)))I(t)\right ] +\theta (C(t)) \\ & =& -\gamma (t)G(t) + C(t) +\theta (C(t)) {}\end{array}$$

(2)

$$\displaystyle\begin{array}{rcl} \mbox{ with }C(t)& =& \gamma (t)G(t)[1 -\mu (\epsilon (t),I(t))](1 - I(t)),{}\end{array}$$

(3)

with given initial values G(0) and I(0). The variable $t \in [0,\infty )$ denotes time,¹ G(t) and I(t) describe the size of governmental forces, and the fraction of insurgents in the population at time t, respectively. Population size is constant over time and normalized to 1 for simplicity. C(t) describes the collateral damages which may result in the increase of insurgents $\theta (C)$. ² It is reasonable to assume that $\theta (C)$ is a positive, strictly monotonically increasing continuous function of collateral damages C.  α and δ are non-negative constants; α is the attrition rate of the government force due to insurgents’ actions, whereas δ is the natural decay rate of soldiers due to natural attrition and defection. The reinforcement rate β(t) as well as the attrition rate γ(t) may be seen either as time dependent decision variables of the government, or as constant fixed parameters in a simplified version of the model.³

Key in the interaction between soldiers and insurgents is the level of intelligence μ(t),(0 ≤ μ(t) ≤ 1). Without knowledge about the location of insurgents (i.e. μ(t) = 0) the government is ’shooting in the dark’, where the probability of reducing insurgents is proportional to the size of the insurgency. On the other hand insurgents can be combated precisely if intelligence is perfect, that is μ(t) = 1. This effect can also be seen by the number of collateral casualties C(t) which is zero under perfect information μ(t) = 1. 

Contrary to the model of Feichtinger et al. (2012) it is assumed that μ(t) cannot be directly chosen by the government, rather it depends on the effort ε(t) ≥ 0 of intelligence gathering (e.g., number of informants) but also on the level of the insurgency, i.e. μ(t) = μ(ε(t), I(t)). We assume that μ(0, I) = 0, the partial derivative with respect to ε being positive, μ _ε  > 0, and that μ _{ε ε}  < 0 which means that μ is concave w.r.t. ε. Additionally a saturation effect in the sense that $\lim _{\epsilon \rightarrow \infty }\mu (\epsilon,I) \leq 1$ should hold. With respect to I the level of intelligence should be hump-shaped. This accounts for the fact that it may be harder to gather information for low fractions of insurgents (as the cooperating population may not be aware of the location of terrorists) as well as for high levels of insurgencies (as nobody would dare to give corresponding information to the government). For the mixed second order partial derivative μ _ε, I we assume that it is positive for small and negative for large values of I. For a possible specification see Eq. (14) below.

In our model the government, as a decision maker, has to decide on the effort ε(t) invested in intelligence as well as on recruitment β(t) and attrition γ(t) to minimize the damage caused by insurgents together with the costs of counter-measures. To keep the analysis simple we assume an additive structure. Therefore we consider the following discounted stream of instantaneous costs over an infinite time horizon

$$\displaystyle{ \int _{0}^{\infty }e^{-\rho t}\left [D(I(t)) + K_{ 0}(G(t)) + K_{1}(\epsilon (t)) + K_{2}(\gamma (t)) + K_{3}(\beta (t))\right ]dt }$$

(4)

as objective value of our intertemporal optimization problem which has to be minimized.

The first term D(I) describes the (monetary) value of damages created by the insurgents which is an important but also problematic issue. Insurgencies always lead to human casualities, and it is almost cynical to measure these losses in monetary terms. Nevertheless, efforts have been made to determine the economic value of a human life (see, e.g., Viscusi and Aldy 2003). Additionally there are also financial damages, such as destroyed infrastructure, which can be evaluated straightforwardly. It is assumed that D(0) = 0 and that damages are an increasing and convex function depending on the size of the insurgency.

The second term K ₀(G) captures the costs of keeping an army of size G. The remaining terms K _i denote the costs of the control variables ε, γ, β, respectively. These cost functions K _j , j = 0, ⋯ , 3 are assumed to be increasing and convex. The positive time preference rate (discount rate) of the government is denoted as ρ. 

Summarizing the control problem and modelling it as an maximization problem leads to

$$\displaystyle{ \max _{\epsilon,\gamma,\beta }\int _{0}^{\infty }e^{-\rho t}\left [-D(I) - K_{ 0}(G) - K_{1}(\epsilon ) - K_{2}(\gamma ) - K_{3}(\beta )\right ]dt }$$

(5)

subject to

$$\displaystyle\begin{array}{rcl} \dot{G}& =& -\alpha I +\beta -\delta G{}\end{array}$$

(6)

$$\displaystyle\begin{array}{rcl} \dot{I}& =& -\gamma G + C +\theta (C){}\end{array}$$

(7)

$$\displaystyle\begin{array}{rcl} \mbox{ where }C& =& \gamma G[1 -\mu (\epsilon,I)](1 - I){}\end{array}$$

(8)

with given initial conditions G(0) and I(0) under the constraints

$$\displaystyle{ 0 \leq \epsilon,\quad 0 \leq \gamma,\quad 0 \leq G,\quad 0 \leq I \leq 1. }$$

(9)

Note that our model does not address any operational requirements and it stipulates that the decision variables are optimized via a cost function. In a more realistic context of the problem a government might have the objective that the number of attacks by insurgents or the fraction of insurgents within the population must never exceed a certain threshold. Also, it might be a requirement that the size of the governmental troops never falls below a certain threshold as this might be seen as a sign of weakness to third parties trying to exploit the conflict. By reinforcement of the troops, one can keep the size of the governmental troops above a threshold. Additionally, more intense attacks by the government’s forces mean a stronger decline of the insurgents leading to less attacks. In order to keep the fraction of the insurgents below a certain threshold, one can attack the insurgents more intensely and put more efforts into intelligence to make counter-insurgency operations more effective. However, a higher recruitment of the government leads to higher capabilities related to counter-insurgency actions. A future task is to investigate how the introduction of such political objectives affects the optimal application of the available control instruments. One could compare the costs of a strict enforcement of such objectives opposed to a policy where the decision maker does not care about the size of the two groups on the short run as long as the long run outcome is favorable. The inclusion of such state constraints will most likely lead to the occurrence of additional steady states, history-dependence and areas in the state space where no solution is feasible.

3 Simplified Model

To show that periodic solutions may be optimal we consider a simplified version of the above model. As the main goal of our analysis is to study the effect of intelligence, the effort ε in increasing this level of intelligence is the only control variable. Recruitment β as well as the strength of fighting insurgents γ are assumed to be constants and do not enter the objective functional. Moreover δ = 0 is chosen and the damage and cost functions are linear; i.e. we assume $D(I) = fI,K_{0}(G) = gG,K_{1}(\epsilon ) =\epsilon$ with positive parameters f, g. 

Therefore this simplified version can be written as

$$\displaystyle{ \max _{\epsilon }\int _{0}^{\infty }e^{-\rho t}\left [-fI - gG-\epsilon )\right ]dt }$$

(10)

subject to the system dynamics

$$\displaystyle\begin{array}{rcl} \dot{G}& =& -\alpha I+\beta {}\end{array}$$

(11)

$$\displaystyle\begin{array}{rcl} \dot{I}& =& -\gamma G + C +\theta (C){}\end{array}$$

(12)

$$\displaystyle\begin{array}{rcl} \mbox{ with }C& =& \gamma G[1 -\mu (\epsilon,I)](1 - I){}\end{array}$$

(13)

where initial values G(0) and I(0) are given.

For simplicity the dependence of the level of intelligence on the effort and on the size of the insurgency is modelled as

$$\displaystyle{ \mu (\epsilon,I) = A\left (1 - \frac{1} {1+\epsilon }\right )I(1 - I), }$$

(14)

a function which shows all features like saturation effect w.r.t. ε and unimodality w.r.t. I required in the general model setup. With this specification the intelligence measures act most efficiently in case that the level of insurgency is about 50 %. Note that by introducing a further parameter this hump of I(1 − I) at I = 0. 5 could be shifted to any arbitrary value within the interval [0, 1]. 

Additionally the constraints

$$\displaystyle{ 0 \leq \epsilon,\quad 0 <A \leq 4,\quad 0 \leq G,\quad 0 \leq I \leq 1 }$$

(15)

have to hold.⁴

3.1 Analysis

We analyse the above optimal control problem by applying Pontryagin’s maximum principle and derive the canonical system of differential equations in the usual way. Note that in our analysis we could not verify any sufficiency conditions and therefore the canonical system only leads to extremals which are only candidates for optimal solutions. First the current value Hamiltonian is built and given by

$$\displaystyle\begin{array}{rcl} H =\lambda _{0}\left [-fI - gG-\epsilon \right ] +\lambda _{1}\{ -\alpha I +\beta \} +\lambda _{2}\{ -\gamma G + C(G,I,\epsilon ) +\theta (C(G,I,\epsilon ))\}\quad & &{}\end{array}$$

(16)

where $\lambda _{1}$ and $\lambda _{2}$ are the time dependent adjoint variables and $\lambda _{0}$ a non-negative constant.⁵

As the optimal control ε has to maximize the Hamiltonian, the first order condition leads to

$$\displaystyle{ \frac{\partial H} {\partial \epsilon } = -\lambda _{0} +\lambda _{2}[1 +\theta ^{{\prime}}(C)]\frac{\partial C} {\partial \epsilon } = 0 }$$

(17)

Remarks

• 1. It is difficult to exclude the anormal case $\lambda _{0} = 0$ in a formal way. Nevertheless it can be easily seen from the Hamiltonian given by (16) that in this case the optimal control ε would either be 0 or unbounded in case that 0 < I < 1 (depending on the sign of the adjoint variable $\lambda _{2}$), and undeterminate otherwise. As these cases are unrealistic we restrict our further analysis to the normal case $\lambda _{0} = 1.$

• 2. To determine the sign of the adjoint variable $\lambda _{2}$ notice that for positive values of $\lambda _{2}$ the Hamiltonian is strictly monotonically decreasing for increasing ε, such that the constraint ε ≥ 0 would become active leading to the boundary solution ε = 0 as value of the optimal effort.

  The adjoint variable $\lambda _{2}$ can be interpreted as shadow price of the state variable I(t) and by economic reasoning we assume that this has to be negative for the cases we are considering in the following.

• 3. As $\lim _{\epsilon \rightarrow \infty }H = -\infty$ there exists an interior maximizer ε of the Hamiltonian if

  $$\displaystyle{ \left.\frac{\partial H} {\partial \epsilon } \right \vert _{\epsilon =0}> 0. }$$

  (18)

  This condition holds for sufficiently small values of $\lambda _{2}$, i.e. iff

  $$\displaystyle{ \lambda _{2} <\frac{-1} {\gamma GAI(1 - I)^{2}[1 +\theta ^{{\prime}}(C)]}. }$$

  (19)

• 4. Under the additional assumption that the effect of collateral damages on the increase of the insurgency is marginally increasing i.e. $\theta (C)$ being convex, the Hamiltonian is concave w.r.t. ε and the first order condition (17) leads to a unique interior solution iff (19) holds. A sigmoid (convex/concave) relationship may be more plausible to describe the effect of collateral damages, but then the Hamiltonian is not concave any more leading to problems when solving for the optimal control variable.

The adjoint variables satisfy the adjoint differential equations

$$\displaystyle\begin{array}{rcl} \dot{\lambda }_{1} =\rho \lambda _{1} -\frac{\partial H} {\partial G} =\rho \lambda _{1} + g\lambda _{0} +\lambda _{2}\left \{\gamma -[1 +\theta ^{{\prime}}(C)]\frac{\partial C} {\partial G}\right \}& &{}\end{array}$$

(20)

$$\displaystyle\begin{array}{rcl} \dot{\lambda }_{2} =\rho \lambda _{2} -\frac{\partial H} {\partial I} =\lambda _{2}\left \{\rho -[1 +\theta ^{{\prime}}(C)]\frac{\partial C} {\partial I} \right \} +\alpha \lambda _{1} + f\lambda _{0}& &{}\end{array}$$

(21)

and the transversality conditions

$$\displaystyle{ \lim _{t\rightarrow \infty }e^{-\rho t}\lambda _{ 1} =\lim _{t\rightarrow \infty }e^{-\rho t}\lambda _{ 2} = 0. }$$

(22)

In analysing dynamical systems the existence of steady states and its stability is of major concern. In the following proposition a necessary condition for the existence of interior steady states is derived.

Proposition

Under the assumption that keeping an army of size G leads to costs gG (i.e. g > 0) and that the shadow price $\lambda _{1}$ of the army is positive, an interior steady state of the optimization model can exist only if the marginal effect of casualties on the increase of insurgents is smaller than the average effect, i.e. only if

$$\displaystyle{ \theta ^{{\prime}}(C) <\frac{\theta (C)} {C} }$$

(23)

at the steady state level. ⁶

Proof

The steady states of the canonical system are solutions of $\dot{G} =\dot{ I} =\dot{\lambda } _{1} =\dot{\lambda } _{2} = 0,$ where the optimal control is implicitly given by (17).

At an interior steady state $\dot{I} = 0$ implies

$$\displaystyle{ \dot{I} = G\left [-\gamma + \frac{C} {G} + \frac{\theta (C)} {G} \right ] = 0 \Rightarrow \gamma -\frac{C} {G} = \frac{\theta (C)} {G} }$$

(24)

As

$$\displaystyle{ \frac{\partial C} {\partial G} = \frac{C} {G} }$$

(25)

$\dot{\lambda }_{1} = 0$ leads to

$$\displaystyle{ \lambda _{1}\rho + g = -\lambda _{2}\left \{\gamma -[1 +\theta ^{{\prime}}(C)]\frac{C} {G}\right \} }$$

(26)

Note that the LHS of (26) is positive, therefore

$$\displaystyle{ \left \{\gamma -\frac{C} {G} -\theta ^{{\prime}}(C)\frac{C} {G}\right \} }$$

(27)

has to be positive. (27) together with (24) leads to

$$\displaystyle{ \frac{\theta (C)} {G} -\theta ^{{\prime}}(C)\frac{C} {G}> 0\quad \mbox{ or equivalently }\frac{\theta (C)} {C}>\theta ^{{\prime}}(C). }$$

(28)

Remarks

• 1. Assuming a power function $\theta (C) = C^{\alpha }$ condition (23) holds iff α < 1, i.e. if the effect of collateral casualties on the inflow of insurgents is marginally decreasing.

  For a linear function $\theta (C) =\theta _{0} +\theta _{1}C$ condition (23) holds iff the intercept $\theta _{0}$ is strictly positive.

• 2. In Feichtinger et al. (2012) $\theta (C) =\theta C^{2}$ is assumed. In their model interior steady states only exist if the utility of keeping an army of size G is larger than the corresponding costs, i.e. if G enters the objective functional positively. Obviously an army of size G may also lead to some benefits as it can be seen as status symbol or it leads also to some level of deterrence. That these utilities, however, compared to keeping costs result in a net benefit seems to be rather unrealistic.

• 3. Note that condition (23) is also required for the existence of interior steady states in the more general model (5)–(9).

In the following we specify the function $\theta (C)$ as linear, i.e. as $\theta (C) =\theta _{0} + (\theta _{1} - 1)C$, with $\theta _{0}> 0,\theta _{1}> 1.$ The first order optimality condition (17) then reduces to

$$\displaystyle{ \frac{\partial H} {\partial \epsilon } = -1 +\lambda _{2}\theta _{1}\frac{\partial C} {\partial \epsilon } = -1 -\frac{A\lambda _{2}\theta _{1}\gamma GI(1 - I)^{2}} {(1+\epsilon )^{2}} = 0 }$$

(29)

which leads to the optimal level of effort

$$\displaystyle{ \epsilon = \sqrt{-A\lambda _{2 } \theta _{1 } \gamma GI(1 - I)^{2}} - 1 }$$

(30)

As the partial derivative of casualities w.r.t. I is given by

$$\displaystyle{ \frac{\partial C} {\partial I} =\gamma G\left (-\frac{\partial \mu } {\partial I}(1 - I) - 1+\mu \right ) =\gamma G\left (\mathop{\underbrace{A \frac{\epsilon }{1+\epsilon }(1 - I)}}\limits _{= \frac{\mu }{ I} }(3I - 1) - 1\right ) }$$

(31)

we have to analyse the canonical system

$$\displaystyle\begin{array}{rcl} \dot{G}& =& -\alpha I +\beta {}\end{array}$$

(32)

$$\displaystyle\begin{array}{rcl} \dot{I}& =& -\gamma G +\theta _{0} +\theta _{1}\gamma G(1-\mu )(1 - I){}\end{array}$$

(33)

$$\displaystyle\begin{array}{rcl} \dot{\lambda }_{1}& =& \rho \lambda _{1} + g +\lambda _{2}\gamma \left [1 -\theta _{1}(1-\mu )(1 - I)\right ]{}\end{array}$$

(34)

$$\displaystyle\begin{array}{rcl} \dot{\lambda }_{2}& =& \alpha \lambda _{1} + f +\lambda _{2}\left [\rho -\theta _{1}\gamma G\left (\mu \left (3 -\frac{1} {I}\right ) - 1\right )\right ]{}\end{array}$$

(35)

$$\displaystyle\begin{array}{rcl} \mu & =& AI(1 - I) -\sqrt{- \frac{AI} {\lambda _{2}\theta _{1}\gamma G}}{}\end{array}$$

(36)

Solutions of the differential equation system (32)–(35) with the level of intelligence μ given by (36) together with initial values G(0) and I(0) where also the transversality conditions hold are extremals and strictly speaking only candidates for an optimal solution as we could not verify any sufficiency conditions so far.

In the following we show that periodic paths may exist as solutions of the dynamical system (32)–(36) by applying the Hopf bifurcation theorem (see, e.g., Guckenheimer and Holmes 1983, for details). This theorem considers the stability properties of a family of smooth, nonlinear dynamic systems for variation of a bifurcation parameter. More precisely, this theorem states that periodic solutions exist if (i) two purely imaginary eigenvalues of the Jacobian matrix exist for a critical value of the bifurcation parameter, such that (ii) the imaginary axis is crossed at nonzero velocity. Note that stable or unstable periodic solutions may occur and to determine its stability further computations, either analytically or numerically are necessary.

Unfortunately, for the canonical system (32)–(35) it is not even possible to find steady state solutions explicitly and therefore we have to base our results on simulations given in the following numerical example.

3.2 Numerical Example

We choose the discount rate ρ as bifurcation parameter. Values for the other parameters are specified as follows:⁷

$$\displaystyle\begin{array}{rcl} \alpha = 0.77,\beta = 0.58,\gamma = 0.26,f\,=\,2.00,g\,=\,0.68,\theta _{0} = 2.83,\theta _{1} = 1.60,A = 3.24& &{}\end{array}$$

(37)

The Jacobian possesses a pair of purely imaginary eigenvalues for the critical discount rate ρ _crit  = 0. 14305948 at the steady state

$$\displaystyle{ G^{\infty } = 13.5712,I^{\infty } = 0.7532,\lambda _{ 1}^{\infty } = 53.9293,\lambda _{ 2}^{\infty } = -40.2585. }$$

(38)

The optimal effort to be invested into intelligence at the steady state level amounts to $\epsilon ^{\infty } = 4.8115$ leading to the level of intelligence $\mu ^{\infty } = 0.4986.$

According to the computer code BIFDD (see Hassard et al. 1981) stable limit cycles occur for discount rates less than ρ _crit . 

Fig. 1

Time path of control variable ε and the states together with the level of intelligence μ along one period of the cycle

To present a cycle and discuss its properties we used the boundary value problem solver COLSYS to find a periodic solution of the canonical system for ρ = 0. 127 by applying a collocation method.

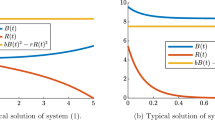
For ρ = 0. 127 the steady state is shifted to $G^{\infty } = 13.655,I^{\infty } = 0.7532,\lambda _{1} = 46.6175,\lambda _{2} = -31.8485$, with an optimal effort of $\epsilon ^{\infty } = 4.1850$ leading to a level of intelligence $\mu ^{\infty } = 0.4861.$ This steady state is marked as a cross in Figs. 2–5. Additionally solutions spiraling towards the persistent oscillation are depicted in these figures.

In Fig. 1 the time path of the control ε as well as the resulting level of intelligence μ together with the two state variables G and I along one period of the cycle can be seen. The length of the period is 19.7762 time units.

Fig. 2

Persistent oscillation in the G∕I-diagram

As can be seen from Figs. 2, 3, 4, and 5 we can distinguish four different regimes along one cyclical solution. In the first phase which could be called ‘increasing terror phase’ both the strength of governmental troops G(t) as well as the size of the insurgency I(t) increase.

In the following phase, called ‘dominant terror phase’ the insurgency increases, but the government reduces its counter-terror measures as this will also reduce the negative impact due to collateral damages.

As the negative effect of collateral damages is reduced also the number of insurgents decreases in the ‘recovery phase’ where G(t) and I(t) both shrink.

Fig. 3

Persistent oscillation in the ε∕μ-diagram

Fig. 4

Persistent oscillation in the I∕ε-diagram

In the last phase the government can be seen as being dominant as G(t) starts to increase again due to the low size of the insurgency, which is still decreasing. Due to an increasing effect of collateral damages the insurgency will start to become larger at the end and the cycle is closed.

Obviously the size of governmental troops G(t) is the leading variable whereas I(t) lags behind. This is caused by the effect of collateral damages and the induced inflow of insurgents.

Having a closer look at the effect of the effort on gathering information on the level of intelligence it turns out that along a fraction of 57. 5 % of the cycle an increasing effort leads to a higher intelligence level, and in 30. 0 % both the effort as well as intelligence are decreasing. Nevertheless there exist rather short phases along the cycle with opposing trends. The level of intelligence is increasing despite a falling effort along 10. 5 % of the periodic solution due to the decreasing size of the insurgency, since then the effort becomes more effective. On the contrary along 2 % even an increasing effort in gathering information does not lead to a higher level of intelligence since, due to an increasing insurgency, it becomes harder to obtain reliable information.

Fig. 5

Persistent oscillation in the I∕μ-diagram

4 Conclusions and Extensions

Surprisingly, Lanchester’s pivotal attrition paradigm has never enriched the optimization scenario.⁸ In the present paper we use optimal control theory to study how a government should apply intelligence efficiently to fight an insurgency. Due to the formal structure of the model, i.e. the multiplicative interaction of the two states with the control variable, complex solutions might be expected. As a first result in that direction a Hopf bifurcation analysis is carried out establishing the possibility of persistent stable oscillations.⁹

Since our analysis can be seen only as a first step, several substantial extensions are possible. The first is to include the ’fist’, i.e. the attrition rate of the insurgents caused by the regime’s forces, in addition to the ‘eye’, i.e. the intelligence level of the government. In particular, we intend to study the optimal mix of these two policy variables. A main question which arises in that context is whether these instruments might behave complementarily or substitutively.¹⁰

Among the further extensions we mention a differential game approach with the government and the insurgents as the two players. Moreover, it would be interesting to study the case where the regime has to fight against two (or more) opponents (insurgents). Additionally following the ideas by Udwadia et al. (2006) the combination of both direct military intervention to reduce the terrorist population and non-violent persuasive intervention to influence susceptibles to become pacifists could be analyzed under aspects of optimization.

Finally we should stress the fact that the model we discussed is not validated by empirical data. Even if this would be the case, the proposed model seems much to simple to deliver policy recommendations for concrete insurgencies.