A Simplified Form of Fuzzy Multiset Finite Automata

Abstract

Fuzzy multiset finite automata represent fuzzy version of finite automata working over multisets. Description of these automata can be simplified to such a form where transition relation is bivalent and only the final states form a fuzzy set. In this paper it is proved that the simplified form preserves computational power of the automata and way of how to perform the corresponding transformation is described.

1 Introduction

Fuzzy multiset finite automata were introduced by Wang et al. in [16]. They represent fuzzy version of finite automata working over multisets (also called bags) which generalize sets in the respect that allow multiplied occurrence of its elements. Whilst finite automata work over strings (i.e. order of the input symbols is strictly determined), work of multiset finite automata over multisets means that at any moment of their computation, any remaining symbol of the input multiset can be processed (see e.g. [4, 9]).

Further contribution to fuzzy multiset finite automata was made in [13] by introducing determinism and by formulating pumping lemmata for languages accepted by both deterministic and non-deterministic fuzzy multiset finite automata. Further explorations of these automata can be easier if we simplify their description. This paper is devoted to the task.

Let us start with some notes concerning fuzzy finite automata whose theory is well elaborated and which can inspire us a lot. Traditionally, the automata are defined with fuzzy set of initial states, fuzzy transition relation, and fuzzy set of final states (cf. e.g. [5, 14]). Substitution of the fuzzy set of initial states by crisp one-element set (i.e. only one initial state is considered with truth value 1) is easy to perform and widely used. Further simplification consisting in change of fuzzy transition relation to crisp one was described under some restricting condition by Bělohlávek in [1] and used in many papers dealing for example with determinization process or minimization of the automata (cf. [12] or [8]).

Contrary to fuzzy finite automata, deterministic and non-deterministic fuzzy multiset finite automata have different computational power (see [13]), therefore Bělohlávek’s approach cannot be used to determinization in the multiset case. Nevertheless, resulting automata with bivalent transition relation will undoubtedly lead due to their simpler form to easier elaboration of fuzzy multiset finite automata theory.

The presented paper is organized as follows. Section 2.1 presents basic notions of multisets and multiset finite automata. Section 2.2 is devoted to fuzzy multiset finite automata. In Sect. 3, simplified fuzzy multiset finite automata are defined and their computational power is proved to be equal to the computational power of standard fuzzy multiset finite automata. Some possibilities of future research are mentioned in Sect. 4.

2 Preliminaries

In the paper we use notation and basic notions from [13].

2.1 Multiset Finite Automata

We assume certain familiarity of the reader with basic notions from formal languages and automata theory (cf. [7, 15]). Therefore, we skip the classical notion of finite state automaton and start with multisets and multiset finite automaton.

We denote by $\mathbf{N}$ the set of all natural numbers including 0. If $\varSigma$ is a finite nonempty set of symbols we call it an alphabet. Cardinality of any alphabet $\varSigma$ is denoted by card $(\varSigma )$.

For any alphabet $\varSigma$, a mapping $\,\sigma : \varSigma \rightarrow \mathbf{N}\,$ is called a finite multiset. Obviously, each usual set $\,U \subseteq \varSigma \,$ is a multiset $\sigma _U$ such that $\sigma _U(x) = 1\,$ iff $\,x \in U$. We use denotation of [10, 11, 13]. So, we denote the set of all multisets over $\varSigma$ by $\varSigma ^{\oplus }$. $\varSigma ^{\oplus }$ is a commutative monoid with operation of addition $\oplus$ and neutral element $\mathbf{0}_{\varSigma }$, defined as follows:

• $(\alpha \oplus \beta )(x) = \alpha (x) + \beta (x)\,$ for all $\, x \in \varSigma$,

• $\mathbf{0}_{\varSigma }(x) = 0\,$ for all $\, x \in \varSigma$.

Further, for any multisets $\,\alpha , \beta \in \varSigma ^{\oplus }$, we define the difference $\alpha \ominus \beta$ and the inclusion $\alpha \sqsubseteq \beta$ by

• $(\alpha \ominus \beta )(x) = \max \{0, \alpha (x) - \beta (x)\}\,$ for all $\, x \in \varSigma$,

• $\alpha \sqsubseteq \beta \,$ iff $\,\alpha (x) \le \beta (x)\,$ for all $\, x \in \varSigma$.

We use the notation $\langle y \rangle$ for singleton multisets, i.e. $\langle y \rangle (x) = 0$ for $x \not = y\,$ and $\,\langle y \rangle (y) = 1$. If $a_i = a \in \varSigma \,$ for $\,i \in \{1,\ldots ,m\}$, we write $\,\langle a \rangle ^m\,$ instead of $\,\langle a_1 \rangle \oplus \ldots \oplus \langle a_m \rangle$. For a multiset $\alpha$, we denote the number of occurrences of a symbol $a \in \varSigma$ in $\alpha$ by $|\alpha |_a$. By cardinality of a multiset $\alpha$ we understand card $(\alpha ) = \sum _{a \in \varSigma }|\alpha |_a$.

The interested reader can find more about multiset theory for example in [2, 3].

Definition 1

A shape multiset finite automaton is an ordered quintuple

$A = (Q, \varSigma , \delta , q_0, F)$ where Q is a nonempty finite set of states, $\varSigma$ is the input alphabet, $q_0$ is the initial state, $F \subseteq Q$ is the set of final states, and $\delta$ is the transition relation $\delta \subseteq Q \times \varSigma \times Q$.

We extend the relation $\delta$ to relation $\delta ^* \subseteq Q \times \varSigma ^{\oplus }\times Q$ in the recursive way:

• 1. $(q, \mathbf{0}_{\varSigma }, r) \in \delta ^*$ iff $r = q$,

• 2. $(q, \alpha , s) \in \delta ^*$ if there are $r \in Q,\ a \in \varSigma$ such that $\langle a \rangle \sqsubseteq \alpha , (q, a, r) \in \delta$ and $(r, \alpha \ominus \langle a \rangle , s) \in \delta ^*$.

The shape multiset language L(A) accepted by the multiset finite automaton A is defined by

$L(A) = \{\alpha \in \varSigma ^{\oplus }|\, (q_0, \alpha , q) \in \delta ^* \text { for some }q \in F\}$.

Otherwise stated, the multiset language L(A) consists of all multisets $\alpha$ such that the automaton A starting its computation in $q_0$ with $\alpha$ on its ‘input’ finishes its work in a final state with $\mathbf{0}_{\varSigma }$ on its ‘input’. Realize that computation of the automaton A does not depend on some strict order of symbols in the ‘input multiset’.

Note that in [10], the transition relation of a multiset finite automaton is not confined only to single symbols of $\varSigma$ but is defined on the same basis as our relation $\delta ^*$ (i.e. instead of symbols of $\varSigma$ it uses multisets over $\varSigma$) which is accompanied by demand of finiteness of such transition relation. However in the same paper, the statement about irrelevance of these differences is made. Namely, there is mentioned mutual transformation between automata of these two definitions without change of the accepted multiset language.

2.2 Fuzzy Multiset Finite Automata

In this paper we consider fuzzy sets with truth values in the unit interval [0, 1], i.e. a fuzzy set in a universe set X is any mapping $A: X \rightarrow [0, 1]$, A(x) being interpreted as the truth degree of the fact that “x belongs to A” and being called membership value. A fuzzy relation R between sets X and Y is defined as a mapping $R: X \times Y \rightarrow [0, 1]$. Analogously, a fuzzy ternary relation $\widetilde{R}$ is defined as a mapping $\widetilde{R}: X \times Y \times Z \rightarrow [0, 1]$. For any fuzzy set A, the set $\text {supp}(A) = \{a \in X|\, A(a)>0\}$ is called support of A.

Definition 2

A fuzzy multiset finite automaton (FMFA) is an ordered quintuple $\,A = (Q, \varSigma , \delta , q_0, F)$ where Q is a nonempty finite set of states, $\varSigma$ is the input alphabet, $q_0$ is the initial state, $F: Q \rightarrow [0, 1]$ is a fuzzy set in Q, and $\delta : Q \times \varSigma \times Q \rightarrow [0, 1]$ is the fuzzy transition relation.

A state $q \in Q$ is called a final state of A if $F(q) > 0$. We extend the fuzzy relation $\delta$ to fuzzy relation $\delta ^*: Q \times \varSigma ^{\oplus }\times Q \rightarrow [0, 1]$ in the following way.

• $\delta ^*(q, \mathbf{0}_{\varSigma }, r) = 0$ for $r \not = q$ and $\delta ^*(q, \mathbf{0}_{\varSigma }, q) = 1$,

• $\delta ^*(q, \alpha , s) = \max \limits _{{ \begin{array}[t]{c}r\! \in \! Q\\[1pt]a\! \in \! \varSigma ,\, \langle a \rangle {{ \sqsubseteq }} \alpha \end{array}} } \{\delta (q, a, r) \wedge \delta ^*(r, \alpha \ominus \langle a \rangle , s)\}$

                     for all $\,\alpha$ of positive cardinality.

The fuzzy multiset language L(A) accepted by the FMFA A is defined by

• $L(A)(\alpha ) = \max \limits _{q \in Q}\left\{ \delta ^*(q_0, \alpha , q)\wedge F(q)\right\}$ for all $\alpha \in \varSigma ^{\oplus }$

and is called a FMFA-language.

Analogously to the note following Definition 1 we should mention that the definition of a fuzzy multiset finite automaton in [16] differs from our definition (taken from [13]) in two respects. First, it uses fuzzy set of initial states. Second, it defines fuzzy transition relation on multisets¹ over $\varSigma$ (and not on symbols of $\varSigma$). Neither of these differences is fundamental. Both of them are removable with help of Theorems 4.1 and 4.2 from [16].

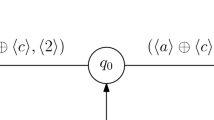
Example 1

Consider FMFA $\,A = (Q, \varSigma , \delta , q_0, F)\,$ where

$Q = \{q_0, q_1, q_2\}$,

$\varSigma = \{a,b\}$,

$\delta (q_0,a,q_1) = 0.8$,

$\delta (q_1,a,q_2) = \delta (q_1,b,q_0) = 0.5$,

$\delta (q_2,b,q_1) = 0.4$,

$\delta (q_i,x,q_j) = 0$ otherwise,

$F(q_0) = 0$, $F(q_1) = 1$, $F(q_2) = 0.3$.

We can illustrate the automaton lucidly with help of Fig. 1 where we utilize graphical representation which is used for fuzzy finite automata (cf. e.g. [6]). In the labelled directed graph, its nodes represent states of the automaton, the initial state is indicated by the arrow pointing at it from nowhere, each final state q is depicted by double circle including the value of F(q) (if the value is missing, the default value 1 is assumed), and each arc in the graph coincides with a non-null transition (if the arc goes from state q to state r and $\delta (q,a,r)=\mu$ then the arc is labelled by $a/\mu$).

Fig. 1

Graphical representation of fuzzy finite automata

Consequently, for example

$\delta ^*(q_1, \langle a \rangle \oplus \langle b \rangle , q_1) \begin{array}[t]{l} = \max \{\delta (q_1, a, q_2) \wedge \delta (q_2, b, q_1), \delta (q_1, b, q_0) \wedge \delta (q_0, a, q_1)\}\, {=}\\[1pt] = \max \{0.5 \wedge 0.4, 0.5 \wedge 0.8\} = 0.5 \end{array}$

Obviously

$\delta ^*(q_0, \langle a \rangle ^3 \oplus \langle b \rangle , q_0) = 0$,

$\delta ^*(q_0, \langle a \rangle ^3 \oplus \langle b \rangle , q_1) = 0$,

$\delta ^*(q_0, \langle a \rangle ^3 \oplus \langle b \rangle , q_2) = 0.5$,

and

$L(A)(\langle a \rangle ^3 \oplus \langle b \rangle ) = \max \left\{ \delta ^*(q_0, \langle a \rangle ^3 \oplus \langle b \rangle , q_2)\wedge F(q_2)\right\} = 0.5 \wedge 0.3 = 0.3$.

It is easy to see that

$L(A)(\alpha ) = \left\{ \begin{array}[c]{ll} 0.8 &{} \text{ if } \, \alpha = \langle a \rangle ,\\[3pt] 0.5 &{} \text{ if } \, |\alpha |_a = |\alpha |_b + 1 > 1,\\[3pt] 0.3 &{} \text{ if } \, |\alpha |_a = |\alpha |_b + 2,\\[3pt] 0 &{} \text{ otherwise }. \end{array}\right. \qquad \qquad \begin{array}[c]{l} \\ \square \end{array}$

Note that in [16], it is proven that the family of all FMFA-languages equals the family of all fuzzy multiset regular languages (which are generated by fuzzy multiset regular grammars).

3 A Simplified Form of Fuzzy Multiset Finite Automata

Definition 3

If a FMFA $A = (Q, \varSigma , \delta , q, F)$ satisfies the condition $\delta : Q \times \varSigma \times Q \rightarrow \{0, 1\}$ we will call it a fuzzy multiset finite automaton in simplified form.

Note that FMFA in simplified form uses (non-fuzzy) transition relation and the only ‘fuzzy’ component is represented by fuzzy set of final states.

Analogously to situation concerning fuzzy automata (see [1]), we are going to explore computational power of the ‘simplified FMFA’.

Theorem 1

Each FMFA-language is accepted by a FMFA in simplified form.

Proof

We will prove the theorem on the basis of ideas from [1] where analogous statement concerned fuzzy (non-multiset) finite automata.

Let L(A) be a FMFA-language accepted by the FMFA $\,A = (Q, \varSigma , \delta , q_0, F)$. Since Q and $\varSigma$ are finite we have finite support of both $\delta$ and F. Hence, $I = \{\delta ^*(q, \alpha , s)| \alpha \in \varSigma ^{\oplus }\wedge q, s \in Q\} \cup \{F(q)| q \in Q\}$ is finite. Therefore the set $\widetilde{Q}$ consisting of all fuzzy sets in Q with truth values in I (i.e. $\widetilde{Q}: Q \rightarrow I$) is finite and can represent a new set of states. Now, consider the ‘simplified FMFA’ $\,\widetilde{A} = (\widetilde{Q}, \varSigma , \bar{\delta }, \bar{q_0}, \widetilde{F})$ where

• $\bar{\delta }: \widetilde{Q} \times \varSigma \times \widetilde{Q} \rightarrow \{0, 1\}$ is a transition relation defined for all $\bar{Q}, \bar{R} \in \widetilde{Q}, a \in \varSigma$ by $\bar{\delta }(\bar{Q}, a, \bar{R}) = \left\{ \begin{array}[c]{ll} 1 &{} \text{ if } \, \bar{R}(q) = \max \limits _{s \in Q}\left\{ \bar{Q}(s) \wedge \delta (s,a,q)\right\} \text{ for } \text{ all } \, q \in Q,\\ 0 &{} \text{ otherwise }, \end{array}\right.$

• $\bar{q_0} \in \widetilde{Q}$ is a fuzzy set defined by $\bar{q_0}(q_0) = 1$ and $\bar{q_0}(q) = 0$ for $q \not = q_0$,

• $\widetilde{F}: \widetilde{Q} \rightarrow I$ is a fuzzy set of fuzzy sets defined by $\widetilde{F}(\bar{Q}) = \max \limits _{q \in Q}\left\{ \bar{Q}(q) \wedge F(q)\right\}$ for all $\bar{Q} \in \widetilde{Q}$.

We claim that $L(A) = L(\widetilde{A})$.

• (I) $L(\widetilde{A})(\mathbf{0}_{\varSigma }) \begin{array}[t]{l} = \max \limits _{\bar{Q} \in \widetilde{Q}}\left\{ \bar{\delta ^*}(\bar{q_0}, \mathbf{0}_{\varSigma }, \bar{Q}) \wedge \widetilde{F}(\bar{Q}) \right\} = \widetilde{F}(\bar{q_0}) = \max \limits _{q \in Q}\left\{ \bar{q_0}(q) \wedge F(q)\right\} =\\ = F(q_0) = F(q_0) \wedge \delta ^*(q_0, \mathbf{0}_{\varSigma }, q_0) = \max \limits _{q \in Q}\left\{ \delta ^*(q_0, \mathbf{0}_{\varSigma }, q) \wedge F(q) \right\} =\\ = L(A)(\mathbf{0}_{\varSigma }). \end{array}$

• (II) For the verification of $L(A)(\alpha ) = L(\widetilde{A})(\alpha )$ with $\alpha \not = \mathbf{0}_{\varSigma }$, we will use the following assertion.

  Assertion: Let $\,\bar{S} \in \widetilde{Q},\ \alpha \in \varSigma ^{\oplus }, \text{ card }\, (\alpha ) = n> 0$. If $\,\bar{\delta ^*}(\bar{q_0}, \alpha , \bar{S}) = 1\,$ then there is a sequence $\,\left( a_i\right) _{i=1}^n, \alpha = \langle a_1 \rangle \oplus \ldots \oplus \langle a_n \rangle$ such that for all $\,q \in Q$, $\bar{S}(q) = \max \limits _{r_i \in Q}\left\{ \delta (q_0, a_1, r_1) \wedge \delta (r_1, a_2, r_2) \wedge \ldots \wedge \delta (r_{n-1}, a_n, q)\right\}$.

  Proof of the assertion: We will use an induction on cardinality of the multiset $\alpha$.

  • (1) If card $(\alpha ) = 1$ then $\alpha = \langle a \rangle$ for some $a \in \varSigma$. By definition of $\bar{\delta }$, we have $\bar{\delta }(\bar{q_0}, a, \bar{S}) = 1$ iff $\bar{S}(q) = \delta (q_0, a, q)$ for all $\,q \in Q$. Since $\bar{\delta }(\bar{q_0}, a, \bar{S}) = \bar{\delta ^*}(\bar{q_0}, \alpha , \bar{S})$, the assertion holds true for $n=1$.

  • (2) Let the assertion hold true for any multiset of cardinality from the set $\{1, \ldots , n\}$ where $n \ge 1$. We will verify its validity for an multiset $\alpha$ of cardinality $n + 1$.

    Assume $\alpha \in \varSigma ^{\oplus }$, $\bar{S} \in \widetilde{Q}$ such that card $(\alpha ) = n+1$ and $\bar{\delta ^*}(\bar{q_0}, \alpha , \bar{S}) = 1$.

    Since

    $1 = \bar{\delta ^*}(\bar{q_0}, \alpha , \bar{S}) =\!\!\! \max \limits _{{ \begin{array}[t]{c}\bar{T}\! \in \! \widetilde{Q}\\[1pt]a\! \in \! \varSigma ,\, \langle a \rangle {{ \sqsubseteq }} \alpha \end{array}} }\!\!\!\! \{\bar{\delta ^*}(\bar{q_0}, \alpha \ominus \langle a \rangle , \bar{T}) \wedge \bar{\delta }(\bar{T}, a, \bar{S})\}$,

    there are $\bar{T} \in \widetilde{Q}, a \in \varSigma , \langle a \rangle \sqsubseteq \alpha$ such that

       $\bar{\delta }(\bar{T}, a, \bar{S}) = 1\,$ and $\,\bar{\delta ^*}(\bar{q_0}, \alpha \ominus \langle a \rangle , \bar{T}) = 1$.

    The first equality implies by definition of $\bar{\delta }$ that

    $\bar{S}(q) = \max \limits _{s \in Q} \{\bar{T}(s) \wedge \delta (s, a, q)\}\ \forall q \in Q$

    and the second equality implies by inductive hypothesis that

    $\exists \left( a_i\right) _{i=1}^n, \alpha \ominus \langle a \rangle = \langle a_1 \rangle \oplus \ldots \oplus \langle a_n \rangle ,\ \forall q \in Q:$

    $\bar{T}(q) = \max \limits _{r_i \in Q}\left\{ \delta (q_0, a_1, r_1) \wedge \ldots \wedge \delta (r_{n-1}, a_n, q)\right\}$.

    If we denote $a_{n+1} = a$ then we obtain that

    $\exists \left( a_i\right) _{i=1}^{n+1}, \alpha = \langle a_1 \rangle \oplus \ldots \oplus \langle a_{n+1} \rangle ,\ \forall q \in Q:$

    $\bar{S}(q) = \max \limits _{s \in Q} \{\max \limits _{r_i \in Q}\left\{ \delta (q_0, a_1, r_1) \wedge \ldots \wedge \delta (r_{n-1}, a_n, s)\right\} \wedge \delta (s, a_{n+1}, q)\} =$

    $= \max \limits _{s \in Q} \{\max \limits _{r_i \in Q}\left\{ \delta (q_0, a_1, r_1) \wedge \ldots \wedge \delta (r_{n-1}, a_n, s) \wedge \delta (s, a_{n+1}, q)\}\right\}$.

    If we denote $r_n = s$ then we get

    $\bar{S}(q) = \max \limits _{r_i \in Q}\left\{ \delta (q_0, a_1, r_1) \wedge \ldots \wedge \delta (r_{n-1}, a_n, r_n) \wedge \delta (r_n, a_{n+1}, q)\right\}$

    and the assertion is proved.

  Now we prove $L(\widetilde{A}) \subseteq L(A)$:

  Consider an arbitrary $\alpha \in \varSigma ^{\oplus }, \alpha \not = \mathbf{0}_{\varSigma }$. Then, with help of the previous assertion (used in fourth equality) we get

  $\begin{array}[t]{ll} L(\widetilde{A})(\alpha ) &{} = \max \limits _{\bar{Q} \in \widetilde{Q}}\left\{ \bar{\delta ^*}(\bar{q_0}, \alpha , \bar{Q}) \wedge \widetilde{F}(\bar{Q}) \right\} =\\ &{} = \max \limits _{{ \begin{array}[t]{c}\bar{Q}\! \in \! \widetilde{Q}\\ \bar{\delta ^*}(\bar{q_0}, \alpha , \bar{Q}) = 1\end{array}} } \widetilde{F}(\bar{Q}) =\\ &{} = \max \limits _{{ \begin{array}[t]{c}\bar{Q}\! \in \! \widetilde{Q}\\ \bar{\delta ^*}(\bar{q_0}, \alpha , \bar{Q}) = 1\end{array}} }\left\{ \max \limits _{q \in Q}\left\{ \bar{Q}(q) \wedge F(q)\right\} \right\} =\\ &{} = \max \limits _{\bar{Q} \in \widetilde{Q}}\left\{ \max \limits _{q \in Q}\left\{ \max \limits _{r_i \in Q}\left\{ \delta (q_0, a_1, r_1) \wedge \ldots \wedge \delta (r_{n-1}, a_n, q)\right\} \! \wedge \! F(q)\right\} \!\right\} \le \\ &{} \le \max \limits _{\bar{Q} \in \widetilde{Q}}\left\{ \max \limits _{q \in Q}\left\{ \delta ^*(q_0, \alpha , q) \wedge F(q)\right\} \right\} =\\ &{} = L(A)(\alpha ). \end{array}$

  For the proof of the opposite inclusion (i.e. $L(A) \subseteq L(\widetilde{A})$), we use the following implication (which is easy to verify):

  Let $\alpha \in \varSigma ^{\oplus }$ and let $\bar{S} \in \widetilde{Q}$ be defined by $\bar{S}(q) = \delta ^*(q_0, \alpha , q)$ for all $q \in Q$. Then $\bar{\delta ^*}(\bar{q_0}, \alpha , \bar{S}) = 1$.

  By the definition,

  $L(A)(\alpha ) = \max \limits _{q \in Q}\left\{ \delta ^*(q_0, \alpha , q) \wedge F(q)\right\}$.

  If we denote $\delta ^*(q_0, \alpha , q) = \bar{S}(q)$ then we have

  $\begin{array}[t]{ll} L(A)(\alpha ) &{} = \max \limits _{q \in Q}\left\{ \bar{S}(q) \wedge F(q)\right\} = \widetilde{F}(\bar{S}) = \widetilde{F}(\bar{S}) \wedge 1 =\\ &{} = \widetilde{F}(\bar{S}) \wedge \bar{\delta ^*}(\bar{q_0}, \alpha , \bar{S}) \le \max \limits _{\bar{Q} \in \widetilde{Q}}\left\{ \bar{\delta ^*}(\bar{q_0}, \alpha , \bar{Q}) \wedge \widetilde{F}(\bar{Q})\right\} =\\ &{} = L(\widetilde{A})(\alpha ). \end{array}$

$\square$

The following corollary is obvious.

Corollary 1

The family of FMFA languages is equal to the family of languages accepted by FMFA in simplified form.

4 Conclusion

In this paper, a simpler form of fuzzy multiset finite automata was introduced and computational power of these automata was proved to be equal to the computational power of standard fuzzy multiset finite automata. The proof is constructive and provides an algorithm for transformation of any fuzzy multiset finite automaton to its version in simpler form.

The simpler form can prove its usefulness in further development of fuzzy multiset finite automata theory. As an immediate tasks we can mention solving equivalence and minimization problems.