Keywords

1 Introduction

In the field of operations research, cutting and packing (C&P) problems are typical combinatorial optimization problems encountered in many industrial segments during the production processes. In general, these problems seek to find the best allocation of some small items into some larger ones to optimize a given objective function and satisfy prescribed constraints.

Therefore, the competitiveness of the modern industries, the result of evolution and global economic growth requires that certain part of the investments should be allocated to the studies related to the production process of the products. The client may not penalize for inefficiencies in the use of raw materials, and the market itself is in charge of extinguishing products uncompetitive. Moreover, the efficient utilization of raw material is necessary to obtain a global competitive edge in a business world. Therefore, is important apply methods to try to improve allocation between small items and come to fast layouts in comparison with manual generation.

A specialization of C&P problem is the placement of irregular figures with characteristics similar to regular cut, but dealing with irregular figures, the nesting problems. This issue impacts upon several manufacturing industries, e.g. furniture, garment, metalware, textile and wood. They have been known as NP-hard [14] due to their difficulty where few exact methods have been reported in the literature [2, 22], where it is possible to find promising solutions by applying methodologies addressed in [21] and also in [10].

According to the typology of [23] (Fig. 1), the nesting problem is classified as a two-dimensional irregular open dimension problem, a problem category in which the set of small items has to be accommodated completely by one or more large objects whose extensions-in at least one dimension can be considered as a variable. More specifically, the problem at hand consists of packing a collection of irregular items (or polygons) onto a rectangular object with a constant width and an unlimited length.

Fig. 1
figure 1

The typology presented in [23]

Full size image

The heuristic methods presented in the literature mostly deal with a class of problems in which the objective is to minimize the length of the master surface used in [3]. Such approaches do not always suite problems where limited master surface is used, such as hides or sheet metals. Packing usually suites the division of problems in which stock material comes in rolls. However, for the case when limited length or bounded stocks are used, bin packing will result in degradation in the utilization of material. Instead, the idea of knapsack problem can be put into practice to serve such purpose.

The packing process aims at minimizing the length of the rectangular object such that no overlap between items occurs and each packed item lies entirely onto the rectangular object. Furthermore, three variations appear depending on rotations of items: rotations of any angles are allowed; rotations of finite number of angles are allowed; and no rotation is allowed. This paper conducts a survey about recent approaches to tackle irregular strip packing problems evidencing three master categories: mathematical programming, metaheuristics and mixed approaches.

Problems involving irregular pieces comprise one of the classes of packing problems. Whatever the constraints or secondary objectives, there are some approaches to find suitable layouts. Several of them may be combined and produce different results, making it harder a shaping a pattern of categories. The Fig. 2 presents a classification adopted to describe different papers within literature.

Fig. 2
figure 2

A schema to describe approaches present in literature using different categories

Full size image

2 Mathematical Programming Approaches

These approaches try to find the global optimal solution. There are few studies in this category due the fact of the high complexity inherent of nesting problems. All approaches have computational potentials restricted to a limit of items. Starting a certain quantity of pieces the optimal solution cannot found in a feasible time.

In this context, [8] presents a constraint logic programming (CLP) to the resolution of nesting problems. A CLP implementation is applied for convex and non-convex polygons. The authors used the no-fit polygon concept to tackle the innate geometric constraints of this type of problem and found the optimal solution for data sets with, maximum, six pieces. Furthermore, [13] described a mixed-integer programming (MIP) model based on [9] for the nesting problem and works as a reference to [2] that proposed a partition on extern space of no-fit polygon that represent all possible positions for the placement in slices, to improve the application of branch and bound approach. In [22] the author also proposed a mixed-integer programming (MIP) model, however, decision variables are binaries and are associated with each discrete point (a dot) of the board, a new name of placement area, and with each piece type. The grid resolution, the board size and the number of different piece types compose the computational cost of this approach.

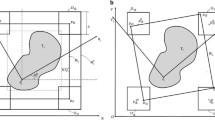
Figure 3 show the form how is represented the elements that compose the model. In Fig. 3a, the board is illustrated with the number of rows and columns, the grid resolution for x and y as well as the possible dots. Geometric features are demonstrated in Fig. 3b, c. In first, Inner-fit polygon (IFP) between a piece type and a rectangular board and to second a set of dots after no-fit polygon generation. Lastly, in Fig. 3d, a feasible solution to a four pieces example.

Fig. 3
figure 3

Representation of Dotted-Board model presented by [22]

Full size image

An advantage of the model is its insensitivity to piece and board geometry, making it easy to extend to more complex problems such as non-convex boards, possibly with defects. In another hand, to tackle real applications, usually, the number of variables that integrate the model is big, making the time of solutions stay slow or infeasible.

3 Heuristics Approaches

A heuristic technique is any approach to solving or improves one methodology that not necessarily, finds optimal solution, but proposes immediate goals. Given the complexity of nesting problems there many approaches that apply a heuristics methods and placement strategies.

Some methods (PARTIAL SOLUTIONS) use the production of layout by analyzing piece to piece. In a reasonable time and computational cost is possible find feasible solution with relative quality. These heuristics have focused on the order that items will be placed, as put the pieces of biggest size first or based on the placement rule chosen, for example, Bottom-Left or using previous criteria of selection for next piece to enter in the stock sheet.

The most used placement rule is Bottom-Left (BL). A popular constructive algorithm to any two-dimensional cutting or packing problem aims to order the pieces and allocate them at feasible positions to a rectangular object, more precisely into its lowest possible location and then closest to its left without overlapping with any placed item, as illustrated by Fig. 4. This process, known as bottom-left heuristic, was first applied to nesting problems by [4], after introduced in [5] for packing an arbitrary collection of rectangular pieces into a rectangular bin so as to minimize the height achieved by any piece. The advantages of this type of approach, as stated by [11], are its speed and simplicity, when compared with more sophisticated methods that may be able to produce solutions of higher quality.

Fig. 4
figure 4

Bottom-left procedure for an input piece. a Regular and b Irregular

Full size image

In the case of two-dimensional cutting, the papers yielded by [7, 15, 16], for instance, considered placement algorithms based on the bottom-left (BL) rule and here the heuristic above was also chosen as placement policy.

The geometric representation of pieces will influence directly on the implementation of the Bottom-left algorithm. Using raster or polygonal representations, the pieces must be moved step by step and for each step, the feasibility is checked. When overlap situation occurs, the previous position is resumed, and a movement towards the bottom is tried. If this bottom movement is feasible, then it proceeds until no movement is allowed in this direction, and returns to the left movement direction. The final piece placement position is found when no more movement to the left or bottom is allowed [6].

A different BL method was proposed by [7]. Aiming fill empty spaces, this technique combines a tabu search and hill-climbing with no-fit polygon to determine feasible positions. The movement of pieces starts in the bottom left side, and the horizontal slide is based on discrete points. Since the vertical movement is realized in a continuous way.

Another issue of placement rule to BL was presented in Oliveira et al. [19] when the authors use a not fixed positions for the pieces on the stock sheet. Thus, the positioning of a new item is not limited horizontally, only vertically. The position of the new item to be inserted on the sheet is determined from the choice of one of three criteria relating to minimizing the growth of the layout length. These are:

  • Minimization of the area of the rectangular enclosure of the newly generated partial solution.

  • Minimization of the length of the rectangular enclosure of the newly generated partial solution.

  • Maximization of the overlap between the rectangular enclosure of the actual partial solution and the rectangular enclosure of the piece to be placed, without allowing overlap between the pieces themselves.

The similar rules to BL heuristic were applied in [6]. The authors used a beam search and a tabu search to try choice the best sequence of position. Each position is represented as a node in a beam search. This search is performed by limiting the number of sheets, each iteration, and a function is defined to evaluate the quality of each node. The value of this feature will guide the expansion of the tree. The complete solutions are represented by us lower height.

Several approaches have focused in the order that the pieces of dataset are placed on the stock sheet. Due the irregular shapes, define the best order to a set of items is not simple. Strategies to solve this problem involves a randomization or a fixed rule, dynamic selection and whether backtracking is permitted.

A random selection is often used to create an initial solution in algorithms that tackle complete solutions. Genetic algorithms are one of the most popular techniques to solve irregular objects packing problems. In general, the chromosome represents an ordered list of pieces to be packed, which is decoded by a fast placement rule [20].

In [11], the author established pre-defined sequences using eight metrics to determine the static order of pieces (Fig. 5). Depending on the criteria, the difficult pieces may be the largest, the longest, the most irregular or simply those that exist in larger quantities.

Fig. 5
figure 5

Eight metrics of [11]

Full size image

Working with dynamic selection is possible manage the next piece to be placed. Through of some criteria, each partial solution is evaluated, and the next piece is picked. Bennell and Song [6, 19] use seven criteria, these are, relative waste, overlap, relative distance, waste minus overlap, relative waste plus relative distance, distance minus overlap, and waste minus overlap plus distance.

Generating a layout piece by piece is the simplest way to find a feasible solution. On the other hand, to try finding better solutions are necessary to apply sophisticated techniques grounded in dynamic sequences.

Another type of approaches to try obtaining good solutions (COMPLETE SOLUTIONS) is implementing local search in complete solutions already found. The layout changes can present an improvement on objective function when executed in a finite number of iterations.

Several papers have been used meta-heuristics and shifts in complete solutions to tackle nesting problems, these we can show [7] Applying Tabu Search, [15] with Simulated Annealing, Genetics Algorithms by [3].

The essential characteristic to define a search strategy outline is the problem representation. These can be modeled as a sequence of pieces led for a placement rule or worked straight in the configuration of layout, realizing changes in the solution pieces.

In [1] the authors characterizing the search in a sequence as a graph problem. The optimal path represents the better order. The BL rule is applied as a position heuristic.

Using a swap neighborhood controlled by a parameter, [19] proposed a probabilistic heuristic called two-exchange. This parameter represents the size of the search in a neighborhood setting the number maximum of changes between pieces in the complete sequence. Furthermore, they used obstruction polygon concept and computational geometry to find the bottom left position even with positions that fill gaps.

In [7] a new constructive heuristic lower left with the capacity to fill gaps in the layout was proposed, which is one of the greatest limitations of the original method. The movement of the items starts in the lower left corner and sliding horizontal is done discreetly, from a grid point, while the movement vertical is continuous. To determine the valid positions, the fit polygon is it used. This technique is combined with the hill-climbing local search and tabu search.

An approach that combines a genetic algorithm and a BL as a constructive heuristics for the position was found in [17]. The codification of chromosome represents a sequence of items. In [3], the authors used the same strategy but a different placement rule.

4 Mixed Approaches

Mathematical programming techniques have been adopted for solving one of the following sub-problems: overlap minimization problem, whose objective is to place all polygons onto a stock sheet with given width and length so that the total amount of overlap between polygons is made as small as possible; compaction problem, which requires a feasible layout and relocates many polygons simultaneously so as to minimize the strip length; and separation problem, which takes an infeasible layout and performs a set of translations of the polygons which eliminates all overlaps and has the minimum total translation.

Another approach [8] proposes a unique approach that overcomes the need for a placement rule by incorporating backtracking mechanisms for each placement point. They work over a discretized stock sheet and use constraint logic programming (CLP) to efficiently try each feasible placement point for each piece given the previously placed pieces. The intrinsic CLP mechanisms to deal with constraints plus specific rules proposed by the authors lead to an algorithm able to solve small problems to optimality efficiently.

In [15], for instance, the authors hybridized simulated annealing and linear programming. Firstly, an initial layout is obtained by a greedy bottom-left placement heuristic, being each piece selected according to a random weighted length criterion. The simulated annealing algorithm guides the search over the solution space where each neighborhood structure handles linear programming models, which are a compaction algorithm (Fig. 6) and a separation algorithm (Fig. 7). An extended local search algorithm based on nonlinear programming is conceived in [18].The algorithm starts with a feasible layout and its length is saved as best length. Then, a new layout is achieved by randomly swapping two polygons in the current solution.

Fig. 6
figure 6

Application of compaction in [15]

Full size image
Fig. 7
figure 7

Application of separation in [15]

Full size image

Within a time limit, the strip length is reduced and a local search method solves overlap minimization problems. If the new placement is feasible, the best solution is updated and its length is further reduced to find even better solutions. Otherwise, the strip length is increased and a local search is invoked, which is guided by Tabu Search techniques in order to escape from local minima. A compaction algorithm is used to improve the results.

By other means, a successful approach that combines a local search method with a guided local search to deal with two-dimensional and three-dimensional nesting problems is proposed in [12]. An initial strip length is found by a fast placement heuristic (e.g., bottom-left). By reducing this value, overlap situations occur, which are removed by a local search that may apply one of the following four changes: horizontal translation; vertical translation; rotation; or flipping. The guided local search is adopted to escape from local minima.

5 Conclusion

The nesting problems are present in several industrial applications. The main objective is to minimize the length of layouts and, consequently, reducing the waste of raw material. For this paper, we categorize the main approaches of literature in three different ways. The mathematical programming, heuristics and mixed approaches.

For specific types of items, certain approaches will work best computational results. However, depending on the shape of polygons, the same may be a decrease in efficiency. The criteria for selection of various positioning method is an outstanding solution to the problem, however the computational complexity involved in such methods is high.

The choice of a category that will serve to grounding an approach of nesting problem can be realized following one of these presented in this paper. However, the specifics attributes inherent of each problem can compose a particular implementation in a special section.