Traffic Flow Optimisation at Sags by Controlling the Acceleration of Some Vehicles

Abstract

Sags are bottlenecks in freeway networks. Nowadays , there is a growing interest in the development of traffic management measures for sags based on the use of in-car systems. This contribution determines the movements that individual (equipped) vehicles should make in order to minimise congestion. Specifically, we optimise the accelerations of some selected vehicles as they move along a one-lane freeway stretch with a sag, setting as objective the minimisation of total travel time. The optimisation results highlight the relevance of two traffic management strategies: (a) motivating drivers to accelerate fast along sags; and (b) limiting the inflow to sags. Also, they suggest ways to apply these strategies in practice by regulating the acceleration of vehicles equipped with in-car systems. These results prove the usefulness of the proposed method as a tool for control measure development.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Sags (or sag vertical curves) are freeway sections along which the gradient increases gradually in the direction of traffic. The capacity of sags is lower than that of sections with other vertical profiles [1]; hence, traffic often becomes congested at sags in high-demand conditions [2]. For example, in Japanese intercity freeways, 60 % of traffic jams occur at sags [1]. The main cause of congestion appears to be that most drivers do not accelerate enough as they move along the vertical curve [3]. Consequently, they keep longer headways than expected given their speed [4]. This leads to periodic formation of stop-and-go waves when traffic demand is sufficiently high [5]. The bottleneck is generally the end of the vertical curve [6]. In the last decades, various traffic control measures have been proposed for mitigating congestion at freeway sags. Most of these measures use variable message signs as actuators [1, 7, 8]. Recently, however, there is a growing interest in developing traffic control measures that use in-car systems as actuators [9, 10]. Although this type of measures have great potential, they are mostly in early phases of development. We argue that, at this stage, it is important to determine how equipped vehicles should move at sags in order to minimise congestion. This would lay the theoretical foundation for the development of effective traffic control applications.

The main goal of this paper is to identify the optimal acceleration behaviour of vehicles equipped with in-car systems at sags and the related effects on traffic flow, assuming low penetration rates. To this end, we optimise the accelerations of some vehicles of a traffic stream as they move along a one-lane freeway stretch with a sag, considering as objective the minimisation of total travel time. This is done for various scenarios defined by the number of controlled vehicles and their positions in the stream. By analysing the results, we identify the main strategies that vehicles equipped with in-car systems should use at sags to minimise congestion.

2 Optimisation Problem

2.1 System Elements

The system consists of a stream of n vehicles moving along a single-lane freeway stretch. Every vehicle is assigned a number i that corresponds to its position in the stream ($i=1, 2, \ldots , n$). The set that contains all numbers i is denoted by N. A total of m vehicles are controlled vehicles. The subset of N that contains the numbers i of these vehicles is denoted by M. Each controlled vehicle is assigned a number j that corresponds to its position in relation to the other controlled vehicles ($j=1, 2, \ldots , m$). The freeway stretch has no ramps and its vertical profile is known.

2.2 State and Control Variables

The state variables are: (a) position of all vehicles along the freeway ($r_i$, $\forall i$); (b) speed of all vehicles ($v_i$, $\forall i$); and (c) amount of freeway gradient compensated by the drivers of all vehicles ($G_{\text {com},i}$, $\forall i$). These variables are the ones needed to determine the trajectories of all vehicles in the space-time plane (see Sect. 2.3). The state at simulation time step $\tau$ is defined as follows:

$$\begin{aligned} \mathbf {x}(\tau ) = \begin{bmatrix} r_1(\tau )&r_2(\tau )&\ldots&r_n(\tau ) \\ v_1(\tau )&v_2(\tau )&\ldots&v_n(\tau ) \\ G_{\text {com},1}(\tau )&G_{\text {com},2}(\tau )&\ldots&G_{\text {com},n}(\tau ) \end{bmatrix} \end{aligned}$$

(1)

The control variables are the maximum accelerations of all controlled vehicles ($u_j$, $\forall j$). Section 2.3 describes how $u_j$ influences the actual vehicle acceleration. The control input at control time step $\kappa$ is defined as follows:

$$\begin{aligned} \mathbf {u}(\kappa ) = \begin{bmatrix} u_1(\kappa )&u_2(\kappa )&\ldots&u_m(\kappa ) \end{bmatrix} \end{aligned}$$

(2)

Different counters are used for simulation and control time steps ($\tau$ and $\kappa$) because the control time step length ($T_\text {c}$) can be assigned a different value than the simulation time step length ($T_\text {s}$), as long as $T_\text {c}$ is a multiple of $T_\text {s}$.

2.3 State Dynamics

The position and speed of all vehicles change over time as follows:

$$\begin{aligned} r_i(\tau +1) = r_i(\tau ) + v_i(\tau ) \cdot T_\text {s} + 0.5 \cdot a_i(\tau ) \cdot T_\text {s}^2 \end{aligned}$$

(3)

$$\begin{aligned} v_i(\tau +1) = v_i(\tau ) + a_i(\tau ) \cdot {T_\text {s}} \end{aligned}$$

(4)

In Eqs. 3 and 4, $a_i(\tau )$ denotes the acceleration of vehicle i at time step $\tau$, which is calculated as follows. For non-controlled vehicles, $a_i(\tau )$ is equal to the acceleration given by the car-following model presented in [11] ($a_{\text {CF},i}(\tau )$). For controlled vehicles, $a_i(\tau )$ is the minimum of the control input ($u_j(\kappa )$) and $a_{\text {CF},i}(\tau )$. Therefore:

$$\begin{aligned} a_i(\tau )= {\left\{ \begin{array}{ll} a_{\text {CF},i}(\tau ) &{} \text {if } i \notin M\\ \min (u_j(\kappa ),a_{\text {CF},i}(\tau )) &{} \text {if } i \in M\\ \end{array}\right. } \end{aligned}$$

(5)

where i and j are the same vehicle, and $\kappa$ is such that $\tau \cdot T_\text {s} \in [\kappa \cdot T_\text {c}, (\kappa +1) \cdot T_\text {c})$.

The car-following model has the following variables: speed, relative speed, spacing, gradient and compensated gradient ($G_{\text {com}}$). The gradient is dependent on the freeway location. The way $G_{\text {com}}$ changes over time is explained in [11].

2.4 Cost Function and Optimisation Problem

The cost function (J) is defined as the total travel time of all vehicles from their initial positions to the arrival point R:

$$\begin{aligned} J(\mathbf x (0),\mathbf x (1),\ldots ,\mathbf x (\tfrac{T}{T_\text {s}}),\mathbf u (0),\mathbf u (1),\ldots ,\mathbf u (\tfrac{T}{T_\text {c}})) = \sum \limits _{i=1}^{n} \left( T_s \cdot \tau _{R,i} + \varDelta t_i \right) \end{aligned}$$

(6)

where $\tau _{R,i}$ denotes the last simulation time step at which vehicle i is upstream of R:

$$\begin{aligned} \tau _{R,i} = \max \left( \tau \text { }| \text { } r_i(\tau ) \le R \right) \end{aligned}$$

(7)

and $\varDelta t_i$ denotes the time required by vehicle i to move from its position at time step $\tau _{R,i}$ to point R, which is calculated by solving the following quadratic equation:

$$\begin{aligned} \frac{a_i(\tau _{R,i})}{2} \cdot (\varDelta t_i)^2 + v_i(\tau _{R,i}) \cdot \varDelta t_i + (r_i(\tau _{R,i}) - R) = 0 \end{aligned}$$

(8)

The discrete-time optimisation problem, which is non-linear and non-convex, can be formulated as the following mathematical program:

Find $\mathbf u ^*(0),\mathbf u ^*(1),\ldots ,\mathbf u ^*(\tfrac{T}{T_\text {c}})$

that minimise $J(\mathbf x (0),\mathbf x (1),\ldots ,\mathbf x (\tfrac{T}{T_\text {s}}),\mathbf u (0),\mathbf u (1),\ldots ,\mathbf u (\tfrac{T}{T_\text {c}}))$

subject to:

$$\begin{aligned} \mathbf {x}(0) = \mathbf {x}_0 \end{aligned}$$

(9)

$$\begin{aligned} \mathbf {u}(\kappa ) \in \mathscr {U}, \text { for } \kappa = 0, 1 , 2, \ldots , \tfrac{T}{T_\text {c}} \end{aligned}$$

(10)

$$\begin{aligned} \mathbf {x}(\tau +1) = \mathbf {f}(\mathbf {x}(\tau ),\mathbf {u}(\kappa )), \text { for } \tau = 0, 1 , 2, \ldots , \tfrac{T}{T_\text {s}} \end{aligned}$$

(11)

where $\kappa$ is such that $\tau \cdot T_\text {s} \in [\kappa \cdot T_\text {c}, (\kappa +1) \cdot T_\text {c})$.

In Eq. 9, $\mathbf {x}_0$ denotes the initial state, which is assumed known. In Eq. 10, $\mathscr {U}$ denotes the admissible control region. T is the total simulation period.

3 Experimental Set-Up

We carried out a series of optimisation experiments that entailed solving the problem presented in Sect. 2.4 (using sequential quadratic programming) for various scenarios. The goal of these experiments was to determine the optimal acceleration behaviour of controlled vehicles at sags (and the related effects on traffic flow), assuming low penetration rates and nearly-saturated traffic conditions.

Eight scenarios were defined. In all scenarios, the traffic stream contains 300 vehicles ($n=$ 300). The scenarios differ in the number of controlled vehicles (m) and their positions in the stream (set M). To define the scenarios, we set the number of controlled vehicles to 0, 1, 2 or 3, and their positions to $\frac{n}{4}$, $\frac{2n}{4}$ and/or $\frac{3n}{4}$. A scenario was defined for every possible configuration of set M.

All other inputs are the same in all scenarios. The simulation time step length ($T_\text {s}$) is 0.5 s and the control time step length ($T_\text {c}$) is 8 s. The total simulation period (T) is 800 s. The freeway stretch can be divided in three consecutive sections: (a) constant-gradient downhill section; (b) sag vertical curve; and (c) constant-gradient uphill section. The sag vertical curve is 600 m long. Upstream and downstream of the sag, the freeway slope is equal to $-0.5$ % and 2.5 %, respectively. Along the vertical curve, the gradient increases linearly over distance. The arrival point used to calculate travel times (R) is 3400 m downstream of the end of the sag. All vehicle-driver units are 4 m long and are assigned the same value for every parameter of the car-following model (see Table 1). At time zero, the initial speed of all vehicles is equal to the desired speed (120  km/h), the first vehicle of the stream is located on the constant-gradient downhill section (3000 m upstream of the sag), and the traffic density is the critical density of that section. Initially, the compensated gradient is equal to the actual gradient for all vehicle-driver units, hence the freeway gradient has no influence on vehicle acceleration. The set of admissible maximum acceleration values is the same for all controlled vehicles and for all control time steps: it contains all real numbers between $-0.5$ and 1.4 m/s$^2$.

Table 1 Values of the car-following model parameters

4 Results

The optimisation results show that the optimal acceleration behaviour of controlled vehicles is defined by two strategies. Sections 4.1 and 4.2 describe the characteristics of these strategies and their effects on traffic flow.

4.1 Primary Strategy

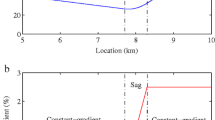
The primary strategy is used by all controlled vehicles in all scenarios. It involves performing a four-phase manoeuvre in the sag area (see for example Fig. 1). The first phase (D1) begins upstream of the sag or right after entering it. During this phase, controlled vehicles decelerate moderately (at the minimum acceleration rate allowed by the controller) and their distance headway increases considerably. During the second phase (A1), which begins halfway through the vertical curve, controlled vehicles accelerate fast (with maximum acceleration rates up to 1 m/s$^2$ or higher) and their distance headway decreases quickly. The third phase (D2) begins on the last part of the vertical curve. In this phase, controlled vehicles decelerate slowly in order to adjust to the behaviour of the leader. Their distance headway continues to decrease because the preceding vehicle is slower. Controlled vehicles catch up with their leader at around the end of the sag. From that point on, controlled vehicles simply accelerate to the desired speed (fourth phase, A2).

Fig. 1

Example of four-phase manoeuvre in the sag area (scenario with $M=\{75\}$). The behaviour of vehicle 75 in the control scenario (C) and the no-control scenario (NC) are shown together for comparison purposes: speed over time (vehicle 75) (a); position over time (vehicles 74 and 75) (b)

Fig. 2

Speed contour plots: no-control scenario (a); the scenario with $M=\{75\}$ (A is region of low traffic speed and limited flow; B is a region of high traffic speed and high flow) (b)

In all cases, the type of manoeuvre described above has two main effects on traffic flow. Firstly, it induces the first group of vehicles located behind the controlled vehicle (up to 85 vehicles in some cases) to accelerate fast along the sag. As a result, traffic speed at the end of the vertical curve (bottleneck) increases and stays moderately high (70–90 km/h) for a particular period (2–3 min), contrary to what happens in the no-control scenario (compare Fig. 2a, b). The main consequence of this increase in traffic speed is that the flow at the bottleneck increases by up to 5 %, which leads to a decrease in total travel time. Secondly, every manoeuvre triggers a stop-and-go wave on the first part of the sag (see Fig. 2b) that temporarily limits the inflow to the vertical curve. Limiting the inflow is beneficial because it slows down the formation of congestion at the end of the sag, hence high levels of sag outflow can be maintained for a longer period of time.

Fig. 3

Speed (a) and time headway (b) of every vehicle at the end of the sag in: (i) the no-control scenario; (ii) the control scenario with $M=\{150\}$ (including the supporting strategy); and (iii) a virtual scenario corresponding to the scenario with $M=\{150\}$ in which the supporting strategy was excluded from the solution

4.2 Supporting Strategy

The supporting strategy is only applied by some controlled vehicles in some scenarios. It consists in performing one or more deceleration-acceleration manoeuvres upstream of the sag, catching up with the preceding vehicle before entering the vertical curve. The characteristics of these manoeuvres are very case-specific, but their overall effect on traffic flow is similar in all cases¹. Essentially, they change the location and severity of congestion upstream of the vertical curve in such a way that the inflow to the bottleneck is slightly lower than if the supporting strategy was not applied. As a result, the primary strategy is able to produce high traffic speeds and flows at the end of the sag for a slightly longer period of time (see for example Fig. 3a, b). This causes additional total travel time savings. It is important to note, however, that in all scenarios the primary strategy is the one that contributes the most to reduce the total travel time.

5 Conclusions

The goal of this paper was to identify the main strategies that define the optimal acceleration behaviour of vehicles equipped with in-car systems at sags and their effects on traffic flow, considering as objective the minimisation of total travel time. To this end, we optimised the accelerations of some vehicles of a traffic stream that moves along a single-lane freeway stretch with a sag. Our findings provide valuable insight into how congestion can be reduced at sags by means of traffic control measures based on the use of in-car systems. More specifically, they highlight the relevance of motivating drivers to accelerate fast along sags and limiting the inflow to the vertical curve. In addition, they indicate ways to do that by regulating the acceleration of equipped vehicles. Our findings also prove the usefulness of the proposed optimisation method as a tool for control measure development. We conclude that this method could be used to identify effective traffic management strategies for other types of bottlenecks, possibly considering alternative control objectives.

Further research is necessary to determine whether the traffic management strategies identified in this paper would also be the most effective in other scenarios (such as scenarios with multi-lane freeways, higher penetration rates and/or lower traffic demand). In addition, further research is necessary to translate the identified strategies into implementable traffic control measures (e.g., cooperative adaptive cruise control applications).