Annihilation of Positrons with Atomic Electrons

Abstract

We analyze various channels for the annihilation of positrons with atomic electrons. Since in the annihilation process a large energy exceeding 1 MeV is released, relativistic analysis is required even in the case of slow positrons. We study in detail the dominative two-photon annihilation process on the Bethe ridge and outside it. We calculate the characteristics of single-quantum annihilation and annihilation followed by knockout of a bound electron to the continuum. In the latter case, the role of the QFM mechanism described in Chap. 9 is important. We consider also annihilation followed by creation of a $\mu ^+\mu ^{-}$ pair and annihilation accompanied by creation of a mesoatom.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

11.1 Two-Photon Annihilation

11.1.1 On the Bethe Ridge: Fast Positrons

Annihilation of a positron with a electron bound in an atom can be followed by radiation of two photons. This process, illustrated by Fig. 11.1, has the largest cross section, at least for small Z, among the various channels of annihilation of positrons in their interactions with atomic electrons, since it can take place on the free electrons. The conservation laws for the free process

$$\begin{aligned} E+m\ =\ \omega _1+\omega _2; \quad \mathbf{p}\ =\ \mathbf{k}_1+\mathbf{k}_2\,, \end{aligned}$$

(11.1)

with E and $\mathbf{p}$ the relativistic energy and three-dimensional momentum of the positron, require that the difference between the energies of the radiated photons be limited by the condition

$$\begin{aligned} \frac{\omega _1-\omega _2 }{\omega _1+\omega _2}\ \le \ \sqrt{\frac{E-m}{E+m}}\,. \end{aligned}$$

(11.2)

Here we have assumed that $\omega _1\ge \omega _2$.

If the condition (11.2) is satisfied and the positron kinetic energy is large enough, i.e., $\xi =\alpha Z E/p \ll 1$, a momentum

$$\begin{aligned} \mathbf{q}\ =\ \mathbf{k}_1+\mathbf{k}_2-\mathbf{p} \end{aligned}$$

(11.3)

is transferred from the nucleus to the bound electron. Following our general approach, we can write for the amplitude of annihilation with any bound electron at the Bethe ridge ($q \sim \mu _b$)

$$\begin{aligned} F(E,\omega _1, \mathbf{q})\ =\ F_0(E,\omega _1)S(q)\,, \end{aligned}$$

(11.4)

with S(q) defined by (9.146). In this chapter, we describe the electrons by single-particle functions.

The amplitude of the free process $F_0$ can be expressed in terms of the amplitude $F_C$ of the Compton scattering on the free electron at rest. While dependence of the latter on the energies of the incoming photon and the ejected electron is $F_C(E_C, \omega _{1C})$, we obtain $F_0(E,\omega _1)=F_C(-E_C,-\omega _{1C})$. This is a manifestation of the general principle of the crossing invariance of the amplitudes. The amplitude of the process in which the system of the particles A and B converts to that of the particles C and D and that in which a particle is changed to its antiparticle are described by the same analytical function of kinematic variables.

Employing (2.80), we obtain for the energy distribution

$$\begin{aligned} \frac{d\sigma }{d\omega _i}\ =\ \frac{d\sigma _0}{d\omega _2}\ =\ \frac{2\pi r_e^2 f_0m}{p^2}\,, \end{aligned}$$

(11.5)

with $d\sigma _0/d\omega _i$ the energy distribution for two-photon annihilation on the free electron, while

$$f_0=\frac{1}{2}\Big [\frac{\omega _1}{\omega _2}+\frac{\omega _2}{\omega _1}+ 2\Big (\frac{m}{\omega _1}+ \frac{m}{\omega _2}\Big )-\Big (\frac{m}{\omega _1}+ \frac{m}{\omega _2}\Big )^2\Big ];$$

see (6.168). The angular distribution can be written as

$$\begin{aligned} \frac{d\sigma }{dt_i}= \frac{d\sigma _0}{dt_i}=\frac{2\pi r_e^2f_0 \omega _1^2}{p(E+m)}; \quad t_i=\frac{\mathbf{p}\cdot \mathbf{k}_i}{pk_i}\,. \end{aligned}$$

(11.6)

The total cross section of annihilation is of order $r_e^2$ for $E-m \sim m$. In the ultrarelativistic limit $E \gg m$, it becomes smaller, i.e., $\sigma \sim r_e^2m/E$. One can see this by employing (11.5). This equation demonstrates also that in the nonrelativistic limit $p\ll m$ (but still $p \gg \eta$), the energy distribution is larger than at $p \sim m$ ($E-m \sim m$). The increase of the total cross section is not so large, since the interval of photon energy values diminishes, i.e., $|\omega _i-m|/m \lesssim p/m$. Thus in the nonrelativistic case, we obtain $\sigma \sim r^2_e m/p$. The corrections to these equations are of order $\alpha ^2Z^2$.

The total cross section for the two-quanta annihilation on a free electron is [1]

$$\begin{aligned} \sigma _0(E)=\frac{\pi r_e^2}{\beta +1}\bigg [\frac{\beta ^2+4\beta +1}{\beta ^2-1}\ln \Big (\beta +\sqrt{\beta ^2-1}\Big )- \frac{\beta +3}{\sqrt{\beta ^2-1}}\bigg ], \end{aligned}$$

(11.7)

with $\beta \ =\ E/m$. In the ultrarelativistic limit $E \gg m$,

$$\begin{aligned} \sigma _0(E)\ =\ \pi r_e^2\frac{m}{E}\Big (\ln {\frac{2E}{m}}-1\Big ). \end{aligned}$$

(11.8)

The cross section for annihilation in interaction with an atom containing N electrons is

$$\begin{aligned} \sigma (E)\ =\ N\sigma _0(E). \end{aligned}$$

(11.9)

In the only experiment on two-quantum annihilation of positrons with atoms [2], the cross section was measured for 300-keV positrons absorbed by atoms of silver ($I_Z=26$ keV). The theoretical results overestimate the measured ones.

In the free process, the values $t_i$ are determined by those of $\omega _i$, i.e.,

$$\begin{aligned} t_1=t_{10}=\frac{p^2+\omega _1^2-\omega _2^2}{2p\omega _1}; \quad t_2=t_{20}=\frac{p^2+\omega _2^2-\omega _1^2}{2p\omega _2}\,. \end{aligned}$$

(11.10)

We shall see that after inclusion of the terms of order $\xi$, the distributions $d\sigma /d\omega _idt_i$ peak at $t_i$, which differ from the values defined by (11.10) by values of order $\alpha ^2Z^2$. We calculate the terms $\sim \xi$ for a hydrogenlike atom. We include the terms linear in $\mathbf{q}$ in the amplitude $F_0$ and the lowest-order correction for interaction between the positron and the nucleus. As in the case of Compton scattering , Coulomb corrections to the propagators provide contributions of order $\xi ^2$. We obtain [3]

$$\begin{aligned} \frac{d\sigma }{d\omega _1d\varOmega _1d\varOmega _2}=\frac{8r_e^2}{\pi ^2}\frac{\eta ^5m\omega _1\omega _2}{pa^4} \bigg [f_0\cdot \Big (1-\frac{2E}{m}L\Big ) - f_1\frac{\mathbf{q}\cdot \mathbf{k_1}}{m\omega _1}-f_2\frac{\mathbf{q} \cdot \mathbf{k_2}}{m\omega _2}\bigg ]. \nonumber \\ \end{aligned}$$

(11.11)

Here $\eta =m\alpha Z$,

(11.12)

while $f_i=\omega _i\partial f_0/\partial \omega _i$ for $i=1,2$, i.e.,

$$f_1=\frac{1}{2}\Big [\frac{\omega _1}{\omega _2}-\frac{\omega _2}{\omega _1}+ 2\frac{m}{\omega _1}\Big (\frac{m}{\omega _1}+\frac{m}{\omega _2}-1\Big )\Big ]; \quad f_2(\omega _1,\omega _2)=f_1(\omega _1 \leftrightarrow \omega _2).$$

Writing

$$ \frac{d\sigma }{d\omega _1d\varOmega _1d\varOmega _2}\ =\ \frac{\omega _1^2d\sigma }{d^3k_1d\varOmega _2}\ =\ \frac{\omega _1^2d\sigma }{d^3 qd\varOmega _2} $$

and integrating over $\mathbf{q}$, we find that the terms proportional to L, $f_1$, and $f_2$ vanish, and we come to the energy distribution $d\sigma /d\omega _2$ in the lowest approximation of the expansion in powers of $\xi$ (11.5). Thus the corrections of order $\xi$ manifest themselves neither in the energy or angular distributions nor in the total cross section.

Integrating the distribution (11.11) over $\varOmega _2$, we obtain

$$\begin{aligned} \frac{d\sigma }{d\omega _1d\varOmega _1}\ =\ \frac{8r_e^2}{3\pi }\frac{m\omega _1}{p\omega _2\eta } \frac{f_0(\omega _1,\omega _2)}{(1+x^2)^3}\Big [1+\alpha ZxF(\omega _1, t_1)\Big ]. \end{aligned}$$

(11.13)

Here

$$\begin{aligned} F(\omega _1,t_1)=\lambda (\omega _1)+\frac{E}{p}\frac{\varPhi (x,t)}{f_0}; \quad \lambda (\omega _1)=\bigg (1-\frac{m}{\omega _1}-\frac{m}{\omega _2}\bigg )\frac{f_1}{f_0} +\frac{f_2}{f_0}- \frac{m}{\omega _2}\,, \nonumber \\ \end{aligned}$$

(11.14)

while

$$\begin{aligned} x=\frac{q_1-\omega _2}{\eta }; \quad \mathbf{q}_1=\mathbf{p}-\mathbf{k}_1; \quad t\equiv \frac{\mathbf{p}{} \mathbf{q}_1}{pq_1}=\frac{p-\omega _1t_1}{q_1}\,. \end{aligned}$$

(11.15)

The function $\varPhi$ is a rather bulky combination of elementary functions. We do not present it here, referring the interested reader to the paper [3]. We provide only an expression for

$$\begin{aligned} \varPhi (0,t)\ =\ \frac{15}{2t^5}\bigg (-1+\frac{7t^2}{6}+\frac{3t^4}{10}+\frac{2-3t^2+t^6}{4t} \ln \frac{1+t}{1-t}\bigg ), \end{aligned}$$

(11.16)

which determines the shift of the positions of the peaks of the distribution (11.11) and the shift of the differential cross sections $d\sigma /dt_1$ at fixed $\omega _1$ and $d\sigma /d\omega _1$ at fixed $t_1$.

In free kinematics, $x=0$, and thus

$$\begin{aligned} \omega _1=\omega _{10}=\frac{m(E+m)}{E+m-pt_1}; \quad \omega _2=\omega _{20}=\frac{m(E+m)}{E+m-pt_2}. \end{aligned}$$

(11.17)

If we now include the corrections of order $\xi$, the peak of the distribution (11.13) is reached at

$$\begin{aligned} x_1=\frac{\alpha Z}{6}\bigg (\lambda (\omega _1)+\frac{E}{p}\frac{\varPhi (0,t_0)}{f_0}\bigg ); \quad t_0=\frac{p-Et_{10}}{E-pt_{10}}, \end{aligned}$$

(11.18)

with $t_{10}$ the value of $t_1$ corresponding to the free kinematics determined by (11.10). At a fixed value of $\omega _1$, the peak of the angular distribution is reached at

$$\begin{aligned} t_1\ =\ t_{10}-\frac{\omega _2\eta }{\omega _1p}x_1\,, \end{aligned}$$

(11.19)

with $t_{10}$ determined by (11.10). The formula for the shift of the position of the energy distribution peak is somewhat more complicated:

$$\begin{aligned} \omega _1=\omega _{10}+\frac{\alpha ^2Z^2}{6}\frac{\omega _1\omega _2}{E+m}\bigg (\lambda (\omega _1) +\frac{E}{p}\frac{\varPhi (0,t_0)}{f_0}+\frac{\omega _2f_1-\omega _1f_2}{f_0(E+m)}-2\bigg ). \end{aligned}$$

(11.20)

Here $t_0$ is defined by (11.18), and the RHS should be taken at $\omega _1=\omega _{10}, \omega _2=\omega _{20}$ corresponding to the free kinematics. The values of $\omega _{n0}$ ($n=1,2$) are given by (11.17). In the nonrelativistic case, (11.17) can be simplified:

$$\begin{aligned} \omega _1\ =\ \omega _{10}+\frac{\eta ^2}{12p}\bigg (\varPhi (0,t_0)-\frac{3p}{m}+O(\frac{p^2}{m^2})\bigg ). \end{aligned}$$

(11.21)

11.1.2 On the Bethe Ridge: Slow Positrons

Now we extend our analysis to the case in which the kinetic energy of the positron is of order the electron binding energy. We must include interaction with the atomic field in the positron wave function. If the ionization potential $I_b$ is not too large, i.e., $I_b \ll m$, the incoming positron can be described by the nonrelativistic function. However, the positron in the intermediate state in Fig. 11.1 carries a large energy and should be described by the relativistic propagator.

Fig. 11.1

Two-quantum annihilation in the interaction of positrons with atomic electrons. The solid lines stand for electrons (positrons). The arrow marks the positron, with the direction of the arrow opposite to that of the positron momentum. The dark blob labels the bound electron. The helix lines are for the photons

Due to the energy conservation law, $\omega _1+\omega _2=2m-I_b \approx 2m$. Introducing ${{{\varvec{\kappa }}}}=\mathbf{k}_1+\mathbf{k}_2$, we see that on the Bethe ridge, $\kappa \sim \mu _b \ll \omega _1+\omega _2$. Thus the energies of the radiated photons are close, i.e., $|\omega _1-\omega _2|\le \kappa \sim \mu _b$, and

$$\begin{aligned} \frac{|\omega _1-\omega _2|}{\omega +\omega _2}\ \lesssim \ \frac{\mu _b}{m}\ \ll \ 1\,. \end{aligned}$$

(11.22)

Each photon carries the energy $\omega _i\approx m\approx 500$ keV. The photons are radiated in nearly opposite directions, with $t_{12}=\mathbf{k}_1\cdot \mathbf{k}_2/\omega _1\omega _2$ close to $-1$.

We carry out calculations for annihilation with the K-shell electrons, describing them by nonrelativistic Coulomb functions. Due to (11.22), the momenta of the intermediate particles in the Feynman diagrams shown in Fig. 11.1 are large enough ($p_{a,b}\gg \eta$), and with an error of order $\eta /m\sim \alpha Z$ can be described by free relativistic propagators.

To obtain the cross section of the process, we can employ results for differential distributions of the Compton scattering on the K electrons with ejection of slow electrons carried out in Sect. 6.4. The distribution $d\sigma _C/d\omega _2dt_{12}$ is represented by (6.162). Employing this result, we obtain

$$\begin{aligned} \frac{d \sigma }{d\omega _1d\kappa }= r_e^2\frac{2^7}{3}\frac{m\eta ^4\xi \kappa ^3(p^2+3\kappa ^2+\eta ^2)}{[(p-\kappa )^2+\eta ^2]^3 [(p+\kappa )^2+\eta ^2]^3}\cdot N(\kappa )(1+t^2_{12}) \end{aligned}$$

(11.23)

for $|\omega _1-m|\lesssim \eta$ and $\kappa \lesssim \eta$. Here

$$\begin{aligned} N(\kappa ) = N^2_+\exp (2\xi \chi ) ; \quad \chi = \arctan {\bigg (\frac{2\eta p}{\kappa ^2-p^2 +\eta ^2}\bigg )}, \end{aligned}$$

(11.24)

with

$$\begin{aligned} N^2_+(\xi )\ =\ \frac{2\pi \xi }{\exp (2\pi \xi )-1}, \end{aligned}$$

(11.25)

in the squared normalization factor of the positron wave function. Recall that $\xi =\eta /p=(I_Z/\varepsilon )^{1/2}$.

On the RHS of (11.23), the last factor is the only term depending on $\omega _1$ with $t_{12}=1-(4m^2-\kappa ^2)/2\omega _1\omega _2$. Taking into account the identity of two photons, we obtain

$$\begin{aligned} \frac{d \sigma }{d\kappa }=\frac{1}{2}\int \limits _{m-\kappa /2}^{m+\kappa /2}d\omega _1\frac{d \sigma }{d\omega _1d\kappa }= r_e^2\frac{2^7}{3}\frac{m\eta ^4\xi \kappa ^4(p^2+3\kappa ^2+\eta ^2)}{[(p-\kappa )^2+\eta ^2]^3 [(p+\kappa )^2+\eta ^2]^3} \cdot N(\kappa ). \end{aligned}$$

(11.26)

This determines the angular distribution

$$ \frac{d\sigma }{dt_{12}}\ =\ \frac{m^2}{\kappa }\frac{d \sigma }{d\kappa }\,, $$

where the distribution $d\sigma /d\kappa$ is given by (11.26) with $\kappa ^2=2m^2(1+t_{12})$. The total cross section can be obtained by integration over $\kappa$, and the integral is saturated at $\kappa \sim \eta$. The cross section is of order $r_e^2\cdot m/p$.

For very slow positrons with $p \ll \eta$, it is reasonable to evaluate

$$\begin{aligned} \exp {(2\xi \chi )}\ =\ \exp {\bigg (4\eta ^2/(\kappa ^2+\eta ^2)\bigg )} \end{aligned}$$

(11.27)

on the RHS of (11.24). In this limit, $\sigma \sim r^2_e\xi ^2 e^{-2\pi \xi }/(\alpha Z)$. The exponential quenching is due to the strong repulsion between the nucleus and the slow positron.

At $\varepsilon \le I_Z$, annihilation with the electrons of multielectron atoms is more complicated, since the correlation between the positron and atomic electrons should be included. The positron captures one of the atomic electrons, creating a new two-particle bound state, the positronium. In the next step, the positronium decays into two photons if the positronium has spin $S=0$, or into three photons for $S=1$. This becomes the dominant annihilation mode [4]. The positron annihilation on molecules is still more complicated, since the vibrational degrees of freedom become involved [5].

11.1.3 Photon Distribution Outside the Bethe Ridge

If the photon energies satisfy the inequality (11.2), we can calculate the angular distribution $d\sigma /dt_1$ for every value of the angle $t_1$. Recall that if $t_1$ is close to $t_{10}$ (i.e., their difference is of order $\alpha Z$), which corresponds to free kinematics and is given by (11.10), the distribution is determined by small recoil momenta $q\sim \eta$. If the values of $t_1$ are not close to $t_{10}$, a large recoil momentum $q \gg \mu _b$ should be transferred to the nucleus.

Following the analysis carried out in Chaps. 3 and 5, we can consider the process as consisting of two steps. The first is scattering of the positron on the atom. In this process, a large momentum q is transferred to the atom. As we have seen in previous chapters, since $q \gg \eta$, this momentum should be transferred to the nucleus. After the scattering, the positron carries momentum $\mathbf{p}'=\mathbf{p}+\mathbf{q}'$ with $\mathbf{q}' \approx \mathbf{q}$, i.e., $|\mathbf{q}' -\mathbf{q}| \ll q$. Since the energy is not transferred in this collision, $|\mathbf{p'}|=p'=p$. In the second step, the scattered positron is annihilated with the bound electron. Here two photons are radiated and a small momentum of order $\mu _b$ is transferred to the nucleus. The angle between the directions of the momenta $\mathbf{k}_1$ and $\mathbf{p}'$ is determined by free kinematics. Thus for $t'=\mathbf{k}_1\mathbf{p}'/k_1p'$, we can write

$$\begin{aligned} t'\ =\ t_{10}\,, \end{aligned}$$

(11.28)

with $t_{10}$ determined by (11.10).

Similar to the case of Compton scattering (8.31), the distribution in photon energy and recoil momentum can be written as

$$\begin{aligned} \frac{d\sigma }{d\omega _1d\varphi dq^2}\ =\ \frac{\langle \psi _i|r^{-2}|\psi _i\rangle }{4\pi } \cdot \frac{d\sigma _0}{d\omega _1d\varphi }\cdot \frac{d\sigma _{e^+A}(\varepsilon )}{dq^2}\,. \end{aligned}$$

(11.29)

Here $\varphi$ is the angle between the planes determined by the vectors $\mathbf{p}$, $\mathbf{q}$ and $\mathbf{p}'$, $\mathbf{k}_1$; $d\sigma _0/d\omega _1d\varphi$ is the differential cross section for the positron two-quanta annihilation with the free electron, while $d\sigma _{eA}$ is that for the scattering of the positron on the atom. At $q\gg \eta$, the latter can be treated in the Born approximation . It is dominated by scattering on the nucleus and can be written similar to (8.32) as

$$\begin{aligned} \frac{d\sigma _{e^+A}(\varepsilon )}{dq^2}\ =\ \frac{d\sigma _{e^+N}(\varepsilon )}{dq^2}\ =\ \frac{|V_{e^+N}(q^2)|^2}{2\pi }\frac{E^2}{p^2}(1-\frac{q^2}{4E^2})\,, \end{aligned}$$

(11.30)

with the positron–nucleus interaction $V_{e^+N}(q^2)=4\pi \alpha Z/q^2$.

The distribution (11.29) can be written in terms of the angular variables of the radiated photon. Writing $q^2=2p^2(1-t_p)$ with $t_p=\mathbf{p}{} \mathbf{p}'/p^2$, we represent (11.30) as

$$\begin{aligned} \frac{d\sigma _{e^+N}(\varepsilon )}{dq^2}=\frac{1}{2p^2}\frac{d\sigma _{e^+N}(\varepsilon )}{dt_p}; \quad \frac{d\sigma _{e^+N}(\varepsilon )}{dt_p}=\frac{4\pi \alpha ^2Z^2}{p^2(1-t_p)^2}\frac{E^2}{p^2} \Big (1-\frac{p^2(1-t_p)}{2E^2}\Big ). \end{aligned}$$

(11.31)

The distribution

$$ \frac{d\sigma _{e^+N}(\varepsilon )}{dt_1}\ =\ \frac{d\sigma _{e^+N}(\varepsilon )}{dt_p}\frac{dt_p}{dt_1} $$

can be obtained using the relation $t_p=t_1t'+(1-t_1^2)^{1/2}(1-t'^2)^{1/2}\cos {\varphi }$ and (11.28). Carrying out integration over $\varphi$, we obtain

$$\begin{aligned} \frac{d\sigma }{d\omega _1dt_1}= \frac{\alpha ^2}{2}\frac{\langle \psi _i|r^{-2}|\psi _i\rangle }{p^2}\cdot \frac{E^2}{p^2} \frac{d\sigma _0}{d\omega _1}\cdot \bigg (\frac{1-t_1t_{10}}{(t_1-t_{10})^2}-\frac{p^2}{2E^2}\frac{1}{|t_1-t_{10}|}\bigg ). \end{aligned}$$

(11.32)

This expression is true outside the Bethe ridge , i.e., at $|t_1-t_{10}|\gtrsim \alpha Z$. On the Bethe ridge, $|t_1-t_{10}| \sim \alpha Z$, and one should use the equations of Sect. 11.1.1.

Another important region outside the Bethe ridge is the one where the energy of one of the photons is much smaller than that of the other one, e.g., $\omega _2 \ll \omega _1$. The distribution of the soft photons is similar to that in Compton scattering; see (8.35):

$$\begin{aligned} \frac{d\sigma }{d\omega _2d\varOmega _1}=\frac{\alpha }{\pi }\cdot \frac{v^2}{\omega _2}\cdot \int \frac{d\varOmega _2}{4\pi }\cdot \frac{1-\tau ^2}{(1-v\tau )^2}\cdot \frac{d\sigma _{s}}{d\varOmega _1}; \quad \tau =\frac{\mathbf{p} \cdot \mathbf{k}_2}{p \omega _2}, \end{aligned}$$

(11.33)

with $\mathbf{v}=\mathbf{p}/{E}$ the velocity of the positron. Here $d\sigma _s$ is the differential cross section of the process without the soft photon. In other words, $\sigma _s$ is the cross section of annihilation with all initial energy converted into the energy of a single photon. This process will be analyzed below.

11.2 Annihilation with Radiation of One Photon

11.2.1 Single-Quantum Annihilation

The possibility of single-quantum annihilation of a positron in its interaction with a bound electron was predicted by Fermi and Uhlenbeck in 1933. They carried out the first calculation of the cross section based on the Born approximation and the Coulomb potential. The result is presented, e.g., in the book [1]. The corresponding Feynman diagram is shown in Fig. 11.2. The process in which one of the bound electrons is annihilated while the others do not change their states,

$$\begin{aligned} e^++A\ =\ A^{+}+\gamma \,, \end{aligned}$$

(11.34)

with A and $A^{+}$ denoting the atom, and the positive ion is crossing-invariant with respect to the photoionization process

$$ \gamma +A\ =\ A^{+}+e^-\,. $$

Thus the cross section can be expressed in terms of the photoionization amplitude $F_{ph}$.

Fig. 11.2

Single-quantum annihilation in interaction of positrons with atomic electrons. The notations are the same as in Fig. 11.1

Denoting the four-vector of the photoelectron in the photoionization process by $P_{ph}$, we can write for the cross section of the single-quantum annihilation

$$\begin{aligned} d\sigma ^+_{ann}\ =\ \frac{1}{v}|F_{ph}(-P_{ph})|^2\frac{\omega ^2d\varOmega }{(2\pi )^2}; \quad \omega \ =\ E+E_b\,, \end{aligned}$$

(11.35)

where v is the positron velocity, and $E_b$ is the total energy of the bound electron annihilated in interaction with the positron. The upper index $+$ indicates that we have a single-charged ion $A^+$ in the final state. The recoil ion obtains large momentum $q \sim m$.

The theory of the process mirrors that for photoionization. Employing the results of Sect. 6.3, we estimate $\sigma ^{+}_{ann} \sim r^2_e\alpha ^4Z^5$. In the hydrogenlike approximation, the cross section of annihilation with the K-shell electrons of the atom with nuclear charge Z is

$$\begin{aligned} \sigma ^{+}_{ann}(E)=\frac{4\pi r_e^2\alpha ^4Z^5}{(\beta +1)^2\sqrt{\beta ^2-1}} \bigg [\beta ^2+\frac{2}{3}\beta +\frac{4}{3}- \frac{\beta +2}{\sqrt{\beta ^2-1}}\ln {(\beta +\sqrt{\beta ^2-1})}\bigg ], \nonumber \\ \end{aligned}$$

(11.36)

where $\beta =E/m$. This equality is true in the lowest order in $\xi =\alpha Z/v$ [1]. The cross section reaches its largest value at $E\approx 2m$. For annihilation of nonrelativistic positrons with $E-m \ll m$,

$$\begin{aligned} \sigma ^{+}_{ann}(E)\ =\ \frac{4\pi r_e^2\alpha ^4Z^5}{3}\frac{p}{m}\,, \end{aligned}$$

(11.37)

while in the ultrarelativistic limit $E \gg m$,

$$\begin{aligned} \sigma ^{+}_{ann}(E)\ =\ 4\pi r_e^2\alpha ^4Z^5\frac{m}{E}\,. \end{aligned}$$

(11.38)

These expressions are true in the lowest order in powers of $\xi =\alpha Z/v$. Besides the hydrogenlike calculations, the cross section of annihilation with K and L electrons was obtained for a number of atoms by employing the screened Coulomb functions [6, 7]. Also, the Z-dependence of the angular distribution has been traced experimentally [8].

11.2.2 Annihilation Followed by Ionization

Single-quantum annihilation can be followed by the knockout of a bound electron to the continuum. In the process,

$$\begin{aligned} e^++A\ =\ A^{++}+e^-+\gamma , \end{aligned}$$

(11.39)

the energy of the positron E, is shared between the electron with energy $E_1$ and the photon carrying the energy $\omega$. Neglecting the binding energies, we can write

$$\begin{aligned} E+2m\ =\ E_1+\omega \,. \end{aligned}$$

(11.40)

In this reaction, a three-dimensional momentum

$$\begin{aligned} \mathbf{q}\ =\ \mathbf{p}_1+\mathbf{k}-\mathbf{p} \end{aligned}$$

(11.41)

is transferred from the nucleus. One can see that this reaction is crossing-invariant with respect to the double photoionization considered in Chap. 9.

Here we focus on the case in which the positron annihilates with one of the 1s electrons, and the second 1s electron is knocked out to the continuum. Let us analyze the contributions of the main mechanisms to the cross section of the process $\sigma ^{++}_{ann}$.

The annihilation removes one of the bound 1s electrons and thus changes the effective charge felt by the second one. This is the familiar shakeoff (SO) mechanism described in Chaps. 3 and 9. The SO determines the spectrum of the electrons at small values of their kinetic energies $\varepsilon _1=E_1-m \sim I_b$. Here the energy of the radiated photon is close to its largest value $\omega =E_1+m-I_b$. It follows from (11.40) that $\varepsilon _1+\omega \ge 2m$, and we can employ the asymptotic expression (9.37). Thus the contribution of the SO mechanism to the cross section $\sigma _{ann}^{++}$ of the reaction expressed by (11.39) is

$$\begin{aligned} \sigma ^{SO}_{ann}(E)=\sigma ^{+}_{ann}(E)C_0 ;\quad C_0=\frac{m}{2\pi ^2\varPhi ^2_{1s}} \int _0^{\infty }d\varepsilon _1 p_1|\varPhi (\varepsilon _1)|^2. \end{aligned}$$

(11.42)

Recall that for helium, $C_0 \approx 0.016$, while the Z-dependence of $C_0$ is traced in Sect. 9.2.

Before annihilation with the atomic electron, the positron can knock out another electron from a bound state. Note that while single-quantum annihilation with a free electron is not possible, a similar process of interaction of the positron with a system of two free electrons in a spin-singlet state can take place [9]. In such a process, the recoil momentum is $q=0$. To find the conditions for this quasifree mechanism (QFM) , note that in free kinematics, $(\mathbf{p}-\mathbf{k})^2=p_1^2$, and $E_1=E_0-\omega$, with $E_0=E+2m$ the largest energy available for the outgoing electron. Since $E_1^2-p_1^2=m^2$, we obtain

$$\begin{aligned} \omega \ =\ \frac{2m\omega _0}{E_0-pt}; \quad t\ =\ \frac{\mathbf{p}\cdot \mathbf{k}}{pk}\,, \end{aligned}$$

(11.43)

with $\omega _0=E+m$ the largest energy available for the photon. Thus the limits for the photon energy are

$$\begin{aligned} \frac{2m\omega _0}{E_0+p}\ \le \ \omega \ \le \ \frac{2m\omega _0}{E_0-p}\,. \end{aligned}$$

(11.44)

For nonrelativistic positrons with $p\ll m$, the energy of the photon and the kinetic energy of the outgoing electron are $\omega \approx 4m/3$ and $\varepsilon _1\approx 2m/3$ respectively. They vary in small intervals of order p / m near these values. In the ultrarelativistic limit $E \gg m$, the energy carried by the photon is limited by the condition $m \le \omega \le E$.

The QFM amplitude is proportional to that of the process on the free electrons; see (9.145). The energy distribution of the radiated photons in the interval determined by (11.44) is

$$\begin{aligned} \frac{d\sigma ^{++}_{ann}}{d\omega }\ =\sigma _1Z^3W(\omega )\frac{m}{p^2}{\mathscr {I}}; \quad \sigma _1=\pi r_e^2\alpha ^4, \end{aligned}$$

(11.45)

with ${\mathscr {I}}$ determined by (9.176);

$$\begin{aligned} W(\omega )=\Bigg (\frac{\varepsilon _1+\omega _0}{ \varepsilon _1\omega _0}\bigg )^2\bigg [EE_1-m^2-\kappa ^2+ (\frac{m\omega }{\omega _0\varepsilon _1})^2(EE_1-2\varepsilon _1\omega _0+m^2+\kappa ^2)\bigg ]; \nonumber \\ \end{aligned}$$

(11.46)

$$ \kappa ^2\ =\ \frac{(E^2-E_1^2)^2-\omega ^4}{4\omega ^2}; \quad \omega _0\ =\ \varepsilon _1+\omega ; $$

see (9.200). Introducing the dimensionless parameters $x=\omega /\omega _0$ and $\gamma =m/\omega _0$, we can write (11.45) and (11.46) as

$$\begin{aligned} \frac{d\sigma ^{++}_{ann}}{dx}\ =\ \sigma _1Z^3W(x)\frac{m}{\varepsilon }{\mathscr {I}}\,, \end{aligned}$$

(11.47)

with

$$\begin{aligned} W(x)\ =\ \gamma \Big (\frac{2-x}{1-x}\Big )^2\bigg [2(x-\gamma )+\Big [1-\Big (\frac{\gamma x}{1-x}\Big )^2\Big ] \Big [\frac{4(1-x)}{x}-\gamma \frac{(2-x)^2}{x^2}\Big ]\bigg ]. \nonumber \\ \end{aligned}$$

(11.48)

The QFM contribution to the cross section $\sigma ^{++}_{ann}$ is

$$\begin{aligned} \sigma ^{QFM}_{ann}(E)=\sigma _1Z^3f(E); \quad f(E)={\mathscr {I}}\frac{m}{\varepsilon }\cdot \int _{x_1}^{x_2}dxW(x), \end{aligned}$$

(11.49)

with the limits of integration

$$\begin{aligned} x_1\ =\ \frac{2m}{E_0+p}\,; \quad x_2\ =\ \frac{2m}{E_0-p}\,, \end{aligned}$$

(11.50)

corresponding to (11.44).

We write $\sigma ^{+}_{ann}(E)=\sigma _1Z^5\varphi (E)$, with

$$ \varphi (E)\ =\ \frac{4m^3}{p(E+m)^2}\Big (\frac{E^2}{m^2}+\frac{2}{3}\frac{E}{m} +\frac{4}{3}-\frac{E+2m}{p}\ln \frac{E+p}{m}\Big ), $$

determined by (11.36). We write also $\sigma ^{QFM}_{ann}(E)=\sigma _1Z^3f(E)$, with f(E) defined by the second equality of (11.49). Similar to the case of double photoionization, the double-to-single ionization ratio can be written as

$$\begin{aligned} R(E)=\frac{\sigma ^{++}_{ann}(E)}{\sigma ^{+}_{ann}(E)}= \frac{\sigma ^{SO}_{ann}(E)+\sigma ^{QFM}_{ann}(E)}{\sigma ^{+}_{ann}(E)}=C_0+ \frac{\sigma ^{QFM}_{ann}(E)}{\sigma ^{+}_{ann}(E)}. \end{aligned}$$

(11.51)

Here we neglected the terms of order $I_b/\varepsilon$. Employing (11.35) and (11.48), we represent the ratio (11.51) as

$$\begin{aligned} R(E)\ =\ \frac{c+\beta (E)}{Z^2};\quad \beta (E)\ =\ f(E)/\varphi (E)\,. \end{aligned}$$

(11.52)

Note that the functions f(E) and $\beta (E)$ depend on the quantum number of ionized states through the factor ${\mathscr {I}}$.

Fig. 11.3

Annihilation of positrons with atomic electrons accompanied by ionization. a Corresponds to the shakeoff (SO) mechanism. b Illustrates the quasifree mechanism (QFM). The notation is the same as in Fig. 11.1

Fig. 11.4

Energy dependence of the cross sections. The horizontal axis is for the positron energy E related to the positron mass m. The vertical line is for the functions f(E), $\varphi (E)$, and $\beta (E)$ defined in Sect. 11.1.2. Reproduced from [9]

Now we focus on elimination of two 1s electrons. We employ the perturbative model developed in Sect. 9.2.2. The amplitude is described by the Feynman diagrams presented in Fig. 11.3. Recall that in this case, the values of the parameters that enter (11.45), (11.49), and (11.52) are ${\mathscr {I}}=1/8$ and $c=0.09$ respectively. The functions f(E), $\varphi (E)$, and $\beta (E)$ are shown in Fig. 11.4. For nonrelativistic positrons with $\varepsilon \ll m$ (but $\varepsilon =E-m\gg I_Z$), we obtain

$$\begin{aligned} \beta (E)\ =\ \frac{1}{9}\cdot \frac{m}{E-m}\,. \end{aligned}$$

(11.53)

Thus at small values of Z and $\varepsilon$, the ratio R can become larger than unity. Hence double ionization can become more probable than a single one. In the ultrarelativistic limit, the two lowest terms of the expansion in powers of m / E provide

$$\begin{aligned} \beta (E)\ =\ \frac{1}{4} \bigg [1+\frac{m}{4E}\Big (11\ln {\frac{E}{m}}+6\ln {2}-\frac{35}{2}\Big )\bigg ]. \end{aligned}$$

(11.54)

The ultrarelativistic asymptotics for the ratio R corresponds to $\beta =1/4$ and is:

$$\begin{aligned} R\ =\ \frac{0.34}{Z^2}.\, \end{aligned}$$

(11.55)

Hence it is just the same as for the double-to-single photoionization ratio. However, in contrast to that case, R(E) exceeds its asymptotic value for every value of the positron energy.

11.3 Annihilation Without Radiation

11.3.1 Annihilation with Ionization

The energy released in the annihilation of a positron with a bound electron can be absorbed by another bound electron. The latter moves to the continuum. Thus the final state of the process consists of the ion with two holes in the electron shell and the ejected electron in the continuum. In this process,

$$ e^{+} +A\ \rightarrow \ A^{++}+e^- , $$

illustrated by Fig. 11.5a, the ejected electron obtains the energy

$$\begin{aligned} E_1\ =\ E+2m \end{aligned}$$

(11.56)

(here we neglected the values of the binding energies). The process cannot take place in a system of free electrons, since it requires a large momentum

$$\begin{aligned} \mathbf{q}\ =\ \mathbf{p}-\mathbf{p}_1 \end{aligned}$$

(11.57)

to be transferred to the nucleus. Since $q \ge p_1-p$, we find, employing (11.56), that $q^2 \ge 4m^2$.

Fig. 11.5

Annihilation of positrons with atomic electrons without radiation. a Ionization; b Creation of $\mu ^{+}\mu ^{-}$ pairs. The muons are shown by bold lines. The other notation is the same as in Fig. 11.1

The amplitude of the process can be written as

$$\begin{aligned} F\ =\ 4\pi \alpha \int d^3r'\bar{\psi }_{-p}(\mathbf{r'})\gamma ^{\mu }\psi _a(\mathbf{r'})\int d^3r D_{\mu \nu }({{{\varvec{\rho }}}})\bar{\psi }_{p_1}(\mathbf{r})\gamma ^{\nu }\psi _b(\mathbf{r})-(a \leftrightarrow b). \end{aligned}$$

(11.58)

Here $\psi _{-p}$ and $\psi _{p_1}$ are the wave functions describing the positron and the ejected electron, $\psi _{a,b}$ are the wave functions of the bound electrons in the states a and b, and ${{{\varvec{\rho }}}}=\mathbf{r}-\mathbf{r}'$. The photon propagator $D_{\mu \nu }$ in the Feynman gauge written in spatial representation is

$$\begin{aligned} D_{\mu \nu }({{{\varvec{\rho }}}})\ =\ g_{\mu \nu }\int \frac{d^3f}{(2\pi )^3} \frac{\exp (i\mathbf{f}{{{\varvec{\rho }}}})}{f^2-\omega ^2-i0};\quad \omega \ =\ E+m. \end{aligned}$$

(11.59)

Hence, (11.58) can be written as

$$\begin{aligned} F\ =\ 4\pi \alpha \int \frac{d^3f}{(2\pi )^3}\frac{A^{\mu }(-\mathbf{f},a) B_{\mu }(\mathbf{f},b)}{f^2-\omega ^2-i0} -(a \leftrightarrow b), \end{aligned}$$

(11.60)

with

$$ A^{\mu }(-\mathbf{f},a)\ =\ \int d^3r'\bar{\psi }_{-p}(\mathbf{r}')\gamma ^\mu \psi _a(\mathbf{r}')\exp (-i\mathbf{f}{} \mathbf{r}'), $$

$$ B_{\mu }(\mathbf{f},b)\ =\ \int d^3r \bar{\psi }_{p_1}(\mathbf{r})\gamma _{\mu }\psi _b(\mathbf{r})\exp (i\mathbf{f}{} \mathbf{r}). $$

Note that $A^{\mu }(-\mathbf{f},a)$ is the matrix element of the single-quantum annihilation of the positron with the bound electron in the state a. Also, $B_{\mu }(\mathbf{f},b)$ is the matrix element for photoionization of state b.

As we have seen in Sect. 3.1.2, a large momentum $q \gg \mu _b$ can be transferred to the nucleus by a bound electron or by a positron in the initial state or by a continuum electron in the final state, and the corresponding contributions to the amplitude are of the same order of magnitude. Thus, although the ejected electron carries the kinetic energy $\varepsilon _1 \ge 2m$, its interaction with the recoil ion should be included. On the other hand, for $\alpha Z \ll 1$, it can be treated perturbatively. The same refers to a description of the positron while its energy is large enough, $\varepsilon _1 \gg I_Z$.

We carry out calculations for the K electrons of the hydrogenlike atom. To obtain the amplitude in the lowest order of the expansion in powers of $\alpha Z$, we describe all electrons and the positron by the FSM functions; see (6.24) and (6.29) [10]. Note that there were earlier calculations for this process in which the bound electrons were described by the Coulomb functions, while the positron and the ejected electron were described by plane waves. As we said before, such calculations do not include all the terms contributing in the leading order in $\alpha Z$.

We obtain for the angular distribution

$$\begin{aligned} \frac{d\sigma }{d\varOmega }= \frac{r_e^2(\alpha Z)^8}{4}\frac{N^2(\xi _1)N_{+}^2(\xi )p_1m^4}{p\omega ^4}T(\theta ); \quad \xi =\frac{\alpha ZE}{p};\quad \xi _1=\frac{\alpha ZE_1}{p_1}. \end{aligned}$$

(11.61)

Here $N^2$ and $N_+^2$ are the squared normalization factors of the ejected electron and of the positron determined by (3.19) and (11.25); $\theta$ is the angle between the directions of the positron and electron momenta $\mathbf{p}$ and $\mathbf{p_1}$. The angular factor

$$\begin{aligned} T(\theta )\ =\ \frac{16m^2}{q^2}\Big (1-\frac{4m^2}{q^2}\Big ) \end{aligned}$$

(11.62)

is the same for all Z. It reaches its largest value $T_{\max }=1$ at $q^2=8m^2$, i.e., at

$$\begin{aligned} \theta \ =\ \theta _0\ =\ \arccos \bigg (1-\frac{4m^2}{\omega ^2}\bigg )^{1/2}. \end{aligned}$$

(11.63)

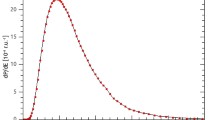
For nonrelativistic positrons $\theta _0 \rightarrow \pi /2$. For ultrarelativistic positrons with $E \gg m$, we obtain $\theta _0 \rightarrow 0$, i.e., the ejected electron moves in the same direction as the positron. An example of the angular distribution is given in Fig. 11.6.

Fig. 11.6

Angular distribution for annihilation with ionization at $E=2m$. The horizontal line is for the angle $\theta$ between the directions of the momenta of the incoming positron and the outgoing electron. The vertical line is for the differential cross section $d\sigma /d\varOmega$ in $\mu b/sterrad$ units. Reproduced from [10]

Integration of the angular distribution (11.61) provides

$$\begin{aligned} \sigma \ =\ 8\pi r_e^2(\alpha Z)^8\frac{N^2(\xi _1)N_{+}^2(\xi )m^6}{p^2\omega ^4} \bigg (\ln \frac{p_1+p}{p_1-p}-\frac{pp_1}{2\omega ^2}\bigg ). \end{aligned}$$

(11.64)

The cross section obtains its largest values, which are of order $r_e^2(\alpha Z)^8$, at $\varepsilon \sim m$. In the ultrarelativistic region $E \gg m$, it decreases as $r_e^2(\alpha Z)^8m^6/E^6$. For the nonrelativistic positrons with $\varepsilon ,p \ll m$, we obtain, putting $E=m$, $E_1=3m$, and $p_1=2\sqrt{2}m$,

$$\begin{aligned} \sigma \ =\ \frac{2^{1/2}\pi r_e^2(\alpha Z)^8}{8}\frac{N^2(\xi _1)N_{+}^2(\xi )m}{p}\,. \end{aligned}$$

(11.65)

Note that if the positron energy is so small that $2\pi \xi \gtrsim 1$, the factor $N_{+}^2(\xi ) \sim 2\pi \xi e^{-2\pi \xi }$ provides exponential quenching of the cross section.

To obtain more accurate expressions for the cross section, we represent the next-to-leading correction in powers of $\alpha Z$ [11]. We must include the $\alpha ^2Z^2$ terms in the expansion of the wave functions of the bound and continuum electron and that of the positron. Such a term for the 1s wave function is determined by (6.53). It is given by the third term on the RHS of (6.48) for the wave function of the ejected electron. Including also a similar correction for the wave function of the positron, we obtain for the angular distribution

$$\begin{aligned} \frac{d\sigma }{d\varOmega }\ =\ 4r_e^2(\alpha Z)^8N^2(\xi _1)N_+^2(\xi )\frac{p_1m^6}{p\omega ^4q^2}T_1(\theta )\,, \end{aligned}$$

(11.66)

with

$$\begin{aligned} T_1(\theta )\ =\ 1-\frac{4m^2}{q^2}+\frac{\pi \eta }{p_1}\bigg (\frac{8mE_1}{q^2}-\frac{2p_1}{q}-1\bigg ). \end{aligned}$$

(11.67)

The total cross section, which includes the lowest $\alpha Z$ correction, is

$$\begin{aligned} \sigma = 8\pi r_e^2(\alpha Z)^8\frac{N^2(\xi _1)N_+^2(\xi )m^6}{p^2\omega ^4} \bigg [\ln \frac{p_1+p}{p_1-p}-\frac{pp_1}{2\omega ^2}- \frac{\pi \eta }{p_1}\Big (\ln \frac{p_1+p}{p_1-p}-\frac{pp_1}{\omega ^2}\Big )\bigg ]. \nonumber \\ \end{aligned}$$

(11.68)

Recall that $m/E_1 <1/3$.

For example, for $Z=82$, we find that (11.64) provides $\sigma =18 \mu b$ for the cross section. Inclusion of the lowest-order correction (11.68) changes the value to $\sigma =15\mu b$.

11.3.2 Annihilation with Creation of $\mu ^+\mu ^-$ Pairs

If the positron is fast enough, it can annihilate with the bound electron, creating a $\mu ^+\mu ^-$ pair; see Fig. 11.5b. The process $e^+e^{-} \rightarrow \mu ^{+}\mu ^{-}$ can take place for the free electrons. The threshold positron energy in the rest frame of the electron is

$$\begin{aligned} {\mathscr {E}}_0\ =\ 2m^2_{\mu }/m\ \approx \ 44\,\mathrm GeV, \end{aligned}$$

(11.69)

with $m_\mu \approx 105$ MeV the muon mass. To obtain the value, we denote the four-momentum of the positron by $p=(E, \mathbf{p})$ and that of the electron at rest by $p'=(m,0)$; the momenta of $\mu ^+$ and $\mu ^{-}$ are $p_1=(E_1, \mathbf{p}_1)$ and $p_2=(E_2, \mathbf{p}_2)$. The value of the threshold energy can be obtained by squaring the momentum conservation equation $p+p'=p_1+p_2$ and noting that $(p_1p_2)\ge m_{\mu }^2$.

If the electron is in a bound state, the three-dimensional momentum $\mathbf{q}=\mathbf{p}-\mathbf{p}_1-\mathbf{p}_2$ can be transferred to the nucleus in the process,

$$ e^{+} +A\ \rightarrow \ A^{+}+\mu ^++\mu ^{-}. $$

The energy conservation law is $E+m-I_b=E_1+E_2$, and the annihilation can take place for $E\ge {\mathscr {E}}$, where the threshold for creation of free $\mu ^-$ and $\mu ^+$ is [12]

$$\begin{aligned} {\mathscr {E}}\ =\ 2m_\mu \ \approx \ 211\,\mathrm MeV \end{aligned}$$

(11.70)

(here we neglected terms of order $m/m_{\mu }$ and $I_b/m_{\mu }$).

The amplitude of the process can be written as

$$\begin{aligned} A=\alpha \int d^3r' \bar{\varphi }_{\mathbf{p}_2}(\mathbf{r}')\gamma _{\mu }\varphi _{{-\mathbf p}_1}(\mathbf{r}')\int d^3r\frac{e^{i\omega R}}{\omega R}\bar{\psi }_{{-\mathbf p}}(\mathbf{r})\gamma ^{\mu }\psi _b(\mathbf{r}); \quad R=|\mathbf{r}-\mathbf{r}'|. \nonumber \\ \end{aligned}$$

(11.71)

Here $\omega =E_1+E_2$ is the total energy of the $\mu ^+\mu ^{-}$ pair; $\psi _{{-\mathbf p}}(\mathbf{r})$ and $\psi _b(\mathbf{r})$ are the wave functions of the positron and the bound electrons. The wave functions $\varphi _{{-\mathbf p}_1}$ and $\varphi _{\mathbf{p}_2}$ describe the positive and negative muons carrying momenta $\mathbf{p}_1$ and $\mathbf{p}_2$ respectively. We employ the Feynman gauge for the photon propagator.

The muon wave functions should be calculated in the atomic field with nucleus of finite size. At large $E \gg m_{\mu }$, the positron can be described by the FSM functions. Recall that the accuracy of the latter can be estimated as $\alpha ^2Z^2/\ell _{eff}$, with $\ell _{eff}$ the effective value of the orbital moment. Since a large momentum $q \sim m_{\mu }$ should be transferred to the nucleus, the process takes place at distances $r \sim 1/m_{\mu }$ from the center of the nucleus. Thus we can estimate $\ell _{eff}=pr \gg 1$.

We shall carry out the calculations in the lowest order of $\alpha Z$. A large momentum $\mathbf{q} \sim m_{\mu }$ can be transferred to the nucleus by any of four charged particles. As we know, transfer of large momenta can be treated perturbatively, and we represent the amplitude A as the sum of four terms,

$$A\ =\ A_a+A_b+A_c+A_d,$$

corresponding to transfer of the momentum q by the bound electron, by the incoming positron, and by the final-state muons $\mu ^{\pm }$ respectively.

We begin with the transfer of the large momentum by the bound electron. At $q \sim m_{\mu }$, we must take into account the finite size of the nucleus. For the wave function of an electron bound in an atom with a nucleus of finite size, we can write, analogously to (2.94),

$$\begin{aligned} \psi _b(\mathbf{q})\ =\ -\frac{8 \pi \eta }{q^4}\frac{{{\varvec{\alpha }}}\mathbf{q}}{2m}\psi _b(r=0)F(q)u_0\,, \end{aligned}$$

(11.72)

with the nonrelativistic function $\psi _b(r=0)$ on the RHS. In further calculations, we employ the notation $N_b=\psi _b(r=0)$. The charge form factor F(q) is normalized by the condition $F(0)=1$. Describing the continuum particles by plane waves, we write in momentum representation

$$\begin{aligned} A_a\ =\ -(4\pi )^2\alpha ^2ZN_bF(q)\frac{\bar{u}(p_2)\gamma _{\mu }u(-p_1)\bar{u}(-p)\tilde{q}\gamma ^\mu u_0}{q^4s}, \end{aligned}$$

(11.73)

with $s\,{=}\,(p_1+p_2)^2\,{=}\,(E_1+E_2)^2-(\mathbf{p}_1+\mathbf{p}_2)^2\,{=}\,(m+E)^2-(\mathbf{p}-\mathbf{q})^2\,{=}\,2mE+2\mathbf{p}{} \mathbf{q}-q^2$ the denominator of the photon propagator. Note that $s \ge 4m_{\mu }^2$.

Transfer of the momentum q by the incoming positron is determined by the lowest-order correction to the plane wave:

$$\begin{aligned} A_b=\, 4\pi \alpha \frac{\bar{u}(p_2)\gamma _{\mu }u(-p_1)}{s}\int \frac{d^3f}{(2\pi )^3} \frac{\bar{u}(-p)\gamma _0(\hat{k} +m)\gamma ^{\mu }u_0}{k^2-m^2}\cdot \frac{-4\pi \alpha ZF(\mathbf{q} + \mathbf{f})}{(\mathbf{q}+\mathbf{f})^2} \psi (\mathbf{f}); \end{aligned}$$

(11.74)

$$ k\ =\ (-E, \mathbf{q}-\mathbf{p}+\mathbf{f})\,. $$

Since the integral over f is saturated by $f\sim \eta \ll q$, we can neglect f everywhere except in the argument of the bound-state wave function. This leads to

$$\begin{aligned} A_b\ =\ (4\pi )^2\alpha ^2ZN_bF(q)\frac{\bar{u}(p_2)\gamma _\mu u(-p_1)\bar{u}(-p)(2E+\tilde{q}) \gamma ^\mu u_0}{q^2as}; \quad a\ =\ 2\mathbf{p}{} \mathbf{q}-q^2. \end{aligned}$$

(11.75)

In a similar way, one can find the contribution of the terms corresponding to the transfer of momentum q by the final-state muons:

$$\begin{aligned} A_c+A_d= & {} \frac{(4\pi )^2\alpha ^2 ZN_bF(q)}{s'q^2}\bigg [2\Big (\frac{E_2}{a_2}-\frac{E_1}{a_1}\Big ) \bar{u}(p_2)\gamma ^{\mu }u(-p_1)\ \nonumber \\&\qquad \,-\ \frac{\bar{u}(p_2)\gamma ^{\mu }\tilde{q}u(-p_1)}{a_1}- \frac{\bar{u}(p_2)\tilde{q}\gamma ^{\mu }u(-p_1)}{a_2}\bigg ]\bar{u}(-p)\gamma _{\mu }u_0\,. \end{aligned}$$

(11.76)

Here $s'=(p+p')^2; \quad a_i=2\mathbf{p}_i\mathbf{q}+q^2$. Since $\psi _b(r=0)=0$ for the bound states with $\ell \ne 0$, only the s states contribute to the amplitude.

Note that the denominator of the photon propagator $s'=(p+p')^2 \approx 2mE$ is much smaller than that in the amplitudes $A_a$ and $A_b$, i.e., $s'/s \sim mE/m_{\mu }^2$. Considering the energies

$$\begin{aligned} E\ \ll \ {\mathscr {E}}_0, \end{aligned}$$

(11.77)

we can put $A=A_c+A_d$ in the main part of the phase volume, since here, $|A_a+A_b| \ll |A_c+A_d|$. Thus the large momentum q is transferred to the nucleus mainly by the final-state muons. In the configuration with $\mathbf{p}_1=\mathbf{p}_2$ directed along $\mathbf{p}$, the sum of the contributions is $A_c+A_d=0$. Hence, in the vicinity of this point, all the terms on the RHS of (11.71) are important. Also, at $\mathbf{p}_1\approx \mathbf{p}_2$, the relative velocity of the outgoing $\mu ^+$ and $\mu ^-$ is small, and they undergo strong attraction; see a similar situation in pair creation by a photon in the field of the nucleus [13].

The differential cross section of the muon pair creation in annihilation with the electrons in the s state can be written as

$$\begin{aligned} d\sigma \ =\ 2\pi \alpha \frac{N_b^2}{m^2E}d\sigma _{\gamma \mu ^+\mu ^-}\,, \end{aligned}$$

(11.78)

with $\sigma _{\gamma \mu ^+\mu ^{-}}$ the cross section for muon pair creation by a photon with energy E and three-momentum $\mathbf{p}$. We consider energies $E \ge 2m_{\mu } \gg m$, and thus we can put $E^2=p^2$. In the limit of a point nucleus $F(q)=1$, the cross section $\sigma _{\gamma \mu ^+\mu ^-}$ can be evaluated analytically. However, this limit works only for very light atoms, for which the cross section is very small. We carry out analysis that takes into account the finite size of the nucleus.

The differential cross section (11.78) can be written as

$$\begin{aligned} d\sigma \ =\ \tau (Z)\frac{m_\mu ^4}{q^4}\frac{p_1p_2}{E^2m_\mu }F^2(q)S(\mathbf{p}_1, \mathbf{p}_2)dE_1dt_1dt_2d\varphi \,. \end{aligned}$$

(11.79)

Here $t_i=\cos {\theta _i}$, $\theta _i$ are the angles between momenta $\mathbf{p}_i$ and $\mathbf{p}$, $\varphi$ is the angle between the planes determined by the vectors $\mathbf{p}_1, \mathbf{p}$ and $\mathbf{p}_2, \mathbf{p}$,

$$\begin{aligned} S(\mathbf{p}_1, \mathbf{p}_2)=4m_{\mu }^2\Big (\frac{E_2}{a_2}-\frac{E_1}{a_1}\Big )^2-m_\mu ^2 q^2\Big (\frac{1}{a_2}-\frac{1}{a_1}\Big )^2+ \end{aligned}$$

(11.80)

$$\frac{2}{a_1a_2}\Big ([\mathbf{p_1}{} \mathbf{q}]^2+ [\mathbf{p_2}{} \mathbf{q}]^2\Big )^2,$$

and

$$\begin{aligned} \tau (Z)\ =\ 4r_\mu ^2(\alpha Z)^2\frac{N_b^2}{m^2m_\mu }; \quad r_\mu \ =\ \frac{\alpha }{m_\mu }\,. \end{aligned}$$

(11.81)

Note that for the K shell of the hydrogenlike atom with point nucleus, we have $N_b^2=\eta ^3/\pi$, and

$$\begin{aligned} \tau (Z)\ =\ \frac{4}{\pi }r_\mu ^2 (\alpha Z)^5 \frac{m}{m_\mu }\ =\ 0.0114 (\alpha Z)^5 \mu b \end{aligned}$$

(11.82)

provides the scale for the cross section $\sigma$. Assuming a uniform distribution in the sphere of radius R for the electric charge of the nucleus, we obtain for the form factor

$$\begin{aligned} F(q)\ =\ \frac{3(\sin {qR}-qR\cos {qr})}{q^3R^3}\,; \quad R\ =\ 1.2\cdot A^{1/3}\,\mathrm Fm \end{aligned}$$

(11.83)

(recall that 1Fm = $10^{-13}$ cm), with A the number of nucleons in the considered nucleus. Since the nonrelativistic wave functions with $\ell \ne 0$ become zero at the origin, only the s atomic electrons contribute to the process. The K electrons provide the leading contribution.

The final-state muon $\mu ^{-}$ can be captured to the atomic bound state. In the process,

$$ e^{+} +A\ \rightarrow \ A^{(\mu )}+\mu ^{+}; $$

$A^{(\mu )}$ denotes the mesoatom, i.e., the atom in which one of the electrons is replaced by the muon $\mu ^{-}$. The amplitude is represented by (11.71) with the wave function $\varphi _{\mathbf{p}_2}(\mathbf{r}')$ of the continuum muon $\mu ^{-}$ replaced by its bound-state function in the field of the atom with the nucleus of finite size. The energy conservation law is now $E+m-I_b=E_1+m_{\mu }-I_b^{(\mu )}$, with the last term the ionization potential of the mesoatom. The cross section is connected with the cross section $\sigma ^{b}_{\gamma \mu ^+\mu ^{-}}$ of the process in which the photon with energy E and three-momentum $\mathbf{p}$ creates a $\mu ^+\mu ^{-}$ pair with the negative muon bound in the atom. In the lowest order of the $\alpha Z$ expansion,

$$\begin{aligned} \sigma =2\alpha (\alpha Z)^3\frac{m}{E}\sigma ^{b}_{\gamma \mu ^+\mu ^{-}}. \end{aligned}$$

(11.84)

To calculate the cross section $\sigma ^{b}_{\gamma \mu ^+\mu ^{-}}$, one needs the wave function of the bound muon in the field of the finite-size nucleus. It can be found by numerical solution of the Dirac equation. Using the relativistic Coulomb functions for describing the bound electrons and the FSM positron wave functions enables us to trace the nuclear charge dependence of the cross section [14]. At characteristic energy $E=10 m_{\mu }\approx 1$ GeV, it is $\sigma =10^{-5}\mu b$ for $Z=60$, yielding $1.5\cdot 10^{-5}\mu b$ for $Z=92$.

At $E \gtrsim {\mathscr {E}}_0$, annihilation on the free electrons becomes possible. In annihilation on a bound electron, a small momentum $q \sim \eta$ is transferred to the nucleus. The total cross section for annihilation on a bound electron is equal to that on a free electron. The latter is [15]

$$\begin{aligned} \sigma _0\ =\ \frac{2\pi }{3} r_e^2 \frac{m}{E}\Big (1+\frac{{\mathscr {E}}_0}{2E}\Big ) \Big (1-\frac{{\mathscr {E}}_0}{E}\Big )^{1/2}. \end{aligned}$$

(11.85)

Thus the cross section for annihilation with an atom containing $N_e$ electrons is $\sigma _A=N_e\sigma _0$. In the vicinity of the threshold $E-{\mathscr {E}}_0\sim m_\mu \alpha ^2$, (11.85) is invalid, since the interaction of the outgoing muons should be taken into account. The RHS of (11.85) obtains a factor that is the wave function of the relative motion of the muons at the origin [13]. Thus at $E \rightarrow {\mathscr {E}}_0$, the cross section has a finite value.

Note that $\mu ^-$ and $\mu ^+$ can form a bound state with binding energy $m_\mu \alpha ^2/4\approx 1.4$ keV. The threshold of this channel is smaller than ${\mathscr {E}}_0$ by that value.

The cross sections $\sigma _0$ and $\sigma _A$ reach their largest values at $E\approx 1.7{\mathscr {E}}_0$. Here $\sigma _0\approx r_e^2m^2/m^2_\mu \approx 1\mu b$, and thus $\sigma \approx N_e[\mu b]$.