Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Forecasting has become an important research area and is applied in many fields such as in sciences, economy, meteorology, politic and to any system if there, exist uncertainty on that system in the future. Before the emergence of mathematical and computer models so called machine learning algorithms, forecasting was carried out by human experts. In this approach, all parameters that are possibly give effect to the system to be forecasted are considered and judged by the experts before producing the forecasting output. Unfortunately, forecasting using human experts is very vague and sometimes arguable since it is totally depends on the expert’s knowledge, experiences an interest. Other than using human experts, there exists other prediction approach: Statistical Prediction Rules which is more reliable and robust [1]. One of the popular methods in Statistical Prediction Rules is Time Series Prediction where it uses a model to forecast future events based on known past events: to forecast future data points before they are measured.

A time series consists of sequence of numbers which explained the status of an activity versus time. In more detail, a time series is a sequence of data points, measured typically at successive times, spaced at (often uniform) time intervals. A time series has features that are easily understood. For instance a stock price time series has a long term trend, seasonal and random variations while a cereal crops price time series contains only seasonal components [2]. There exist many approaches to perform time series forecasting. Among the approaches are Box-Jenkins Approach (ARMA/ARIMA) [3], Regression analysis [4], Artificial Neural Networks (ANN) [5], Fuzzy Logic (FL) [6] and Genetic Algorithms [GA] [7]. However among them, the computational intelligence technique such as ANN, FL and GA are getting more attention in time series forecasting because they are non-linear in nature and able to approximate easily complex dynamically system [8–11].

In its typical implementation, ANN will be trained by using the existing set of previous data. After the ANN reaches its optimized performance, the training process is stopped. Then the optimized ANN will be used to estimate the forthcoming output based on the current received inputs. This form of implementation is called as offline mode and is implemented in real-world, especially in power generator station [12, 13]. However, studies shown forecasting in the offline mode has several disadvantages. The major disadvantage is that the ANN parameters must be updated from time to time to suite with the various changing of the incoming data. This requires the ANN to be trained again by including the latest available data for the training. If the updating process is neglected, the ANN will generate incorrect forecasting whenever they receive unseen input data beyond the training data set. In situation where the data are non-stationary, the offline forecaster will be under performance, unless it is continuously being updated to track non-stationarities. This calls for online forecasting technique, where the parameters of the ANN will be adaptive to the latest available data.

2 Materials and Methods

2.1 Radial Basis Function

The Radial basis function (RBF) neural networks typically have three layers: an input layer, a hidden layer with a non-linear RBF activation function and a linear output layer. Each layer consists of one or more nodes depending on the design. The nodes in input layer are connected to the nodes in hidden layer while the nodes in hidden layer are connected to the nodes in the output layer via linear weights [14]. The output from each node in the hidden layer is given as:

$$ Z_{j} =\Phi \left( {||v(t) - c_{j} (t)||} \right)\quad j = 1, 2, 3\ldots \ldots \ldots n_{h} . $$
(1)

where \( c_{j} \left( t \right) \) and n h representing the RBF centre and number of hidden nodes, \( v\left( t \right) \) is the input vector to the RBF and \( \Phi ( \bullet ) \) representing the temporary activation function while ||•|| represents the Euclidean distance between the input vector and RBF centre. The initial value of the RBF centre, \( c_{j} \left( t \right) \) is given by taking the first data of the series as the RBF centre. The activation function \( \Phi ( \bullet ) \) used is Thin Plate Spline given by \( \Phi \left( a \right) = a^{2} \log \left( a \right) \), where a = \( a = ||v(t) - c_{j} (t)|| \) is Euclidean distance. The Euclidean distance for each hidden node is given by:

Euclidean distance,

$$ a_{j} = \sqrt {\sum\limits_{i = 1}^{n} {\left( {c_{ij} (t) - v_{j} (t)} \right)^{2} } } . $$
(2)

where c ij (t) = RBF centre for the j-th hidden node and i-th input, and \( v_{i} (t) \) = the i-th input. The RBF output is given by:

$$ y_{k} (t) = w_{k0} + \sum\limits_{j = 1}^{{n_{h} }} {w_{kj} }\Phi \left( {||v(t) - c_{j} (t)||} \right);\quad k = 1,2,3, \ldots \ldots m. $$
(3)

where \( w_{kj} \), is the weight between hidden node and output node and m is the number of output node.

2.2 Adaptive Learning Algorithms

Two parameters, namely, the RBF centre in hidden nodes and weights between the hidden nodes and the output nodes were updated using the Adaptive Fuzzy C-Means Clustering (AFCMC) and the Exponential Weighted Recursive Least Square (e-WRLS) algorithms respectively [15, 16].

Adaptive Fuzzy C-Means Clustering. Give initial value to \( c_{j} \)(0), μ(0) and q, where 0 ≤ μ(0) ≤ 1.0 and 0 ≤ q ≤ 1.0 (the typical value is between 0.30 to 0.95 respectively). Then compute the Euclidean distance d j (t) between input v(t) and centre c j (t). Obtain the shortest distance, d s (t) longest distance d l (t), nearest centret c s (t) and distant centre c l (t).

For j = 1 to j = n c , where n c  = number of RBF centre,

  1. (a)

    Updates the square distance between centre and input v(t) using:

    $$ \gamma (t) = \frac{1}{{n_{c} }}\sum\limits_{k = 1}^{{n_{c} }} {\mathop {\left[ {||v(t) - c_{k} (t)||} \right]}\nolimits^{2} } . $$
    (4)
  2. (b)

    if j ≠ s that is if that centre is not c s centre, updates the centre by referring to:

    $$ \Delta c_{j} = \mu (t)\vartheta (t)\left[ {v(t) - c_{j} (t - 1)} \right]. $$
    (5)

    where

    $$ \vartheta (t) = \left\{ {\begin{array}{*{20}l} {D_{l} \left( t \right)D_{j} \left( t \right)\exp \left[ { - D_{a} \left( t \right)} \right]} \hfill & {if\,d_{j} > 0} \hfill \\ {D_{l} \left( t \right)\exp \left[ { - D_{a} \left( t \right)} \right]} \hfill & {if\,d_{j} = 0} \hfill \\ \end{array} } \right.. $$
    (6)

    and

    \( D_{l} \left( t \right) = \frac{\gamma \left( t \right)}{{d_{l}^{2} }} \),\( D_{j} \left( t \right) = \frac{{d_{a}^{2} \left( t \right)}}{{d_{j}^{2} \left( t \right)}} \) and \( D_{a} \left( t \right) = \frac{{d_{a}^{2} \left( t \right)}}{\gamma \left( t \right)} \) with a = s if d s (t) > 0 and a = z

    if d s (t) = 0, (d z (t) = smallest nonzero distance between v(t) and c j (t)).

  3. (c)

    updates c s (t) using

    $$ \Delta c_{s} \left( t \right) = \mu \left( t \right)\varphi \left( t \right)\left[ {v\left( t \right) - c_{s} \left( {t - 1} \right)} \right] . $$
    (7)

Where

$$ \begin{aligned} \varphi \left( t \right) = \left\{ {\begin{array}{*{20}l} {\exp \left( { - \frac{{d_{s}^{2} \left( t \right)}}{\gamma \left( t \right)}} \right)} \hfill & {if\,d_{s} \left( t \right) > 0.} \hfill \\ 0 \hfill & {if\,d_{s} \left( t \right) = 0.} \hfill \\ \end{array} } \right. \hfill \\ \hfill \\ \end{aligned} $$
(8)

Measure the distance between c s (t) with all centres, \( h_{k} \left( t \right) = \left( {\left\| {c_{s} \left( t \right) - c_{k} \left( t \right)} \right\|} \right) \), k = 1, 2, 3, … n c and k ≠ s. If the shortest distance h c (t), is \( h_{c} \left( t \right) < \mu \left( t \right)d_{a} \left( t \right) \), move the nearest distance, c c (t) to new location based on:

$$ \Delta c_{c} \left( t \right) = - \frac{{\mu \left( t \right)d_{a}^{2} \left( t \right)}}{{d_{l}^{2} \left( t \right)}}\left( {c_{c} \left( t \right) - c_{s} \left( t \right)} \right). $$
(9)

Set t = t + 1, and repeat the above for each data sample. The diffusion coefficient \( \mu \left( t \right) \), is updates by using:

$$ \mu \left( t \right) = \mu \left( 0 \right)\exp \left( { - \frac{{qt^{2} }}{{n_{c}^{2} }}} \right) + \frac{{\exp \left( { - q\mu \left( {t - 1} \right)} \right)}}{{n_{c} }}. $$
(10)

Exponential Weighted Recursive Least Square. Set \( \hat{\beta }_{0}^{j} = 0 \) and construct matrix P 0 = αI. The typical value for α is 104 ≤ α ≤ 106 and I is Identity matrix of \( n_{h} \) (number of hidden nodes). Read the output from the hidden nodes, \( X_{k}^{T} \), and calculate K k and P k+1 using:

$$ K_{k} = \frac{{P_{k} X_{k + 1} }}{{\lambda + X_{k + 1}^{T} P_{k} X_{k + 1} }}, $$
(11)

and

$$ P_{k + 1} = \frac{{P_{k} }}{\lambda }\left\{ {I - K_{k} X_{k + 1}^{T} } \right\}. $$
(12)

where λ is a forgetting factor with its typical value of 0.95 ≤ λ ≤ 0.99. The λ can also be computed by:

$$ \lambda \left( t \right) = \lambda_{0} \lambda \left( {t - 1} \right) + \left( {1 - \lambda_{0} } \right). $$
(13)

where λ 0 = 0.99. Estimates \( \hat{\beta }_{k + 1}^{j} \) by using:

$$ \hat{\beta }_{k + 1}^{j} = \hat{\beta }_{k}^{j} + K_{k} \left[ {y_{k + 1} - X_{k + 1}^{T} \hat{\beta }_{k}^{j} } \right]. $$
(14)

Set k = k + 1, k = 1, 2, 3, … N where N is the number of data. Repeat steps 2–4 till converges. Because \( \xi \left(k \right) \) cannot be computed, \( \hat{\varepsilon }\left(k \right) \) is used to replace \( \xi \left(k \right) \) where \( \hat{\varepsilon }\left(k \right) \), is measurement error and can be computed by \( \hat{\varepsilon }\left(k \right) = y\left(k \right) - \hat{y}(k) \) where \( \hat{y} = X_{k}^{T} \hat{\beta}_{k - 1}. \)

3 Results and Discussion

3.1 Data

The forecasting performance is evaluated by using two simulated data and one real data. The simulated data are the Mackey-Glass nonlinear time series and Set A from Santa Fe Competition (SantaFe-A), while the real data is the IBM Stock Price data. The forecasting based on time series produced by the Mackey-Glass equation is regarded as a criterion for comparing the ability of different predicting method and is used in many time series forecasting researches [17, 18]. The SantaFe-A data were recorded from a Far-Infrared-Laser in a chaotic state. These data were chosen because they are a good example of the complicated behavior that can be seen in a clean, stationary, low-dimensional non-trivial physical system for which the underlying governing equations dynamics are well understood. The IBM data are the daily closing price of IBM stock from January 1, 1980 to October 8, 1992 [19].

3.2 Forecaster Optimization

The selection of input lag and the number of hidden node in the RBF have strong impact on the performance of a neural network based forecaster [3]. In parallel to this, the analysis on input selection (input lag) and number of hidden node that produce the optimized forecaster is conducted. The analysis starts by setting the RBF input with the data at elapsed time (t−1)(t−2) … (t−8)(t−9)(t−10) and increasing the hidden nodes one by one until it reaches 50. For each number of hidden nodes, the R2 value for one step ahead forecasting were recorded. The same process is repeated for the other input lag as tabulated in Table 1. The R2 values obtained from the analysis were plotted and the number of hidden node which gives the highest R2 values for all five input lags was used in the analysis to obtain the correct number of input lag. This analysis was conducted by setting the hidden node to the value obtained and varies the input lag from (t−1) to (t−1)(t−2) … (t−98)(t−99)(t−100). Table 2 shows the input lag and the number of hidden node which produce the best multiple steps ahead forecasting performance for the three data.

Table 1 List of input lags used to determine the correct number of hidden node
Full size table
Table 2 The best input lag and number of hidden node for the three data
Full size table

3.3 Forecasting Performance

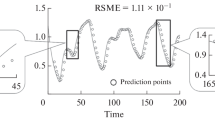
The findings obtained from the analyses in Sect. 3.2 were used to construct a universal online RBF forecaster for Mackey Glass data, SantaFe-A data and IBM Stock Price data. The performance of the forecaster to forecast the three data were tested. Figure 1 presented one to four steps ahead forecasting for the last 500 Mackey Glass data. For SantaFe-A data, due to the nature of data which is too fluctuating, only the last 100 actual and forecasted data are displayed in Fig. 2. Figure 3 presented the forecasting on 500 IBM Stock Price data. From plots in Figs. 1, 2, and 3, it can be observed that the online RBF forecaster is able to produce reliable and close forecasted values in most of the time. For both data, the input lags and number of hidden nodes which produce the best forecasting performance and the R2 values for one to four steps ahead forecasting are presented in Table 3.

Fig. 1
figure 1

One to four steps ahead forecasting for the last 500 Mackey Glass data

Full size image
Fig. 2
figure 2

One to four steps ahead forecasting for the last 100 SantaFe-A data

Full size image
Fig. 3
figure 3

One to four steps ahead forecasting for the last 500 IBM data

Full size image
Table 3 RMSE and R2 values for one to four steps ahead forecasting obtained by the online RBF forecaster
Full size table

The forecasting performance of the online RBF forecaster versus the offline RBF forecaster was also evaluated. Table 4 presents the RMSE and R2 values for four steps ahead forecasting achieved by the offline RBF forecaster.

Table 4 RMSE and R2 values for one to four steps ahead forecasting obtained by the offline RBF forecaster
Full size table

For Mackey Glass data, the performance of the offline RBF for one step ahead forecasting are slightly lower to compare with the online RBF. However for multiple steps ahead forecasting, the performance of offline RBF was absolutely poorer where significant deviations were recorded as the forecasting distance increases. The analysis on IBM stock price data also favors online RBF over offline RBF. It can be noted that the offline RBF is able to produce good one step ahead forecasting with 91 % accuracy. However it is considered low to compare with the accuracy obtained by online RBF which is 99 %. For other forecasting distance, namely two to four steps ahead, the offline RBF was failed to generate the acceptable forecasting performance. The forecasting performance obtained by the two, three and four steps ahead was lower than 0.6 and can be regarded as poor to compare with online RBF.

The superiority of online RBF over offline RBF on the Mackey Glass and IBM stock price data can be explained by the nature of the data themselves. It can be observed that both data display different patterns over times especially in the first half and second half of the data. Therefore by using the first half of the data for training are insufficient for the offline RBF to cover all patterns that were exhibited by the data in the next second half. This finding shows that the offline RBF is unable to generate good forecasting for any system which shows chaotic and non-stationary patterns over time.

However, different observation was obtained from the analysis on SantaFe-A data. For this data, the offline RBF produces higher performance in one to four steps ahead forecasting to compare with online RBF. This is again can be explained by the data itself where it can be noted that SantaFe-A data exhibit almost consistent patterns throughout the time. In brief, it can be said that the data is repeating themselves over times. Therefore by training the offline RBF using the first 500 data repeatedly was enough to cover the next 500 testing data. While for online RBF, continuous learning contributes to over fitting which degraded its forecasting ability.

4 Conclusion

More and more fields including science, financial, economy and meteorological adapt time series forecasting to solve uncertainty situation or outcomes in their respective fields. Due to the nature that problems to be solved are affected much by other parameters which change over time, the requirement of the online forecasting model is practical in real-world applications. This paper presented a tool to perform online multiple steps ahead time series forecasting using Radial Basis Function, which shows reliable and accurate forecasting capability.