Keywords

1 Introduction

In many applications, like in the porous media flow simulation where we model flow of water, gas and oil in reservoirs and aquifers, we need to numerically solve partial differential equations with highly heterogeneous coefficients representing for instance the permeability. It is known that high contrast in the coefficients causes many standard numerical methods to perform badly.

Domain decomposition methods are among the efficient solvers for systems of equations arising from the finite element discretizations of elliptic partial differential equations, cf. [22], and Additive Schwarz Methods (ASM) are among the most popular domain decomposition methods, cf. e.g. [3, 11, 15, 16] and references therein. In classical overlapping Additive Schwarz Methods the domain is divided into overlapping subdomains, where local subproblems are defined, and a coarse problem is defined globally for the scalability, cf. [22]. If subdomains are such that, in each subdomain, the variations in the coefficients are not too large, it is well known, that classical coarse spaces yield methods that are robust with respect to the variation, cf. e.g. [4, 15, 22]. In the recent years, the research has extended to highly heterogeneous coefficients, cf. e.g. [5–10, 14, 17–21, 23, 24]. In some of those works, the construction of coarse spaces have been based on enriching their coarse spaces with eigenfunctions of some generalized eigenvalue problems, cf. [1, 6, 7, 9, 14, 21], resulting in methods that are robust with respect to any heterogeneity. This has been the source of our inspiration in this paper.

We propose a parallel additive Schwarz preconditioner for the finite element discretization of the self-adjoint elliptic second order problem in 3D with highly heterogeneous and highly varying coefficients. Preconditioned conjugate gradients method (cf. [12]) is used to solve the resulting preconditioned system. The preconditioner is based on the abstract Schwarz framework where the solution space is decomposed into subspaces associated with the overlapping subdomains, and a specially constructed multiscale coarse space associated with the wire basket of the decomposition, which is then enriched with functions based on solving generalized eigenvalue problems defined locally over each face. The present work is an extension to 3D of the recent work of [9] in 2D. The obtained bounds are independent of the geometries of the subdomains, and the heterogeneities in the coefficients.

The remainder of this paper is organized as follows, in Sect. 2 we present the finite element discretization. In Sect. 3 we present our coarse space introducing the multiscale finite element functions and the functions based on generalized eigenvalue problem on each face. Section 4 contains a description of the overlapping additive Schwarz preconditioner, and in Sect. 5 we briefly discuss the implementation issues.

2 Finite Element Discretization

The aim is to find an approximation to the solution of the following self-adjoint second order elliptic differential problem: find \(u^*\in H^1_0(\varOmega )\) such that

$$\begin{aligned} a(u^*,v)=f(v)\qquad \forall v \in H^1_0(\varOmega ), \end{aligned}$$
(1)

where

$$\begin{aligned} a(u,v)= & {} \int _\varOmega \alpha (x) (\nabla u)^T\nabla v \,d x, \qquad f(v) = \int _\varOmega f v \, d x. \end{aligned}$$
(2)

Here \(\varOmega \) is a polygonal domain in the three dimensional space, \(f \in L^2(\varOmega )\) and \(\alpha \) is a strictly positive and bounded function. Hence, we can always scale \(\alpha \) by its minimal value; we further assume that \(\alpha \ge 1\).

We introduce a quasi-uniform triangulation of the domain \(\varOmega \), denoting it with \(T_h(\varOmega )=T_h=\{\tau \}\), which consists of tetrahedrons \(\tau \), and we let \(h=\max _{\tau \in T_h}\mathrm {diam}(\tau )\) be the parameter of \(T_h\), cf. e.g. [2] for more details.

Let \(V_h\) be the finite element space of continuous functions which are piecewise linear over the triangulation \(T_h\) and zero on the boundary \(\partial \varOmega \). The degrees of freedom are associated with the nodes or nodal points which are the vertices of tetrahedrons.

Note that on each element \(\tau \in T_h\) the gradient \(\nabla u_{|\tau }\) is a constant vector, hence for \(u,v\in V^h\) we have \(\int _\tau \alpha (x)\nabla u^T \nabla v \,d x= (\nabla u_{|\tau }^T \nabla v_{|\tau }) \int _\tau \alpha (x)\, d x\), hence we can assume that \(\alpha (x)\) is piecewise constant over the elements of \(T_h\).

Remark 1

We can also consider a more general case when our differential problem is defined with the following symmetric bilinear form

$$ \int _\varOmega (\nabla u)^T A(x) \nabla v \, dx, $$

where \(A(x) \in (L^\infty (\varOmega ))^{3 \times 3}\) is symmetric, and strictly positive definite over \(\varOmega \) in the following sense:

$$\exists \, C_1,C_0>0, \; \forall x \in \varOmega , \; \forall \xi \in \mathbb {R}^3 \qquad C_0\xi ^T\xi \le \xi ^TA(x)\xi \le C_1\xi ^T\xi .$$

We can scale A and assume that \(C_0=1\) and the entries of A are piecewise constant functions over the elements of \(T_h\). If the condition number of \(A_{|\tau }\) in any \(\tau \in T_h\) remain uniformly bounded, we remark that the result of this paper holds true also for this case.

The discrete FEM problem is formulated as follows: find \(u_h \in V_h\) such that

$$\begin{aligned} a(u_h,v)=f(v) \qquad \forall v \in V_h. \end{aligned}$$
(3)

The problem has a unique solution by the Lax-Milgram lemma and there are error estimates, see e.g. [2] and references therein. By formulating the discrete problem in the standard nodal basis \(\{\phi _i\}_{x_i\in \varOmega _h}\), we get the following system of algebraic equations

$$\begin{aligned} A_h \varvec{u}_h=\varvec{f}_h \end{aligned}$$
(4)

where \(A_h=(a(\phi _i,\phi _j))_{i,j}\), \(\varvec{f}_h=(f_j)_{x_j\in \varOmega _h}\) with \(f_j=\int _\varOmega f(x)\psi _i\,dx\), and \(\varvec{u}_h=(u_i)_i\) with \(u_i=u_h(x_i)\). Here \(u_h=\sum _{x_i\in \varOmega _h} u_i \phi _i\). The resulting system is symmetric and in general very ill-conditioned; any standard iterative method may perform badly due to the ill-conditioning of the system.

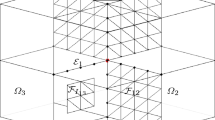
In this paper we present a method for solving such systems using the preconditioned conjugate method (cf. [12]) and propose an additive Schwarz preconditioner (cf. [22]). Let \(\varOmega \) be partitioned into a collection of disjoint open and connected substructures \(\varOmega _k\), such that \( \overline{\varOmega }=\bigcup _{k=1}^N\overline{\varOmega }_k. \) We assume that the triangulation \(T_h\) is aligned with the subdomains \(\varOmega _k\), that is any \(\tau \in T_h\) is contained in one subdomain, hence, each subdomain \(\varOmega _k\) inherits the local triangulation \(T_h(\varOmega _k)=\{\tau \in T_h: \tau \subset \varOmega _k\}\). Such a partition may be computed by a mesh partitioning software like e.g. METIS, cf. [13]. We make an additional assumption that the number of subdomains which share a vertex or an edge of an element of \(T_h\) is bounded by a constant. An important role is played by the interface \(\varGamma =\bigcup _{k=1}^N \partial \varOmega _k{\setminus } \partial \varOmega \). The non-empty intersection of two subdomains \(\partial \varOmega _i\cap \partial \varOmega _j\) not on \(\partial \varOmega \) is either a collection of 2D faces of elements of \(T_h\), in which case we say that \(\mathcal {\overline{F}}_{i j}=\partial \varOmega _i\cap \partial \varOmega _j\) is a generalized closed face, or it is a collection of closed edges of elements of \(T_h\), in which case we say that \(\mathcal {\overline{E}}_{i j}=\partial \varOmega _i\cap \partial \varOmega _j\) is a generalized closed edge, or it is a vertex of \(T_h\). We define the wire basket of this partition as the sum of the closed edges of the elements of \(T_h\), which are not on \(\partial \varOmega \) but are contained in more than two substructures, in other words those contained in any generalized edge, and we denote the wire basket by \(\mathcal {W}\). We also define the local wire basket \(\mathcal {W}_i=\mathcal {W}\cap \partial \varOmega _i\) which will play a crucial role in our analysis. We define the sets of nodal points, \(\varOmega _h,\partial \varOmega _h,\varOmega _{k,h}\), \(\mathcal {F}_{k l,h}\), \(\mathcal {E}_{k l,h}\), \(\mathcal {W}_{k, h}\) etc., as the sets of vertices of elements of \(T_h\), which are in \(\varOmega ,\partial \varOmega ,\varOmega _k\), \(\mathcal {F}_{k l}\), \(\mathcal {E}_{k l}\), \(\mathcal {W}_k\) etc., respectively.

3 Coarse Space

In our method, the key role is played by the global coarse space which is a space of discrete harmonic functions (cf. Sect. 3.1 below) and which consists of two space components: the multiscale coarse space component and the generalized face based eigenfunction space component.

3.1 Discrete Harmonic Extensions

We start by defining the discrete harmonic extensions. Local subspaces \(V_{h,k}\) are defined as restrictions, of the space \(V_h\) to \(\overline{\varOmega }_k\), that is

$$\begin{aligned} V_{h,k}=\{u_{|\overline{\varOmega }_k}: u\in V_h\}=\{v\in C(\overline{\varOmega }_k): v_{|\tau }\in \mathcal {P}_1(\tau ), \tau \in T_h( \varOmega _k ), v_{|\overline{\varOmega }_k\cap \partial \varOmega }=0 \}, \end{aligned}$$

and we let

$$ V_{h,k}^0=V_{h,k}\cap H^1_0(\varOmega _k). $$

Let the local discrete harmonic extension operator \(\mathcal {H}_k:V_{h,k}\rightarrow V_{h,k}\) be defined as the unique solution to the following local problem:

$$\begin{aligned} \left\{ \begin{array}{rcl} a_k(\mathcal {H}_k u,v)&{}=&{}0 \qquad \forall v\in V_{h,k}^0\\ \mathcal {H}_k u &{}=&{} u \quad \mathrm {on} \quad \partial \varOmega _k. \end{array} \right. \end{aligned}$$
(5)

where \(a_k(u,v)=\int _{\varOmega _k} \alpha (x)\nabla u^T \nabla v\, d x\). A function \(u \in V_{h,k}\) is discrete harmonic in \(\varOmega _k\) if \(u_{|\overline{\varOmega }_k}=\mathcal {H}_k u \in V_{h,k}\). For \(u\in V_h\), if all its restrictions to local subdomains are discrete harmonic then u is said to be piecewise discrete harmonic over the partition. Note that a discrete harmonic function in \(V_{k,h}\) is uniquely defined by its values at the nodal points in \(\partial \varOmega _{k,h}\).

3.2 Multiscale Coarse Space Component

We define the multiscale component of the coarse space here. We need a few extra definitions. Let \(V_h(\mathcal {F}_{k l})\) be the space of all traces of functions from \(V_h\) onto \(\mathcal {\overline{F}}_{k l}\) and let \(V_{h,0}(\mathcal {F}_{k l})\) be its subspace of functions taking zero values at the nodal points of \(\mathcal {W}_h\cap \mathcal {F}_{k l,h}\), i.e. the nodal points on the boundary of \(\mathcal{F}_{kl}\).

Note that as \(\alpha \) is piecewise constant over \(T_h\), it may have jumps across the 2D common faces of two neighboring elements (i.e. tetrahedrons) in \(T_h\). For any face \(f\subset \mathcal {F}_{k l}\) we define \(\overline{\alpha }_f=\max \{ \alpha _{|\tau _1},\alpha _{|\tau _2}\}\) where \(\tau _1\in T_h(\varOmega _k)\) and \(\tau _2\in T_h(\varOmega _l)\) are two neighboring elements such that f is their common face.

With each face \(\mathcal {F}_{k l}\), we associate a bilinear form \(a_{\mathcal {F}_{k l},h}:V_h(\mathcal {F}_{k l})\times V_h(\mathcal {F}_{k l})\rightarrow \mathbb {R}\), which is defined as

$$ a_{\mathcal {F}_{k l},h}(u,v)= \sum _{f \subset \mathcal {F}_{k l}} \int _f \overline{\alpha }_f \nabla u \nabla v \, d s, $$

where the sum is over the 2D faces of the elements of \(T_h\) forming the face \(\mathcal {F}_{k l}\), and the integral is over each such 2D face. Note that \(u\in V_h(\mathcal {F}_{k l})\) is continuous, and its restriction to such a face f is a linear polynomial.

Analogously, associated with the face \(\mathcal {F}_{k l}\), we define a scaled discrete weighted \(L^2\) inner product, a symmetric bilinear form \(b_{\mathcal {F}_{k l},h}:V_h(\mathcal {F}_{k l})\times V_h(\mathcal {F}_{k l})\rightarrow \mathbb {R}\), as

$$ b_{\mathcal {F}_{k l},h}(u,v)= \sum _{x \in \mathcal {F}_{k l,h}} \overline{\alpha }_x u(x) \, v(x), $$

where \(\overline{\alpha }_x=\max _{x\in \partial \tau }\alpha _{|\tau }\), i.e. is equal to the maximal value of \(\alpha _{|\tau }\) over all elements \(\tau \) sharing the node x as a vertex.

Finally, we introduce the multiscale coarse space component \(V_{ms}\subset V_h\) as the space of functions whose degrees of freedom are associated with the nodal points of \(\mathcal {W}_h\). For any function \(u \in V_{ms}\), on each face \(\mathcal {F}_{k l}\), it is defined as the solution of the following generalized face problem,

$$\begin{aligned} \left\{ \begin{array}{rcl} a_{\mathcal {F}_{k l},h} (u_{|\mathcal {F}_{k l}},v) &{}=&{}0 \qquad \forall v\in V_{h,0}(\mathcal {F}_{k l})\\ u_{|\mathcal {F}_{k l}} &{}=&{} u \quad \mathrm {on} \quad \partial \mathcal {F}_{k l}=\mathcal {W}\cap \mathcal {\overline{F}}_{k l}. \end{array} \right. \end{aligned}$$
(6)

and inside each subdomain, it is defined as the discrete harmonic extension in the sense of (5). So, once \(u\in V_{ms}\) is known at the nodal points of \(\mathcal{W}_h\), its values at the nodal points of each face can be computed by solving (6), and then its values at the nodal points of each subdomain can be computed by solving (5).

Proposition 1

The problem (6) has a unique solution.

Proof

Note that if the form \(a_{\mathcal {F}_{k l},h} (v,v)\) is zero for any \(v \in V_{h,0}(\mathcal {F}_{k l})\), then it means that v is constant on each 2D face \(f \subset \mathcal {F}_{k l}\). The continuity of v yields that v is equal to a single constant over all 2D faces contained in \(\mathcal {F}_{k l}\). Finally this constant is zero because v is zero at the nodal points on the wire basket (boundary of the face). This proves that the form is positive definite in \(V_{h,0}(\mathcal {F}_{k l})\).

Let \(\hat{u}\) be a function equal to u at the nodal points of \(\partial \mathcal {F}_{k l}\) and equal to zero at all nodal points in the interior of the face \(\mathcal {F}_{k l}\), i.e. not belonging to \(\mathcal {W}_h\). Then \(\tilde{u}:= u_{\mathcal {F}_{k l}}-\hat{u}\) is in \(V_{h,0}(\mathcal {F}_{k l})\) and we can rewrite (6) as: find \(\tilde{u} \in V_{h,0}(\mathcal {F}_{k l})\) such that

$$ a_{\mathcal {F}_{k l},h} (\tilde{u},v) =-a_{\mathcal {F}_{k l},h} (\hat{u},v) \qquad \forall v\in V_{h,0}(\mathcal {F}_{k l}), $$

which obviously has a unique solution due the positive definiteness of the bilinear form in \(V_{h,0}(\mathcal {F}_{k l})\).

Finally \(u \in V_{ms}\) is discrete harmonic in \(\varOmega _k\) and thus the values of u in \(\varOmega _{k,h}\) are uniquely defined by its values on the wire basket and on faces using (5). We note that the dimension of \(V_{ms}\) equals the number of all nodes in the set \(\mathcal {W}_h\).

3.3 Generalized Face Based Eigenfunction Space Component

We introduce a face based generalized eigenvalue problem: find \((\lambda ,\psi )\in \mathbb {R} \times V_{h,0}(\mathcal {F}_{k l})\) such that

$$\begin{aligned} a_{\mathcal {F}_{k l},h} (\psi ,v) = \lambda b_{\mathcal {F}_{k l},h} (\psi ,v) \qquad \forall v\in V_{h,0}(\mathcal {F}_{k l}) \end{aligned}$$
(7)

Since both bilinear forms are symmetric and positive definite in \(V_{h,0}(\mathcal {F}_{k l})\), there exist real and positive eigenvalues and their respective \(b_{\mathcal {F}_{k l},h}\)-orthogonal and normalized eigenvectors satisfying (7) such that

$$ 0<\lambda _1^{\mathcal {F}_{k l}}\le \lambda _2^{\mathcal {F}_{k l}}\le \ldots \le \lambda _M^{\mathcal {F}_{k l}}, $$

and

$$b_{\mathcal {F}_{k l},h} (\psi _j^{\mathcal {F}_{k l}},\psi _i^{\mathcal {F}_{k l}})=0\quad j\not =i, \qquad b_{\mathcal {F}_{k l},h} (\psi _j^{\mathcal {F}_{k l}},\psi _j^{\mathcal {F}_{k l}})=1. $$

Here M is the dimension of \(V_{h,0}(\mathcal {F}_{k l})\).

For any \(1\le n \le M \) we can define a orthogonal projection: \(\pi _n^{\mathcal {F}_{k l}}:V_{h,0}(\mathcal {F}_{k l}) \rightarrow span\{\psi _j^{\mathcal {F}_{k l}}\}_{j=1}^n \subset V_{h,0}(\mathcal {F}_{k l})\) as

$$\begin{aligned} \pi _n^{\mathcal {F}_{k l}} v= \sum _{j=1}^n b_{\mathcal {F}_{k l},h} (v,\psi _j^{\mathcal {F}_{k l}})\psi _j^{\mathcal {F}_{k l}}. \end{aligned}$$
(8)

By a simple algebraic argument (similar to those in [21] or [9]) we get the following lemma.

Lemma 1

The operator \(\pi _n^{\mathcal {F}_{k l}}\) is \(a_{\mathcal {F}_{k l},h}\)-orthogonal projection and moreover

$$\begin{aligned} \Vert v-\pi _n^{\mathcal {F}_{k l}} v\Vert ^{2}_{b,\mathcal {F}_{k l}}\le \frac{1}{\lambda _{n+1}^{\mathcal {F}_{k l}}} \Vert v-\pi _n^{\mathcal {F}_{k l}} v\Vert ^{2}_{a,\mathcal {F}_{k l}} \quad \forall v\in V_{h,0}(\mathcal {F}_{k l}), \end{aligned}$$

where \(\Vert v\Vert _{a,\mathcal {F}_{k l}}^2= a_{\mathcal {F}_{k l},h}(v, v)\) and \(\Vert v\Vert _{b,\mathcal {F}_{k l}}^2= b_{\mathcal {F}_{k l},h}(v, v)\).

We further assume that a nonnegative number \(n(\mathcal {F}_{k l})\), not greater than the dimension of \(V_{h,0}(\mathcal {F}_{k l})\), is known or given for each face \(\mathcal {F}_{k l}\). Then for each eigenvector \(\psi _j^{\mathcal {F}_{k l}}\), \(1\le j \le n(\mathcal {F}_{k l})\) we define \(\varPsi _j^{\mathcal {F}_{k l}} \in V_h\) which is equal to \(\psi _j^{\mathcal {F}_{k l}}\) on the face \(\mathcal {F}_{k l}\), zero on the remaining faces and everywhere on the wire basket \(\mathcal {W}\), and finally discrete harmonic inside each subdomain in the sense of (5) defining uniquely its values at all interior nodes of the subdomain. We are now able to introduce the face based eigenfunction space component which is

$$ V_{h,n}^{\mathcal {F}_{k l}}=span\{\varPsi _j^{\mathcal {F}_{k l}}\}_{j=1}^{n(\mathcal {F}_{k l})}, \qquad \forall \mathcal {F}_{k l}\subset \varGamma . $$

Finally, our coarse space is defined as follows:

$$\begin{aligned} V_0:=V_{ms} + \sum _{\mathcal {F}_{k l}\subset \varGamma } V_{h,n}^{\mathcal {F}_{k l}}. \end{aligned}$$
(9)

4 Additive Schwarz Method (ASM) Preconditioner

We define our preconditioner utilizing the abstract framework of ASM, i.e. we introduce a decomposition of the global space \(V_h\) into the sum of smaller subspaces of \(V_h\), and define symmetric positive definite bilinear forms on the subspaces; cf. [22]. In our present work, we consider only the original bilinear form a(u, v), i.e. (2), on each subspace.

The coarse space is defined in the previous section, cf. (9). The local subspace \(V_k\) associated with the subdomain \(\varOmega _k\), is defined as the space of all functions \(u\in V_h\) which take the value zero at all nodal points that lie outside \(\overline{\varOmega }_k\). It is easy to see that \(V_h= \sum _{k=1}^N V_k\). Now, including the coarse space, we have the following decomposition:

$$ V_h=V_0+\sum _{k=1}^N V_k. $$

The additive Schwarz operator \(T:V_h\rightarrow V_h\) is defined in terms of the projection like operators, \(T_k, k=0\cdots N\), as follows, i.e. \( T=T_0 + \sum _{k=1}^N T_k, \) where the coarse space projection like operator, \(T_0: V_h\rightarrow V_0\), is defined as

$$ a(T_0u,v)=a(u,v) \qquad \forall v\in V_0, $$

and the local subspace projection operators, \(T_k:V_h\rightarrow V_k\), are defined as

$$ a(T_ku,v)=a(u,v) \qquad \forall v\in V_k, \qquad k=1,\ldots ,N.$$

Under the Schwarz framework, the problem (3) is then reformulated as the following equivalent preconditioned system,

$$\begin{aligned} T u_h=g, \end{aligned}$$
(10)

where \(g=g_0+\sum _{k=1}^N g_k \) with \(g_0=T_0u_h^*\), \(g_k=T_ku_h^*\), \(k=1,\ldots ,N\), and \(u_h^*\) the exact solution. Note that the right hand side vectors, \(g_k, k=0\cdots ,N,\) can be calculated without explicitly knowing the exact solution.

4.1 An Estimate of the Condition Number

We present the main result of this paper, namely, an estimate of the condition number of the preconditioned system (3), which is given in the following theorem.

Theorem 1

There exist positive constants c and C such that

$$\begin{aligned} c(1+ \max _{\mathcal {F}_{k l}}(\lambda _{n+1}^{\mathcal {F}_{k l}})^{-1})^{-1}\, a(u,u) \le a(Tu,u)\le & {} C \, a(u,u) \qquad \forall u \in V_h, \end{aligned}$$

where \(\lambda _{n+1}^{\mathcal {F}_{k l}}\) and \(n=n(\mathcal {F}_{k l})\) are as defined in Sect. 3.3, and c, C are constants independent of \(\alpha ,h\) and the number of subdomains.

A Sketch of the Proof. The proof is based on the abstract Schwarz framework, where we need to verify the three key assumptions of the framework, see [22] for the framework. The first two assumptions, that is, the local stability and strengthened Schwarz-Cauchy inequalities, follow immediately from standard arguments. The last assumption, that is the assumption on the stable decomposition, is less trivial.

We propose the following decomposition of u, \(u=u_0+\sum _{i=1}^N u_i\), with \(u_i\in V_i\) for \(i=0,\ldots ,N\). For any \(u \in V_h\) we let \(u_0\in V_0\) be defined as follows. Let \(u_{ms} \in V_{ms}\) be equal to u at all nodes of \(\mathcal {W}_h\). The restriction of \(u-u_{ms}\) to a face \(\mathcal {F}_{k l}\) is then a function in \(V_{h,0}(\mathcal {F}_{k l})\). Let \(u_{k l} \in V_{h,n}^{\mathcal {F}_{k l}}\) be equal to \(\pi _n^{\mathcal {F}_{k l}}(u-u_{ms})\) (cf. (8)). Note that \(u_{k l}\) is zero at all wire basket nodes and discrete harmonic inside subdomains. Now, by letting \(u_0=u_{ms}+\sum _{\mathcal {F}_{k l}\subset \varGamma } u_{k l}\), and \(u_i = I_h(\theta _i(u-u_0))\), where \(\{\theta _i\}\) is the standard partition of unity with respect to the partition \(\{{\varOmega }_i\}\) and \(I_h\) the standard nodal interpolation operator.

Now using the above decomposition, and the estimates of Lemma 1 we can show that

$$ a(u_0,u_0)+\sum _{k=1}^Na(u_k,u_k) \le C (1+ \max _{\mathcal {F}_{k l}}(\lambda _{n+1}^{\mathcal {F}_{k l}})^{-1} ) a(u,u), $$

where C is a constant independent of \(\alpha ,h\) and number of subdomains. The proof of the theorem then follows from the abstract Schwarz framework, cf. e.g. [22].

Remark 2

The idea is to collect eigenfunctions with the smallest eigenvalues (bad eigenmodes) into the coarse space, whereby removing their influence on the convergence. Normally, the bad modes are associated with the channels (regions with large coefficients) crossing the interface \(\mathcal {F}_{k l}\). The number of eigenfunctions, \(n(\mathcal {F}_{k l})\), required for the robustness, can either be preassigned from experience or chosen adaptively by setting a threshold and choosing those eigenfunctions whose eigenvalues are smaller than the threshold.

Remark 3

Although, an explicit dependence on the mesh parameters does not appear in the convergence estimate of Theorem 1, it is not difficult to tell that this dependence is somehow hidden in the eigenvalues of the face eigenvalue problems, and as soon as the influence of the bad eigenmodes have been removed, it will start to show, at least numerically. However, if we choose the threshold, cf. Remark 2, to be in the order of \(\frac{h}{H}\), it is straightforward to see that the convergence will be in the order of \(\frac{H}{h}\).

5 Implementation Issues

In this section, we briefly discuss the implementation of our ASM preconditioner. We propose to use the preconditioned conjugate gradient iteration (cf. e.g. [12]) for the system (10). Constructing the coarse space requires the solution of the generalized eigenvalue problem (7) on each subdomain face (interface), the first few eigenfunctions corresponding to the smallest eigenvalues are then included in the coarse space. Prescribing a threshold \(\lambda _0\), and then computing the eigenpairs with eigenvalues smaller than \(\lambda _0\), we can get an automatic way to enrich the coarse space. The simplest way would be to compute a fixed number of eigenpairs, e.g. \(n=5\) or so, this may however not guarantee robustness as the number of channels crossing a face may be much larger. In each step of PCG we compute a residual vector which requires solving the coarse problem and local subproblems, cf. [22]. All these problems are independent so they can be solved in parallel. The local subdomain problems are solved locally on their respective subdomains. The coarse problem is global, and although its dimension equals the number of nodes on the wire basket plus the number of local eigenfunctions, the coarse stiffness matrix is quite sparse. However, if we add too many of the eigenfunctions, the coarse space may become too large and the coarse problem too expensive, on the other hand, if we add too few eigenfunctions then the condition number may be too large and the convergence of the iterative scheme too slow.