Bio-Inspired Algorithms and Preferences for Multi-objective Problems

Abstract

Multi-objective optimization evolutionary algorithms have been applied to solve many real-life decision problems. Most of them require the management of trade-offs between multiple objectives. Reference point approaches highlight a preferred set of solutions in relevant areas of Pareto frontier and support the decision makers to take more confidence evaluation. This paper extends some well-known algorithms to work with collective preferences and interactive techniques. In order to analyse the results driven by the online reference points, two new performance indicators are introduced and tested against some synthetic problem.

1 Introduction

Multi-objective optimization problems (MOPs) simultaneously optimize a set of objective functions. Formally posed, a MOP can be defined as $\min \varvec{F}(\varvec{x}) = \left\{ f_1(\varvec{x}),\ldots ,f_k(\varvec{x})\right\}$, where $\varvec{x}=\left\langle x_1,\cdots , x_n\right\rangle \in \varOmega$ is an n-dimensional vector of decision variables. The solution of a MOP is a (possibly infinite) Pareto-optimal set $P_S=\left\{ \varvec{x}\in \varOmega |\not {\exists }\varvec{y}\in \varOmega :\varvec{y}\prec \varvec{x}\right\}$ that contains all the elements of $\varOmega$ that not Pareto-dominated ($\prec$) by any other element [2]. Elements of $P_S$ represent different trade-offs between the objective functions values. The projection of $P_S$ through $F()$ is known as the Pareto-optimal front, $P_F$.

The application of evolutionary algorithms to MOPs has prompted the creation of multi-objective optimization evolutionary algorithms (MOEAs) [2]. They approximate the $P_S$ as a discrete set of points.

Having a solution to a MOP, a decision maker (DM) must identify which of those solutions are the ones that satisfy her/his preferences and would be realized in practice. This task can be rather complex and requires in-depth knowledge of the problem being solved, something that is impossible in many practical situations.

Reference points and interactive techniques can be used to mitigate these inconveniences and support the DM in reaching a proper specification. These approaches also allow the optimization algorithm to focus on areas of interest and thus reaching satisfactory solutions at a lower computational cost.

In practice, however, optimization problems pose difficulties in defining a priori reference points or preferences. In this regard, collective intelligence reference points obtained by the interaction and aggregation of multiple opinions can be used to produce an accurate representation of preferences and, hence, reference points. This approach can also eliminate the unilateral choice bias that can be introduced by a single DM. Collective environments can improve MOEAs with cognitive and subjective evaluation to find better solutions in more relevant regions of $P_F$.

This work incorporates online interactive collective preferences and interactive behaviour into three existing MOEAs: NSGA-II [6], SPEA2 [12] and SMS-EMOA [1] and, therefore, introduces a collective intelligence version of them. Similarly, while working in this task it became evident the lack of adequate performance indicators that take into account preferences. Therefore, as part of the paper are also introduced two new performance indicators that are used to evaluate the quality of the $P_F$ approximation driven by the online collective preferences.

The paper proceeds with Sect. 2 that covers some required formal foundations regarding reference points and collective intelligence. Section 3 introduces the novel interactive MOEAs. Subsequently, Sect. 4 presents the new performance indicators that are to be used later on. After that, Sect. 5 analyzes the performance of the algorithms when faced with benchmark problem. Finally, conclusive remarks and future work directions are put forward.

2 Foundations

Preferences are user-defined parameters and denote values or subjective impressions regarding the trade-offs points. It transforms qualitative feelings into quantitative values to bias the search during the optimization phase and restrict the objective space. In this sense, a reliable preference vector improves the trade-off answers obtained.

The reference point approach concentrates the search of Pareto non-dominated solutions near a selected point. It is based on the achievement scalarizing function that uses a reference point to capture the desired values of the objective functions. Let $\varvec{z}^{0}$ be a reference point for an n-objective optimization problem of minimizing $F(\varvec{x}) = \left\{ f_1(\varvec{x}), ..., f_k(\varvec{x}) \right\}$, the reference point scalarizing function can be stated as follows:

$$\begin{aligned} \sigma \left( \varvec{z}, \varvec{z}^{0}, \varvec{\lambda }, \rho \right) =\max \limits _{i=1,...,k} \left\{ \lambda _i(z_i-z_i^{0}) \right\} +\rho \sum \limits _{i=1}^{k} \lambda _i\left( z_i-z_i^{0}\right) , \end{aligned}$$

(1)

where $\varvec{z} \in \mathcal {Z}$ is one objective vector, $\varvec{z}^{0} = \left\langle z_1^{0},...,z_k^{0} \right\rangle$ is a reference point vector, $\sigma$ is a mapping from $\mathbb {R}^k$ onto $\mathbb {R}$, $\varvec{\lambda } = \left\langle \lambda _1,..., \lambda _k \right\rangle$ is a scaling coefficients vector, and $\rho$ is an arbitrary small positive number. Therefore, the achievement problem can be rebuilt as: $\min \sigma \left( \varvec{z}, \varvec{z}^{0}, \varvec{\lambda }, \rho \right)$.

A subset $X$ of $\mathbb {R}^n$ is convex if for any two pair of solutions $x^1, x^2 \in X$ and $\alpha \in [0,1]$, the following condition is true: $\alpha x^1+(1-\alpha )x^2 \in X$. The intersection of all the convex sets containing a given subset $X$ of $\mathbb {R}^n$ is called the convex hull of $X$. The convex hull of a set of points is the smallest convex set that contains the points.

The convex hull of individual minima (CHIM) is the set of points in $\mathbb {R}^k$ that are convex combinations of $F_i^*- F^*$:

$$\begin{aligned} \mathcal {H}=\left\{ \varPhi \beta : \beta \in \mathbb {R}^k, \sum \limits _{i=1}^k \beta _i=1, \beta _i\ge 0 \right\} \end{aligned}$$

(2)

where $x_i^*$ is the global minimizers of $f_i(\varvec{x})$, $\forall i \in \{1,\cdots , k\}$. Let $F_i^*= F(x_i^*), \forall i \in \{1,\cdots , k\}$; and $\varPhi$ is a pay-off matrix $k \text { x } k$ whose the $i^{th}$ column is $F_i^*- F^*$.

Since the beginning of 2000, the development of social network technologies and interactive online systems has promoted a broader understanding of the “intelligence” concept. A new phenomenon appeared based not only on the cognition of one individual, but also placed on a network of relationships with other people and the external world. The field known as collective intelligence (COIN) [9] is defined as the self-organized group intelligence arisen from participatory and collaboration actions of many individuals. Shared tasks or issues are handled by singular contributions in such a manner that their aggregation process creates better results and solves more problems than each particular contribution separately.

Inside collective environment, contributions come from different people. Clustering algorithms distinguish the users with similar preferences to perform a cooperative evolution or decision making choice. A mixture model is a probabilistic model to reveal distributions of observations in the overall population. Given a data set $Y=\{\varvec{y}_1,\ldots ,\varvec{y}_N\}$ where $\varvec{y}_i$ is a d-dimensional vector measurement with the points created from density $p(\varvec{y})$, a finite mixture model is defined as:

$$\begin{aligned} p\left( \varvec{y}|\varTheta \right) =\sum \limits _{k=1}^{K}\alpha _kp_k\left( \varvec{y}|z_k,\theta _k \right) \end{aligned}$$

(3)

Let $K\ge 1$ be the number of components, $p_k\left( \varvec{y}|z_k,\theta _k \right)$ be the mixture components where each k is a density or distribution over $p\left( \varvec{y}\right)$ and parameters $\theta _k$, $\varvec{z}=\left\langle z_1,\ldots ,z_k \right\rangle$ be a K-ary random variable defining the identity of the mixture component that produced $\varvec{y}$ and $\alpha _k=p_k\left( z_k \right)$ are the mixture weights representing the probability that $\varvec{y}$ was generated by component k. Hence, the parameters for a mixture model is $\varTheta = \{ \alpha _1,\ldots ,\alpha _K,\theta _1,\ldots ,\theta _K\}$, $1\le k \le K$.

The Central Limit Theorem [8], explains why many applications that are influenced by a large number of random factors have a probability density function that approximates a Gaussian distribution. Let Y be a sequence of random variables that are identically and independently distributed, with mean $\mu$ and variance $\sigma ^2$. The distribution of the normalised sum $S_n = \frac{1}{\sqrt{n}}(\varvec{y}_1 + \ldots + \varvec{y}_N)$ approaches the Gaussian distribution, $G(\mu ,\sigma ^2)$, as $n\rightarrow \infty$.

In a Gaussian mixture model, each of the K components is a Gaussian density with parameters $\theta =\{\varvec{\mu _k},\varSigma _k\}$, $\varvec{y} \in \mathbb {R}^d$ and function as:

$$\begin{aligned} p_k\left( \varvec{y}|\theta _k\right) = \frac{1}{ \left( 2\pi \right) ^{d/2} |\varSigma _k|^{1/2}}e^{-\frac{1}{2}\left( \varvec{y} - \varvec{\mu }_k\right) ^t \varSigma ^{-1}_k\left( \varvec{y}-\varvec{\mu }_k\right) } \end{aligned}$$

(4)

3 Interactive Algorithms

Interactive genetic algorithms (IGA) were successfully applied to get feedbacks of transitional results during the evolution process. IGA incorporates external evaluation to support problems whose optimization objectives are complex to be defined by a-priori exact functions. It employs users’ subjectivities as fitness values to drive the search engine.

As the purpose of this study is the enhancement of MOEAs through the use of the collective preferences, interactive genetic algorithms are an appropriate technique to support this goal. The new algorithms are extensions of the classical MOEAs: NSGA-II, SPEA2 and SMS-EMOA. The main changes on the original methods are the incorporation of COIN into the selection procedure; the transformation of the continuous evolutionary process into an interactive one; and the adoption of reference points to drive the search towards relevant regions in Pareto-optimal front.

3.1 CI-NSGA-II

One of the new algorithms is a variation of NSGA-II [6]. The NSGA-II is a non-domination based genetic algorithm for multi-objective optimization. It adopts two main concepts: a density information for diversity and a fast non-dominated sorting in the population. The crowding distance uses the size of the largest cuboid enclosing two neighboring solutions to estimate the density of points in the front. The non-dominated sorting places each individual into a specific front such that the first front $\tau _1$ is a non-dominant set, the second front $\tau _2$ is dominated only by the individuals in $\tau _1$ and so on. Each solution inside the front $\tau _n$ receives a rank equal to its non-domination level n.

The selection operator uses the rank ($i_{rank}$) and crowding distance ($i_{dist}$) in a binary tournament. The partial order $\prec _{c}$ between two individuals i and j, for example, prefers the minor domination rank if they are from different fronts or otherwise, the one with higher values of crowding distance.

$$\begin{aligned} i \prec _{c} j := i_{rank} < j_{rank} \vee (i_{rank} = j_{rank} \wedge i_{dist} > j_{dist}) \end{aligned}$$

(5)

In Algorithm 1, the new CI-NSGA-II converts the original NSGA-II into an interactive process. The subroutine CollectiveContributions() suspends the evolution progress and submits some individuals from population to the users’ evaluation. In this research, the individuals received can be analyzed in two different ways: (a) a pairwise comparison allows the selection of the best candidate between two or more individuals; (b) a dynamic game scenario stimulates the participant creativity to improve or produce new individuals. Both approaches discover online reference points.

Inside collective environment, the contributions come from different people. Assuming the Central Limit Theorem [8], the inputs have a distribution that is approximately Gaussian. Therefore, after each collective interaction, the subroutine ExpectationMaximization() gets the users’ collaboration as a Gaussian Mixture model to emulate the evaluation landscape of all participants’ preferences.

The expectation maximization approach creates online reference points ($\varTheta$) for search optimization. Whether the user’s collaboration is a simple vote on the best individual presented to him (pairwise comparison) or a complete re-edited individual, the clustering algorithm distinguishes the users with similar preferences to perform a cooperative evolution and a decision making choice through the collective reference points.

The procedure ReferencePointDistance() calculates the minimum distance from each point in the population to the nearest collective reference points in $\varTheta$. This way, the point near the reference point is favoured and stored in the new population. CI-NSGA-II develops a partial order similar to the NSGA-II procedure, but replaces the crowding distance operator by the distance to collective reference points ($i_{ref}$).

$$\begin{aligned} i \prec _{c} j := i_{rank} < j_{rank} \vee (i_{rank} = j_{rank} \wedge i_{ref} < j_{ref}) \end{aligned}$$

(6)

CI-NSGA-II prioritizes the points close to the online collective reference point. The algorithm consumes preference information to explore satisfactory solutions for DMs.

3.2 CI-SMS-EMOA

The SMS-EMOA [1] is a steady-state algorithm that applies the non-dominated sorting as a ranking criterion and the hypervolume measure (S) as a selection operator.

After the non-domination ranking, the next step is to update the last front population, $P_{worst}$. It replaces the member with the minimum contribution to $P_{worst}$ hypervolume by a new individual that increases the hypervolume covered by the population.

The new algorithm CI-SMS-EMOA converts the original SMS-EMOA into an interactive process. The CollectiveContributions() and ExpectationMaximization() subroutines have the same purpose and work as the CI-NSGA-II.

The selection operation, performed by the COIN Selection() procedure, prefers individuals with minor domination rank ($i_{rank}$). If they belong to the same front, the one with the maximum contribution to the hypervolume of the set and the closest reference point distance ($i_{ref}$) is selected.

A procedure Hype-RefPoint Distance() gets the hypervolume contribution (S) and calculates the minimum distance from each solution in the population to the nearest collective reference points in $\varTheta$. This way, the point with high hypervolume value and short reference point distance is favoured and stored in the new population.

3.3 CI-SPEA2

The strength pareto evolutionary algorithm 2 (SPEA2) [12] developed a fitness assignment strategy based on the number of individuals that one solution dominates and it is dominated by. SPEA2 implements elitism by keeping an external population (archive) of size N. The archive preserves the best solutions since the beginning of the evolution.

The strength ST(i) for each individual i is the number of population members it dominates: $ST(i)=|\{ j : j \in P_t \oplus \bar{P}_t\wedge i \prec j \}|$; where $\oplus$ is the multiset union, $P_t$ and $\bar{P}_t$ are the population and archive population at generation t, respectively. The fitness F(i) for a individual i is given by the strength of its dominators: $F(i)= \sum ST(j)$; where $j \in P_t \vee \bar{P}_t$, $j \prec i$. High values of F(i) means the individual i is dominated by many others and $F(i)=0$ corresponds to a non-dominated individual.

SPEA2 uses a nearest density estimation technique, adapted from the kNN method, to distinguish individuals having the same fitness values. This density function is a function of the distance to the k-th nearest data point and it is added to the fitness function F.

In the new algorithm CI-SPEA2, subroutine COIN Selection() computes the strength of all individuals and the non-dominated members are copied to the archive $\bar{P}_t$. The k-th nearest data point used to calculate the original density function in SPEA2 was substituted by the collective reference points $\varTheta$. If the archive $\mid \bar{P}_t\mid \le N$, the algorithm chooses the nearest individuals to the collective reference point until the archive size is reached. Otherwise, if $\mid \bar{P}_t\mid > N$, it removes the more distant ones proportionally to the number of individuals in each reference point cluster. This way, the archive keeps the same distribution of points around its reference points.

4 Performance Indicators

Several performance indicators are used to evaluate the outcome sets of MOEAs. They measure the quality of the Pareto front approximation and allow comparison between different algorithms. There exist a variety of approaches that analyse the distribution of points in objective function space and the accuracy in terms of convergence.

The Pareto-optimal front coverage indicator, $D_{S \rightarrow P_F}$, is a proximity indicator that defines the distance between an achieved approximation set S and their closest counterpart in the current Pareto-optimal front:

$$\begin{aligned} D_{S \rightarrow P_F}(S)= \frac{1}{|S|}\sum \limits _{\varvec{x} \in S} \min _{\varvec{x'} \in P_S}\left\{ d\left( \varvec{x},\varvec{x'} \right) \right\} , \end{aligned}$$

(7)

where d is the Euclidean distance between two points. Small values of $D_{S \rightarrow P_F}$ indicate proximity to the $P_F$.

However, some others indicators like: coverage of two sets, diversity and the hypervolume could not be employed in this study. Because their values depend on the spread of solutions in the whole Pareto front and, on contrary, the proposed algorithms aim to obtain subsets of solutions close to the collective reference points. There is a lack of performance indicators that focus only on the proportion of occupied area in $P_F$. For that reason, the following subsection presents two new ones.

4.1 Referential Cluster Variance Indicator

Instead of a good spread of solutions along $P_F$, the method proposed in this work wants to obtain subsets of solutions close to the collective reference point. In this context, a small cluster variance means the individuals from the sample $Y=\{\varvec{y}_1,\ldots ,\varvec{y}_N\}$ of size N are clustered closely around the population mean ($\mu$) or the reference point ($\varvec{z}^0$). A low dispersion for a group of preferred points in $P_F$ denotes a better efficiency of the approach tested. The referential cluster variance indicator $\kappa$ is represented as follows:

$$\begin{aligned} \kappa = \frac{1}{N}\sum \limits _{i=1}^N \left( \varvec{y_i}-\mu \right) ^2 \end{aligned}$$

(8)

In cases with more than one collective reference point ($\varvec{z}^j$), the points are clustered based on the closest distance to one of the reference points: $C_j=\{\varvec{a} \in \mathbb {R}^k : \Vert \varvec{a} - \varvec{z}^j \Vert \le \Vert \varvec{a} - \varvec{z}^i \Vert , \forall i\}$. Cluster $C_j$ consists of all points for which $\varvec{z}^j$ is the closest. The referential cluster variance is calculated to each cluster separately.

4.2 Hull Volume Indicator

Convex hull is a well-known geometric object widely used in various fields such as: shape analysis, pattern recognition, geographical information systems, image processing, etc. It has been also applied in the multi-objective optimization scenario.

The Normal Boundary Intersection method (NBI) [4] projects elements of the CHIM towards the boundary $\partial \mathcal {Z}$ of the objective space $\mathcal {Z}$ through a normal vector N. The intersection point between $\partial \mathcal {Z}$ and N the normal pointing is a Pareto optimal point, if the $P_F$ surface is convex. Martínez and Coello [10] introduced an archiving strategy based on the CHIM to find evenly distributed points along the $P_F$. Their convex hull multi-objective evolutionary algorithm (CH-MOEA) uses an archiving mechanism that stores non-dominated solutions which are orthogonal to each point of CHIM ($h \in \mathcal {H}$). Likewise, Shan-Fan et al. [11] presented a MOEA where the non-dominated solutions are picked out from dominated solutions by the quick convex hulls algorithm.

The idea of convex hull can be borrowed and applied as a performance indicator to measure the quality of the non-dominated points around the collective reference points. Connecting the closest final points to each reference point will produce a facet representation of the $P_F$. The volume of the convex hull can be used as a scalar indicator for the distribution of points in $P_F$. Small values of the hull volume ($\varPsi$) indicate concentrate points.

Non-convex problems can use alpha shapes to determine a concave hull of theirs points in $P_F$. The alpha shape is a subgraph of the Delaunay triangulation. The value of alpha ($\alpha$) controls the geometric design of the shape. For large $\alpha$ values the shape approaches to the boundary of the convex hull. On the other hand, as $\alpha$ decreases the shape shows more cavities.

5 Experimental Results

This section presents some results of CI-NSGA-II, CI-SPEA2 and CI-SMS-EMOA. The scalable multi-objective test problems from the ZDT, DTLZ and WFG problem sets [2] have a known optimal front and can be used to benchmark the outcome of the algorithms. Their features cover different classes of MOPs: convex $P_F$, non-contiguous convex parts, non-convex, multi-modal, etc. For those reasons, the test problems subject the new algorithms to distinct optimization difficulties and compare their results.

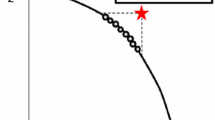
The experiment emulates the collectivity by developing some virtual DMs (robots). Each robot has a predefined point in the objective space which will be used to direct robots’ votes in a pairwise comparison between two individuals from Pareto front. Therefore, the robot votes on a solution according to the closest distance between its predefined point and each of the two candidates. Figure 1 illustrates candidates c1 and c2 with their respectively distances to the predefined point, d1 and d2. As $d1<d2$, the robot would vote on c1. The robots create the collective reference points with a better reasoning strategy than simply random choice. It is important to notice that the collective reference point is built on the similarity of answers (votes) after the Gaussian Mixture model and cannot be confused with the robots’ predefined points.

Very few MOEAs consider more than one user for reference point selection or evolutionary interaction. They neglect a collective scenario where many users could actively interact and take part of the decision process throughout the optimization. Furthermore, the new algorithms choose the reference points interactively. The references are not defined a-priori, like the R-NSGA-II from Deb [7], nor indicated by the DM as the middle point in the Light Beam approach [5]. Rather, all the references are discovered online with the support of a genuine collective intelligence of many users.

Fig. 1.

The robot’s predefined point will choose candidate c1 because the distance $d1<d2$.

Fig. 2.

Indicators for WFG2 and DTLZ2 tests.

In this experiment, the robots abstract the collectivity within a controlled environment. So the algorithms can be tested, compared and better understood in their working principles. The quantity of online reference points is directly related to the number of k clusters in the Gaussian Mixture model.

The front coverage ($D_{S \rightarrow P_F}$), the referential cluster variance ($\kappa$) and the hull volume ($\varPsi$) indicators were used to measure the quality of the algorithms. In addition to the Gaussian Mixture model, the K-means algorithm was implemented to bring a different clustering technique into the analysis of the algorithms. But the performance of Gaussian Mixture for these benchmarking cases was consistently better.

After 30 independent executions per algorithm on each test problem, the box plots were used to represent and support a valid judgment of the quality of the solutions and how different algorithms compare with each other. Figure 2 shows the distribution of the performance indicators for WFG2 and DTLZ2 problems in the form of box plots.

Although box plots allow a visual comparison of the results, it is necessary to go beyond reporting the descriptive statistics of the performance indicators and apply a statistical hypothesis test. The Conover-Inman procedure [3] is a non-parametric method for testing equality of population medians. It can be implemented in a pairwise manner to determine if the results of one algorithm were significantly better than those of the other. A significance level, $\alpha$, of 0.05 was used for all tests. Table 1 contains the results of the statistical analysis for all the test problems based on the mean values.

Table 1. Results of the Conover-Inman statistical hypothesis tests based on the mean values. Green cells (+) denote cases where the algorithm in the row statistically was better than the one in the column. Cells marked in red ($-$) are cases where the method in the column yielded statistically better results when compared to the method in the row.

The process of discovering the best algorithm is rather difficult as it implies cross-examining and comparing the results of their performance indicators. Figure 3 present a more integrative representation by grouping their indicators. A higher value of average performance ranking implies that the algorithm consistently achieved lower values of the indicators being assessed. In this case, lower values mean better convergence to $P_F$ and higher concentration around the collective reference points. For a given set of algorithms $A_1, \ldots , A_K$, a set of P test problem instances $\varPhi _1, \ldots , \varPhi _P$, the function $\delta$ is defined as:

$$\begin{aligned} \delta \left( A_i, A_j, \varPhi _p \right) = {\left\{ \begin{array}{ll} 1 &{} \quad \text {if }A_i \gg A_j \text { solving } \varPhi _p\\ 0 &{} \quad \text {otherwise} \end{array}\right. } \end{aligned}$$

(9)

where the relation $A_i \gg A_j$ defines if $A_i$ is better than $A_j$ when solving the problem instance $\varPhi _p$ in terms of the performance indicators: $D_{S \rightarrow P_F}$, $\kappa$ and $\varPsi$. Relying on $\delta$, the performance index $P_p(A_i)$ of a given algorithm $A_i$ when solving $\varPhi _p$ is then computed as: $P_p(A_i)= \sum \limits _{j=1, j \ne i}^K \delta \left( A_i, A_j, \varPhi _p \right)$.

The CI-NSGA-II with Gaussian Mixture model consistently outperformed the others algorithms in most cases. Concerning the convergence indicator, CI-NSGA-II was ranked best in 16 of 21 test functions, except for ZDT1, ZDTL6, DTLZ1, WFG6 and WFG8. The CI-SPEA2 and CI-SMS-EMOA have a similar performance on WFG tests. It is worth noticing that ZDT4 experiment demonstrated a premature convergence around the online reference points. A better control of the extent of obtained solutions must be investigated to avoid this behaviour.

Fig. 3.

Average performance ranking across ZDT, DTLZ and WFG test problems.

In summary, the interactive MOEAs and their collective reference points proved to be well matched for the range of ZDT, DTLZ and WFG test problems.

6 Final Remarks

In this work we have introduced new algorithms to improve the successive stages of evolution via dynamic group preferences. The interactive algorithms can apprehend people’s heterogeneity and common sense to guide the search through relevant regions of Pareto-optimal front.

The new approaches have been tested successfully in benchmarking problems. Two different performance indicators were presented with the intention to measure the proportion of occupied area in $P_F$.

Currently, we have been exploring different features of the evolutionary process, such as: the usage of COIN as a local search for new individuals and opening the population for users’ update to augment its quality. Replacing the robots by human collaborators, this research has a simulated environment¹ that represents the facility location problem. In this context, individuals from the evolutionary algorithm population are distributed to the participants who have to fix and change the position arrangement or the resource distribution in the scenario. This simulated environment promotes the collaboration and supports rational improvements in the quality of the population. The algorithms (CI-NSGA-II, CI-SMS-EMOA, CI-SPEA2) introduced and compared here are used to iteratively refine the search parameters with collective preferences.

In the near future, we plan to work on creative solutions unfolded by the participants and possibly explore non-explicit objectives hidden in more complex scenario. Furthermore, we intent to apply directional information from the collective reference points during the evolution process. This way, the technique can extract the intelligence of the crowds and, at the same time, minimize the interruptions of the algorithm.