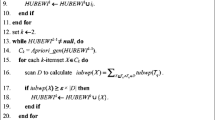Probabilistic Maximal Frequent Itemset Mining Over Uncertain Databases

Abstract

We focus on the problem of mining probabilistic maximal frequent itemsets. In this paper, we define the probabilistic maximal frequent itemset, which provides a better view on how to obtain the pruning strategies. In terms of the concept, a tree-based index PMFIT is constructed to record the probabilistic frequent itemsets. Then, a depth-first algorithm PMFIM is proposed to bottom-up generate the results, in which the support and expected support are used to estimate the range of probabilistic support, which can infer the frequency of an itemset with much less runtime and memory usage; in addition, the superset pruning is employed to further reduce the mining cost. Theoretical analysis and experimental studies demonstrate that our proposed algorithm spends less computing time and memory, and significantly outperforms the TODIS-MAX[20] state-of-the-art algorithm.

H. Li—This research is supported by the National Natural Science Foundation of China(61100112,61309030), Beijing Higher Education Young Elite Teacher Project(YETP0987), Discipline Construction Foundation of Central University of Finance and Economics, Key project of National Social Science Foundation of China(13AXW010), 121 of CUFE Talent project Young doctor Development Fund in 2014 (QBJ1427).

1 Introduction

Frequent itemset mining is one of the traditional and important fields in data mining, which discovers itemsets whose occurrences are larger than a specified threshold. Many efficient algorithms and methods have been developed in the recent years [1]. In such methods, a very important assumption is, however, the mined transactions are exact no matter they are static or increasingly updated.

When new applications are developed and new requirements are met, uncertainty exists often. As an example, Table 1 shows an animal monitor system, which use the cameras to distinguish 3 pandas with names “PanPan”, “TuanTuan”, and “YuanYuan” among other animals, as well observe their appearances. Nevertheless, the digital image recognition method is not accurate enough to recognize each panda. Thus, each panda will annotated by a probability to present the existence [2], and we call it the attribute-uncertainty. This new feature brings us new challenges, which cannot be well addressed by the traditional frequent itemset mining methods. The existing uncertain data mining methods can be categorized into two types. One is to achieve the expected frequent itemsets [6–17], another is to obtain the probabilistic frequent itemsets [18–30].

Table 1. An uncertain database example

1.1 Motivation

When mining frequent itemsets over exact databases, it has been presented the frequent itemsets are redundant. Many itemset compression methods have been proposed, such as maximal itemset [3], closed itemset [4] and non-derivable itemset [5]. If the users do not care the support of an itemset, but only want to know whether it is frequent, the maximal frequent itemset is the best choice since it is the most efficient method to represent the frequent itemsets. Similarly, if we want to discover frequent itemsets over uncertain databases, to obtain the maximal frequent itemsets can not only make the mining results easier to use, but also reduce the computing cost and memory size. Therefore, in this paper, we investigate how to efficiently discover the maximal frequent itemsets over an attribute-uncertainty model based uncertain database.

1.2 Challenges and Contributions

To address our proposed problem, an intuitive consideration is to enumerate all the probabilistic frequent itemsets and then to filter the maximal frequent itemsets. This method was proposed in [20] named pApriori, which introduced the divide-and-conquer method to mine the vertical databases, and used a one-bound estimating method to evaluate the frequency of itemsets. Then, a new method TODIS-MAX[20] was proposed for further improvement. Besides all the techniques used in pApriori, TODIS-MAX also presented its own optimizations. It used a top-down method, which generated the itemsets from supersets to subsets, and thus can efficiently used the pruning strategy when generating the infrequent itemsets. Also, it proposed a method to compute the probability density function of the subsets from the supersets, which can further reduce the computing cost. To our best knowledge, TODIS-MAX is the most efficient algorithm to achieve the maximal frequent itemsets from uncertain databases.

However, there are still some problems for addressing: (1) the top-down method may meet a bottleneck when the count of probabilistic frequent 1-items increases, which will result in an exponentially increase of the probabilistic infrequent itemsets, and this is hard to handle even though the time complexity can be reduced to O(n). (2) The value to decide the probabilistic infrequent itemsets is not tight enough, which makes itemsets in multi-levels have to be recomputed. (3) If an itemset is frequent, the computing cost is still high since the time complexity is $O(nlog^{2}n)$ in the worst case. Accordingly, new problems are posed: How to reduce the most of exponentially increased itemsets? How to further decrease the computing cost of the frequent itemsets? And how to efficiently achieve the maximal frequent itemsets?

In this paper, we address these problems and make the following contributions.

• 1. We focus on the problem of probabilistic maximal frequent itemset mining over uncertain databases, and define the probabilistic maximal frequent itemset, which is in line to the traditional definition over exact database, and supplies us a better pruning method.

• 2. We introduce a compact data structure PMFIT to maintain the information of probabilistic frequent itemsets, which in a bottom-up manner, can efficiently organize the mining results for the itemset search. Then the PMFIM algorithm is proposed to depth-first discover the probabilistic maximal frequent itemsets. In this algorithm, we propose a probabilistic support estimation method, which can compute the upper bound and the lower bound of the probabilistic support with a much low cost. The method when together used with PMFIT, yields a significantly better performance. Plus, we use the super pruning strategy to further reduce the mining cost.

• 3. We compare our algorithm with the TODIS-MAX[20] on 2 synthetic datasets and 3 real-life datasets. Our experimental results show that our algorithm is much more effective and efficient.

The rest of this paper is organized as follows. In Sect. 2 we present the preliminaries and then define the problem. Section 3 introduces the data structures, and illustrates our algorithm in detail. Section 4 evaluates the performance with theoretical analysis and experimental results. Finally, Sect. 5 concludes this paper.

2 Preliminaries and Problem Definition

2.1 Preliminaries

Given a set of distinct items $\varGamma =\{i_{1},i_{2},\cdots ,i_{n}\}$ where $|\varGamma |=n$ denotes the size of $\varGamma$, a subset $X \subseteq \varGamma$ is called an itemset; suppose each item $x_{t}(0<t\le |X|)$ in X is associated with an occurrence probability $p(x_{t})$, we call X an uncertain itemset, which is denoted as $X=\{x_{1},p(x_{1});x_{2},p(x_{2});\cdots ;x_{|X|},p(x_{|X|})\}$, and the probability of X is $p(X)=\varPi _{i=1}^{|X|}p(x_{i})$. We call the list $\{p(x_{1}), p(x_{2}),\cdots , p(x_{|X|})\}$ the probability density function. An uncertain transaction UT is an uncertain itemset with an ID. An uncertain database UD is a collection of uncertain transactions $UT_{s}(0<s \le |UD|)$. Given an uncertain itemset X, the count it occurs in an uncertain database is called the support, denoted $\varLambda (X)$.

Two definitions of the frequent itemset for uncertain data have been proposed. One is based on the the expected support, another is based on the probabilistic support.

Definition 1

(Expected Frequent Itemset [6]) Given an uncertain database UD, an itemset X is an $\lambda$-expected frequent itemset if its expected support $\varLambda ^{E}(X)$ is not smaller than minimum support $\lambda$. Here $\varLambda ^{E}(X)=\sum _{UT \in UD}\{p(X)|X \subseteq UT\}$.

Definition 2

(Probabilistic Frequent Itemset [26]) Given the minimum support $\lambda$, the minimum probabilistic confidence $\tau$ and an uncertain database UD, an itemset X is a probabilistic frequent itemset if the probabilistic support $\varLambda ^{P}_{\tau }(X) \ge ~\lambda$. $\varLambda ^{P}_{\tau }(X)$ is the maximal support of itemset X with probabilistic confidence $\tau$, i.e., $\varLambda ^{P}_{\tau }(X)=Max\{i|P_{\varLambda (X) \ge i} > \tau \}$.

2.2 Problem Definition

Definition 3

(Probabilistic Maximal Frequent Itemset) Given the minimum support $\lambda$, the minimum probabilistic confidence $\tau$ and an uncertain database UD, an itemset X is a probabilistic maximal frequent itemset if it is a probabilistic frequent itemset and is not covered by the other probabilistic frequent itemsets.

From Definition 3, one can easily see that the support information of an probabilistic frequent itemset $Y \subset X$ can be estimated from the probabilistic maximal frequent itemset X without having to read from the database anymore.In other words, for a probabilistic maximal frequent itemset X, any itemset Y that $Y \subset X$ satisfy the following statement: The probability of Y’s support no smaller than $\lambda$ is larger than $\tau$.

Problem Statement: Based on the previous definition, we present our addressed problem as follows. Given an uncertain database UD, the minimum support $\lambda$, the minimum probabilistic confidence $\tau$, we are required to explore all probabilistic maximal frequent itemsets from UD.

3 Probabilistic Maximal Frequent Itemset Mining Method

3.1 Data Structures

Probabilistic Mining Frequent Itemset Tree. To accelerate the searching and pruning speed, we design a simple but effective index named PMFIT(Probabilistic Maximal Frequent Itemset Tree), in which each node $n_{X}$ denotes an itemset X; $n_{X}$ is a 6-tuple $<item, sup, esup, psup,lb,ub>$, in which item denotes the last item of the current itemset X, sup is the support, esup is the expected support, and psup is the probabilistic support. lb and ub separately represent the lower bound and upper bound of probabilistic support. Except the root node, each node has a pointer to its parent node. PMFIT can be constructed by our proposed algorithm in Sect. 3.5. Figure 1 is the PMFIT from the 6 transactions. For an example, $n_{A}$ denotes itemset $\{A\}$ with the support 3, the expected support 1.9, and the probabilistic support 3. As can be seen, 13 nodes are probabilistic frequent itemsets, only 3 nodes are probabilistic maximal frequent itemsets.

Fig. 1.

Probabilistic maximal frequent itemset tree(PMFIT) for $\lambda =3$, $\tau =0.1$

Probabilistic Maximal Frequent Itemset Collection. Since the final results do not have to maintain the probabilities of each item, we employed a traditional bitmap based collection to store the probabilistic maximal frequent itemsets, which can help us perform the superset pruning, so that a better performance can be achieved.

3.2 Probabilistic Support Computing

Since the probabilistic density function of itemset X in two transactions $T_{1}$ and $T_{2}$ can be computed with the convolution between the probabilistic density function in $T_{1}$ and the probabilistic density function in $T_{2}$, the divide-and-conquer method proposed in [20] is also employed in our paper. That is, the uncertain database will be split into two parts to separately compute the probabilistic density function, and this operation will be recursively conducted until the sub-database has only one transaction. The convolution can be computed with a Fast Fourier Transformer, which, given the size of the uncertain database n, will efficiently reduce the time complexity from $O(n^{2})$ to $O(nlog^{2}(n))$.

3.3 Items Reordering

Bayardo stated that ordering items with increasing support can reduce the search space [3]; together with other pruning strategies, it can further reduce the cost of the support computing. In this paper, we employ the similar heuristic rule with a little differences. That is, the items will be ordered by their expected supports rather their supports. This is due to the instinctive observation that two itemsets occurring in the same transactions may have different probability and thus have various expected supports. As a simple example in Fig. 1, itemset ${\{B\}}$ and itemset $\{C\}$ occur in four transactions, which means their supports are both 4, nevertheless, the expected supports are 2.8 and 2.6 separately. As a result, we believe using expected support to sort the items will make the algorithm more efficient. Note that even though probabilistic support is the best to be used in sorting the items, we did not use it. This is due to the fact that computing the probabilistic support is much more time-consumed, which, in comparison to computing the expected support, may has a worse performance when the minimum support is low. Choosing the expected support to sort the items are verified effective in our experiments; we find both methods achieve almost the same search space, but computing the expected support is much more efficient.

3.4 Pruning Strategies

We propose pruning strategies to improve the performance. A tight bounds are supplied to infer the range of probabilistic support, or even can ignore the computing of probabilistic support; in addition, a superset pruning method inspired by the traditional mining algorithm is employed.

The Bounds of Probabilistic Support. When mining the probabilistic maximal frequent itemsets over an n-transactions uncertain database, the probabilistic support is not important for the users, so we try to find a method to estimate the frequency of an itemset rather directly compute the probabilistic support.

Theorem 1

For an itemset X in uncertain database UD, given the minimum probabilistic confidence $\tau$, we can get the lower bound and upper bound of the probabilistic support $\varLambda ^{P}_{\tau }(X)$, denoted lb($\varLambda ^{P}_{\tau }(X)$) and ub($\varLambda ^{P}_{\tau }(X)$) as follows.

$$\begin{aligned} {\left\{ \begin{array}{ll} lb(\varLambda ^{P}_{\tau }(X)) = \varLambda ^{E}(X)-\sqrt{-2\varLambda ^{E}(X) ln(1-\tau )}\\ ub(\varLambda ^{P}_{\tau }(X)) = \frac{2\varLambda ^{E}(X)-ln\tau +\sqrt{ln^{2}\tau -8\varLambda ^{E}(X) ln\tau }}{2}\end{array}\right. }\end{aligned}$$

(1)

Proof

For the itemset X, we use $\varepsilon$ to denote the expected support $\varLambda ^{E}(X)$, also, we use t to denote the probabilistic support $\varLambda ^{P}_{\tau }(X)$, which, according to Definition 2, satisfies the following equations.

$$\begin{aligned} {\left\{ \begin{array}{ll}P_{\varLambda (X) \ge t} > \tau \Leftrightarrow P_{\varLambda (X) > t-1} > \tau \\ P_{\varLambda (X) \ge t+1} \le \tau \Leftrightarrow P_{\varLambda (X) > t} \le \tau \end{array}\right. }\end{aligned}$$

(2)

(1) If we set $t=(1+\xi )\varepsilon$, i.e., $\xi =\frac{t}{\varepsilon }-1$, where $\xi \ge 0$, that is, $t \ge \varepsilon$, then based on the Chernoff Bound, $P_{\varLambda (X) \ge t} = P_{\varLambda (X)\ge (1+\xi )\varepsilon } \le e^{-\frac{\xi ^{2}\varepsilon }{2+\xi }}$; based on the first inequality of Eq. 2, we can get $\tau < e^{-\frac{\xi ^{2}\varepsilon }{2+\xi }} = e^{-\frac{(t-\varepsilon )^{2}}{t+\varepsilon }}$; that is to say, when $t \ge \varepsilon$,$\frac{2\varepsilon -ln\tau -\sqrt{ln^{2}\tau -8\varepsilon ln\tau }}{2} <t<\frac{2\varepsilon -ln\tau +\sqrt{ln^{2}\tau -8\varepsilon ln\tau }}{2}$. Since $\frac{2\varepsilon -ln\tau -\sqrt{ln^{2}\tau -8\varepsilon ln\tau }}{2} \le \varepsilon$, we can obtain the following inequality.

$$\begin{aligned} t<\frac{2\varepsilon -ln\tau +\sqrt{ln^{2}\tau -8\varepsilon ln\tau }}{2} \quad \quad \quad \quad \quad if \quad t \ge \varepsilon \end{aligned}$$

(3)

(2) If we set $t=(1-\xi ')\varepsilon$, i.e., $\xi '=1-\frac{t}{\varepsilon }$, where $\xi ' \ge 0$, that is, $t \le \varepsilon$, then based on the Chernoff Bound, $P_{\varLambda (X) > t} = P_{\varLambda (X) > (1-\xi ')\varepsilon } > 1-e^{-\frac{\xi '^{2}\varepsilon }{2}}$; based on the second inequality of Eq. 2, we can get $\tau > 1-e^{-\frac{\xi '^{2}\varepsilon }{2}}$, i.e., $-\sqrt{-\frac{2ln(1-\tau )}{\varepsilon }}<\xi '<\sqrt{-\frac{2ln(1-\tau )}{\varepsilon }}$, then when $t \le \varepsilon$, $\varepsilon -\sqrt{-2\varepsilon ln(1-\tau )} <t<\varepsilon +\sqrt{-2\varepsilon ln(1-\tau )}$. Since $\varepsilon \le \varepsilon +\sqrt{-2\varepsilon ln(1-\tau )}$, we can get the following inequality.

$$\begin{aligned} t > \varepsilon -\sqrt{-2\varepsilon ln(1-\tau )} \quad \quad \quad \quad if \quad t \le \varepsilon \end{aligned}$$

(4)

From Eqs. 3 and 4, we can conclude that no matter t is larger or smaller than the $\varepsilon$, it is definitely within the range of ($\varepsilon -\sqrt{-2\varepsilon ln(1-\tau )}$, $\frac{2\varepsilon -ln\tau +\sqrt{ln^{2}\tau -8\varepsilon ln\tau }}{2}$). Consequently, we can determine the lower bound is $\varLambda ^{E}(X)-\sqrt{-2\varLambda ^{E}(X) ln(1-\tau )}$, and the upper bound is $\frac{2\varLambda ^{E}(X)-ln\tau +\sqrt{ln^{2}\tau -8\varLambda ^{E}(X) ln\tau }}{2}$. $\blacksquare$

Theorem 1 provides us two pruning strategies. For an itemset X, if the upper bound $\frac{2\varepsilon -ln\tau +\sqrt{ln^{2}\tau -8\varepsilon ln\tau }}{2}$ is not larger than the minimum support $\lambda$, then X is a probabilistic infrequent itemset. Also, if the lower bound $\varepsilon -\sqrt{-2\varepsilon ln(1-\tau )} \ge \lambda$, then X is definitely a probabilistic frequent itemset. We can see that for an uncertain database with size n, if the minimum support $\lambda$ is not within this range, we can successfully hit the target.

Example 1

Using the uncertain dataset in Fig. 1 as the example. If we set the minimum support $\lambda =1$ and the minimum probabilistic confidence $\tau =0.1$, then for itemset $\{A\}$, the lower bound is 1.3, which is larger than 1, then itemset $\{A\}$ is a frequent itemset. Further, if we set the minimum support $\lambda =5$ and the minimum probabilistic confidence $\tau =0.1$, then for itemset $\{AB\}$, the upper bound is 4.7, which is smaller than 5, and thus itemset $\{AB\}$ is an infrequent itemset.

Superset Pruning. According to our definition, an itemset being probabilistic maximal frequent must satisfy two conditions. (1) the probabilistic support is not smaller than the minimum support; (2) it is not covered by any other probabilistic frequent itemsets. Both computing are needed, then the computing with lower computing cost should be conducted firstly. As the above mentioned, computing the probabilistic support requires $O(nlog^{2}(n))$ time complexity, which can be improved to O(n) with our method. However, to scan the existing probabilistic maximal frequent itemsets, assuming whose size is m, requires at most O(m) time complexity. Based on the definition of probabilistic maximal frequent itemset, m is much smaller than n. Consequently, for a new generated itemset, we will first decide whether it is cover by a super itemset, then, if not, compute the bounds or the probabilistic support. This strategy can be extended for further pruning. That is, for a probabilistic maximal frequent itemset $X=\{x_{1}x_{2}\cdots x_{n}\}$, if they are the last n items in the sorted items list, then items $x_{2},\cdots ,x_{n}$ can be pruned directly for further computing. We can see from Fig. 1, since $\{CDE\}$ is an itemset in which the items are the last three ones in the sorted items list, then $\{D\}$, $\{E\}$ will be removed, and the computing for all their descendants can be pruned.

3.5 Algorithm Description

In this section, we propose a depth-first algorithm named PMFIM(Probabilistic Maximal Frequent Itemset Mining) to build the bottom-up organized tree, that is, the subsets will be computed first, and then the supersets will be generated if their subsets are all frequent. We discover the itemsets with this manner since the probabilistic frequent itemset also has the apriori property. The algorithm can be conducted in five steps. Algorithm 1 shows the pseudo code of Step 3–5.

Step 1: We get all the distinct items and sort them in an incremental order according to their expected supports before we build the PMFIT; during the process, the items with the support or the upper bound lower than the minimum support will be initially pruned.

Step 2: The PMFIT is initialed with only one root node, which represent the null itemset.

Step 3: For a parent node, we begin to generate the child node, and compute the related information to decide whether it is frequent. First, if the child node is covered by one of the maximal frequent itemsets, it is not a maximal but a frequent itemset; specially, if all the items in it are the last ones in the sorted items list, we can determine that all the right nodes are not the final results, and the loop will be ended immediately. Second, after computing the support, the expected support and the support bounds, if the upper bound is not larger than the minimum support, then it is an infrequent itemset; if the lower bound is not smaller than the minimum support, then it is a frequent itemset. Finally, if we can not determine the frequency by the previous value, we need to compute the probabilistic support and compare it to the minimum support.

Step 4: If a child node is frequent, we will recall Step 3 for it; otherwise, it will be pruned.

Step 5: If a node has no children and is not in the final results, it is a probabilistic maximal frequent itemset. We can add it into the probabilistic maximal frequent itemset collection. Because of our depth-first mining manner, there is no need to remove the subset from the collection.

Complexity. The overall time complexity of the PMFIM algorithm depends on the database size n, the minimum support $\lambda$, the minimum probabilistic confidence $\tau$, and the count of PMFIT nodes t. For each new generated node, there are three possible computing cost. The first is O(m) where m is the count of current probabilistic maximal frequent itemsets; the second is O(n); the third is $O(nlog^{2}n)$. Generally, $m < n < nlog^{2}n$; thus, the worst time complexity is $O(nlog^{2}n)$. Nevertheless, as will be demonstrated in our experiments, the count of probabilistic support computing is greatly small, which guarantee that the performance can be improved significantly.

4 Experiments

We conducted the experiments to evaluate the performance of PMFIM. The state-of-the-art algorithm TODIS-MAX[20], which has been presented much more efficient than pApriori, was used as the evaluation method. While TODIS-MAX focused on the tuple-uncertainty based databases, we re-implemented it for the attribute-uncertainty based databases. The dataset size |UD|, the relative minimum support $\lambda _{r}$(=$\frac{\lambda }{|UD|}$), and the minimum probabilistic confidence $\tau$ are the main elements that may affect the uncertain data mining, which, as a result, were used to compare the algorithms in runtime and memory cost.

4.1 Running Environment and Datasets

Both algorithms were implemented with C++, compiled with Visual Studio 2010 running on Microsoft Windows 7 and performed on a PC with a 2.90GHZ Intel Core i7-3520M processor and 8GB main memory. We evaluated the algorithms on 2 synthetic datasets generated by the IBM synthetic data generator and 3 real-life datasets [25]. The detailed data characteristics are shown in Table 2. We used the item correlation to show the density of an uncertain database, that is, a smaller correlation value denotes a denser data.

Table 2. Uncertain dataset characteristics

4.2 Effect of Relative Minimum Support

We set a fixed minimum probabilistic confidence and compared the performance of the two algorithms when the relative minimum support was changed.

Running Time Cost Evaluation. As can be seen in Fig. 2, the runtime cost of the two algorithms reduced linearly with a decrease of the relative minimum support. Plus, to compare our algorithm to TODIS-MAX, we can observe the following results. On the one hand, when the relative minimum support was high, the runtime cost of the TODIS-MAX method was a little lower than the PMFIM over most of the datasets. This is due to the advantage of the top-down mining manner in TODIS-MAX, that is, a faster pruning will be employed if the supersets are not frequent, which is more useful when performing over dense dataset. On the other hand, when the relative minimum support became lower, the performance of TODIS-MAX turned worse significantly, which can also be clearly noticed over denser datasets. As shown in the figure, over the densest dataset CONNECT4, PMFIM achieved almost a thousand time faster than TODIS-MAX when the relative minimum support was 0.7, and then, the TODIS-MAX can be almost not measured since the runtime cost increased too much; over the KOSARAK, the sparsest dataset, our algorithm can also achieved hundreds-fold speedup when the relative minimum support was 0.05. This outperforming further increased when the relative minimum support turned smaller. This is also because of the different mining fashions: TODIS-MAX employed the top-down method, which, when the relative minimum support was small, may use more frequent items to generate infrequent itemsets, whose size will exponentially increased along with the count of frequent items. Even though TODIS-MAX employed the expected support to prune certain computing, the rest computing was still too large to conduct. In comparison to that, our algorithm was a bottom-up method, i.e., only frequent itemsets were generated; with the help of superset pruning, the computing will not increase sharply when the relative minimum support became lower.

Fig. 2.

Running time cost vs relative minimum support

Memory Cost Evaluation. We also compared the maximal memory usages of the two algorithms. As shown in Fig. 3, similar to the runtime cost, the memory usages decreased when the relative minimum support increased. In addition, we can see that in a majority of cases TODIS-MAX used more memory than our algorithm. Since our algorithm employed the divided-and-conquer method proposed in TODIS-MAX, the running memory cost was similar when the relative minimum support was high. Nevertheless, when it became low, the memory usage of TODIS-MAX will increased exponentially. Again, it was because of the massively generated infrequent itemsets. Besides, the lattice used in TODIS-MAX was another reason that use more memory. Note that we did not show the memory cost of TODIS-MAX when the relative minimum support was low, this is because that the runtime cost was too high to perform the TODIS-MAX algorithm in limited time.

Fig. 3.

Memory cost vs relative minimum support

4.3 Effect of Data Size

We evaluated the scalability of the two algorithms, that is, we performed the algorithms w.r.t. different data sizes, which are shown in Fig. 4. The T25I15D320K dataset was used as the evaluation dataset. We separately got the first n(from 20 K to 320 K) transactions to conduct the algorithms. Plus, the relative minimum support and the minimum probabilistic confidence were set to the fixed values. Note even though the relative minimum support was fixed, the minimum support changed since the data size was different. As shown in Fig. 4(a), when the dataset turned larger, the runtime cost of the two algorithms also increased, but the PMFIM algorithm was much more stable when the dataset became larger. This presents that our algorithm can accurate estimate most of the probabilistic supports no matter how the data size increased. However, in Fig. 4(b), with the increasing size of transactions, the memory cost of both algorithms increase linearly. It is reasonable since we showed the maximal memory cost during running; thus, once we directly computed the probabilistic support, the memory will be more used for more transactions.

4.4 Effect of Minimum Probabilistic Confidence

Definition 2 shows that a larger minimum probabilistic confidence may result in a less possibility that an itemset becomes frequent, which will reduce the computing cost and the memory usage. We evaluated two algorithms for different minimum probabilistic confidences(from 0.00001 to 0.1) when the relative minimum support was fixed.

Fig. 4.

Effect of data size for $\lambda _{r}=0.1$, $\tau =0.9$

Figures 5 and 6 separately presented the runtime cost and the memory usage. To our surprise, we find that when the minimum probabilistic confidence increased, both the runtime and the memory cost of the two algorithms kept almost unchanged. This shows that the minimum probabilistic confidence had little effect on the performance of the algorithms. It is due to the reason that the probabilistic density function was highly sparse when the dataset size was large, which results that most of the minimum probabilistic confidence can slightly change the probabilistic support, and thus can almost not change the types of the itemsets.

Fig. 5.

Runtime cost vs minimum probabilistic confidence

Fig. 6.

Memory cost vs minimum probabilistic confidence

5 Conclusions

In this paper we studied the behavior of probabilistic maximal frequent itemset mining over uncertain databases. We defined the probabilistic maximal frequent itemset, which is much reasonable and can supply more pruning considerations. Based on this, an extended enumeration tree named PMFIT was introduced to efficiently index and maintain the probabilistic frequent itemsets. A bottom-up algorithm named PMFIM, mining in a depth-first manner, was proposed, in which we used the support and the expected support to estimate whether an itemset is frequent, which greatly reduced the computing cost and memory usage; in addition, a superset pruning method was employed to further improve the mining performance. Our extensive experimental studies show that our PMFIM algorithm achieved thousands or more faster speed than TODIS-MAX, and also significantly outperformed in memory cost.