Efficient Local Representations of Graphs

Abstract

Informally, an efficient local representation of a graph G is a scheme in which we assign short labels (representable by a “small” number of bits, hence efficient) to G’s vertices so that we can determine if two vertices are adjacent simply by examining the labels assigned to the pair of vertices (hence local). For some classes of graphs (such as planar graphs), one can devise local representations, but for others (such as bipartite graphs), this is not possible.

We present a conjecture due to Muller [22] and to Kannan, Naor, and Rudich [15] that distinguishes those hereditary classes of graphs (closed under induced subgraphs) for which an efficient local representation is feasible from those for which it is not.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Notation All graphs in this chapter are simple: their edges are undirected, and they have neither loops nor multiple edges. For a graph G = (V, E), the number of vertices is nearly always denoted by the letter n. The notation v ∼ w indicates that vertices v and w are adjacent, i.e., vw ∈ E. For a positive integer n, we write [n] for the set {1, 2, …, n}. We write lgn for the base-2 logarithm of n. We also write logn but that is invariably wrapped in big-oh notation, so the base is irrelevant.

6.1 Seeking an Efficient Data Structure for Graphs

The efficient local representation of graphs problem is due to Muller [22] and to Kannan, Naor, and Rudich [15].

Here’s the overarching question: How do we efficiently represent a graph in a computer?

Perhaps the simplest method is via an adjacency matrix; the memory to store this matrix uses $\Theta (n^{2})$ bits, but this may be wasteful if the graph does not have too many edges. In the latter case, adjacency lists may be a better option. See, for example, [8, 12], or [31] for a discussion of data structures one may use to represent a graph.

If we think of a graph as modeling relations between its vertices, then determining if two vertices are adjacent “should” only depend on some shared property of the two nodes under consideration.

To illustrate our thoughts, we begin by discussing interval representations of graphs.

6.1.1 Interval Representations of Graphs

Let G be a graph. We say that G has an interval representation if we can assign to each vertex v ∈ V (G) a real interval J _v so that for distinct vertices v and w we have

$$\displaystyle{v \sim w\;\Longleftrightarrow\;J_{v} \cap J_{w}\not =\varnothing.}$$

For example, let G be the path graph with 1 ∼ 2 ∼ 3 ∼ 4. The following assignment

$$\displaystyle{1\mapsto [1,3],\quad 2\mapsto [2,5],\quad 3\mapsto [4,7],\quad \text{and}\quad 4\mapsto [6,8].}$$

gives an interval representation for G. See [11] and [19]. Interval representations of graphs are a special case of intersection representations [7, 12, 21, 24, 25].

This representation provides a terrific way to store a graph in a computer. For each vertex, we only need to hold two numbers: the left and right end points of its interval. To check if two vertices are adjacent, we just do some quick checks on four numbers.

How much storage space does such a representation consume? We might be concerned that we may need a great deal of precision to specify the intervals’ end points. However, it’s not hard to show that if G has an interval representation, then we can find a representation in which the end points are distinct values¹ in [2n].

This implies that for each vertex of the graph, we hold a scant O(logn) bits of information, and we can test adjacency simply by examining the information attached to just the two vertices of interest.

Informally, this is what we mean by an efficient local representation of a graph. To each vertex v we attach a “short” [hence efficient] label ℓ(v), and adjacency between vertices v and w can be tested via a calculation whose inputs are just ℓ(v) and ℓ(w) [hence local as we do not consider labels on any other vertices nor do we reference a global data structure such as an adjacency matrix].

Sadly, interval representations are not the ideal we seek because not all graphs admit such a representation. A moment’s doodling shows that the four cycle C ₄ has no such representation.

Graphs that have interval representations are called interval graphs, and for that family, an efficient local representation is available. What about other families of graphs?

6.1.2 Additional Examples

Trees

Let T be a tree with n vertices. Arbitrarily select a vertex of T to be called the root and give the edges directions so that on any path to the root, all edges point toward the root. Thus every vertex (other than the root) has a unique parent.

We now attach labels to the vertices of T. Each label ℓ(v) is an ordered pair of integers (a _v , b _v ) drawn from the set [n]. The a-values are assigned arbitrarily; the only requirement is that they be distinct. The b-labels depend on the direction of the edge. If the edge from v to w is oriented v → w, then b _v  = a _w . That is, the second element of v’s label is the first element of v’s parent. Since the root r does not have a parent, its label is simply (a _r , a _r ). See Figure 6.1.

Fig. 6.1

An efficient local representation for a tree. Each label is an ordered pair (a, b). Observe that the a-values are distinct. The vertex labeled (5, 5) is the root and the b-label of every other vertex is the a-label of its parent

We now observe that the vertex labels are 2lgn bits in length, and testing vertices for adjacency only requires examining the labels of the two vertices:

$$\displaystyle{ v \sim w\;\Longleftrightarrow\;a_{v} = b_{w}\ \text{ or }\ a_{w} = b_{v}. }$$

(6.1)

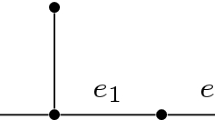
This efficient local representation method easily extends from trees to acyclic graphs (forests). Indeed, the scheme works for graphs that are not trees. For example, consider an n-cycle and label its vertices, in order, as follows:

$$\displaystyle{(1,2)\quad (2,3)\quad (3,4)\quad \cdots \quad (n - 1,n)\quad (n,1).}$$

Test (6.1) applies here as well.

Planar Graphs

We can extend this technique to planar graphs. The minimum degree of planar graph is at most 5. Let G be a planar graph with n vertices and assume that V (G) = [n]. Here is how we label V (G).

Let v be a vertex of minimum degree. The label we assign to v is a tuple of the form ℓ(v) = (v; v ₁, v ₂, v ₃, v ₄, v ₅) where the v _i ’s are v’s neighbors (or 0s if v has fewer than 5 neighbors). Now delete v from G and repeat. Since G − v is planar, we select a vertex, say w, of minimum degree in G − v and assign to it the label ℓ(w) = (w; w ₁, w ₂, w ₃, w ₄, w ₅) where the w _i ’s are (up to) five of its neighbors in G − v. Delete w and continue until the entire graph is consumed. This labeling uses 6lgn bits per vertex.

Once this labeling is created, we can test the adjacency of any two vertices x and y just by examining their labels ℓ(x) = (x; x ₁, …, x ₅) and ℓ(y) = (y; y ₁, …, y ₅): we simply check if x = y _i or y = x _i for some i.

k-Degenerate Graphs

The representation method we presented for planar graphs relies on an idea that we can generalize. For a positive integer k, a graph G is called k-degenerate if δ(H) ≤ k for all subgraphs H ⊆ G. We write $\mathcal{D}_{k}$ for the set of k-degenerate graphs. Note that trees are 1-degenerate and planar graphs are 5-degenerate.

The labeling method we used for planar graphs readily extends to graphs in $\mathcal{D}_{k}$. Let G be an n-vertex graph in $\mathcal{D}_{k}$. Without loss of generality we assume V (G) = [n]. Choose a minimum degree vertex v of G, and let ℓ(v) = (v; v ₁, v ₂, …, v _k ) where the v _i s are neighbors of v (or 0s if d(v) < k). Delete v from G and repeat. The labels assigned to vertices use (k + 1)lgn bits, and adjacency testing is the same as for planar graphs.

Complete Multipartite (Turan) Graphs

It is no surprise that interval graphs have efficient local representations; this is nearly immediate from their definition. The existence of efficient local representations for trees and planar graphs are instances of the same idea that shows graphs in $\mathcal{D}_{k}$ have efficient local representations. Here is another example to illustrate the central idea.

Recall that a graph G is a complete multipartite graph if we can partition its vertex set as $V (G) = I_{1} \dot{\cup }\cdots \dot{\cup } I_{k}$ where each I _j is an independent set, and for i ≠ j, every vertex in I _i is adjacent to every vertex in I _j .

Here’s an efficient local representation. Given the partition of V (G), let ℓ(v) = j if v ∈ I _j . We have v ∼ w exactly when ℓ(v) ≠ ℓ(w). Since the number of parts in the partition of G is at most n, the number of bits used in the labels is bounded by lgn, and so this is an efficient local representation.

Circular Arc Graphs

The family of circular arc graphs [32] are a natural extension of interval graphs. In this case, we assign to each vertex v of a graph G an arc A _v of some fixed circle. Vertices v and w are adjacent exactly when their arcs A _v and A _w intersect.

As in the case of interval graphs, there is no loss of generality in assuming that the 2n end points of the arcs representing G are distinct and therefore may placed at the corners of a regular 2n-gon. Therefore, the arcs can be described using just 2lgn bits, and hence we have an efficient local representation.

String Graphs

The family of string graphs [16, 17] generalize the circular arc graphs. In a circular arc graph, each vertex is represented by a special type of curve: an arc on a fixed circle. In a string graph, we use arbitrary planar curves. A graph G is a string graph provided we can assign to each vertex v a curve S _v in the plane so that vertices v and w are adjacent if and only if $S_{v} \cap S_{w}\not =\varnothing$. As shown by Sinden [29], not all graphs are string graphs.

Clearly a string representation of a graph is local, but is it efficient? Clearly we cannot represent an arbitrary curve with just a handful of bits. Is there a trick (such as the one we used for interval and circular arc graphs) that enables us to bound the number of bits needed for each vertex? We shall see that the answer is no (Proposition 2.5).

6.2 Efficient Local Representations

6.2.1 Main Definitions

The problem can be described as follows. Let $\mathcal{P}$ be a property of graphs. We want to know if $\mathcal{P}$-graphs have efficient local representations. This means n-vertex graphs in $\mathcal{P}$ can be labeled with “short” labels—O(logn) bits—and adjacency can be tested just by comparing the labels on two vertices. The adjacency test is the same for all graphs with property $\mathcal{P}$.

Let’s be more precise. By a graph property we mean an isomorphism-closed set of graphs: $G \in \mathcal{P}\wedge H\cong G\Longrightarrow H \in \mathcal{P}$. It is sometimes more comfortable to refer to a property as a class of graphs.

A graph property $\mathcal{P}$ is hereditary if it is closed under taking induced subgraphs; that is, $G \in \mathcal{P}\wedge H \leq G\Longrightarrow H \in \mathcal{P}$ (where H ≤ G denotes that H is an induced subgraph of G). It is natural in this context to focus on hereditary properties because if G has an efficient local representation, then G − v does as well.

Local representations are associated with graph classes (and not with individual graphs).

Definition 2.1.

Let $\mathcal{P}$ be a hereditary property of graphs. A local representation for $\mathcal{P}$ is a symmetric function $A: \mathbb{Z}^{+} \times \mathbb{Z}^{+} \rightarrow \{ 0,1\}$ such that for every graph $G \in \mathcal{P}$ there is a labeling function $\ell: V (G) \rightarrow \mathbb{Z}^{+}$ such that for distinct vertices v, w of G, we have v ∼ w ⇔ A[ℓ(v), ℓ(w)] = 1.

In other words, A is an adjacency test used by all graphs in $\mathcal{P}$. Each graph G in $\mathcal{P}$ has its own labeling function ℓ, and adjacency of two distinct vertices can be tested by applying the test A to the labels assigned to the pair.

[Note that Definition 2.1 requires that the vertex labels be positive integers, but in the examples in Section 6.1, the labels are tuples of integers. This is a minor technicality as we could perform kludges such as converting a pair of nonnegative integers (a, b) into a ternary number by writing a and b in binary and separating the values with a 2, like this: (18, 11) ↦ 1001021011 _three.]

Definition 2.1 omits any notion of efficiency and, consequently, is not interesting. Indeed, all hereditary properties have local representations using this definition; here’s how.

Let G be any graph and assume that V (G) = [n]. We label vertex v by ℓ(v) = [v; a(v)] where a(v) is an n-tuple of 0s and 1s that indicates the neighbors of v. That is, the jth entry in a(v) is 1 exactly when v ∼ j. Stated differently, a(v) is the v ^th row of G’s adjacency matrix. The test function A applied to labels ℓ(v) = [v; a(v)], and ℓ(w) = [w; a(w)] simply returns the w ^th entry in a(v).

In other words, if we allow long labels, the neighborhood of a vertex can be trivially encoded in the label. We therefore impose a bound on the size of the vertex labels. We have previously expressed this as a bound on the number of bits that specify the label as being O(logn). These bits can be merged to form a single positive integer, and the restriction on the number of bits translates to requiring labels to lie in a set of the form [n ^k] where k is a given positive integer.

Definition 2.2.

Let $\mathcal{P}$ be a hereditary property of graphs. An efficient local representation for $\mathcal{P}$ is a symmetric function $A: \mathbb{Z}^{+} \times \mathbb{Z}^{+} \rightarrow \{ 0,1\}$ and a positive integer k such that every graph $G \in \mathcal{P}$ there is a labeling function ℓ: V (G) → [n ^k] (where n =  | V (G) | ) such that for distinct vertices v, w of G we have v ∼ w ⇔ A[ℓ(v), ℓ(w)] = 1.

As before, the adjacency test A depends only on the property $\mathcal{P}$. Likewise the positive integer k is fixed for the class (does not depend on n). That labels take values in [n ^k] is tantamount to saying that the labels are (at most) klgn bits in length. It is in this sense, the representation is (space) efficient.

6.2.2 The Problem

When we failed to restrict the number of bits in the labels, the class of all graphs $\mathcal{G}$ has a local representation. The interesting question is: What happens when we require efficiency? Is there an efficient local representation for all graphs?

This would be fantastic, but not surprisingly, the answer is no. To see why, we use a counting argument. To that end, we recall the definition of the speed of a hereditary property of graphs [1, 28].

Definition 2.3.

Let $\mathcal{P}$ be a hereditary property of graphs and let n be a positive integer. Define $\mathcal{P}(n)$ to be the number of graphs in $\mathcal{P}$ with vertex set [n]. The function $\mathcal{P}(\cdot )$ is called the speed of the property.

For example, let $\mathcal{G}$ denote the class of all graphs. Then $\mathcal{G}(n) = 2^{\binom{n}{2}}$. Or let $\mathcal{P}$ be the property of having at most one edge. The set of graphs with vertex set [n] that has at most one edge consists of the edgeless graph $\overline{K_{n}}$ and $\binom{n}{2}$ graphs with exactly one edge. Therefore $\mathcal{P}(n) = 1 + \binom{n}{2}$.

To show that not all hereditary properties admit an efficient local representation, we prove the following.

Proposition 2.4.

Let $\mathcal{B}$ be the class of bipartite graphs. Then $\mathcal{B}$ does not admit an efficient local representation.

Proof.

Suppose for contradiction that $\mathcal{B}$ admits an efficient local representation (A, k). Let n be a positive integer.

Every $G \in \mathcal{B}$ with V (G) = [n] has a labeling function ℓ: [n] → [n ^k], and, necessarily, different graphs have different labeling functions.

The number of functions from [n] to [n ^k] is n ^kn which implies that $\mathcal{B}(n) \leq n^{kn}$. However, it is easy to see that $\mathcal{B}(n) \geq 2^{n^{2}/4 }$ which exceeds n ^kn once n is large enough.

In a similar spirit, we show that the class of string graphs does not admit an efficient local representation.

Proposition 2.5.

Let $\mathcal{S}$ be the class of string graphs. Then $\mathcal{S}$ does not admit an efficient local representation.

Proof.

Recall that a graph G is a split graph [10] provided we can partition V (G) = K ∪ I where K is a clique and I is an independent set. We show that the class of string graphs contains all split graphs. Since the number of split graphs on vertex set [n] is at least as large as the number of bipartite graphs on [n], the result follows exactly as in the proof of Proposition 2.4.

Let G be a split graph with V (G) = K ∪ I. To see that G is a string graph, assign disjoint curves to the vertices in I. For the vertices in K, we choose curves that emanate from a common point. If v ∈ K is adjacent to i ₁, i ₂, …, i _d  ∈ I, then v’s curve can be chosen to intersect the disjoint curves that represent i ₁, i ₂, …, i _d while avoiding all other I-curves as in Figure 6.2. □ 

Fig. 6.2

We present a split graph and its string representation. The curves representing the vertices in the independent set I = { 6, 7, 8, 9} are the disjoint vertical line segments. The curves representing the vertices in the clique K = { 1, 2, 3, 4, 5} must intersect each other and exactly those curves for vertices in I to which they are adjacent. For example, the curve representing vertex 1 intersects vertical segments 6, 7, and 9, but not 8

Note that the key fact we used in the proof of Proposition 2.4 is that there are too many graphs on n vertices. In order for a hereditary property $\mathcal{P}$ to admit an efficient local representation, the speed of $\mathcal{P}$ must be bounded by a function of the form n ^kn for a specific integer k.

Thus a hereditary property can fail to have an efficient local representation if it contains too many graphs—it violates the “speed limit” $\mathcal{P}(n) \leq n^{kn}$ for all fixed values of k.

What else could go wrong? That’s a great question. Raised by [15] and [22], this is the question we offer our readers and present as our contribution to this compendium of favorite conjectures:

Conjecture 2.6 (Muller 1987; Kannan, Naor, Rudich 1992).

Let $\mathcal{P}$ be a hereditary property of graphs. Then $\mathcal{P}$ admits an efficient local representation if and only if there is an integer k such that $\mathcal{P}(n) \leq n^{kn}$ .

6.3 Challenging Examples

Conjecture 2.6 holds for a wide swath of hereditary graph properties including some we have considered (acyclic graphs, planar graphs, interval graphs, circular arc graphs) and many more we have not (such as permutation graphs [9] and threshold graphs [20]).

The following examples are—as best we know—possible counterexamples. The challenge is to find efficient local representations for these classes or show that none exist. See [2, 6], or [21] to find other hereditary classes as possible challenges.

Line Segment Intersection Graphs 

The class of line segment intersection graphs lies between interval and string graphs. A graph G is a line segment intersection graph if we can assign to each v ∈ V (G) a planar line segment L _v in such a way that v ∼ w if and only if $L_{v} \cap L_{w}\not =\varnothing$. Let $\mathcal{L}$ denote the class of line segment intersection graphs. See [3, 5, 18, 24].

Using the techniques described in [26], one can derive an upper bound for $\mathcal{L}(n)$ of the form n ⁴ⁿ, and so—if we believe Conjecture 2.6—this class should admit an efficient local representation.

Creating a local representation is easy; checking that it is efficient is difficult! Here’s the representation. If $G \in \mathcal{L}$, then we know there is an assignment v ↦ L _v mapping vertices to line segments. These line segments can be represented as a 4-tuple of numbers (x, y, z, w) that specify the end points of the segment as (x, y) and (z, w). It’s easy to check that there is no loss of generality in assuming that these coordinates are positive rational numbers (because $\mathbb{Q}^{2}$ is dense in $\mathbb{R}^{2}$). Therefore the labeling becomes an 8-tuple of integers. (Furthermore, by clearing denominators, we may assume all the coordinates are positive integers and a 4-tuple will suffice.)

Checking adjacency (i.e., intersection of the line segments) can be reduced to evaluating a pair of polynomial functions on the end points (details in [26]).

The only issue that remains is this: How many bits do we need to specify the end points? Do we need a high level of precision, or can this be accomplished with O(logn) bits?

Cographs 

The class of complement reducible graphs [4], or cographs for short, can be described recursively as follows:

• K ₁ is a cograph.

• If G is a cograph, so is its complement $\overline{G}$.

• If G and H are cographs, then so is their disjoint union. (This is the graph formed by simply taking copies of G and H on disjoint vertex sets and no additional edges.)

Let $\mathcal{C}$ denote the class of cographs. It is easy to see that $\mathcal{C}$ is a hereditary property. It is well known that cographs are exactly those graphs that do not contain the path P ₄ as an induced subgraph.

With a bit of work, an upper bound of the form $\mathcal{C}(n) \leq n^{kn}$ can be derived. See sequence A000669 in [30].

Therefore, if Conjecture 2.6 holds, property $\mathcal{C}$ admits an efficient local representation.

Tolerance Graphs 

The class of tolerance graphs [13, 14] may be considered as a generalization of interval graphs. We say that a graph G has a tolerance representation if we can assign to each vertex v of G a pair (I _v , t _v ) where I _v is a closed, real interval and t _v is a positive real number so that v ∼ w in G if and only if the length of the intersection I _v ∩ I _w is at least min{t _v , t _w }. Graphs with such a representation are called tolerance graphs.

An application of the methods in [26] gives a speed bound of the form n ³ⁿ, and therefore tolerance graphs satisfy the hypothesis of Conjecture 2.6. Do they satisfy the conclusion?

Geometric Graphs 

Let $(\mathcal{X},d)$ be a metric space. A graph G has a geometric representation in $(\mathcal{X},d)$ if there is a mapping $f: V (G) \rightarrow \mathcal{X}$ such that v ∼ w if and only if d[f(v), f(w)] ≤ 1. See [23].

A particularly natural example is $\mathcal{X} = \mathbb{R}^{2}$ together with the Euclidean metric. In this case, we can think of such graphs as having an intersection representation by unit discs.

Still with the Euclidean metric, for $\mathcal{X} = \mathbb{R}^{k}$, the number of geometric graphs with vertex set [n] is bounded by an expression of the form n ^kn and therefore satisfies the hypothesis of Conjecture 2.6. Do they satisfy the conclusion?

6.4 Variations

There are some natural variations on the core problem to consider.

6.4.1 Computation Concerns

We have focused on space-efficient representations. Each vertex holds a modest quantity of information. The combined information held by two vertices is sufficient to determine if they are adjacent. But at what cost? The authors of [15] also require that the function A(⋅ , ⋅ ) be efficiently computable—in time polynomial in the size of the inputs. That is, the number of computational steps to check if v and w are adjacent in an n vertex graph should be bounded by an expression of the form (logn)^t for some fixed exponent t.

This is a perfectly reasonable requirement but appears to make this difficult problem only harder. Their conjecture (which we may dub the strong efficient local representation conjecture) is that hereditary properties that satisfy the speed limit $\mathcal{P}(n) \leq n^{kn}$ have an efficient local representation A that is polynomial-time computable. Clearly the strong version of the conjecture implies the weaker.

6.4.2 Other Label Sizes

Why do we want label sizes with O(logn) bits? This size is natural because already to name the vertices (e.g., specify vertex names in [n]) requires lgn bits. Thus the desire that ℓ(v) be represented in O(logn) bits is akin to saying that the labels are “about the same size” as the vertex names.

If, however, we are willing to modify this requirement, we can generate a host of additional problems.

Suppose we permit vertex labels to be larger—say, $O(\sqrt{n})$ bits. Then, presumably, such local representations could encompass more hereditary graph properties. If this is permitted, can we represent all hereditary properties that satisfy the speed limit $\mathcal{P}(n) \leq n^{kn}$? For the case of $O(\sqrt{n})$ bits, the counting argument shows that the properties must obey a bound of the form $n^{k\sqrt{n}}$; if $\mathcal{P}$ does obey such a bound, must it admit an $O(\sqrt{n})$ bits-per-vertex local representation?

On the other hand, we might consider using smaller labels, i.e., with o(logn) bits per vertex. As an extreme example, suppose $\mathcal{P}$ is the property of being a complete bipartite graph. Then we can label vertices with just a single bit (0 for vertices in one part of the bipartition and 1 for vertices in the other) and use the function A(x, y) = 1[x ≠ y].

Using the results in [28], we have the following result from [27].

Theorem 4.1.

Let $\mathcal{P}$ be a hereditary property of graphs and let k be a positive number with $k < \frac{1} {2}$ . If, for all n sufficiently large, we have $\mathcal{P}(n) \leq n^{kn}$ , then $\mathcal{P}$ admits a local representation in which the labels have O(1) bits.□

In other words, the “super efficient” [o(logn) bits per vertex] local representation conjecture is true. Furthermore, if a property has a representation using o(logn) bits per vertex, then it has a representation using a constant number of bits per vertex.