Circuit Double Covers of Graphs

Abstract

The circuit double cover conjecture (CDC conjecture) is easy to state: For every 2-connected graph, there is a family $\mathcal{F}$ of circuits such that every edge of the graph is covered by precisely two members of $\mathcal{F}$. The CDC conjecture (and its numerous variants) is considered by most graph theorists as one of the major open problems in the field. The CDC conjecture, Tutte’s 5-flow conjecture, and the Berge-Fulkerson conjecture are three major snark family conjectures since they are all trivial for 3-edge-colorable cubic graphs and remain widely open for snarks. This chapter is a brief survey of the progress on this famous open problem.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

16.1 Introduction

The circuit (cycle) double cover conjecture (CDC conjecture) is easy to state: For every 2-connected graph, there is a family $\mathcal{F}$ of circuits such that every edge of the graph is covered by precisely two members of $\mathcal{F}$. As an example, if a 2-connected graph is properly embedded on a surface (without crossing edges) in such a way that all faces are bounded by circuits, then the collection of the boundary circuits will “double cover” the graph.

The CDC conjecture (and its numerous variants) is considered by most graph theorists as one of the major open problems in the field. One reason for this is its close relationship with topological graph theory, integer flow theory, graph coloring, and the structure of snarks.

The CDC conjecture was presented as an “open question” by Szekeres [66] for cubic graphs (as we will see soon in Theorem 1, it is equivalent for all bridgeless graphs). The conjecture was also independently stated by Seymour in [62] for all bridgeless graphs. An equivalent version of the CDC conjecture was proposed by Itai and Rodeh [36] that every bridgeless graph has a family $\mathcal{F}$ of circuits such that every edge is contained in one or two members of $\mathcal{F}$.

For the origin of the conjecture, some mathematicians gave the credit to Tutte. According to a personal letter from Tutte to Fleischner [73], he said, “I too have been puzzled to find an original reference. I think the conjecture is one that was well established in mathematical conversation long before anyone thought of publishing it.” It was also pointed out in the survey paper by Jaeger [41] that “it seems difficult to attribute the paternity of this conjecture” and also pointed out in some early literature (such as [23]) that “its origin is uncertain.” This may explain why the CDC conjecture is considered as “folklore” in [7] (Unsolved problem 10). Some early investigations related to the conjecture can be traced back to publications by Tutte in 1949 [70, 73].

Most material presented in this chapter follows the pioneering survey papers by Jaeger (1985 [41]), and Jackson (1993 [37]), and the monographs Integer Flows and Cycle Covers of Graphs (1997 [78]) Circuit Double Covers of Graphs (2007 [79]) by the author.

The circuit double cover conjecture is obviously true for 2-connected planar graphs since the boundary of every face is a circuit and the set of the boundaries of all faces forms a circuit double cover of an embedded graph. One might attempt to extend this observation further to all 2-connected graphs embedded on some surfaces. However, it is not true that any embedding of a 2-connected graph is free of a handle bridge. That is, the boundary of some face may not be a circuit. This leads to an even stronger open problem in topology known as the strong embedding conjecture: Can we find an embedding of a 2-connected graph G on some surface $\Sigma$ such that the boundary of every face is a circuit? See [27, 50] or Conjecture 3.10 in [7] for more information.

The following theorem summarizes some structure of a minimal counterexample to the circuit double cover conjecture (see [41]).

Theorem 1.

If G is a minimum counterexample to the circuit double cover conjecture, then:

• (1) G is simple, 3-connected, and cubic;

• (2) G has no nontrivial 2 or 3-edge cut;

• (3) G is not 3-edge colorable; and

• (4) G is not planar.

Thus, most graphs considered in this chapter are cubic and bridgeless.

For a 3-edge-colorable cubic graph, we have an even stronger result for even subgraph double cover. The following theorem was formulated by Jaeger [41]. (The equivalence of (1) and (2) was also applied in [62].)

Theorem 2.

Let G be a cubic graph. Then the following statements are equivalent:

• (1) G is 3-edge colorable;

• (2) G has a 3-even subgraph double cover; and

• (3) G has a 4-even subgraph double cover.

16.2 Faithful Circuit Cover and Petersen Minor-Free Graphs

The concept of faithful circuit cover is not only a generalization of the circuit double cover problem but also an inductive approach to the CDC conjecture in a very natural way.

Let $\mathcal{Z}^{+}$ be the set of all positive integers and $\mathcal{Z}^{\star }$ be the set of all nonnegative integers.

Definition 1.

Let G be a graph and $w: E(G) \rightarrow \mathcal{Z}^{+}$. A family $\mathcal{F}$ of circuits (or even subgraphs) of G is a faithful circuit cover (or faithful even subgraph cover, respectively) with respect to w if each edge e is contained in precisely w(e) members of $\mathcal{F}$.

Figure 16.1 shows an example of a faithful circuit cover of (K ₄, w) where $w: E(K_{4}) \rightarrow \{ 1,2\}$. Here w ⁻¹(1) induces a Hamilton circuit and w ⁻¹(2) induces a perfect matching (a pair of diagonals).

Fig. 16.1

Faithful circuit cover – an example

It is obvious that the circuit double cover is a special case of the faithful circuit cover problem by choosing the weight w to be 2 for every edge.

Definition 2.

Let G be a graph. A weight $w: E(G) \rightarrow \mathcal{Z}^{+}$ is Eulerian if the total weight of every edge cut is even. And (G, w) is called an Eulerian weighted graph.

Definition 3.

Let G be a graph. An Eulerian weight $w: E(G) \rightarrow \mathcal{Z}^{+}$ is admissible if, for every edge-cut T and every e ∈ T,

$$\displaystyle{w(e) \leq \frac{w(T)} {2}.}$$

And (G, w) is called an admissible Eulerian weighted graph if w is Eulerian and admissible.

If G has a faithful circuit cover $\mathcal{F}$ with respect to a weight $w: E(G) \rightarrow \mathcal{Z}^{+}$, then the total weight of every edge cut must be even since, for every circuit C of $\mathcal{F}$ and every edge-cut T, the circuit C must use an even number of distinct edges of the cut T. With this observation, the requirements of being Eulerian and admissible are necessary for faithful circuit covers.

Problem 1.

Let G be a bridgeless graph with $w: E(G) \rightarrow \mathcal{Z}^{+}$. If w is admissible and Eulerian, does G have a faithful circuit cover with respect to w?

Unfortunately, Problem 1 is not always true. The Petersen graph P ₁₀ with an Eulerian weight w ₁₀ (see Figure 16.2) does not have a faithful circuit cover: where the set of weight 2 edges induces a perfect matching of P ₁₀ and the set of weight 1 edges induces two disjoint pentagons.

Fig. 16.2

$(P_{10},w_{10})$

For a given weight $w: E(G) \rightarrow \mathcal{Z}^{+}$, denote

$$\displaystyle{E_{w=i}\ =\ \{e \in E(G):\ w(e) = i\}.}$$

Like many mainstream research areas in graph theory, 3-edge coloring plays a central role in the study of the faithful circuit cover problem. The following is one of the most frequently used lemmas in this field.

Lemma 1 (Seymour [62]).

Let G be a cubic graph and $w: E(G) \rightarrow \{ 1,2\}$ be an Eulerian weight. Then the following statements are equivalent:

• (1) G is 3-edge colorable; and

• (2) G has a faithful 3-even subgraph cover with respect to w.

Since the 4-color theorem is equivalent to 3-edge colorings for all bridgeless cubic planar graphs, an immediate corollary of Lemma 1 is the following early result (Theorem 3) by Seymour. An alternative proof of Theorem 3 (slightly stronger) is provided by Fleischner [15] without using the 4-color theorem.

Theorem 3 (Seymour [62], and Fleischner [15, 18]).

If G is a planar, bridgeless graph associated with an Eulerian weight $w: E(G) \rightarrow \{ 1,2\}$ , then G has a faithful circuit cover with respect to w.

Theorem 3 was further generalized for Petersen minor-free graphs as follows.

Theorem 4 (Alspach, Goddyn and Zhang [1, 3]).

Let G be a graph without a Petersen minor and $w: E(G) \rightarrow Z^{+}$ be an admissible Eulerian weight. Then G has a faithful circuit cover with respect to w.

16.3 Integer Flows

The concept of integer flow was introduced by Tutte [70], [71] as a generalization of the map coloring problems. This section is a brief survey of circuit covering theorems arising from the integer flow theory. Readers are referred to [40, 65, 78] of the comprehensive surveys in this area.

The following are some of classical results in flow theory.

Theorem 5 (Jaeger [38, 39]).

Every 4-edge-connected graph admits a nowhere-zero 4-flow.

Theorem 6 (Jaeger [39], Kilpatrick [44]).

Every bridgeless graph admits a nowhere-zero 8-flow.

Theorem 6 is further improved by Seymour in the following theorem.

Theorem 7 (Seymour [63]).

Every bridgeless graph admits a nowhere-zero 6-flow.

With the application of the following lemma, the flow theorems can be stated as even subgraph covering problems.

Lemma 2 (Matthews [52]).

Let r be a positive integer. A graph G admits a nowhere-zero 2 ^r -flow if and only if G has an r-even subgraph cover.

Thus, the following are corollaries of Theorems 5 and 6.

Corollary 1 (Jaeger [40]).

Every 4-edge-connected graph has a 2-even subgraph cover, and every bridgeless graph has a 3-even subgraph cover.

With an elementary operation, symmetric difference, between even subgraphs, one can further state the above corollary as theorems for even subgraph double covers and 4-covers.

Corollary 2 (Jaeger [40]).

Every 4-edge-connected graph has a 3-even subgraph double cover.

Corollary 3 (Bermond, Jackson and Jaeger [5]).

Every bridgeless graph has a 7-even subgraph 4-cover.

Applying Theorem 7, Fan proved the following even subgraph cover result.

Theorem 8 (Fan [13]).

Every bridgeless graph has a 10-even subgraph 6-cover.

The following is a combination of Corollary 3 and Theorem 8.

Theorem 9 ( [13]).

For each even integer k greater than two, every bridgeless graph has an even subgraph k-cover.

Theorem 9 is therefore a partial result for the following conjectures.

Conjecture 1 (Seymour [62]).

Let $w: E(G) \rightarrow \mathcal{Z}^{+}$ be an admissible Eulerian weight of a bridgeless graph G such that $w(e) \equiv 0\bmod 2$ for each edge e ∈ E(G). Then G has a faithful circuit cover of w.

Conjecture 2 (Goddyn [26]).

Let $w: E(G) \rightarrow \mathcal{Z}^{+}$ be an admissible Eulerian weight of a bridgeless graph G. If w(e) ≥ 2 for every edge e of G, then (G, w) has a faithful circuit cover.

Corollary 3 can also be considered as a partial result for the Berge-Fulkerson conjecture. The following is an equivalent version of the conjecture.

Conjecture 3 (Berge and Fulkerson [22]).

Every bridgeless cubic graph has a 6-even subgraph 4-cover.

16.4 Small Oddness

Definition 4.

Let S be an even subgraph of a cubic graph G. A component C of S is odd (or even) if C contains an odd (or even, respectively) number of vertices of G.

Definition 5.

Let G be a bridgeless cubic graph. For a spanning even subgraph S of G, the oddness of S, denoted by odd(S), is the number of odd components of S. For the cubic graph G, the oddness of G, denoted by odd(G), is the minimum of odd(S) for all spanning even subgraph S of G.

The following are some straightforward observations.

Fact.

A cubic graph G is 3-edge colorable if and only if odd(G) = 0.

Fact.

The oddness of every cubic graph must be even.

Note that determination of the oddness of a cubic graph is a hard problem since determining the 3-edge colorability of a cubic graph is an NP-complete problem [31].

Theorem 10 (Huck and Kochol [35] and [32, 45]).

Let G be a bridgeless cubic graph with oddness at most 2. Then G has a 5-even subgraph double cover.

Theorem 10 was further improved by Huck [34] (a computer-assisted proof) and independently by Häggkvist and McGuinness [30], for oddness 4 graphs.

Theorem 11 (Huck [34], Häggkvist and McGuinness [30]).

Let G be a bridgeless cubic graph with oddness at most 4. Then G has a circuit double cover.

For a 3-edge-colorable cubic graph G ₁ and an edge e ∈ E(G ₁), it is obvious that the suppressed cubic graph $G_{2} = \overline{G_{1} - e}$ is of oddness at most 2. And, therefore, a bridgeless cubic graph containing a Hamilton path is also of oddness at most 2. The following is a corollary of Theorem 10.

Corollary 4 (Tarsi [67]; Or see [25] for a simplified proof).

Every bridgeless graph containing a Hamilton path has a 6-even subgraph double cover.

Note that every 3-edge-colorable cubic graph (Theorem 2) has a 3-even subgraph double cover, while every oddness 2 cubic graph has a 5-even subgraph double cover. The following is a conjecture for all bridgeless graphs.

Conjecture 4 (Preissmann [58] and Celmins [9]).

Every bridgeless graph has a 5-even subgraph double cover.

16.5 Strong Circuit Double Cover

Circuit Extension and Strong CDC

Note that in the Eulerian (1, 2)-weighted Petersen graph (P ₁₀, w ₁₀) (see Figure 16.2), $E_{w_{10}=1}$ induces two disjoint circuits. How about an Eulerian (1, 2)-weighted graph (G, w) for which E _w = 1 induces a single circuit? The following is an open problem that addresses possible faithful covers for such weighted graphs.

Conjecture 5 (Strong circuit double cover conjecture, Seymour, see [17] p. 237, and [18], also see [24]).

Let w be an Eulerian (1, 2)-weight for a 2-edge-connected, cubic graph G. If the subgraph of G induced by weight 1 edges is a circuit, then (G, w) has a faithful circuit cover.

Conjecture 5 has an equivalent statement.

Let G be a 2-edge-connected cubic graph and C be a circuit of G; then the graph G has a circuit double cover $\mathcal{F}$ with $C \in \mathcal{F}$.

Definition 6.

Let C be a circuit of a 2-edge-connected cubic graph G. A strong circuit (even subgraph) double cover of G with respect to C is a circuit (even subgraph) double cover $\mathcal{F}$ of G with $C \in \mathcal{F}.$ (As an abbreviation, $\mathcal{F}$ is called a strong CDC of G with respect to C.)

Conjecture 5 is obviously stronger than the circuit double cover conjecture. Conjecture 6 (Sabidussi Conjecture) is a special case of Conjecture 5 that the given circuit is dominating.

Conjecture 6 (Sabidussi and Fleischner [16], and Conjecture 2.4 in [2]).

Let G be a cubic graph such that G has a dominating circuit C. Then G has a circuit double cover $\mathcal{F}$ such that the given circuit C is a member of $\mathcal{F}$.

The following is a general question for circuit extension.

Problem 2 (Seymour [64], also see [20, 47]).

For a 2-edge-connected cubic graph G and a given circuit C of G, does G contain a circuit C′ with $V (C) \subseteq V (C')$ and $E(C)\neq E(C')$?

Definition 7.

A circuit C of a graph G is extendable if G contains another circuit C′ such that $V (C) \subseteq V (C')$ and E(C) ≠ E(C′). And the circuit C′ is an extension of C (or simply a C-extension).

Problem 2 proposes a possible recursive approach to Conjecture 5.

Proposition 1 (Kahn, Robertson, Seymour [43], also see [10, 64], personal communication, 2012).

If Problem  2 is true for every circuit in every 2-edge-connected cubic graph, then Conjecture  5 is true.

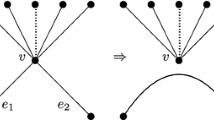
Note that not every circuit is extendable; the graph in Figure 16.3 is an example discovered by Fleischner ([15, 17, 19, 20]) in which a circuit C does not have an extension.

Fig. 16.3

The circuit C (of length $16 = n - 2$) is not extendable

Definition 8.

Let G be a 2-edge-connected, cubic graph and C be a circuit of G. If C is not extendable, then C is called a stable circuit of G.

Note that the graph G illustrated in Figure 16.3 is a $\oplus _{3}$-sum of two copies $G/P_{1},G/P_{2}$ of the Petersen graphs (where P ₁, P ₂ are two components of $G -\{ e_{0},e_{1},e_{2}\}$).

Proposition 2 (Fleischner).

The circuit C illustrated in Figure  16.3 is stable.

In [20] and [47], infinite families of stable circuits are constructed by Fleischner and Kochol. Some of them are cyclically 4-edge-connected snarks [47].

Recently, a computer-aided search [8] discovered stable circuits for some cyclically 4-edge-connected snarks of order n, for every even integer $n \in \{ 22,\ldots,36\}$. However, the existence of stable circuits does not disprove the strong CDC conjecture for those snarks: the computer-aided proof further verifies the strong CDC conjecture for all of those small snarks (cyclically 4-edge-connected snarks of order at most 36). Note that 3-edge-colorable graphs are not counterexamples to any faithful cover problem (Lemma 1), and graphs with nontrivial 2- or 3-edge cut can be reduced to graphs of smaller orders.

Proposition 3 (Brinkmann, Goedgebeur, Hägglund and Markström [8]).

The strong circuit double cover conjecture holds for all bridgeless cubic graphs of order at most 36.

Note that, for the stable circuit C illustrated in Figure 16.3, $\vert V (G) - V (C)\vert = 2$. Although it is not extendable, it is not a counterexample to the strong circuit double cover conjecture. However, for all cubic graphs, the strong CDC conjecture remains open if a circuit C is of length n − 2.

Extension-Inheritable Properties

Definition 9. A given property $\mathcal{P}$ is extension-inheritable, if for any pair (G, C) with property $\mathcal{P}$,

• (1) The property $\mathcal{P}$ guarantees the existence of a C-extension C′, and

• (2) The reduced pair $(\overline{G - (E(C) - E(C'))},C')$ also has the same property $\mathcal{P}$.

Fleischner [19], by applying the lollipop method introduced in [68], discovered the first extension-inheritable property: circuit of length at least n − 1.

With the same approach as for Proposition 1, we have the following lemma.

Lemma 3.

If a pair (G,C) has some extension-inheritable property $\mathcal{P}$ , then the graph G has a circuit double cover containing C.

In the remaining part of this section, following the approach in [21], some extension-inheritable properties are summarized.

Definition 10.

A spanning tree T of a graph H is called a Y-tree if T consists of a path $x_{1}\ldots x_{t-1}$ and an edge $x_{t-2}x_{t}$. A Y -tree is called a small-end Y -tree if $d_{H}(x_{1}) \leq 2$.

A Hamilton path $x_{1}\ldots x_{t}$ of H is called a small-end Hamilton path if $d_{H}(x_{1}) \leq 2$.

The following is a list of some known extension-inheritable properties where G is a 2-edge-connected cubic graph and C is a circuit of G.

• (1) C is a Hamilton circuit of G (C. A. B. Smith; see [68, 69] or [72] p. 243).

• (2) |V (G) − V (C)|≤ 1 (Fleischner [19]; also see [21]).

• (3) |V (G) − V (C)|≤ 2 and, in the case of $\vert V (G) - V (C)\vert = 2$ , the distance between two vertices of V (G) − V (C) is 3 (Fleischner and Häggkvist [21]; see Figure  16.4).

  Fig. 16.4

  

  An extendable circuit missing two vertices

• (4) |V (G) − V (C)|≤ 4 and G − V (C) is connected (Fleischner and Häggkvist [21]).

• (5) |V (G) − V (C)|≤ 6 and G − V (C) is connected [54].

• (6) $H = G - V (C)$ has a small-end Hamilton path (see Figure  16.5). (Fleischner and Häggkvist [28].)

  Fig. 16.5

  

  An extendable circuit missing a small-end Hamilton path

• (7) $H = G - V (C)$ has either a small-end Hamilton path or a small-end Y -tree (see Figures  16.5 and  16.6).

  Fig. 16.6

  

  An extendable circuit missing a small-end Y -tree

• (8) $H = G - V (C)$ is of order at most 13 and has a Hamilton path or a Y -tree [54].

Semi-Extension of Circuits

If a circuit C is not extendable, the graph G may still have a strong CDC containing C. In this section, we present a relaxed definition for circuit extendibility (introduced in [12]), by which the strong CDC conjecture (Conjecture 5) is true if every circuit of 2-connected cubic graphs has a semi-extension (Theorem 12 and Conjecture 7).

Before the introduction of the new concept of semi-extension, we first introduce the definition of Tutte bridge.

Definition 11.

Let H be a subgraph of G. A Tutte bridge of H is either a chord e of H ($e = xy\notin E(H)$ with both x, y ∈ V (H)) or a subgraph of G consisting of one component Q of G − V (H) and all edges joining Q and H (and, of course, all vertices of H adjacent to Q).

For a Tutte bridge B _i of H, the vertex subset $V (B_{i}) \cap V (H)$ is called the attachment of B _i and is denoted by A(B _i ) (see Figure 16.7).

Fig. 16.7

Two Tutte bridges $B_{1},B_{2}$ of a circuit C

Definition 12.

Let C and D be a pair of distinct circuits of a 2-connected cubic graph G. Let $J_{1},\ldots,J_{p}$ be the components of $C \bigtriangleup D$. The circuit D is a semi-extension of C if, for every Tutte bridge B _i of $C \cup D$,

• (1) Either the attachment $A(B_{i}) \subseteq V (D)$, or

• (2) $A(B_{i}) \subseteq V (J_{j})$ for some $j \in \{ 1,\ldots,p\}$.

Note that a semi-extension D of C may not contain all the vertices of C.

It is easy to see that the concept of circuit semi-extension is a generalization of circuit extension: for a C-extension D, every Tutte bridge B _i has its attachment $A(B_{i}) \subseteq V (D)$ (since each J _j contains no vertex of V (C) − V (D)).

Conjecture 7 (Esteva and Jensen [12]).

For every 2-connected cubic graph G, every circuit C of G has a semi-extension.

Theorem 12 (Esteva and Jensen [12]).

If Conjecture  7 is true for every 2-connected cubic graph, then the strong circuit double cover conjecture is true.

Further Generalizations

Similar to Definition 12 and Theorem 12, the concept of semi-extension can be further generalized as follows.

Definition 13.

Let G be a 2-connected cubic graph, C be a circuit, and D be a nonempty even subgraph of G with components $D_{1},\ldots,D_{q}$. Let $J_{1},\ldots,J_{p}$ be the components of $C \bigtriangleup D$. The even subgraph D is a weak semi-extension of C if, for every Tutte bridge B _i of $C \cup D$,

• (1) Either the attachment $A(B_{i}) \subseteq V (J_{j})$ for some $j \in \{ 1,\ldots,p\}$, or

• (2) $A(B_{i}) \subseteq V (D_{h})$ for some $h \in \{ 1,\ldots,q\}$.

Conjecture 8.

For every 2-connected cubic graph G, every circuit C of G has a weak semi-extension.

With a similar proof to that of Theorem 12, we have the following result.

Proposition 4.

If Conjecture  8 is true for every 2-connected cubic graph, then the strong circuit double cover conjecture is true.

16.6 Kotzig Frames

Spanning Kotzig Subgraphs

Definition 14. A cubic graph H is called a Kotzig graph if H has a 3-edge-coloring $c: E(H) \rightarrow \{ 1,2,3\}$ such that $c^{-1}(i) \cup c^{-1}(j)$ is a Hamilton circuit of H for every pair i, j ∈ { 1, 2, 3}. (Equivalently, H is a Kotzig graph if it has a 3-circuit double cover.) The coloring c is called a Kotzig coloring of H.

Obviously, 3K ₂, K ₄, Möbius ladders M _2k+1 for every k ≥ 0, the Heawood graph, and the dodecahedron graph are examples of Kotzig graphs.

The study of CDC for graphs containing some spanning subgraphs that are subdivisions of Kotzig graphs was initially started in [24]. Later, it was further generalized in [29].

Definition 15.

A graph H is a spanning minor of another graph G if G has a spanning subgraph that is a subdivision of H. If H is a Kotzig graph, then we say G has a spanning Kotzig minor.

Theorem 13 (Goddyn [24], also see [29]).

If a graph G has a Kotzig graph as a spanning minor, then G has a 6-even subgraph double cover.

The concept of spanning Kotzig minor is further generalized in [24] and [29].

Definition 16.

Let H be a cubic graph with a 3-edge-coloring $c: E(H) \rightarrow \mathcal{Z}_{3}$ such that

(∗) edges in colors 0 and μ(μ ∈ { 1, 2}) induce a Hamilton circuit.

Let F be the even 2-factor induced by edges in colors 1 and 2. If, for every even subgraph $S \subseteq F$, switching colors 1 and 2 of the edges of S yields a new 3-edge coloring having the same property (∗), then the 3-edge-coloring c is called a semi-Kotzig coloring. A cubic graph H with a semi-Kotzig coloring is called a semi-Kotzig graph.

Similar to semi-Kotzig graphs, various generalizations, variations, or relaxations of Kotzig graphs have been introduced in [29], such as switchable-CDC graph, iterated Kotzig graph, etc. Analogies and stronger versions of Theorem 13 have been obtained for those generalizations or variations ([24, 29]).

Kotzig Frames: Disconnected Spanning Subgraphs

If a cubic graph G has an even 2-factor, then the graph G has many nice properties: G is 3-edge colorable, G has a circuit double cover, etc. Inspired by the structure of even 2-factors, Häggkvist and Markström [29] introduced the following concept which extends the investigation of connected spanning minors to disconnected cases.

Definition 17.

Let G be a cubic graph. A spanning subgraph H of G is called a frame of G if G∕H is an even graph.

Definition 18.

Let G be a cubic graph. A frame H of G is called a Kotzig frame (or semi-Kotzig frame) of G if, for each non-circuit component H _j of H, the suppressed graph $\overline{H_{j}}$ is a Kotzig graph (or semi-Kotzig graph, respectively).

We have discussed cubic graphs with connected Kotzig frames (Theorem 13) and some of its generalizations. Those are results about frames with only one component. In this section, graphs with disconnected frames will be further studied.

The following is a generalization of Theorem 13.

Theorem 14 (Häggkvist and Markström [29]).

If a cubic graph G has a Kotzig frame that contains at most one non-circuit component, then G has a 6-even subgraph double cover.

Similarly, Theorem 14 is further generalized for semi-Kotzig frames and other frames ([29]).

Theorem 15 (Ye and Zhang [74]).

If a cubic graph G contains a semi-Kotzig frame with at most one non-circuit component, then G has a 6-even subgraph double cover.

The following conjecture about semi-Kotzig frames was originally proposed in [29] for Kotzig frames, iterated Kotzig frames, and switchable-CDC frames.

Conjecture 9.

Let G be a cubic graph with semi-Kotzig frame. Then G has a circuit double cover.

Some partial results for Conjecture 9 can be found in [11, 29, 80], etc.

16.7 Orientable Cover

Attempts to prove the CDC conjecture have led to various conjectured strengthenings, such as the faithful circuit cover problem (Problem 1), strong circuit double cover problem (Conjecture 5), even covering problems (Conjectures 1 and 2), 5-even subgraph double cover problem (Conjecture 4), etc. Verification of any of those stronger problems will imply the CDC conjecture.

In this chapter, we present another type of variation of the double cover problem: directed circuit double covering. These are, in general, much stronger than the CDC problem. And some of them have already been completely characterized.

Historically, the paper by Tutte [70] on orientable circuit double cover is the earliest published article related to the CDC problem.

Orientable Double Cover

Definition 19. Let G = (V, E) be a graph and D be an orientation of E(G). A directed even subgraph H of the directed graph D(G) is a subgraph of D(G) such that for each vertex v of H, the indegree of v equals the outdegree of v.

Definition 20.

• (1) Let $\mathcal{F} =\{ C_{1},\ldots,C_{r}\}$ be an even subgraph double cover of a graph G. The set $\mathcal{F}$ is an orientable even subgraph double cover if there is an orientation D _μ on E(C _μ ), for each $\mu = 1,\ldots,r$, such that

  • (i) $D_{\mu }(C_{\mu })$ is a directed even subgraph, and

  • (ii) For each edge e contained in two even subgraphs C _α and C _β ($\alpha,\beta \in \{ 1,\ldots,r\}$), the directions of $D_{\alpha }(C_{\alpha })$ and $D_{\beta }(C_{\beta })$ are opposite on e.

• (2) An orientable k-even subgraph double cover $\mathcal{F}$ is an orientable even subgraph double cover consisting of k members. (See Figure 16.8.)

  Fig. 16.8

  

  An orientable 4-even subgraph double cover of K ₄

The following theorem was originally proved by Tutte [70] for cubic, bipartite graphs and reformulated and generalized by Jaeger [40].

Theorem 16 (Tutte [70]).

A graph G admits a nowhere-zero 3-flow if and only if G has an orientable 3-even subgraph double cover.

Tutte proved the following theorem in [70] for cubic graphs, and later this was generalized by Jaeger (see [39] or see [41]) and Archdeacon [4].

Theorem 17 (Tutte [70], Jaeger [39], Archdeacon [4]).

A graph G admits a nowhere-zero 4-flow if and only if G has an orientable 4-even subgraph double cover.

The following conjecture is proposed for general graphs.

Conjecture 10 (Archdeacon [4] and Jaeger [40]).

Every bridgeless graph has an orientable 5-even subgraph double cover.

16.8 Girth, Embedding, Small Cover

Girth

The girth of a smallest counterexample to the circuit double cover was first studied by Goddyn [23], in which a lower bound 7 of girth was found. Later, this bound was improved as follows: at least 8 by McGuinness [53] and at least 9 by Goddyn [24] (a girth bound of 10 was also announced in [24]). The following theorem, proved with a computer-aided search, remains the best bound up to today.

Theorem 18 (Huck [33]).

The girth of a smallest counterexample to the circuit double cover conjecture is at least 12.

It was conjectured in [42] that cyclically 4-edge-connected snarks have bounded girth. If this conjecture were true, then the circuit double cover conjecture would follow immediately by Theorem 18 (or an earlier result in [23] for girth 7). But this is not the case: in [46], Kochol gave a construction of cyclically 5-edge-connected snarks of arbitrarily large girths.

However, Theorem 18 (or its earlier results) remains useful in the studies of some families of embedded graphs with small genus since the girth of such graphs is bounded.

Small Genus Embedding

The circuit double cover conjecture is trivial if a bridgeless graph is planar: the collection of face boundaries is a double cover. How about graphs embeddable on surfaces other than a sphere? Although it is known that every bridgeless graph has a 2-cell embedding on some surface, it is not guaranteed that face boundaries are circuits.

The following early results verified the circuit double cover conjecture for graphs embeddable on some surfaces with small genus.

Theorem 19 (Zha [75–77]).

Let G be a bridgeless graph. If G has a 2-cell embedding on a surface with at most 5 crosscaps, or at most 2 handles, then G has a circuit double cover.

Theorem 19 was recently further generalized by Mohar to the following theorem for surfaces with larger genus.

Theorem 20 (Mohar [55]).

Let $\mathcal{G}$ be the family of all bridgeless graphs each of which has a 2-cell embedding on some surface with Euler characteristic ξ ≥−31. Then every member of $\mathcal{G}$ has a circuit double cover.

Small Circuit Double Covers

The following conjectures were proposed by Bondy in [6].

Conjecture 11 (Bondy [6]).

Every 2-edge-connected simple graph G of order n has a circuit double cover $\mathcal{F}$ such that $\vert \mathcal{F}\vert \leq n - 1$.

Conjecture 12 (Bondy [6]).

Every 2-edge-connected simple cubic graph G (G ≠ K ₄) of order n has a circuit double cover $\mathcal{F}$ such that $\vert \mathcal{F}\vert \leq \frac{n} {2}$.

The equivalent relation (Theorem 21) between the circuit double cover conjecture and a small circuit double cover conjecture (Conjecture 12) is proved in [49].

Theorem 21 (Lai, Yu and Zhang [49]).

If a simple cubic graph G (G ≠ K ₄ ) has a circuit double cover, then the graph G has a circuit double cover containing at most $\frac{\vert V (G)\vert } {2}$ circuits.

Conjecture 11 has been verified for some families of graphs ([14, 48, 51, 56, 57, 59–61]).