Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

A jet formed by the injector nozzle is highly dynamic and thus subject to an intensive turbulent exchange with the ambient air. Most available knowledge of the dynamics of water jets has been obtained almost exclusively by experimental measurements and is generally restricted to photographic observation of the jet form and the axial velocity distribution within the jet. In principle, by neglecting the fluid friction loss at the injector, the overall jet speed is directly obtained from the Bernoulli equation and equals \( \sqrt{2gH} \) where H is the pressure head at the injector inlet. The measurement of the velocity distribution in the jet was almost exclusively conducted by the use of Pitot tubes (Berntsen et al. 2001; Brekke 2005). The accuracy of this measurement technique is very limited. So one was, for example, unable to measure the velocity distribution where the streamlines are curved. The photographic method was mainly used to investigate the jet expansion and instability. Both the velocity measurements by means of Pitot tubes and photographic flow visualizations are unable to fully capture the hydrodynamic features of high-speed jets.

A decisive advance in experimental measurements of the jets in Pelton turbines could be achieved by applying laser measurement methods, i.e., the laser Doppler anemometry (LDA); see Zhang et al. (2000a, b, 2003) and Zhang and Parkinson (2001). A summary of important knowledge from measurements can be found in Zhang and Casey (2007). These investigations have helped to systematically understand the jet mechanics and the stability behaviors.

The following sections discuss, after a brief explanation of the LDA technique, the general characterization of jet flows based on experimental measurements at a model injector. For the purpose of considering the common features of the jet flow, there is no need to distinguish between model turbines and their prototypes.

4.1 Laser Doppler Anemometry

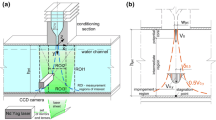
The LDA method is a widely used method for flow investigations. It is highly accurate and nonintrusive and shows the high time-resolution capability. Detailed descriptions of the working principles and the applications of the LDA method can be found, for example, in Durst et al. (1987), Albrecht et al. (2003), Ruck (1987), and Zhang (2010). The development of the LDA method in the past three decades includes both hardware and software development on the one hand and the development that are directed to application methods (Zhang 2004a, b, 2005) on the other hand. To measure the jet under water, Richter and Leder (2006) as well as Hüttmann et al. (2007) directly used a submergible LDA system. For measurements of jets in Pelton turbines, the applicability of the LDA method has been demonstrated by attaching a small wedge of Plexiglas on the jet according to Fig. 4.1. Such a window method aims to smooth the rough and turbulent jet surface, so that the laser beams are enabled to be transmitted into the jet. The disturbance in the flow, as caused by the wedge, is limited to the turbulent boundary layer of a thickness less than 0.1 mm on the surface of the wedge. The LDA method has been demonstrated to be highly accurate for high-speed jet measurements, even in areas of the jet with curved streamlines. Especially, the LDA method has been confirmed as the only effective method to precisely measure the secondary flows in the jet. For this purpose the dual measurement method (DMM) was developed (Zhang and Parkinson 2001, 2002) and has also been generally extended (Zhang 2005).

Fig. 4.1
figure 1

Water jet and optical configuration of LDA measurements (Zhang et al. 2000b)

Full size image

For more about the LDA application methods under many other measurement conditions, see Zhang (2010).

Based on LDA measurements at a model injector, the most important features of the jet flow are discussed and summarized below.

4.2 Axially Symmetric Jet Flow

Although the jet flow property strongly depends on the flow form at the injector inlet, the simplest case is considered first, as the inlet flow is fully developed in a straight circular pipe. The flow before entering the injector is therefore axially symmetric. Correspondingly, one expects an axially symmetric jet flow. Figure 4.2 shows such expected velocity distributions that are measured at various cross sections along the jet. They represent axial velocity components and have been normalized by the theoretical value of \( \sqrt{2gH} \). Based on these first measurements, the following general properties of the jet flow can be observed:

Fig. 4.2
figure 2

Axial velocity distributions in a jet generated by an injector with straight inlet flow

Full size image
  1. 1.

    In the center of the jet, a clearly separated jet core with a velocity deficit can be recognized. It is simply due to the boundary layer development on the needle surface and is partly equalized along the jet flow. The energy loss associated with the velocity deficit can be determined from measurements on the second measurement section (2D 0), where all streamlines are straight and parallel. The calculation shows that the related overall head loss is about 0.3 %. Since the nozzle opening in this case corresponds to the nominal operation point, the head loss of about 0.3 % can be considered to be general in all injectors under the nominal flow rate.

    The nonuniform velocity distribution in a jet section also means that for calculations of the overall mass, momentum, and energy flow rates each time the different mean velocities have to be applied according to the following definitions:

    $$ {\overline{C}}_{\mathrm{M}}=\frac{8}{d_0^2}{\displaystyle {\int}_0^{d_0/2}c\cdot r\cdot \mathrm{d}r,} $$
    (4.1)
    $$ {\overline{C}}_{\mathrm{I}}=\frac{8}{d_0^2{\overline{C}}_{\mathrm{M}}}{\displaystyle {\int}_0^{d_0/2}{c}^2\cdot r\cdot \mathrm{d}r,} $$
    (4.2)
    $$ \overline{C_{\mathrm{E}}^2}=\frac{8}{d_0^2{\overline{C}}_{\mathrm{M}}}{\displaystyle {\int}_0^{d_0/2}{c}^3\cdot r\cdot \mathrm{d}r.} $$
    (4.3)

    Corresponding calculations on the second measurement section according to Fig. 4.2 show that the difference between the three mean velocities is negligibly small (\( {\overline{C}}_{\mathrm{I}}/{\overline{C}}_{\mathrm{M}}=1.0001 \), \( \overline{C_{\mathrm{E}}^2}/{\overline{C}}_{\mathrm{M}}^2=1.0004 \)). For this reason, it is practically not necessary to distinguish between three mean velocities.

  2. 2.

    In the first measurement section, the axial velocity increases linearly from the jet core to the jet surface. This nonconstant velocity profile indicates that the jet contracting has not yet completed up to here. Since as a consequence all streamlines are curved, there is a pressure increase towards the jet core. Accordingly, the flow velocity decreases, while the total pressure remains constant. This is also the reason why the normalized mean velocity at this jet section is obviously smaller than unity. It should be mentioned here that such a velocity distribution at the section with curved streamlines cannot be measured with a Pitot tube. The use of a Pitot tube requires that all streamlines there are straight and parallel. Obviously the accurate LDA measurements also enable the jet waist section to be located and identified.

  3. 3.

    According to the above points, the flow in the first measurement section of the jet is still found to operate under acceleration. The nonuniform velocity profile in the area outside the jet core is indicative of curved streamlines in the jet. It must be noted here that the corresponding streamline curvature can be calculated from the measured velocity profile.

    For this purpose the jet is considered in a cylindrical coordinate system. Since it does not possess any circumferential velocity component, the streamline is described simply by

    $$ {r}^{\prime }=\frac{\mathrm{d}r}{\mathrm{d}z}=\frac{c_{\mathrm{r}}}{c_{\mathrm{z}}}. $$
    (4.4)

    Taking into account that the velocity components c r and c z in general are functions of the spatial coordinates, i.e., \( {r}^{\prime }=f\left(r,\ z\right) \), it further follows from Eq. (4.4) that

    $$ {r}^{{\prime\prime} }=\frac{{\mathrm{d}}^2r}{\mathrm{d}{z}^2}=\frac{1}{c_{\mathrm{z}}^2}\left[{c}_{\mathrm{z}}\left(\frac{\partial {c}_{\mathrm{r}}}{\partial z}+\frac{\partial {c}_{\mathrm{r}}}{\partial r}\frac{\mathrm{d}r}{\mathrm{d}z}\right)-{c}_{\mathrm{r}}\left(\frac{\partial {c}_{\mathrm{z}}}{\partial z}+\frac{\partial {c}_{\mathrm{z}}}{\partial r}\frac{\mathrm{d}r}{\mathrm{d}z}\right)\right]. $$
    (4.5)

    Restricting ourselves to the streamlines in further considerations, the streamline equation \( \mathrm{d}r/\mathrm{d}z={c}_{\mathrm{r}}/{c}_{\mathrm{z}} \), according to Eq. (4.4), is inserted into the above equation. In addition, potential flow is also assumed so that \( \partial {c}_{\mathrm{r}}/\partial z=\partial {c}_{\mathrm{z}}/\partial r \). With the assumption \( {c}_{\mathrm{r}}/{c}_{\mathrm{z}}\ll 1 \), Eq. (4.5) is then simplified to

    $$ {r}^{{\prime\prime} }=\frac{1}{c_{\mathrm{z}}}\frac{\partial {c}_{\mathrm{z}}}{\partial r}, $$
    (4.6)

    and the curvature of the streamlines is given by

    $$ \frac{1}{R}=\frac{r^{{\prime\prime} }}{{\left(1+{r^{\prime}}^2\right)}^{3/2}}\approx {r}^{{\prime\prime} }=\frac{1}{c_{\mathrm{z}}}\frac{\partial {c}_{\mathrm{z}}}{\partial r}. $$
    (4.7)

    Since the velocity gradient \( \partial {c}_{\mathrm{z}}/\partial r \) can be obtained from the measured velocity profile that has been shown in Fig. 4.2, the radius of curvature of the streamlines can be directly calculated. Table 4.1 shows some results of the exploited measurements at three pressure heads of 10, 20, and 30 m.

    Table 4.1 Radii of curvature of streamlines while passing through the first measurement section according to Fig. 4.2 (Zhang and Casey 2007)
    Full size table

    It can be confirmed that due to the almost equal radii of curvature of the streamlines at the measurement sections, all streamlines remain unchanged for different pressure heads. The jet flows are therefore similar.

    The curvature of streamlines in the jet has the additional consequence that the pressure increases towards the jet axis. The corresponding pressure gradient can be determined from the momentum equation. The Euler equation for the radial velocity component is given in this case by

    $$ -\frac{1}{\rho}\frac{\mathrm{d}p}{\mathrm{d}r}={c}_{\mathrm{r}}\frac{\partial {c}_{\mathrm{r}}}{\partial r}+{c}_{\mathrm{z}}\frac{\partial {c}_{\mathrm{r}}}{\partial z}. $$
    (4.8)

    Assuming potential flow, which is free of rotation, one has \( \frac{\partial {c}_{\mathrm{r}}}{\partial z}-\frac{\partial {c}_{\mathrm{z}}}{\partial r}=0 \). Due to \( \frac{\partial {c}_{\mathrm{z}}}{\partial r}=\frac{c_{\mathrm{z}}}{R} \) from Eq. (4.7), one obtains

    $$ \frac{\partial {c}_{\mathrm{r}}}{\partial z}=\frac{c_{\mathrm{z}}}{R}. $$
    (4.9)

    The pressure gradient in the jet at the considered measurement section is calculated from Eq. (4.8) with \( {c}_{\mathrm{r}}\approx 0 \); the result is

    $$ \frac{1}{\rho}\frac{\mathrm{d}p}{\mathrm{d}r}=-{c}_{\mathrm{z}}\frac{\partial {c}_{\mathrm{z}}}{\partial r}=-\frac{c_{\mathrm{z}}^2}{R}. $$
    (4.10)

    Such an expression of the pressure gradient is analogous to that of a potential vortex (see Sect. 6.1.2).

  4. 4.

    Except for the flow velocity in the surface region of the jet, the jet speed remains constant up to a distance 7D 0. From the mass conservation law, it can be concluded that the jet diameter should remain unchanged as well. That this is realistic will be demonstrated in the next section.

Based on measurements of high-speed jet flows under the simplest flow conditions in the injector, the most important properties of the jet flow could be revealed in this section.

4.3 Jet Expansion

In the measurements shown in Fig. 4.2, it has been confirmed that the jet speed and thus the jet diameter remain almost unchanged over a distance of about 7D 0. This property is a corroboration of the high quality of the jet flow with negligible energy loss. Based on the observations as well as the photographic recordings, however, it has often been reported that the jet usually suffers from an expansion of about 0.2° to 0.5°. Such an excessive jet expansion in reality cannot be correct. For this reason, the jet is assumed to have an expansion angle α (Fig. 4.3). Because of the constant flow rate \( \overset{.}{Q}=A\overline{C} \), the change in the mean speed along the jet is calculated to be

Fig. 4.3
figure 3

Definition of the jet expansion

Full size image
$$ \frac{\mathrm{d}\overline{C}}{\mathrm{d}z}=-\frac{\overline{C}}{A}\frac{\mathrm{d}A}{\mathrm{d}z}. $$
(4.11)

The jet section is given by \( A=\pi {r}^2 \) from which it follows that

$$ \frac{\mathrm{d}A}{\mathrm{d}z}=2\pi r\frac{\mathrm{d}r}{\mathrm{d}z}=2\pi r \tan \alpha . $$
(4.12)

The specific kinetic energy of the jet flow is given by \( e={\overline{C}}^2/2 \). Its change along the jet is then obtained as

$$ \frac{\mathrm{d}e}{e\mathrm{d}z}=2\frac{\mathrm{d}\overline{C}}{\overline{C}\mathrm{d}z}. $$
(4.13)

By substituting Eqs. (4.11) and (4.12) into Eq. (4.13) and with \( {d}_0=2{r}_0 \) for the jet diameter, one, finally, obtains the change in the specific kinetic energy along the jet in the form

$$ \frac{\Delta e}{e}=-\left(8 \tan \alpha \right)\frac{\Delta z}{d_0}. $$
(4.14)

For a typical distance of the jet flow path, say \( \Delta z/{d}_0=4 \), and a jet expansion angle of 0.2°, the energy loss according to Eq. (4.14) is estimated to be 11 %. Such an extent of the energy loss is actually by no means realistic. According to Eq. (4.14), a loss in kinetic energy of about 1 % within a distance of \( \Delta z/{d}_0=4 \) corresponds to a jet expansion of only 0.02°. From this assessment it can be concluded that the apparent jet expansion observed in practice is obviously only limited to the jet surface and is, therefore, insignificant in terms of the energy loss. The apparent jet expansion arises most likely only from the turbulent momentum exchange with the ambient air.

4.4 Secondary Flows in the Jet and the Jet Stability

In practice , the injector of a Pelton turbine is usually found downstream of a bend of a pipe (Fig. 2.3) which may be part of the distributor. A fully developed turbulent flow in a long straight pipe is no longer available. This is always the case at a vertical turbine with more than two injectors which are distributed around the Pelton wheel. The inflow to each injector is strongly influenced by the distributor design and is no longer axially symmetric but possesses secondary flow structure. In principle, all axial irregularities or disturbances in the flow can be effectively diminished when the flow is accelerated while passing through the injector. This could be confirmed by an arranged measurement of the jet flow. Despite the interferences of the needle supporting ribs or artificially enhanced disturbances in the injector, no notable change in the jet flow could be identified (Zhang et al. 2000b). However, the existing vortex cells in the flow behave differently. According to the conservation law of angular momentum for frictionless flow, the rotation retains undiminished in the jet. Figure 4.4 shows the corresponding secondary flows which were measured in two sections: downstream of a 90° bend of the pipe and in the jet, respectively. The same model injector as in Fig. 4.2 was used. The high measurement resolution for very small secondary flow velocities in the considered jet section was achieved by means of the dual measurement method (DMM) which was developed by Zhang (2005).

Fig. 4.4
figure 4

Secondary flow structures in the flow after a 90° bend and in the jet, respectively, and the formation of the water-droplet string on the jet surface, from Zhang and Casey (2007)

Full size image

In Fig. 4.4, two well-structured rotating flow zones within the jet section can be confirmed. They are similar to the structure of the secondary flow at the injector inlet. Although such a secondary flow in the jet is sufficiently low against the axial flow, it can influence the jet nature decisively. The secondary flow in the jet takes a form so that two streams meet together on that jet side which corresponds to the inside of the pipe bend. Due to the free surface of the jet, the merger of two streams brings about the water to locally escape from the jet. The direct visible outcome is the formation of a string of longitudinal water droplets on the surface of the jet. Such water droplets behave as a disruptive factor for the mechanical parts of the turbine. By reaching the Pelton bucket, they could cause local damage to the bucket material. In a multi-jet Pelton turbine , the next injector must be protected against the impingement of such water droplets. The protection shelter which is commonly used in practice directly suffers from the strong droplet impingement and thus damage (Fig. 4.5).

Fig. 4.5
figure 5

Protection shelter in the form of a washbasin and the material damage because of the impingement of water-droplet strings

Full size image

In order to improve the jet quality in Pelton turbines, the formation of the water-droplet string on the jet surface has to be effectively suppressed. Since the cause of such an undesirable phenomenon is located upstream of the injector inlet, i.e., downstream of the pipe bend, the application of sharp pipe bends should be avoided if possible. The installation of a flow-straightening grid before or within the injector to break down the secondary flow structure is not always realistic, as this could cause additional head losses and enhance the risk of nozzle clogging. For this reason, it is rather difficult to reduce the swirling flow structure in the jet.