Keywords

1 Introduction. Basic Formulae of the Mindlin’s Gradient Elasticity Theory

Classical linear theory of elasticity is not capable to describe multi-scale phenomena as effects of meso-scale, micro-scale or nano-scale in primarily macro-scale problems because it leaves out of account that materials have microstructure. A lot of improvements of classical elasticity theory have been done in order to explain such effects. One of the first significant contributions was done by Mindlin (1964). His first strain gradient theory of linear elasticity implies the existence of an additional term in the definition of the potential energy W:

$$\begin{aligned} W = \int \limits _{B}^{}\left[ \frac{1}{2} \varvec{\tau } : \varvec{\varepsilon } + \frac{1}{2} \varvec{\mu } \ \vdots \ \varvec{\kappa }\right] \mathrm {d}V , \end{aligned}$$
(1)

where \(\varvec{\varepsilon }\) stands for the classical strain tensor, \(\varvec{\tau }\) is the Cauchy stress tensor, \(\varvec{\mu }\) is the double stress tensor and \(\varvec{\kappa }\) is the micro-deformation gradient tensor. The nabla-operator is denoted by \(\nabla \) and can be defined in Cartesian coordinate system as \(\nabla = {\varvec{e}}_i \frac{\partial }{\partial x_i}\), \(\int _{B}^{}\mathrm {d}V \) designates integration over the volume of a body B.

Form II Mindlin’s strain gradient elasticity theory proposes to define tensor \(\varvec{\kappa }\) as the gradient of the macroscopic strain:

$$\begin{aligned} \varvec{\kappa } = \nabla \varvec{\varepsilon }. \end{aligned}$$
(2)

The simplest variant of this theory widely used in the literature, with roots in Aifantis (1992), Altan and Aifanis (1997), defines the double stress tensor as follows

$$\begin{aligned} \varvec{\mu } = l_s^2 \nabla \varvec{\tau }, \end{aligned}$$
(3)

where \(l_s\) denotes gradient elasticity parameter which has dimension of length.

In the framework of considering gradient theory, the well known expressions for classical stress and strain tensors are valid:

$$\begin{aligned} \varvec{\varepsilon } = \frac{1}{2}(\nabla {\varvec{u}} + (\nabla {\varvec{u}})^T), \end{aligned}$$
(4)
$$\begin{aligned} \varvec{\tau } = {\varvec{C}} : \varvec{\varepsilon }. \end{aligned}$$
(5)

Here \({\varvec{u}}\) stands for the displacement vector and \({\varvec{C}}\) is the fourth-order tensor of elastic moduli.

By substitution (2) and (3) into (1), one can obtain the expression for the potential energy by using only the classical stress and strain tensors:

$$\begin{aligned} W = \int \limits _{B}^{}\left[ \frac{1}{2}\varvec{\tau } : \varvec{\varepsilon } + \frac{1}{2} l_s^2 \nabla \varvec{\tau } \ \vdots \ \nabla \varvec{\varepsilon }\right] \mathrm {d}V. \end{aligned}$$
(6)

The kinetic energy has an additional term as well:

$$\begin{aligned} T = \int \limits _{B}^{} \left[ \frac{1}{2}\rho \dot{{\varvec{u}}}\cdot \dot{{\varvec{u}}} + \frac{1}{2}\rho l_d^2 \nabla \dot{{\varvec{u}}} : \nabla \dot{{\varvec{u}}} \right] \mathrm {d}V, \end{aligned}$$
(7)

where \(\rho \) stands for the mass density, upper dots indicate the differentiation with respect to time and \(l_d\) is the second gradient coefficient called micro inertia coefficient with the dimension of length.

The work done by external forces alongside with two classical terms has two additional ones:

$$\begin{aligned} W_{\mathrm {ext}} = \int \limits _{B}^{} {\varvec{F}} \cdot {\varvec{u}} \mathrm {d}V + \int \limits _{\partial B_P}^{} {\varvec{P}} \cdot {\varvec{u}} \mathrm {d}S + \int \limits _{\partial B_R}^{} {\varvec{R}} \cdot ( {\varvec{n}} \cdot \nabla {\varvec{u}}) \mathrm {d}S + \oint \limits _{\partial \partial B_E}^{} {\varvec{E}} \cdot {\varvec{u}} \mathrm {d}l, \end{aligned}$$
(8)

where \({\varvec{F}}\) stands for the body force per unit volume, \({\varvec{P}}\) is the traction force, \({\varvec{R}}\) is the double traction force, \(\int _{\partial B} \mathrm {d}S\) denotes integration over the surface of the body, \({\varvec{n}}\) is the unit vector normal to the surface, \( {\varvec{E}}\) is the force distributed on the wedges \({\partial \partial B_E}\) of the body surface, \(\oint _{\partial \partial B_E}^{} \mathrm {d}l\) denotes integration over these wedges. For simplicity, external loadings at possible corners of the wedges (see, for instance, Polizzotto 2012) have been excluded in the formulation above.

By substitution of (6)–(8) into Hamilton’s principle for independent variation \(\delta {\varvec{u}}\) between fixed limits of \({\varvec{u}}\) at times \(t_0\) and \(t_1\)

$$\begin{aligned} \delta \int \limits _{t_0}^{t_1} (T-W) \mathrm {d}t + \int \limits _{t_0}^{t_1} \delta W_{\mathrm {ext}} \mathrm {d}t = 0, \end{aligned}$$
(9)

one can obtain the equation of motion of elastic continuum with micro-structure:

$$\begin{aligned} \nabla \cdot \varvec{\tau } - l_s^2 \nabla \cdot \varDelta \varvec{\tau } + {\varvec{F}} = \rho \ddot{{\varvec{u}}} - \rho l_d^2 \varDelta \ddot{{\varvec{u}}} \ \ \text {in} \ \ B \end{aligned}$$
(10)

and expressions for the external forces (Mindlin 1964; Polizzotto 2012):

$$\begin{aligned} \varvec{P} = \varvec{n} \cdot (\varvec{\tau } - l_s^2 \varDelta \varvec{\tau }) - l_s^2 \nabla _s \cdot (\varvec{n} \cdot \nabla \varvec{\tau }) + l_s^2 (\nabla _s \cdot \varvec{n})\varvec{n} \otimes \varvec{n} : \nabla \varvec{\tau } + \rho l^2_{d} \varvec{n} \cdot \nabla \ddot{\varvec{u}}\ \text {on} \ \partial B_P, \end{aligned}$$
(11a)
$$\begin{aligned} {\varvec{R}} = l_s^2 {\varvec{n}} \otimes {\varvec{n}} : \nabla \varvec{\tau } \ \text {on} \ \partial B_R, \end{aligned}$$
(11b)
$$\begin{aligned} {\varvec{E}} = l_s^2 {\varvec{s}} \cdot {\varvec{L}} : \varvec{[} {\varvec{n}} \otimes {\varvec{n}} \cdot \nabla \varvec{\tau } \varvec{]} \ \text {on} \ \partial \partial B_E, \end{aligned}$$
(11c)

where \(\varDelta = \nabla ^2\) stands for the Laplacian, \(\nabla _s\) being the surface part of the nabla-operator: \(\nabla _s = \nabla - {\varvec{n}} \otimes {\varvec{n}} \cdot \nabla \), \({\varvec{s}}\) being the unit vector tangent to C and \({\varvec{L}}\) is the third order Levi-Civita tensor. The bold face brackets in (11c) indicate that the enclosed quantity is the difference of its values, at \(\partial \partial B\) on the two portions of \(\partial B\) that intersect at \(\partial \partial B\).

2 Weak Form

Vector equation of motion (10) within a framework of the gradient elasticity theory is partial differential equation with high order derivatives. It can be solved analytically only in the simplest cases. The most common way of solving continuum mechanics problems numerically is to use the family of Finite Element Methods. In order to get the numerical solution, it is necessary to begin with definition of the weak form of the equation:

Definition 3.1

For a given loading \({\varvec{F}} \in [L^2(B)]^3\) find the deformation vector \({\varvec{u}} \in {\varvec{U}}\) such that

$$\begin{aligned} a({\varvec{u}},{\varvec{w}}) = l({\varvec{w}}) \ \forall \ {\varvec{w}} \in {\varvec{W}} \subset [H^2(B)]^3, \end{aligned}$$
(12)

where the bilinear form \(a:{\varvec{U}} \times {\varvec{W}} \rightarrow \mathbb {R}^3\) and the load functional \(l: {\varvec{W}} \rightarrow \mathbb {R}^3\), respectively, are defined as

$$\begin{aligned} a({\varvec{u}},{\varvec{w}}) = \int \limits _{B}^{} [ \varvec{\tau }(\varvec{\epsilon } ({\varvec{u}})) : \varvec{\epsilon } ({\varvec{w}}) + l_s^2 \nabla \varvec{\tau }(\varvec{\epsilon } ({\varvec{u}})) \ \vdots \ \nabla \varvec{\epsilon } ({\varvec{w}}) + \rho \ddot{{\varvec{u}}} \cdot {\varvec{w}} + \rho l_d^2 \nabla \ddot{{\varvec{u}}} : \nabla {\varvec{w}} ] dV , \end{aligned}$$
(13)
$$\begin{aligned} l({\varvec{w}}) = \int \limits _{B}^{} {\varvec{F}} \cdot {\varvec{w}} \mathrm {d}V + \int \limits _{\partial B_P}^{} {\varvec{P}} \cdot {\varvec{w}} \mathrm {d}S + \int \limits _{\partial B_R}^{} {\varvec{R}} \cdot ( {\varvec{n}} \cdot \nabla {\varvec{w}}) \mathrm {d}S + \oint \limits _{\partial \partial B_E}^{} {\varvec{E}} \cdot {\varvec{w}} \mathrm {d}l. \end{aligned}$$
(14)

Here \({\varvec{U}}\) is a subspace of Sobolev space \([H^2(B)]^3\) and each function from this subspace satisfies the Dirichlet boundary conditions:

$$\begin{aligned} {\varvec{U}} = \{{\varvec{u}} \in [H^2(B)]^3 \ | \ {\varvec{u}}_{|\partial B_u} = {\varvec{u}}_0, \ {\varvec{u}}_{|C_u} = {\varvec{u}}_c, \ {\varvec{n}} \cdot \nabla {\varvec{u}}_{|\partial B_D} = {\varvec{d}} \} \subset [H^2(B)]^3. \end{aligned}$$
(15)

Functions from \({\varvec{W}}\) satisfy the homogeneous Dirichlet boundary conditions:

$$\begin{aligned} {\varvec{W}} = \{{\varvec{w}} \in [H^2(B)]^3 \ | \ {\varvec{w}}_{|\partial B_u} = 0, \ {\varvec{w}}_{|C_u} = 0, \ {\varvec{n}} \cdot \nabla {\varvec{w}}_{|\partial B_D} = 0 \} \subset [H^2(B)]^3. \end{aligned}$$
(16)

Galerkin’s method suggests to represent an approximate solution (trial function) and test function by using a finite number of basis functions

$$\begin{aligned} {\varvec{u}}^h = \sum _{i=1}^{n}{\varvec{u}}_i \varphi _i, \ \ \ \ \ \ \ \ \ \ {\varvec{w}}^h = \sum _{i=1}^{n}{\varvec{w}}_i \varphi _i, \end{aligned}$$
(17)

at that \({\varvec{u}}^h \in {\varvec{U}}^h\) and \({\varvec{w}}^h \in {\varvec{W}}^h\), where \({\varvec{U}}^h\) and \({\varvec{W}}^h\) are finite-dimensional approximations of \({\varvec{U}}\) and \({\varvec{W}}\):

$$\begin{aligned} {\varvec{U}}^h \subset {\varvec{U}}, \ \ {\varvec{W}}^h \subset {\varvec{W}}. \end{aligned}$$
(18)

An important fact arises from (18) for a conforming method: the solution space must be a subspace of Sobolev space \([H^2(B)]^3\). It means that basis functions \(\varphi _i\) must provide at least \(C^1\) continuity from element to element. Classical Lagrange basis functions can provide only \(C^0\) continuity and consequently they are not suitable for solving the gradient elasticity problems. There are a lot of different modifications of Galerkin’s methods but probably the most universal and advanced one is Isogeometric Analysis introduced by Hughes et al. (2005).

3 Isogeometric Analysis

Isogeometric Analysis (IGA) can be considered as the “next generation” of the finite-element methods family. It has been under development at a quick rate during last 10 years. The main idea of IGA is to use the non-uniform rational B-splines (NURBS) as basis functions \(\varphi _i\). This peculiarity causes a lot of advantages of IGA methods such as the exact representation of the problem geometry. Interested readers advised to reach for the book devoted to Isogeometric Analysis (Cottrell et al. 2009).

In the context of the gradient elasticity theory the most important property of IGA is the \(C^{p-1}\) continuity provided across the elements boundaries in each parametric direction. Here p is an order of the NURBS basis functions in one of the directions. The NURBS basis is constructed by using 1D B-spline basis functions which can be defined by using Cox-de Boor recursion formula:

$$\begin{aligned} N_{i,p}(\xi )&= \frac{\xi -\xi _i}{\xi _{i+p}-\xi _i} N_{i,p-1}(\xi ) + \frac{\xi _{i+p+1}-\xi }{\xi _{i+p+1}-\xi _{i+1}} N_{i+1,p-1}(\xi ) \ \ \mathrm {for} \ \ p = 1,2,3,\ldots \nonumber \\ N_{i,0}(\xi )&= {\left\{ \begin{array}{ll} 1 &{}\text {if } \xi _i \le \xi \le \xi _{i+1};\\ 0 &{}\text {otherwise}. \end{array}\right. } \end{aligned}$$
(19)

Definition of 3D NURBS basis functions is presented below:

$$\begin{aligned} R_{i,j,k}^{p,q,r}(\xi , \eta , \zeta ) = \frac{\displaystyle N_{i,p}(\xi ) N_{j,q}(\eta ) N_{k,r}(\zeta ) w_{i,j,k}}{\displaystyle \sum _{\hat{i}=1}^{n} \sum _{\hat{j}=1}^{m} \sum _{\hat{k}=1}^{l} N_{\hat{i},p}(\xi ) N_{\hat{j},q}(\eta ) N_{\hat{k},r}(\zeta )w_{\hat{i},\hat{j},\hat{k}}}, \end{aligned}$$
(20)

where \(w_{i,j,k}\) are weight coefficients.

4 Numerical Results

This section is devoted to results of numerical solutions of some benchmark problems which were obtained from (10)–(11) by dimension reduction. For more results the interested reader can look at Niiranen et al. (2015a, b).

4.1 Static Rod in Tension

Consider a straight prismatic rod of constant cross section area A and length L. The displacement along the longitudinal axis x are denoted by u. Material of the rod is isotropic with Young’s modulus E and gradient coefficient \(l_s\). According to Papargyri-Beskou et al. (2010), the governing equilibrium equation of this rod in terms of displacements can be written as follows (body force is set to be zero):

$$\begin{aligned} AE(u''-l_s^2u'''') = 0 \ \text {in} \ [0,L]. \end{aligned}$$
(21)

Boundary conditions for the gradient rod under tension are assumed to be:

$$\begin{aligned} u|_{x=0}=0,&\ \ P|_{x=L} \equiv AE(u'-l_s^2u''')|_{x=L}=P_0, \nonumber \\ u'|_{x=L}=0,&\ \ R|_{x=0} \equiv AE l_s^2u''|_{x=0}=0. \end{aligned}$$
(22)

Solution for the problem (21)–(22) can be found analytically. It means that this problem can be used for the examination of the IGA applicability for solving of 1D problems of the gradient elasticity theory.

Fig. 1
figure 1

\(L^2\), \(H^1\) and \(H^2\) norms of error of the stretched rod displacements for different order of the NURBS basis functions

Full size image

Convergence curves for different orders p of the NURBS basis functions presented on Fig. 1 seem to follow the next formula:

$$\begin{aligned} ||u-u^h||_m \le ch^{\beta } ||u||_{p+1}, \end{aligned}$$
(23)

where \(||\cdot ||_m\) denotes the norm corresponding to the Sobolev space \(H^m(L)\), \(u^h\) is the approximate solution, c is an unknown constant and h is the element size. Convergence rate is denoted by \(\beta \) and expression for it depends on the degree of the Sobolev norm m of the solution error. In context of the gradient elasticity \(H^2\) norm is the energy norm and its convergence rate equals to \(\beta = p-1\). For \(L^2\) norm (or \(H^0\) norm) the convergence rate equals to \(\beta = min\{p+1, \ 2(p-1)\}\) and for \(H^1\) norm it is equal to \(\beta = p\). These results are in agreement with the theoretical analysis in Niiranen et al. (2015b) and Cottrell et al. (2009).

Fig. 2
figure 2

Dimensionless axial strains of the stretched rod for different values of the gradient elasticity parameter

Full size image

Figure 2 represents the dimensionless strain of stretched rod along axis x for the different values of the gradient parameter \(l_s\):

$$\begin{aligned} \hat{\varepsilon } = \frac{\varepsilon _{\mathrm {gr}}}{\varepsilon _\mathrm {c}(x/L=1)}. \end{aligned}$$
(24)

In distinction from the classical theory for which strain \(\varepsilon _{\mathrm {c}}\) is uniform along the rod axis, the gradient theory gives strain \(\varepsilon _{\mathrm {gr}}\) which is not uniform. It means that 1D gradient elasticity can explain the local elongation and further fracture in the middle of a tension specimen: primarily plastic deformations will most likely occur in a zone of the maximum elastic strain.

4.2 2D Dynamic Problem

Consider a square domain \(\varOmega \) with the side length \(L = 10\) mm. Material properties are defined by Lame parameters \(\lambda \) and \(\mu \), mass density \(\rho \) (they are assumed to be equal to the parameters of standard steel), and gradient coefficients \(l_s = 1\) mm and \(l_d = 0.5\) mm. The governing equation of motion of 2D domain in plane strain/stress state can be written as follows (body force is set to be zero):

$$\begin{aligned} (1-l_s^2\varDelta )(\mu \varDelta {\varvec{u}}+(\lambda + \mu )\nabla \nabla \cdot {\varvec{u}}) = \rho \ddot{{\varvec{u}}} - \rho l_d^2 \varDelta \ddot{{\varvec{u}}} \ \ \text {in} \ \varOmega . \end{aligned}$$
(25)

Boundary conditions are assumed to be

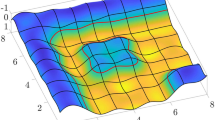
$$\begin{aligned} {\varvec{u}} \cdot {\varvec{s}}|_{\partial \varOmega } = 0; \ \ {\varvec{P}} \cdot {\varvec{n}}|_{\partial \varOmega } = 0; \ \ {\varvec{R}}|_{\partial \varOmega } = 0. \end{aligned}$$
(26)

Numerical solution for the spectral problem (25) and (26) is presented in Table 1. As one can see, gradient elasticity theory changes the body eigen frequencies and difference between results of classical and gradient elastic theories rises with increasing of the frequency number.

Table 1 Eigenfrequencies of a 2D square domain
Full size table