Multiscale Modeling of Nanoreinforced Composites

Abstract

In this chapter, we present different multiscale modeling techniques to determine the elastic and interfacial properties of carbon nanotube (CNT)-reinforced polymer composites. The elastic properties of CNT-reinforced composite (hereinafter the “nanocomposite”) are obtained in a two-step approach. First, at the nanoscale level, molecular dynamics (MD) and atomistic-based continuum (ABC) techniques are used to determine the effective elastic properties of a representative volume element (RVE) that is comprised of a nanofiller and its immediate surrounding. Second, at the microscale level, several micromechanics models and hybrid Monte Carlo finite-element (FE) simulations are used to determine the bulk properties of nanocomposite. The interfacial properties are determined through pullout test using MD and ABC techniques. The effect of length, diameter, agglomeration, waviness, defects, and orientation of CNTs on the elastic and interfacial properties of nanocomposites is also investigated. The development of multiscale modeling and the proper selection of simulation parameters are discussed in detail. The results of several studies are presented and compared to show the inherited limitations in each technique.

1.1 Introduction

CNTs are lighter than aluminum (density ∼1.4 g/cm³; Iijima 1991; Gao et al. 1998), are stronger than steel (Young’s modulus >1 TPa; Treacy et al. 1996; Krishnan et al. 1998; Shen and Li 2004), have large fracture strain (Wong et al. 1997; Yu et al. 2000) and high aspect ratio (Qian et al. 2000), and are more thermally conductive than copper (>2500 W⁄mK; Hone et al. 1999; Yang 2005; Awad and Ladani 2015). Due to these remarkable properties, CNTs have emerged as a promising reinforcement for polymer-based nanocomposites (Li and Chou 2003a; Shen and Li 2004; Tsai et al. 2010). It is believed that few weight percentages of CNTs can significantly improve the mechanical , thermal , and physical properties of their nanocomposites (Coleman et al. 2006a; Spitalsky et al. 2010; Rahmat and Hubert 2011).

Several experimental studies have been carried out to study the mechanical properties of nanocomposites . An earlier attempt was made by Schadler et al. (1998) to measure the mechanical properties of nanocomposite under tension and compression loadings. They reported that the compression modulus is higher than that of the tensile modulus, indicating the load transfer to CNTs from the matrix is higher in compression. Allaoui et al. (2002) managed to double Young’s modulus and yield strength of the nanocomposite by adding 1 and 4 wt% of multiwalled CNTs , respectively, compared to the pure epoxy matrix. Uniform dispersion of CNTs resulted in a 250–300 % increase in the storage modulus of epoxy nanocomposite at 20–30 wt% of CNTs due to the strong interfacial bonding between CNTs and epoxy resin (Gou et al. 2004). Qian et al. (2000) investigated the load transfer in multiwalled CNT –polystyrene composites and reported an increase in the tensile modulus and strength by ∼39 and 25 %, respectively, at 1 wt% of CNTs . Meguid and Sun (2004) showed that the homogeneous dispersion of CNTs in the epoxy matrix can improve the tensile and shear strengths of the resulting synthesized nanocomposite. However, at higher CNT concentrations, the mechanical properties of the nanocomposite were found to deteriorate due to the formation of CNT agglomerates, which act as stress concentrators. The multifunctionality of nanocomposites was also investigated experimentally. For example, Park et al. (2002) synthesized a polyimide composite reinforced with CNTs and reported improved mechanical , thermal , electrical, and optical properties.

The mechanical performance of nanocomposites is significantly influenced by the interfacial cohesion between the CNT and the surrounding matrix. Higher interfacial shear strength (ISS) is an indicator of better stress transfer from the polymer matrix to the embedded CNTs and hence an enhanced reinforcement effect (Desai and Haque 2005). Several experimental studies used direct methods such as pullout test and indirect methods such as fragmentation test and Raman spectroscopy to investigate the interfacial characteristics of nanocomposites. For instance, Wagner et al. (1998) estimated the interfacial shear stress between the multiwalled CNTs and the polymer based on the fragmentation test to be as high as 500 MPa, which is more than one order of magnitude compared to the conventional composites. Micro-Raman spectroscopy was used by Ajayan et al. (2000) to measure the local mechanical behavior of single-walled CNT bundles in the epoxy nanocomposite. They noticed that the efficiency of stress transfer and hence the enhancement of the mechanical properties is lower than expected due to the sliding of CNTs within the bundle. Cooper et al. (2002) used scanning probe microscope tip to pull out individual single- and multiwalled CNT ropes from epoxy matrix. The ISS of both the cases was found in the range of 35–376 MPa. This relatively high value of the ISS was attributed to the formation of strong ultrathin epoxy layer at the interface. This layer exits as a result of the formation of covalent bonds between CNTs and the surrounding polymer molecules, which originate from the defects on the CNTs .

The efficiency of CNTs in reinforcing the matrix depends on several parameters such as chirality, aspect ratio, defects, alignment, degree of waviness, chemical functionalization, agglomeration, and aggregation in the prepared nanocomposite system (Gojny et al. 2005; Coleman et al. 2006b; Wang et al. 2012). A significant number of experimental and numerical studies have been conducted so far to study the influence of these parameters on the mechanical performance of nanocomposites . Due to the atomic nature of CNTs , we cannot use the existing analytical and numerical techniques of traditional reinforced fiber composites for studying the mechanical properties of nanocomposites (Zeng et al. 2008). In nanocomposites, the bonding between the embedded CNTs and the polymer originates mainly from the weak nonbonded van der Waals (vdW) and Coulombic interactions (Han and Elliott 2007). However, chemical functionalization of CNTs can introduce some strong interfacial covalent bonds between the nanotube walls and the polymer chains leading to a stronger nanocomposite (Xiao et al. 2015). Due to these inherited limitations in conventional modeling techniques of composite materials, different multiscale modeling techniques were developed to address the length scale effect and to determine the effective properties of nanocomposites.

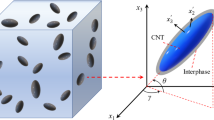
In general, multiscale modeling of nanocomposites is carried out in two stages, as shown in Fig. 1.1 (Wernik 2013). The first stage usually addresses different issues related to the atomic structure of CNTs and the surrounding polymer at the nanoscale level. Mainly, MD simulations and ABC modeling technique are used in the first stage. Because of the nonbonded interactions between the CNT and the matrix and the formation of a strong ultrathin polymer layer at their interface, a representative volume element (RVE ) is needed to capture the interfacial and mechanical properties of the resulting nanocomposite (Alian et al. 2015a). The results of the atomistic simulations are then used as an input to the second stage. Analytical and numerical micromechanical techniques are used in the second stage to determine the bulk properties of the nanocomposite (Wernik and Meguid 2014). The RVE from the first stage is used here as an equivalent effective fiber embedded in the bulk matrix.

Fig. 1.1

Modeling steps involved in the multiscale model

In this chapter, we cover the basics of multiscale modeling techniques utilized for CNT -reinforced composites. In particular, the application of each model in studying the elastic and interfacial properties is presented. The results predicted by multiscale models have been validated with those of experimental data reported in the literature. The influence of CNT morphology and dispersion on the interfacial and mechanical properties is investigated to determine the best method to prepare nanocomposites with optimal properties. The effect of CNT dispersion is investigated considering the two cases: aligned and randomly distributed CNTs , while the effect of agglomeration is investigated by considering CNT bundles of different sizes. CNTs with different curvatures are modeled as well to study the effect of their waviness on the mechanical behavior of nanocomposites. The results of the conducted investigations are presented and compared to show the inherited limitations in each modeling technique.

This chapter is organized as follows. Following this Introduction, the basics of MD and its applications in nanocomposites are described in Sect. 1.2. The basics of ABC technique and its application in determining the elastic and interfacial properties of nanocomposites are presented in Sect. 1.3. The micromechanical procedure based on Mori–Tanaka technique is reviewed and subsequently used to study the effect of CNT agglomeration, waviness, and dispersion on the bulk properties of nanocomposite in Sect. 1.4. Finally, Monte Carlo method and FE technique are then combined in Sect. 1.5 as an alternative method to Mori–Tanaka technique. Numerical and analytical results are presented for each modeling technique at the end of each section.

1.2 Molecular Modeling

MD simulations offer an appropriate and effective means to deal with large nanoscale systems and relatively longer simulation times compared to density functional theory (DFT) simulations and have been extensively used for determining the interfacial and mechanical properties of nanocomposites . MD has been also a very valuable tool for studying the effect of CNT agglomeration, waviness, aspect ratio, defects, and functionalization on the mechanical behavior of nanocomposites. For example, Frankland et al. (2003a) used MD simulations to calculate the longitudinal and transverse Young’s moduli of polymer nanocomposite reinforced with long and short CNTs . Grujicic et al. (2007) studied the effect of chemical functionalization on the mechanical properties of multiwalled CNT –vinyl ester epoxy composites using MD simulations. Their results showed that introducing covalent bonds between CNTs and the surrounding polymer results in significant improvements in the transverse elastic properties of the nanocomposite. Alian et al. (2015b) studied the effect of CNT agglomeration on the elastic properties of CNT –epoxy composites by modeling different RVEs reinforced with bundles of CNTs . Their results showed that the CNT agglomerates dramatically reduce the effective properties of epoxy nanocomposites.

1.2.1 Basics of MD Simulations

MD is a computational method that was firstly introduced into theoretical physics by Alder and Wainwright (1957) to simulate elastic collisions between hard spheres. Since then, MD has become an important and attractive computational tool for many research fields including chemical physics, biochemistry, and materials science. MD allows to study relatively large molecular systems that cannot be simulated using quantum mechanics-based techniques such as DFT and ab initio approaches due to the enormous computational cost (Srivastava et al. 2003). The main purpose of MD simulations is to simulate the time-dependent behavior of the system by calculating the current and future position and velocity of each atom using Newton’s equations of motion. This information can be used later to calculate the averaged mechanical , physical, and thermal properties of the system (van Gunsteren and Berendsen 1990).

The initial position and velocity of each atom of the system must be known at the beginning of the MD simulation. This initial data is randomly generated based on statistical mechanics and the required average temperature of the system. Then, the trajectories of the atoms are determined by solving the Newton’s equations of motion of the interacting atoms of the system:

$$ {\overset{\rightharpoonup }{F}}_{\kern-.15em i}={m}_i\ {\overset{\rightharpoonup }{a}}_{\kern-.15em i} $$

(1.1)

where ${\overset{\rightharpoonup }{F}}_{\kern-.15em i}$, m _i , and ${\overset{\rightharpoonup }{a}}_{\kern-.15em i}$ are the acting force, mass, and acceleration of atom i, respectively. The interatomic forces are the gradient of the total potential energy, V, of the system:

$$ {\overset{\rightharpoonup }{F}}_{\kern-.15em i}=-\nabla\ V\left(\overset{\rightharpoonup }{r}\right) $$

(1.2)

The velocity, ${\overset{\rightharpoonup }{v}}_{\kern-.15em i}$, and displacement vector, ${\overset{\rightharpoonup }{r}}_{\kern-.15em i}$, of each atom are the first and second derivatives of the acceleration:

$$ {\overset{\rightharpoonup }{a}}_{\kern-.15em i}=\frac{d{\overset{\rightharpoonup }{v}}_{\kern-.15em i}}{dt} $$

(1.3)

$$ {\overset{\rightharpoonup }{v}}_{\kern-.15em i}=\frac{d{\overset{\rightharpoonup }{r}}_{\kern-.15em i}}{dt} $$

(1.4)

Using Eqs. (1.1), (1.3), and (1.4), we obtain the following differential equation:

$$ -\nabla\ V\left(\overset{\rightharpoonup }{r}\right)={m}_i\ \frac{d^2{\overset{\rightharpoonup }{r}}_{\kern-.15em i}}{d{t}^2} $$

(1.5)

The most popular algorithm to integrate the resulting equations of motion of the system is the Verlet algorithm (Verlet 1967). In this algorithm, Newton’s equations of motion are approximated by a Taylor series expansion as a time series:

$$ r\left(t+\delta t\right)=r(t)+v(t)\ \delta t+\frac{1}{2}a(t)\ \delta {t}^2+\frac{1}{6}\frac{d^3r(t)}{d{t}^3}\ \delta {t}^3+\mathrm{O}\left(\delta {t}^4\right) $$

(1.6)

$$ r\left(t-\delta t\right)=r(t)-v(t)\ \delta t+\frac{1}{2}a(t)\ \delta {t}^2-\frac{1}{6}\frac{d^3r(t)}{d{t}^3}\ \delta {t}^3+\mathrm{O}\left(\delta {t}^4\right) $$

(1.7)

Adding the above two equations and moving the $r\left(t-\delta t\right)$ term to the right-hand side, we obtain

$$ r\left(t+\delta t\right)=2r(t)-\mathrm{r}\left(t-\delta t\right)+a(t)\ \delta {t}^2+\mathrm{O}\left(\delta {t}^4\right) $$

(1.8)

This is the general form of the Verlet algorithm for MD , where δt is the time step of the analysis; accuracy significantly increases with the decrease in this time step because it is a function of the fourth order of δt. The value of a(t) is determined from Eq. (1.5), which depends on the location of the atom. Here, we use the positions from the previous and current time steps and acceleration of the current step to predict the trajectory of the atom. The instantaneous velocity v(t) of each atom can be later calculated using Taylor series expansion, as follows:

$$ v(t)=\frac{r\left(t+\delta t\right)-r\left(t-\delta t\right)}{2\delta t}+\mathrm{O}\left(\delta {t}^3\right) $$

(1.9)

The accuracy of the velocity is a function of δt ³ implying that it has lower accuracy than the position which is a function of δt ⁴. The kinetic energy K(t) and the averaged instantaneous temperature T of the system, based on the equipartition theory, can be calculated using the obtained velocities using the following relations:

$$ K(t)=\frac{1}{2}{\sum}_i{m}_i\ {\left({v}_i(t)\right)}^2 $$

(1.10)

$$ T(t)=\frac{2}{3}\frac{K(t)}{N\ {K}_{\mathrm{B}}} $$

(1.11)

where K _B is the Boltzmann constant . The averaged stress tensor of the MD unit cell is defined in the form of virial stress (Zhou 2003), as follows:

$$ \sigma =\frac{1}{V}\ {\displaystyle {\sum}_{i=1}^N}\left(\frac{m_i}{2}{v_i}^2 + {F}_i\ {r}_i\right) $$

(1.12)

where V is the volume of the MD unit cell and v _i , m _i , r _i , and F _i are the velocity, mass, position, and force acting on the ith atom, respectively.

The total potential energy of the system can be defined by interatomic potentials or molecular mechanics force fields which describe how the atoms interact with each other (LeSar 2013). The selected interatomic potential or force field for the system under investigation must be very accurate for the quantum mechanical process and to yield reliable results. These potentials and force fields have been developed by several researchers based on quantum mechanics calculations and then validated by comparing their results with experimental tests (Brenner 2000; LeSar 2013). The general expression for the total atomistic potential energy of the system can be written as a many-body expansion that depend on the position of one, two, three atoms or more at a time (LeSar 2013):

$$ V\left({\overset{\rightharpoonup }{r}}_{\kern-.25em 1},{\overset{\rightharpoonup }{r}}_{\kern-.25em 2},\dots .,{\overset{\rightharpoonup }{r}}_{\kern-.25em N}\right)={\sum}_i^N{V}_1\left({\overset{\rightharpoonup }{r}}_{\kern-.25em i}\right)+{\sum}_{i,j}^N{V}_2\left({\overset{\rightharpoonup }{r}}_{\kern-.25em i},{\overset{\rightharpoonup }{r}}_{\kern-.25em j}\right)+{\sum}_{i,j,k}^N{V}_3\left({\overset{\rightharpoonup }{r}}_{\kern-.25em i},{\overset{\rightharpoonup }{r}}_{\kern-.25em j},{\overset{\rightharpoonup }{r}}_{\kern-.25em ik}\right)+\dots $$

(1.13)

where V ₁ is the one-body term (energy of the isolated atom i due to an external force field such as the electrostatic force), V ₂ is the two-body term (pairwise interactions of the atoms i and j such as Lennard–Jones potential (Jones 1924)), V ₃ is the three-body term (three-body interactions and usually called many-body interactions such as Tersoff and Brenner potentials), N is the number of atoms in the system, and ${\overset{\rightharpoonup }{r}}_{\kern-.15em i}$ is the position vector of atom i (Tersoff 1988; Brenner 1990). However, most of the polymeric systems need a more generalized interatomic potential which is mainly defined based on geometrical parameters such as bond lengths, angles, and rotation. To tackle this problem, many force fields were developed (LeSar 2013). The total energy in force fields consists of two parts: the first one is concerned with the bonded interactions of the covalently bonded atoms, and the second is concerned with the nonbonded interactions originating from the relatively weak long-range electrostatic and vdW forces:

$$ V=\underset{V_{\mathrm{bonded}}}{\underbrace{{\displaystyle \sum }{V}_r+{\displaystyle \sum }{V}_{\theta }+{\displaystyle \sum }{V}_{\varphi }}}+\underset{V_{\mathrm{non}\hbox{-} \mathrm{bonded}}}{\underbrace{{\displaystyle \sum }{V}_{\mathrm{vdW}}+{\displaystyle \sum }{V}_{\mathrm{elec}}}} $$

(1.14)

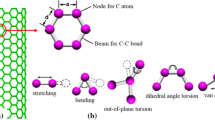
where V _r term is for oscillations about the equilibrium bond length (i.e., bond stretching), V _θ term is for oscillations of 3 atoms about an equilibrium bond angle (i.e., bond angle bending), V _φ term is for torsional rotation of 4 atoms about a central bond (i.e., dihedral angle torsion), V _vdW term is for a nonbonded vdW interactions, and V _ele term is for a nonbonded electrostatic interactions (Li and Chou 2003a). The components of the potential energy due to the bonded interactions are shown in Fig. 1.2.

Fig. 1.2

Schematic of both bonded and nonbonded interactions between the atoms of a small molecule

All MD simulations are being conducted under specified conditions. These ensembles are characterized by fixed values of the following thermodynamic variables: potential energy, temperature, pressure, volume, and total number of particles. The most commonly used ensembles in MD simulations are:

• Micro-canonical ensemble: constant number of atoms, volume, and energy (N,V,E)

• Isothermal–isobaric ensemble: constant number of atoms, temperature, and pressure (N,T,P)

• Canonical ensemble: constant number of atoms, temperature, and volume (N,V,T)

There is a common sequence that can be followed to build an MD model and perform a successful simulation. The first step is to build the initial structure of the system using software such as NanoEngineer, Materials Studio, Packmol, etc. This step consumes a significant time of the work as it usually requires the building of small units of the system and dispersing them in a large MD unit cell. The second step is to minimize the structure by changing the initial location of the atoms to reduce the total potential energy of the system and to relieve the residual stresses. The third step is assigning an initial velocity to each atom based on the targeted average temperature of the system. The fourth is to equilibrate the minimized structure to obtain the system at targeted initial conditions (pressure, volume, temperature ). Finally, conducting the required analysis and measuring the system properties of interest.

1.2.2 Modeling of Nanocomposite and Its Constituents

In this section, we will present modeling of CNTs , epoxy, and nanocomposites using MD simulations (see Fig. 1.3). The main objective is to obtain the atomic-level elastic and interfacial properties of the nanocomposite. All MD simulations will be performed with large-scale atomic/molecular massively parallel simulator (LAMMPS; Plimpton 1995) using either the consistent valence force field (CVFF; Dauber-Osguthorpe et al. 1988) or the adaptive intermolecular reactive bond order (AIREBO) potential (Stuart et al. 2000). CVFF has been used successfully by several researchers to predict the mechanical properties of CNTs , epoxy polymers, and CNT –epoxy composites (Alian et al. 2015b; Li et al. 2012; Tunvir et al. 2008). AIREBO has been also used by many researchers for CNTs , hydrocarbons, and polymers consisting of only carbon and hydrogen such as polyethylene (Coluci et al. 2007; Zang et al. 2009). Conjugate gradient algorithm is used to minimize the total potential energy of the initial configurations. The structure is considered to be optimized once the change in the total potential energy of the system between subsequent steps is less than 1.0 × 10⁻¹⁰ kcal/mol. Velocity Verlet algorithm is used to integrate the equations of motion in all MD simulations. Periodic boundary conditions are imposed on all directions of the MD unit cells. The cutoff distance for the nonbonded interaction is set to 14.0 Å (Haghighatpanah and Bolton 2013).

Fig. 1.3

Molecular structures of (a) (5,5) armchair CNT , (b) RVE consists of SWCNT embedded in polymer, and (c) pullout of CNT bundle from epoxy matrix

1.2.2.1 Modeling of CNTs

In this section, MD simulations are conducted to determine the elastic properties of pristine SWCNTs using AIREBO interatomic potential. The effect of CNT diameter size on its mechanical properties is investigated considering different armchair SWCNTs, with diameter ranging from ∼6 to ∼35 Å, as shown in Fig. 1.4.

Fig. 1.4

Schematics of different CNTs adopted in the study: (a) (5, 5) CNT , (b) (10, 10) CNT , and (c) (20, 20) CNT

The transversely isotropic elastic moduli of the armchair CNTs are determined using the strain energy density–elastic constant relations. The following four loading conditions are imposed on the CNT : axial tension for axial Young’s modulus (E ₁) and major Poisson’s ratio (ν ₁₂), torsional moment for axial shear modulus (G₁₂), in-plane biaxial tension for plane strain bulk modulus (K₂₃), and in-plane shear for in-plane shear modulus (G₂₃). Schematic representations of these loading conditions are depicted in Fig. 1.5. The equations written underneath the figures indicate the respective strain energy densities (U) stored in the CNT due to the applied strain.

Fig. 1.5

Loading conditions used to determine the elastic constants of the CNT : (a) tensile, (b) twist, (c) in-plane biaxial tension, and (d) in-plane shear

The equivalent-continuum structure of a CNT is assumed to be annular cylinder by considering its effective wall thickness as 3.4 Å (Hao et al. 2008), and its area is determined as $A=2\pi rt$, where r is the outer radius of the CNT and t is its wall thickness. The sequence of the MD simulations is as follows: first, the initial structures of the generated CNTs are first optimized using the conjugate gradient algorithm to obtain the nanotube configurations of minimum energy. Subsequently, the minimized structures of the CNTs are equilibrated for 50 ps in the constant temperature and volume canonical (NVT) ensemble using a 0.5 fs time step at 300 K. Then, a defined strain increment of 0.1 % is applied to the CNTs followed by potential energy minimization. During each loading step, one end of the CNT is fixed, while a prescribed load/displacement is applied to the other end. In case of axial tension, an incremental axial displacement is applied to the top end. In case of twisting moment, an incremental tangential displacement was applied to the top end while constraining its motion in the radial direction to maintain the presumed cylindrical shape of the CNT . In case of in-plane biaxial tension, all atoms of the CNT were subjected to two-dimensional plane strain condition by axially constraining the two ends of the CNT . In case of in-plane shear condition, the CNT is subjected to in-plane shear in such a way that its circular cross section deforms into an elliptical shape. Finally, this loading step is repeated until the strain reaches up to 3 %. Under each strain increment, the change in potential energy that is equivalent to the stored strain energy in the CNTs is used to determine the elastic properties based on the relation between the deformation energy density and the elastic constants.

Five types of armchair CNTs (5, 5), (10, 10), (15, 15), (20, 20), and (25, 25) are considered in the current analysis to study the effect of nanotube diameter on the elastic moduli of CNTs . The MD results show that the elastic coefficients of the CNTs decrease as the diameter of a CNT increases (see Fig. 1.6a–d).

Fig. 1.6

Effect of vacancy defects on (a) axial Young’s modulus, (b) axial shear modulus, (c) plane strain bulk modulus, and (d) in-plane shear modulus of (5,5) armchair CNT

1.2.2.2 Modeling of Pure Epoxy

MD simulations are conducted to determine the isotropic elastic moduli of epoxy material using CVFF. We will model a specific two-component epoxy material based on diglycidyl ether of bisphenol A (DGEBA) epoxy resin and triethylenetetramine (TETA) curing agent, which is typically used in the aerospace industry (see Fig. 1.7). The volumetric bulk (K) and shear (G) moduli of the epoxy will be determined by applying volumetric and three-dimensional shear strains, respectively.

Fig. 1.7

Molecular structures of (a) epoxy resin (DGEBA) and (b) curing agent (TETA)

During the curing process, the hydrogen atoms in the amine groups of the curing agent react with the epoxide groups of the resin forming covalent bonds, which result in a highly cross-linked epoxy structure. The resin/curing agent weight ratio in the epoxy polymer was set to 2:1 in order to achieve the best elastic properties (Wernik 2013). The cross-linked polymer structure consisted of 80 DGEBA molecules cross-linked with 40 molecules of curing agent TETA. The cross-linked structure was utilized to form a 3D structure of epoxy. This structure was then used to build the epoxy system in the subsequent MD simulations of both neat epoxy and CNT –epoxy composite.

The neat epoxy model was generated by randomly placing 5 cross-linked structures in a cubic simulation box of size 150 Å × 150 Å × 150 Å to form a system containing ∼25,000 atoms, as shown in Fig. 1.8a. The MD unit cell was compressed gradually to the targeted dimensions of 60 Å × 60 Å × 60 Å through 25 consecutive steps. At each compression step, the atoms coordinates were remapped to fit inside the compressed box, and then the updated structure was optimized by minimizing its potential energy to obtain a relaxed configuration, as shown Fig. 1.8b.

Fig. 1.8

The simulation box containing 400 chains of DGEBA and 200 chains of TETA (a) placed randomly in a simulation box of size 150 Å × 150 Å × 150 Å and (b) equilibrated after being compressed into a cube of size 60 Å × 60 Å × 60 Å

The optimized system was then equilibrated at room temperature in the constant temperature and volume canonical (NVT) ensemble over 200 ps using a 0.5 fs time step at 300 K. The compressed system was equilibrated for another 200 ps in the isothermal–isobaric (NPT) ensemble at 300 K and 1 atm to generate an epoxy system with the correct density. This equilibration step resulted in an equilibrated amorphous structure with an average density of 1.1 g/cm³. At the end, the structure is again equilibrated for another 200 ps in the NVT ensemble at 300 K. In order to determine the bulk modulus of the epoxy, the simulation box was volumetrically strained in both tension and compression by applying equal uniform strains along the three axes. The bulk modulus was calculated by

$$ K=\frac{\sigma_h}{\varepsilon_v} $$

(1.15)

where ε _v and σ _h are the volumetric strain and the averaged hydrostatic stress, respectively. In order to determine the average shear modulus, equal shear strains were applied on the simulation box in xy, xz, and yz planes. The shear modulus was calculated by

$$ G=\frac{\tau_{ij}}{\gamma_{ij}}, i\ne j $$

(1.16)

where τ _ij and γ _ij denote the averaged shear stress and shear strain, respectively. In each loading case, strain increments of 0.25 % were applied along a particular direction by uniformly expanding or shearing the simulation box and updating the atoms coordinates to fit within the new dimensions. After each strain increment, the MD unit cell was equilibrated using the NVT ensemble at 300 K for 10 ps. Then, the stress tensor is averaged over an interval of 10 ps to reduce the effect of fluctuations. These steps were repeated again in the subsequent deformation increments. The procedure was stopped when the total strain reached up to 2.5 %. Based on the calculated bulk and shear moduli, Young’s modulus (E) and Poisson’s ratio (ν) were determined as follows:

$$ E=\frac{9KG}{3K+G}\kern0.5em \mathrm{and}\kern0.5em \nu =\frac{3K-2G}{2\left(3K+G\right)} $$

(1.17)

The predicted elastic properties of the epoxy from the conducted MD simulations are found to be consistent with the experimentally measured moduli of a similar epoxy, as summarized in Table 1.1 (Littell et al. 2008).

Table 1.1 Elastic moduli of the epoxy material

1.2.2.3 Modeling of CNT –Epoxy Interface

The structure of the polymer matrix at the vicinity of the CNT surface differs from the bulk polymer far from the interface due to the formation of an ultrathin polymer layer at the CNT –epoxy polymer (Cooper et al. 2002). This ultrathin layer consists of a highly packed crystalline polymer, which has higher elastic properties than the amorphous bulk polymer (Coleman et al. 2004). In this section, the interface thickness of the CNT –epoxy composites will be determined using MD simulations. In order to obtain the actual CNT –epoxy properties using multiscale modeling technique, the size of the RVE must be large enough to incorporate the interface layer. Armchair (5,5) CNT of length 76 Å is used in the present study. Interface thickness is an important parameter in calculating the actual volume fraction of CNTs in composite. The cylindrical molecular structure of the (5,5) SWCNT is treated as an equivalent solid cylindrical fiber (Kundalwal and Ray 2012; Thostenson and Chou 2003) for determining its volume fraction in the nanocomposite RVE :

$$ {v}_{\mathrm{CNT}}\cong \frac{f_n\ {N}_{\mathrm{CNT}}\ \pi\ {\left({D}_{\mathrm{CNT}}+{h}_{\mathrm{vdW}}\right)}^2\ {L}_{\mathrm{CNT}}}{4{V}_{\mathrm{cell}}} $$

(1.18)

where D _CNT and L _CNT denote the respective diameter and length of a CNT , h _vdW is the vdW equilibrium distance between a CNT and the surrounding polymer matrix, N _CNT is the number of CNTs in the bundle, f _n is a factor based on the shape of the bundle of CNTs , and V _cell is the volume of the RVE .

In order to determine the thickness of the interface layer, we performed MD simulations for a system consisting of a CNT surrounded by epoxy structures using the same steps as adopted in the pure epoxy case without any further chaining between the epoxy molecules. This approach does not address how the interfacial layer thickness changes with the epoxy chain growth during reaction curing, but we can determine the average interfacial layer thickness when the MD system reaches an equilibrium state. Figure 1.9 shows the radial distribution function (RDF) of the epoxy atoms surrounding the embedded CNT after the equilibration. The variation of the RDF along the radial direction represents the change of the epoxy structure in the vicinity of the embedded CNT . It may be observed from Fig. 1.9 that the RDF of the epoxy atoms is zero at a radial distance of 0.56 nm and reaches its maximum value of 160 atoms/nm³ at the radial distance of 0.77 nm. Then, it starts to fluctuate around an average value of 110 atoms/nm³. This result indicates that the value of the vdW equilibrium distance h _vdW is ∼2.75 Å and the thickness of CNT –epoxy matrix interface layer is ∼3.0 Å. The obtained values of the interfacial layer thickness and the equilibrium separation distance were used to select the appropriate RVE sizes for MD simulations of nanocomposites in the next section.

Fig. 1.9

RDF of the epoxy atoms around the embedded CNT

1.2.2.4 Modeling of Nanocomposite Containing Agglomerated CNTs

CNTs have a tendency to agglomerate and aggregate into bundles due to poor dispersion of CNTs and their high surface energy and surface area (Dumlich et al. 2011). The presence of CNT agglomerates and aggregates deteriorates the interfacial properties of the nanocomposite resulting in limited stress transfer and load sharing (Alian et al. 2015b). Therefore, the issue of agglomeration of CNTs needs to be addressed. The effect of agglomeration is investigated by modeling RVEs reinforced with CNT bundles of different sizes. Three RVEs are constructed to represent an epoxy matrix containing a (1) single CNT , (2) bundle of three CNTs , and (3) bundle of seven CNTs (see Fig. 1.10). Each RVE will be used as an effective fiber in the micromechanical model to calculate the effective elastic moduli of the nanocomposite at the microscale level, as shown in Fig. 1.1. All MD simulations are conducted using CVFF force field.

Fig. 1.10

MD unit cells containing a (a) single CNT , (b) bundle of three CNTs , and (c) bundle of seven CNTs

The initial distance between the adjacent CNTs in the bundle was taken to be 3.4 Å, which is equivalent to the intertube separation distance in multiwalled CNTs . The RVEs are assumed to be transversely isotropic with the 3-axis being the axis of symmetry. Therefore, only five independent material constants are required to fully define the elastic stiffness matrix. The constitutive relationship of the transversely isotropic RVE is given by

$$ \left[\begin{array}{c}{\sigma}_{11}\\ {}{\sigma}_{22}\\ {}{\sigma}_{33}\\ {}{\sigma}_{23}\\ {}{\sigma}_{13}\\ {}{\sigma}_{12}\end{array}\right]=\left[\begin{array}{cccccc}{\mathrm{C}}_{11}& {\mathrm{C}}_{12}& {\mathrm{C}}_{13}& 0& 0& 0\\ {}{\mathrm{C}}_{12}& {\mathrm{C}}_{11}& {\mathrm{C}}_{13}& 0& 0& 0\\ {}{\mathrm{C}}_{13}& {\mathrm{C}}_{13}& {\mathrm{C}}_{33}& 0& 0& 0\\ {}0& 0& 0& {\mathrm{C}}_{44}& 0& 0\\ {}0& 0& 0& 0& {\mathrm{C}}_{44}& 0\\ {}0& 0& 0& 0& 0& \left({\mathrm{C}}_{11}-{\mathrm{C}}_{12}\right)/2\end{array}\right]\left[\begin{array}{c}{\varepsilon}_{11}\\ {}{\varepsilon}_{22}\\ {}{\varepsilon}_{33}\\ {}{\varepsilon}_{23}\\ {}{\varepsilon}_{13}\\ {}{\varepsilon}_{12}\end{array}\right] $$

(1.19)

where σ _ij and ε _ij are the respective stress and strain components with (i, j = 1, 2, 3, 4, 5, 6) and C _ij represents the elastic coefficients of the RVE . The MD simulation box in each case was constructed by randomly placing cross-linked epoxy structures around an individual CNT or a CNT bundle. The CNT volume fraction is kept the same in all RVE ∼6.5 %. The details of the three RVEs are summarized in Table 1.2. To determine the five elastic constants, the RVEs were subjected to five different loading conditions: longitudinal tension, transverse tension, in-plane tension, in-plane shear, and out-of-plane shear. The steps involved in the MD simulations of the RVEs are the same as adopted in the previous section for pure epoxy. The boundary and loading conditions that have been applied to the RVE to determine the corresponding five independent elastic coefficients of the RVE are listed in Table 1.3.

Table 1.2 Parameters used in the RVE

Table 1.3 Effective elastic coefficients of the RVEs and corresponding displacement fields

Table 1.4 summarizes the outcome of the MD simulations. It may be observed from the results that the elastic properties of the RVEs are significantly higher than those of the neat epoxy. It is also clear from the results that the CNT agglomeration reduces the reinforcing effect of the embedded CNTs , which eventually degrades the bulk elastic moduli of the nanocomposites . The axial elastic coefficients, C₃₃, of the RVEs containing bundles of three and seven CNTs decreased by some 21 and 38.5 %, respectively, as compared with the RVE containing an individual CNT . The CNT agglomeration is also found to reduce the transverse elastic coefficients of the RVEs . For example, the transverse elastic coefficient, C₁₁, of the RVEs containing bundles of three and seven CNTs decreased by 11.0 and 22.9 %, respectively, compared with the RVE containing an individual CNT .

Table 1.4 Material properties of the nanocomposite RVE containing either an individual CNT or its bundle

The effective elastic moduli of the RVE are related to the effective elastic stiffness components as follows:

$$ {\mathrm{E}}_{33}={\mathrm{C}}_{33}-\frac{2{\mathrm{C}}_{{}_{23}}^2}{{\mathrm{C}}_{12}+{\mathrm{C}}_{11}} $$

(1.20)

$$ {\mathrm{E}}_{11}={\mathrm{E}}_{22}=\frac{\left({\mathrm{C}}_{11}-{\mathrm{C}}_{12}\right)\ \left({\mathrm{C}}_{11}{\mathrm{C}}_{33}+{\mathrm{C}}_{12}{\mathrm{C}}_{33}-2{\mathrm{C}}_{23}^{{}^2}\right)}{{\mathrm{C}}_{11}{\mathrm{C}}_{33}-{\mathrm{C}}_{23}^2} $$

(1.21)

$$ {\mathrm{G}}_{12}=\frac{\left({\mathrm{C}}_{11}-{\mathrm{C}}_{12}\right)}{2} $$

(1.22)

$$ {\mathrm{G}}_{13}={\mathrm{G}}_{23}={\mathrm{C}}_{44} $$

(1.23)

$$ {\mathrm{K}}_{12}=\frac{{\mathrm{C}}_{11}+{\mathrm{C}}_{12}}{2} $$

(1.24)

where E₃₃, E₁₁, G₂₃, G₁₂, and K₁₂ are the effective axial Young’s, transverse Young’s, axial shear, transverse shear, and bulk moduli of the nanocomposite, respectively.

1.2.2.5 Modeling of Nanocomposite Containing Wavy CNTs

CNTs have a tendency to bend in the prepared nanocomposites due to their relatively high aspect ratio and low bending stiffness (Falvo et al. 1997). In order to investigate the effect of CNT waviness on the mechanical performance of their nanocomposites, we conducted MD simulations to determine the elastic moduli of nanocomposites reinforced with straight and wavy CNTs using CVFF force field. Sinusoidal armchair (5,5) CNT of shape factor α (a/λ) 0.77 and length 256 Å is used in the simulations (see Fig. 1.11a). Due to the symmetry of the appiled boundary and loading conditions, only half of a complete sine-wave CNT was modeled (Matveeva et al. 2014). The MD simulation box in each case was constructed by randomly placing cross-linked epoxy structures around the embedded CNT (see Fig. 1.11b), and its size in each case was adjusted in such a way that the CNT volume fraction remains constant at 2.5 %. The details of the seven RVEs are summarized in Table 1.5.

Fig. 1.11

(a) A schematic representation of a wavy CNT showing the main parameters that control curvature.(b) MD unit cell reinforced with wavy CNT (α = 0.8)

Table 1.5 Parameters used in the RVEs

Curved CNTs have reinforcement effects on both the chord and the transverse directions; therefore, the RVE is considered to be orthotropic. Nine independent material constants are required to fully define the elastic stiffness tensor of the orthotropic RVE . The constitutive relationship of the orthotropic RVE is given by

$$ \left[\begin{array}{c}{\sigma}_{11}\\ {}{\sigma}_{22}\\ {}{\sigma}_{33}\\ {}{\sigma}_{23}\\ {}{\sigma}_{13}\\ {}{\sigma}_{12}\end{array}\right]=\left[\begin{array}{cccccc}{\mathrm{C}}_{11}& {\mathrm{C}}_{12}& {\mathrm{C}}_{13}& 0& 0& 0\\ {}{\mathrm{C}}_{12}& {\mathrm{C}}_{22}& {\mathrm{C}}_{23}& 0& 0& 0\\ {}{\mathrm{C}}_{13}& {\mathrm{C}}_{23}& {\mathrm{C}}_{33}& 0& 0& 0\\ {}0& 0& 0& {\mathrm{C}}_{44}& 0& 0\\ {}0& 0& 0& 0& {\mathrm{C}}_{55}& 0\\ {}0& 0& 0& 0& 0& {\mathrm{C}}_{66}\end{array}\right]\left[\begin{array}{c}{\varepsilon}_{11}\\ {}{\varepsilon}_{22}\\ {}{\varepsilon}_{33}\\ {}{\varepsilon}_{23}\\ {}{\varepsilon}_{13}\\ {}{\varepsilon}_{12}\end{array}\right] $$

(1.25)

The nine independent stiffness constants can be determined by applying six loading conditions on the RVE : uniaxial tension and compressions in all directions and in-plane shears in 1–2, 2–3, and 1–3 planes. The steps involved in the MD simulations are the same as those adopted for the pure epoxy and RVE reinforced with agglomerated CNTs . The boundary and loading conditions applied to the RVE are listed in Table 1.6.

Table 1.6 Effective elastic coefficients of the RVEs and corresponding displacement fields

Table 1.7 summarizes the outcome of the MD simulations. It may be observed from the results that the CNT waviness reduces the reinforcing effect of CNTs , which eventually degrades the bulk elastic moduli of the nanocomposites .

Table 1.7 Material properties of the nanocomposite RVE containing straight or wavy CNT at ~1.8 vol.%

1.2.2.6 CNT Pullout Simulations

The mechanical performance of nanocomposites depends on the efficiency of stress transfer between the polymer matrix and the embedded CNTs . Due to the difficulties associated with experimental studies of the interfacial properties of nanocomposites on the atomic scale, a significant number of analytical models have been developed, and numerical studies have also been conducted to study these nanocomposites (Wernik et al. 2012). For instance, in an effort to understand the main factors that govern the interfacial adhesion, Lordi and Yao (2000) used force-field-based molecular mechanics calculations to determine the binding energies and sliding frictional stresses between CNTs and a range of polymer matrices. Their results show that binding energies and frictional forces slightly affect the strength of the interface. Liao and Li (2001) used molecular mechanics simulations to study the interfacial characteristics of a CNT -reinforced polystyrene composite due to nonbonded electrostatic and vdW interactions and reported the interfacial shear stress approximately to be ∼160 MPa. Frankland and Harik (2003b) used MD simulations to pull out a CNT from a crystalline polymer matrix. Based on their MD results, they developed an interfacial friction model based on the pullout force, an effective viscosity, and the strain rate. Li et al. (2011) studied the effects of CNT length, diameter, and wall number on the interfacial properties of CNT –polyethylene composite using MD simulations. Their results showed that the ISS does not depend on the CNT length, but it is proportional to the CNT diameter.

In this section, we will determine the ISS of an epoxy nanocomposite using MD simulations. The MD simulation box is constructed using the same steps as mentioned previously herein. During the pullout simulation, one end of the fully embedded CNT is extracted from the matrix at constant velocity of $1\times {10}^{-5}\;\mathring{\mathrm{A}} /\mathrm{fs}$ in the NVT ensemble at 300 K (Yang et al. 2012a). The periodic boundary conditions were removed along the axial direction of the CNT , and the polymer atoms are constrained during the pullout simulation (Li et al. 2011). The pullout force and the average ISS are then determined based on the work done during the pullout test. Typical snapshots during CNT pullout from the epoxy matrix are shown in Fig. 1.12. The corresponding ISS is determined by dividing the pullout force by the initial interfacial area, $A=\pi\ {d}_{\mathrm{CNT}}\ {l}_{\mathrm{CNT}}$, where d _CNT and l _CNT are the diameter and length of the embedded CNT , respectively.

Fig. 1.12

Snapshots of CNT -reinforced epoxy composite at various displacements during the CNT pullout simulation

Five different CNT lengths up to 200 Å were modeled to study the effect of CNT length on the interfacial properties . Figure 1.13 shows the effect of embedded CNT lengths on the ISS of a nanocomposite with an interfacial thickness of 3.4 Å. The ISS of the CNT –polymer composite system exhibits a decaying length trend similar to traditional fiber composites (Herrera-Franco and Drzal 1992).

Fig. 1.13

Effect of CNT length on the ISS

The effect of CNT size on the interfacial properties was investigated by modeling RVEs reinforced with SWCNT of different diameters. The smallest CNT is of (5, 5) chirality and 6.78 Å diameter, while the largest is of (18, 18) chirality and 24.4 Å diameter. Figure 1.14 shows that the ISS decreases approximately linearly with the increase of the CNT diameter. The effect of the interface thickness on the ISS of nanocomposite is investigated by modeling the CNT –epoxy RVEs with different interface thicknesses ranging from 2.2 to 4.25 Å. The measured ISS was found to decrease with increasing the interfacial thickness, as shown in Fig. 1.15. This dependence is attributed to the fact that vdW interactions between any two atoms become weaker with the increase of their atomic separation distance.

Fig. 1.14

Effect of CNT diameter on the ISS

Fig. 1.15

Effect of interface thickness on the ISS

1.3 ABC Mechanics Technique

Due to the computational cost of MD simulations, another atomistic technique was developed to model CNT and its nanocomposite by replacing their structures with equivalent-continuum elements. In this method, in contrast to the traditional continuum modeling techniques, the discrete nature of the structure is considered by replacing the carbon–carbon covalent bond and the interatomic interaction with beam and truss elements, respectively. In general, ABC simulations are conducted using conventional finite element analysis (FEA) packages by modeling (1) CNTs as space frame structures; (2) bonded interactions using beam, truss, and spring elements; and (3) nonbonded interactions using nonlinear truss elements (Nasdala and Ernst 2005).

1.3.1 Basics of ABC Technique

At the nanoscale level, the total interatomic potential energy of the system can be described as the sum of individual energy contributions from bonded- and nonbonded interactions:

$$ V={\displaystyle \sum }{V}_r+{\displaystyle \sum }{V}_{\theta }+{\displaystyle \sum }{V}_{\varphi }+{\displaystyle \sum }{V}_{\omega }+{\displaystyle \sum }{V}_{\mathrm{vdW}} $$

(1.26)

where the terms V _r , V _θ , V _φ , V _ω , and V _vdW represent the bond-stretch interaction, bond angle bending, dihedral angle torsion, improper (out-of-plane) torsion, and nonbonded vdW interaction, respectively (Li and Chou 2003a). Figure 1.16 shows schematic representations of these interatomic potential energies.

Fig. 1.16

Interatomic interactions in atomic structures

Li and Chou (2003a) modeled the deformation of CNTs by modeling their structures as geometrical frame-like structures in which each atom acts as a joint of connecting load-bearing beam members which represent C–C covalent bonds where the interatomic potential energies are linked to the strain energies. They described the first four terms of the interatomic potential energy for the bonded interactions using harmonic approximation assuming only small deformations. In addition, they merged the potential energy from the dihedral angle torsion and the improper torsion into a single equivalent term. As a result, the total potential energy due to the covalent bonding can be calculated using only three terms as follows:

$$ {V}_r=\frac{1}{2}\ {k}_r{\left(r-{r}_{\mathrm{o}}\right)}^2=\frac{1}{2}\ {k}_r\Delta {r}^2 $$

(1.27)

$$ {V}_{\theta }=\frac{1}{2}\ {k}_{\theta }{\left(\theta -{\theta}_{\mathrm{o}}\right)}^2=\frac{1}{2}\ {k}_{\theta}\Delta {\theta}^2 $$

(1.28)

$$ {V}_{\tau }={V}_{\varphi }+{V}_{\omega }=\frac{1}{2}\ {k}_{\tau}\Delta {\varphi}^2 $$

(1.29)

where k _r is the bond-stretching force constant, k _θ is the bond angle-bending force constant, k _τ is the torsional resistance, Δr is the bond-stretching increment, Δθ is the bond angle change, and Δφ is the angle change of bond twisting. Then, they used beam elements to replace C–C bonds by equating the beam strain energy due to axial deformation, pure bending, and pure torsion due to the total potential energy of the bond. The governing parameters that characterize the beam elements are axial stiffness (EA), bending stiffness (EI), and torsional stiffness (GJ) (see Fig. 1.17) and can be calculated as follows:

Fig. 1.17

Beam element under (a) axial tension, (b) pure bending, and (c) torsion

$$ \frac{\mathrm{EA}}{L}={k}_r,\;\frac{\mathrm{EI}}{L}={k}_{\theta },\;\frac{\mathrm{GJ}}{L}={k}_{\tau } $$

(1.30)

Later, Li and Chou (2003b) determined the elastic properties of multiwalled CNTs by modeling them as space frame structures using connected beam elements where the vdW interactions between the CNT walls were modeled as nonlinear truss elements (see Fig. 1.18).

Fig. 1.18

(a) CNT modeled as a frame-like structure based on beam elements and (b) a double-wall CNT and a schematic representation of the truss elements used to model the intertube vdW interactions

1.3.2 Modeling of Nanocomposites

A more advanced and generalized ABC model was developed by Wernik and Meguid (2010) based on the modified Morse potential to study the nonlinear elastic response of SWCNTs under tensile and torsional loadings. The stretching and angle-bending components in the interatomic potential were modeled by nonlinear rotational spring and beam elements, respectively, as shown in Fig. 1.19. The following equations were used to describe the bond-stretching and angle-bending components of the modified Morse potential:

Fig. 1.19

Schematic representations of (a) a hexagonal lattice of CNT and (b) the connecting structural elements used to model C–C covalent bond

$$ {V}_{\mathrm{modified}\_\mathrm{morse}\_\mathrm{potential}}={V}_{\mathrm{bond}\_\mathrm{stretching}}+{V}_{\mathrm{angle}\_\mathrm{bending}} $$

(1.31)

$$ {V}_{\mathrm{bond}\_\mathrm{stretching}}={D}_e\left({\left[1-{ \exp}^{-\beta \left(r-{r}_{\mathrm{o}}\right)}\right]}^2-1\right) $$

(1.32)

$$ {V}_{\mathrm{angle}\_\mathrm{bending}}=\frac{1}{2}\ {k}_{\theta }{\left(\theta -{\theta}_{\mathrm{o}}\right)}^2\left[1+{k}_{\mathrm{sextic}\ }{\left(\theta -{\theta}_{\mathrm{o}}\right)}^4\right] $$

(1.33)

where r, θ, D _e , β, k _θ , and k _sextic are parameters of the potential.

The results of their ABC simulations showed that armchair CNTs offer a better reinforcement for the nanocomposite due to their superior properties compared to all other types of CNTs . For example, the induced initial damage on the CNT wall expanded more rapidly in the case of zigzag CNTs , as shown in Fig. 1.20. However, zigzag CNTs showed a higher resistance to torsional buckling by having a higher angle of twist for each buckling mode in comparison to the armchair CNTs (see Fig. 1.21).

Fig. 1.20

CNTs at different fracture stages under tensile loading condition (Wernik and Meguid 2010)

Fig. 1.21

CNTs buckling under torsional loading (Wernik and Meguid 2010)

Meguid et al. (2013) extended their model to incorporate vdW interactions between neighboring atoms of the CNT and the polymer matrix by modeling the weak nonbonded interactions as truss elements. They used the modified model to study the interfacial and mechanical properties of nanocomposites . They used LJ interatomic potential to describe the vdW interactions between the embedded CNT and the surrounding polymer matrix, as given below:

$$ {V}_{\mathrm{LJ}}=4\mu \left[{\left(\frac{\psi }{r}\right)}^{12}-{\left(\frac{\psi }{r}\right)}^6\right] $$

(1.34)

where μ is the depth of energy well and its value indicates the bond strength, ψ is the distance at which E _LJ is zero and known as the effective diameter of the hard sphere atom, and r is the distance between the two atoms. To model the surrounding polymer matrix, a specific two-component epoxy was used based on a DGEBA and TETA formulation. The Young’s modulus and Poisson’s ratio of the epoxy matrix were taken to be 1.07 GPa and 0.28, respectively. The epoxy was modeled using higher-ordered 3D, 10-node solid tetrahedral elements with quadratic displacement behavior as shown in Fig. 1.22.

Fig. 1.22

Schematic representation of the CNT –epoxy interface

Figure 1.23 shows a schematic of the displacement boundary conditions applied during the pullout process. The nodes in the CNT are constrained from any radial displacements, and an incremental axial displacement boundary condition is applied to the top of CNT nodes to initiate the pullout process. The force required to withdraw the CNT from the matrix is evaluated over the course of the pullout process by summing the reaction forces at the upper CNT nodes. The corresponding ISS was determined by dividing the maximum pullout force by the initial interfacial area, $A=\pi\;dl$, where d and l are the diameter and length of the embedded CNT , respectively. The pullout model was used to study the effect of CNT length and diameter on the pullout force and the interfacial shear strength (Figs. 1.24 and 1.25). The pullout force was found to increase with increasing CNT diameter, while it was found to be independent of the CNT length. The ISS was found to decrease with increasing the CNT diameter and length.

Fig. 1.23

Schematic drawing showing (a) the three-phase model that consists of the polymer, the reinforcing CNT , and interface layer; (b) pullout of a CNT from matrix to determine the ISS of the nanocomposite

Fig. 1.24

Effect of geometrical parameters on the pullout force of a SWCNT from epoxy matrix. (a) Effect of CNT diameter. (b) Effect of CNT length (Meguid et al. 2013)

Fig. 1.25

Effect of geometrical parameters on the ISS of CNT –epoxy composite. (a) Effect of CNT diameter. (b) Effect of CNT length (Meguid et al. 2013)

Wernik and Meguid (2014) then used their model to determine the elastic properties of a transversely isotropic nanoscale RVE consists of a SWCNT, the surrounding polymer matrix, and their interface (see Fig. 1.26). The five stiffness constants required to fully describe the elastic behavior of the RVE were determined by applying five different sets of boundary conditions on the RVE and equating the total strain energies of the RVE and an equivalent representative fiber, exhibiting the same geometrical and mechanical characteristics, under identical sets of loading conditions as listed in Table 1.3 (assuming 2–3 planes of symmetry in the current case). Table 1.8 summarizes the obtained stiffness constants and the corresponding elastic moduli of the RVE from the ABC simulations.

Fig. 1.26

Geometrical dimensions of the RVE and the equivalent effective fiber represent CNT –epoxy composite with 32 % CNT volume fraction (Wernik and Meguid 2014)

Table 1.8 Stiffness constants and the corresponding elastic moduli of the RVE from the ABC simulations

1.4 Micromechanics Modeling

Multiscale modeling of nanocomposites can be conducted using a two-step scheme. First, the effective elastic properties of a RVE that account for the nanofiller and its immediate surrounding are determined using an appropriate atomistic modeling technique. This RVE is subsequently homogenized into an effective fiber with the same dimensions but with uniform properties (Yang et al. 2012b). Second, established micromechanical techniques such as Mori–Tanaka technique are then used to determine the mechanical properties of the nanocomposites on a macroscopic scale using the effective fiber as the reinforcing fiber in the polymer matrix. Odegard and coworkers (2003, 2005) developed a sequential multiscale model in which the CNT , polymer matrix, and interface were all combined and modeled as an effective continuum fiber using an equivalent-continuum modeling method. Then Mori–Tanaka method was employed to determine the bulk properties of a nanocomposite reinforced with aligned and randomly orientated effective fibers for varied CNT lengths and concentrations. Selmi et al. (2007) compared the predicted elastic properties of CNT -based polymers using different micromechanical techniques including various extensions of the Mori–Tanaka method. Their comparative study showed that the two-level Mori–Tanaka/Mori–Tanaka (MT–MT) approach delivers the most accurate predictions compared to experimental results. In this section, we will use Mori–Tanaka method to scale up the elastic properties of the pure epoxy and the effective fiber, which are determined using MD simulations, to the bulk level. This method has been successfully employed to similar problems by many researchers (Jam et al. 2013; Sobhani Aragh et al. 2012).

Mori–Tanaka model can be developed by utilizing the elastic properties of the nanocomposite containing transversely isotropic aligned CNT or the orthotropic wavy CNT and the isotropic elastic properties of the pure epoxy. In case of two-phase composite, where the inhomogeneity is randomly orientated in the three-dimensional space, the following relation can be used to determine the effective stiffness tensor [C] of the nanocomposite:

$$ \left[C\right]=\left[{C}^m\right]+{v}_{\mathrm{RVE}}\left\langle \left(\left[{C}^{\mathrm{RVE}}\right]-\left[{C}^m\right]\right)\right\rangle \left(\left[A\right]{\left[{v}_m\left[I\right]+{v}_{\mathrm{RVE}}\ \left\langle \left[A\right]\right\rangle \right]}^{-1}\right) $$

(1.35)

in which the mechanical strain concentration tensor [A] is given by

$$ \left[A\right]={\left[\left[I\right]+\left[{S}^{\mathrm{RVE}}\right]{\left(\left[{C}^m\right]\right)}^{-1}\left(\left[{C}^{\mathrm{RVE}}\right]-\left[{C}^m\right]\right)\right]}^{-1} $$

(1.36)

where [C ^m] and [CRVE] are the stiffness tensors of the epoxy matrix and the RVE , respectively; [I] is an identity matrix; v _m and v _RVE represent the volume fractions of the epoxy matrix and the RVE , respectively; and [S ^RVE] indicate the Eshelby tensor (Mori and Tanaka 1973). The specific form of the Eshelby tensor for the RVE inclusion given by Qiu and Weng (1990) is utilized herein.

It may be noted that the elastic coefficient matrix [C] directly provides the values of the effective elastic properties of the nanocomposite, where the RVE is aligned with the 3-axis. In case of random orientations of CNTs , the terms enclosed with angle brackets in Eq. (1.35) represent the average value of the term over all orientations defined by transformation from the local coordinate system of the RVE to the global coordinate system. The transformed mechanical strain concentration tensor for the RVEs with respect to the global coordinates is given by

$$ \left[A\right]={\left[\left[I\right]+\left[{S}^{\mathrm{RVE}}\right]{\left(\left[{C}^m\right]\right)}^{-1}\left(\left[{C}^{\mathrm{RVE}}\right]-\left[{C}^m\right]\right)\right]}^{-1} $$

(1.37)

where t _ij are the direction cosines for the transformation and are given by

$$ {t}_{11}= \cos \phi\ \cos \psi - \sin \phi\ \cos \gamma\ \sin \psi,\ {t}_{12}= \sin \phi\ \cos \psi + \cos \phi\ \cos \gamma\ \sin \psi, {t}_{13}= \sin \psi\ \sin \gamma,\ {t}_{21}=- \cos \phi\ \sin \psi - \sin \phi\ \cos \gamma\ \cos \psi, {t}_{22}=- \sin \phi\ \sin \psi + \cos \phi\ \cos \gamma\ \cos \psi,\ {t}_{23}= \sin \gamma\ \cos \psi,\ {t}_{31}= \sin \phi\ \sin \gamma, {t}_{32}=- \cos \phi\ \sin \gamma, \mathrm{and}\kern0.2em {t}_{33}= \cos \gamma $$

Consequently, the random orientation average of the dilute mechanical strain concentration tensor [A] can be determined by using the following equation:

$$ \left\langle \left[A\right]\right\rangle =\frac{{\displaystyle {\int}_{-\pi}^{\pi }}{\displaystyle {\int}_0^{\pi }}{\displaystyle {\int}_0^{\pi /2}}\left[{\tilde {A}}\right]\left(\phi,\ \gamma,\ \psi \right)\ \sin \gamma\ \mathrm{d}\phi \mathrm{d}\gamma \mathrm{d}\psi\ }{{\displaystyle {\int}_{-\pi}^{\pi }}{\displaystyle {\int}_0^{\pi }}{\displaystyle {\int}_0^{\pi /2}}\ \sin \gamma\ \mathrm{d}\phi \mathrm{d}\gamma \mathrm{d}\psi } $$

(1.38)

where ϕ, γ, and ψ are the Euler angles as shown in Fig. 1.27. It may be noted that the averaged mechanical strain concentration tensors given by Eqs. (1.36) and (1.38) are used for the cases of aligned and random orientations of CNTs , respectively, in Eq. (1.35).

Fig. 1.27

Relationship between the local coordinates (1, 2, 3) of the RVE and the global coordinates (1′, 2′, 3′) of the bulk composite

The effect of CNT orientation on the bulk properties was investigated by considering polymer reinforced with aligned and randomly oriented CNTs , as shown in Fig. 1.28. The effect of CNT agglomeration was investigated by considering effective fibers representing RVEs reinforced with bundle of three CNTs and bundle of seven CNTs . The maximum CNT volume fraction (V _CNT) considered in the nanocomposite is 5 % because CNT concentrations above this loading are not normally realized (Wernik and Meguid 2014).

Fig. 1.28

Schematic representations of RVE reinforced with (a) aligned CNTs and (b) randomly dispersed CNTs

Unless otherwise stated, the bulk elastic properties of the nanocomposite are relate to the aligned nanocomposite RVEs along the 3-axis. Let us first demonstrate the effect of agglomeration of CNTs on the effective elastic properties of the aligned CNT -reinforced epoxy composite. Figure 1.29a–d shows the variations of the effective axial Young’s modulus (E₃₃), the transverse Young’s modulus (E₁₁), the effective axial shear modulus (G₂₃), and the transverse shear modulus (G₁₂) of the nanocomposite with the CNT volume fraction. The elastic moduli increase with increasing CNT volume fraction and decrease with increasing the CNT bundle size. The results show clearly that the CNT agglomerates significantly reduce the elastic moduli.

Fig. 1.29

Variation of the (a) axial Young’s modulus, (b) the transverse Young’s modulus, (c) the effective axial shear modulus, and (d) the transverse shear modulus of the nanocomposite containing aligned CNTs with the CNT volume fraction

The orientations of the CNT reinforcement in the polymer matrix can vary over the volume of the nanocomposite. Therefore, studying the properties of nanocomposites reinforced with randomly oriented CNTs is of a great importance. For such investigation, CNTs or their bundles are considered to be randomly dispersed in the epoxy matrix over the volume of the nanocomposite. As expected, this case provides the isotropic elastic properties for the resulting nanocomposite. Figure 1.30a, b illustrates the variations of the effective Young’s (E) and shear (G) moduli of the nanocomposite with the CNT loading. These results clearly demonstrate that the randomly dispersed CNTs improve the effective Young’s and shear moduli of the nanocomposite over those of the transverse Young’s modulus (E₁₁) and the shear moduli (G₁₂ and G₂₃) of the nanocomposite reinforced with aligned CNTs . This is attributed to the fact that the CNTs are homogeneously dispersed in the epoxy matrix in the random case, and hence, the overall elastic properties of the resulting nanocomposite improve in comparison to the aligned case. These findings are also consistent with the previously reported findings by Odegard et al. (2003) and Wernik and Meguid (2014). It may also be observed that both E and G decrease with the increase of the number of CNTs in the bundle, and this effect becomes more pronounced at higher CNT volume fractions.

Fig. 1.30

Variation of the (a) Young’s modulus and (b) the shear modulus of the nanocomposite containing randomly oriented CNTs with the CNT volume fraction

1.5 Large-Scale Hybrid Monte Carlo FEA Simulations

Finite element (FE) analysis with the aid of Monte Carlo technique offers a unique opportunity to study the local mechanical behavior and also the overall properties of CNT -reinforced polymer composites under large deformations and specific boundary conditions (Wernik 2013). Complementary to the traditional micromechanical techniques, large-scale three-dimensional (3D) FE models of polymer matrix reinforced with enough number of randomly oriented CNTs are used to predict the average properties of the nanocomposite at a certain CNT volume fraction. Simulation is carried out for several times to yield better averaged results with less scattering. This technique uses the effective elastic moduli of the RVE and the pure epoxy obtained from the atomistic simulations as an input into the analysis.

Here, we will describe the large-scale FE model developed by Wernik and Meguid (2014) to study CNT –epoxy composites. First, a constitutive model for both the effective fiber and the surrounding epoxy polymer that accounts for the material nonlinearities was determined using ABC technique. They benefited from the available nonlinear material models which represent an advantage over the linear elastic micromechanical models. The multi-linear elastic material model was used to describe the nonlinear behavior of the nanocomposite constituents allowing the full response of the composite to be determined when subjected to large deformations. Figure 1.31 shows a FE unit cell that represents a composite loaded with 1.0 % CNT volume fraction.

Fig. 1.31

Hybrid Monte Carlo FEA computational cell model in its (a) unmeshed and (b) fully meshed form. The model utilizes a CNT volume fraction of 1.0 % and a CNT aspect ratio of 100 (from Wernik 2013)

Higher-ordered 3D, 10-node solid tetrahedral elements with quadratic displacement behavior were used to mesh both the polymer and representative fibers. Periodic boundary conditions were imposed on the FE computational cell. This model represents perfectly straight reinforcing representative fibers of diameter 2.4 nm and aspect ratio of 100. The main disadvantage of this method is the enormous computational cost that is required for such simulations. As a result, a great attention should be given in selecting the cell size that provides accurate results with reasonable computational cost. The RVE was then subjected to a tensile strain up to 10 % by displacing the nodes located at the upper surface while fixing the nodes located at the lower surface. The constitutive relations of the RVE were then evaluated by dividing the total reaction force by the cross-sectional area at each iteration of the simulation. Figure 1.32 shows the predicted constitutive response of the FE unit cell under tensile load plotted against experimental measurements for an epoxy matrix reinforced with the same CNT concentration (0.5 wt%).

Fig. 1.32

Predicted constitutive response of nano-reinforced adhesives under tensile load (from Wernik 2013)