Special Continuous Probability Distributions

Abstract

Particular continuous distributions encountered on a daily basis are discussed: the simplest uniform distribution, the exponential distribution characterizing the decay of unstable atoms and nuclei, the ubiquitous normal (Gauss) distribution in both its general and standardized form, the Maxwell velocity distribution in its vector and scalar form, the Pareto (power-law) distribution, and the Cauchy (Lorentz, Breit–Wigner) distribution suitable for describing spectral line shapes and resonances. Three further distributions are introduced ($\chi ^2$-, Student’s t- and F-distributions), predominantly used in problems of statistical inference based on samples. Generalizations of the exponential law to hypo- and hyper-exponential distributions are presented.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

In this chapter we become acquainted with the most frequently used continuous probability distributions that physicists typically deal with on a daily basis.

1 Uniform Distribution

Its name says it all: the uniform distribution describes outcomes of random experiments—a set of measured values of a random variable—where all values between the lowest (a) and the highest possible (b) are equally probable. A bus that runs on a 15-min schedule, will turn up at our stop anywhere between $a=0\,\mathrm {min}$ and $b=15\,\mathrm {min}$ from now: our waiting time X is a continuous random variable distributed uniformly between a and b, which one denotes as

$$ X \sim U(a,b). $$

The probability density corresponding to the uniform distribution U(a, b) is

$$\begin{aligned} f_X(x) = \left\{ \begin{array}{rcl} \displaystyle {1\over b-a} &{};&{} \quad a \le x \le b , \\ 0 &{};&{} \quad \mathrm {elsewhere} , \end{array} \right. \end{aligned}$$

(3.1)

(Fig. 3.1 (left)) and its distribution function is

$$ P(X \le x) = F_X(x) = \left\{ \begin{array}{rcl} 0 &{};&{} x < a , \\ \displaystyle {x-a\over b-a} &{};&{} a \le x \le b , \\ 1 &{};&{} x > b . \end{array} \right. $$

If we show up at the bus stop at a random instant, the probability that our waiting time will not exceed $10\,\mathrm {min}$, is

$$ P(X \le 10) = F_X(10) = {10-0\over 15-0} = {2\over 3} . $$

Fig. 3.1

[Left] The probability density of the uniform distribution U(a, b). [Right] The probability density of the exponential distribution with parameter $\lambda$

Example

On a hot day, a house-fly mostly sits still, but occasionally takes off to stretch its legs. Suppose that the time T of its buzzing around is uniformly distributed between 0 and $30\,\mathrm {s}$, i.e. $T \sim U(0,30)$. What is the probability that it will fly for more than $20\,\mathrm {s}$ (event A) given that it flies for more than $10\,\mathrm {s}$ (condition B)? Due to the additional information B the probability density is no longer $f_T(t) = 1/30\,\mathrm {s}$ but $\widetilde{f}_T(t) = 1/((30$–$10)\mathrm {s}) = 1/20\,\mathrm {s}$, hence

$$ P\bigl (T> 20\,\mathrm {s} \, | \, T > 10\,\mathrm {s}\bigr ) = \int _{20\,\mathrm {s}}^{30\,\mathrm {s}} \widetilde{f}_T(t) \, \mathrm {d}t = {30\,\mathrm {s} - 20\,\mathrm {s} \over 20\,\mathrm {s} } = {1\over 2} . $$

The same result can be obtained by using the original density $f_T(t)$ and direct application of the conditional probability formula:

$$ P(A|B) = { P(A \cap B) \over P(B) } = { P(A) \over P(B) } = \int _{20\,\mathrm {s}}^{30\,\mathrm {s}} f_T(t) \, \mathrm {d}t \biggl / \int _{10\,\mathrm {s}}^{30\,\mathrm {s}} f_T(t) \, \mathrm {d}t = { 1/3 \over 2/3 } = {1\over 2} . $$

No matter how trivial the example is, do not forget that computing a conditional probability imposes a restriction on the sample space!    $\triangleleft$

2 Exponential Distribution

The exponential distribution is used to describe processes in which the probability of a certain event per unit time is constant: the classical example is the time-dependence of the radioactive decay of nuclei, but it is also used in modeling the distribution of waiting times in queues or durations of fault-free operation (lifetimes) of devices like light bulbs or computer disks.

The decay of an unstable atomic nucleus is a random process par excellence (see also Sects. C.3 and 3.2.1). For a single nucleus, it is impossible to predict the precise moment of its decay; the probability for it to decay in some time interval depends only on the length of this interval, $\Delta t$, not on the age of the nucleus. We say that the nuclei “do not age” and that radioactive decay is a “memory-less” process: suppose that we have been waiting in vain for time t for the nucleus to decay; the probability that the decay finally occurs after $t+{\Delta t}$, is independent of t,

$$\begin{aligned} P( T> t + {\Delta t} \, | \, T> t ) = P( T > {\Delta t} ) . \end{aligned}$$

(3.2)

If the interval $\Delta t$ is short enough, we can assume that the decay probability is proportional to $\Delta t$, and then the only choice becomes

$$ P(\mathrm {decay}) = \lambda {\Delta t} \qquad \mathrm {or} \qquad P(\mathrm {no~decay}) = 1 - \lambda {\Delta t} , $$

where $\lambda = 1/\tau$ is the decay probability per unit time [$\mathrm {s}^{-1}]$, also called the decay constant, while $\tau$ is the characteristic or decay time. The probability that a nucleus has not decayed yet after $n{\Delta t}$ is $(1-\lambda {\Delta t})^n$. The probability that it has not decayed after a longer time $t = n{\Delta t}$, meaning that it will decay at some time $T > t = n{\Delta t}$, is therefore

$$\begin{aligned} P(T > t) = \lim _{n\rightarrow \infty } ( 1 - \lambda {\Delta t} )^n = \lim _{n\rightarrow \infty } \left( 1 - {\lambda t\over n} \right) ^n = \mathrm {e}^{-\lambda t} . \end{aligned}$$

(3.3)

Since $P(T > t) = 1 - P(T \le t) = 1 - F_T(t)$, we can immediately calculate the corresponding probability density,

$$\begin{aligned} f_T(t) = {\mathrm {d}F_T(t)\over \mathrm {d}t} = {\mathrm {d}\over \mathrm {d}t} \left( 1 - \mathrm {e}^{-\lambda t} \right) = \lambda \, \mathrm {e}^{-\lambda t} , \qquad t \ge 0 , \end{aligned}$$

(3.4)

shown in Fig. 3.1 (right). (As an exercise, check the validity of (3.2)!) Let us think in a complementary way: the probability that the nucleus has not decayed until time t must equal the probability that it will decay at some instant from t until $\infty$, i.e. the corresponding integral of the density we have just derived. Indeed

$$ \int _t^\infty f_T(t')\,\mathrm {d}t' = \int _t^\infty \lambda \, \mathrm {e}^{-\lambda t'}\,\mathrm {d}t' = \mathrm {e}^{-\lambda t} . $$

It is incredible how many wrong interpretations of these considerations can be heard, so let us reiterate: Equation (3.3) gives the probability that until time t the nucleus has not decayed. At time zero this probability equals 1 and exponentially drops to zero henceforth: every unstable nucleus will decay at some time. The rate of change of the number of nuclei—nuclei still available for decay—is given by the differential equation ${\mathrm {d}N(t)/\mathrm {d}t} = - \lambda N(t)$ with the initial condition $N(t=0) = N_0$, and its solution is

$$\begin{aligned} N(t) = N_0 \, \mathrm {e}^{-\lambda t} . \end{aligned}$$

(3.5)

The decay constant $\lambda$ is determined experimentally by counting the number of decays R(t) until time t. Since $N_0 = N(t) + R(t)$, it follows from above that $\mathrm {e}^{-\lambda t} = 1 - R(t)/N_0$, therefore

$$ \lambda t = - \log \left( 1 - {R(t)\over N_0} \right) . $$

By fitting this functional dependence to the measured data we extract $\lambda = 1/\tau$.

Mini-example Two counters in a bank are busy serving a single customer each: the first person has just arrived, while the other has been there for 10 min. Which counter should we choose in order to be served as quickly as possible? If the waiting times are exponentially distributed, it does not matter.    $\triangleleft$

Example

You do not believe the Mini-example? Let the variable T measure the time between consecutive particle hits in a Geiger–Müller counter, where T is exponentially distributed, with a characteristic time of $\tau = 84\,\mathrm {s}$ [1]. The probability that we detect a particle ${\Delta t} = 30\,\mathrm {s}$ after the counter has been switched on, is

$$\begin{aligned} P\bigl ( T \le {\Delta t} \bigr ) = F_T({\Delta t}) = 1 - \mathrm {e}^{-{\Delta t}/\tau } \approx 0.30 . \end{aligned}$$

(3.6)

Now imagine that we switch on the detector and three minutes ($t=180\,\mathrm {s}$) elapse without a single particle being detected. What is the probability to detect a particle within the next $\Delta t = 30\,\mathrm {s}$? Intuitively we expect that after three minutes the next particle is “long over-due”. But we need the conditional probability

$$ P( T \le t+{\Delta t} \,|\, T> t ) = { P( t < T \le t+{\Delta t} ) \over P (T > t)} . $$

Here

$$ P( t < T \le t+{\Delta t} ) = F_T(t\,+\,{\Delta t}) - F_T(t) = \left[ 1 - \mathrm {e}^{-(t+{\Delta t})/\tau } \right] - \left[ 1 - \mathrm {e}^{-t/\tau } \right] \approx 0.035 $$

and $P( T > t ) = 1 - F_T(t) = \mathrm {e}^{-t/\tau } \approx 0.117$, thus $P( T \le t+{\Delta t} \,|\, T > t ) = 0.035/0.117 \approx 0.30$, which is the same as (3.6). The fact that we have waited 3 minutes without detecting a particle, has no influence whatsoever on the probability of detection within the next $30\,\mathrm {s}$.    $\triangleleft$

Example

Customers A and B arrive simultaneously at two bank counters. Their service time is an exponentially distributed random variable with parameters $\lambda _\mathrm {A}$ and $\lambda _\mathrm {B}$, respectively. What is the probability that B leaves before A?

Let $T_\mathrm {A}$ and $T_\mathrm {B}$ be random variables measuring the actual service time. The probability that A has not been served until $t_\mathrm {A}$ is $\mathrm {e}^{-\lambda _\mathrm {A}t_\mathrm {A}}$. The corresponding probability for customer B is $\mathrm {e}^{-\lambda _\mathrm {B}t_\mathrm {B}}$. Since the waiting processes are independent, their joint probability density is the product of individual probability densities:

$$ f_{T_\mathrm {A},T_\mathrm {B}}\bigl (t_\mathrm {A},t_\mathrm {B}\bigr ) = \lambda _\mathrm {A}\,\mathrm {e}^{-\lambda _\mathrm {A}t_\mathrm {A}} \cdot \lambda _\mathrm {B}\,\mathrm {e}^{-\lambda _\mathrm {B}t_\mathrm {B}} . $$

Therefore the required probability is

$$ P\bigl ( T_\mathrm {B} < T_\mathrm {A} \bigr ) \!=\! \int _0^\infty \!\!\mathrm {d}t_\mathrm {A} \int _0^{t_\mathrm {A}} f_{T_\mathrm {A},T_\mathrm {B}}\bigl (t_\mathrm {A},t_\mathrm {B}\bigr ) \, \mathrm {d}t_\mathrm {B} \!=\! \int _0^\infty \!\!\mathrm {d}t_\mathrm {A} \lambda _\mathrm {A}\,\mathrm {e}^{-\lambda _\mathrm {A}t_\mathrm {A}} \left( 1 - \mathrm {e}^{-\lambda _\mathrm {B}t_\mathrm {A}} \right) \!=\! {\lambda _\mathrm {B} \over \lambda _\mathrm {A} + \lambda _\mathrm {B}} . $$

The limits are also sensible: if the clerk serving B is very slow ($\lambda _\mathrm {B}\rightarrow 0$), then $P\bigl ( T_\mathrm {B} < T_\mathrm {A} \bigr ) \rightarrow 0$, while in the opposite case $P\bigl ( T_\mathrm {B} < T_\mathrm {A} \bigr ) \rightarrow 1$.    $\triangleleft$

The conviction that exponential distributions are encountered only in random processes involving time in some manner, is quite false. Imagine a box containing many balls with diameter d. The fraction of black and white balls is p and $1-p$, respectively [2]. We draw the balls from the box and arrange them in a line, one touching the other. Suppose we have just drawn a black ball. What is the probability that the distance x between its center and the center of the next black ball is exactly iD, ($i=1,2,\ldots$)? We are observing the sequences of drawn balls or “events” of the form

so the required probability is obviously

$$ P(x = iD) = (1-p)^{i-1}p . $$

Since these events are exclusive, the corresponding probability function is a sum of all probabilities for individual sequences:

$$ F_X(x) = P(x \le iD) = p + (1-p)p + \cdots + (1-p)^{i-1}p = 1 - (1-p)^i . $$

Abbreviating $D=1/n$ and $np = \lambda$ this can be written as

$$ F_X(x) = 1 - \left( 1 - {\lambda \over n} \right) ^{nx} , $$

since $i = x/D = nx$. Suppose we take the limits $n\rightarrow \infty$ and $p\rightarrow 0$ (i.e. there are very few black balls in the box and they have very small diameters), such that $\lambda$ and x remain unchanged: then $F_X(x) \rightarrow 1 - \mathrm {e}^{-\lambda x}$, and the corresponding density is $f_X(x) = {\mathrm {d}F_X/\mathrm {d}x} = \lambda \, \mathrm {e}^{-\lambda x}$, which is indeed the same as (3.4).

2.1 Is the Decay of Unstable States Truly Exponential?

The exponential distribution offers an excellent phenomenological description of the time dependence of the decay of nuclei and other unstable quantum-mechanical states, but its theoretical justification implies many approximations and assumptions, some of which might be questionable in the extremes $t/\tau \ll 1$ and $t/\tau \gg 1$. Further reading can be found in [3] and the classic textbooks [4–6].

3 Normal (Gauss) Distribution

It is impossible to resist the temptation of beginning this Section by quoting the famous passage from Poincaré’s Probability calculus published in 1912 [7]:

[The law of the distribution of errors] does not follow from strict deduction; many seemingly correct derivations are poorly argued, among them the one resting on the assumption that the probability of deviation is proportional to the deviation. Everyone trusts this law, as I have recently been told by Mr. Lippmann, since the experimentalists believe it is a mathematical theorem, while the theorists think it is an experimental fact.¹

The normal (Gauss) distribution describes—at least approximately—countless quantities from any sphere of human existence and Nature, for example, diameters of screws being produced in their thousands on a lathe, body masses of people, exam grades and velocities of molecules. A partial explanation and justification for this ubiquity of the Gaussian awaits us in Sect. 6.3 and in particular in Chap. 11. For now let us simply become acquainted with the bell-shaped curve of its two-parameter probability density

$$\begin{aligned} f_X(x) = {1\over \sqrt{2\pi }\sigma } \mathrm {exp}\left( -{(x-\mu )^2 \over 2\sigma ^2} \right) , \qquad -\infty< x < \infty , \end{aligned}$$

(3.7)

shown in Fig. 3.2 (top).

Fig. 3.2

[Top] Normal distribution ${N}(\mu =1.5,\sigma ^2=0.09)$ with average (mean) $\mu$ and positive parameter $\sigma$ determining the peak width. Regardless of $\sigma$ the area under the curve equals one. [Bottom] Standardized normal distribution N(0, 1)

The definition domain itself makes it clear why the normal distribution is just an approximation in many cases: body masses can not be negative and exam grades can not be infinite . The distribution is symmetric around the value of $\mu$, while the width of its peak is driven by the standard deviation $\sigma$; at $x=\mu \pm \sigma$ the function $f_X$ has an inflection. The commonly accepted “abbreviation” for the normal distribution is ${N}(\mu ,\sigma ^2)$. In Chap. 4 we will see that $\mu$ is its average or mean and $\sigma ^2$ is its variance.

The cumulative distribution function corresponding to density (3.7) is

$$ F_X(x) = P(X \le x) = \int _{-\infty }^x f_X(t) \, \mathrm {d}t = {1\over 2} \left[ 1 + \mathrm {erf}\left( {x-\mu \over \sqrt{2}\sigma } \right) \right] , $$

where

$$\begin{aligned} \mathrm {erf}(z) = {2\over \sqrt{\pi }} \int _0^z \mathrm {e}^{-t^2} \mathrm {d}t , \qquad \mathrm {erf}(-z) = -\mathrm {erf}(z) , \end{aligned}$$

(3.8)

is the so-called error function which is tabulated (see Tables D.1 and D.2 and the text below). The probability that a continuous random variable, distributed according to the density (3.7), takes a value between a and b, is

$$\begin{aligned} P(a \le X \le b) = F_X(b) - F_X(a) = {1\over 2} \left[ \mathrm {erf}\left( {b-\mu \over \sqrt{2}\sigma } \right) - \mathrm {erf}\left( {a-\mu \over \sqrt{2}\sigma } \right) \right] . \end{aligned}$$

(3.9)

3.1 Standardized Normal Distribution

When handling normally distributed data it makes sense to eliminate the dependence on the origin and the width by subtracting $\mu$ from the variable X and divide out $\sigma$, thereby forming a new, standardized random variable

$$ Z = {X-\mu \over \sigma } . $$

The distribution of Z is then called standardized normal and is denoted by N(0, 1) (zero mean, unit variance). It corresponds to the probability density

$$\begin{aligned} f_Z(z) = {1\over \sqrt{2\pi }}\,\mathrm {e}^{-z^2/2} , \end{aligned}$$

(3.10)

while the distribution function is

$$\begin{aligned} \Phi (z) = P(Z \le z) = {1\over 2} + {1\over \sqrt{2\pi }}\int _0^z \mathrm {e}^{-t^2/2} \, \mathrm {d}t = {1\over 2} \left[ 1 + \mathrm {erf}\left( {z\over \sqrt{2}} \right) \right] . \end{aligned}$$

(3.11)

The values of definite integrals of the standardized normal distribution

$$\begin{aligned} {1\over \sqrt{2\pi }} \int _0^{z} \mathrm {e}^{-t^2/2} \mathrm {d}t = {1\over 2} \, \mathrm {erf}\left( {z\over \sqrt{2}} \right) \end{aligned}$$

(3.12)

for z between 0 and 5 in steps of 0.01, which is sufficient for everyday use, are listed in Table D.1. The abscissas $x=\mu \pm n\sigma$ or $z=\pm n$ ($n=1,2,\ldots$) are particularly important. The areas under the curve $f_Z(z)$ on these intervals,

$$ P_{n\sigma } = P(\mu -n\sigma \le X \le \mu +n\sigma ) = P(-n \le Z \le n) = \mathrm {erf}\left( {n\over \sqrt{2}} \right) , $$

are equal to

$$\begin{aligned} P_{1\sigma } \approx 0.683 , \quad P_{2\sigma } \approx 0.955 , \quad P_{3\sigma } \approx 0.997 , \quad P_{4\sigma } \approx 0.9999367 \ldots \end{aligned}$$

(3.13)

(see Fig. 3.2 (bottom)) and tell us what fraction of the data (diameters, masses, exam grades, velocities) is within these—completely arbitrary—intervals and what fraction is outside. For example, if we establish a normal mass distribution of a large sample of massless particles (smeared around zero due to measurement errors), while a few counts lie above $3\sigma$, one may say: “The probability that the particle actually has a non-zero mass, is $0.3\%$.” But if the distribution of measurement error is indeed Gaussian, then even the extreme $0.3\%$ events in the distribution tail may be genuine! However, by increasing the upper bound to $4\sigma$, $5\sigma$,... we can be more and more confident that the deviation is not just a statistical fluctuation. In modern nuclear and particle physics the discovery of a new particle, state or process the mass difference or the signal-to-noise ratio must typically be larger than $5\sigma$.

Example

(Adapted from [1].) The diameter of the computer disk axes is described by a normally distributed random variable $X=2R$ with average $\mu =0.63650\,\mathrm {cm}$ and standard deviation $\sigma =0.00127\,\mathrm {cm}$, as shown in the figure. The required specification (shaded area) is $(0.6360\pm 0.0025)\,\mathrm {cm}$. Let us calculate the fraction of the axes that fulfill this criterion: it is equal to the probability $P(0.6335\,\mathrm {cm} \le X \le 0.6385\,\mathrm {cm})$, which can be computed by converting to the standardized variables $z_1 = (0.6335\,\mathrm {cm} - \mu )/\sigma = -2.36$, corresponding to the lower specified bound, and $z_2 = (0.6385\,\mathrm {cm} - \mu )/\sigma = 1.57$, which corresponds to the upper one. Hence the probability is $P(-2.36 \le Z \le 1.57)$ and can be computed by using the values from Table D.1 (see also Fig. D.1):

$$\begin{aligned}P(-2.36 \le Z \le 1.57)= & {} P(Z \le 1.57) - P(Z \le -2.36) \\= & {} P(Z \le 1.57) - \bigl [ 1 - P(Z \le 2.36) \bigr ] \\= & {} {\textstyle {1\over 2}} + 0.4418 - \left[ 1 - \left( {\textstyle {1\over 2}} + 0.4909 \right) \right] = 0.9327 . \end{aligned}$$

If the machining tool is modified so as to produce the axes with the required diameter of $0.6360\,\mathrm {cm}$, but with the same uncertainty as before, $\sigma$, the standardized variables become $z_2 = -z_1 = (0.6335$–$0.6360\,\mathrm {cm})/\sigma = 1.97$, thus

$$ P(z_1 \le Z \le z_2) = P(-z_2 \le Z \le z_2) = 2\,P(0 \le Z \le z_2) = 2\cdot 0.4756 = 0.9512 . $$

The fraction of useful axes is thereby increased by about $2\%$.

3.2 Measure of Peak Separation

A practical quantity referring to the normal distribution is its full width at half-maximum (FWHM), see double-headed arrow in Fig. 3.2 (top). It can be obtained by simple calculation: $f_X(x)/f_X(0) = 1/2$ or $\mathrm {exp}[-x^2/(2\sigma ^2)] = 1/2$, hence $x = \sigma \sqrt{2\log 2}$. The $\mathrm {FWHM}$ is just twice this number,

$$ \mathrm {FWHM} = 2\sqrt{2\log 2}\,\sigma \approx 2.35 \, \sigma . $$

$\mathrm {FWHM}$ offers a measure of how well two Gaussian peaks in a physical spectrum can be separated. By convention we can distinguish neighboring peaks with equal amplitudes and equal $\sigma$ if their centers are at least FWHM apart (Fig. 3.3).

Fig. 3.3

Illustration of the measure of peak separation. The centers of the fourth and fifth peak from the left are 0.3 apart, which is just slightly above the value of $\mathrm {FWHM}=0.24$ for individual peaks, so they can still be separated. The three leftmost peaks can also be separated. The structure at the right consists of two peaks which are too close to each other to be cleanly separated. In practice, similar decisions are almost always complicated by the presence of noise

4 Maxwell Distribution

The Maxwell distribution describes the velocities of molecules in thermal motion in thermodynamic equilibrium. In such motion the velocity components of each molecule, ${\varvec{v}}=(v_x,v_y,v_z)$, are stochastically independent, and the average velocity (as a vector) is zero. The directions x, y and z correspond to kinetic energies $mv_x^2/2$, $mv_y^2/2$ and $mv_z^2/2$, and the probability density in velocity space at given temperature T decreases exponentially with energy. The probability density for ${\varvec{v}}$ is the product of three one-dimensional Gaussian densities:

$$\begin{aligned} f_{\varvec{V}}({\varvec{v}}) = \left( {1\over \sqrt{2\pi } \, \sigma } \right) ^3 \mathrm {exp}\left( -{v_x^2+v_y^2+v_z^2\over 2\sigma ^2} \right) = \left( {1\over 2\pi \sigma ^2} \right) ^{3/2} \mathrm {exp}\left( -{v^2\over 2\sigma ^2} \right) , \end{aligned}$$

(3.14)

where $v^2 = v_x^2 + v_y^2 + v_z^2$ and $\sigma ^2 = k_\mathrm {B} T/m$. The distribution over ${\varvec{v}}$ is spherically symmetric, so the appropriate distribution in magnitudes $v = |{\varvec{v}}|$ is obtained by evaluating $f_{\varvec{V}}({\varvec{v}})$ in a thin spherical shell with volume $4\pi v^2\mathrm {d}v$, thus

$$\begin{aligned} f_V(v) = {\mathrm {d}F_V\over \mathrm {d}v} = \left( {m\over 2\pi k_\mathrm {B} T} \right) ^{3/2} 4\pi v^2 \, \mathrm {exp}\left( - {mv^2\over 2k_\mathrm {B} T} \right) . \end{aligned}$$

(3.15)

An example of such distribution for nitrogen molecules at temperatures 193 and $393\,\mathrm {K}$ is shown in Fig. 3.4 (left).

Fig. 3.4

[Left] Maxwell distribution of velocities of nitrogen molecules at $T=193\,\mathrm {K}$ and $T=393\,\mathrm {K}$. See also Fig. 4.1 (right) and Problem 3.10.4. [Right] Pareto distribution with parameters $b\equiv x_\mathrm {min}$ (minimum value on the abscissa) and a (shape parameter)

5 Pareto Distribution

Probability distributions of many quantities that can be interpreted as random variables have relatively narrow ranges of values. The height of an average adult, for example, is $180\,\mathrm {cm}$, but nobody is 50 or $500\,\mathrm {cm}$ tall. The data acquired by the WHO [8] show that the body mass index (ratio of the mass in kilograms to the square of the height in meters) is restricted to a range between $\approx$15 and $\approx$50.

But one also frequently encounters quantities that span many orders of magnitude, for example, the number of inhabitants of human settlements (ranging from a few tens in a village to tens of millions in modern city conglomerates). Similar “processes” with a large probability for small values and small probability for large values are: frequency of specific given names, size of computer files, number of citations of scientific papers, number of web-page accesses and the quantities of sold merchandise (see Example on p. 97), but also quantities measured in natural phenomena, like step lengths in random walks (anomalous diffusion), magnitudes of earthquakes, diameters of lunar craters or the intensities of solar X-ray bursts [9–11]. A useful approximation for the description of such quantities is the Pareto (power law) distribution with the probability density

$$\begin{aligned} f_X(x) = \displaystyle {ab^a\over x^{a+1}} = {a\over b} \left( {b\over x} \right) ^{a+1} , \qquad 0 < b \le x , \end{aligned}$$

(3.16)

where b is the minimal allowed x (Fig. 3.4 (right)), and a is a parameter which determines the relation between the prominence of the peak near the origin and the strength of the tail at large x. It is this flexibility in parameters that renders the Pareto distribution so useful in modeling the processes and phenomena enumerated above. As an example, Fig. 3.5 (left) shows the distribution of the lunar craters in terms of their diameter, and Fig. 3.5 (right) shows the distribution of solar X-ray bursts in terms of their intensity.

Fig. 3.5

[Left] Distribution of lunar craters with respect to their diameter, as determined by researchers of the Lunar Orbiter Laser Altimeter (LOLA) project [12, 13] up to 2011. [Right] The distribution of hard X-rays in terms of their intensity, measured by the Hard X-Ray Burst Spectrometer (HXRBS) between 1980 and 1989 [14]. The straight lines represent the approximate power-law dependencies, also drawn in the shaded areas, although the Pareto distributions commence only at their right edges ($x \ge x_\mathrm {min}$)

The Pareto distribution is normalized on the interval $[b,\infty )$ and frequently one does not use its distribution function $F_X(x) = P(X \le x)$ but rather its complement,

$$\begin{aligned} 1 - F_X(x) = P(X > x) = \int \limits _x^\infty f_X(t) \, \mathrm {d}t = ab^a \int \limits _x^\infty {\mathrm {d}t\over t^{a+1}} = \left( {b\over x} \right) ^a , \qquad x \ge b , \end{aligned}$$

(3.17)

as it is easier to normalize and compare it to the data: the ordinate simply specifies the number of data points (measurements, events) that were larger than the chosen value on the abscissa. By plotting the data in this way, one avoids histogramming in bins, which is not unique. The values $x_\mathrm {min}=b$ should not be set to the left edge of the interval on which measurements are available (e.g. $20\,\mathrm {m}$ in LOLA measurements), but to the value above which the description in terms of a power-law appears reasonable ($\approx$50 $\mathrm {m}$). The parameter a can be determined by fitting the power function to the data, but in favor of better stability [9] we recommend the formula

$$ a = n \left[ \sum _{i=1}^n \log {x_i\over b} \right] ^{-1} , $$

which we derive later ((8.11)).

Hint If we wish to plot the cumulative distribution for the data $\{ x_i, y_i \}_{i=1}^n$, we can use the popular graphing tool Gnuplot. We first sort the data, so that $x_i$ are arranged in increasing order (two-column file data). The cumulative distribution can then be plotted by the command

5.1 Estimating the Maximum $\varvec{x}$ in the Sample

Having at our disposal a sample of n measurements presumably originating from a power-law distribution with known parameters a and b, a simple consideration allows us to estimate the value of the largest expected observation [9]. Since we are dealing with a continuous distribution, we should refer to the probability that its value falls in the interval $[x,x+\mathrm {d}x]$. The probability that a data point is larger than x, is given by (3.17), while the probability for the opposite event is $1-P(X > x)$. The probability that a particular measurement will be in $[x,x+\mathrm {d}x]$ and that all others will be smaller is therefore $[1 - P(X > x)]^{n-1} f_X(x)\,\mathrm {d}x$. Because the largest measurement can be chosen in n ways, the total probability is

$$ n \left[ 1 - P(X > x) \right] ^{n-1} f_X(x) \, \mathrm {d}x . $$

The expected value of the largest measurement—such quantities will be discussed in the next chapter—is obtained by integrating x, weighted by the total probability, over the whole definition domain:

$$\begin{aligned}\overline{x}_\mathrm {max}= & {} n \int _b^\infty x f_X(x) \left[ 1 - P(X > x)\right] ^{n-1}\,\mathrm {d}x = na \int _b^\infty \left( {b\over x} \right) ^a \left[ 1 - \left( {b\over x} \right) ^a \right] ^{n-1}\,\mathrm {d}x \\= & {} nb \int _0^1 t^{n-1} (1-t)^{-1/a} \, \mathrm {d}t = nb \, B \left( n, {a-1\over a} \right) , \end{aligned}$$

where B(p, q) is the beta function. We have substituted $t = 1-(b/x)^a$ in the intermediate step. For the sample in Fig. 3.5 (left), which contains $n=1513$ data points, $a=2.16$ and $b=0.05\,\mathrm {km}$, we obtain $x_\mathrm {max} \approx 2.5\,\mathrm {km}$. If the sample were ten times as large, we would anticipate $x_\mathrm {max} \approx 7.1\,\mathrm {km}$.

6 Cauchy Distribution

The Cauchy distribution with probability density

$$\begin{aligned} f_X(x) = {1\over \pi }{1\over 1+x^2} , \qquad -\infty< x < \infty , \end{aligned}$$

(3.18)

is already familiar to us from the Example on p. 41. In fact, we should have discussed it along with the exponential, as the Fourier transform of the exponential function in the time scale is the Cauchy function in the energy scale:

$$\begin{aligned} g(t) = \mathrm {e}^{-|t|/\tau } \quad \Longrightarrow \quad {1\over 2\pi } \int _{-\infty }^\infty g(t) \, \mathrm {e}^{-\mathrm {i}\,2\pi \nu t} \,\mathrm {d}t = {1\over \pi } {1/\tau \over (1/\tau )^2 + 4\pi ^2\nu ^2} . \end{aligned}$$

(3.19)

In other words, the energy distribution of the states decaying exponentially in time is given by the Cauchy distribution. It is therefore suitable for the description of spectral line shapes in electromagnetic transitions of atoms and molecules (Fig. 3.6 (left)) or for modeling the energy dependence of cross-sections for the formation of resonances in hadronic physics (Fig. 3.6 (right)). With this in mind, it makes sense to furnish it with the option of being shifted by $x_0$ and with a parameter s specifying its width:

$$\begin{aligned} f_X(x;x_0,s) = {1\over \pi } {s\over s^2 + (x-x_0)^2} . \end{aligned}$$

(3.20)

Fig. 3.6

[Left] A spectral line in the emission spectrum of silicon (centered at $\lambda =254.182\,\mathrm {nm}$) at a temperature of $19{,}000\,\mathrm {K}$ and particle density $5.2\,\times \,10^{22}/\mathrm {m}^3$ [15], along with the Cauchy (Lorentz) approximation. Why the agreement with the measured values is imperfect and how it can be improved will be revealed in Problem 6.9.2. [Right] Energy dependence of the cross-section for scattering of charged pions on protons. In this process a resonance state is formed whose energy distribution in the vicinity of the maximum can also be described by the Cauchy (Breit–Wigner) distribution

In spectroscopy the Cauchy distribution is also known as the Lorentz curve, while in the studies of narrow, isolated resonant states in nuclear and particle physics it is called the Breit–Wigner distribution: in this case it is written as

$$ f(W;W_0,\Gamma ) = {1\over \pi } {\Gamma /2\over (W-W_0)^2 + \Gamma ^2/4} , $$

where $W_0$ is the resonance energy and $\Gamma$ is the resonance width.

7 The $\varvec{\chi ^2}$ distribution

The $\chi ^2$ distribution, a one-parameter probability distribution with the density

$$\begin{aligned} f_{\chi ^2}(x; \nu ) = {1\over 2^{\nu /2}} {1\over \Gamma \bigl (\nu /2\bigr )} x^{\nu /2-1} \mathrm {e}^{-x/2} , \qquad x > 0 , \end{aligned}$$

(3.21)

will play its role in the our discussion on statistics (Chaps. 7–10). The parameter $\nu$ is called the number of degrees of freedom. The probability density of the $\chi ^2$ distribution for four values of $\nu$ is shown in Fig. 3.7. The corresponding distribution function is

$$ F_{\chi ^2}(x; \nu ) = P\left( X \le x \right) = {1\over 2^{\nu /2}} {1\over \Gamma \bigl (\nu /2\bigr )} \int _0^x t^{\nu /2-1} \mathrm {e}^{-t/2} \, \mathrm {d}t . $$

In practical work one usually does not need this definite integral but rather the answer to the opposite question, the cut-off value x at given P. These values are tabulated: see Fig. D.1 (top right) and Table D.3.

Fig. 3.7

The density of the $\chi ^2$ distribution for four different parameters (degrees of freedom) $\nu$. The maximum of the function $f_{\chi ^2}(x; \nu )$ for $\nu > 2$ is located at $x = \nu -2$. For large $\nu$ the $\chi ^2$ density converges to the density of the normal distribution with average $\nu -2$ and variance $2\nu$. The thin curve just next to $f_{\chi ^2}(x; 10)$ denotes the density of the N(8, 10) distribution

8 Student’s Distribution

The Student’s distribution (or the t distribution)² is also a one-parameter probability distribution that we shall encounter in subsequent chapters devoted to statistics. Its density is

$$\begin{aligned} f_T(x; \nu ) = {1\over \sqrt{\nu } \, B\left( {\nu \over 2},{1\over 2}\right) } \, \left( 1 + {x^2\over \nu } \right) ^{-(\nu +1)/2} , \qquad -\infty< x < \infty , \end{aligned}$$

(3.22)

where $\nu$ is the number of degrees of freedom and B is the beta function. The graphs of its density for $\nu =1$, $\nu =4$ and $\nu =20$ are shown in Fig. 3.8. In the limit $\nu \rightarrow \infty$ the Student’s distribution tends to the standardized normal distribution.

Fig. 3.8

The density of the Student’s (t) distribution with $\nu =1$, $\nu =4$ and $\nu =20$ degrees of freedom. The distribution is symmetric about the origin and approaches the standardized normal distribution N(0, 1) with increasing $\nu$ (thin curve), from which it is hardly discernible beyond $\nu \approx 30$

9 $\varvec{F}$ distribution

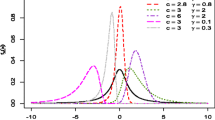
The F distribution is a two-parameter distribution with the probability density

$$\begin{aligned} f_F(x;\nu _1,\nu _2) = \left( {\nu _1\over \nu _2} \right) ^{\nu _1/2} { \Gamma \bigl ((\nu _1+\nu _2)/2\bigr ) \over \Gamma \bigl (\nu _1/2\bigr ) \Gamma \bigl (\nu _2/2\bigr ) } \, x^{{\nu _1/2}-1} \left( 1 + {\nu _1\over \nu _2}\,x \right) ^{-(\nu _1+\nu _2)/2} , \end{aligned}$$

(3.23)

where $\nu _1$ is the number of degrees of freedom “in the numerator” and $\nu _2$ is the number of degrees of freedom “in the denominator”. Why this distinction is necessary will become clear in Sect. 7.2.3: there we shall compare ratios of particular random variables, distributed according to (3.23). The probability densities of the F distribution are shown in Fig. 3.9 for several typical $(\nu _1,\nu _2)$ pairs.

Fig. 3.9

[Left] The probability density of the F distribution for $\nu _1=10$ degrees of freedom (numerator) and three different degrees of freedom $\nu _2$ (denominator). [Right] The density of the F distribution for $\nu _2=10$ and three different values of $\nu _1$

10 Problems

10.1 In-Flight Decay of Neutral Pions

A complicated transformation of a uniform distribution may still turn out to be a uniform distribution, as we learn by solving the classical problem in relativistic kinematics, the in-flight neutral pion decay to two photons, $\pi ^0\rightarrow \gamma +\gamma$. Calculate the energy distribution of the decay photons, $\mathrm {d}N/\mathrm {d}E_\gamma$!

Let the $\pi ^0$ meson fly in the laboratory frame along the z-axis with velocity $v_\pi$. The decay in the $\pi ^0$ rest frame is isotropic. Due to azimuthal symmetry ($\phi$) this implies a uniform distribution over the cosine of the angle $\theta ^*$ (see Sect. C.2.2):

$$ f(\cos \theta ^*) = {\mathrm {d}N\over \mathrm {d}(\cos \theta ^*)} = {1\over 2} , \qquad -1 \le \cos \theta ^*\le 1 , $$

where $\theta ^*$ is the emission angle of the first photon in the rest frame, as shown in the figure:

The energy distribution of the photons is obtained by the derivative chain-rule:

$$\begin{aligned} {\mathrm {d}N\over \mathrm {d}E_\gamma } = {\mathrm {d}N\over \mathrm {d}(\cos \theta ^*)} {\mathrm {d}(\cos \theta ^*)\over \mathrm {d}E_\gamma } = {1\over 2} {\mathrm {d}(\cos \theta ^*)\over \mathrm {d}E_\gamma } . \end{aligned}$$

(3.24)

We therefore need to establish a relation between $\theta ^*$ and $E_\gamma$, and it is offered by the Lorentz transformation from the $\pi ^0$ rest frame to the laboratory frame. Of course, the energies of the photons in the rest frame are equal, $E_{\gamma ,1}^*= E_{\gamma ,2}^*= E_\gamma ^*= p_\gamma ^*c = m_\pi c^2/2$, and their four-vectors are

$$ \bigl ( E_{\gamma ,i}^*, p_{\gamma x,i}^*c, \, p_{\gamma y,i}^*c, \, p_{\gamma z,i}^*c \bigr ) = \textstyle {1\over 2} m_\pi c^2 \bigl ( 1, \pm \sin \theta ^*, 0, \pm \cos \theta ^*\bigr ) , \qquad i=1,2 . $$

The Lorentz transformation that gives us their energies in the laboratory frame is

$$ E_{\gamma ,i} = \gamma E_{\gamma ,i}^*+ \gamma \beta p_{\gamma z,i}^*c = \textstyle {1\over 2} m_\pi c^2 \gamma \bigl ( 1 \pm \beta \cos \theta ^*\bigr ) , $$

where $\beta = {v_\pi /c} = {p_\pi c/E_\pi }$ and $\gamma = {1/\sqrt{1-\beta ^2}} = {E_\pi /(m_\pi c^2)}$. It follows that

$$ {\mathrm {d}E_{\gamma ,i}\over \mathrm {d}(\cos \theta ^*)} = \textstyle {1\over 2} m_\pi c^2 \gamma \beta = \textstyle {1\over 2} p_\pi c $$

i.e.

$$ {\mathrm {d}(\cos \theta ^*)\over \mathrm {d}E_\gamma } = {2\over p_\pi c} . $$

When this is inserted in (3.24), we obtain the required energy distribution, which is indeed uniform:

$$ {\mathrm {d}N\over \mathrm {d}E_\gamma } = {1\over p_\pi c} , $$

namely on the interval between the minimal and maximal values

$$ E_{\gamma }^\mathrm {min} = \textstyle {1\over 2}(E_\pi - p_\pi c) = \textstyle {1\over 2} E_\pi (1-\beta ) , \qquad E_{\gamma }^\mathrm {max} = \textstyle {1\over 2}(E_\pi + p_\pi c) = \textstyle {1\over 2} E_\pi (1+\beta ) . $$

Let us check our findings by a simple simulation, observing the decay of pions with a velocity of 0.7c ($\beta = 0.7$). We use a computer to generate 100000 uniformly distributed values $-1\le \cos \theta ^*\le 1$ (Fig. 3.10 (left)), and then use each of these values to calculate the photon energies in the laboratory frame, $E_{\gamma ,1}$ and $E_{\gamma ,2}$. A uniform distribution over $E_\gamma$ on the interval between $E_\gamma ^\mathrm {min}$ and $E_{\gamma }^\mathrm {max}$ should appear. It can be seen in Fig. 3.10 (right) that we were not mistaken.

Fig. 3.10

The $\pi ^0\rightarrow \gamma +\gamma$ decay. [Left] Uniform distribution of events over $\cos \theta ^*$ in the $\pi ^0$ rest frame. [Right] Uniform energy distribution of the decay pions in the laboratory frame

10.2 Product of Uniformly Distributed Variables

(Adapted from [17].) Let two continuous random variables X and Y be described by a known probability density $f_{X,Y}(x,y)$. Calculate the probability density $f_Z(z)$ of the product random variable $Z=XY$ in the most general case and in the case that X and Y are independent. Discuss the special case of independent variables X and Y, both of which are uniformly distributed on the interval (0, 1).

Define the domain $\mathcal{D} = \{ (x,y): xy < z\}$ (shown for positive z as the shaded region in the figure) which determines the distribution function of the variable Z:

$$ P\bigl ( (X,Y) \in \mathcal{D} \bigr ) = F_Z(z) = \int _0^{\infty } \mathrm {d}y \int _{-\infty }^{z/y} f_{X,Y}(x,y) \, \mathrm {d}x +\int _{-\infty }^0 \mathrm {d}y \int _{z/y}^\infty f_{X,Y}(x,y) \, \mathrm {d}x . $$

To facilitate the determination of integration boundaries, the intervals of four integrations in this equation—read from left to right—are denoted by numbers 1 to 4 in the figure. (The derivation for negative z proceeds analogously.) The corresponding probability density is then obtained by differentiation:

$$ f_Z(z) = {\mathrm {d}F_Z(z)\over \mathrm {d}z} = \int _0^\infty {1\over y}\,f_{X,Y}\left( {z\over y}, y \right) \,\mathrm {d}y - \int _{-\infty }^0 {1\over y}\,f_{X,Y}\left( {z\over y}, y \right) \,\mathrm {d}y . $$

If X and Y are independent, possessing probability densities $f_X(x)$ and $f_Y(y)$, one has $f_{X,Y}(x,y) = f_X(x)f_Y(y)$, thus

$$\begin{aligned} f_Z(z) = \int _0^\infty {1\over y}\,f_X\left( {z\over y} \right) f_Y(y) \,\mathrm {d}y - \int _{-\infty }^0 {1\over y}\,f_X\left( {z\over y} \right) f_Y(y) \,\mathrm {d}y . \end{aligned}$$

(3.25)

The product of uniformly distributed variables X and Y is always positive and less than 1, hence the probability density $f_Z(z)$ of the variable $Z=XY$ may be non-zero only on the interval (0, 1). On this interval it can be determined by using (3.25), in which only the first term survives due to this very requirement, and even here the integrand is positive only if $0< z/y < 1$ and $0< y < 1$, i.e. when $z< y < 1$. It follows that

$$ f_Z(z) = \int _z^1 {\mathrm {d}y \over y} = - \log z , \qquad 0< z < 1 , $$

while $f_Z(z)=0$ elsewhere.

10.3 Joint Distribution of Exponential Variables

Let X and Y be independent random variables distributed exponentially with parameters $\lambda _1=1$ and $\lambda _2=3$,

$$ f_X(x) = \lambda _1 \, \mathrm {e}^{-\lambda _1 x} , \qquad f_Y(y) = \lambda _2 \, \mathrm {e}^{-\lambda _2 y} , \qquad x, y \ge 0 . $$

Imagine a square region $S = [0,a]\,\times \,[0,a]$. Calculate the value of a, for which the probability that a randomly drawn (x, y) pair falls into S, equals 1 / 2. Calculate the conditional joint probability density of the variables X and Y, given that $X \ge a$ and $Y \ge a$.

The variables X and Y are independent, hence their joint probability density is

$$ f_{X,Y}(x,y) = f_X(x) f_Y(y) = \lambda _1 \lambda _2 \, \mathrm {e}^{-\lambda _1 x} \mathrm {e}^{-\lambda _2 y} , \qquad x, y \ge 0 . $$

The probability that a random pair of values (x, y) finds itself in S, equals

$$ P_{aa} \equiv P\bigl ( 0 \le X \le a, 0 \le Y \le a \bigr ) = \int _0^a \int _0^a f_{X,Y}(x,y) \, \mathrm {d}x \, \mathrm {d}y = \left( 1 - \mathrm {e}^{-\lambda _1 a} \right) \left( 1 - \mathrm {e}^{-\lambda _2 a} \right) . $$

We are looking for a such that $P_{aa} = 1/2$. This equation is best solved by Newton’s method, in spite of its known pitfalls: with the function $f(x) = (1 - \mathrm {e}^{-\lambda _1 x})(1\,-\,\mathrm {e}^{-\lambda _2 x})-1/2$ (plot it!) and its derivative $f'(x) = \lambda _1 \mathrm {e}^{-\lambda _1 x} + \lambda _2 \mathrm {e}^{-\lambda _2 x} - (\lambda _1 + \lambda _2) \mathrm {e}^{-(\lambda _1+\lambda _2) x}$ we start the iteration $x_{n+1} = x_n - f(x_n)/f'(x_n)$, $n=0,1,2,\ldots$  With the initial approximation $x_0=0.5$ just a few iteration steps lead to $a = x_\infty \approx 0.7987$.

We first form the conditional distribution function

$$\begin{aligned}F_{X,Y} \bigl ( x,y | X\ge a, Y\ge a \bigr )= & {} P \bigl ( X\le x, Y\le y | X\ge a, Y\ge a \bigr ) \\= & {} { P\bigl ( a\le X\le x \cap a\le Y\le y \bigr ) \over P\bigl ( X\ge a \cap Y\ge a \bigr ) } = { P( a\le X\le x ) P( a\le Y\le y ) \over P( X\ge a ) P( Y\ge a ) } \\= & {} { \int _a^y \mathrm {d}v \int _a^x f_{X,Y}(u,v) \, \mathrm {d}u \over \int _a^\infty \mathrm {d}v \int _a^\infty f_{X,Y}(u,v) \, \mathrm {d}u } = { \bigl ( \mathrm {e}^{-\lambda _1 a} - \mathrm {e}^{-\lambda _1 x} \bigr ) \bigl ( \mathrm {e}^{-\lambda _2 a} - \mathrm {e}^{-\lambda _2 y} \bigr ) \over \mathrm {e}^{-\lambda _1 a} \mathrm {e}^{-\lambda _2 a} } , \end{aligned}$$

where we have taken into account that X and Y are independent. The probability density can then be calculated by differentiating $F_{X,Y}$ with respect to x and y:

$$ f_{X,Y}\bigl ( x,y | X\ge a, Y\ge a \bigr ) = {\partial ^2\over \partial x\partial y} F_{X,Y} \bigl ( x,y | X\ge a, Y\ge a \bigr ) = \lambda _1 \lambda _2 \mathrm {e}^{-\lambda _1 (x-a)} \mathrm {e}^{-\lambda _2 (y-a)} . $$

We should also check the normalization which must be fulfilled—as for any probability density—also for the calculated conditional density. Indeed we find

$$ \int _a^\infty \int _a^\infty f_{X,Y}\bigl ( x,y | X \ge a, Y \ge a \bigr ) \, \mathrm {d}x \, \mathrm {d}y = 1 , $$

where $[a,\infty ]^2$ is the definition domain of the conditional joint probability density.

10.4 Integral of Maxwell Distribution over Finite Range

What fraction of nitrogen ($\mathrm {N}_2$) molecules at temperature $T=393\,\mathrm {K}$ have velocities between $v_1 = 500$ and $v_2 = 1000\,\mathrm {m/s}$, if the velocity distribution is of the Maxwell type (see Fig. 3.4 (left))?

Let us rewrite (3.15) in a slightly more compact form

$$ f_V(v) = \sqrt{16 \alpha ^3 \over \pi } \, v^2 \,\mathrm {e}^{-\alpha v^2} , \qquad \alpha = \sqrt{m\over 2k_\mathrm {B}T}\,\,{.} $$

The required fraction of molecules is equal to the definite integral of the probability density from $v_1$ to $v_2$,

$$ P(v_1 \le V \le v_2) = \int _{v_1}^{v_2} f_V(v) \, \mathrm {d}v = \sqrt{16 \alpha ^3 \over \pi } \int _{v_1}^{v_2} v^2 \, \mathrm {e}^{-\alpha v^2} \, \mathrm {d}v . $$

Such integrals are typically handled by resorting to integration by parts, in which the power of the variable x in the integrand is gradually reduced:

$$\begin{aligned}\int x^n \, \mathrm {e}^{-\alpha x^2} \mathrm {d}x= & {} -{1\over 2\alpha } \int x^{n-1} (-2\alpha x) \, \mathrm {e}^{-\alpha x^2} \, \mathrm {d}x \\= & {} -{1\over 2\alpha } \left[ x^{n-1} \, \mathrm {e}^{-\alpha x^2} - \int (n-1) x^{n-2} \, \mathrm {e}^{-\alpha x^2} \, \mathrm {d}x \right] . \end{aligned}$$

In our case we only need the integral with $n=2$, therefore

$$ I(v) = \int \limits _0^v x^2 \, \mathrm {e}^{-\alpha x^2} \, \mathrm {d}x = {1\over 2\alpha } \int \limits _0^v \mathrm {e}^{-\alpha x^2} \, \mathrm {d}x -{1\over 2\alpha } \, v \, \mathrm {e}^{-\alpha v^2} = {\sqrt{\pi }\over 4\alpha ^{3/2}} \, \mathrm {erf}\left( \sqrt{\alpha }\,v \right) -{v\over 2\alpha } \, \mathrm {e}^{-\alpha v^2} . $$

From Table D.2 we read off $\mathrm {erf}(\sqrt{\alpha }v_1) \approx 0.4288$ and $\mathrm {erf}(\sqrt{\alpha }v_2) \approx 0.4983$, and all that is needed is to merge the expressions to

$$ P(v_1 \le V \le v_2) = \sqrt{16\alpha ^3\over \pi }\bigl [ I(v_2) - I(v_1) \bigr ] \approx 0.5065 . $$

(The result by computing the $\mathrm {erf}$ functions accurately is 0.5066.)

10.5 Decay of Unstable States and the Hyper-exponential Distribution

Organic scintillator is a material in which charged particles promote electrons to excited states, which get rid of the excess energy by photon emission. The time dependence of the intensity of emitted light can be approximated by a sum of two independent excitation mechanisms (occurring almost instantaneously) and de-excitations proceeding with two different decay times, as shown in Fig. 3.11. Write down the corresponding probability density and the functional form of the decay curve. Generalize the expressions to multiple time components. Does the same physical picture apply to a mixture of radioactive isotopes, if each of them has only a single decay mode?

Fig. 3.11

Typical time dependence of a light pulse emanating from an organic scintillator: in this case, the total intensity consists of a fast relaxation component with decay time $\tau _1 = 30\,\mathrm {ns}$ (frequency $70\%$) and a slow one with decay time $\tau _2 = 150\,\mathrm {ns}$ ($30\%$)

The mechanisms of light generation in scintillators are poorly understood, but the predominant opinion seems to be that the type of relaxation (fast or slow) is determined already during excitation. We are thus dealing with exclusive (incompatible) events, hence the probability density is

$$ f_T(t) = P \lambda _1 \, \mathrm {e}^{-\lambda _1 t} + (1-P) \lambda _2 \, \mathrm {e}^{-\lambda _2 t} . $$

The time dependence of the light curve is then given by the distribution function:

$$ N(t)/N_0 = 1 - F_T(t) = 1 - \int _0^t f_T(t')\,\mathrm {d}t' = P \, \mathrm {e}^{-\lambda _1 t} + (1-P) \, \mathrm {e}^{-\lambda _2 t} . $$

Obviously one can generalize this to multiple (k) time components by writing

$$\begin{aligned} f_T(t) = \sum _{i=1}^k P_i \lambda _i \, \mathrm {e}^{-\lambda _i t} , \qquad \sum _{i=1}^k P_i = 1 . \end{aligned}$$

(3.26)

The distribution with such probability density is known as the k-phase hyper-exponential distribution. It can be used to model the superposition of k independent events, e.g. the response time of a system of k parallel computer servers, in which the ith server is assigned with probability $P_i$ to handle our request, and the distribution of its service time is exponential with parameter $\lambda _i$ (Fig. 3.12 (left)). Such a distribution also describes the lifetime of a product manufactured on several parallel assembly lines or in factories with different levels of manufacturing quality.

Fig. 3.12

[Left] A set of k parallel independent processes (“phases”) with a single output, described by the hyper-exponential distribution. [Right] An illustration of the decay modes of a sample of unstable particles

At first sight, radioactive decay in a sample containing various isotopes (for example, a mixture of $^{137}\mathrm {Cs}$, $^{235}\mathrm {U}$ and $^{241}\mathrm {Am}$) resembles such a k-phase process. But the key difference is that the decays of individual isotopes are not mutually exclusive: in a chosen time interval ${\Delta t}$ we might detect the decay of a single isotope, two, or all three. In this case the hyper-exponential distribution is not justified.

Similar conclusions can be drawn for the decay of unstable particles with multiple decay modes, each occurring with a distinct probability. Suppose that particle $\mathrm {X}$ decays into the final state $\mathrm {A}$ consisting of two or more lighter particles. The usual decay law (3.5) applies:

$$ \dot{N}_{\mathrm {X}\rightarrow \mathrm {A}}(t) = -\lambda _\mathrm {A} N(t) . $$

If multiple final states $\mathrm {A}, \mathrm {B}, \mathrm {C}, \ldots \,$ are allowed, we must sum over all contributions: the time derivative of the number of particles still available for decay at time t is

$$ \dot{N}(t) = \dot{N}_{\mathrm {X}\rightarrow \mathrm {anything}}(t) = \dot{N}_{\mathrm {X}\rightarrow \mathrm {A}}(t) +\dot{N}_{\mathrm {X}\rightarrow \mathrm {B}}(t) + \cdots = -\bigl ( \lambda _\mathrm {A} + \lambda _\mathrm {B} + \cdots \bigr ) N(t) \equiv -\lambda N(t) . $$

The extinction of N is therefore driven by a single time constant, $\lambda = \lambda _\mathrm {A} + \lambda _\mathrm {B} + \cdots$ ! Just prior to the decay, Nature does not think about the type of the final state, but rather just chooses the time of the decay by exponential law with parameter $\lambda$,

$$ N(t) = N_0 \, \mathrm {e}^{-\lambda t} = N_0 \, \mathrm {e}^{-t/\tau } , $$

where $\tau$ is the average decay time. Instead of $\tau$ we sometimes prefer to specify the conjugated variable in the Heisenberg sense (time and energy, position and linear momentum, angle and angular momentum), known as the total decay width:

$$ \Gamma = {\hbar \over \tau } = \hbar \lambda = \hbar \bigl ( \lambda _\mathrm {A} + \lambda _\mathrm {B} + \cdots \bigr ) = \Gamma _\mathrm {A} + \Gamma _\mathrm {B} + \cdots . $$

The total width $\Gamma$ is a sum of the partial widths $\Gamma _\mathrm {A}$, $\Gamma _\mathrm {B}$, $\ldots$  It is only at the very moment of decay that the particle randomly “picks” a certain final state. The probabilities for the transitions to specific final states can be expressed by branching ratios or branching fractions: for individual decay modes we have

$$\begin{aligned} \mathrm {Br}_\mathrm {A} = { \displaystyle {\dot{N}_{\mathrm {X}\rightarrow \mathrm {A}}} \over \displaystyle {\dot{N}_{\mathrm {X}\rightarrow \mathrm {anything}}} } = { \Gamma _\mathrm {A} \over \Gamma } , \qquad \mathrm {Br}_\mathrm {B} = { \Gamma _\mathrm {B} \over \Gamma } , \qquad \mathrm {Br}_\mathrm {C} = { \Gamma _\mathrm {C} \over \Gamma } , \qquad \ldots \end{aligned}$$

(3.27)

Conservation of probability (a particle must decay into some final state after all) of course ensures

$$ \mathrm {Br}_\mathrm {A} + \mathrm {Br}_\mathrm {B} + \mathrm {Br}_\mathrm {C} + \cdots = 1 . $$

As an example, Table 3.1 shows the partial widths and branching fractions in the decay of the $\mathrm {Z}^0$ bosons produced in collisions of electrons and positrons at invariant energies around $91\,\mathrm {GeV}$; see Fig. 3.12 (right). From the total decay width we compute the average decay time $\tau = \hbar /\Gamma \approx 2.6\,\times \,10^{-25}\mathrm {s}$. The energy dependence of the $\mathrm {Z}^0$ resonance is described by the Breit-Wigner distribution (Fig. 3.6 (right)) with the center at approximately $91.2\,\mathrm {GeV}$ and a width of about $2.5\,\mathrm {GeV}$.

Table 3.1 The dominant decay modes of the $\mathrm {Z}^0$ boson, the corresponding partial decay widths and the branching fractions

10.6 Nuclear Decay Chains and the Hypo-exponential Distribution

In nuclear decay chains an unstable nucleus decays with characteristic time $\tau _1$ to a lighter nucleus, which in turn decays with characteristic time $\tau _2$ to an even lighter nucleus, and so on. Such decay chains with consecutive emissions (mostly $\alpha$ particles or electrons) are typical of heavy nuclei. Figure 3.13 (left) shows a segment of the uranium decay chain where each subsequent isotope has a single decay mode, but with a different characteristic time. Find the probability distribution to describe such processes!

Fig. 3.13

[Left] A segment of the uranium decay chain where only one type of decay is allowed at each stage. [Center] Depiction of k serial processes with a single output, described by the hypo-exponential distribution. [Right] Illustration of a nuclear decay chain; compare it to Fig. 3.12 (right)

Suppose that the decay chain is initiated by type 1 isotopes with no daughter nuclei present at time zero, and that no other isotope decays into this type. The time evolution of the decay chain is then governed by the set of differential equations

$$\begin{aligned}\dot{N}_1= & {} - \lambda _1 N_1 , \\ \dot{N}_2= & {} - \lambda _2 N_2 + \lambda _1 N_1 , \\ \dot{N}_3= & {} - \lambda _3 N_3 + \lambda _2 N_2 , \\ \cdots= & {} {-}\cdots , \end{aligned}$$

with initial conditions

$$ N_1(0) = N_0 , \qquad N_2(0) = N_3(0) = \cdots = 0 . $$

We already know the solution of the first line:

$$ N_1(t) = N_0 \, \mathrm {e}^{-\lambda _1 t} . $$

The next component of the chain is obtained by first multiplying the second line of the system by $\mathrm {e}^{\lambda _2 t}$ and exploiting the previously calculated solution for $N_1(t)$,

$$ \mathrm {e}^{\lambda _2 t} \dot{N}_2(t) = - \lambda _2 \, \mathrm {e}^{\lambda _2 t} N_2 + \lambda _1 N_0 \, \mathrm {e}^{(\lambda _2-\lambda _1) t} . $$

We move the first term on the right to the left,

$$ \mathrm {e}^{\lambda _2 t} \dot{N}_2(t) + \lambda _2 \, \mathrm {e}^{\lambda _2 t} N_2 = \left( \mathrm {e}^{\lambda _2 t} {N}_2(t) \right) ^\cdot = \lambda _1 N_0 \, \mathrm {e}^{(\lambda _2-\lambda _1) t} , $$

and integrate to get

$$ \mathrm {e}^{\lambda _2 t} {N}_2(t) = {\lambda _1\over \lambda _2-\lambda _1} N_0 \, \mathrm {e}^{(\lambda _2-\lambda _1) t} + C . $$

The constant C is dictated by the condition $N_2(0)=0$, whence $C=-\lambda _1 N_0 / (\lambda _2-\lambda _1)$ and

$$ N_2(t) = {\lambda _1\over \lambda _1-\lambda _2} N_0 \left[ \mathrm {e}^{-\lambda _2 t} - \mathrm {e}^{-\lambda _1 t} \right] . $$

The same trick can be used to obtain the remaining elements of the chain: in the ith line of the system we always multiply $\dot{N}_i$ by $\mathrm {e}^{\lambda _i t}$, carry over $-\lambda _i \, \mathrm {e}^{\lambda _i t}N_i$ to the left where it can be joined with its neighbor into a derivative of a product, grab the result from the previous step, and integrate. For the third element of the chain, for example, we obtain

$$ N_3(t) = \lambda _1 \lambda _2 N_0 \left[ {\mathrm {e}^{-\lambda _1 t} \over (\lambda _2-\lambda _1)(\lambda _3-\lambda _1)} +{\mathrm {e}^{-\lambda _2 t} \over (\lambda _1-\lambda _2)(\lambda _3-\lambda _2)} +{\mathrm {e}^{-\lambda _3 t} \over (\lambda _1-\lambda _3)(\lambda _2-\lambda _3)} \right] . $$

It is obvious that this can be generalized to

$$\begin{aligned} N_k(t) = \sum _{i=1}^k \left( \prod _{{j=1\atop j\ne i}}^k {\lambda _j \over \lambda _j-\lambda _i} \right) \lambda _i \, \mathrm {e}^{-\lambda _i t} , \end{aligned}$$

(3.28)

except that we must replace $\lambda _k \rightarrow N_0$ in the numerator of all fractions. Such a distribution, which in general describes a sum of independent , exponentially distributed variables, each with its own parameter $\lambda _i$, is called hypo-exponential.