Towards the General Theory of Global Planar Bifurcations

Abstract

This is an outline of a theory to be created, as it was seen in April 2015. An addendnum to the proofs at the end of the chapter describes the recent developments.

To Christiane Rousseau, a wonderful mathematician and organizer of scientific life, and a dear friend.

Theory of planar bifurcations has a long and glorious history. It may be split into two parts: local and nonlocal bifurcations. Local bifurcations appeared first in the works of Poincaré. The most famous of them is the Poincaré–Andronov–Hopf bifurcation. The second part deals with the bifurcations of separatrix polygons, the polycycles. The simplest ones are separatrix loops of hyperbolic saddles and homoclinic curves of saddle-nodes. This part may be also called “semilocal bifurcations” because the perestroikas occur in arbitrary narrow neighborhoods of the polycyles. After the first founding works of Andronov and his school, this part started to develop intensively since 1980s. We plan to show that there is a third part, not yet developed, that may be called “global bifurcations.” The main new effect in this theory may be called “sparking saddle connections.” They were discovered by Malta–Palis in the early 1980s and described below.

This survey is aimed to outline the first steps in the development of this theory. All the new theorems below are “theorems”: the proofs are not yet written.

13.1 Global Bifurcations in Generic One-Parameter Families

13.1.1 Basic Definitions

In 1985 Arnold suggested a program of development of the global bifurcation theory in the plane. Begin with some classical notions necessary to understand his text quoted below.

Definition 1.

Let M be a manifold, not necessary closed, and B be a parameter space, a ball in $\mathbb{R}^{k}$. Two families of vector fields $\{v_{\varepsilon }\},\{w_{\varepsilon }\}$ on M with the parameter space $B \ni \varepsilon$ are topologically equivalent provided that there exists a skew product homeomorphism

$$\displaystyle\begin{array}{rcl} & H: B \times M \rightarrow B \times M,& {}\\ & (\varepsilon,x)\mapsto (h(\varepsilon ),H(\varepsilon,x)), & {}\\ \end{array}$$

where h is a homeomorphism B → B, such that for any $\varepsilon \in B$ the homeomorphism $H(\varepsilon,\cdot )$ is an orbital topological equivalence between the vector fields $v_{\varepsilon }$ and $w_{h(\varepsilon )}$.

Definition 2.

Two families above are weakly equivalent if in the previous definition H is no more a homeomorphism. Namely, H is no more continuous in $\varepsilon$, remaining a homeomorphism of M to M for any fixed $\varepsilon$.

Definition 3.

A local family of vector fields on M is a germ on M ×{ 0} of families $\{v_{\varepsilon }(x)\},\ x \in M,\ \varepsilon \in (B,0)$. That is, the base B is replaced by a germ of a base (B, 0). Local topological equivalence and weak equivalence of local families is a correspondent equivalence of some representatives of these families provided that the corresponding homeomorphism of the bases brings the critical parameter value zero of one base to that of another.

Definition 4.

A local family of vector fields on M is globally (weakly) structurally stable provided that it is (weakly) topologically equivalent to all the nearby families. The term globally may be omitted. It recalls that the family is considered in the whole phase space.

13.1.2 Arnold’s Program

The text in this subsection, except for the last sentence is a quotation from the survey [1].

Although even local bifurcations is high codimensions (at least three) on a disc are not fully investigated, it is natural to discuss nonlocal bifurcations in multiparameter families of vector fields on a two-dimensional sphere. For their description, it is necessary to single out the set of trajectories defining perestroikas in these families.

Definitions and Examples (V.I. Arnol’d 1985)

Definition 5.

A finite subset of the phase space is said to support a bifurcation if there exists an arbitrarily small neighborhood of this subset and a neighborhood of the bifurcation values of the parameter (depending on it) such that, outside this neighborhood of the subset, the deformation (at values of the parameter from the second neighborhood ) is topologically trivial.

Example 1.

Any point of a saddle connection (including both saddles) supports a bifurcation, even if one adds to it any other points. In a system with two saddle connections an interior point on one connection supports a bifurcation only with a point on the other connection.

Definition 6.

The bifurcation support of a bifurcation is the union of all minimal sets supporting a bifurcation (“minimal” means not containing a proper subset that supports a bifurcation).

Example 2.

In a system with one saddle connection (bifurcating in a standard way), the support coincides with the saddle connection, including its endpoints, the saddles.

Definition 7.

Two deformations of vector fields with bifurcation supports $\Sigma _{1}$ and $\Sigma _{2}$ are said to be equivalent on their supports if there exist arbitrarily small neighborhoods of the supports, and neighborhoods of the bifurcation values of the parameters depending on them, such that the restrictions of the families to these neighborhoods of the supports are topologically equivalent, or weakly equivalent, over these neighborhoods of bifurcation values.

Example 3.

All deformations of vector fields with a simple saddle connection are equivalent to each other, independent of the number of hyperbolic equilibria or cycles in the system as a whole.

Example 4.

Four-parameter deformations of a vector field close to a cycle of multiplicity four are weakly topologically equivalent, but, generally, not equivalent: the classification of such deformations with respect to topologically equivalence involves functional invariants.

Conjecture (V.I. Arnol’d 1985).

For a generic l-parameter family of vector fields on S ²:

• 1) On their supports, all deformations are equivalent to a finite number of deformations (the number depends only upon l).

• 2) Any bifurcation diagram is (locally) homeomorphic to one of a finite number (depending only upon l) of generic examples.

• 3) There exist versal and weakly structurally stable deformations.

• 4) The family is globally weakly structurally stable.

• 5) The bifurcation supports consist of a finite number (depending only upon l) of (singular) trajectories.

• 6) The number of points in a minimal supporting set is bounded by a constant depending only on l.

Certainly proofs or counterexamples to the above conjectures are necessary for investigating nonlocal bifurcations in generic l-parameter families.

The bifurcation supports defined in this subsection will be sometimes called small supports, because large supports will be defined below.

13.1.3 Sparking Saddle Connections

The key feature of the global planar bifurcations are the connections named in the title.

The simplest example of sparking saddle connections occurs for one semistable cycle, with two hyperbolic saddles: one inside and one outside the cycle. The following theorem appears first in [16]; we quote it from [7].

Theorem 1.

Suppose that a vector field X in the plane contained in a generic one-parameter family $X_{\varepsilon }(X_{0} = X)$ has a semistable limit cycle L. Let this field has two hyperbolic saddles: one inside and the other outside the cycle. Suppose that the separatrix of one saddle winds to the cycle as $t \rightarrow +\infty$ and the separatrix of the other one does not the same as $t \rightarrow -\infty$. Then on one side of $\varepsilon = 0$ , there exist two limit cycles that tend to L as $\varepsilon \rightarrow 0$ : one is stable and the other is unstable. For $\varepsilon$ on the other side of $\varepsilon = 0$ , there exist no limit cycles near L. Moreover, there exists a sequence of parameter values of the form

$$\displaystyle{\varepsilon _{n} = \frac{1} {n^{2}}(c + o(1)),\ c\neq 0,}$$

such that the field $X_{\varepsilon _{n}}$ has a saddle connection for any n large enough.

The bifurcation diagram is not an isolated point (as it happens in all the classical examples of generic one-parameter families), but rather a sequence of points converging to the critical parameter values. Subsequent points in this sequence are marked by subsequent natural numbers: $\varepsilon _{m},\varepsilon _{m+1},\ldots$. The vector field corresponding to $\varepsilon _{n}$ has a saddle connection that makes n circuits around the interior saddle, before closure.

13.1.4 Another Kind of Sparking Saddle Connections

Breaking of a homoclinic loop of a saddle may also generate sparking saddle connections.

Theorem 2.

Suppose that a planar vector field X met in a generic one-parameter family has a separatrix loop, and the saddle value (trace of the linearization) is negative. Suppose that this vector field has a unique saddle inside the separatrix loop, with one or two incoming separatrixes winding towards the separatrix loop of the first saddle in the negative time, and exactly two other singular points, a sink and a source, inside the loop, see Fig. 13.1. Then on one side of the critical parameter value the field has a stable hyperbolic cycle with one saddle inside and one outside. On the other side of the critical value there is a countable number of bifurcation points related to saddle connections between the two saddles mentioned above. The number of circuits of these connections around the interior saddle tends to infinity as the parameter tends to the critical value.

Fig. 13.1

Two phase portraits of a separatrix loop with a saddle inside corresponding to the critical parameter values; the sinks inside the loops are not shown

Fig. 13.2

Different locations of Cherry cells

13.1.5 The Definitions Revisited

Let us describe the bifurcation support of the Malta–Palis bifurcation. A minimal set supporting the bifurcation consists of one point on the semistable cycle. Indeed, for any neighborhood of this point there exists a neighborhood of the critical parameter value such that for any non-zero bifurcation parameter value from the second neighborhood the corresponding sparkling saddle connections cross the first neighborhood. The representative of the local Malta–Palis family having the second neighborhood as the base, with the first neighborhood deleted from the phase space, is topologically trivial.

The union of all the minimal sets supporting the bifurcation, that is, the bifurcation support, is the semistable cycle only. In its small neighborhood sparkling saddle connections are not visible at all. So the bifurcations in this neighborhood do not describe the bifurcations in the Malta–Palis family.

Consider another example, namely, a vector field with a homoclinic trajectory of a saddle-node of multiplicity two in assumption that this field occurs in a typical one-parameter family. The minimal set supporting the bifurcation is unique in this case. It is the saddle-node singular point itself. Indeed, the vector field in any domain that contains this point is structurally unstable. On the other hand, the same vector field in the domain with a neighborhood of the saddle-node deleted is structurally stable because it is met in a typical one-parameter family and thus has no more degeneracies. Hence, the bifurcation support consists of one point, the saddle-node itself. Yet, the bifurcation, the generation of a limit cycle, happens in a neighborhood of the whole homoclinic curve. The bifurcation support is not relevant to this bifurcation.

This is a reason to introduce new definitions.

Below we give a definition of a large bifurcation support. It is motivated by the following natural question: what does it mean that two bifurcations in two local families of vector fields on the 2-sphere are essentially the same? The answer: the local families are weakly equivalent makes no sense. We may extend two phase portraits with the same bifurcation by different structurally stable elements, and the local families would become nonequivalent.

The definition of the large bifurcation support below is aimed to answer the question above. It is adjusted, in particular, to the bifurcations of sparking saddle connections and homoclinic curves of saddle-nodes. We deal first with nonlocal families, then with local ones.

Definition 8.

Consider a family of vector fields on a sphere S ² with a parameter base B. Let $D \subset B$ be the bifurcation diagram of the family. A closed set $C \subset D \times S^{2}$ is called a bifurcation carrier if for any neighborhood U of C and for any point b ∈ D the corresponding local family on $(B,b) \times S^{2}\setminus U$ is topologically trivial; moreover, the carrier is the minimal closed set with this property.

Example 5.

A bifurcation carrier in the Malta–Palis bifurcation is a countable set having exactly one point on each of the sparkling separatrixes, and one point of the semistable cycle.

Definition 9.

A large bifurcation support of type one for a nonlocal family is a minimal closed set that contains all the carriers of the bifurcations in the family.

Example 6.

The large bifurcation support of type one in the Malta–Palis family consists of all the sparkling saddle connections with the saddles included, plus the semistable cycle, all located in D × S ² over the corresponding bifurcation values. This support consists of an infinite number of the phase curves in the family.

We do not define the large bifurcation support of type two for nonlocal families, and pass to local families instead.

Definition 10.

A large bifurcation support of type one for a local family with zero critical value of the parameter is a minimal closed set $\Sigma \subset \{ 0\} \times S^{2}$ with the following properties. For any neighborhood U of $\Sigma$ in S ² there exists a neighborhood V of 0 in B such that the large bifurcation support of the representative of the local family with the base V belongs to V × U.

Example 7.

The large bifurcation support of type one in the local Malta–Palis family consists of the semistable cycle and the separatrixes that wind to and from it, the corresponding saddles included. This support consists of a finite number of orbits, namely, five: two saddles, two separatrixes, and a cycle.

Example 8.

There are two different large bifurcation supports of type one for the local family described in Theorem 2. They are shown in Fig. 13.1.

This is the first part of the definition of the large bifurcation support. The second part is the following:

Definition 11.

A singular curve of a vector field on a two sphere is a curve for which the phase portrait of the field in any neighborhood of the closure of the curve is topologically nonequivalent to that for any other phase curve with a nearby initial condition.

Example 9.

A separatrix of a hyperbolic saddle, or a boundary curve of a parabolic sector of a saddle-node, is a singular curve.

Definition 12.

Consider a local family and take all the non-hyperbolic singular points of the critical vector field. Consider all the sequences of cycles and singular curves in the product B × S ² that correspond to the parameter values converging to zero, and whose distance to at least one of these singular points tends to zero. The upper topological limit of these sequences (the set of all points whose arbitrary neighborhoods intersect infinitely many terms of the sequence) constitutes the large bifurcation support of type two.

Example 10.

The large bifurcation support of type two for the polycycles apple and halfapple shown in Fig. 13.7 below consists of these polycycles.

Definition 13.

A large bifurcation support for a local family is the union of the corresponding large bifurcation supports of type one and type two.

Definition 14.

The bifurcations in two local families are called equivalent, if these families are weakly equivalent in some neighborhoods of their large bifurcation supports, and the linking homeomorphism over each base point is an isotopy, that is, may be extended to the homeomorphism of the whole sphere.

Problem 1.

Prove that for any k there is an open and dense set in the space of k-parameter local families of vector fields in the two sphere such that for any fixed family from this set the following holds. There exists a neighborhood of the fixed family such that for any two local families from this neighborhood the week topological equivalence of these two families in some neighborhoods of their large supports implies the same equivalence of the families on the whole sphere, provided that the vector fields corresponding to the critical parameter values are orbitally topologically equivalent.

Theorem 3.

All the bifurcations that occur in generic nonlocal one-parameter families of vector fields on the two sphere have at most countable bifurcation carriers.

Theorem 4.

All the generic local one-parameter families of vector fields in S ² have large bifurcation supports that consist of a finite number of phase curves.

Theorem 5.

There are exactly two classes of topological equivalence of bifurcations in the local families described in Theorem 2. Their large bifurcation supports are shown in Fig.  13.1.

13.1.6 Classification of Global Bifurcations in the Local One-Parameter Families on the Sphere

In all the classification theorems below the bifurcations in local families are considered in some neighborhood of their large supports.

Theorem 6.

There are exactly six generic one-parameter families in the plane, up to topological equivalence, whose “small” representatives, that is nonlocal families corresponding to sufficiently small neighborhoods of the critical parameter value, have finite carriers. These carriers consist of exactly one point.

These six bifurcations are all classical:

• breaking of a saddle-node singular point having no homoclinic loop;

• breaking of a saddle-node singular point having a homoclinic loop;

• Andronov–Hopf bifurcations;

• vanishing or splitting of a semistable limit cycle;

• breaking of a separatrix loop of a hyperbolic saddle;

• breaking of a saddle connection of two different saddles.

All other bifurcations occur due to sparkling saddle connections.

Note that an arbitrary finite number of saddles may be involved in the formation of sparking saddle connections related both to semistable cycles and to saddle connections. So, an infinite number of pairwise topologically nonequivalent generic 1-parameter families occurs, see Fig. 13.3.

Fig. 13.3

Complicated large bifurcation supports

Theorem 7.

There is an infinite number of local one-parameter families of vector fields on the two sphere pairwise topologically nonequivalent on their large supports. There are two classes of them having an infinite bifurcation diagram: those that correspond to semistable cycle and to a separatrix loop with sparkling saddle connections. The large supports of the corresponding bifurcation consist of the cycle (in the first case), the separatrix loop (in the second case), and the separatrixes of the hyperbolic saddles that wind onto them either in the positive, or in the negative time, in both cases. Two local one-parameter families of vector fields on a two sphere whose large bifurcation support contains a separatrix loop are topologically equivalent if the large supports of the corresponding bifurcations are isotopic: may be transformed one into another by a homeomorphism of the ambient sphere, and the vector fields corresponding to the critical parameter values are orbitally topologically equivalent.

There is but a finite number of classes of topological equivalence of local one-parameter families whose large bifurcation supports contain a semistable limit cycle and are isotopic, provided that the vector fields corresponding to the critical parameter values are orbitally topologically equivalent.

The large supports in the theorem above always consist of a finite number of phase curves. Examples are shown in Fig. 13.3. The combinatorics of these supports may be very complicated. May be, it might be described by some oriented graphs.

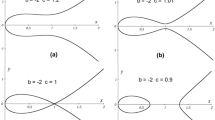
Example 11.

The large support of the bifurcation in the Malta–Palis family consists of the semistable cycle and the separatrixes of two saddles that wind onto it from inside and from outside. Four different cases occur, see Fig. 13.2.

Note that Cherry cells enter the game, and their different location corresponds to topologically nonequivalent families.

We conclude this section by the following:

Conjecture 1.

If two generic one-parameter local families of vector fields on the two sphere are equivalent in the neighborhoods of their large supports, then they are also equivalent in the basins of the attraction/repulsion of their (small) supports.

13.2 Bifurcations in Two-Parameter Families

13.2.1 Local Bifurcations

There is one (and only one!) local bifurcation in the two-parameter families that is quite new in comparison with those previously studied. This is the Bogdanov–Takens bifurcation. Its investigation was a revolution in the bifurcation theory, and opened a new period of its development.

Note that other famous two-parameter families in the plane:

• the families investigated by Zoladek;

• the so-called resonances 1: 2, 1: 3 investigated by Horozov;

• the resonance 1: 4, investigated by many authors but not yet fully studied,

are factorizations of higher dimensional problems, and do not belong to the subject of our survey.

More traditional are problems that occur in codimension 1, but have supplementary degeneracies. These are bifurcations of saddle-nodes and Andronov–Hopf bifurcations. Nothing interesting occurs in these families with two parameters. Three singular points may be generated in the first family instead of two. Two limit cycles occur in the second family instead of one.

Let us say a few words about the multiparameter case. Floris Takens investigated generation of limit cycles in the unfolding of a vector fields

$$\displaystyle{ v(z) = iz + az^{k+1}z^{k}+\ldots,\ a\neq 0 }$$

(13.1)

written in its resonant normal form. Such a field occurs in generic k-parameter families. Its unfolding generates no more than k limit cycles.

An unfolding of a vector field on a line

$$\displaystyle{v(x) = ax^{k+1}+\ldots,\ a\neq 0}$$

that occurs in generic k-parameter families can generate no more that k + 1 singular points.

The phase portraits of these families in both cases are easily investigated.

A striking discovery was made by Roussarie: topological classification of these families has functional moduli provided that the number of parameters is high enough: three for the Andronov–Hopf family and four for the bifurcation of a multiple limit cycle.

Theorem 8 (Roussarie [18]).

For a generic three-parameter unfolding of a vector field (13.1) with k = 3 there exists a functional invariant of topological classification. This invariant is a one-parameter family of diffeomorphisms of a cycle.

On the other hand, any generic unfolding of a germ (13.1) is weakly topologically equivalent to one of a finite number of “standard” local families. So in what follows we speak about weak equivalence only.

13.2.2 Semilocal Bifurcations in Two-Parameter Families

At the end of 1980s a Moscow graduate student Anna Kotova collected a “zoo” of all polycycles that may occur in generic two- and three-parameter families [14]. There are “individual polycycles” (separatrix polygons homeomorphic to a circle), “collections of polycycles” (finite unions of individual polycycles), and one “ensemble”: a continuous family of polycycles that occur in a generic three-parameter family. We postpone the description of this ensemble to the next section.

Later on, S. Trifonov investigated the cyclicity of all individual polycyles in the “Kotova zoo,” [22].

Here we present these results for codimension two. All the polycycles below have there own names. They are shown in Figs. 13.4, 13.5, 13.6, 13.7, 13.8, 13.9 and listed in the figure captions.

Fig. 13.4

A rigged loop: a separatix loop of a hyperbolic saddle with a zero saddle value (trace of eigenvalues)

Fig. 13.5

A lune (left); a heart (right)

Fig. 13.6

An eight shaped figure (collection of three polycyles: two separatrix loops and their union)

Fig. 13.7

An “apple and halfapple”

Fig. 13.8

Boundary homoclinic loop of a saddle-node

Fig. 13.9

Twin saddle-nodes

Trifonov proved that no polycycle in this list has cyclicity larger than 2. On the other hand, my former student Grozovski investigated the bifurcations of the collection “apple,”and found that three limit cycles may be generated by a two-parameter unfolding of this collection. This is the simplest case when the number of cycles generated is larger than the number of parameters.

Let us say a few words about the bifurcations of a separatrix loop. It is investigated now in full generality for the families with an arbitrary number of parameters. In modern terms the result is the following:

Theorem 9.

A separatrix loop that occurs in a generic k-parameter family may generate no more than k limit cycles.

This result was obtained by Andronova–Leontovich in the late 1940s; the sketch of the proof with the main ideas was published in [15]. Unfortunately, she never published the full proof. A complete proof of this result was obtained by Roussarie (an upper estimate) [17]. In [8] its sharpness was proved.

13.2.3 Polycycles and Sparkling Separatrixes

Conjecture 2.

Sparkling separatrixes may occur for all the polycyles listed above, except for the twin saddle-node.

Problem 2.

Describe the corresponding global bifurcations. In particular, are Arnold’s Conjectures 3 and 4 true for two-parameter families?

13.2.4 Synchronized Sparkling Saddle Connections

Consider a semistable limit cycle with two saddle separatrixes winding on it from outside and two winding from inside, Fig. 13.10.

Fig. 13.10

Large bifurcation support for a family with synchronized saddle connections

The question is: when two saddle connections may occur simultaneously under the bifurcation in this family?

As proved in [16], this cannot happen in generic one-parameter families. But it can happen in two-parameter ones [7, 9]. Let us describe this bifurcation in more detail.

Consider the parameter depending Poincaré map P of the semistable cycle corresponding to some transversal $\Gamma$. Denote the two parameters by $\varepsilon,\delta$. Then the Poincaré map will be $P(x,\varepsilon,\delta ),\ x \in \Gamma$. Suppose that $\varepsilon$ is “responsible” for the breaking of the semistable cycle: the semistable cycle corresponds to $\varepsilon = 0$ and vanishes for $\varepsilon> 0$. By Ilyashenko and Yakovenko [10], there exists a vector field $w_{\varepsilon,\delta }$ on $\Gamma$ that generates $P(\cdot,\varepsilon,\delta )$ as a time one phase flow transformation in the domain $\varepsilon \geq 0$, where the cycle vanishes. Moreover, the coordinate x on $\Gamma$ and the parameters may be so chosen that

$$\displaystyle{w_{\varepsilon,\delta }(x) = \frac{x^{2}+\varepsilon } {1 + a(\varepsilon,\delta )x}.}$$

Let $E_{j}(\varepsilon,\delta )$ and $I_{j}(\varepsilon,\delta )$ be the x-coordinates of the intersections of the separatrixes with $\Gamma$, continuous in $\varepsilon,\delta$. Separatrixes passing through $E_{j}(\varepsilon,\delta )$ and$I_{j}(\varepsilon,\delta )$ coincide iff for some natural k,

$$\displaystyle{P^{k}(E_{ j}(\varepsilon,\delta ),\ \varepsilon,\delta ) = I_{j}(\varepsilon,\delta ).}$$

This is equivalent to

$$\displaystyle{ g_{w_{\varepsilon,\delta }}^{k}(E_{ j}(\varepsilon,\delta )) = I_{j}(\varepsilon,\delta ). }$$

(13.2)

If this happens simultaneously for j = 1 and 2, then the two separatrixes coincide simultaneously, they “meet” after k turns from E _j to I _j . Consider a “time function” corresponding to the field $w_{\varepsilon,\delta }$ ($x_{0} \in \Gamma$ is arbitrary):

$$\displaystyle{ T(x,\varepsilon,\delta ) =\int _{ x_{0}}^{x} \frac{d(\xi )} {w_{\varepsilon,\delta }(\xi )} }$$

(13.3)

Equation (13.2) is equivalent to

$$\displaystyle{ T(I_{j}(\varepsilon,\delta ),\varepsilon,\delta ) - T(E_{j}(\varepsilon,\delta ),\varepsilon,\delta ) = k. }$$

(13.4)

If these equalities hold for a sequence $(\varepsilon _{k},\delta _{k}) \rightarrow 0$ as $k \rightarrow \infty$, we have a sequence of simultaneous (twin) saddle connections corresponding to $(\varepsilon _{k},\delta _{k})$; the number of winds of this connections near the cycle that have vanished is k. Equation (13.4) for j = 1 and 2, imply

$$\displaystyle{T(E_{1}(\varepsilon _{k},\delta _{k}),\varepsilon _{k},\delta _{k}) - T(E_{2}(\varepsilon _{k},\delta _{k}),\varepsilon _{k},\delta _{k}) = T(I_{1}(\varepsilon _{k},\delta _{k}),\varepsilon _{k},\delta _{k}) - T(I_{2}(\varepsilon _{k},\delta _{k}),\varepsilon _{k},\delta _{k}).}$$

Passing to the limit, as $\varepsilon \rightarrow 0,\ \delta \rightarrow 0$, we get

$$\displaystyle{T(E_{1},0,0) - T(E_{2},0,0) = T(I_{1},0,0) - T(I_{2},0,0).}$$

Consider a function

$$\displaystyle\begin{array}{rcl} S(\varepsilon,\delta ) = [T(E_{1},(\varepsilon,\delta ),\varepsilon,\delta ) - T(E_{2}(\varepsilon,\delta ),\varepsilon,\delta )] - [T(I_{1}(\varepsilon,\delta ),\varepsilon,\delta ) - T(I_{2}(\varepsilon,\delta ),\varepsilon,\delta )].& &{}\end{array}$$

(13.5)

The previous equality implies

$$\displaystyle{S(0,0) = 0.}$$

Let $\frac{\partial S} {\partial \varepsilon } (0,0)\neq 0$. Then the “synchronization curve” S = 0 is transversal to $\varepsilon = 0$. Hence, the synchronization curve intersects transversally the curves of saddle connections between E ₁ and I ₁ making k turns, $k \rightarrow \infty$. The intersection points correspond to synchronized connections between E ₂, I ₂ and E ₁, I ₂. The bifurcation diagram is shown in Fig. 13.11.

Fig. 13.11

The bifurcation diagram in a family with two synchronized saddle connections

We will turn back to this bifurcation in the study of quasigeneric families.

13.2.5 Sparkling Saddle Connections for Two Semistable Cycles

In two-parameter families two semistable cycles may occur. Any finite number of saddles may be added “for free.” Consider first the bifurcation with two separate semistable cycles and four saddles involved, see Fig. 13.12.

Fig. 13.12

Two separate semistable cycles

Let $\varepsilon = 0$ correspond to the left semistable cycle, and δ = 0 to the right one. The bifurcation diagram in the domain $\varepsilon \geq 0,\ \delta \geq 0$ is shown in Fig. 13.13.

Fig. 13.13

Bifurcation diagram in a family with two separate semistable cycles, domain $\varepsilon \geq 0,\ \delta \geq 0$

Second, consider two semistable cycles one inside another, with two saddles, one outside the larger one, another inside the smaller one. Sparkling saddle connections will occur when both cycles disappear, Fig. 13.14.

Fig. 13.14

Two semistable cycles, one inside another

13.2.6 Synchronized Connections and Complicated Bifurcation Diagrams in Two-Parameter Families

Consider now a more complicated case: two semistable cycles one inside another, with a saddle I inside, E outside, and B between them.

The large bifurcation support of this family is schematically shown in Fig. 13.15. The bifurcation diagram is presented in Fig. 13.15 too.

Fig. 13.15

More complicated location of saddles and bifurcation diagram in the domain $\varepsilon \geq 0,\ \delta \geq 0$

The “horizontal” curves correspond to connections between the saddles I and B. Black vertical curves correspond to connections between B and E that involve the lower separatrix L of B; the red ones correspond to those that involve the upper separatrix U.

Any of these lines is marked by an integer number: a number of full turns made by the connection around the interior saddle I. The intersections between vertical and horizontal curves correspond to simultaneous saddle connections, see Fig. 13.16.

Fig. 13.16

Simultaneous saddle connections in the family considered

There are three connections in Fig. 13.16: one between I and B, one between B and E, and the third is a compound connection between I and E, the union of the previous two.

There are also hyperbola-shaped arcs in the bifurcation diagram that correspond to the connections between E and I. They are marked by the number n of full circuits that they make around I. These curves pass through the points of synchronized connections with indexes k and m; in this case, $n = k + m$. We call them “arcs of long connection.”

There are alternating thick and thin arcs on the horizontal curves. Thin ones correspond to the case when the unstable separatrix of E enters the interior domain of the (vanished) small semistable cycle; thick ones correspond to the case when this separatix enters the Cherry cell of B, see Fig. 13.17.

Fig. 13.17

Role of Cherry cells

13.2.7 An Infinite Number of Samples of the Bifurcation Diagrams

Theorem 10.

There exists an infinite number of topologically nonequivalent germs of bifurcation diagrams in generic two-parameter families of vector fields in the two sphere.

Sketch of the Proof.

As an example one may suggest a series of local families with the large bifurcation supports consisting of two semistable cycle, one saddle I inside both, one in between, and j saddles outside both cycles. The large support of the corresponding bifurcation is shown in Fig. 13.18.

Fig. 13.18

Infinite series of large supports that correspond to an infinite set of topologically nonequivalent germs of bifurcation diagrams

We claim that the germs of the bifurcation diagrams for these families are topologically nonequivalent for different values of j. In more detail, denote the saddle inside the inner cycle by I, the one between the cycles by B, and the saddles outside both cycles, by $E_{1},\ldots,E_{j}$. Let $\varepsilon,\ \delta$ be the parameters of the family such that $\varepsilon = 0\ (\delta = 0)$ corresponds to the presence of the larger (respectively, smaller) semistable cycle. Then, in the domain $\varepsilon> 0,\ \delta> 0$, there are two sequences of pairwise disjoint “vertical” and “horizontal” curves. The first sequence tends to $\varepsilon = 0$ and corresponds to the sparkling saddle connections between B and E _j that occur when the larger semistable cycle vanishes. The second sequence tends to δ = 0 and corresponds to sparkling saddle connections between I and B.

The two sequences together form sort of a grid $\Sigma$, with the rectangle-like cells. It is similar to the one shown in Fig. 13.13, but a bit more complicated. The nodes of this grid correspond to simultaneous saddle connection, see Fig. 13.16.

A third family $\Lambda$ of bifurcation curves occurs. It corresponds to saddle connections between I and E _j . The bifurcation curves of this family are similar to those shown in Fig. 13.14. But they are dashed because of the presence of the Cherry cells between two cycles, see Fig. 13.15, left.

The whole bifurcation diagram is similar to the one shown in Fig. 13.15, right, but more complicated. There is an infinite number of cells of the grid $\Sigma$ that tend to zero and intersect exactly j arcs of the third family $\Lambda$. No cell intersects more than j arcs.

This number j is a topological invariant of the bifurcation diagram constructed. Thus a countable number of germs of pairwise topologically nonequivalent germs of bifurcation diagrams in generic two-parameter families on the sphere occurs.

This completes the sketch of the proof of Theorem 10. □ 

13.2.8 Quasigeneric Families with a Continuum of Topologically Nonequivalent Bifurcation Diagrams

Intuitively speaking, a quasigeneric family is a “corrupted generic family”: one (and exactly one) genericity condition is violated.

Theorem 11.

There exists a class of quasigeneric two-parameter families whose bifurcation diagram has a numeric modulus of the topological classification. Consequently, for this class of local families there exists a continual set of pairwise topologically nonequivalent germs of bifurcation diagrams.

Sketch of the Proof.

Consider a two-parameter family with two separate semistable cycles and six saddles involved, see Fig. 13.19.

Fig. 13.19

Large support of a quasigeneric family whose bifurcation diagram has numeric modulus of topological classification

Let the saddles depend on the parameters $\varepsilon,\delta$, as well as the “first” intersection points of the separatrixes winding to and from the first cycle. Denote these points by $E_{1}(\varepsilon,\delta )$ and $E_{2}(\varepsilon,\delta )$ for exterior saddles, $I_{1}(\varepsilon,\delta )$ and $I_{2}(\varepsilon,\delta )$ for interior saddles. Let $w_{\varepsilon,\delta }$ be the same as in Sect. 13.2.4, and S be the synchronization function (13.5). One of the genericity assumptions for the family is

$$\displaystyle{S(0,0)\notin \mathbb{Z}.}$$

In this case, the bifurcation diagram in the family is like the diagram in Fig. 13.13.

Suppose now that the genericity assumption above fails; for instance,

$$\displaystyle{S(0,0) = 0.}$$

In a quasigeneric family the curve $\lambda$:

$$\displaystyle{S(\varepsilon,\delta ) = 0}$$

is transversal both to $\varepsilon = 0$ and δ = 0 at zero. The bifurcation diagram for this family is a combination of two: the one shown in Fig. 13.11, and the other from Fig. 13.13. It is plotted in Fig. 13.20.

Fig. 13.20

Bifurcation diagram with a numeric modulus of topological classification

Roughly speaking, the slope of the curve $\lambda$ at zero is a topological invariant of the bifurcation diagram described above.

Let us make a precise statement. Let $T(x,\varepsilon,\delta )$ be the time function corresponding to the Poincaré map of the first cycle, see (13.3), and $R(x,\varepsilon,\delta )$ be the similar function for the second cycle. Let us make a parameter change:

$$\displaystyle{\Phi: (\mathbb{R}^{+},0) \times (\mathbb{R}^{+},0) \rightarrow (\mathbb{R}^{+},\infty ) \times (\mathbb{R}^{+},\infty )}$$

defined as follows:

$$\displaystyle{(\varepsilon,\delta )\mapsto \tau (\varepsilon,\delta ),\ \sigma (\varepsilon,\delta ),}$$

where

$$\displaystyle\begin{array}{rcl} & \tau (\varepsilon,\delta ) = T(E_{1}(\varepsilon,\delta ),\varepsilon,\delta ) - T(I_{1}(\varepsilon,\delta ),\ \varepsilon,\delta ),& {}\\ & \sigma (\varepsilon,\delta ) = R(E(\varepsilon,\delta ),\varepsilon,\delta ) - R(I(\varepsilon,\delta ),\ \varepsilon,\delta ), & {}\\ \end{array}$$

The saddle connections between E ₁ and I ₁ that intersect $\Gamma _{1}\ k + 1$ times correspond to the line τ = k. Similar connections between E and I correspond to $\sigma = k$. So the bifurcation diagram of the family contains the grid:

$$\displaystyle{\tau \in \mathbb{Z}^{+} + k_{ 0},\ \sigma \in \mathbb{Z}^{+} + m_{ 0}}$$

for some $k_{0},m_{0} \in \mathbb{Z}^{+}$.

The numbering of the lines of the grid is defined up to adding O(1). So the curve $\Phi (\lambda )$ may be given by a function

$$\displaystyle{\sigma =\varphi (\tau ).}$$

It is easy to prove that there exists a limit

$$\displaystyle{\omega =\lim _{\tau \rightarrow \infty }\frac{\varphi (\tau )} {\tau }.}$$

We claim that this limit is an invariant of the topological classification of the bifurcation diagrams of the class considered. Indeed, for any integral value τ = k > 0, the integer part of $\varphi (k)$ is the number m of the horizontal line such that $\Phi (\lambda )$ intersects the segment

$$\displaystyle{\{(\tau,\sigma )\vert \tau = k,\ \sigma \in [m,m + 1]\}.}$$

This number is topologically well-defined modulo an additional term O(1) non depending on m. Then $\varphi +O(1)$ is well defined topologically. Hence, the limit ω is topologically well defined. In other words, ω is a topological invariant of the bifurcation diagram of the family. This completes the sketch of the proof of the theorem. □ 

13.3 Global Bifurcations in Generic Three-Parameter Families

As of now, this subject is almost untouched. An exclusion is the so-called ensemble “lips,” a continual set of polycycles that occurs in generic three-parameter families.

13.3.1 Ensemble “Saddle Lips”

Consider a vector field v ₀ with the following three degeneracies: v ₀ has two saddle-nodes whose parabolic sectors are turned “face to face”: a continuum of the phase curves that emerge one sector enter the other one; moreover, the separatrixes of the hyperbolic sectors of the saddle-nodes coincide, see Fig. 13.21.

Fig. 13.21

Ensemble saddle—lips

The field v ₀ has a continual family of polycycles: they all contain a mutual separatrix of the two saddle-nodes, the saddle-nodes included, and the phase curves that emerge one saddle-node and enter the other one, one curve for each polycycle.

This family of polycycles is bounded by the separatrixes of two saddles: E lying outside the polycycles described above, and I lying inside. The large bifurcation support for the unfolding of the ensemble “saddle lips” is the union of all the polycycles of the ensemble.

The bifurcation diagrams of this family may be unboundedly complicated. Namely, for a graph $\Gamma$ of any generic monotonic function [0, 1] → [0, 1] there exists a vector field v ₀ in the class described above, with the following property. The bifurcation diagram of a generic unfolding of v ₀ is a surface with singularities. It contains a surface homeomorphic to a cone over the Legendre transformation of $\Gamma$, see Fig. 13.22.

Fig. 13.22

A piece of a bifurcation diagram for the ensemble “saddle—lips”

This surface may have an arbitrary large number of self intersections. Thus, there exists an infinite number of bifurcation diagrams for such families; these diagrams are pairwise topologically nonequivalent [14].

Bifurcations in the ensemble “lips” without two saddles E and I is studied in [14]. Bifurcations in the same ensemble with the saddle E included and I deleted is studied in [20]. The global bifurcations in the ensemble described are not yet studied. In particular, it is unclear, whether this ensemble admits sparkling saddle connections, whatever it means.

In the English translation of Arnold et al. [1] there is a remark made by Arnold that follows the text quoted above:

Recently A. Kotova and V. Stanzo found a counterexample to Conjecture 2. Little is now known: even for families of structurally stable and quasigeneric vector fields, Conjectures 3 and 4 (the only nontrivial in this case) are unproved.

In what follows, we will discuss these conjectures in full generality, not only for families of structurally stable and quasigeneric vector fields.

13.3.2 Ensemble “Shark”

In three-parameter families a new kind of sparkling saddle connections may occur. Consider a polycycle with at least one saddle-node singular point on it. Suppose that a separatrix of some saddle enters the parabolic sector of this saddle-node. Then, after the saddle-node disappears, the separatrix may start to wind in a neighborhood of a polycycle that have vanished, and produce a variety of saddle connections with the other separatrixes.

As an illustration consider an ensemble “shark,” see Fig. 13.23. The name comes from the figure that resembles the mouth full of teeth. When both saddle-nodes disappear, an enormous variety of saddle connections may occur. It is unclear whether or not the generic unfolding of such ensembles is structurally stable.

Fig. 13.23

An ensemble “shark”

13.3.3 Extended Collection “Half-Apple and Loop”

A collection of polycycles named in the title may occur in a generic three-parameter family. It is shown in Fig. 13.24. There are three degeneracies for the field v ₀ with such a collection:

Fig. 13.24

A collection “apple-loop”

• a separatrix loop of a hyperbolic saddle E;

• a saddle-node S;

• a connection between S and E: the separatrix of the hyperbolic sectors of the saddle-node coincides with the incoming separatrix of S.

Note that the outcoming separatrix of E may enter the parabolic sector of the saddle-node S without increasing the rate of degeneracy.

Separatrixes of hyperbolic saddles winding from the saddle loop inside it do not increase the rate of degeneracy, see Fig. 13.25.

Fig. 13.25

Large bifurcation support with the “apple-loop” collection as a subset: vector field v ₀

The same holds true for the separatrixes that enter the saddle-node S from outside the polycycle. When the saddle-node disappears, and the connections are broken, a lot of sparkling saddle connections may occur, see Fig. 13.26.

Fig. 13.26

A possible phase portrait in the unfolding of the field v ₀ from the previous picture

Problem 3.

Are the generic unfoldings of the ensemble “shark” or a polycycle “halfapple and loop” with extra saddles structurally stable?

The abundance of saddle connections that may occur makes the positive answer very plausible.

13.3.4 Kotova Zoo Revisited

A polycycle that may occur in a generic k-parameter family is defined not only by its geometry. For instance, the first polycycle in the Kotova zoo for the two-parameter families is a separatrix loop with a zero saddle value, see Fig. 13.4.

Definition 15.

A rigged polycycle is a polycycle with some additional restrictions on the jets of the corresponding vector field at the vertexes or at the edges of the polycycle.

We mention here some rigged polycycles from the Kotova zoo for three-parameter families.

• A separatrix loop with a zero saddle value and zero Melnikov integral:

  $$\displaystyle{I =\int _{\gamma }\mathop{\mathrm{d}iv}v\,dt,}$$

  where γ is the separatrix loop, t its time parametrization.

• An eight shaped figure, see Fig. 13.6, with a zero saddle value.

Definition 16.

A large support that contains rigged polycycles is called rigged large supports

Definition 17.

Two rigged large supports are equivalent if they are isotopic, and the isotopy respects the rigging relations: these relations are the same for the phase curves of two supports that are mapped to each other by the isotopy.

These definitions will be used in the next section.

13.4 Global Bifurcations with Many Parameters

No results are known to the author in general theory of global planar bifurcations with the number of parameters greater than three. Here we state some problems only.

13.4.1 Supports and Their Basins

Definition 18.

A basin of an invariant set A of a planar vector field is the set of all points whose α- or ω-limit sets belong to A.

Example 12.

All the phase curves that wind to or from a semistable cycle belong to the basin of this cycle. Their union equals this basin.

Problem 4.

Is it true that the large bifurcation support of a local finite-parameter family belongs to the basin of the small bifurcation support?

Conjecture 3.

The answer is “yes” for generic one-parameter families.

By definition, two local families are weakly equivalent when they are equivalent in some neighborhoods of their large bifurcation supports. The following problem is aimed to increase the domain where two families are equivalent.

Problem 5.

Is it correct that two weakly equivalent local families are in fact weakly equivalent in the basins of their large bifurcation supports?

Again, the answer seems to be affirmative for the generic one-parameter families.

13.4.2 Bifurcational Stability

Recall our main result about generic one-parameter families.

Two local one-parameter families are topologically equivalent iff the large supports of the corresponding bifurcations are isotopic and do not contain semistable cycles; moreover, vector fields corresponding to zero parameter value are orbitally topologically equivalent, see Theorem 7.

This property gives rise to the following definition:

Definition 19.

A class of local families is (strongly) bifurcationally stable provided that the following holds. Two local families of this class are topologically equivalent iff their large supports of the corresponding bifurcations are isotopic, and vector fields corresponding to zero parameter values are orbitally topologically equivalent. The latter assumption is required in two definitions to follow. This class is bifurcationally stable if the equivalence above follows from the isotopy of the rigged large supports. This class is weakly bifurcationally stable if the isotopy class of the rigged large support corresponds to a finite number of topological types of local families.

Problem 6.

Describe (strongly and weakly) bifurcationally stable classes of local families.

We expect that the “majority” of local families are not bifurcationally stable in any sense. The more interesting are the classes that are bifurcationally stable.

Conjecture 4.

The following local families are bifurcationally stable:

• k-parameter families with a rigged separatrix loop that may be met in generic k-parameter but not in (k − 1)-parameter families;

• k-parameter families with a homoclinic curve of a saddle-node of the multiplicity k.

Problem 7.

What may be said about the bifurcational stability of local families whose small supports are rigged polycycles met in generic two-parameter families?

In contrast to the global bifurcation theory of k-parameter families, the semilocal one, related to bifurcations of polycycles, is more elaborated.

13.5 Bifurcations of Polycycles

This is a rich theory, and we discuss here only a few results from it. We start with the polynomial case.

13.5.1 Bifurcational Approach to the Hilbert’s 16th Problem

This approach is due to Roussarie. It is related to the following form of Hilbert’s 16th problem:

Problem 8.

Prove that for any n there exists H(n), a Hilbert number, such that a planar polynomial vector field of degree no greater than n can have no more than H(n) limit cycles.

For what follows, we recall some well-known definitions.

An oriented polycycle is a finite union of cyclically enumerated singular points (the vertexes) and phase curves that connect the vertexes (the edges) with the following properties:

• the vertexes with the different numbers may coincide; the edges may not;

• the edge number j connects the vertexes O _j and O _j+1;

• the time orientation of the edge number j is from O _j to O _j+1;

• the first vertex (edge) follows the last one (cyclicity of the enumeration).

Semilocal bifurcations are considered in the neighborhoods of the polycycles. Two semilocal bifurcations of polycycles are equivalent if there exists two neighborhoods of the polycycle where two local families are weakly topologically equivalent.

Definition 20.

A limit cycle is generated by an unfolding of a polycycle if there exists a family of limit cycles depending on the parameter of the unfolding such that the limit cycles of the family tend to the polycycle in sense of the Hausdorff distance as the parameter tends to the critical value.

Definition 21.

The cyclicity of a polycycle in a family is the maximal number of limit cycles that may be generated by this polycycle in this family.

Conjecture 5 (Roussarie, [19]).

Any polycycle that occurs in a family of planar polynomial vector fields of degree no greater than given n has a finite cyclicity.

Theorem 12 ([19]).

The above conjecture implies the existence of Hilbert number H(n) for any n.

13.5.2 The Dumortier–Roussarie–Rousseau Program

In [2] the authors listed all the rigged polycycles that may occur in the family of the quadratic vector fields. Their number appeared to be 121. It is sufficient to prove the finite cyclicity of any of them in the family of quadratic vector fields, in order to prove the existence of H(2). Up to now more than 80 polycycles are studied and their finite cyclicity is proved. This partial success is a strong indication that H(2) really exists.

13.5.3 The Arnold’s Program for the Polycycles

It seems that the Arnold’s program is perfectly adjusted to the study of bifurcations of polycycles. But the problem seems to be very difficult. Indeed, the Conjecture 2: Any bifurcation diagram is (locally) homeomorphic to one of a finite number (depending only upon l) of generic examples is closely related to the following:

Conjecture 6 (Hilbert–Arnold Conjecture, [6]).

For any k, a polycycle met in a typical k-parameter family, has but a finite cyclicity.

13.5.4 Present Status of the Hilbert–Arnold Conjecture

The conjecture is proved for the so-called elementary polycycles: those that have vertexes as singular points whose eigenvalues are not simultaneously zero.

Theorem 13 ([10]).

Elementary polycycles met in a typical k-parameter families have but a finite cyclicity.

Later on this cyclicity was estimated by V. Kaloshin, [12, 13]

Theorem 14 ([11]).

The cyclicity of an elementary polycycle met in a typical k-parameter family is no greater than $2^{25k^{2} }$.

Kaloshin suggested to estimate the cyclicity of polycycles with a fixed number n of vertices that may be met in generic k-parameter families. Kaleda and Schurov obtained this estimate.

Theorem 15 ([11]).

The cyclicity of an elementary polycycle with n vertexes met in a typical k-parameter family is no greater than C(n)k ³ⁿ.

13.5.5 Finiteness Theorem for Generic k-Parameter Families

There’s no doubt that the following theorem is true:

Theorem 16.

A vector field met in typical k-parameter family has but a finite number of limit cycles.

Yet the theorem remains unproved.

13.5.6 Back to the Hilbert–Arnold Problem

One of the equivalent forms of the finiteness theorem for limit cycles is the following nonaccumulation theorem:

Theorem 17 ([3, 5]).

Limit cycles of an analytic vector field cannot accumulate to a polycycle of this field.

Classical Seidenberg–Lefshez–Bendixson–Dumortier theorem reduces this statement to the case when the polycycle in the theorem is elementary.

The question arises: may the general Hilbert–Arnold problem be reduced to Theorem 13 by sort of desingularization in the families?

13.5.7 Desingularization in the Families

The question above was investigated by S. Trifonov.

Definition 22.

Say that a family of vector fields is quasielementary if any field of the family either has but a finite number of singular points and they are all elementary (such fields are called elementary) or has a whole curve of singular points, and becomes elementary after a division of its components by a common non-invertible analytic factor.

Theorem 18 ([21]).

Any analytic finite-parameter family of vector fields, after a special desingularization process, may be transformed to a quasielementary family of vector fields.

13.5.8 Trifonov Phenomenon

Note that a quasielementary family may not be equivalent to a family of elementary vector fields. Indeed, a vector field with a curve of singular points may correspond to an isolated parameter value. This particular vector field may be transformed into an elementary one by the division by a non-invertible function. But the nearby vector fields have no common factor of their components. Thus the whole quasielementary family cannot be transformed into an elementary one. This effect called the Trifonov phenomenon prevents the reduction of the general Hilbert–Arnold problem to Theorem 13.

13.5.9 Back to the Arnold’s Program

Definition 23.

A nest of a planar vector field with a finite number of singular points in an open subset Z in the phase plane such that

• Z is homeomorphic to an annulus;

• the boundary curves of the annulus Z are limit cycles;

• Z contains no singular points of the field.

A nest is said to be maximal if it is not a proper subset of another nest.

Definition 24.

Consider vector fields v ₁ and v ₂. Let Z _j be the union of maximal nests of v _j , j = 1, 2. We say that v ₁ and v ₂ are equivalent modulo limit cycles if the restriction of v ₁ to $\overline{\mathbb{R}\setminus Z_{1}}$ is orbitally topologically equivalent to the restriction of v ₂ to $\overline{\mathbb{R}^{2}\setminus Z_{2}}$ (the bar denotes the closure of the set).

Definition 25.

Two families $\{v_{\varepsilon }\}$ and $\{w_{\varepsilon }\}$ of vector fields in the total spaces B × M and B′ × M′ are weakly equivalent modulo limit cycles, if there exists a map

$$\displaystyle{H: B \times M \rightarrow B' \times M,\quad (\varepsilon,x)\mapsto (\varphi (\varepsilon ),h_{\varepsilon }(x)),}$$

where $h_{\varepsilon }$ is a homeomorphism M → M′ not necessary continuous in $\varepsilon$, such that $h_{\varepsilon }$ is a topological equivalence of $v_{\varepsilon }$ and $w_{\varphi }(\varepsilon )$, modulo limit cycles.

The following problem is inspired by Arnold’s conjectures from Sect. 13.1.2:

Problem 9.

Is it correct that for any k there is but a finite number of pairwise topologically nonequivalent generic k-parameter unfoldings of polycycles in their neighborhoods modulo limit cycles?

Addendum. In a recent preprint: Yu. Ilyashenko, Yu. Kudryashov, I. Schurov, An open set of structurally unstable families of vector fields in the two-sphere, arXiv:1506.06797 [math.DS], an open set of three parameter families named in the title was constructed.