Keywords

1 Introduction to Supply Chain Planning Under Uncertainty

Supply chain planning (SCP) consists of strategic, tactical and operational decision making problems of a supply chain network. Strategic decisions are related to supply chain design and configuration over a long term whilst tactical planning is related to those decisions affecting the efficient usage of the various resources. Also, operational planning is related to the detailed scheduling, sequencing, assigning loads, etc., in a short term planning horizon. The same facet of all above-mentioned problems is the decision making in a real world and with respect to future situation. In real world, vagueness may be arise with semantic description of events and phenomena, i.e., planning of supply chains in many cases may require human descriptions, judgments, statements and evaluations about the future conditions. These affairs are performed through the natural languages and in respect to this fact that in natural language the words are mostly appeared vaguely and imprecisely [98], the supply chain planning input data may be tainted with uncertainty . On the other hand, with respect to lack of information about the future situations, we need to predict the future, and in prediction of the future conditions, imprecision may be arise due to inherent errors and ambiguity. Therefore, supply chain planning problems are accompanied by imprecision and vagueness due to prediction errors and imprecise descriptions, respectively. Nevertheless, is it necessary to consider these uncertainties when planning of supply chains? According to Klibi et al. [32] any supply chain planning decision model, which is developed based on deterministic conditions has no assurance for acceptable performance in any plausible future situation. They also mentioned that in some cases it is not sufficient to only consider business as usual random variables such as demand, prices and exchange rate but one should include extreme and catastrophe events such as natural disasters and terrorist attacks. Therefore, it is necessary to have a specific strategy in facing with uncertainty in supply chain planning.

Accordingly, in this chapter, different types of uncertainty and their associated sources are first introduced and analyzed. Thereafter, various approaches used to cope with uncertainty in supply chain planning problems are discussed and a hyper conceptual framework is proposed for coping with uncertainty in SCP problems. Since the focus of this chapter is on the application of fuzzy mathematical programming in SCP area, the other sections of the chapter are dedicated to classification, review and description of fuzzy programming methods developed in the relevant literature.

1.1 Definition and Scope

According to Rosenhead et al. [71], certainty can be defined as the condition of decision making in which there is no element of chance intervene between decisions and their outcomes. Also, Zimmermann [98] defined the certainty as the situation that is definitely known, input parameters have predetermined values and there is no doubt in the occurrence of events. On the contrary, uncertainty is vagueness in reaching the target values and/or imperfect information about the input parameters or environmental conditions in which the decisions are made. Galbraith [19] also mentioned that uncertainty is the difference between the amount of information that is required to make the decision and the amount of available information. This definition implicitly unveils one of the important origins of uncertainty that is ‘imperfect information’. There is also a distinction between uncertainty and risk. In the classical risk management, risk is defined as the product of probability and severity of an extreme event [23]. According to above-mentioned definitions, it can be concluded that uncertainty is a value neutral concept (i.e. includes both the chance for gain and the chance of damage), while risk is a negative concept and worthy of avoidance. As explained by Stewart [77], uncertainty gives rise to risk and in the risky situations undesirable outcomes could occur.

In an attempt for choosing an appropriate strategy for uncertainty management in supply chain planning area, it is necessary to understand the sources of uncertainty related to supply chain networks. According to Simangunsong et al. [76], identifying a full list of supply chain uncertainty sources is a precursor to develop appropriate portfolio of uncertainty management strategies.

An early classification was suggested by Davis [10] who mentioned three sources of uncertainty in the supply chain planning context including the demand, supply and process uncertainties. Later, this classification was supported by other researchers including van der Vaart et al. [85] and Gupta and Maranas [22]. Afterwards, Mason-Jones and Towill [49] added a fourth source to those suggested by Davis [10] called control uncertainty, which is related to the capability of a supply chain to transform the orders of customers to production flows by means of information flows. They denominated their model as the circle model which involves four uncertainty sources: (1) demand side uncertainty, (2) supply side uncertainty, (3) control uncertainty and (4) process uncertainty. The model advices that reducing uncertainty in each of these sources can lead to cost reduction.

Another taxonomy is proposed by Christopher and Peck [9], which classifies the risk sources into three categories as follows: (1) internal risk (process and control), (2) external risk and (3) network dependent risk (supply and demand). They also extended a framework for managing and mitigating the risks related to each source. Klibi et al. [32] identified uncertainty sources from the supply chain perspective and in a more detailed view. Table 1 integrates different prominent classifications for sources of uncertainty available in the literature. In the review paper of Simangunsong et al. [76], fourteen sources of uncertainty extracted from the literature are introduced. Simangunsong et al. [76] classify uncertainty management strategies into two broad categories: (1) reducing uncertainty , (2) coping with uncertainty. Their classification is summarized in Fig. 1. The first strategy (i.e. reducing uncertainty) disables or reduces uncertainty at its sources such as using the better forecasting approaches for demand predictions or integrating the organizations across the supply chain to achieve better collaboration between them. The latter strategy refers to one which tries to minimize the impact of uncertainty on the performance of supply chain instead of reducing the sources of uncertainty. Various analytical approaches (e.g. mathematical methods) are usually used when implementing these strategies. As early as 1993, Davis [10] suggested three strategies to cope with uncertainty: (1) TQM (total quality control), (2) new product design and (3) supply chain redesign. The first two strategies participate in reducing the process uncertainty while supply chain redesign can alleviate the demand and supply side uncertainties. In addition, van der Vorst and Beulens [85] proposed two other strategies of reducing the uncertainty: (1) collaboration with key suppliers and customers (2) reducing the role of human in supply chain processes. The first one aims to control the demand and supply uncertainties while the latter tries to reduce process uncertainty. It should be noted that the concept of collaboration has been studied broadly in supply chain management and one important prerequisite of this concept is the advanced integration of supply chain members. Furthermore, collaboration leads to uncertainty reduction in various uncertainty categories including demand, supply, process and control uncertainties. Another prerequisite of collaboration that is worthy of attention is information sharing alongside the supply chain. Other strategies such as flexibility in supply side [21, 66, 73], lead time management [66], insurance against disasters [31, 69, 79] are also suggested in the relevant literature.

Table 1 Different classifications for sources of uncertainty
Full size table
Fig. 1
figure 1

Different strategies in facing with uncertainty along with some examples

Full size image

1.2 Different Types of Uncertainty

Different classifications of uncertainty have ever been proposed in the literature from the different viewpoints. Tang [79] classified supply chain risks into operational and disruption risks. Operational risks are related to those uncertainties that intrinsically are involved in supply chain operations such as demand and cost uncertainty, equipment malfunction, etc. Also, disruption risks are related to those events with low-likelihood but high-severity impact, caused by natural and man-made disasters or technological threats like employee strikes. Interested readers can consult with Torabi et al. [80, 82] for more information. Another classification was expressed by Klibi et al. [32] where various types of uncertainty were categorized into three groups: (1) Randomness, (2) Hazard and (3) Deep uncertainty. They explained that randomness is characterized by random variables related to business-as-usual events while hazard is characterized by low-likelihood but high-impact extreme events. Furthermore, deep uncertainty is related to unavailability of information about likelihood of future plausible events. Mula et al. [52] classified uncertainty into two main categories: (1) flexibility in constraints and goals (2) uncertainty in data. The first category is characterized by the flexibility in satisfying the constraints and/or in target values of goals. Uncertainty in data can be also classified into two categories: (1) randomness, that stems from the random nature of some events and parameters and (2) epistemic uncertainty, which is related to lack of knowledge about the exact value of some ill-defined and imprecise data, which are often in the form of linguistic attributes and qualitative/judgmental data extracted from field experts. According to above-mentioned classification, the intuitive taxonomy for uncertainty can be presented by considering two dimensions: (1) the impact of uncertainty and (2) the nature of imprecision. The proposed taxonomy is illustrated in Fig. 2.

Fig. 2
figure 2

Taxonomy of uncertainty

Full size image

1.3 Overview of Different Approaches Used to Cope with Uncertainty

Both the qualitative and quantitative approaches are applied by researchers and practitioners to handle uncertainty in SCP problems. As mentioned by Peidro et al. [57] quantitative modelling approach includes (1) analytical methods, (2) artificial intelligence methods, (3) simulation based methods, and (4) hybrid methods. This classification, along with some examples for each category is shown in Fig. 3. Since this chapter focuses on fuzzy programming methods, relevant mathematical models are elaborated in the rest of this chapter. However, it should be noted that stochastic programming (e.g. [4, 61]) and robust optimization (e.g. [62]) are the other major methods broadly used in the extant literature. Although there are many research works in the area of SCP, which focus on developing efficient methods to cope with uncertainty, there is a need for a general conceptual/methodological framework which enables the decision makers to systemically confront with uncertainty in SCP problems.

Fig. 3
figure 3

Different categories of quantitative modeling approaches along with some examples (adopted from Peidro et al. [58] with some modifications)

Full size image

Figure 4 shows the proposed methodological/conceptual framework for handling the uncertainty in SCP area. The conceptual framework comprises of four phases: (1) SCN risk analysis: this phase is set out to select important sources of uncertainty based on the corresponding likelihood and severity which subjectively or objectively attribute to the concerned sources; (2) Scenario development and sampling: this phase is intended to provide a plausible portfolio of scenarios or the possible states for the concerned system in the future. Scenario must be transparent, probable, relevant and compatible; (3) Solution approach: it means selecting an analytical method for modeling the uncertainty including the stochastic, fuzzy and robust programming; (4) Modeling resilience, robustness and responsiveness: decisions which are obtained from a solution method, must be remain feasible under almost all future scenarios. In addition, robustness in facing with tensions, rapidity in returning to the equilibrium state and maintaining a good level of performance in a critical condition are the measures of resilience.

Fig. 4
figure 4

Conceptual/methodological framework for modeling approach in coping with uncertainty

Full size image

To conclude this section, Fig. 5 classifies different mathematical programming methods used to deal with uncertainty in SCP problems with respect to the taxonomy of uncertainty provided in Fig. 2.

Fig. 5
figure 5

Classification of analytical methods with respect to the nature of uncertainty

Full size image

2 Fuzzy Mathematical Programming Models for Supply Chain Planning

As it was mentioned in the previous sections, supply chain planning problems’ input data may be subject to uncertainties with different natures and sources. Imprecision associated with subjective estimations, which are based on human judgments or preferences, vagueness and flexibility in objectives and constraints, random nature of some parameters or inexactness in input data, are the examples of different types of uncertainty . Fuzzy set theory is among the main approaches that particularly, manipulate the uncertainty which arises from ambiguity in data and/or vagueness of target values of objectives and constraints. The imprecision can be stemmed from absence of sharp boundaries in definitions, flexibility and vagueness in objectives and constraints, subjective estimations for values of input data and lastly when the historical data does not exist sufficiently or the conditions of problem do not satisfy the presumptions of probability theory.

Fuzzy mathematical programming methods (FMPM) can be classified into two main categories ([53, 81]; Pishvaee and Torabi [60]): (1) flexible programming and (2) possibilistic programming . Flexible programming is used to deal with vagueness in target values of objectives and/or flexibility of constraint’s satisfaction while possibilistic programming is applied to cope with ambiguous (i.e. imprecise) input data (i.e., epistemic uncertainty). Beside the traditional categories of FMPM (i.e. the flexible and possibilistic programming), two other types of modeling approaches called fuzzy stochastic programming and robust fuzzy programming have recently been proposed in the literature. Fuzzy stochastic programming and/or stochastic fuzzy programming, which are frequently used interchangeably (see for instance [5, 85]; Mohammadi et al. [51]) are able to handle those situations in which there are both probabilistic randomness and possibilistic imprecision in data. Also, robust fuzzy programming (see [59, 63]) enables the decision maker to be benefited from the advantages of both robust optimization and FMP approaches. To show the applicability of fuzzy mathematical programming in the context of supply chain planning, Table 2 briefly reviews and classifies a number of important FMP models developed in the literature.

Table 2 Classification of some important FMPMs developed in the area of SCP
Full size table

2.1 Possibilistic Programming

Since the 1950s stochastic programming has been used broadly for the sake of handling randomness uncertainty in the input parameters. However, stochastic programming has some limitations in practice: (1) The low level of computational efficiency, (2) the need for sufficient and reliable historical data and (3) the inability in modelling subjective parameters and concepts ([41]; Pishvaee and Torabi [60]). It is obvious that in most of real-life problems the aforementioned limitations become significant drawbacks in the application and usefulness of stochastic programming approach.

As a powerful alternative, possibilistic programming (PP) provides a framework which can appropriately handle the epistemic uncertainty in input parameters. In PP, a possibilistic distribution is attributed to an uncertain parameter, which shows the degree of possibility of occurrence for each possible value in the related support. Figure 6 summarizes some of the important and popular PP methods which are used broadly in the literature.

Fig. 6
figure 6

Classification of various possibilistic programming methods

Full size image

For confronting the imprecise resources and technological coefficients in optimization models, Ramik [68] supposed that all the technological and resource coefficients are L-R fuzzy numbers and by the use of self-inclusion concept, they concluded that the inequalities with imprecise resources and technological coefficients are fuzzy inequalities. Accordingly, they proposed the use of fuzzy ranking methods to handle the imprecise parameters in such mathematical programming problems. Tanaka et al. [78] formulated the uncertain input parameters as symmetric triangular fuzzy numbers and based on extension principle they defined satisfaction level of \(\alpha\) for each constraint including imprecise parameters. They defined \(\alpha\) as a priori parameter which is specified by the decision maker. While most of developed approaches in the literature considered the constraints with imprecise resources and technological coefficients in the form of inequalities, Dubois and Prade [14] proposed their approach for different forms of constraints, especially equality constraints, and introduced two viewpoints in confronting a possibilistic constraint: (1) soft and (2) hard approach. In the first approach, by the use of possibility index, they defined the concept of \(\alpha\)-weak feasibility and in the second approach, by the use of necessity index, the concept of \(\alpha\)-hard feasibility was proposed. Notably, the uncertain equality constraints are substituted by two inequalities.

The imprecision of objective function parameters is a common issue which should be handled in optimization problems. Lai and Hwang [37] supposed that these imprecise coefficients in the objective function have triangular possibly distributions. They proposed the substitution of the main objective function by three functions which consist of the most possible, the most pessimistic and the most optimistic value of the main objective function. They stated that for solving the equivalent multi-objective model it is possible to use every multi criterion decision making (MODM) techniques. Rommelfanger et al. [70] assumed that the vector of parameters in objective function is an interval-valued coefficient vector. They substituted the main imprecise objective function by two deterministic objective functions. They also proposed a new approach for the models which their objective function’s coefficients have general convex possibility distribution (i.e., it is not necessary to have only triangular or trapezoidal shapes).

Using the concept of exceedance and strict exceedance defined by Dubois and Prade [16], Negi [55] developed an approach which maximizes the minimum possibility degree of objective function and constraints. Jiménez et al. [29] proposed a new PP approach based on the Jiménez [28] ranking method and the concepts regarding the expected interval (EI) and expected value (EV) of imprecise parameters.

According to the approach used for dealing with possibilistic chance constraints, possibilistic programming approaches can be classified into measure-based possibilistic programming and non-measure-based possibilistic programming methods. In measure-based possibilistic programming, the crisp counterpart of the original problem is constructed based on a fuzzy measure (e.g. necessity measure). However, a Non-measure based possibilistic programming applies other techniques such as fuzzy ranking methods to form the crisp equivalent model. According to Pishvaee et al. [64], there are three main categories in measure-based possibilistic programming as follows: (1) expected value models (2) chance constrained programming (3) depended chance constrained programming. The first approach uses an expected value operator for every imprecise parameter in the objective function and constraints. It can be applied more conveniently without increasing the computational complexity of the original model compared to the two other methods but at the same time it has no control on the confidence level of chance constraints. The second approach is able to control the satisfaction level of constraints by the use of \(\alpha\)-level concept; but also increases the computational complexity since it adds a new constraint for each objective function of the original model. The third approach is somehow similar to the second one but it provides more conservative decision for the decision maker since it gives more importance to maximization of satisfaction levels.

Dubois and Prade [16] defined two basic fuzzy measures including the possibility (Poss) and necessity (Nes) measures. While the first is extremely optimistic, the second is extremely pessimistic. The authors provide definitions for possibility and necessity measure based expected value operators as well as proposing methods for measuring the possibility and necessity of a chance constraint. By the use of these operators different possibilistic programming methods are extended in the literature. Another measure which is proposed by Liu and Liu [42, 43] is credibility measure. Credibility measure can be defined as the average of possibility and necessity measures. Also, Liu and Liu [42, 43] extended an expected value operator based on credibility measure. They developed both expected value and fuzzy chance constrained programming frameworks based on credibility measure. More recently, Xu and Zhou [91] defined Me measure which is an extension to credibility measure. By means of a parameter, this measure is able to adjust the degree of optimism or pessimism in measuring the fuzziness. They also proposed a possibilistic chance constrained programming approach based on Me measure, which was then extended by Torabi et al. [82].

2.1.1 Possibilistic Programming Models for Supply Chain Planning

In this section, firstly, a possibilistic programming model for supply chain network design problem is introduced. This model is adapted from Pishvaee et al. [63] work. Secondly, the method applied in this paper to achieve the crisp counterpart is described. The supply chain under consideration is of a single-product, three-echelon type, which comprises multiple production centers, distribution centers and costumer zones. Aiming at completely fulfill the demands of costumer zones, products are produced in production centers and delivered to customers through one or more distribution centers. The locations and amounts of demands are predefined. There are various candidate positions for establishing capacitated production and distribution centers. In addition, there are various candidate production technologies when a new production center is established in a location. The model must make several decisions regarding the locations and numbers of production and distribution centers as well as the amount of products which are transported between every two nodes of the network. Also the production technology must be specified for every established production center. The indices, parameters and variables that are used in mathematical formulation are as follows.

  • Indices:

i :

index of potential locations for plants \(i = 1,\, \ldots ,\,I\)

j :

index of potential locations for distribution centers \(j = 1,\, \ldots ,\,J\)

k :

index of fixed locations of customers \(k = 1,\, \ldots ,\,K\)

m :

index of different production technologies available for plants \(m = 1,\, \ldots ,\,M\)

  • Parameters:

\(d_{k}\) :

demand of customer zone k

\(f_{i}^{m}\) :

fixed cost of opening plant i with production technology m

\(g_{j}^{{}}\) :

fixed cost of opening distribution center j

\(c_{ij}^{{}}\) :

shipping cost per product unit from plant i to distribution center j

\(a_{jk}^{{}}\) :

shipping cost per product unit from distribution center j to customer k

\(\rho_{i}^{m}\) :

production cost per unit of product at plant i with production technology m

\(\tau_{i}^{{}}\) :

maximum capacity of plant i

\(\varphi_{j}^{{}}\) :

maximum capacity of distribution center j

  • Variables:

\(u_{ij}^{m}\) :

quantity of products produced at plant i with technology m and shipped to distribution center j

\(q_{jk}^{{}}\) :

quantity of products shipped from distribution center j to customer k

\(x_{i}^{m}\) :

\(= \left\{ {\begin{array}{*{20}l} 1 & {{\text{if a plant with technology}}\;m\;{\text{is opened at location }}i} \\ 0 & {\text{otherwise}} \\ \end{array} } \right.\)

y j :

\(= \left\{ {\begin{array}{*{20}l} 1 & {{\text{if a distribution center is opened at location}}\;j,} \\ 0 & {\text{otherwise}} \\ \end{array} } \right.\)

By the use of above-mentioned notations, the formulation of the concerned supply chain network design problem is shown in below.

$${\text{Min W}} = \sum\limits_{i} {\sum\limits_{m} {f_{i}^{m} x_{i}^{m} } } + \sum\limits_{j} {g_{j} y_{j} } + \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{m} {(\rho_{i}^{m} + c_{ij} )u_{ij}^{m} } } } + \sum\limits_{j} {\sum\limits_{k} {a_{jk} q_{jk} } }$$
(1)
$${\text{s}} . {\text{t}} .\;\;\sum\limits_{j} {q_{jk} \ge d_{k} ,\quad \forall\;k,}$$
(2)
$$\sum\limits_{i} {\sum\limits_{m} {u_{ij}^{m} } } = \sum\limits_{k} {q_{jk} } ,\quad \forall\;j,$$
(3)
$$\sum\limits_{j} {u_{ij}^{m} \le x_{i}^{m} \tau_{i}^{{}} } ,\mathop {}\nolimits^{{}} \forall\;i,\,m,$$
(4)
$$\sum\limits_{k} {q_{jk} \le y_{j} \varphi_{j} ,} \quad \forall\;j,$$
(5)
$$\sum\limits_{m} {x_{i}^{m} } \le 1\quad \forall\;i,$$
(6)
$$x_{i}^{m} ,y_{j} \in \left\{ {0,\,1} \right\},\quad \forall\;i,j,m,$$
(7)
$$u_{ij}^{m} ,q_{jk} \ge 0,\quad \forall\;i,\,j,\,m.$$
(8)

Equation (1) is the objective function of the problem which minimizes the total cost and includes summation of fixed opening costs, variable production costs and transportation costs. Constraint (2) is related to ensuring the full satisfaction of demands of all customers. Equation (3) shows material flow balance at each distribution center. Constraints (4) and (5) enforce capacity restrictions on plants and distribution centers and additionally ensure that if a facility is not opened, there will be no shipping from the related location. Equation (6) states that at most one technology can be attributed to each potential plant. Finally, Eqs. (7) and (8) are related to binary and non-negatively decision variables respectively.

As it is mentioned in the relevant literature [58, 62] most of the parameters of supply chain network design problems (e.g. capacities, demand of customers and transportation costs) contaminated by uncertainty in real-world situations because of fluctuation of parameters over the long-term horizon. To cope with this issue, a possibilistic chance constrained programming model is developed here.

For convenience, the supply chain network design model can be summarized in a compact form as follows:

$$\begin{array}{*{20}l} {\text{Min}} \hfill & {z = fy + cx} \hfill \\ {s.t.} \hfill & {Ax \ge d,} \hfill \\ {} \hfill & {Bx = 0,} \hfill \\ {} \hfill & {Sx \le Ny,} \hfill \\ {} \hfill & {Tx \le 1,} \hfill \\ {} \hfill & {y \in \left\{ {0,1} \right\},\quad x \ge 0.} \hfill \\ \end{array}$$
(9)

where the vectors f, c, and d are related to fixed-opening costs, variable transportation and production costs and demands, respectively. The matrices A, B, C, N, S and T are technological coefficient matrices of the constraints. Also, y and x are the vectors of binary decision variables and continuous decision variables, respectively.

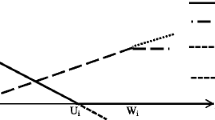
The vectors f, c, and d and coefficient matrix N which respectively are related to fixed opening costs, variable transportation costs, demands and capacity of facilities are the imprecise parameters in the model. Here, trapezoidal possibility distribution (see Fig. 7) is attributed to uncertain parameters. Each trapezoidal possibility distribution can be defined by four prominent points, e.g. \(\tilde{\xi } = (\xi_{(1)} ,\,\xi_{(2)} ,\,\xi_{(3)} \,,\xi_{(4)} )\). It is obvious that if \(\xi_{(2)} = \xi_{(3)}\), the attributed trapezoidal possibility distribution is reduced into a triangular form. The expected value operator is used to defuzzify the objective function and the necessity measure is applied to cope with chance constraints including imprecise parameters.

Fig. 7
figure 7

The trapezoidal possibility distribution of fuzzy parameter \(\tilde{\xi }\)

Full size image

Accordingly, the equivalent possibilistic chance constrained programming model can be formulated as follows:

$$\begin{array}{*{20}l} {\text{Min}} & {{\text{E}}[z] = {\text{E}}[\tilde{f}]y + {\text{E}}[\tilde{c}]x} \\ {s.t.} & {{\text{N}}ec\left\{ {Ax \ge \tilde{d}} \right\} \ge \alpha ,} \\ {} & {Bx = 0,} \\ {} & {{\text{N}}ec\left\{ {Sx \le \tilde{N}y} \right\} \ge \beta ,} \\ {} & {Tx \le 1,} \\ {} & {y \in \left\{ {0,1} \right\},\quad x \ge 0.} \\ \end{array}$$
(10)

Notably, the expected value used for defuzzification of the objective function was firstly developed by Yager [92]. Assume that \(\tilde{\xi }\) is a fuzzy number and its membership function is defined as follow:

$$\mu_{{\tilde{\xi }}} (x) = \left\{ {\begin{array}{*{20}l} {f_{{\tilde{\xi }}} (x),} & {if\;\xi_{(1)} \le x < \xi_{(2)} } \\ {1,} & {if\;\xi_{(2)} \le x \le \xi_{(3)} } \\ {g_{{\tilde{\xi }}} (x),} & {if\;\xi_{(3)} < x \le \xi_{(4)} } \\ {0,} & {if\;x < \xi_{(1)} \;or\;x > \xi_{(4)} } \\ \end{array} } \right.$$

\(E^{*} (\tilde{\xi })\) and \(E_{*} (\tilde{\xi })\) are the upper and lower expected (mean) values of \(\tilde{\xi }\) that can be defined as follow [15, 24]:

$$E^{*} (\tilde{\xi }) = \xi_{(3)} + \int\limits_{{\xi_{(3)} }}^{{\xi_{(4)} }} {g_{{\tilde{\xi }}}^{{}} (x)\,{\text{d}}x}$$
(11)
$$E_{*} (\tilde{\xi }) = \xi_{(2)} - \int\limits_{{\xi_{(1)} }}^{{\xi_{(2)} }} {f_{{\tilde{\xi }}} (x)\,{\text{d}}x}$$
(12)

The expected interval (EI) and expected value (EV) of \(\tilde{\xi }\) based on Eqs. (11) and (12), can be defined as follow [15, 24]:

$$EI[\tilde{\xi }] = [E_{*} (\tilde{\xi }),\,E^{*} (\tilde{\xi })]$$
(13)
$$EV[\tilde{\xi }] = \frac{{E_{*} (\tilde{\xi }) + \,E^{*} (\tilde{\xi })}}{2}$$
(14)

If \(\tilde{\xi }\) is a trapezoidal fuzzy number (see Fig. 7), then we have:

$$EI[\tilde{\xi }] = \left[ {\frac{{\xi_{(1)} + \xi_{(2)} }}{2},\,\frac{{\xi_{(3)} + \xi_{(4)} }}{2}} \right]$$
(15)
$$EV[\tilde{\xi }] = \frac{{\xi_{(1)} + \xi_{(2)} + \xi_{(3)} + \xi_{(4)} }}{4}$$
(16)

Let r be a real number. According to Dubois [13], Dubois and Prade [16] necessity (Nec) of \(\tilde{\xi } \le r\) can be defined as follows:

$${\text{Nec}}\left\{ {\tilde{\xi } \le r} \right\} = 1 - \mathop {\sup }\limits_{x > r} \mu_{{\tilde{\xi }}} (x) = 1 - {\text{Pos}}\left\{ {\tilde{\xi } > r} \right\}$$
(17)

Therefore, the necessity of \(\tilde{\xi } \le r\) can be stated as follows:

$${\text{N}}ec\left\{ {\tilde{\xi } \le r} \right\} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\xi_{(4)} \le r,} \hfill \\ {\frac{{r - \xi_{(3)} }}{{\xi_{(4)} - \xi_{(3)} }},} \hfill & {\xi_{(3)} \le r \le \xi_{(4)} ,} \hfill \\ {0,} \hfill & {\xi_{(3)} \ge r.} \hfill \\ \end{array} } \right.$$
(18)

Based on Eqs. (17) and (18) and with respect to Dubois and Prade [18] and Luhandjula [45], it can be proved that:

$${\text{N}}ec\left\{ {\tilde{\xi } \le r} \right\} \ge \alpha \,\, \Leftrightarrow \,\,r \ge (1 - \alpha )\xi_{(3)} + \alpha \xi_{(4)} .$$
(19)

As there is an assumption that all of uncertain parameters in formulation (11) have trapezoidal possibility distribution, the equivalent crisp model for formulation (11) can be given as follows:

$$\begin{array}{*{20}l} {\text{Min}} \hfill & {{\text{E}}[z] = \left( {\frac{{f_{(1)} + f_{(2)} + f_{(3)} + f_{(4)} }}{4}} \right)y + \left( {\frac{{c_{(1)} + c_{(2)} + c_{(3)} + c_{(4)} }}{4}} \right)x} \hfill \\ {s.t.} \hfill & {Ax \ge (1 - \alpha )d_{(3)} + \alpha d_{(4)} ,} \hfill \\ {} \hfill & {Bx = 0,} \hfill \\ {} \hfill & {Sx \le \left[ {(1 - \beta )N_{(2)} + \beta N_{(1)} } \right]y,} \hfill \\ {} \hfill & {Tx \le 1,} \hfill \\ {} \hfill & {y \in \left\{ {0,\,1} \right\},\quad x \ge 0.} \hfill \\ \end{array}$$
(20)

2.2 Flexible Programming

In a fuzzy environment the meaning of objective function and constraints are somehow different from their classical hard meanings. For example, if a decision maker decides to “decrease the cost considerably”, he/she may prefer to reach some aspiration levels (i.e., flexible targets) rather than strictly minimize the cost. Additionally, “≤”, “=” and “≥” signs in a constraint might not be meant in the strict mathematical sense and slight violation is allowed. In these cases, the fuzzy distributions are attributed to these soft constraints and objective functions based on the preferences of decision makers (DMs). In this framework, the value of attributed membership function shows the degree of DMs’ satisfaction. Luhandjula [45] named this sort of fuzzy mathematical programing as ‘Flexible programming’ .

Flexible programming models can be categorized into two groups [97]: (1) symmetric and (2) non-symmetric. The first one describes the models which both objective function and constraints have flexibility in reaching the target values. In the second category only constraints have fuzzy nature. Figure 8 illustrates some well-known flexible programming methods according to above-mentioned classification.

Fig. 8
figure 8

Classification of different methods of flexible programming

Full size image

Verdegay [87] provided the crisp equivalent parametric programming model for the flexible programming problem with fuzzy constraints. Werners [89] studied the non-symmetric flexible programming problem and proposed a method in which two extreme values of objective function were used to construct a fuzzy membership function in order to attain the satisfaction degree of objective function. Zimmermann [96] applied the Zadeh’s max-min operator to solve the symmetric flexible programming problem model. Chanas [7] argued that due to lack of knowledge about the fuzzy feasible region, the fuzzy membership function of objective function cannot be determined from the beginning. He proposed a framework in which the attributed fuzzy membership is specified using an interactive process.

2.2.1 Flexible Programming Models for Supply Chain Planning

Consider the supply chain network design problem described in Sect. 2.1.1. In that problem it was assumed that capacities, demand of customers, fixed opening costs and variable transportation costs are imprecise parameters. In this section, it is assumed that the demand and capacity constraints are flexible (i.e., soft constraints) and slight violation is allowed. For example, in demand constraints symbol \(\tilde{ \ge }\) is regarded as fuzzy version of \(\ge\) which implies that demand of a customer zone must be essentially less than or somehow similar to the number of products that are delivered to the customer zone. According to Pishvaee and Khalaf [59] and Torabi et al. [83], the model can be represented as follows:

$$\begin{array}{*{20}l} {\text{Min}} \hfill & {z = cx + fy} \hfill \\ {{\text{s}}.{\text{t}}} \hfill & {Ax\tilde{ \ge }d} \hfill \\ {} \hfill & {Bx = 0} \hfill \\ {} \hfill & {Sx\tilde{ \ge }Ny} \hfill \\ {} \hfill & {Ty \le 1} \hfill \\ {} \hfill & {y \in \left\{ {0,1} \right\}, \quad x \ge 0} \hfill \\ \end{array}$$
(21)

Based on Cadenas and Verdegay [3], the violation of soft constraints can be modeled by the use of fuzzy numbers (in this case by \(\tilde{t}\) and \(\tilde{r}\) denoting the maximum allowable tolerances). Therefore, model (21) is rewritten as follows:

$$\begin{array}{*{20}l} {\text{Min}} \hfill & {z = cx + fy} \hfill \\ {s.t.} \hfill & {Ax \ge d - \tilde{t}\left( {1 - \alpha } \right)} \hfill \\ {} \hfill & {Bx = 0} \hfill \\ {} \hfill & {Sx \le Ny + \left[ {\tilde{r}\left( {1 - \beta } \right)} \right]y} \hfill \\ {} \hfill & {Ty \le 1} \hfill \\ {} \hfill & {y \in \left\{ {0,1} \right\}, \quad x \ge 0} \hfill \\ \end{array}$$
(22)

where minimum satisfaction level of flexible constraints are controlled by \(\alpha\) and \(\beta\). Now, we intended to defuzzify formulation (22) based on the fuzzy ranking method suggested by Yager [92, 93]. For this, assume that \(\tilde{t}\) and \(\tilde{r}\) are triangular fuzzy numbers and they are represented by their pessimistic, most possible and optimistic values (i.e., \(\tilde{t} = (t^{p} ,t^{m} ,t^{o} )\) and \(\tilde{r} = (r^{p} ,r^{m} ,r^{o} )\)). These fuzzy numbers can be defuzzified as follows:

$$\left( {t^{m} + \frac{{\varphi_{t} - \varphi_{t}^{{\prime }} }}{3}} \right)$$
(23)
$$\left( {r^{m} + \frac{{h_{r} - h_{r}^{{\prime }} }}{3}} \right)$$
(24)

where parameters \(\varphi_{t}\) and \(\varphi_{t}^{{\prime }}\) (\(h_{r}\) and \(h_{r}^{{\prime }}\)) are lateral margins of the triangular fuzzy number \(\tilde{t}\) (\(\tilde{r}\)) and are defined in Eqs. (25) and (24).

$$\varphi_{t} = t^{o} - t^{m}$$
(25)
$$\varphi_{t}^{{\prime }} = t^{m} - t^{p}$$
(26)

By the use of Eqs. (23) and (24), the crisp counterpart of model (22) is as follows.

$$\begin{array}{*{20}l} {\text{Min}} \hfill & {z = cx + fy} \hfill \\ {s.t.} \hfill & {Ax \ge d - \left( {t^{m} + \frac{{\varphi_{t} - \varphi_{t}^{{\prime }} }}{3}} \right)\left( {1 - \alpha } \right)} \hfill \\ {} \hfill & {Bx = 0} \hfill \\ {} \hfill & {Sx \le Ny + \left[ {\left( {r^{m} + \frac{{h_{r} - h_{r}^{{\prime }} }}{3}} \right)\left( {1 - \beta } \right)} \right]y} \hfill \\ {} \hfill & {Ty \le 1} \hfill \\ {} \hfill & {y \in \left\{ {0,1} \right\},\quad x \ge 0} \hfill \\ \end{array}$$
(27)

Notably, the applied method is capable of supporting different kinds of fuzzy numbers as well as various fuzzy ranking methods when converting the soft constraints to their flexible constraints. Also, the minimum satisfaction level for constraints should be determined in the range of \(0 \le \alpha ,\;\beta \le 1\), subjectively by the decision maker.

2.3 Robust Fuzzy Mathematical Programming

Robust optimization provides a set of risk-averse approaches in confronting with uncertainty, which attempts to obtain a robust solution. A solution is robust, if it has feasibility robustness and optimality robustness, simultaneously [59, 63]. A solution has feasibility robustness if it is feasible under almost all possible realization of uncertain parameters and has optimality robustness if the value of objective function for the obtained solution would remain close to optimal value or have minimum (undesirable) deviation from the optimal value for (almost) all possible values of uncertain parameters. Both of feasibility robustness and optimality robustness could be used as two performance indicators, which examine the validity of a solution for an uncertain problem irrespective of the type of applied uncertainty programming approach.

Pishvaee et al. [63] classify robust optimization approaches into three main categories: (1) hard worst case robust optimization (2) soft worst case robust optimization, and (3) realistic robust optimization. In the first approach, the solution remains feasible under all possible values of uncertain parameters while the worst case value of objective function is optimized. This approach is applicable for those situations in which maximum immunization against uncertainty is needed (e.g. military cases). The second approach argues that it is very unlikely that all of uncertain parameters get their extreme worst case values at the same time. In this approach, similar to the worst case approach, the worst case value of objective function is optimized; however, the feasibility robustness level is not planned for the worst case value. Finally, the third approach seeks to attain a trade-off among the average performance of the objective function, worst case value of the objective function and feasibility robustness. As mentioned before, feasibility robustness and optimality robustness can be used in evaluation of a solution for the problems tainted with uncertainty regardless of the type of uncertainty. Therefore, we can also look for robustness in fuzzy environment and control the feasibility and optimality robustness of a solution. As a pioneer work in this field, Pishvaee et al. [63] proposed three robust possibilistic programming approaches, which are able to control the feasibility and optimality robustness in different degrees. These include: (1) hard worst-case robust possibilistic programming (HWRPP), (2) soft worst-case robust possibilistic programming (SWRPP) and (3) realistic robust possibilistic programming. The first one optimizes the worst possible value of objective function as well as immunizing the solution against the worst-case values of uncertain parameters. This method is indifferent to the forms of uncertain parameters and only considers their extreme worst values. Therefore, there is no need to determine the possibility distributions of uncertain parameters and it is sufficient to only know the support range of each possibility distributions. The second method optimizes the worst value of objective function while considering the penalty cost for constraints’ violations. Thus, this approach is more flexible than HWRPP, because the violation of constraints is permissible to some extent. The third approach attempts to achieve a reasonable trade-off between the average performance, feasibility robustness and optimality robustness. As was mentioned in Sect. 2, the fuzzy mathematical programming consists of possibilistic programming and flexible programming. Until now we introduced some approaches that unified possibilistic programming and robust optimization in the literature. Interested readers can consult with Pishvaee and Khalaf [59] in which new models called robust flexible programming and robust mixed flexible-possibilistic programming have been introduced.

2.3.1 Robust Fuzzy Programming Models for Supply Chain Planning

Consider the supply chain network design problem discussed in Sect. 2.1.1 where capacities, demand of customers, fixed opening costs and variable transportation costs were imprecise parameters formulated by some possibility distributions. Now, based on Pishvaee et al. [63] and for the sake of considering and controlling feasibility and optimality robustness in the mentioned problem, it is reformulated by realistic, hard worst case and soft worst case robust possibilistic programming methods.

  • Realistic robust possibilistic programming model

At first, consider the formulation (20), where vectors f, c, d and coefficient matrix N denote the imprecise parameters regarding the fixed opening costs, variable transportation costs, demands and capacities, respectively. Based on formulation (20), the realistic robust possibilistic formulation of the concerned problem is as follows:

$$\begin{array}{*{20}l} {\text{Min}} \hfill & {{\text{E}}[{\text{z]}} + \gamma (z_{\hbox{max} } - z_{\hbox{min} } ) + \delta [d_{(4)} - (1 - \alpha )d_{(3)} - \alpha d_{(4)} ]} \hfill \\ {} \hfill & { + \pi [\beta N_{(1)} + (1 - \beta )N_{(2)} - N_{1} ]y} \hfill \\ {s.t.} \hfill & {Ax \ge (1 - \alpha )d_{(3)} + \alpha d_{(4)} ,} \hfill \\ {} \hfill & {Bx = 0,} \hfill \\ {} \hfill & {Sx \le \left[ {\beta N_{(1)} + (1 - \beta )N_{(2)} } \right]y,} \hfill \\ {} \hfill & {Tx \le 1,} \hfill \\ {} \hfill & {y \in \left\{ {0,1} \right\},\quad x \ge 0,\;\;0.5 < \alpha ,\;\;\beta \le 1.} \hfill \\ \end{array}$$
(28)

The first term of objective function is the expected value of z. By minimization of the expected value of total cost, the average performance is improved. The second term, \(\gamma (z_{\hbox{max} } - z_{\hbox{min} } )\), indicates the difference between the best (z min ) and worst (z max ) possible values of z. Equation (29) defines these two values.

$$\begin{aligned} z_{\hbox{max} } & = f_{(4)} y + c_{(4)} x, \\ z_{\hbox{min} } & = f_{(1)} y + c_{(1)} x, \\ \end{aligned}$$
(29)

Also, \(\gamma\) indicates the relative importance of \((z_{\hbox{max} } - z_{\hbox{min} } )\) compared to the other terms of objective function. Therefore, \(\gamma (z_{\hbox{max} } - z_{\hbox{min} } )\) controls the maximum deviation from the expected optimal value of objective function (i.e. it controls optimality robustness of the solution). Furthermore, \([d_{(4)} - (1 - \alpha )d_{(3)} - \alpha d_{(4)} ]\) represents the difference between the worst possible value of imprecise demand and the value that is used in right hand side of the chance constraint. Also, \(\delta\) is the unit penalty cost for unsatisfied demand. Therefore, the third term, \(\delta [d_{(4)} - (1 - \alpha )d_{(3)} - \alpha d_{(4)} ]\), indicates the possible violation cost of demand constraint and it is used to control the feasibility robustness of the solution. Similar discussion can be performed for the fourth term in the objective function, i.e., \(\pi [\beta N_{(1)} + (1 - \beta )N_{(2)} - N_{1} ]y\).

Based on the above-mentioned definitions and descriptions, we can say that formulation (22) seeks to reach a reasonable trade-off between the average performance, optimality robustness and feasibility robustness. It should be noted that when the technological coefficients (i.e., matrix N) is tainted with uncertainty the model becomes non-linear (because of multiplication of N and \(\beta\)). To escape from the complexity of such non-linear model, a linearization method is also proposed in Pishvaee et al. [63].

  • Hard worst case robust possibilistic programming model (HWRPP)

In the hard worst case robust programming approach, the solution must be remain feasible under all possible values of imprecise parameters while the worst case value of objective function is optimized. The worst case approach provides the maximum conservation against uncertainty and therefore it is a fully risk-averse approach. Based on above-mentioned descriptions, we can represent the hard worst case robust possibilistic version of the concerned supply chain network design problem (1)–(8) as follows:

$$\begin{array}{*{20}l} {\text{Min}} \hfill & {\sup (z)} \hfill \\ {s.t.} \hfill & {Ax \ge \sup (\tilde{d}),} \hfill \\ {} \hfill & {Bx = 0,} \hfill \\ {} \hfill & {Sx \le \inf (\tilde{N})y,} \hfill \\ {} \hfill & {Tx \le 1,} \hfill \\ {} \hfill & {y \in \left\{ {0,1} \right\},\quad x \ge 0.} \hfill \\ \end{array}$$
(30)

By assuming that the possibility distributions of imprecise parameters are of trapezoidal shape, model (30) can be rewritten as follows:

$$\begin{aligned} & {\text{Min}}\,\,\,\,\,z_{\hbox{max} } \\ & s.t.\,\,\,\,\,\,Ax \ge d_{(4)} , \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,Bx = 0, \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,Sx \le N_{(1)} y, \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,Tx \le 1, \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,y \in \left\{ {0,1} \right\},\,\,\,\,\,\,x \ge 0. \\ \end{aligned}$$
(31)

Notably, HWRPP model does not rely on the form of possibility distribution and it is sufficient to only know the worst possible value of imprecise parameters. It is noteworthy that some other robust possibilistic programming models are also developed by Pishvaee et al. [63] and applied in the literature for coping with uncertainty in different supply chain planning problems (e.g. [51, 95]).

  • Robust flexible programming model

Based on model (27), the robust flexible programming model proposed by Pishvaee and Khalaf [59] can be formulated as follows:

$$\begin{array}{*{20}l} {\text{Min}} \hfill & {E = cx + fy + \gamma \left[ {\left( {t^{m} + \frac{{\varphi_{t} - \varphi_{t}^{{\prime }} }}{3}} \right)\left( {1 - \alpha } \right)} \right] + \theta \left[ {\left( {r^{m} + \frac{{h_{r} - h_{r}^{{\prime }} }}{3}} \right)\left( {1 - \beta } \right)} \right]y} \hfill \\ {s.t.} \hfill & {Ax \ge d - \left( {t^{m} + \frac{{\varphi_{t} - \varphi_{t}^{{\prime }} }}{3}} \right)\left( {1 - \alpha } \right)} \hfill \\ {} \hfill & {Bx = 0} \hfill \\ {} \hfill & {Sx \le Ny + \left[ {\left( {r^{m} + \frac{{h_{r} - h_{r}^{{\prime }} }}{3}} \right)\left( {1 - \beta } \right)} \right]y} \hfill \\ {} \hfill & {Ty \le 1} \hfill \\ {} \hfill & {y \in \left\{ {0,1} \right\}, \quad x \ge 0,\;\;0 \le \alpha ,\beta \le 1} \hfill \\ \end{array}$$
(32)

The last two terms of objective function calculates the total penalty cost of possible violation on soft constraints (i.e., feasibility robustness) while the first two terms are the original objective function of model (27). Indeed, the third and fourth terms represent the difference between the two extreme values of the right hand side of flexible constraints which are defined as follows:

$$\left( {t^{m} + \frac{{\varphi_{t} - \varphi_{t}^{{\prime }} }}{3}} \right)\left( {1 - \alpha } \right) = d - \left[ { d - \left( {t^{m} + \frac{{\varphi_{t} - \varphi_{t}^{{\prime }} }}{3}} \right)\left( {1 - \alpha } \right)} \right]$$
(33)
$$\left[ {\left( {r^{m} + \frac{{h_{r} - h_{r}^{{\prime }} }}{3}} \right)\left( {1 - \beta } \right)} \right]y = \left[ {Ny + \left[ {\left( {r^{m} + \frac{{h_{r} - h_{r}^{{\prime }} }}{3}} \right)\left( {1 - \beta } \right)} \right]y} \right] - Ny$$
(34)

Also, penalty costs are considered for each unit of violation on soft constraints which are presented via parameters \(\upgamma\) and \(\uptheta\) in the proposed model. It should be noted that the model optimizes the values of satisfaction levels (i.e., \(\upalpha\) and \(\upbeta\)) as two variables. As a result, there is no need for iterative subjective experiments by setting different values of \(\upalpha\) and \(\upbeta\). The proposed model belongs to the category of realistic robust programming since it tries to make a reasonable balance between the cost of robustness (i.e., the third and fourth terms of objective function) and the overall performance of the concerned problem (i.e., the first and second terms of objective function). Similar to model (28), the multiplication of N and \(\upbeta\) results in non-linearity of model (32) and therefore a linearization method is provided in Pishvaee and Khalaf [59]. Moreover, some other robust flexible and possibilistic-flexible programming methods are also proposed in Pishvaee and Khalaf [59].

2.4 Fuzzy-Stochastic Programming

Generally there are two main types of uncertainty including fuzziness and randomness. However, in some real world situations, fuzziness and randomness maybe appear simultaneously. We may encounter a random situation whose outcomes are not crisp numbers but fuzzy elements, i.e., in the form of linguistic descriptions. As an example, a situation can be considered in which a group of people are randomly selected and asked about the future weather in a particular day and they response in the form of linguistic descriptions such as “hot”, “very hot” “more or less hot”. Another example of facing with hybrid uncertainty is a model in which a constraint has a random RHS while technological coefficients of the constraint are imprecise parameters extracted from expert opinion in the form of fuzzy numbers.

To cope with an uncertain situation in which the fuzziness and randomness appear simultaneously (i.e., mixed fuzzy-stochastic data), various concepts are proposed in the literature: (1) fuzzy random variable which is introduced by Kwakernaak [35, 36] and refers to a random element whose prominent values are fuzzy; (2) random fuzzy variable which is developed by Liu and Liu [45] and refers to a fuzzy element taking random values as its prominent values; (3) probability of a fuzzy event [94]; (4) probabilistic set [25]; (5) linguistic probabilities [12].

As mathematical programming approaches in the form of linear and mixed integer linear are broadly used in the area of supply chain planning , now we present a classification of fuzzy-stochastic linear programming problems according to Luhandjula [47] and thereafter a number of them are introduced. Luhandjula [47] classified fuzzy stochastic linear programming models as follows:

  • Flexible stochastic linear problems

  • Inclusive-constrained linear programming with fuzzy random variable coefficients

  • Inequality-constrained linear programming with fuzzy random variable coefficients

  • Linear programming with random variables and fuzzy numbers

In flexible stochastic linear problems, since coefficients in constraints and objective functions have random distributions, the objective functions and constraints might not be meant in the strict mathematical sense and slight violations for constraints are permitted. To cope with these problems some symmetric (e.g. [48]; Luhandjula [44] and non-symmetric (e.g. [5, 6] approaches can be found in the literature. In some problems, constraints state that the possible region of LHS occurrence including some ill-defined parameters must be involved in the satisfactory region. In these cases, the problem is in the form of Inclusive-constrained and if it includes fuzzy random variables, the methodology proposed by Luhandjula [47] might be useful.

Inequality-constrained model with fuzzy random variable coefficients is a mathematical programming model in which constraints are in the form of inequality and all of coefficients are in the form of fuzzy random variables. Katagiri and Ishii [30] developed an approach for dealing with these problems in the linear form. Some problems include both random coefficients and fuzzy coefficients simultaneously. To cope with these problems, Luhandjula [46] proposed an approach and applied it in a problem in which the coefficients of the technological matrix are fuzzy numbers while the coefficients of RHS include gamma random variables.

Last but not the least, a supply chain mater planning problem with random fuzzy data is addressed by Vafa Arani and Torabi [84]. In the proposed model, market demand of final products and technical coefficients of the marketable securities are supposed to be random fuzzy variables.

2.4.1 Fuzzy Stochastic Programming Model for Supply Chain Planning

If sufficient and reliable historical data is available for a parameter, a probability distribution can be plausibly attributed to the parameter. For example, consider the demand constraint of formulation (21). It is not a far-fetched situation that the company has recorded its customer orders for a long time and based on this historical data we can attribute a probability distribution to the demands.

$$\begin{array}{*{20}l} {\text{Min}} \hfill & {z = fy + cx} \hfill \\ {s.t.} \hfill & {Ax\tilde{ \le }d,} \hfill \\ {} \hfill & {Bx = 0,} \hfill \\ {} \hfill & {Sx \le Ny,} \hfill \\ {} \hfill & {Tx \le 1,} \hfill \\ {} \hfill & {y \in \left\{ {0,1} \right\},\quad x \ge 0.} \hfill \\ \end{array}$$
(35)

where d is a random variable with cumulative distribution function F and “\(\tilde{ \le }\)” is the flexible version of “\(\le\)”. Now, in a bid to achieve the crisp counterpart of demand constraint we refer to Chakraborty [5] who attributed a membership function to the probability of fuzzy event \((\tilde{P}(Z\tilde{ \le } z))\) as Eq. (36), where Z is a random variable and we are about to calculate the probability of \(Z\tilde{ \le }z\) which “\(\tilde{ \le }\)” denotes the fuzzy nature of the inequality:

$$\mu_{{\tilde{P}\left( {Z\tilde{ \le } z} \right)}} \left( r \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {if\;\;F\left( z \right) = r} \hfill \\ {\frac{{F\left( {z +\Delta z} \right) - r}}{{F\left( {z +\Delta z} \right) - F(z)}},} \hfill & {if \;\;F(z) \le r \le F(z +\Delta z)} \hfill \\ 0 \hfill & {if\;\;r > F(z +\Delta z)} \hfill \\ \end{array} } \right.$$
(36)

Therefore, firstly we should obtain the membership function of \(\tilde{P}(d\tilde{ \le }Ax)\) where d (demand) is a random variable with cumulative function F and r is the target value which determines the satisfaction chance of the concerned constraint. Accordingly, the membership function is formulated as follows:

$$\mu_{{\tilde{P}\left( {d\tilde{ \le } Ax} \right)}} \left( r \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {if\;\;F\left( {Ax} \right) = r} \hfill \\ {\frac{{F\left( {Ax +\Delta Ax} \right) - r}}{{F\left( {Ax +\Delta Ax} \right) - F\left( {Ax} \right)}},} \hfill & {if\;\; F\left( {Ax} \right) \le r \le F\left( {Ax +\Delta Ax} \right)} \hfill \\ 0 \hfill & { if\;\;r > F\left( {Ax +\Delta Ax} \right)} \hfill \\ \end{array} } \right.$$
(37)

\(\Delta Ax\) is determined exogenously by decision maker and it is equal to the maximum allowable amount for violation of the constraint. Now, we can replace the demand constraint by \(\mu_{{\tilde{P}\left( {d\tilde{ \le } Ax} \right)}} \left( r \right) \ge \alpha\) and convert the original model into an equivalent \(\alpha\)-parametric model in which different solutions are obtained for different values of \(\alpha\). It should be noted that the linearity of the replaced equation depends on the linearity of cumulative distribution function of the corresponding random variable.

3 Case Study

As a sample application of fuzzy programming approaches in the context of supply chain planning , a real medical device industrial case is presented in this section. The case study is adopted from Pishvaee et al. [65]. The studied case is an Iranian single-use medical needle and syringe (SMNS) producer entitled AVAPezeshk (AVAP) (www.avapezeshk.com). AVAP has approximately 70 % of the market in Iran and has a production plant with about 600 million production capacity per year for satisfying the customers’ demand. SMNS is a broadly used medical device as WHO [90] stated, 16 billion injections are carried out annually. On the other hand, reusing unsterilized needles and syringes leads to 8–16 million hepatitis B, 2.3–4.7 million hepatitis C and 80,000–160,000 human immunodeficiency virus (HIV) infections per year [90]. Therefore, the efficient management of end-of-life (EOL) SMNS can diminish its undesirable social and environmental effects. There are three main options for EOL SMNS as follows: (1) incineration, (2) safe landfill and (3) recycling by steel and plastic recycling centers. The first method is widely used due to its cost efficiency despite its significant environmental burden like air pollution. The second method also has some adverse environmental impacts and the third is employed rarely due to possibility of infection of end-of-life medical needle. The underling structure of the concerned supply chain is depicted in Fig. 9. Both forward and reverse streams involved in this network. Through the forward flow, new products are transported to customer zones to satisfy demands (unmet demand is not permitted) while in reverse flow, the EOL products which are returned after the consumption, are collected and disassembled by collection centers and then are shipped to recycling, landfill and Incineration centers.

Fig. 9
figure 9

The structure of AVAP supply chain network

Full size image

In Pishvaee et al. [65], a mathematical model is elaborated to address the problem of AVAP supply chain network redesign. The proposed mathematical model determines the number, location and technology of production centers, the number, location and capacity of collection centers as well as the best strategies for returned EOL products aiming to achieve a reasonable trade-off between three dimensions of sustainability, i.e., economical, environmental and social aspects.

The input parameters of the problem are tainted with epistemic uncertainty due to incompleteness and unreliable data. Therefore, it is necessary to refer to an expert for estimating uncertain parameters. In the view of this fact, a group of experts and managers has been formed to attribute a trapezoidal fuzzy number to each uncertain parameter according to their knowledge. The credibility-based chance constrained programming approach which is proposed by Liu and Liu [45, 46] (an briefly described in Sect. 2.1.1) is applied to deal with the concerned possibilistic model. To cope with this multi-objective model a posteriori approach is selected in which the weights of economic, environment and social objectives must be assigned before solving the model. By referring to AVAP managers’ opinions, higher weight is given to economic objective. Particularly, the range 0.8–1 is attributed to the weight of economic objective while the range of 0–0.15 is selected for environment and social objectives. The step size is set to 0.05 and the minimum confidence level of chance constraints is set as 0.9. The above-mentioned model is solved by GAMS 22.9.2 optimization software. As Fig. 10 shows, in the network with objective function weight of (1, 0, 0), in comparison to the network formed for weight vector (0.8, 0.15, 0.05) less collection centers are established and their locations are more centralized. While production centers are located in the same positions for both of instances, the more cost-oriented network, i.e., (1, 0, 0) prefers using the cost-efficient production technology type and the other uses the environmental friendly production technologies. Also, the network with the weight of (0.8, 0.15, 0.05) suggests to open some recycling centers while the network with the weight of (1, 0, 0) selects safe landfill method as the EOL strategy.

Fig. 10
figure 10

The illustration of SC network nodes under different importance weight of OFs (adopted form [65]). aImportance weight: (1, 0, 0). bImportance weight: (0.8, 0.15, 0.05)

Full size image

4 Future Research Directions

Given the current state-of-the-art literature in assessing the uncertainty and the application of fuzzy mathematical programming methods in supply chain planning , there are various avenues for further research as follows:

  • Considering hazard and deep uncertainty in supply chain risk assessment and imbedding these sorts of uncertainty in decision support models in the context of supply chain planning .

  • Assessing and fostering resilience and robustness in different types of decision support models, e.g. mathematical programming models.

  • Lack of mathematical approaches for hybrid uncertain environments in spite of the fact that most of uncertain models involve multiple types of uncertainties. Therefore, there is a serious need for developing novel methods capable of dealing with mixed uncertainties.

  • Since most of real life problems are of large size, and traditional exact solution methods can only solve small to moderate-sized problem instances, devising tailored solution approaches including heuristics, meta-heuristics or Mat-heuristics (the interoperation of meta-heuristics and mathematical programming techniques) would be of particular interest.

  • Controlling the robustness in other flexible and possibilistic programming methods by unifying robust optimization approaches with these methods, can be regarded as an attractive future research direction.

  • Since the robust possibilistic programming and robust flexible programming models are in their infancy, various future researches can be conducted in this regard.