A Survey on Models and Methods for Solving Fuzzy Linear Programming Problems

Abstract

Fuzzy Linear Programming (FLP), as one of the main branches of operation research, is concerned with the optimal allocation of limited resources to several competing activities on the basis of given criteria of optimality in fuzzy environment. Numerous researchers have studied various properties of FLP problems and proposed different approaches for solving them. This work presents a survey on models and methods for solving FLP problems. The solution approaches are divided into four areas: (1) Linear Programming (LP) problems with fuzzy inequalities and crisp objective function, (2) LP problems with crisp inequalities and fuzzy objective function, (3) LP problems with fuzzy inequalities and fuzzy objective function and (4) LP problems with fuzzy parameters. In the first area, the imprecise right-hand-side of the constraints is specified with a fuzzy set and a monotone membership function expressing the individual satisfaction of the decision maker. In the second area, a fuzzy goal and corresponding tolerance is defined for each coefficient of decision variables in the objective function. In the third area, both the coefficients of decision variables in the objective function and the right-hand-side of the constraints are specified by fuzzy goals and corresponding tolerances. In the fourth area, some or all parameters of the LP problem are represented in terms of fuzzy numbers. In this contribution, some of the most common models and procedures for solving FLP problems are analyzed. The solution approaches are illustrated with numerical examples.

1 Introduction

Linear programming (LP) is concerned with the optimal allocation of limited resources to several competing activities on the basis of given criteria of optimality. In conventional LP problems the observed data or parameters are usually imprecise because of incomplete information. Imprecise evaluations are primarily the result of unquantifiable, incomplete and non-obtainable information. Fuzzy Sets theory could be used to represent such imprecise data in LP by generalizing the notion of membership in a set, and a fuzzy LP (FLP) problem appears in a natural way.

In this context, Tanaka et al. [35] first proposed the theory of fuzzy mathematical programming based on the fuzzy decision framework of Bellman and Zadeh [2]. The first formulation of FLP to address the impreciseness of the parameters in LP problems with fuzzy constraints and objective functions has been introduced by Zimmerman [43]. Tanaka and Asai [34] proposed a possibilistic LP formulation where the coefficients of the decision variables were crisp while the decision variables were fuzzy numbers. Verdegay [38] presented the concept of a fuzzy objective based on the fuzzification principle and used this concept to solve FLP problems. Herrera et al. [17] examined the fuzzified version of the mathematical problem assuming that the coefficients are represented in terms of fuzzy numbers and the relations in the definition of the feasible set are also fuzzy. Zhang et al. [42] proposed an FLP where the coefficients of the objective function are assumed to be fuzzy. They showed how to convert the FLP problems into multi-objective optimization problems with four objective functions. Gupta and Mehlawat [15] studied a pair of fuzzy primal-dual LP problems and calculated duality results using an aspiration level approach. Hatami-Marbini and Tavana [16] proposed a new method for solving LP problems with fuzzy parameters. Their method provides an optimal solution that is not subject to specific restrictive conditions and supports the interactive participation of the decision maker in all steps of the decision-making process. Kheirfam and Verdegay [20] carried out a sensitivity analysis on the right-hand-side of the constraints and the coefficients of the objective function for a fuzzy quadratic programming problem. Wan and Dong [39] developed a new possibility LP with trapezoidal fuzzy numbers. They proposed the auxiliary multi-objective programming with four objectives to solve the corresponding possibility LP.

Numerous researchers have studied various properties of FLP problems and proposed different approaches for solving them. Because of existing different assumptions and sources of fuzziness in the parameters, the definition of FLP problem is not unique. Bector and Chandra [1] have classified FLP problems into four following Categories:

• Type 1: LP problems with fuzzy inequalities and crisp objective function

• Type 2: LP problems with crisp inequalities and fuzzy objective function

• Type 3: LP problems with fuzzy inequalities and fuzzy objective function

• Type 4: LP problems with fuzzy parameters

In the FLP problems of Type 1 is assumed that the fuzziness of the available resources is characterized by the membership function over the tolerance range. Verdegay [37] proved that the optimal solution of a problem of this type can be found by use of solving an equivalent crisp parametric LP problem assuming that the objective function is crisp. Werners [40], on the other hands, considered that the objective function should be fuzzy because of fuzzy inequality constraints and proposed a non-symmetric model for solving the FLP problem of Type 1.

In the FLP problems of Type 2 is assumed the coefficient of decision variables in the objective function cannot be precisely determined. For solving a problem of Type 2, Verdegay [37] proposed an equivalent cost parametric LP problem. In addition, Verdegay [38] proved that for a given problem of Type 2 there always exist a problem of Type 1 and has a same solution.

The FLP problem of Type 3 is a combination of Type 1 and Type 2 problems. This means that not only a goal and its corresponding tolerance are considered for the objective function, but also a tolerance for each fuzzy constraint is known. Two important approaches for solving this kind of FLP problems are Zimmerman’s approach [44] and Chanas’s approach [3]. In the proposed approach by Zimmerman is assumed that the goal and its corresponding tolerance of the objective function are given initially. According to this approach, the optimal solution of such problem can be found by solving a crisp LP problem. On the other hand, in the proposed approach by Chanas [3], the goal and its corresponding tolerance are determined by solving two LP problems. Then based on the obtained results and the optimal solution of a crisp parametric LP problem, the optimal solution of such FLP problem is determined.

In the FLP problems of Type 4, the some or all parameters of the problems under consideration may be fuzzy numbers and the inequalities may be interpreted in terms of fuzzy rankings. The solution approaches for solving the problems of Type 4 can be classified into two general groups: Simplex based approach and Non-simplex based approach. In the simplex based approach, the classical simplex algorithms such as primal simplex algorithm, dual simplex algorithm and primal-dual simplex algorithm are generalized for solving LP problems with fuzzy parameters. In this approach, the comparison of fuzzy numbers is done by use of linear ranking functions. On the other hand, in the non-simplex based approach, such FLP problems are first converted into equivalent crisp problems, which are then solved by the standard methods.

Maleki et al. [29] consider a kind of FLP problem in which only the coefficients of decision variables in the objective function are represented in terms of trapezoidal fuzzy numbers. They first proved the fuzzy analogues of some important theorems of LP and then extended the primal simplex algorithm in fuzzy sense to obtain the optimal solution of the LP problems with fuzzy cost coefficients. After that, Nasseri and Ebrahimnejad [30] generalized the dual simplex algorithm in fuzzy sense for solving the same problem based on duality results developed by Mahdavi-Amiri and Nasseri [27]. Another approach namely primal-dual simplex algorithm in fuzzy sense has been proposed by Ebrahimnejad [7] that unlike the dual simplex algorithm does not require a dual feasible solution to be basic. Using these algorithms the sensitivity analysis for the same problem was discussed in [6].

Maleki et al. [29] used the crisp solution of the LP problem with fuzzy cost coefficients as an auxiliary problem, for finding the fuzzy solution of fuzzy variable linear programming (FVLP) problems in which the right-hand-side vectors and decision variables are represented by trapezoidal fuzzy numbers. Mahdavi-Amiri and Nasseri [28] showed that the auxiliary problem is indeed the dual of the FVLP problem and proved duality results by a natural extension of the results of crisp LP. Using these results, Mahdavi-Amiri and Nasseri [28] and Ebrahimnejad et al. [13] developed two new methods in fuzzy sense, namely the fuzzy dual simplex algorithm and the fuzzy primal-dual simplex algorithm, respectively, for solving the FVLP problem directly and without any need of an auxiliary problem. Ebrahimnejad and Verdegay [12] and Ebrahimnejad [8] generalized the bounded simplex algorithms in fuzzy sense for solving that kind of FVLP problems in which some or all variables are restricted to lie within fuzzy lower and fuzzy upper.

Ganesan and Veeramani [14] introduced a type of fuzzy arithmetic for symmetric trapezoidal fuzzy numbers and then proposed a primal simplex method for solving FLP problems in which the coefficients of the constraints are represented by real numbers and all the other parameters as well as the variables are represented by symmetric trapezoidal fuzzy numbers. Nasseri et al. [31] discussed a concept of duality for the same FLP problems and derived the weak and strong duality theorems. Based on these duality results, Ebrahimnejad and Nasseri [11] proposed a duality approach for the same problem for situation in which a fuzzy dual feasible solution is at hand. Kumar and Kaur [23] proposed an alternative method for solving the existing symmetric FLP problem. Ebrahimnejad and Tavana [10] proposed a novel method for solving the same FLP problem which is simpler and computationally more efficient than the above mentioned algorithms.

Kheirfam and Verdegay [19] formulated a new type of FLP problems, namely symmetric fully fuzzy linear programming (SFFLP) problem in which all parameters as well as the decision variables were represented by symmetric trapezoidal fuzzy numbers. Then they established the duality and complementary slackness for the same problems and from the obtained results presented a fuzzy dual simplex for solving SFFLP problems.

For solving the LP problems with fuzzy cost coefficients according to non-simplex based approach some auxiliary programming problems are first defined. The three approaches proposed by Lai and Hwang [25], Rommenlfanger et al. [33] and Delgado et al. [4] are the main approaches for solving this kind of FLP problems.

The proposed approaches by Ramik and Ramanek [32], Tanaka et al. [36] and Dubois and Prade [5] belonging to non-simplex based approach can be used to solve the FLP problems involving fuzzy numbers for the coefficients of the decision variables in the constraints and the right-hand-side of the constraints. Ramik and Ramanek [32] first defined the concept of fuzzy inequality and then converted each fuzzy constraint into three or four crisp constraints depending on triangular and trapezoidal membership functions, respectively. Tanaka et al. [36], based on the concept of $\alpha$-cut, proposed an auxiliary problem for solving this kind of FLP problems by assuming symmetric triangular membership functions for the fuzzy parameters. Dubois and Prade [5] provided two cases of “soft” and “hard” equivalent constraints for the fuzzy constraints of the FLP problem under consideration. Then they expressed the soft and hard constraints by means of $\alpha$-weak feasibility and $\alpha$-hard feasibility, respectively, leading to two separate auxiliary problems.

The FLP problems involving fuzzy numbers for the decision variables, the coefficients of the decision variables in the objective function, the coefficients of the decision variables in the constraints and the right-hand-side of the constraints, is called fully FLP (FFLP) problems. Hosseinzadeh Lotfi et al. [18] considered the FFLP problems where all the parameters and variables were triangular fuzzy numbers. Kumar et al. [24] using arithmetic operations and definition of fuzzy equality, first converted each fuzzy equality constraint into several crisp constraints and then optimized the rank of fuzzy objective function over the obtained crisp feasible space. In contrast to most existing approaches which provide crisp solution, their method not only gives fuzzy optimal solution but also preserve the form of non-negative fuzzy optimal solution and optimal objective function.

The purpose of this chapter is to shortly describe models and methods following the above four types of FLP problems, in order to provide the reader a clear view of the main results produced along the last 50 years on this key research area.

2 Preliminaries

In this section, some necessary concepts and backgrounds on fuzzy arithmetic are reviewed [6, 14, 22, 28, 29].

Definition 1

The characteristic function $\mu_{A}$ of a crisp set $A$ assigns a value of either one or zero to each individual in the universal set $X$. This function can be generalized to a function $\mu_{{\tilde{A}}}$ such that the values assigned to the element of the universal set $X$ fall within a specified range i.e., $\mu_{{\tilde{A}}} :\;X \to [0,1]$. The assigned value indicates the membership grade of the element in the set $\tilde{A}$. Larger values denote the higher degrees of set membership.

The function $\mu_{{\tilde{A}}}$ is called membership function and the set $\tilde{A} = \left\{ {\left( {x,\mu_{{\tilde{A}}} (x)} \right)\left| {x \in X} \right.} \right\}$ defined by $\mu_{{\tilde{A}}}$ for each $x \in X$ is called a fuzzy set.

Definition 2

Given a fuzzy set $\tilde{A}$ defined on universal set of real numbers $X$ and any number $\alpha \in [0,1]$, the $\alpha$-cut of is defined as $[\tilde{A}]_{\alpha } = \left\{ {x \in X;\mu_{{\tilde{A}}} (x) \ge \alpha } \right\}$.

Definition 3

A fuzzy set $\tilde{A}$, defined on universal set of real numbers ${\mathbb{R}}$, is said to be a fuzzy number if its membership function has the following characteristics:

• $\tilde{A}$ is convex, i.e.

  $$ \forall x,y \in {\mathbb{R}},\forall \lambda \in [0,1],\mu_{{\tilde{A}}} \left( {\lambda x + (1 - \lambda )y} \right) \ge \min \left\{ {\mu_{{\tilde{A}}} (x),\mu_{{\tilde{A}}} (y)} \right\}, $$

• $\tilde{A}$ is normal, i.e., $\exists \bar{x} \in {\mathbb{R}};\mu_{{\tilde{A}}} (\bar{x}) = 1,$

• $\mu_{{\tilde{A}}}$ is piecewise continues.

Definition 4

A fuzzy number $\tilde{A}$ is said to be a positive (negative) fuzzy number if for each $x \le 0(x \ge 0),\mu_{{\tilde{A}}} (x) = 0$.

Definition 5

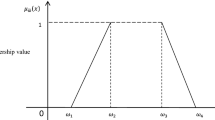
A fuzzy number $\tilde{a} = (a_{1} ,a_{2} ,a_{3} ,a_{4} )$ is said to be a trapezoidal fuzzy number if its membership function is given by (see Fig. 1).

Fig. 1

A trapezoidal fuzzy number $\tilde{a} = (a_{1} ,a_{2} ,a_{3} ,a_{4} )$

$$ \mu_{{\tilde{a}}} (x) = \left\{ {\begin{array}{*{20}c} {\frac{{x - a_{1} }}{{a_{2} - a_{1} }},} & {a_{1} \le x \le a_{2} ,} \\ {1,} & {a_{2} \le x \le a_{3} ,} \\ {\frac{{a_{4} - x}}{{a_{4} - a_{3} }},} & {a_{3} \le x \le a_{4} .} \\ \end{array} } \right. $$

Definition 6

A trapezoidal fuzzy number $\tilde{a} = (a_{1} ,a_{2} ,a_{3} ,a_{4} )$ is said to be a symmetric trapezoidal fuzzy number if $a_{2} - a_{1} = a_{4} - a_{3}$. Assuming $a_{2} - a_{1} = a_{4} - a_{3} = \alpha$, a symmetric trapezoidal fuzzy number is denoted by $\tilde{a} = (a_{2} - \alpha ,a_{2} ,a_{3} ,a_{3} + \alpha )$.

Definition 7

Two trapezoidal fuzzy numbers $\tilde{a} = (a_{1} ,a_{2} ,a_{3} ,a_{4} )$ and $\tilde{b} = (b_{1} ,b_{2} ,b_{3} ,b_{4} )$ are said to be equal, i.e. $\tilde{a} = \tilde{b}$ if and only if $a_{1} = b_{1} ,a_{2} = b_{2} ,a_{3} = b_{3}$ and $a_{4} = b_{4}$.

Definition 8

A trapezoidal fuzzy number $\tilde{a} = (a_{1} ,a_{2} ,a_{3} ,a_{4} )$ is said to be a non-negative trapezoidal fuzzy number if and only if $a_{1} \ge 0$.

Definition 9

A fuzzy number $\tilde{a} = (a_{1} ,a_{2} ,a_{3})$ is said to be a triangular fuzzy number if its membership function is given by

$$ \mu_{{\tilde{a}}} (x) = \left\{ {\begin{array}{*{20}l} {\frac{{x - a_{1} }}{{a_{2} - a_{1} }},} & {a_{1} \le x \le a_{2} ,} \\ {\frac{{a_{3} - x}}{{a_{3} - a_{2} }},} & {a_{2} \le x \le a_{3} .} \\ \end{array} } \right. $$

Definition 10

Let $\tilde{a} = (a_{1} ,a_{2} ,a_{3} ,a_{4} )$ and $\tilde{b} = (b_{1} ,b_{2} ,b_{3} ,b_{4} )$ be two trapezoidal fuzzy numbers. Then the arithmetic operations on $\tilde{a}$ and $\tilde{b}$ are given by:

• $\tilde{a} + \tilde{b} = (a_{1} + b_{1} ,a_{2} + b_{2} ,a_{3} + b_{3} ,a_{4} + b_{4} )$

• $\tilde{a} \otimes \tilde{b} = (m_{1} ,m_{2} ,m_{3} ,m_{4} )$, where

  $$ \begin{aligned} m_{1} & = \min \left\{ {a_{1} b_{1} ,a_{1} b_{4} ,a_{4} b_{1} ,a_{4} b_{4} } \right\},\quad m_{2} = \min \left\{ {a_{2} b_{2} ,a_{2} b_{3} ,a_{3} b_{2} ,a_{3} b_{3} } \right\}, \\ m_{3} & = \max \left\{ {a_{1} b_{1} ,a_{1} b_{4} ,a_{4} b_{1} ,a_{4} b_{4} } \right\},\quad m_{4} = \max \left\{ {a_{2} b_{2} ,a_{2} b_{3} ,a_{3} b_{2} ,a_{3} b_{3} } \right\}, \\ \end{aligned} $$

• $k > 0,k\tilde{a} = (ka_{1} ,ka_{2} ,ka_{3} ,ka_{4} ),$

• $k < 0,k\tilde{a} = (ka_{4} ,ka_{3} ,ka_{2} ,ka_{1} ).$

Definition 11

For any two fuzzy numbers $\tilde{a}$ and $\tilde{b}$, the operations ${\text{MIN}}$ and ${\text{MAX}}$ are defined as follows:

$$ \begin{aligned} {\text{MIN}}\left( {\tilde{a},\tilde{b}} \right)(z) & = \mathop {\sup }\limits_{z = \min (x,y)} \min \left[ {\mu_{{\tilde{a}}} (x),\mu_{{\tilde{b}}} (y)} \right] \\ {\text{MAX}}\left( {\tilde{a},\tilde{b}} \right)(z) & = \mathop {\sup }\limits_{z = \max (x,y)} \min \left[ {\mu_{{\tilde{a}}} (x),\mu_{{\tilde{b}}} (y)} \right] \\ \end{aligned} $$

Theorem 1

Let ${\text{MIN}}$ and ${\text{MAX}}$ be binary operations on the set of all fuzzy numbers $F({\mathbb{R}})$ defined in Definition 11 . Then, the triple $\left\langle {F({\mathbb{R}}),{\text{MIN}},{\text{MAX}}} \right\rangle$ is a distributive lattice.

Remark 1

The lattice $\left\langle {F({\mathbb{R}}),{\text{MIN}},{\text{MAX}}} \right\rangle$ can also be expressed as the pair $\left\langle {F({\mathbb{R}}),\,\preceq \,}\right\rangle$, where $\preceq$ is a partial ordering defined as:

$$ \begin{aligned} & \tilde{a}\,\preceq\, \tilde{b} \Leftrightarrow {\text{MIN}}\left( {\tilde{a},\tilde{b}} \right) = \tilde{a}\;{\text{or}},\;{\text{alternatively}}, \\ & \tilde{a}\,\preceq \,\tilde{b} \Leftrightarrow {\text{MAX}}\left( {\tilde{a},\tilde{b}} \right) = \tilde{b}. \\ \end{aligned} $$

Remark 2

For any two trapezoidal fuzzy numbers $\tilde{a} = (a_{1} ,a_{2} ,a_{3} ,a_{4} )$ and $\tilde{b} = (b_{1} ,b_{2} ,b_{3} ,b_{4} )$, ${\text{MAX}}\left( {\tilde{a},\tilde{b}} \right) = \tilde{b}$ or $\tilde{a}\,\preceq\, \tilde{b}$ if and only if $a_{1} \le b_{1} ,a_{2} \le b_{2} ,a_{3} \le b_{3}$ and $a_{4} \le b_{4}$.

Definition 12

A ranking function is a function $\Re :\;F({\mathbb{R}}) \to {\mathbb{R}}$ that maps each fuzzy number into the real line, where a natural order exists. A ranking function $\Re$ is said to be a linear ranking function if $\Re (k\tilde{a}_{1} + \tilde{a}_{2} ) = k\Re (\tilde{a}_{1} ) + \Re (\tilde{a}_{2} )$ for any $k \in {\mathbb{R}}$.

Remark 3

For a trapezoidal fuzzy number $\tilde{a} = (a_{1} ,a_{2} ,a_{3} ,a_{4} )$, one of the most linear ranking functions introduced by Yager [41] is $\Re (\tilde{a}_{1} ) = \frac{{a_{1} + a_{2} + a_{3} + a_{4} }}{4}.$

Remark 4

For a triangular fuzzy number $\tilde{a} = (a_{1} ,a_{2} ,a_{3} )$, Yager’s linear ranking function is reduced to $\Re (\tilde{a}_{1} ) = \frac{{a_{1} + 2a_{2} + a_{3} }}{4}.$

3 LP with Fuzzy Inequalities and Crisp Objective Function

The general model of LP problems with fuzzy inequalities and crisp objective function is formulated as follows:

$$ \begin{aligned} & \max z = \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \\ & s.t.\;\;g_{i} (x) = \sum\limits_{j = 1}^{n} {a_{ij} x_{j} \,\precsim\, b_{i} ,} \quad i = 1,2, \ldots ,m, \\ & \quad \quad x_{j} \ge 0,\quad j = 1,2, \ldots ,n. \\ \end{aligned} $$

(1)

In model (1), $\precsim$ is called “less than or equal to” and it is assumed that tolerance $p_{i}$ for each constraint is given. This means that the decision maker can accept a violation of each constraint up to degree $p_{i}$. In this case, constraints $g_{i} (x)\,\precsim\, b_{i} ,$ are equivalent to $g_{i} (x) \le b_{i} + \theta p_{i} ,(i = 1,2, \ldots ,m)$, where $\theta \in [0,1]$.

Verdegay [37] and Werners [40] considered two solution methods namely nonsysmmetric method and symmetric method, respectively, for solving the FLP problem (1). In what follows, theses solution approaches are discussed.

3.1 Verdegay’s Approach

Verdegay [37] proved that the FLP problem (1) is equivalent to crisp parametric LP problem when the membership functions of the fuzzy constraints are continues and non-increasing functions. According to his approach, the membership functions of the fuzzy constraints of problem (1) can be modeled as follows:

$$ \mu_{i} \left( {g_{i} (x)} \right) = \left\{ {\begin{array}{*{20}l} {1,} & {g_{i} (x) < b_{i} ,} \\ {1 - \frac{{g_{i} (x) - b_{i} }}{{p_{i} }},} & {b_{i} \le g_{i} (x) \le b_{i} + p_{i} ,} \\ {0,} & {g_{i} (x) > b_{i} + p_{i} .} \\ \end{array} } \right. $$

(2)

In this case, FLP problem (1) is equivalent to:

$$ \begin{aligned} & \max z = \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \\ & s.t.\;\;\mu_{i} \left( {g_{i} (x)} \right) \ge \alpha ,\quad i = 1,2, \ldots ,m, \\ & \quad \quad \alpha \in [0,1],\quad x_{j} \ge 0,\quad j = 1,2, \ldots ,n. \\ \end{aligned} $$

(3)

Now, by substituting membership functions (2) into problem (3), the following crisp parametric LP problem is obtained:

$$ \begin{aligned} & \max z = \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \\ & s.t.\;\;g_{i} (x) = \sum\limits_{j = 1}^{n} {a_{ij} x_{j} } \le b_{i} + (1 - \alpha )p_{i} ,\quad i = 1,2, \ldots ,m, \\ & \quad \quad \alpha \in [0,1],\quad x_{j} \ge 0,\quad j = 1,2, \ldots ,n. \\ \end{aligned} $$

(4)

It should be note that for each $\alpha \in [0,1]$, an optimal solution is obtained. This indicates that the solution with $\alpha$ grade of membership function is actually fuzzy.

Example 1

[26] Consider the following FLP problem:

$$ \begin{aligned} & \max z = 4x_{1} + 5x_{2} + 9x_{3} + 11x_{4} \\ & s.t.\;\;g_{1} (x) = x_{1} + x_{2} + x_{3} + x_{4} \le 15, \\ & \quad g_{2} (x) = 7x_{1} + 5x_{2} + 3x_{3} + 2x_{4} \le 120, \\ & \quad g_{3} (x) = 3x_{1} + 5x_{2} + 10x_{3} + 15x_{4} \le 100, \\ & \quad x_{1} ,x_{2} ,x_{3} ,x_{4} \ge 0. \\ \end{aligned} $$

(5)

Assume that the first and third constrains are imprecise and their maximum tolerances are 3 and 20, respectively, i.e. $p_{1} = 3$ and $p_{3} = 20$. Then, according to (4), the following crisp parametric LP problem is solved:

$$ \begin{aligned} & \max z = 4x_{1} + 5x_{2} + 9x_{3} + 11x_{4} \\ & s.t.\;\;g_{1} (x) = x_{1} + x_{2} + x_{3} + x_{4} \le 15 + 3(1 - \alpha ), \\ & \quad \quad g_{2} (x) = 7x_{1} + 5x_{2} + 3x_{3} + 2x_{4} \le 120, \\ & \quad \quad g_{3} (x) = 3x_{1} + 5x_{2} + 10x_{3} + 15x_{4} \le 100 + 20(1 - \alpha ), \\ & \quad \quad x_{1} ,x_{2} ,x_{3} ,x_{4} \ge 0. \\ \end{aligned} $$

(6)

By use of the parametric technique the optimal solution and the optimal objective value are obtained as follows:

$$ \begin{aligned} x^{*} & = \left( {7.14 + 1.43(1 - \alpha ),0,7.86 + 1.57(1 - \alpha ),0} \right), \\ z^{*} & = 99.29 + 19.86(1 - \alpha ) \\ \end{aligned} $$

(7)

3.2 Werners’s Approach

In the symmetric method proposed by Werners [40], it is assumed that the objective function of problem (1) should be fuzzy because of fuzzy inequality constraints. For doing this, he calculated the lower and upper bounds of the optimal values by solving the standard LP problems (8) and (9), respectively, as follows:

$$ \begin{aligned} & z^{l} = \max z = \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \\ & s.t.\;\;\sum\limits_{j = 1}^{n} {a_{ij} x_{j} } \le b_{i} ,\quad i = 1,2, \ldots ,m, \\ & \quad \quad x_{j} \ge 0,\quad j = 1,2, \ldots ,n. \\ \end{aligned} $$

(8)

$$ \begin{aligned} & z^{u} = \max z = \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \\ & s.t.\;\;\sum\limits_{j = 1}^{n} {a_{ij} x_{j} \le b_{i} + p_{i} ,} \quad i = 1,2, \ldots ,m, \\ & \quad \quad x_{j} \ge 0,\quad j = 1,2, \ldots ,n. \\ \end{aligned} $$

(9)

In this case, the membership function of the objective function is defined as follows:

$$ \mu_{0} (z) = \left\{ {\begin{array}{*{20}l} {1,} & {z > z^{u} ,} \\ {1 - \frac{{z^{u} - z}}{{z^{u} - z^{l} }},} & {z^{l} \le z \le z^{u} ,} \\ {0,} & {z < z^{l} .} \\ \end{array} } \right. $$

(10)

Now, problem (1) can be solved by solving the following problem, a problem of finding a solution that satisfies the constraints and goal with the maximum degree:

$$ \begin{aligned} & \max z = \alpha \\ & s.t.\;\;\mu_{0} (z) \ge \alpha , \\ & \quad \;\;\mu_{i} \left( {g_{i} (x)} \right) \ge \alpha ,\quad i = 1,2, \ldots ,m, \\ & \quad \;\;\alpha \in [0,1],\quad x_{j} \ge 0,\quad j = 1,2, \ldots ,n. \\ \end{aligned} $$

(11)

By substituting the membership functions of the constraints given in (2) and the membership function of the objective function given in (10) into problem (11), the following crisp LP problem is obtained:

$$ \begin{aligned} & \max \alpha \\ & s.t.\;\;\sum\limits_{j = 1}^{n} {c_{j} x_{j} \ge z^{l} - (1 - \alpha )(z^{u} - z^{l} ),} \\ & \quad \quad g_{i} (x) = \sum\limits_{j = 1}^{n} {a_{ij} x_{j} \le b_{i} + (1 - \alpha )p_{i} ,\quad i = 1,2, \ldots ,m,} \\ & \quad \quad \alpha \in [0,1],\quad x_{j} \ge 0,\quad j = 1,2, \ldots ,n. \\ \end{aligned} $$

(12)

Example 2

[22] Consider the following FLP problem:

$$ \begin{aligned} & \max z = 0.4x_{1} + 0.3x_{2} \\ & s.t.\;\;g_{1} (x) = x_{1} + x_{2} \le \mathop {400}\limits^{ \sim } , \\ & \quad \;\;g_{2} (x) = 2x_{1} + x_{2} \le \mathop {500}\limits^{ \sim } , \\ & \quad \;\;x_{1} ,x_{2} \ge 0. \\ \end{aligned} $$

(13)

where the membership functions of the fuzzy constraints are defined by:

$$ \mu_{1} (x) = \left\{ {\begin{array}{*{20}l} {1,} & {g_{1} (x) < 400,} \\ {1 - \frac{{g_{1} (x) - 400}}{100},} & {400 \le g_{1} (x) \le 500,} \\ {0,} & {g_{1} (x) > 500.} \\ \end{array} } \right. $$

(14)

$$ \mu_{2} (x) = \left\{ {\begin{array}{*{20}l} {1,} & {g_{2} (x) < 500,} \\ {1 - \frac{{g_{2} (x) - 500}}{100},} & {500 \le g_{2} (x) \le 600,} \\ {0,} & {g_{2} (x) > 600.} \\ \end{array} } \right. $$

(15)

Then, the lower and upper bounds of the objective function are calculated by solving the following two crisp LP problems (16) and (17), respectively:

$$ \begin{aligned} & z^{l} = \max z = 0.4x_{1} + 0.3x_{2} \\ & s.t.\;\;g_{1} (x) = x_{1} + x_{2} \le 400, \\ & \quad \;\;g_{2} (x) = 2x_{1} + x_{2} \le 500, \\ & \quad \;\;x_{1} ,x_{2} \ge 0. \\ \end{aligned} $$

(16)

$$ \begin{aligned} & z^{u} = \max z = 0.4x_{1} + 0.3x_{2} \\ & s.t.\;\;g_{1} (x) = x_{1} + x_{2} \le 500, \\ & \quad \;\;g_{2} (x) = 2x_{1} + x_{2} \le 600, \\ & \quad \;\;x_{1} ,x_{2} \ge 0. \\ \end{aligned} $$

(17)

Solving two problems (16) and (17) give $z^{l} = 130$ and $z^{u} = 160$, respectively. Then, the membership function $\mu_{0}$ of the objective function is defined as follows:

$$ \mu_{0} (z) = \left\{ {\begin{array}{*{20}l} {1,} & {z > 160,} \\ {1 - \frac{160 - z}{30},} & {130 \le z \le 160,} \\ {0,} & {z < 130.} \\ \end{array} } \right. $$

(18)

Then, according to problem (12), the FLP problem (13) becomes:

$$ \begin{aligned} & \max \alpha \\ & s.t.\;\;0.4x_{1} + 0.3x_{2} \ge 130 - 30(1 - \alpha ), \\ & \quad \;\;g_{1} (x) = x_{1} + x_{2} \le 400 + 100(1 - \alpha ), \\ & \quad \;\;g_{2} (x) = 2x_{1} + x_{2} \le 500 + 100(1 - \alpha ), \\ & \quad \;\;\alpha \in [0,1],\quad x_{1} ,x_{2} \ge 0,\quad j = 1,2, \ldots ,n. \\ \end{aligned} $$

(19)

The optimal solution of the problem (19) is $x^{*} = \left( {x_{1}^{*} ,x_{2}^{*} } \right) = (100,350),\alpha^{ * } = 0.5$. The optimal value of the objective function is then calculated by

$$ z^{*} = 0.4x_{1}^{*} + 0.3x_{2}^{*} = 145. $$

4 LP with Crisp Inequalities and Fuzzy Objective Function

The general from of LP problems with crisp inequalities and fuzzy objective function can be formulated as follows:

$$ \begin{aligned} & \mathop {\max} \limits^{ \sim } z = \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \\ & s.t.\;\;g_{i} (x) = \sum\limits_{j = 1}^{n} {a_{ij} x_{j} } \le b_{i} ,\quad i = 1,2, \ldots ,m, \\ & \quad \;\;x_{j} \ge 0,\quad j = 1,2, \ldots ,n. \\ \end{aligned} $$

(20)

Assume that the membership function of the fuzzy objective be given by

$$ \phi (c) = \inf \left\{ {\phi_{1} (c_{1} ),\phi_{2} (c_{2} ), \ldots ,\phi_{n} (c_{n} )} \right\} $$

(21)

In this case, Verdegay [38] proved that if the membership function $\phi_{j} (c_{j} ):{\mathbb{R}} \to [0,1],(j = 1,2, \ldots ,n)$, are continues and strictly monotone, then the fuzzy optimal solution of problem (20) can be obtained by solving the following parametric LP problem:

$$ \begin{aligned} & \max z = \sum\limits_{j = 1}^{n} {\phi_{j}^{ - 1} (1 - \alpha )x_{j} } \\ & s.t.\;\;g_{i} (x) = \sum\limits_{j = 1}^{n} {a_{ij} x_{j} } \le b_{i} ,\quad i = 1,2, \ldots ,m, \\ & \quad \;\;\alpha \in [0,1],\quad x_{j} \ge 0,\quad j = 1,2, \ldots ,n. \\ \end{aligned} $$

(22)

Example 3

[38] Consider the following FLP problem:

$$ \begin{aligned} & \mathop {\max} \limits^{ \sim } z = c_{1} x_{1} + 75x_{2} \\ & s.t.\;\;g_{1} (x) = 3x_{1} - x_{2} \le 2, \\ & \quad \;\;g_{2} (x) = x_{1} + 2x_{2} \le 3, \\ & \quad \;\;x_{1} ,x_{2} \ge 0. \\ \end{aligned} $$

(23)

where the membership function $\phi_{1}$ for $c_{1}$ is given by:

$$ \phi_{1} (c_{1} ) = \left\{ {\begin{array}{*{20}l} {1,} & {c_{1} > 115,} \\ {\frac{{(c_{1} - 40)^{2} }}{5625},} & {40 \le c_{1} \le 115,} \\ {0,} & {c_{1} < 40.} \\ \end{array} } \right. $$

(24)

Then, we have $\phi_{1}^{ - 1} (t) = 40 + 75\sqrt t$. Now, according to model (20) we have to solve the following problem:

$$ \begin{aligned} & \max z = \left( {40 + 75\sqrt {1 - \alpha } } \right)x_{1} + 75x_{2} \\ & s.t.\;\;g_{1} (x) = 3x_{1} - x_{2} \le 2, \\ & \quad \;\;g_{2} (x) = x_{1} + 2x_{2} \le 3, \\ & \quad \;\;\alpha \in [0,1],\quad x_{1} ,x_{2} \ge 0. \\ \end{aligned} $$

(25)

By use of the parametric technique, the optimal solution of problem (25) is $x^{*} = (x_{1}^{*} ,x_{2}^{*} ) = (1,1)$. The fuzzy set of the objective function values of the objective function is then obtained as follows:

$$ \left\{ {(75 + c_{1} ),\frac{{(c_{1} - 40)^{2} }}{5625}} \right\},\quad 40 \le c_{1} \le 115. $$

5 LP with Fuzzy Inequalities and Fuzzy Objective Function

The general from of LP problems with fuzzy inequalities and fuzzy objective function can be formulated as follows:

$$ \begin{aligned} & \mathop {\max}\limits^{ \sim } z = \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \\ & s.t.\;\;g_{i} (x) = \sum\limits_{j = 1}^{n} {a_{ij} x_{j} \,\precsim \,b_{i} ,\quad i = 1,2, \ldots ,m,} \\ & \quad \;\;x_{j} \ge 0,\quad j = 1,2, \ldots ,n. \\ \end{aligned} $$

(26)

In what follows, two solution approaches for solving FLP of type (26) are explored.

5.1 Zimmerman’s Approach [43]

According to this approach, the membership functions $\mu_{i} (i = 1,2, \ldots ,m)$ of the fuzzy constraints are given by (2). Also, it is required to have an aspiration level $z_{0}$ for the objective function. In this case, problem (26) can be described as follows:

$$ \begin{aligned} & Find\;x \\ & s.t.\;\;z = \sum\limits_{j = 1}^{n} {c_{j} x_{j} \,\succsim \,z_{0} } \\ & \quad \;\;g_{i} (x) = \sum\limits_{j = 1}^{n} {a_{ij} x_{j} \,\precsim\, b_{i} ,\quad i = 1,2, \ldots ,m,} \\ & \quad \;\;x_{j} \ge 0,\quad j = 1,2, \ldots ,n. \\ \end{aligned} $$

(27)

Assuming $p_{0}$ be the permissible tolerance for the objective function, the membership function $\mu_{0}$ of the fuzzy objective is given by

$$ \mu_{0} (z) = \left\{ {\begin{array}{*{20}l} {1,} & {z > z_{0} ,} \\ {1 - \frac{{z_{0} - z}}{{p_{0} }},} & {z_{0} - p_{0} \le z \le z_{0} ,} \\ {0,} & {z < z_{0} - p_{0} .} \\ \end{array} } \right. $$

(28)

In this case, to solve the fuzzy system of inequalities (27) corresponding to problem (26), the following crisp LP problem is solved:

$$ \begin{aligned} & \max \alpha \\ & s.t.\;\;\mu_{0} (z) \ge \alpha , \\ & \quad \;\;\mu_{i} \left( {g_{i} (x)} \right) \ge \alpha ,\quad i = 1,2, \ldots ,m, \\ & \quad \;\;\alpha \in [0,1],\quad x_{j} \ge 0,\quad j = 1,2, \ldots ,n. \\ \end{aligned} $$

(29)

By substituting the membership functions of the fuzzy constraints given in (2) and the membership function of the objective function given in (28) into problem (29), the following crisp LP problem is obtained:

$$ \begin{aligned} & \max \alpha \\ & s.t.\;\;\sum\limits_{j = 1}^{n} {c_{j} x_{j} \ge z_{0} - (1 - \alpha )p_{0} ,} \\ & \quad \;\;\sum\limits_{j = 1}^{n} {a_{ij} x_{j} } \le b_{i} + (1 - \alpha )p_{0} ,\quad i = 1,2, \ldots ,m, \\ & \quad \;\;\alpha \in [0,1],\quad x_{j} \ge 0,\quad j = 1,2, \ldots ,n. \\ \end{aligned} $$

(30)

It needs to point out that if $(x^{*} ,\alpha^{*} )$ is an optimal solution of the crisp LP problem (30), then it is said to be an optimal solution of the FLP problem (26) with $\alpha^{*}$ as the degree up to which the aspiration level $z_{0}$ of the decision maker is satisfied.

Example 4

[43] Consider the following FLP problem:

$$ \begin{aligned} & \mathop {\max}\limits^{ \sim } z = x_{1} + x_{2} \\ & s.t.\;\;g_{1} (x) = - x_{1} + 3x_{2} \,\precsim\, 21, \\ & \quad \;\;g_{2} (x) = x_{1} + 3x_{2} \,\precsim \,27, \\ & \quad \;\;g_{3} (x) = 4x_{1} + 3x_{2} \,\precsim\, 45, \\ & \quad \;\;g_{4} (x) = 3x_{1} + x_{2} \le 30, \\ & \quad \;\;x_{1} ,x_{2} \ge 0. \\ \end{aligned} $$

(31)

Assume that $z_{0} = 14.5,p_{0} = 2,p_{1} = 3,p_{2} = 6,$ and $p_{3} = 6$. To obtain the optimal solution of problem (31), we have to solve the following crisp LP problem with regard to problem (30):

$$ \begin{aligned} & \max \alpha \\ & s.t.\;\;z = x_{1} + x_{2} \ge 14.5 - 2(1 - \alpha ) \\ & \quad \;\;g_{1} (x) = - x_{1} + 3x_{2} \le 21 - 3(1 - \alpha ), \\ & \quad \;\;g_{2} (x) = x_{1} + 3x_{2} \le 27 - 6(1 - \alpha ), \\ & \quad \;\;g_{3} (x) = 4x_{1} + 3x_{2} \le 45 - 6(1 - \alpha ), \\ & \quad \;\;g_{4} (x) = 3x_{1} + x_{2} \le 30, \\ & \quad \;\;x_{1} ,x_{2} \ge 0. \\ \end{aligned} $$

(32)

The optimal solution of the crisp LP problem (32) is $(x_{1}^{*} ,x_{2}^{*} ,\alpha^{*} ) = (6,7.75,0.625)$ with the optimal objective function value $z^{*} = 13.75$. Then, $(x_{1}^{*} ,x_{2}^{*} ) = (6,7.75)$ is the optimal solution of the FLP problem (31).

5.2 Chanas’s Approach

In this approach, it is assumed that the decision maker cannot provide initially the goal and its tolerance for the objective function. Chanas [3] therefore proposed first to solve the following problem and then present the results to the decision maker to estimate the goal and the tolerance of the objective function:

$$ \begin{aligned} & \max z = \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \\ & s.t.\;\;g_{i} (x) = \sum\limits_{j = 1}^{n} {a_{ij} x_{j} \,\precsim\, b_{i} ,\quad i = 1,2, \ldots ,m,} \\ & \quad \;\;x_{j} \ge 0,\quad j = 1,2, \ldots ,n. \\ \end{aligned} $$

(33)

In this problem, the membership functions of the fuzzy constraints are assumed as Eq. (2). Therefore, following the Verdegay’s approach [38] and assuming $\theta = 1 - \alpha$ the problem (33) becomes:

$$ \begin{aligned} & \max z = \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \\ & s.t.\;\;g_{i} (x) = \sum\limits_{j = 1}^{n} {a_{ij} x_{j} } \le b_{i} + \theta p_{i} ,\quad i = 1,2, \ldots ,m, \\ & \quad \;\;\theta \in [0,1],\quad x_{j} \ge 0,\quad j = 1,2, \ldots ,n. \\ \end{aligned} $$

(34)

The optimal solution of the parametric LP problem (34) can be found by use of the parametric techniques. For a given $\theta$, assume that $x^{*} (\theta )$ and $z^{*} (\theta )$ are, respectively an optimal solution and the corresponding optimal objective value of the parametric LP problem (34). Then, the following constrains are hold:

$$ \mu_{i} \left( {g_{i} (x^{*} (\theta ))} \right) \ge 1 - \theta ,\quad i = 1,2, \ldots ,m, $$

(35)

On the other hand, in the case of $p_{i} > 0$, for every non-zero basic solution, there is at least one $i$ such that $\mu_{i} \left( {g_{i} (x^{*} (\theta ))} \right) = 1 - \theta$. This follows that the common degree of the constraints satisfaction is $\mu_{c} \left( {g(x^{*} (\theta ))} \right) = \min_{1 \le i \le m} \mu_{i} \left( {g_{i} (x^{*} (\theta ))} \right) = 1 - \theta$. This means that for every $\theta$, a solution can be obtained which satisfies all the constraints with degree $1 - \theta$. Now, such solution is presented to the decision maker to determine the goal $z_{0}$ of the objective function and its tolerance $p_{0}$. Therefore, the membership function $\mu_{0}$ of the objective function becomes:

$$ \mu_{0} (z^{*} (\theta )) = \left\{ {\begin{array}{*{20}l} {1,} & {z^{*} (\theta ) > z_{0} ,} \\ {1 - \frac{{z_{0} - z^{*} (\theta )}}{{p_{0} }},} & {z_{0} - p_{0} \le z^{*} (\theta ) \le z_{0} ,} \\ {0,} & {z^{*} (\theta ) < z_{0} .} \\ \end{array} } \right. $$

(36)

In this case, the final optimal solution $x^{*} (\theta^{*} )$ of the FLP problem (26) will exist at:

$$ \mu_{D} (\theta^{*} ) = \max \left\{ {\mu_{D} (\theta )} \right\} = \mu_{c} \left( {g(x^{*} (\theta ))} \right) = \max \left\{ {\min \left\{ {\mu_{o} (\theta ),\mu_{c} (\theta )} \right\}} \right\} $$

This approach can be summarized as follows:

Step 1::

Solve the parametric LP problem (34) to determine $x^{*} (\theta )$ and $z^{*} (\theta )$.

Step 2::

Determine an appropriate value $\theta$ to get $z_{0}$ and choose $p_{0}$.

Step 3::

Obtain the membership function $\mu_{0} (z^{*} (\theta ))$ as (36).

Step 4::

Set $\mu_{c} = \mu_{0} = 1 - \theta$ to find $\theta^{*}$.

Step 5::

The optimal solution of the FLP problem (26) is $x^{*} (\theta^{*} )$ with the optimal objective value $z^{*} (\theta^{*} )$.

Example 5

Again, consider the FLP problem (31) with $p_{1} = 3, \, p_{2} = 6,$ and $p_{3} = 6$.

The solution procedure is illustrated as follows:

Step 1::

According to problem (34), the following parametric LP problem should be solved:

$$ \begin{aligned} & \max z = x_{1} + x_{2} \\ & s.t.\;\;g_{1} (x) = - x_{1} + 3x_{2} \le 21 + 3\theta , \\ & \quad \;\;g_{2} (x) = x_{1} + 3x_{2} \le 27 + 6\theta , \\ & \quad \;\;g_{3} (x) = 4x_{1} + 3x_{2} \le 45 + 6\theta , \\ & \quad \;\;g_{4} (x) = 3x_{1} + x_{2} \le 30, \\ & \quad \;\;\theta \in [0,1],\quad x_{1} ,x_{2} \ge 0. \\ \end{aligned} $$

(37)

The optimal solution is $x^{*} (\theta ) = \left( {x_{1}^{*} (\theta ),x_{2}^{*} (\theta )} \right) = \left( {6,7 + 2\theta } \right)$ with $z^{*} (\theta ) = 13 + 2\theta$.

Step 2::

Assume $z_{0} = 14$ and choose $p_{0} = 1$.

Step 3::

Now, the membership function $\mu_{0} (z^{*} (\theta ))$ is then given by

$$ \mu_{0} (z^{*} (\theta )) = \left\{ {\begin{array}{*{20}l} {1,} & {13 + 2\theta > 14,} \\ {1 - \frac{{14 - \left( {13 + 2\theta } \right)}}{1} = 2\theta ,} & {13 \le 13 + 2\theta \le 14,} \\ {0,} & {13 + 2\theta < 14.} \\ \end{array} } \right. $$

(38)

Step 4::

In order to find $\theta^{*}$, we set $\mu_{c} = \mu_{0} = 1 - \theta$. We obtain $2\theta = 1 - \theta$ and then $\theta^{*} = \frac{1}{3}$.

Step 5::

The optimal solution is then $x^{*} \left( {\frac{1}{3}} \right) = \left( {x_{1}^{*} \left( {\frac{1}{3}} \right),x_{2}^{*} \left( {\frac{1}{3}} \right)} \right) = \left( {6,\frac{23}{3}} \right)$ with $z^{*} \left( {\frac{1}{3}} \right) = 13 + \frac{2}{3} = 13.667$.

6 LP with Fuzzy Parameters

In this section, different solution approaches for solving several kinds of LP problems with fuzzy parameters are explored.

The solution approaches are classified into two general groups: Simplex based approach and Non-simplex based approach. In the simplex based approach, the classical simplex algorithms such as primal simplex algorithm and dual simplex algorithm are generalized for solving LP problems with fuzzy parameters. In the non-simplex based approach, such FLP problems are first converted into equivalent crisp problems, which are then solved by the standard methods. In what follows, these approaches are explored to find the optimal solution of LP problems with fuzzy parameters.

6.1 The Simplex Based Approach

In this section, the simplex based approach for solving several kinds of LP problems with fuzzy parameters is explored. In such approach, the comparison of fuzzy numbers is done by use of linear ranking functions.

6.1.1 LP with Fuzzy Cost Coefficients

The general from of LP problems with fuzzy cost coefficients can be formulated as follows:

$$ \begin{aligned} & \max \tilde{z} \approx \sum\limits_{j = 1}^{n} {\tilde{c}_{j} x_{j} } \\ & s.t.\;\;\sum\limits_{j = 1}^{n} {a_{ij} x_{j} \le b_{i} ,\quad i = 1,2, \ldots ,m,} \\ & \quad \;\;x_{j} \ge 0,\quad j = 1,2, \ldots ,n. \\ \end{aligned} $$

(39)

This problem can be rewritten as follows:

$$ \begin{aligned} & \max \tilde{z} \approx \tilde{c}x \\ & s.t.\;\;Ax \le b, \\ & \quad \;\;x \ge 0. \\ \end{aligned} $$

(40)

where $b = (b_{1} ,b_{2} , \ldots ,b_{m} ) \in {\mathbb{R}}^{m} ,\;\tilde{c} = (\tilde{c}_{1} ,\tilde{c}_{2} , \ldots ,\tilde{c}_{n} ) \in F\left( {\mathbb{R}} \right)^{n}$, $A = (a_{ij} )_{m \times n} \in {\mathbb{R}}^{m \times n}$ and $x = (x_{1} ,x_{2} , \ldots ,x_{n} ) \in {\mathbb{R}}^{n}$.

In what follows, the solution approach proposed by Maleki et al. [29] for solving the FLP problem (40) is explored. The other approaches can be found in [7, 30].

Consider the system of equality constraints of (40) where $A$ is a matrix of order $(m \times n)$ and $rank(A) = m$. Therefore, $A$ can be partitioned as $[\begin{array}{*{20}c} {B,} & N \\ \end{array} ]$, where $B_{m \times m}$ is a nonsingular matrix with $rank(B) = m$. Let $y_{j}$ is the solution of $By_{j} = a_{j}$. Moreover, the basic solution $x = (x_{B} ,x_{N} ) = (B^{ - 1} b,0)$ is a solution of $Ax = b$. This basic solution is feasible, whenever $x_{B} \ge 0$. Furthermore, the corresponding fuzzy objective function value is obtained as $\tilde{z} \approx \tilde{c}_{B} x_{B} ,\tilde{c}_{B} = (\tilde{c}_{{B_{1} }} ,\tilde{c}_{{B_{2} }} , \ldots ,\tilde{c}_{{B_{m} }} )$.

Suppose $J_{N}$ is the set of indices associated with the current non-basic variables. For each non-basic variable $x_{j} ,j \in J_{N}$ the fuzzy variable $\tilde{z}_{j}$ is defined as $\tilde{z}_{j} \approx \tilde{c}_{B} B^{ - 1} a_{j} = \tilde{c}_{B} y_{j}$.

Maleki et al. [29] stated the following important results in order to improve a feasible solution and to provide unbounded criteria and the optimality conditions for the FLP problem (40) with equality constraints.

Theorem 1

If for a basic feasible solution with basis $B$ and objective value $\tilde{z},\tilde{z}_{k} \prec \tilde{c}_{k}$ for some non-basic variable $x_{k}$ while $y_{k} \,\nleq\, {0}$ , then a new feasible solution can be obtained as follows with objective value $\tilde{z}_{new} = \tilde{z} - (\tilde{z}_{k} - {\tilde{\tilde{c}}}_{k} )x_{k}$ , such that $\tilde{z}\,\preceq\, \tilde{z}_{new}$.

$$ \begin{aligned} x_{{B_{r} }} & = x_{k} = \theta = \frac{{\bar{b}_{r} }}{{y_{rk} }} = \mathop {\min }\limits_{1 \le i \le m} \left\{ {\frac{{\bar{b}_{i} }}{{y_{ik} }}\left| {y_{ik} > 0} \right.} \right\}, \\ x_{{B_{i} }} & = \bar{b}_{i} - y_{ik} \frac{{\bar{b}_{r} }}{{y_{rk} }},\quad i = 1,2, \ldots ,m,\quad i \ne r, \\ x_{j} & = 0,\quad j \in J_{N} ,\quad j \ne k. \\ \end{aligned} $$

Theorem 2

If for a basic feasible solution with basis $B$ and objective value $\tilde{z},\tilde{z}_{k} \prec \tilde{c}_{k}$ for some non-basic variable $x_{k}$ while $y_{k} \le 0$ , then the optimal solution of the FLP problem (40) is unbounded.

Theorem 3

The basic solution $x = (x_{B} ,x_{N} ) = (B^{ - 1} b,0)$ is an optimal solution for the FLP problem (40) if $\tilde{z}_{j} \,\succeq \,\tilde{c}_{j}$ for all $j \in J_{N}$.

Now we are in a position to summarize the fuzzy primal simplex algorithm [29] for solving the FLP problem (40).

Algorithm 1: Fuzzy Primal Simplex Algorithm (Maximization Problem)

• Initialization step

• Choose a starting feasible basic solution with basis $B$.

• Main steps

  • 1. Solve the system $Bx_{B} = b$. Let $x_{B} = B^{ - 1} b,x_{N} = 0$, and $\tilde{z} = \tilde{c}_{B} x_{B}$.

  • 2. Solve the system $\tilde{w}B = \tilde{c}_{B}$. Let $\tilde{w} = \tilde{c}_{B} B^{ - 1}$.

  • 3. Calculate $\tilde{z}_{j} = \tilde{c}_{B} B^{ - 1} a_{j} = \tilde{w}a_{j}$ for all $j \in J_{N}$. Find the rank of $\tilde{z}_{j} - \tilde{c}_{j}$ for all $j \in J_{N}$ based on ranking function $\Re$ given in Remark 3 and let $\Re (\tilde{z}_{k} - \tilde{c}_{k} ) = \min_{{j \in J_{N} }} \left\{ {\Re (\tilde{z}_{j} - \tilde{c}_{j} )} \right\}$. If $\Re (\tilde{z}_{k} - \tilde{c}_{k} ) \ge 0$, then stop with the current basic solution as an optimal solution.

  • 4. Solve the system $By_{k} = a_{k}$ and let $y_{k} = B^{ - 1} a_{k}$. If $y_{k} \le 0$ then stop with the conclusion that the problem is unbounded.

    If $y_{k} \,\nleq\, 0$, then $x_{k}$ enters the basis and $x_{Br}$ leaves the basis providing that

    $$ \frac{{\bar{b}_{r} }}{{y_{rk} }} = \mathop {\min }\limits_{1 \le i \le m} \left\{ {\frac{{\bar{b}_{i} }}{{y_{ik} }}\left| {y_{rk} > 0} \right.} \right\}. $$

  • 5. Update the basic $B$ where $a_{k}$ replace $a_{Br}$, update the index set $J_{N}$ and go to (1).

Example 6

[29] Consider the following FLP problem:

$$ \begin{aligned} & {\text{Max}}\,\tilde{z} \approx (5, 8, 2, 5)x_{1} + (6, 10, 2, 6) x_{2} \\ & s.t.\;\;2x_{1} + 3x_{2} \le 6, \\ & \quad \;\;5x_{1} + 4x_{2} \le 10, \\ & \quad \;\;x_{1} ,x_{2} \ge 0. \\ \end{aligned} $$

(41)

After introducing the slack variables $x_{3}$ and $x_{4}$ we obtain the following FLP problem:

$$ \begin{aligned} & {\text{Max}}\;\tilde{z} \approx (5, 8, 2, 5)x_{1} + (6, 10, 2, 6) x_{2} \\ & s.t.\;\;2x_{1} + 3x_{2} + x_{3} = 6, \\ & \quad \;\;5x_{1} + 4x_{2} + x_{4} = 10, \\ & \quad \;\;x_{1} ,x_{2} ,x_{3} ,x_{4} \ge 0. \\ \end{aligned} $$

(42)

The steps of Algorithm 1 for solving the FLP problem (42) are presented as follows:

Iteration 1

The starting feasible basic is $B = [\begin{array}{*{20}c} {a_{3} ,} & {a_{4} } \\ \end{array} ] = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right]$. Thus, the non-basic matrix $N$ is $N = [\begin{array}{*{20}c} {a_{1} ,} & {a_{2} } \\ \end{array} ]= \left[ {\begin{array}{*{20}c} 2 & 3 \\ 5 & 4 \\ \end{array} } \right]$.

Step 1::

We find the basic feasible solution by solving the system $Bx_{B} = b$:

$$ \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{3} } \\ {x_{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 6 \\ {10} \\ \end{array} } \right] $$

Solving this system leads to $x_{{B_{1} }} = x_{3} = 6$ and $x_{{B_{2} }} = x_{4} = 10$. The non-basic variables are $x_{1} = 0,x_{2} = 0$ and the fuzzy objective value is $\tilde{z} = \tilde{c}_{B} x_{B} = 0$.

Step 2::

We find $\tilde{w}$ by solving the fuzzy system $\tilde{w}B = \tilde{c}_{B}$:

$$ (\tilde{w}_{1} ,\tilde{w}_{2} )\left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {(0,0,0,0)} \\ {(0,0,0,0)} \\ \end{array} } \right] \Rightarrow \tilde{w}_{1} = \tilde{w}_{2} = (0,0,0,0) $$

Step 3::

We calculate $\tilde{z}_{j} - \tilde{c}_{j} = \tilde{w}a_{j} - \tilde{c}_{j}$ for all $j \in J_{N} = \left\{ {1,2} \right\}$:

$$ \begin{aligned} & \tilde{z}_{1} - \tilde{c}_{1} = \tilde{w}a_{1} - \tilde{c}_{1} = \left( {(0,0,0,0),(0,0,0,0)} \right)\left[ {\begin{array}{*{20}c} 2 \\ 5 \\ \end{array} } \right] - (5,8,2,5) = ( - 8, - 5,5,2) \\ & \tilde{z}_{2} - \tilde{c}_{2} = \tilde{w}a_{2} - \tilde{c}_{2} = \left( {(0,0,0,0),(0,0,0,0)} \right)\left[ {\begin{array}{*{20}c} 3 \\ 4 \\ \end{array} } \right] - (6,10,2,6) = ( - 10, - 6,6,2) \\ \end{aligned} $$

Computing the rank of $\tilde{z}_{1} - \tilde{c}_{1}$ and $\tilde{z}_{2} - \tilde{c}_{2}$ based on ranking function given in Remark 3 leads to $\Re (\tilde{z}_{1} - \tilde{c}_{1} ) = - \frac{29}{4}$ and $\Re (\tilde{z}_{2} - \tilde{c}_{2} ) = - 9$. Therefore,

$$ \min \left\{ {\Re (\tilde{z}_{1} - \tilde{c}_{1} ) = - \frac{29}{2},\Re (\tilde{z}_{2} - \tilde{c}_{2} ) = - 9} \right\} = \Re (\tilde{z}_{2} - \tilde{c}_{2} ) = - 9 $$

Step 4::

We find $y_{2}$ by solving the system $By_{2} = a_{2}$:

$$ \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {y_{12} } \\ {y_{22} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 3 \\ 4 \\ \end{array} } \right] \Rightarrow y_{2} = \left[ {\begin{array}{*{20}c} {y_{12} } \\ {y_{22} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 3 \\ 4 \\ \end{array} } \right] $$

Step 5::

The variable $x_{B\,r}$ leaving the basis is determined by the following test:

$$ \min \left\{ {\frac{{\bar{b}_{1} }}{{y_{12} }},\frac{{\bar{b}_{2} }}{{y_{22} }}} \right\} = \min \left\{ {\frac{6}{3},\frac{10}{4}} \right\} = \frac{6}{3} = 2 $$

Hence, $x_{{B_{1} }} = x_{3}$ leaves the basis.

Step 6::

We update the basis $B$ where $a_{2}$ replaces $a_{{B_{1} }} = a_{3}$:

$$ B = [a_{2} ,a_{4} ] = \left[ {\begin{array}{*{20}c} 3 & 0 \\ 4 & 1 \\ \end{array} } \right] $$

Also, we update $J_{N} = \left\{ {1,2} \right\}$ as $J_{N} = \left\{ {1,3} \right\}$.

This process is continued and after two more iterations the optimal basis $B = [a_{2} ,a_{1} ] = \left[ {\begin{array}{*{20}c} 3 & 2 \\ 4 & 5 \\ \end{array} } \right]$ is found. The optimal solution and the optimal objective function value of the FLP problem (41) are therefore given by:

$$ x^{*} = \left( {x_{1}^{*} ,x_{2}^{*} ,x_{3}^{*} ,x_{4}^{*} } \right) = \left( {\frac{6}{7},\frac{10}{7},0,0} \right),\quad \tilde{z}^{*} = \left( {\frac{90}{7},\frac{148}{7},\frac{32}{7},\frac{96}{7}} \right) $$

(43)

6.1.2 LP Problem with Fuzzy Decision Variables and Fuzzy Right-Hand-Side of the Constraints

The LP problem involving fuzzy numbers for the decision variables and the right-hand-side of the constraints is called fuzzy variables linear programming problem (FVLP) problem and is formulated as follows:

$$ \begin{aligned} & \min \tilde{z} = c\tilde{x} \\ & s.t.\;\;A\tilde{x}\,\succeq\, \tilde{b}, \\ & \quad \;\;\tilde{x}\,\succeq \,\tilde{0}. \\ \end{aligned} $$

(44)

In what follows, two solution approaches proposed by Maleki et al. [29] and Mahdavi-Amiri and Nasseri [28] for solving the FVLP problem (44) are explored. The other approaches can be found in [12, 13].

6.1.3 Maleki et al.’s Approach

Maleki et al. [29] introduced an auxiliary problem, having only fuzzy cost coefficients, for an FVLP problem and then used its crisp solution for obtaining the fuzzy solution of the FVLP problem. In order to describe this approach, we reformulate the FVLP problem (44), with respect to the change of all the parameters and variables, as the following FVLP problem:

$$ \begin{aligned} & \min \tilde{u} = \tilde{w}b \\ & s.t.\;\;\tilde{w}A\,\succeq \,\tilde{c}, \\ & \quad \;\;\tilde{w}\,\succeq \,\tilde{0}. \\ \end{aligned} $$

(45)

Maleki et al. [29] considered the FLP problem (40) as the fuzzy auxiliary problem for the FVLP problem (45) and studied the relation between the FVLP problem (45) and the fuzzy auxiliary problem (40). In fact, they proved that if $x_{B} = B^{ - 1} b$ is an optimal basic feasible solution of the auxiliary problem (40) then $\tilde{w} = \tilde{c}_{B} B^{ - 1}$ is a fuzzy optimal solution of the FVLP problem (45).

Example 7

[28, 29] Consider the following FVLP problem:

$$ \begin{aligned} & {\text{Min}}\;\tilde{z} \approx 6\tilde{x}_{1} + 10\tilde{x}_{2} \\ & s.t.\;\;2\tilde{x}_{1} + 5\tilde{x}_{2} \,\succeq\, (5,8,2,5), \\ & \quad \;\;3\tilde{x}_{1} + 4\tilde{x}_{2} \,\succeq\, (6,10,2,6), \\ & \quad \;\;\tilde{x}_{1} ,\tilde{x}_{2} \,\succeq\, \tilde{0}. \\ \end{aligned} $$

(46)

Now, we solve this problem using the solution approach proposed by Maleki et al. [29]. To do this, we rewrite the FVLP problem (46) with respect to the change of all the parameters and variables as follows:

$$ \begin{aligned} & {\text{Min}}\;\;\tilde{u} \approx 6\tilde{w}_{1} + 10\tilde{w}_{2} \\ & s.t.\;\;2\tilde{w}_{1} + 5\tilde{w}_{2} \,\succeq \,(5,8,2,5), \\ & \quad \;\;3\tilde{w}_{1} + 4\tilde{w}_{2} \,\succeq\, (6,10,2,6), \\ & \quad \;\;\tilde{w}_{1} ,\tilde{w}_{2} \,\succeq \,\tilde{0} \\ \end{aligned} $$

(47)

The fuzzy auxiliary problem corresponding to the FVLP problem (47) is defined as follows:

$$ \begin{aligned} & {\text{Max}}\;\tilde{z} \approx (5,8,2,5)x_{1} + (6,10,2,6)x_{2} \\ & s.t.\;\;2x_{1} + 3x_{2} \le 6, \\ & \quad \;\;5x_{1} + 4x_{2} \le 10, \\ & \quad \;\;x_{1} ,x_{2} \ge 0. \\ \end{aligned} $$

(48)

The fuzzy auxiliary problem (48) is exactly the LP problem with fuzzy costs given in (41). Thus, the optimal solution given in (43) is its optimal solution. Now, since the basis $B = [a_{2} ,a_{1} ] = \left[ {\begin{array}{*{20}c} 3 & 2 \\ 4 & 5 \\ \end{array} } \right]$ is the optimal basis of the fuzzy auxiliary problem (48) or (41), the fuzzy optimal solution of the FVLP problem (47) is obtained as follows based on the formulation $\tilde{w} = \tilde{c}_{B} B^{ - 1}$:

$$ \begin{aligned} \tilde{w}^{*} & = \left( {\tilde{w}^{*}_{1} ,\tilde{w}^{*}_{2} } \right) = \left( {(6,10,2,6),(5,8,2,5)} \right)\left[ {\begin{array}{*{20}c} {\frac{5}{7}} & {\frac{ - 2}{7}} \\ {\frac{ - 4}{7}} & {\frac{3}{7}} \\ \end{array} } \right] \\ & = \left( {\left( {\frac{ - 2}{7},\frac{30}{7},\frac{30}{7},\frac{38}{7}} \right),\left( {\frac{ - 5}{7},\frac{12}{7},\frac{18}{7},\frac{19}{7}} \right)} \right) \\ \end{aligned} $$

(49)

This means that the optimal solution of FVLP problem (46) is as follows:

$$ \tilde{x}^{*} = \left[ {\begin{array}{*{20}c} {\tilde{x}_{1}^{*} } \\ {\tilde{x}_{2}^{*} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left( {\frac{ - 2}{7},\frac{30}{7},\frac{30}{7},\frac{38}{7}} \right)} \\ {\left( {\frac{ - 5}{7},\frac{12}{7},\frac{18}{7},\frac{19}{7}} \right)} \\ \end{array} } \right] $$

(50)

Unlike the non-simplex based approach, this approach doesn’t increase the number of the constraint of the primary FLP problem. Another advantage of this approach is to produce the fuzzy optimal solution that provides possible outcomes with certain degree of memberships to the decision maker. However, the fuzzy optimal solution by use of this approach may be not non-negative. For instance the value of $\tilde{x}_{1}^{*}$ in the fuzzy optimal solution (50) is non-negative as there is negative part in this fuzzy number.

6.1.3.1 Mahdavi-Amiri and Nasseri’s Approach

Mahdavi-Amiri and Nasseri [28] proved that the fuzzy auxiliary problem introduced by Maleki et al. [29] is the dual of the FVLP problem. Hence, they introduced a fuzzy dual simplex algorithm for solving the FVLP problem directly on the primary problem and without solving any fuzzy auxiliary problem.

Mahdavi-Amiri and Nasseri [28] defined the dual problem of the FVLP problem (44) as follows:

$$ \begin{aligned} & \max \tilde{u} = w\tilde{b} \\ & s.t.\;\;wA \le c, \\ & \quad \;\;w \ge 0. \\ \end{aligned} $$

(51)

We see that only the coefficients of the objective function of this problem are fuzzy numbers. Thus, it plays the role of the auxiliary problem for the FVLP problem (44).

A summary of the fuzzy dual simplex algorithm proposed by Mahdavi-Amiri and Nasseri [28] for solving FVLP problem (44) is given as follows.

Algorithm 2: Fuzzy Dual Simplex Algorithm (Minimization Problem)

• Initialization step

• Choose a starting dual feasible basic solution with basis $B$.

• Main steps

  • 1. Solve the system $B\tilde{x}_{B} = \tilde{b}$. Let $\tilde{x}_{B} = B^{ - 1} \tilde{b} = \tilde{\bar{b}}$, and $\tilde{z} \approx c_{B} \tilde{x}_{B}$.

  • 2. Find the rank of $\tilde{\bar{b}}_{i}$ for all $1 \le i \le m$ based on ranking function $\Re$ given in Remark 3 and let $\Re \left( {\tilde{\bar{b}}_{i} } \right) = \min_{1 \le i \le m} \left\{ {\Re \left( {\tilde{\bar{b}}_{i} } \right)} \right\}$. If $\Re \left(\tilde{\bar{b}}_{r} \right) \ge 0$, then stop with the current basic solution as an optimal solution.

  • 3. Solve the system $By_{j} = a_{j}$ for all $j \in J_{N}$ and let $y_{j} = B^{ - 1} a_{j}$. If $y_{rj} \ge 0$ for all $j \in J_{N}$ then stop with the conclusion that the FVLP problem is infeasible.

  • 4. Solve the system $wB = c_{B}$. Let $w = c_{B} B^{ - 1}$. Calculate $z_{j} = wa_{j}$ for all $j \in J_{N}$. If $y_{rj} \,\ngeq\, 0$ for all $j \in J_{N}$, then $\tilde{x}_{{B_{r} }}$ leaves the basis and $\tilde{x}_{k}$ enters the basis providing that

    $$ \frac{{z_{k} - c_{k} }}{{y_{rk} }} = \mathop {\min }\limits_{{j \in J_{N} }} \left\{ {\left. {\frac{{z_{j} - c_{j} }}{{y_{rk} }}} \right|y_{rk} < 0} \right\}. $$

  • 5. Update the basis $B$ where $a_{k}$ replaces $a_{Br}$, update the index set $J_{N}$ and go to (1).

Example 8

Again, consider the FVLP problem (46). Now, we solve this problem using the solution approach proposed by Mahdavi-Amiri and Nasseri [28]. To do this, we rewrite the FVLP problem (46) as follows in order to obtain a dual feasible solution with identity basis where $\tilde{x}_{3}$ and $\tilde{x}_{4}$ are fuzzy surplus variables:

$$ \begin{aligned} & {\text{Min}}\;\tilde{z} \approx 6\tilde{x}_{1} + 10\tilde{x}_{2} \\ & s.t.\;\; {-}2\tilde{x}_{1} - 5\tilde{x}_{2} + \tilde{x}_{3} \approx ( - 8, - 5,5,2), \\ & \quad \;\; {-} 3\,\tilde{x}_{1} - 4\tilde{x}_{2} + \tilde{x}_{4} \approx ( - 10, - 6,6,2), \\ & \quad \;\;\tilde{x}_{1} ,\tilde{x}_{2} ,\tilde{x}_{3} ,\tilde{x}_{4} \,\succeq \,\tilde{0}. \\ \end{aligned} $$

(52)

The steps of Algorithm 2 for solving the FVLP problem (52) are explored as follows:

Iteration 1

The starting dual feasible basic is $B = [a_{3} ,a_{4} ] = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right]$. Thus, the non-basic matrix $N$ is $N = [a_{1} ,a_{2} ] = \left[ {\begin{array}{*{20}c} { - 2} & { - 5} \\ { - 3} & { - 4} \\ \end{array} } \right]$.

Step 1::

We find the basic solution by solving the fuzzy system $B\tilde{x}_{B} = \tilde{b}$:

$$ \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\tilde{x}_{3} } \\ {\tilde{x}_{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {( - 8, - 5,5,2)} \\ {( - 10, - 6,6,2)} \\ \end{array} } \right] \Rightarrow \left[ {\begin{array}{*{20}c} {\tilde{x}_{3} } \\ {\tilde{x}_{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {( - 8, - 5,5,2)} \\ {( - 10, - 6,6,2)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\tilde{\bar{b}}_{1} } \\ {\tilde{\bar{b}}_{2} } \\ \end{array} } \right] $$

The fuzzy objective function value is obtained based on the formulation $\tilde{z} \approx c_{B} \tilde{x}_{B}$:

$$ \tilde{z} \approx \left( {0,0} \right)\left[ {\begin{array}{*{20}c} {( - 8, - 5,5,2)} \\ {( - 10, - 6,6,2)} \\ \end{array} } \right] = (0,0,0,0) $$

Step 2::

We find the rank of $\tilde{\bar{b}}_{1}$ and $\tilde{\bar{b}}_{2}$ by use of ranking function $\Re$ given in Remark 3. Hence we have $\Re \left(\tilde{\bar{b}}_{1} \right) = - \frac{29}{4}$ and $\Re \left( {\tilde{\bar{b}}_{2} } \right) = - 9$. Therefore,

$$ \min \left\{ {\Re \left( {\tilde{\bar{b}}_{1} } \right) = - \frac{29}{4},\Re \left( {\tilde{\bar{b}}_{2} } \right) = - 9} \right\} = \Re \left( {\bar{b}_{2} } \right) = - 9\,\ngeq\, 0 $$

Step 3::

We find $y_{j}$ for all $j \in J_{N} = \left\{ {1,2} \right\}$ by solving the system $By_{j} = a_{j}$:

$$ \begin{aligned} \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {y_{11} } \\ {y_{21} } \\ \end{array} } \right] & = \left[ {\begin{array}{*{20}c} { - 2} \\ { - 3} \\ \end{array} } \right] \Rightarrow y_{1} = \left[ {\begin{array}{*{20}c} {y_{11} } \\ {y_{21} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - 2} \\ { - 3} \\ \end{array} } \right] \\ \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {y_{12} } \\ {y_{22} } \\ \end{array} } \right] & = \left[ {\begin{array}{*{20}c} { - 5} \\ { - 4} \\ \end{array} } \right] \Rightarrow y_{2} = \left[ {\begin{array}{*{20}c} {y_{12} } \\ {y_{22} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - 5} \\ { - 4} \\ \end{array} } \right] \\ \end{aligned} $$

Step 4::

We find $w$ by solving the system $wB = c_{B}$:

$$ (w_{1} ,w_{2} )\left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right] \Rightarrow w_{1} = w_{2} = 0 $$

Now, we calculate $z_{j} - c_{j} = wa_{j} - c_{j}$ for all $j \in J_{N} = \left\{ {1,2} \right\}$:

$$ \begin{aligned} z_{1} - c_{1} & = wa_{1} - c_{1} = \left( {0,0} \right)\left[ {\begin{array}{*{20}c} { - 2} \\ { - 3} \\ \end{array} } \right] - 6 = - 6 \\ z_{2} - c_{2} & = wa_{2} - c_{2} = \left( {0,0} \right)\left[ {\begin{array}{*{20}c} { - 5} \\ { - 4} \\ \end{array} } \right] - 10 = - 10 \\ \end{aligned} $$

The variable $\tilde{x}_{{B_{2} }} = \tilde{x}_{4}$ leaves the basis and the variable $\tilde{x}_{k}$ entering the basis is determined by the following test:

$$ \min \left\{ {\frac{{z_{1} - c_{1} }}{{y_{21} }},\frac{{z_{2} - c_{2} }}{{y_{22} }}} \right\} = \min \left\{ {\frac{ - 6}{ - 3},\frac{ - 10}{ - 4}} \right\} = \frac{ - 6}{ - 3} = 2 $$

Hence, $x_{k} = x_{1}$ enters the basis.

Step 5::

We update the basis $B$ where $a_{1}$ replaces $a_{{B_{2} }} = a_{4}$:

$$ B = [a_{3} ,a_{1} ] = \left[ {\begin{array}{*{20}c} 1 & { - 2} \\ 0 & { - 3} \\ \end{array} } \right] $$

Also, we update $J_{N} = \left\{ {1,2} \right\}$ as $J_{N} = \left\{ {2,4} \right\}$.

This process is continued and after two more iterations, the optimal solution of the FVLP problem (44) is given as follows, which is matched with that given in (50) obtained by Maleki et al.’s approach [29]:

$$ \tilde{x}^{*} = \left[ {\begin{array}{*{20}c} {\tilde{x}_{1}^{*} } \\ {\tilde{x}_{2}^{*} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left( {\frac{ - 2}{7},\frac{30}{7},\frac{30}{7},\frac{38}{7}} \right)} \\ {\left( {\frac{ - 5}{7},\frac{12}{7},\frac{18}{7},\frac{19}{7}} \right)} \\ \end{array} } \right] $$

It should be note that the advantages and disadvantages of this approach are same with the Maleki et al.’s approach [29].

6.1.4 LP Problem with Fuzzy Cost Coefficients, Fuzzy Decision Variables and Fuzzy Right-Hand-Side of the Constraints

Ganesan and Veeramani [14] formulated a LP problem in which the cots coefficients, decision variables and the values of the right-hand-side are represented by symmetric trapezoidal fuzzy numbers while the elements of the coefficient matrix are represented by real numbers. This problem can be formulated as follows:

$$ \begin{aligned} & \max \tilde{z} \approx \tilde{c}\tilde{x} \\ & s.t.\;\;A\tilde{x} \approx \tilde{b}, \\ & \quad \;\;\tilde{x}\,\succeq\, \tilde{0}. \\ \end{aligned} $$

(54)

In what follows, two solution approaches are reviewed for solving FLP problem (54). The other approaches can be found in [10, 23].

6.1.4.1 Ganesan and Veeramani’s Approach

Ganesan and Veeramani [14] introduced a new type of fuzzy multiplication and fuzzy ordering for symmetric trapezoidal fuzzy numbers and then proposed a simplex based method for solving SFFLP problem (55) without converting it into crisp LP problem.

Definition 13

Let $\tilde{a} = (a_{2} - \alpha ,a_{2} ,a_{3} ,a_{3} + \alpha )$ and $\tilde{b} = (b_{2} - \beta ,b_{2} ,b_{3} ,b_{3} + \beta )$ be two symmetric trapezoidal fuzzy numbers. The new type of multiplication on $\tilde{a}$ and $\tilde{b}$ has been defined in [14] as follows:

$$ \tilde{a}\tilde{b} \approx \left( {p - w - \gamma ,p - w,p + w,p + w + \gamma } \right) $$

where

$$ \begin{aligned} p & = \left( {\frac{{a_{2} + a_{3} }}{2}} \right)\left( {\frac{{b_{2} + b_{3} }}{2}} \right),\quad w = \frac{{t_{2} - t_{1} }}{2},\quad t_{1} = \min \left\{ {a_{2} b_{2} ,a_{2} b_{3} ,a_{3} b_{2} ,a_{3} b_{3} } \right\}, \\ t_{2} & = \max \left\{ {a_{2} b_{2} ,a_{2} b_{3} ,a_{3} b_{2} ,a_{3} b_{3} } \right\},\quad \gamma = \left| {a_{3} \beta + b_{3} \alpha } \right|. \\ \end{aligned} $$

Definition 14

For any two symmetric trapezoidal fuzzy numbers $\tilde{a} = (a_{2} - \alpha ,a_{2} ,a_{3} ,a_{3} + \alpha )$ and $\tilde{b} = (b_{2} - \alpha ,b_{2} ,b_{3} ,b_{3} + \alpha )$ the relations $\preceq$ and $\approx$ have been defined in [14] as follows:

$$ \begin{aligned} \tilde{a}\,\preceq\, b & \Leftrightarrow \frac{{a_{2} + a_{3} }}{2} \le \frac{{b_{2} + b_{3} }}{2} \\ \tilde{a} \approx b & \Leftrightarrow \frac{{a_{2} + a_{3} }}{2} \approx \frac{{b_{2} + b_{3} }}{2} \\ \end{aligned} $$

Remark 5

It should be note that the ordering defined in Definition 14 is same as with the ordering defined in terms of linear ranking function in Remark 3. This means that the linear ranking function given in Remark 3 for any symmetric trapezoidal fuzzy numbers $\tilde{a} = (a_{2} - \alpha ,a_{2} ,a_{3} ,a_{3} + \alpha )$ is reduced to

$$ \Re (\tilde{a}) = \frac{{a_{2} - \alpha + a_{2} + a_{3} + a_{3} + \alpha }}{4} = \frac{{a_{2} + a_{3} }}{2} $$

Now, consider a system of $m$ simultaneous fuzzy linear equations involving symmetric trapezoidal fuzzy numbers in $n$ unknowns $A\tilde{x} = \tilde{b}$. Let $B$ be any matrix formed by $m$ linear independent of $A$. In this case, the solution $\tilde{x} = (\tilde{x}_{B} ,\tilde{x}_{N} ) = (B^{ - 1} \tilde{b},\tilde{0})$ is a fuzzy basic solution. Let $y_{j}$ and $\tilde{w}$ be the solutions to $By_{j} = a_{j}$ and $\tilde{w}B = \tilde{c}_{B}$, respectively. Define $\tilde{z}_{j} = \tilde{c}_{B} B^{ - 1} a_{j} = \tilde{w}a_{j}$. Based on these results, Ganesan and Veeramani [14] proved fuzzy analogues of some important theorems of LP leading to a new method for solving FLP problem (54) without converting it into a crisp LP problem.

Algorithm 3: Symmetric fuzzy primal simplex algorithm (Maximization Problem)

• Initialization step

• Choose a starting dual feasible basic solution with basis $B$. Form the initial tableau as Table 1.

  Table 1 The initial simplex tableau

• Main steps

  • 1. Calculate $\tilde{z}_{j} - \tilde{c}_{j}$ for all $j \in J_{N}$ where $J_{N}$ is the index set of non-basic variables. Suppose that $\tilde{z}_{j} - \tilde{c}_{j} = (h_{j}^{2} - \alpha_{j} ,h_{j}^{2} ,h_{j}^{3} ,h_{j}^{3} + \alpha_{j} )$. Let

    $$ h_{k}^{2} + h_{k}^{3} = \mathop {\max }\limits_{{j \in J_{N} }} \left\{ {h_{j}^{2} + h_{j}^{3} } \right\}. $$

    If $h_{k}^{2} + h_{k}^{3} \ge 0$, then stop with the current basic solution as an optimal solution.

  • 2. Solve the system $By_{k} = a_{k}$ and let $y_{k} = B^{ - 1} a_{k}$. If $y_{k} \le 0$ then stop with the conclusion that the problem is unbounded. Otherwise, suppose $\tilde{\bar{b}}_{i} = \left( {\bar{b}_{i}^{2} - \alpha_{i} ,\bar{b}_{i}^{2} ,\bar{b}_{i}^{3} ,\bar{b}_{i}^{3} + \alpha_{j} } \right)$. In this case, then $\tilde{x}_{k}$ enters the basis and $\tilde{x}_{{B_{r} }}$ leaves the basis providing that

    $$ \frac{{\bar{b}_{r}^{2} + \bar{b}_{r}^{3} }}{{y_{rk} }} = \mathop {\min }\limits_{1 \le i \le m} \left\{ {\left. {\frac{{\bar{b}_{i}^{2} + \bar{b}_{i}^{3} }}{{y_{ik} }}} \right|y_{rk} > 0} \right\} $$

  • 3. Update the tableau by pivoting on $y_{rk}$ and go to (1).

Example 9

[11] Consider the following FLP problem:

$$ \begin{aligned} & {\text{Max}}\;\tilde{z} \approx (11,13,15,17)\tilde{x}_{1} + (9,12,14,17)\tilde{x}_{2} \\ & s.t.\;\;12\tilde{x}_{1} + 13\tilde{x}_{2} \,\preceq\, (469,475,505,511), \\ & \quad \;\;12\tilde{x}_{1} + 15\tilde{x}_{2} \,\preceq\, (460,465,495,500), \\ & \quad \;\;\tilde{x}_{1} ,\tilde{x}_{2} \,\succeq \,\tilde{0}. \\ \end{aligned} $$

(55)

After introducing the slack variables $\tilde{x}_{3}$ and $\tilde{x}_{4}$ we obtain the initial fuzzy primal simplex tableau as Table 2.

Table 2 The initial simplex tableau of Example 8

By considering $\tilde{x}_{1}$ and $\tilde{x}_{4}$ as the entering variable the leaving variable, respectively, and then by pivoting on $y_{21} = 12$, we obtain the next tableau as Table 3.

Table 3 The optimal tableau of Example 8

Since $h_{2}^{2} + h_{2}^{3} \ge 0$ and $h_{4}^{2} + h_{4}^{3} \ge 0$, the algorithm stops and Table 3 is the optimal tableau.

6.1.4.2 Ebrahimnejad and Nasseri’s Approach

In the proposed approach by Ganesan and Veeramani [14] it is assumed that a fuzzy primal feasible basic solution of the problem (54) is at hand. For situation in which a primal fuzzy feasible basic solution is not at hand, but there is a fuzzy dual feasible basic solution, Ebrahimnejad and Nasseri [9] generalized the fuzzy analogue of the dual simplex algorithm of LP to the FLP problem under consideration. A summary of their method for a minimization problem in tableau format is given as follows.

Algorithm 4: Symmetric Fuzzy Dual Simplex Algorithm (Minimization Problem)

• Initialization step

• Choose a starting primal feasible basic solution with basis $B$. Form the initial tableau as Table 1. Suppose $\tilde{z}_{j} - \tilde{c}_{j} = (h_{j}^{2} - \alpha_{j} ,h_{j}^{2} ,h_{j}^{3} ,h_{j}^{3} + \alpha_{j} )$, so we have $h_{j}^{2} + h_{j}^{3} \ge 0$ for all $j$.

• Main steps

  • 1. Suppose $\tilde{\bar{b}} = B^{ - 1} \tilde{b}$. If $\tilde{\bar{b}} = B^{ - 1} \tilde{b}$ then stop; the current fuzzy solution is optimal.

    Else, suppose $\tilde{\bar{b}}_{i} = \left( {\bar{b}_{i}^{2} - \alpha_{i} ,\bar{b}_{i}^{2} ,\bar{b}_{i}^{3} ,\bar{b}_{i}^{3} + \alpha_{j} } \right)$ and let

    $$ \bar{b}_{r}^{2} + \bar{b}_{r}^{3} = \mathop {\min }\limits_{1 \le i \le m} \left\{ {\bar{b}_{i}^{2} + \bar{b}_{i}^{3} } \right\} $$

  • 2. If $y_{rj} \ge 0$ for all $j$, then stop; the FLP problem under consideration is infeasible.

    Else, $\tilde{x}_{{B_{r} }}$ leaves the basis and $\tilde{x}_{k}$ enters to the basis providing that

    $$ \frac{{h_{k}^{2} + h_{k}^{3} }}{{y_{rk} }} = \mathop {\min }\limits_{1 \le j \le n} \left\{ {\left. {\frac{{h_{j}^{2} + h_{j}^{3} }}{{y_{rj} }}} \right|y_{rj} < 0} \right\} $$

  • 3. Update the tableau by pivoting on $y_{rk}$ and go to (1).

Example 9

[10] Consider the following FLP problem:

$$ \begin{aligned} & {\text{Min}}\;\tilde{z} \approx (1,4,8,13)\tilde{x}_{1} + (2,4,6,8)\tilde{x}_{2} + (1,2,4,5)\tilde{x}_{3} \\ & s.t.\;\;3\tilde{x}_{1} + 4\tilde{x}_{2} + 2\tilde{x}_{3} \,\succeq\, (3,6,10,13), \\ & \quad \;\;4\tilde{x}_{1} + 2\tilde{x}_{2} + \tilde{x}_{3} \,\succeq\, (2,4,6,8), \\ & \quad \;\;2\tilde{x}_{1} + \tilde{x}_{2} + \tilde{x}_{3} \,\succeq\, (1,2,6,7), \\ & \quad \;\;\tilde{x}_{1} ,\tilde{x}_{2} ,\tilde{x}_{3} \,\succeq \,\tilde{0}. \\ \end{aligned} $$

(56)

After introducing the surplus variables $\tilde{x}_{4} ,\tilde{x}_{5}$ and $\tilde{x}_{6}$ the initial fuzzy dual simplex tableau is given as Table 4.

Table 4 The initial tableau of Example 9

After two iterations of the Algorithm 4, the optimal tableau is obtained as Table 5.

Table 5 The optimal tableau of Example 9

In contrast to the FVLP problem considered in [28, 29], in the FLP problem introduced by Ganesan and Veeramini [14], not only the decision variables and the right-hand-side of the constraints are fuzzy, but also the coefficients of decision variables in objective function are fuzzy. However, the proposed approaches for solving FLP problem considered in [14] are valid only for situation in which the parameters are represented by symmetric trapezoidal fuzzy numbers. But, the proposed methods [28, 29] for solving FVLP problems are applicable to both symmetric and non-symmetric trapezoidal fuzzy numbers. Also, unlike the non-simplex based approach and similar to the existing approaches [28, 29] in solving FVLP problems, this approach doesn’t increase the number of the constraint of the primary FLP problem. In addition, although these approaches [9, 14] give fuzzy optimal solution, but, the fuzzy optimal solution by use of these approaches may be not non-negative, too. For instance the value of $\tilde{x}_{3}^{*} = ( - 31, - 20,40,51)$ in the fuzzy optimal solution of Example 8 (see Table 3) and the value of $\tilde{x}_{1}^{*} = \left( {\frac{ - 9}{5},\frac{ - 2}{5},\frac{6}{5},\frac{13}{5}} \right)$ in the optimal solution of Example 9 (see Table 5) are non-negative as there are negative parts in these fuzzy solutions.

6.1.5 LP Problem with Fuzzy Cost Coefficients, Fuzzy Decision Variables, Fuzzy Coefficients Matrix and Fuzzy Right-Hand-Side of the Constraints

Kheirfam and Verdegay [19] defined a new type of FLP problems in which all parameters and decision variables were represented by symmetric trapezoidal fuzzy numbers. This problem, named as symmetric fully fuzzy linear programming (SFFLP), can be represented with the following model:

$$ \begin{aligned} & \max \tilde{z} = \tilde{c}\tilde{x} \\ & s.t.\;\;\tilde{A}\tilde{x} \approx \tilde{b}, \\ & \quad \;\;\tilde{x}\,\succeq \,\tilde{0}. \\ \end{aligned} $$

(57)

Kheirfam and Verdegay [19] introduced a new type of fuzzy inverse and division for symmetric trapezoidal fuzzy numbers and then proposed a simplex based method for solving SFFLP problem (57) without converting it to crisp LP problem.

Definition 15

Let $\tilde{a} = (a_{2} - \alpha ,a_{2} ,a_{3} ,a_{3} + \alpha )$ and $\tilde{b} = (b_{2} - \beta ,b_{2} ,b_{3} ,b_{3} + \beta )$ be symmetric trapezoidal fuzzy number and symmetric non zero trapezoidal fuzzy number, respectively. Two new types of arithmetic operations on $\tilde{a}$ and $\tilde{b}$ have been defined in [19] as follows:

• $$ \frac{1}{{\tilde{b}}} = \tilde{b}^{ - 1} \approx \left( {\left[ {\frac{2}{{b_{2} + b_{3} }} - w} \right] - \beta ,\left[ {\frac{2}{{b_{2} + b_{3} }} - w} \right],\left[ {\frac{2}{{b_{2} + b_{3} }} + w} \right],\left[ {\frac{2}{{b_{2} + b_{3} }} + w} \right] + \beta } \right) $$

where $w = \frac{{t_{2} - t_{1} }}{2},t_{2} = \mathop {\max }\limits_{j = 2,3} \left\{ {\frac{1}{{\bar{b}_{j} }}} \right\},t_{1} = \mathop {\min }\limits_{j = 2,3} \left\{ {\frac{1}{{\bar{b}_{j} }}} \right\},\frac{1}{{\bar{b}_{j} }} = \left\{ {\begin{array}{*{20}l} {\frac{1}{{b_{j} }},} & {b_{j} \ne 0,} \\ {0,} & {b_{j} = 0.} \\ \end{array} } \right.$

• $$ \frac{{\tilde{a}}}{{\tilde{b}}} \approx \left( {\left[ {\frac{{a_{2} + a_{3} }}{{b_{2} + b_{3} }} - w} \right] - \gamma ,\left[ {\frac{{a_{2} + a_{3} }}{{b_{2} + b_{3} }} - w} \right],\left[ {\frac{{a_{2} + a_{3} }}{{b_{2} + b_{3} }} + w} \right],\left[ {\frac{{a_{2} + a_{3} }}{{b_{2} + b_{3} }} + w} \right] + \gamma } \right) $$

where $w = \frac{{t_{2} - t_{1} }}{2},t_{2} = \mathop {\max }\limits_{i,j = 2,3} \left\{ {\frac{{a_{i} }}{{\bar{b}_{j} }}} \right\},t_{1} = \mathop {\min }\limits_{i,j = 2,3} \left\{ {\frac{{a_{i} }}{{\bar{b}_{j} }}} \right\},\gamma = \left| {a_{3} \beta + b_{3} \alpha } \right|.$

A symmetric trapezoidal fuzzy matrix $\widetilde{A} = \left[ {\tilde{a}_{ij} } \right]_{m \times n}$ is any rectangular array of symmetric trapezoidal fuzzy numbers. For any values of indices $i$ and $j$, the ijth minor of the square matrix $\tilde{A} = \left[ {\tilde{a}_{ij} } \right]_{n \times n}$, denoted by $\tilde{A}_{ij}$, is the $(n - 1) \times (n - 1)$ sub-matrix of $\tilde{A}$ obtained by deleting the ith row and the jth column of $\tilde{A}$. In this case, determinant $\tilde{A}$, denoted by $\left| {\tilde{A}} \right|$, is computed as follows [19]:

• For $n = 1,\left| {\tilde{A}} \right| = \tilde{a}_{11}$.

• For $n = 2,\left| {\tilde{A}} \right| = \tilde{a}_{11} \tilde{a}_{22} - \tilde{a}_{12} \tilde{a}_{21}$.

• For $n > 2,\left| {\tilde{A}} \right| = \sum\limits_{j = 1}^{n} {( - 1)^{i + j} } \tilde{a}_{ij} \left| {\tilde{A}_{ij} } \right|$, for any value of index $i = 1,2, \ldots ,n$.

A square matrix $\tilde{A} = \left[ {\tilde{a}_{ij} } \right]_{n \times n}$, is called singular if $\left| {\tilde{A}} \right| = \tilde{0}$. In other case, it said to be non-singular fuzzy matrix and its inverse is calculated by $\tilde{A}^{ - 1} = \frac{(1,1,0,0)}{{\left| {\tilde{A}} \right|}}\left[ {( - 1)^{i + j} \left| {\tilde{A}_{ij} } \right|} \right]_{n \times n}$.

Now, we are in a position to summary the proposed method by Kheirfam and Verdegay [19] solving the SFFLP problem (57).

Suppose a fuzzy basic feasible solution of problem (57) with basis $\tilde{B}$ is at hand. Let $\tilde{y}_{j}$ and $\tilde{w}$ be the solutions to $\tilde{B}\tilde{y}_{j} = \tilde{a}_{j}$ and $\tilde{w}\tilde{B} = \tilde{c}_{B}$, respectively. Define $\tilde{z}_{j} = \tilde{c}_{B} \tilde{B}^{ - 1} \tilde{a}_{j} = \tilde{w}\tilde{a}_{j}$. Using these notations, Kheirfam and Verdegay [19] developed and presented for first time an original dual simplex algorithm for solving the SFFLP problem (57).

Algorithm 5: Symmetric Fully Fuzzy Dual Simplex Algorithm (Maximization Problem)

• Initialization step

• Let $\tilde{B}$ be a basis for the SFFLP problem (57) such that $\tilde{z}_{j} - \tilde{c}_{j} = \left( {h_{j}^{2} - \alpha_{j} ,h_{j}^{2} ,h_{j}^{3} ,h_{j}^{3} + \alpha_{j} } \right)\,\succeq\, \tilde{0}$ for all $j$, i.e. $h_{j}^{2} + h_{j}^{3} \ge 0$. Form the initial tableau as Table 6.

  Table 6 Tableau of the SFFLP problem

• Main steps

  • 1. Suppose $\tilde{\bar{b}} = \tilde{B}^{ - 1} \tilde{b}$. If $\tilde{\bar{b}}\,\succeq \,\tilde{0}$ then stop; the current fuzzy solution is optimal.

    Else, suppose $\tilde{\bar{b}}_{i} = \left( {\bar{b}_{i}^{2} - \alpha_{i} ,\bar{b}_{i}^{2} ,\bar{b}_{i}^{3} ,\bar{b}_{i}^{3} + \alpha_{j} } \right)$ and let

    $$ \bar{b}_{r}^{2} + \bar{b}_{r}^{3} = \mathop {\min }\limits_{1 \le i \le m} \left\{ {\bar{b}_{i}^{2} + \bar{b}_{i}^{3} } \right\} $$

  • 2. If $\tilde{y}_{rj} = \left( {y_{rj}^{2} - \alpha_{rj} ,y_{rj}^{2} ,y_{rj}^{3} ,y_{rj}^{3} - \alpha_{rj} } \right)\,\succeq\, \tilde{0}$ for all $j$, i.e. $y_{rj}^{2} + y_{rj}^{3} \ge 0$, then stop; the SFFLP problem (57) is infeasible.

    Else, $\tilde{x}_{{B_{r} }}$ leaves the basis and $\tilde{x}_{k}$ enters the basis providing that

    $$ \frac{{{h}_{k}^{2} + {h}_{k}^{3} }}{{y_{rk}^{2} + y_{rk}^{3} }} = \mathop {\max }\limits_{1 \le j \le n} \left\{ {\left. {\frac{{{h}_{j}^{2} + {h}_{j}^{3} }}{{y_{rj}^{2} + y_{rj}^{3} }}} \right|y_{rj}^{2} + y_{rj}^{3} < 0} \right\} $$

  • 3. Update the tableau by pivoting on $\tilde{y}_{rk}$ and go to (1).

Example 10

[19] Consider the following SFFLP problem:

$$ \begin{aligned} & {\text{Max}}\;\tilde{z} \approx ( - 4, - 2,2,5)\tilde{x}_{1} + ( - 3, - 2,0,1)\tilde{x}_{2} \\ & s.t.\;\;(1,2,4,5)\tilde{x}_{1} + ( - 5, - 3, - 1,1)\tilde{x}_{2} + (1,1,1,1)\tilde{x}_{3} \approx ( - 6, - 4, - 4,2), \\ & \quad \;\;( - 3, - 2,0,1)\tilde{x}_{1} + ( - 4, - 2,4,6)\tilde{x}_{2} + (1,1,1,1)\tilde{x}_{4} \approx ( - 4, - 1,5,8), \\ & \quad \;\;\tilde{x}_{1} ,\tilde{x}_{2} ,\tilde{x}_{3} ,\tilde{x}_{4} \,\succeq\, \tilde{0}. \\ \end{aligned} $$

(59)

The first dual feasible simplex tableau is showed in Table 7.

Table 7 The initial simplex tableau of Example 10

Since $\bar{b}_{1}^{2} + \bar{b}_{1}^{3} < 0$, thus $\tilde{x}_{{B_{1} }} = \tilde{x}_{3}$ leaves the basis and according to test given in step (2) of Algorithm 5, $\tilde{x}_{2}$ is the entering variable. By pivoting $\tilde{y}_{12} = ( - 5, - 3, - 1,1)$ on the new tableau shown in Table 8 is obtained.

Table 8 The optimal tableau of Example 8

Since $\tilde{\bar{b}}_{1} = \left( {\frac{ - 28}{3},\frac{2}{3},\frac{10}{3},\frac{40}{3}} \right) \succ \tilde{0}$ and $\tilde{\bar{b}}_{2} = \left( {\frac{ - 308}{3}, - 13,13,\frac{308}{3}} \right) \approx \tilde{0}$, the current solution is optimal. Thus, the optimal solution of the problem (59) is

$$ \tilde{x}^{*} = \left[ {\begin{array}{*{20}c} {\tilde{x}_{1}^{*} } \\ {\tilde{x}_{2}^{*} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left( {0,0,0,0} \right)} \\ {\left( {\frac{ - 28}{3},\frac{2}{3},\frac{10}{3},\frac{40}{3}} \right)} \\ \end{array} } \right] $$

(60)

In contrast to the FVLP problem considered in [28, 29] and the FLP problem introduced by Ganesan and Veeramini [14], in the FLP problem considered by Kheirfam and Verdegay [19] all parameters and decision variable are specified in terms of fuzzy data. In addition, the solution approach proposed by Kheirfam and Verdegay [19], not only gives fuzzy optimal solution, but also doesn’t increase the number of the constraint of the primary FLP problem. However, similar to the existing approaches in [9, 14, 28, 29], the fuzzy optimal solution given by use of this approach may be not non-negative. For instance the value of $\tilde{x}_{2}^{*} = \left( {\frac{ - 28}{3},\frac{2}{3},\frac{10}{3},\frac{40}{3}} \right)$ in the fuzzy optimal solution (60) is non-negative as there is negative part in this fuzzy solution.

6.2 The Non-simplex Based Approach

In this section, the non-simplex based approach for solving two kinds of LP problems with fuzzy parameters is explored. In such approach, the fuzzy constraints are first converted to crisp ones based on arithmetic operations on fuzzy numbers and then the standard method are used for solving the crisp problem. Such approach increases the number of functional constraints and thus directly effects the computational time of the simplex method.

6.2.1 LP Problem with Fuzzy Coefficients Matrix and Fuzzy Right-Hand-Side of the Constraints

The general form of LP problems in which the right-hand-side of the constraints and the coefficients of the constraint matrix are fuzzy numbers, can be formulated as follows [32]:

$$ \begin{aligned} & \max z = \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \\ & s.t.\;\;\sum\limits_{j = 1}^{n} {\tilde{a}_{ij} x_{j} } \,\preceq\, \tilde{b}_{i} ,\quad i = 1,2,\ldots,m, \\ & \quad \;\;x_{j} \ge 0,\quad j = 1,2,\ldots,n. \\ \end{aligned} $$

(61)

Let us assume that all fuzzy numbers are triangular. Thus, $\tilde{a}_{ij}$ and $\tilde{b}_{i}$ are represented as $\tilde{a}_{ij} = (a_{1,ij} ,a_{2,ij} ,a_{3,ij} )$ and $\tilde{b}_{i} = (b_{1,i} ,b_{2,i} ,b_{3,i} )$, respectively. Hence, FLP problem (61) can be reformulated as follows:

$$ \begin{aligned} & \max z = \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \\ & s.t.\;\;\sum\limits_{j = 1}^{n} {(a_{1,ij} ,a_{2,ij} ,a_{3,ij} )x_{j} \,\preceq\, (b_{1,i} ,b_{2,i} ,b_{3,i} ),\quad i = 1,2,\ldots,m,} \\ & \quad \;\;x_{j} \ge 0,\quad j = 1,2,\ldots,n. \\ \end{aligned} $$

(62)

Equivalently, with regard to Remarks 1 and 2, the FLP (62) can be rewritten as follows:

$$ \begin{aligned} & \max z = \sum\limits_{j = 1}^{n} {c_{j} x_{j} } \\ & s.t.\;\;\sum\limits_{j = 1}^{n} {a_{1,ij} x_{j} \le b_{1,i} ,\quad i = 1,2,\ldots,m,} \\ & \quad \;\;\sum\limits_{j = 1}^{n} {a_{2,ij} x_{j} \le b_{2,i} ,\quad i = 1,2,\ldots,m,} \\ & \quad \;\;\sum\limits_{j = 1}^{n} {a_{3,ij} x_{j} \le b_{3,i} ,\quad i = 1,2,\ldots,m,} \\ & \quad \;\;x_{j} \ge 0,\quad j = 1,2,\ldots,n. \\ \end{aligned} $$

(63)

The optimal solution of crisp LP problem (63) can be considered as the solution of the FLP problem (61) [32].

Example 11

[26] Consider the following FLP problem:

$$ \begin{aligned} & {\text{Max}}\;z = 5x_{1} + 4x_{2} \\ & s.t.\;\;(2,4,5)x_{1} + (2,5,6)x_{2} \,\preceq\, (19,24,32), \\ & \quad \;\;(3,4,6)x_{1} + (4,5,6)x_{2} \,\preceq \,(6,12,19) \\ & \quad \;\;x_{1} ,x_{2} \ge 0. \\ \end{aligned} $$

(64)

This problem is converted into the following crisp LP problem with regard to problem (63):

$$ \begin{aligned} & {\text{Max}}\;z = 5x_{1} + 4x_{2} \\ & s.t.\;\;2x_{1} + 2x_{2} \le 19, \\ & \quad \;\;4x_{1} + 5x_{2} \le 24, \\ & \quad \;\;5x_{1} + 6x_{2} \le 32, \\ & \quad \;\;3x_{1} + 4x_{2} \le 6, \\ & \quad \;\;4x_{1} + 5x_{2} \le 12, \\ & \quad \;\;6x_{1} + 6x_{2} \le 19, \\ & \quad \;\;x_{1} ,x_{2} \ge 0. \\ \end{aligned} $$

(65)

Solving this problem gives the optimal solution as $x^{*} = \left( {x_{1}^{*} ,x_{1}^{*} } \right) = (1.5,3),z^{*} = 19.5$.

The optimal solutions obtained by this approach are real numbers, which represent a compromise in terms of fuzzy numbers involved. In addition, this approach increases the number of functional constraints and thus this proposed need more computation cost than the simplex based approach.

6.2.2 Fully Fuzzy LP Problem [24]

The FLP problem in which all the parameters as well as the decision variables are represented by fuzzy numbers is called FFLP problem. The general form of FFLP problem can be formulated as follows:

$$ \begin{aligned} & \max \tilde{z} \approx \sum\limits_{j = 1}^{n} {\tilde{c}_{j} \otimes \tilde{x}_{j} } \\ & s.t.\;\;\sum\limits_{j = 1}^{n} {\tilde{a}_{ij} \otimes \tilde{x}_{j} } \approx \tilde{b}_{i} ,\quad i = 1,2,\ldots,m, \\ & \quad \;\;\tilde{x}_{j} \,\succeq\, \tilde{0},\quad j = 1,2,\ldots,n. \\ \end{aligned} $$

(66)

Let us assume that all fuzzy numbers are triangular. Thus $\tilde{a}_{ij}, \tilde{x}_{ij}, \tilde{c}_{j}$ and $\tilde{b}_{i},$ are represented as $\tilde{a}_{ij} = (a_{1,ij} ,a_{2,ij} ,a_{3,ij} )$ $\tilde{x}_{j} = (x_{1,j} ,x_{2,j} ,x_{3,j} )$ $\tilde{b}_{i} = (b_{1,i} ,b_{2,i} ,b_{3,i} )$ and $\tilde{b}_{i} = (b_{1,i} ,b_{2,i} ,b_{3,i} )$, respectively. Hence, FLP problem (66) can be reformulated as follows:

$$ \begin{aligned} & \max\tilde{z} \approx \sum\limits_{j = 1}^{n} {(c_{1,j} ,c_{2,j} ,c_{3,j} ) \otimes (x_{1,j} ,x_{2,j} ,x_{3,j} )} \\ & s.t.\;\;\sum\limits_{j = 1}^{n} {(a_{1,ij} ,a_{2,ij} ,a_{3,ij} ) \otimes (x_{1,j} ,x_{2,j} ,x_{3,j} )} \approx (b_{1,i} ,b_{2,i} ,b_{3,i} ),\quad i = 1,2,\ldots,m, \\ & \quad \;\;(x_{1,j} ,x_{2,j} ,x_{3,j} )\;{\text{is}}\;{\text{a}}\;{\text{non}}\;{\text{negative}}\;{\text{trinagular}}\;{\text{fuzzy}}\;{\text{number}},\quad j = 1,2,\ldots,n. \\ \end{aligned} $$

(67)

Assuming $(a_{1,ij} ,a_{2,ij} ,a_{3,ij} ) \otimes (x_{1,ij} ,x_{2,ij} ,x_{3,ij} ) = (m_{1,ij} ,m_{2,ij} ,m_{3,ij} )$ and using ranking function given in Remark 4 for the objective function, the FLP (67) can be rewritten as follows:

$$ \begin{aligned} & \max \Re (\tilde{z}) = \Re \left( {\sum\limits_{j = 1}^{n} {(c_{1,j} ,c_{2,j} ,c_{3,j} ) \otimes (x_{1,j} ,x_{2,j} ,x_{3,j} )} } \right) \\ & s.t.\;\;\sum\limits_{j = 1}^{n} {(m_{1,ij} ,m_{2,ij} ,m_{3,ij} )} \approx (b_{1,i} ,b_{2,i} ,b_{3,i} ),\quad i = 1,2,\ldots,m, \\ & \quad \;\;(x_{1,j} ,x_{2,j} ,x_{3,j} )\;{\text{is}}\;{\text{a}}\;{\text{non}}\;{\text{negative}}\;{\text{trinagular}}\;{\text{fuzzy}}\;{\text{number}},\quad j = 1,2,\ldots,n. \\ \end{aligned} $$

(68)

Using Definitions 10 and 7, the FLP problem (68) becomes:

$$ \begin{aligned} & \max \Re (\tilde{z}) = \Re \left( {\sum\limits_{j = 1}^{n} {(c_{1,j} ,c_{2,j} ,c_{3,j} ) \otimes (x_{1,j} ,x_{2,j} ,x_{3,j} )} } \right) \\ & s.t.\;\;\sum\limits_{j = 1}^{n} {m_{1,ij} } = b_{1,i} ,\quad i = 1,2,\ldots,m, \\ & \quad \;\;\sum\limits_{j = 1}^{n} {m_{2,ij} } = b_{2,i} ,\quad i = 1,2,\ldots,m, \\ & \quad \;\;\sum\limits_{j = 1}^{n} {m_{3,ij} } = b_{3,i} ,\quad i = 1,2,\ldots,m, \\ & \quad \;\;x_{1,j} \ge 0,\quad x_{2,j} - x_{1,j} \ge 0,\quad x_{3,j} - x_{2,j} \ge 0,\quad j = 1,2,\ldots,n. \\ \end{aligned} $$

(69)

The optimal solution of the crisp LP problem (69) can be considered as the optimal solution of the FFLP problem (66).

Example 12

[24] Consider the following FFLP problem:

$$ \begin{aligned} & {\text{Max}}\;z = (1,6,9) \otimes (x_{1,1} ,x_{1,2} ,x_{1,3} ) + (2,3,8) \otimes (x_{2,1} ,x_{2,2} ,x_{2,3} ) \\ & s.t.\;\;(2,3,4)(x_{1,1} ,x_{1,2} ,x_{1,3} ) + (1,2,3)(x_{2,1} ,x_{2,2} ,x_{2,3} ) = (6,16,30), \\ & \quad \;\;( - 1,1,2)(x_{1,1} ,x_{1,2} ,x_{1,3} ) + (1,3,4)(x_{2,1} ,x_{2,2} ,x_{2,3} ) = (1,17,30) \\ & \quad \;\;(x_{1,1} ,x_{1,2} ,x_{1,3} )\;{\text{and}}\;(x_{2,1} ,x_{2,2} ,x_{2,3} )\;{\text{are}}\;{\text{non}}\;{\text{negative}}\;{\text{fuzzy}}\;{\text{numbers}} .\\ \end{aligned} $$

(70)

This problem is converted into the following crisp LP problem with regard to problem (69):

$$ \begin{aligned} & {\text{Max}}\,\Re (\tilde{z}\,) = \,\frac{1}{4}\left[ {\left( {x_{1,1} + 2x_{1,2} + 12x_{2,1} + 6x_{2,2} + 9x_{3,1} + 8x_{2,3} } \right)} \right] \\ & s.t.\;\;2x_{1,1} + x_{2,1} = 6, \\ & \quad \;\; - x_{1,3} + x_{2,1} = 1, \\ & \quad \;\;3x_{1,2} + 2x_{2,2} = 16, \\ & \quad \;\;x_{1,2} + 3x_{2,2} = 17, \\ & \quad \;\;4x_{1,3} + 3x_{2,3} = 30, \\ & \quad \;\;2x_{1,3} + 4x_{2,3} = 30, \\ & \quad \;\;x_{1,1} \ge 0,\quad x_{1,2} - x_{1,1} \ge 0,\quad x_{1,3} - x_{1,2} \ge 0, \\ & \quad \;\;x_{2,1} \ge 0,\quad x_{2,2} - x_{2,1} \ge 0,\quad x_{2,3} - x_{2,2} \ge 0. \\ \end{aligned} $$

(71)

The optimal solution of the crisp LP problem (71) is as follows:

$$ x_{1,1}^{*} = 1,\quad x_{1,2}^{*} = 2,\quad x_{1,3}^{*} = 3,\quad x_{2,1}^{*} = 4,\quad x_{2,2}^{*} = 5,\quad x_{2,3}^{*} = 6 $$

(72)

Hence, the fuzzy optimal solution of the FFLP problem (70) is

$$ \tilde{x}^{*} = \left( {\tilde{x}_{1}^{*} ,\tilde{x}_{2}^{*} } \right) = \left( {\left( {x_{1,1}^{*} ,x_{1,2}^{*} ,x_{1,3}^{*} } \right),\left( {x_{2,1}^{*} ,x_{2,2}^{*} ,x_{2,3}^{*} } \right)} \right) = \left( {\left( {1,2,3} \right),\left( {4,5,6} \right)} \right) $$

(73)

Putting the fuzzy optimal solution (73) in the objective function of the problem (70) gives $\tilde{z}^{*} = (9,27,75)$.

In contrast to the proposed approaches in [32], Kumar et al.’s method [24] gives fuzzy optimal solution. In contrast to the simplex based approach [9–11, 14, 19, 21, 28–30], Kumar et al.’s method [24] gives non-negative fuzzy optimal solutions.

7 Conclusions

In the conventional LP problems it is assumed that the parameters of the problem are exactly known, but there may be some situations in formulating real-life problems where the parameters are not known in a precise way. A frequently used manner to represent the imprecision in parameters is by means of fuzzy numbers that enlarges the range of applications of LP. Many different techniques have been used in the literature to solve the LP problems in fuzzy environment. In this contribution, a taxonomy and review of some of these techniques for solving four categories of FLP problems was provided. The limitations and advantages of each category were also pointed out. Moreover, the solution approaches were illustrated with several numerical examples.