Intervention-Autonomous Underwater Vehicle Multibody Models for Dynamic Manipulation Tasks

Abstract

Free floating autonomous underwater manipulation is still an open research topic; an important challenge is offered by dynamic manipulation, where the vehicle maintains relevant velocities during manipulation tasks. To develop new control architectures, a precise modelling of the mechanisms involved in the manipulation tasks is needed. The focus of this paper is the multibody modelling and the control of an Intervention-Autonomous Underwater Vehicle (I-AUV). An accurate model of the whole system has been developed, including vehicle-fluid interaction. A suitable 3D contact model has been developed for the contact between the gripper and the object to be manipulated. A control strategy for the whole I-AUV system is proposed, comprising a suitable grasp planning strategy. Finally, an evaluation of the I-AUV control system performances have been carried out.

9.1 Introduction

Nowadays Autonomous Underwater Vehicles (AUVs) are quite widespread. These vehicles can undoubtedly lead to substantial economic and technological benefits. In the technical evolution of the AUVs the following important topics are still characterized by many open problems: the dynamic performances and the control of the vehicle, the mobile tele-manipulation of a single vehicle (with relevant vehicle velocity) and the cooperation among vehicles. In this paper, the modelling and the control architecture of an AUV specifically thought for the underwater mobile manipulation, usually called I-AUV (Intervention-AUV), are described.

Currently, a considerable number of operations in sea-rescue, research and maintenance of oil rig appliances, got ahead using Unmanned Underwater Vehicles (UUVs), need manipulation capacity to be concluded successfully [1–7]. In a such scenario, most of the intervention missions at high depths are faced up by remotely controlled vehicles equipped with one or more robotic arms (Intervention-ROVs), representing until today the standard technology in that field [8]. The ROVs for assistance, which can be teleoperated for long periods, are usually controlled with a master-slave approach [5, 6]. This kind of strategy has some limitations: the operator must be skilled with special type of training, underwater communication is often difficult and a significant delay in the control loop can be present. To overcome these limitations, many researchers are now focused on what appears as the AUV natural evolution, i.e. the autonomous underwater vehicles equipped with manipulator arms, the I-AUVs [4, 7–15].

One important contribution to the development of the state of the art of the I-AUV is due to TRIDENT, an European project lasting for 3 years and started in 2010 [4, 16]. The aim of TRIDENT was the development of new methodologies to complete manipulation assistances in non-structured underwater environments, through a cooperative team composed of an AUV equipped with a robotic arm at 7 degrees of freedoms (DOFs) and an ASC (Autonomous Surface Craft): the latter is an autonomous surface vehicle, whose aim is to replace, in the application near to the coast, the support ship with crew necessary to the running of the AUV. In March 2014 PANDORA project [17] has demonstrated free floating grasping and valve turning in tank. However in both cases the vehicle is in a hovering phase and not in “mobile navigation”. In fact, autonomous underwater robotic manipulation with free-floating base is far from reaching an industrial product. This is particularly true in the framework of dynamic manipulation, where relevant vehicle velocities are required (in contrast with hovering manipulation).

Concerning control strategies, the problem is still open as well. Vehicle- manipulator decoupled control strategies have been mostly studied until now, which independently control the AUV and the robotic arm [8, 15]; these strategies offer simpler hardware and software implementation and require less knowledge of the system parameters compared to arm-vehicle coupled control techniques [2, 8].

In this paper, a detailed 3D multibody model of the I-AUV system (vehicle, arm, gripper, object to be manipulated and fluid interaction [1, 18]) has been developed to test the proposed control strategy. Moreover, a suitable 3D contact model has been developed for the contact between the gripper and the object to be manipulated. For what concerns the control technique, a decoupled vehicle-manipulator strategy has been employed [2, 8]. This kind of techniques offers simpler hardware implementation and is more robust against the knowledge of the system parameters with respect to arm-vehicle coupled strategies. In addition, exploiting the hand kinematics, the control of the gripper has been further decoupled from the arm control: this way, the performances of the I-AUV are improved while maintaining higher vehicle velocities. Furthermore, a grasp planning algorithm, based on optical cameras [19], is proposed.

The models and the control architecture have been validated simulating a suitable test case using the software Matlab$^{\circledR }$. The proposed techniques, after further tests, will be used in opportune hardware tests in the framework of existing projects such as the Italian research project SUONO (Safe Underwater Operations iN Oceans) and the European research project ARROWS, coordinated by the MDM Lab of the University of Florence, to obtain initial experimental results [20].

9.2 I-AUV Multibody Modelling

9.2.1 I-AUV Description

The vehicle possesses 6 DOFs and is equipped with a manipulator arm, which is assumed to be a serial robot with 7 DOFs. On top of the wrist a 6-DOFs gripper is mounted: the latter has 3 fingers, each one composed of 2 phalanxes connected by rotational joints. The reference frames are shown in Fig. 9.1, linked to each rigid body and used to calculate the hydrodynamic terms.

Fig. 9.1

Structure of the I-AUV, equipped with a robotic arm and a gripper

9.2.2 I-AUV Kinematic and Dynamic Model

The analysis of the I-AUV model has been divided into two parts, separating the study of the vehicle model from the analysis of the manipulation system (i.e. the arm and the gripper). Geometrical and physical data have been set according to technical literature [21–23]. In this context, it is assumed that the gripper is rigidly connected to the robotic arm. The models are completely developed in Matlab-Simulink$^{\circledR }$ environment.

SNAME notation has been used [1]; hence, the kinematic model of the AUV is defined in terms of $\varvec{\eta }$ and $\varvec{\nu }$ vectors. $\varvec{\eta }$ represents the position $\left( \varvec{\eta }_{1}\right)$ and the orientation $\left( \varvec{\eta }_{2}\right)$ written in the fixed reference frame $<n>$; $\varvec{\nu }$ include the linear $\left( \varvec{\nu }_{1}\right)$ and the angular $\left( \varvec{\nu }_{2}\right)$ velocities described into the body reference frame $<b>$. Both the fixed and the body reference frames use the NED directions.

The relations between $\dot{\varvec{\eta }}$ and $\varvec{\nu }$ can be written using the following expression:

$$\begin{aligned} \dot{\varvec{\eta }} = J^{n}_{b}\left( \varvec{\eta _{2}}\right) \,\varvec{\nu } , \end{aligned}$$

(9.1)

where

$$\begin{aligned} J^{n}_{b}\left( \varvec{\eta _{2}}\right) \ = \begin{bmatrix} R^{n}_{b}\left( \varvec{\eta _{2}}\right)&0_{3\times 3} \\ 0_{3\times 3}&T^{n}_{b}\left( \varvec{\eta _{2}}\right) \end{bmatrix} . \end{aligned}$$

(9.2)

$R^{n}_{b}(\varvec{\eta }_{2})$ is the rotation matrix between frame $<n>$ and frame $<b>$, and $T^{n}_{b}\left( \varvec{\eta _{2}}\right)$ is the transformation matrix between angular velocity and the time derivative of Euler angles (and its form depends on the particular choice of Euler angles).

The dynamic model of the vehicle is defined as follows [1]:

$$\begin{aligned} M_{RB} \dot{\varvec{\nu }} + C_{RB}(\varvec{\nu })\varvec{\nu }= \varvec{\tau }_H (\varvec{\nu },\varvec{\nu }_C) + \varvec{g} (\varvec{\eta }) + \varvec{\tau }, \end{aligned}$$

(9.3)

where $M_{RB}$ and $C_{RB} (\varvec{\nu })$ are, respectively, the mass matrix and the Coriolis and centrifugal effect matrix. $\varvec{g}(\varvec{\eta })$ and $\varvec{\tau }$ are the contribution due to the gravity effects and the external forces and moments (due to the motors and to the interaction with the arm) applied to the vehicle as to the body reference frame $<b>$. These contributes are referred to the rigid body characteristics. Instead, the hydrodynamic effects ${\varvec{\tau }_H}(\varvec{\nu },{\varvec{\nu }_C})$ are partially decoupled from the dynamical equation in order to use the classical multibody modelling techniques. In particular, buoyancy and hydrodynamic effects are introduced into the model by means of generalized Lagrangian forces applied to each body of the multibody system. From the classic equation of motion for an underwater vehicle [1] and the absolute velocity $\varvec{\nu }$ written in the body reference frame $\varvec{\nu }=\varvec{\nu }_r + \varvec{\nu }_c$ (where $\varvec{\nu }_r$ is the relative velocity and $\varvec{\nu }_c$ is the current velocity), the following expression for ${\varvec{\tau }_H}(\varvec{\nu },{\varvec{\nu }_C})$ can be extracted:

$$\begin{aligned} \varvec{\tau }_H&= - M_A \dot{\varvec{\nu }}_r + C_{RB}\left( \varvec{\nu }_r\right) \varvec{\nu }_c +C_{RB}\left( \varvec{\nu }_c\right) \varvec{\nu }_r \nonumber \\&\quad + C_{RB}\left( \varvec{\nu }_c\right) \varvec{\nu }_c - C_A\left( \varvec{\nu }_r\right) \varvec{\nu }_r - D\left( \varvec{\nu }_r\right) \varvec{\nu }_r . \end{aligned}$$

(9.4)

where $M_A$ is the added mass matrix due to the fluid viscosity, $C_A$ is the Coriolis and centrifugal added effects, and $D \left( \varvec{\nu }_r\right)$ is the damping matrix. The interaction among the different system bodies and the fluid has been modelled by means of appropriate CFD analyses [1, 18, 24, 25]; the mathematical coupling between the multibody model and the fluid equations has been efficiently performed through the toolbox SimMechanics$^{\circledR }$. In particular, as regards the CFD analyses, ANSYS$^{\circledR }$ CFX software has been used to evaluate the elements of the matrices $M_{A}$, $C_{A}$ and $D \left( \varvec{\nu }_r\right)$ for different values of $\varvec{\nu }$, $\dot{\varvec{\nu }}$ and for different motions of the vehicle.

It is useful to express the forces and moments by dimensionless coefficients, to use them in any condition of similarity. Concerning the effects of the hydrodynamic resistance, the elements of the damping matrix $D \left( \varvec{\nu }_r\right)$ are evaluated expressing the forces and torques through the following six dimensionless parameters:

• front, lateral and vertical drag coefficients:

  $$\begin{aligned} \begin{matrix} C_{D_{x}}=\frac{F_{x}}{\frac{1}{2}\rho _{a}A_{f}v^{2}}&C_{D_{y}}=\frac{F_{y}}{\frac{1}{2}\rho _{a}DLv^{2}}&C_{D_{z}}=\frac{F_{z}}{\frac{1}{2}\rho _{a}DLv^{2}} \end{matrix} \end{aligned}$$

• roll, pitch and yaw resistance coefficients:

  $$\begin{aligned} \begin{matrix} C_{M_{x}}=\frac{M_{x}}{\frac{1}{2}\rho _{a}A_{f}D^{3}\omega ^{2}}&C_{M_{y}}=\frac{M_{y}}{\frac{1}{2}\rho _{a}DL^{4}\omega ^{2}}&C_{M_{z}}=\frac{M_{z}}{\frac{1}{2}\rho _{a}DL^{4}\omega ^{2}} \end{matrix} \end{aligned}$$

where the used symbols are: speed v, angular velocity $\omega$, frontal area $A_{f}$, diameter D, fluid density $\rho _{a}$, length L, and $F_{i}$, $M_{i}$ are force and moment (all of them acting on the $\mathbf i$ axis). The geometrical and physical characteristics of the vehicle are based on the literature and are defined in Table 9.1.

Table 9.1 I-AUV data

The I-AUV is provided of a robotic arm with 7 DOFs installed on the bow of the vehicle, in the middle of its lower part. For the kinematic model of the robotic arm (Fig. 9.2), the joint coordinates $\mathbf q =[\theta _{1} \ \theta _{2} \ldots \ \theta _{7}]^T$ and the end-effector pose $\mathbf x = [x \ y \ z \ \phi \ \theta \ \psi ]^T$ are defined. According to the Denavit–Hartenberg (D–H) approach, Table 9.2 collects the D–H parameters extracted for the arm. The main kinematic equations used to entirely describe the redundant manipulator are respectively, for the direct kinematics and for the differential kinematics:

Fig. 9.2

Arm kinematic scheme

Table 9.2 Denavit–Hartenberg parameters of the arm

$$\begin{aligned} T^0_7 = T^0_7 \left( \mathbf q \right) \end{aligned}$$

(9.5)

$$\begin{aligned} \mathbf v _{e}=\begin{bmatrix} \dot{\mathbf{p }}_{e} \\ \varvec{\omega }_{e} \end{bmatrix} ={J}\dot{\mathbf{q }} , \end{aligned}$$

(9.6)

where $T^0_7 \in \mathbb {R}^{4\text {x}4}$ is the homogeneous transformation matrix between the base reference frame $<0>$ fixed to the AUV and the end-effector reference frame $<7>$, $\mathbf q \in \mathbb {R}^{7\text {x}1}$ is the vector of the joint variables, $\dot{\mathbf{p }}_{e}$ is the time derivative of the end-effector position and $\dot{\mathbf{q }}$ is the time derivative of the joint coordinates $\mathbf q$. The redundant DOFs are used to solve secondary tasks (e.g. the avoidance of the singularity or the minimization of the kinetic energy) [2].

The dynamic model of the robotic arm is simulated through the multibody techniques described before, in which each rigid body is modelled as follows:

$$\begin{aligned} M_{l}^i \dot{\varvec{\nu }}_{l}^{i} + C_{l}^i(\varvec{\nu }_l^i )\varvec{\nu }_l^i = \varvec{\tau }_H^i (\varvec{\nu }_l^i ,\varvec{\nu }_{lC}^i) + \mathbf g ^i (\varvec{\eta }_l^i ) + \varvec{\tau }_l^i , \end{aligned}$$

(9.7)

where $M_{l}^i$ represents the mass matrix, $C_{l}^i (\varvec{\nu }_l^i )$ is the Coriolis and centrifugal effect matrix of the ith link. $\mathbf g ^i(\varvec{\eta }_l^i )$ and $\varvec{\tau }_l^i$ are respectively the contribution due to the gravity effects and the external forces (i.e. the torques of the actuators and the force arising from the interaction with the adjacent links) applied to the link (Table 9.3). The ith link characteristics define these contributes. As described before, the hydrodynamic effects ${\varvec{\tau }_{H}^i}(\varvec{\nu }_l^i ,{\varvec{\nu }_{lC}^i})$ are partially decoupled from the dynamic equation in order to use the classical multibody techniques to solve the problem. In particular, these actions have been implemented in each body belonging to the I-AUV system (vehicle, links of the arm and gripper); the simulated effects include hydrostatic and hydrodynamics effects due to the added masses, drag and lift forces and buoyancy effects, implemented similarly to Eq. (9.4).

Table 9.3 Arm and forearm data

Fig. 9.3

Three-dimensional model of the gripper with the 3D contact model

9.2.3 Gripper Multibody Model

A 3D model of the gripper is shown in Fig. 9.3. Each finger consists of two rotational joints connecting the hand to the first phalanx and the two phalanxes. A spherical tip is rigidly connected to the second phalanx. Using the D–H convention, the point where the first phalanx connects to the hand is the origin of reference frame 7 (for each finger), while the middle point of the finger is the origin of frame 8 and the end of the second phalanx is the origin of frame 9. Axis directions are chosen so that a positive value for D–H parameter $\theta$ corresponds to finger’s opening. The reference frame 7$'$, visible in Fig. 9.3, which is the frame attached to the end effector of the arm, is tied to the frame 7$''$ (palm of the hand) by a constant transformation matrix; the same applies for the fingers’ frames 7 with respect to the palm frame. Finally, a frame is attached to the end of each fingertips, rotated by $45^{\circ }$ with respect to the axis of the second phalanx. These frames are the end-effector (ee) frames of each finger. Mass and inertia values of the hand and the fingers are shown in Table 9.4.

Table 9.4 Gripper data

Each finger is locally equivalent to a planar 2-DOFs manipulator, whose kinematics have been used; D–H parameters for one finger are reported in Table 9.5. The dynamic model of a finger in joint space is expressed by the well known relation

$$\begin{aligned} B(\mathbf q )\ddot{\mathbf{q }}+C(\mathbf q ,\dot{\mathbf{q }})+\mathbf g (\mathbf q )+J_{f}^{T}{} \mathbf h _{e}=\varvec{\tau }_{f} , \end{aligned}$$

(9.8)

where B is the inertia matrix, $C(\mathbf q ,\dot{\mathbf{q }})$ and $\mathbf g (\mathbf q )$ include centrifugal, Coriolis and gravitational effects, $J_{f}$ is the finger Jacobian matrix, $\mathbf h _{e} \in \mathbb {R}^{6 \times 1}$ is the vector of forces/torques due to interactions with the environment and $\varvec{\tau }_{f}$ are the joint torques. As for the vehicle and the arm, multibody modelling techniques have been used for the gripper.¹

Table 9.5 Denavit–Hartenberg parameters of the finger

Contact model

This section describes the model that simulates the contact between the spherical tips of the gripper’s fingers and the object to be manipulated. The contact model has the following features [26]:

• contact point: it is assumed that there is a single contact point;

• hard finger contact: tangential forces arise due to friction;

• 3D model: even if the model has been created to govern the contact of the specific test case, its geometrical background is easily adaptable to different cases; thus, it is a complete three-dimensional model.

Figure 9.3 presents the notation used in the model: $\mathbf c _{o}$, $R_{o}$ denote the pose of the object in the inertial frame; $\mathbf p _{f}$, $\mathbf p _{o}$ and $\mathbf v _{f}$, $\mathbf v _{o}$ represent the position and the velocity of the contact points on the fingertip and on the object, respectively. $\mathbf D =\mathbf p _{f}-\mathbf p _{o}$ is the distance between the contact points, and $\mathbf N$ is the contact normal (pointing outwards the object); finally, let $\mathbf s =\mathbf v _{o}-\mathbf v _{f}$ denote the sliding between the surfaces in contact (i.e. the difference between the contact points velocities).

The algorithm can be divided into two steps: firstly the position of the contact points is determined, along with their (vectorial) distance $\mathbf D$; if there is penetration (i.e. $\rho =\mathbf D ^{T}{} \mathbf N$ becomes negative), the contact forces are computed according to the model presented in the following section [27].

Hard finger contact has been considered: three components of force are transmitted at contact; one is normal to the surface, while the others are frictional (tangential) forces. Normal force follows a spring-damper model: let

$$\begin{aligned} s_{N}=\mathbf s ^{T} \mathbf N \end{aligned}$$

(9.9)

denote the value of the component of the sliding vector along $\mathbf N$; then, normal contact force on the object is given by

$$\begin{aligned} \mathbf f _{N}=(k_{n}\rho - c_{n} s_{N}) \mathbf N , \end{aligned}$$

(9.10)

for $k_{n}>0$, $c_{n}>0$. The tangential force is composed of static and kinetic friction; the friction coefficient $\mu$ follows the law:

$$\begin{aligned} \mu (||\mathbf s _{t}||)=\mu _{k}+(\mu _{s}-\mu _{k})e^{-k || \mathbf s _{t}||} , \end{aligned}$$

(9.11)

where $\mathbf s _{t}=\mathbf s -s_{n}{} \mathbf N$ is the tangential sliding, $\mu _{s}>\mu _{k}$ are the static and kinetic friction coefficients and $k>0$ is a tunable parameter. Tangential force exerted on the object is then:

$$\begin{aligned} \mathbf{f }_{t}=- \mu ||\mathbf{f }_{N}|| \frac{\mathbf{s }_{t}}{||\mathbf{s }_{t}||} . \end{aligned}$$

(9.12)

Finite slope can be assumed for $\mu (||\mathbf s _{t}||)$ for small sliding values, to avoid chattering problems during simulations. As a contact between two steel surfaces has been considered, the chosen contact parameters [28] are reported in Table 9.6.

Table 9.6 Contact model parameters

9.2.4 Camera Model

During the grasp planning phase a pose estimation algorithm based on optical sensors (cameras) has been used, which gives the position of the center of mass of the object $\mathbf c _{o}$ and its orientation $R_{o}$ with respect to the arm; thus, it is necessary to give a mathematical model of such sensors. In this context, the pinhole model has been used: this model offers a high computational efficiency [29].

9.3 I-AUV Control

The control system has to make sure that the system can autonomously reach the object to be manipulated and execute the planned task on it.

It has been assumed that all the DOFs of the system are controlled. Actuating forces and torques and their variations have been limited by means of saturations and rate limiters, to simulate the presence of a real actuator [1, 30–32]. At the same time, navigation sensors have been modelled [33].

I-AUVs’ control techniques can be divided into two categories [8]. A first set simultaneously controls the vehicle and the manipulation system [14], subjugating the first to the latter. The second set of techniques makes use of a decoupled approach [15, 34]: the arm manipulates the object while the vehicle tracks its own reference trajectory; the effects of one subsystem on the other are considered as disturbances.

Because of its simplicity and robustness with respect to unknown parameters of the system, the second approach has been chosen. Moreover, exploiting the kinematics of the gripper, the control of the fingers has been further decoupled from the control of the arm: once the desired pose for the fingertips is known, it is indeed possible to univocally determine, from purely geometrical considerations, the desired pose of the arm’s end effector.

Fig. 9.4

Control architecture of the I-AUV

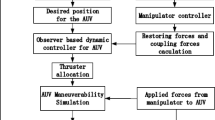
A block diagram of the control architecture is shown in Fig. 9.4. Filled lines represents physical interactions, while dashed lines stand for functional dependence. The global trajectories of the system’s components must permit the manipulation of the object; the dotted line connecting the vehicle’s and the manipulator’s trajectory planning blocks indicates that, even if the two references are virtually independent because of the adopted decoupled strategy, the AUV’s trajectory must allow the arm to reach the object.

Indeed, the whole control system follows a “backward strategy”: during manipulation, the contact points on the object are computed by the grasp planning algorithms; then, a suitable smooth trajectory that takes the fingertips on such points is generated. The positional control of the fingers is in charge of following this trajectory closely. The geometrical decoupling algorithm allows the computation of the reference trajectory of the arm, which is kinematically controlled. Finally, an admissible reference trajectory for the AUV is generated, and a SISO PID control is applied to each DOF of the vehicle [1].

9.3.1 Trajectory Generation of the Manipulation System

The contact points on the object surface constitute the desired values of the reference trajectory; the desired orientation is chosen so that the approach axis of a fingertip frame points inwards the object [35]. The reference trajectory is generated as convex combination of initial and final pose. Let us consider position trajectory generation first: let x denote the generic (scalar) position variable; its desired trajectory is then chosen as

$$\begin{aligned} x(t)=\lambda (t) x_{i}+(1-\lambda (t))x_{d} , \end{aligned}$$

(9.13)

where $x_{i}$ and $x_{d}$ represent the initial and the desired value of x and $\lambda (t)$ is a parameter that continuously (and with continuous derivatives) varies from 1 to 0. This ensures a smooth transition between the initial and the desired values. The continuity of the trajectory is maintained even if the desired value $x_{d}$ varies with time.

For orientation trajectory generation, initial and desired orientations are expressed as unit quaternions $\mathbf q _{i}$ and $\mathbf q _{d}$ [36]; then, Spherical Linear intERPolation (SLERP) is applied, in order to compute a constant angular velocity rotation:

$$\begin{aligned} \mathbf q (t)=\frac{sin\left( 1-\lambda (t) \right) \theta }{sin(\theta )}{} \mathbf q _{i}+\frac{sin(t\theta )}{sin(\theta )}{} \mathbf q _{d}, \quad \theta =cos^{-1}\left( \mathbf q _{i}^{T}{} \mathbf q _{d}\right) . \end{aligned}$$

(9.14)

While the I-AUV is patrolling, searching for the object to be manipulated, the arm is kept at rest position. It is assumed that a camera is mounted on the palm of the gripper. Supposing that the shape of the object is known a priori, as soon as the object enters the field of view of the camera the POSIT algorithm (Pose from Orthography and Scaling with ITerations [37] can be executed to obtain an estimation of the pose of the object itself. Then, the arm’s reference trajectory is changed so as to ensure that the object is kept inside the field of view of the camera all the time. During manipulation, the arm’s reference trajectory is obtained by means of a geometrical algorithm that determines the pose of the end effector of the arm from the knowledge of the fingertips pose. The solution is unique, and the solving process is composed of just a few steps. To overcome the problem of obtaining exact values for the hydrodynamic coefficients of the arm (whereof only an estimation is available), a kinematic control has been preferred to a dynamic control strategy. A Closed Loop Inverse Kinematic Control (CLIK) has been chosen [38], exploiting the arm’s redundancy to keep the manipulator far from singularities.

9.3.2 Trajectory Generation of the AUV

As the definition of dynamic manipulation implies, the AUV never stops during the execution of the task; furthermore, the vehicle must constantly keep the object inside the arm and gripper workspace so as the manipulation takes place.

The AUV is controlled by means of a decoupled PID strategy: six PID controllers have been used, one for each degree of freedom of the vehicle [1]. The control law is:

$$\begin{aligned} \mathbf u _{AUV}^{th}=H^{\dagger }{} \mathbf u _{AUV} , \end{aligned}$$

(9.15)

where

$$\begin{aligned} \mathbf u _{AUV}=J^{n}_{b}\varvec{\tau }_{PID}+\mathbf g (\varvec{\eta }) , \end{aligned}$$

(9.16)

being $\varvec{\tau }_{PID}$ a $6 \times 1$ vector of PID action on the pose error $\mathbf e _{\varvec{\eta }}$. $J^{n}_{b}$ is the AUV Jacobian matrix, $\mathbf g (\varvec{\eta })$ a term of gravity compensation, and $H^{\dagger }$ is a generalized pseudo-inverse of the propeller matrix H [1], which maps the vector of thruster forces $\mathbf S$ into the vector of forces/torques acting on the vehicle:

$$\begin{aligned} \varvec{\tau }=H\mathbf S . \end{aligned}$$

(9.17)

In the considered case, $\mathbf S =[S_1\ S_2\ S_3\ S_4\ S_5\ S_6]^T$; hence, the propeller matrix is square and it has the form:

$$\begin{aligned} H = \left[ {\begin{array}{*{20}{c}} {{\mathbf{v }_1}} &{} {{\mathbf{v }_2}} &{} {{\mathbf{v }_3}} &{} {{\mathbf{v }_4}} &{} {{\mathbf{v }_5}} &{} {{\mathbf{v }_6}} \\ {{\mathbf{P }_{m1}} \times {\mathbf{v }_1}} &{} {{\mathbf{P }_{m2}} \times {\mathbf{v }_2}} &{} {{\mathbf{P }_{m3}} \times {\mathbf{v }_3}} &{} {{\mathbf{P }_{m4}} \times {\mathbf{v }_4}} &{} {{\mathbf{P }_{m5}} \times {\mathbf{v }_5}} &{} {{\mathbf{P }_{m6}} \times {\mathbf{v }_6}} \\ \end{array}} \right] , \end{aligned}$$

(9.18)

where $\mathbf P _{mi}$ for $i=$ 1–6 is the propeller position vector in body reference frame and $\mathbf v _i$ for $i=$ 1–6 is the unitary vector of the thrust direction.

9.4 Numerical Simulations

In this section, the dynamic behaviour of the whole I-AUV system has been simulated during the execution of a predefined dynamic manipulation task (whose scheme is presented in Fig. 9.5).

Fig. 9.5

Description of the performed manipulation task

Table 9.7 Simulation data

The task consists of grasping a cylindrical object lying on the sea floor, and it is composed of the following steps:

• the I-AUV, starting from rest, accelerates for 5 s until steady-state speed is reached;

• as soon as the cylinder enters the field of view of a camera mounted on the palm of the gripper (eye-in-hand configuration), the reference trajectory is changed so as to align the camera focal axis with the line connecting the palm of the gripper to the position of the center of mass of the object (estimated by the POSIT algorithm); this way, the cylinder is kept inside the field of view of the camera all the time;

• when a threshold distance between the gripper and the object is reached, the arm is lowered and the gripper grasps the cylinder;

• the cylinder is lifted and carried as the arm reaches a final “rest” configuration (i.e. the cylinder carried vertically under the bow of the vehicle).

It is worth noting that the AUV never stops during the execution of the task, which is a fundamental requirement for a correct dynamic manipulation task.

For the ease of reading, reported data (unless stated otherwise) are expressed in an inertial reference frame whose x axis is aligned with the forward direction of the vehicle, z axis is directed toward the sea surface, and y axis forms a right-handed coordinate system. Without loss of generality, the origin of this frame is chosen coincident with the initial position of the center of mass of the AUV. The object lies on the sea floor at about $- 0.6$ m under the vehicle (initial depth). The described task has been simulated using Matlab-Simulink$^{\circledR }$ software. A fixed step solver (ODE5-Dormand-Price) has been chosen to increase affinity with real hardware.

Three simulations have been carried out, at different vehicle’s speeds: 0.1, 0.2 and 0.25 m/s; this makes possible the analysis of the effect of increasing speed on the performances of the control system. Table 9.7 summarizes the main parameters of the simulations and the cylinder properties. At higher speed, the I-AUV fails to execute the task correctly; however, this is not due to a control architecture fault, but to the physical length of the links of the arm which impose a limit on the window of time allowed for manipulation.

Fig. 9.6

3D trajectory

Fig. 9.7

Pose error of the AUV

Figure 9.6 reports the three-dimensional trajectory of the vehicle, the gripper, the fingertips and the object obtained during the fastest simulation.

Figure 9.7 shows the behaviour of the AUV during the three simulations: the error along the direction of forward motion is very small, its value increasing with the speed of the vehicle: this is because the AUV always accelerates for 5 s, thus higher steady-state speed equals higher acceleration values, which decrease the performance of the PID controller. Y-motion, roll and yaw angular errors are neglectable. Initial errors on the z-axis motion and on the pitch angle, not affected by speed, are due to the total buoyancy of the system: while the vehicle has positive buoyancy (1 %), the arm and the gripper tend to sink the I-AUV; in addition, since the manipulation system is mounted centrally on the front side of the AUV, it has the effect of leaning the vehicle forward. However, these errors are kept small and rejected in time.

Fig. 9.8

Position error of the arm

Fig. 9.9

Cylinder position

Arm position errors, visible in Fig. 9.8, are expressed in a local coordinate system whose origin coincides with the shoulder of the manipulator and whose initial orientation is the same as the inertial frame. Aside from the initial error (due to gravity), Fig. 9.8 shows that the error increases as the AUV moves faster; however, it is kept small during the execution of the manipulation task. Fingertips position errors are very similar to the arms ones, thus they are not reported.

Figure 9.9 shows the position of the center of mass of the cylinder on each axis. Plots have been divided according to x, y and z coordinates. It is clearly visible the time when the object is grabbed and then lifted (motion on the x and z axis, respectively); transversal motion is neglectable (Table 9.8).

9.5 Conclusion

This paper describes a detailed multibody model of an I-AUV to study a suitable control architecture for manipulation tasks. In particular, to better analyse the effectiveness of the multibody models, the most challenging autonomous manipulation (dynamic manipulation) has been considered. Dynamic manipulation denotes manipulation tasks executed while the vehicle maintains relevant velocities, further complicating the execution of the mission due to the dynamic interaction between the AUV and the manipulator. A complete multibody model of the I-AUV system has been derived, including interaction with the fluid and contact with the object to be manipulated. The I-AUV is controlled by means of a decoupled vehicle-manipulator strategy, further decoupling the control of the gripper exploiting the hand kinematics.

Different relative speeds between the I-AUV and the object, in the same simulation scenario, have been simulated with satisfying results, showing how the developed multibody models and the adopted strategy allow the execution of the task. As concerns future investigations, different simulation scenarios are required to establish the maximum velocity that can be maintained during the manipulation phase. Further improvements are scheduled, with special attention given to data acquisition and to autonomous calculations, before the application of the proposed strategy in the framework of the Italian project SUONO and of the FP7 European project ARROWS.

Table 9.8 Minimum AUV speed