GPU-Accelerated Real-Time Mesh Simplification Using Parallel Half Edge Collapses

Abstract

Mesh simplification is often used to create an approximation of a model that requires less processing time. We present the results of our approach to simplification, the parallel half edge collapse. Based on the half edge collapse that replaces an edge with one of its endpoints, we have devised a simplification method that allows the execution of half edge collapses on multiple vertex pairs of a mesh in parallel, using a set of per-vertex boundaries to avoid topological inconsistencies or mesh foldovers. This approach enables us to remove up to several thousand vertices of a mesh in parallel, depending on the model and mesh topology. We have developed an implementation that allows to exploit the parallel capabilities of modern graphics processors, enabling us to compute a view-dependent simplification of triangle meshes in real-time.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Highly detailed polygonal models are commonly used for visually appealing scenes. The triangle count still poses an important factor in performance considerations. A wide variety of simplification operators have been devised that can be used to reduce the complexity of 3-d models. Falling back on these operators a plethora of algorithms and approaches have been developed to create simplifications of given objects. Over the last decade various algorithms have been presented that are designed to utilize the parallel processing power of modern GPUs to speed up the simplification process (Papageorgiou and Platis [9]) with some focussing on calculating the simplified results in real-time such as Hu et al. [3] or DeCoro and Tatarchuk [4].

We present the results of our approach, the parallel half edge collapse. It is designed to provide a parallel solution to simplification of manifold triangle meshes that can be executed on a GPU.

1.1 Previous Work

Hoppe et al. [2] present the edge collapse. This operator replaces an edge of a triangle mesh with a single vertex, so effectively removing a vertex and one or two triangles. A more restrictive version is the half edge collapse, where the position of the replacement vertex cannot be freely chosen, but is one of the endpoints of the collapsed edge. The edge collapse has the disadvantage that it may create foldovers in the mesh as well as topological inconsistencies [6].

In Hoppe [5], this operator and its inverse - the vertex split - are used to describe an algorithm to coarsen or refine a mesh. Given a detailed mesh Hoppe performs a series of edge collapses on it, storing the applied operations in a data structure. Then the mesh is represented using the coarse version and a series of refinement operations (vertex splits) that can be used to compute the desired refinement of the mesh. In Hu et al. [3] (with further explanation in [8]) this approach is adapted for execution on a GPU. While Hoppe defines a series of strictly iterative operations, Hu et al. replace Hoppe’s data structure with a tree that defines dependencies between the precomputed edge collapses/vertex splits. This improved algorithm allows for a parallel execution and improved performance.

Another method of simplification is the cell collapse originally described in Rossignac and Borrell [1]. Here a number of cells is superimposed over the mesh with all vertices within a cell being combined into a single vertex. While this allows for fast generation of a coarse mesh, it has the disadvantage of ignoring the topology of the mesh which can result in low quality simplifications.

DeCoro and Tatarchuk [4] have adapted this approach to be executed on programmable graphics hardware. Their algorithm executes three passes over the mesh: cell creation, calculation of replacement position for each cell and generation of the decimated mesh.

Papageorgiou and Platis [9] present an algorithm that executes multiple edge collapses in parallel. However, they do not rely on precomputed data structures. Their approach divides a mesh into a series of independent areas. In each area an edge collapse can be safely executed without influencing another one. The algorithm is designed to be executed on a GPU, with the steps of computation of independent areas and performing a series of edge collapses in parallel being repeated until the desired simplification is achieved. This speeds up the computation, but does not provide real-time simplification.

In [10] we presented the concept of our approach, the parallel half edge collapse. In this paper we want to introduce further details of this algorithm and discuss the results of this approach in detail.

1.2 Algorithm Overview

The parallel half edge collapse aims to provide a view-dependent, real time simplification of a triangle mesh. The goal is to compute the simplification at run-time without relying on pre-computed operations. The simplification operator used is the half edge collapse. We determine a set of vertices R that are to be removed from the mesh and the complementary set S (remaining vertices of the mesh). Vertices are removed by performing half edge collapses on edges of the mesh that connect vertices in R with a vertex in S (removing the vertex in R and replacing the edge with the vertex in S), while executing as many of these operations as possible in parallel. To avoid mesh foldovers or topological inconsistencies - even when neighbouring vertices are removed at the same time - we compute a set of per-vertex boundaries to determine if a half edge collapse would cause any of the aforementioned issues. Since only vertices in R that have a neighbour in S can be removed using this approach, we apply multiple iterations of the parallel half edge collapse until all vertices in R have been processed. After each iteration, we execute a reclassification step. This analyses the remaining vertices in R taking changes in the topology and surface shape into account and may move them from R to S to avoid low quality simplifications.

2 Classification

The vertex classification analyses all vertices of a triangle mesh and assigns each one to either R or S. This step is divided into the vertex analysis and the initial classification.

Vertex analysis is performed before the simplification. For each vertex V an error value e(V) is computed. The initial classification falls back on e(V), applies scaling based on camera data like view vector and distance between camera and vertex and compares the result to a user-defined threshold u which leads to the creation of S and R.

2.1 Static Vertex Error

The static vertex error is calculated using a geometric error metric. We chose the average distance between the neighbouring vertices and the tangential plane of V for this purpose. The tangential plane is constructed from the position of V as well as the normal vector stored in V and expressed as $ax + by + cz + d = 0$ with $t = [a, b, c, d]$. For each neighbouring vertex $N_i$ with the position $n = [n_x, n_y, n_z, 1]$ the quadratic distance from the tangential plane $d(V, N_i) = (t \bullet n)^2$ is calculated with e(V) being the average quadratic distance.

$$\begin{aligned} e(V) = \frac{\sum ^m_{i=1}(d(V, N_i))}{m} \end{aligned}$$

(1)

Since this metric is computed per-vertex and does not take a possible removal of neighbouring vertices into account, a large user threshold u could potentially select a large number of - if not all - vertices for removal. This could severely limit parallelism or in case of all vertices being marked for removal prevent a simplification at all. A metric manipulation is applied as a part of the error computation to avoid these issues.

2.2 Vertex Error Manipulation

This step aims to select a number of vertices from the mesh and assign them an error value $e(V) > u$ to guarantee their classification into S. We apply a layered version of the error manipulation. Layer $L_0$ contains the vertices that are assigned $e(V) > u$. Every additionally created layer selects additional points and manipulates their vertex error with a user selected value assigned to the layer.

For this approach a number of vertices has to be selected for each layer:

• Bounding box computation and creation of a set of points $P(L_0) = \{P_0^0, P_1^0,\ldots , P_n^0\}$ within the bounding box with equal axial distance $d(L_0)$ between points.

• Creation of additional layers $L_i$ with points $P(L_i) = \{P_1^i, P_2^i, \ldots P_o^i\}$ created at halfway points between the points in $L_{i-1}$ ($d(L_i) = \frac{d(L_{i-1})}{2}$, $i > 0$, 2-dimensional example on the left in Fig. 1).

• Generation of volume $B(P_j^i)$ for each point. $B(P_j^i)$ is centered around $P_j^i$ and has a side length of $d(L_i)$ (trimmed to the bounding box). Right side of Fig. 1 shows the volumes for the first two sample layers.

• For each volume: determination of all vertices $V(P_j^i)$ within the volume

• For each volume: selection of one vertex from $V(P_j^i)$ and manipulation of the vertex error

Fig. 1.

Example point generation (left to right: layer $L_0$, layer $L_1$, layer $L_2$) and volumes for $L_0$ and $L_1$

Points $P_j^i$ may not correspond to vertices of the mesh. For each $P_j^i$ a vertex is selected from within the corresponding volume $B(P_j^i)$ if applicable. For a point $P_j^i$ with position $p_j^i$ and a vertex $V_k$ with position $v_k$ we calculate the weighted error $m(V_k, P_j^i)$ using the maximum side length l of the volume $B(P_j^i)$ as follows:

$$\begin{aligned} m(V_k, P_j^i) = (l - |p_j^i - v_k|)^2 * e(V_k) \end{aligned}$$

(2)

For each volume the vertex with the maximum weighted error is used for error manipulation. The weighted error takes the static vertex error and the distance between $P_j^i$ and $V_k$ into account. The weighted error is designed to preferably select vertices closer to $P_j^i$, to achieve a more uniform distribution of vertices with a manipulated per-vertex error, while taking the original error value into account, to avoid keeping vertices with little influence to the surface shape in the simplified mesh.

3 Boundary Computation and Testing

The per-vertex boundaries are used to avoid half edge collapses causing mesh foldovers or topological inconsistencies. Due to the parallel nature of this approach, we cannot rely on simple methods of testing for such occurrences (e.g. a maximum rotation of triangle normals before and after a collapse).

3.1 Boundaries

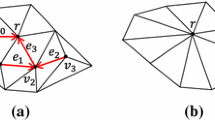
The per-vertex boundaries B(V) are a set of planes that is computed for each vertex V that has at least one neighbour in S (subsequently referred to as removal candidates). Each triangle containing V adds one or more planes to B(V). Boundary planes are constructed based on how many vertices of a triangle are removal candidates (Boundary 1, 2 and 3 for 1, 2, and 3 removal candidates respectively) and use the camera position E. The parallel execution of half edge collapses has to be taken into account and the need for communication avoided. The planes are defined only to allow replacement positions for a removal candidate that would not cause a foldover or inconsistency, no matter what collapse - if any at all - is chosen for the other removal candidate in this triangle. This can lead to possible valid combinations of half edge collapses being blocked with boundaries 2 and 3.

Fig. 2.

Boundaries 1, 2 and 3

Boundary 1 (Vertices $V_1$, $V_2$ and removal candidate $V_r$, Fig. 2 left). A single plane p is constructed. It contains the vectors $\overrightarrow{V_1 - E}$ and $\overrightarrow{V_2 - E}$ as well as the points $V_1$ and $V_2$.

Boundary 2 (Vertex $V_1$ and removal candidates $V_{r1}$, $V_{r2}$, Fig. 2 middle). Two planes $p_1$ and $p_2$ are constructed. Plane $p_1$ is constructed using the vectors $\overrightarrow{V_{r1} - V_{r2}}$ and $\overrightarrow{V_1 - E}$ as well as the point $V_1$. Plane $p_2$ is constructed from $\overrightarrow{V_1 - E}$, $\overrightarrow{\frac{V_{r1} + V_{r2}}{2} - V_1}$ and $V_1$.

Boundary 3 (Removal candidates $V_{r1}$, $V_{r2}$ and $V_{r3}$, Fig. 2 right). Two planes $p_1$ and $p_2$ are constructed for each removal candidate. They both contain the centroid S. For $V_{r1}$, plane $p_1$ contains the vectors $\overrightarrow{V_{r2} - V_{r1}}$ and $\overrightarrow{S - E}$ as well as the point S. Plane $p_2$ for $V_{r1}$ is constructed from $\overrightarrow{V_{r3} - V_{r1}}$ and $\overrightarrow{S - E}$ and lies through the point S.

Each possible half edge collapse for a removal candidate V needs to be tested against these boundaries to avoid foldovers or topological inconsistencies:

• Selection of all triangles T(V) containing V

• For each triangle in T(V) determination of the appropriate boundary

• Construction of boundary planes and adding them to B(V)

• Testing of each possible half edge collapse against all planes in B(V)

Each possible half edge collapse for V has to be tested against each plane in B(V) individually. If any intersection between the edge and any plane in B(V) exists, the half edge collapse is considered invalid. This test can be simplified by adapting the orientation of the plane normals with regards to V. The test checks, if the dot product between the plane normal and the removal candidate V, as well as the dot product between the second vertex of an edge $V'$ and the plane normal share the same sign. Planes are constructed so that the dot product of the plane normal and V have the same sign for all planes in B(V). This reduces the test of a half edge collapse against a single plane in B(V) to a dot product and the checking of the sign of the resulting value.

3.2 Half Edge Collapse Selection

The selection of one half edge collapse for each removal candidate is based on the approach by Garland and Heckbert [7]. We take Garland’s and Heckbert’s approach, compute their error value $\bigtriangleup (V')$ for each valid replacement position and execute the half edge collapse with the lowest error. While Garland and Heckbert update their vertex error by computing a new error value from the errors of $V_1$ and $V_2$, we deviate from this approach. We do not update the error value, but rather compute it at every step for the current intermediate mesh.

4 Deadlock Prevention and Reclassification

Since boundary 2 and 3 can block valid combinations of half edge collapses, it is possible for a deadlock to appear where two or more removal candidates mutually block each other and the simplification cannot be completed. Only boundary 1 always computes a correct result that does not block any valid half edge collapses. To avoid this, we create two sets of boundaries per removal candidate. B(V) contains the boundaries as described above. $B'(V)$ is created with the planes of boundary 1 for all triangles containing V. This creates two results for each vertex: Result $r_1$ from checking with planes in B(V) which allows to select a valid half edge collapse. Result $r_2$ from $B'(V)$ tells if any half edge collapse is allowed when not taking parallel execution into account. If $r_1$ and $r_2$ block all half edge collapses, the vertex cannot be removed and is reclassified. If only $r_1$ blocks all half edge collapses, the parallel execution prevents removal, the vertex remains in R and is considered as “ignored”, excluding it from the removal candidates until at least one neighbour has been processed (either removed or reclassified).

After each removal step the list of removal candidates is updated. The initial vertex error is recomputed for all removal candidates using the current intermediate mesh. Since some neighbours of removal candidates are to be removed we adapt the metric here. We use the maximum distance between the tangential plane and the neighbours that are to remain in the mesh. Like the static vertex error, the updated vertex error is compared to the threshold and the vertex is reclassified if necessary.

5 Implementation

We have devised an implementation of the parallel half edge collapse using CUDA to be able to analyse our algorithm.

We had to extend per-vertex data for our algorithm. Each vertex stores a vertex error that is used to classify the vertex and updated for removal candidates after each iteration. Since boundary computation relies on the number of removal candidates in a triangle, it is also necessary to store if a vertex is “marked” as removal candidate.

The parallel half edge collapse requires information about all neighbouring vertices. It is necessary to create an additional buffer that serves as data storage containing a triangle strip for each vertex of the original mesh. The neighbouring triangles are used for two purposes during the execution of the parallel half edge collapse: boundary computation and calculation of the vertex error. Both applications need the geometric data, but do not rely on knowledge of the orientation of the triangle. Since the triangle fan is stored per vertex in this data structure, we can minimize storage requirements by only storing a list of neighbouring vertices in the correct order.

A second data structure is used to maintain a list of removal candidates. After the initial classification all removal candidates are determined by searching the neighbours of all those vertices, that are selected to remain in the mesh, for vertices to be removed. At the start of the removal step, the stored vertices are distributed among the threads executing the simplification. After the removal step has been completed, the list is repopulated with the new removal candidates for the next step.

We actually maintain two lists of removal candidates. Given that we assign each CUDA thread a vertex from this list, we can never guarantee that we actually have less vertices than cores. After the cores have completed processing the first assigned candidates, the list may still be partially populated. To avoid this issue, we use a separate input and output list, swapping them after each step.

6 Results

Figure 3 shows an example of a simplification of the Stanford Bunny in comparison to the original mesh (left) while Fig. 4 shows examples for other models that were simplified.

Fig. 3.

Original model (left), simplified version (about 93 % reduction in triangles, right)

Fig. 4.

Simplifications of the model Armadillo, Dragon and Happy Buddha (93 %–95 % of triangles removed) from the Stanford 3-d scanning repository

Fig. 5.

Wireframe models of test case 1–5. See Table 1 for details.

We calculated several simplifications of the Stanford Bunny to achieve comparable results, assess processing time and find bottlenecks and weaknesses. All measurements were taken using a Geforce GTX 670 GPU with 1344 cores. The original mesh of the Stanford Bunny consists of 35 947 vertices that form 69 451 triangles. For the purpose of our measurements we compared 5 separate simplifications, ranging from 48 831 to 7 059 triangles. Beside the overall runtime and the number of triangles of the simplified mesh, we also analysed the number of iterations, including the number of vertices processed in each iteration. Given that our approach is executed on a GPU, we want a high number of processed vertices with each iteration to be able to fully utilize the cores of the GPU and increase the efficiency of the simplification. We measured the runtime of the individual steps of the simplification process and analysed the impact of the manipulation of the initial vertex error to the process.

Figure 5 shows the resulting wireframes for all 5 simplifications. Table 1 shows an overview of the results, including the number of triangles the simplified mesh is made up of, the number of triangles removed, the required iterations and the processing time in milliseconds. These results show the rise in necessary iterations to process all vertices marked by the vertex analysis. Table 2 shows the number of removed triangles and processing times for the additional models.

Table 1. Test cases data overview (triangles, triangles removed, number of iterations and processing time in milliseconds)

Table 2. Data of simplifications of additional models (triangles, triangles removed and processing time in milliseconds)

Fig. 6.

Silhouette comparison

Figure 6 shows a comparison of a section of the image between the original (left) and a simplified version (right). This visualizes that the silhouette of the object is well preserved while the triangle count of the surface greatly reduced.

We further analysed the number of vertices processed in each step, which uncovered a problem with the execution of the parallel half edge collapse. A high grade of simplification causes a larger number of necessary iterations. We observed a high number of processed vertices in the early iterations of each simplification. During later iterations the number of vertices available for a half edge collapse dropped significantly.

Fig. 7.

Vertices removed in each iteration (left) and runtime analysis (right)

The chart on the left in Fig. 7 shows the number of vertices that were removed in each step. As mentioned earlier, the GPU used for the test cases offers 1344 cores. The implementation assigns each CUDA thread an individual vertex to process and to remove. As this diagram illustrates, there are one or more steps in several test cases where not all cores of the GPU can be utilized due to an insufficient number of removal candidates. Especially test cases with a high number of triangles removed suffer from this problem. This issue may be further escalated by the mesh topology. A disadvantageous mesh topology can cause some vertices not to have a neighbour in S until most vertices marked for removal have been processed, effectively delaying the completion of the simplification process. Another issue we identified, that can cause this behaviour, is the deadlock prevention we implemented. As our approach can only recognize a possible deadlock once the subsequent iteration has started, the deadlock prevention could potentially delay the completion of the simplification process. Since it can mark a number of vertices as “to be ignored”, the removal of those vertices may be distributed over several iterations, that might otherwise be unnecessary. In a worst-case scenario the only vertices left waiting for removal could be ignored ones with the topology only allowing a single removal per iteration.

The chart on the right in Fig. 7 shows the cumulative runtime of the reclassification, deadlock detection and parallel half edge collapse steps of the simplification process for all five test cases. It is obvious that the majority of the processing time is used for the execution of the parallel half edge collapse itself, while reclassification and deadlock prevention take up less than 20 % of the total run-time.

Another important factor proved to be the error manipulation during the error computation for the static vertex error. It does not only serve to guarantee the functionality of the algorithm, but it also provides additional vertices in S that are regularly spaced out. This has the effect of reducing the necessary number of iterations when many vertices are removed. Experiments with our implementation showed that the error manipulation has very little measurable impact on the test cases 1 and 2 where most vertices in R could be removed in the first iteration. In test case 5, however, the error manipulation caused a large reduction in necessary iterations, reducing them by a factor of 4, increasing parallelism and reducing run-time.

The last factor we analysed is memory usage. The parallel half edge collapse mainly relies on the fan data buffer as well as the buffers for the removal candidates and the vertex error that is stored in the vertex data. The execution needed 2.3 (Bunny), 11.2 (Armadillo), 29.9 (Dragon) and 35.2 (Buddha) megabytes for the tested models.

6.1 Comparison to Existing Algorithms

Given that the parallel half edge collapse is designed for computing the simplification in real-time, the most similar approaches are Hu et al. [3, 8] and DeCoro and Tatarchuk [4]. While Papageorgiou and Platis [9] present an algorithm that aims to execute multiple edge collapses in parallel, they do not aim at real-time execution of the simplification. Even though their algorithm is faster than iterative approaches like the quadric error metric by Garland and Heckbert [7], they still take up to several seconds to compute the simplification. This fact leads to its omission for this comparison.

While Hu et al. provide real-time refinement of a triangle mesh, their approach is a parallel version of progressive meshes presented by Hoppe [5] and is not designed to calculate the complete simplification during rendering. It rather executes incremental changes in the form of vertex splits and edge collapses between frames. They report update times ranging from 10 ms (about 100 000 triangles) to nearly 70 ms (about 450 000 triangles) using a Nvidia GeForce 8800GTX GPU. Given that Hu et al. like Hoppe base their approach on a pre-simplified mesh that can be refined, their approach is to be described as bottom-up. The parallel half edge collapse on the other hand is a top-down approach. Due to these facts, a direct comparison of run times between these algorithms is not really meaningful.

DeCoro and Tatarchuk recalculate the simplification during image generation, but their approach is mainly designed to provide fast simplification time. It does not preserve manifold connectivity and tends to produce overall low quality (Fig. 8). Given that the parallel half edge collapse is a top-down approach, it has the disadvantage of higher execution time when producing coarser meshes. The approach by DeCoro and Tatarchuk has the advantage of producing a much more stable and predictable runtime. They report taking 13 ms to create a simplification of the Stanford Bunny on a “DirectX 10 GPU”.

Fig. 8.

Comparison with DeCoro and Tatarchuk [4] (right)

7 Future Work

The current calculation of the vertex error and its application during the initial classification only rely on geometrical data of the vertex. The classification of neighbouring vertices is not taken into account. As a result a large number of vertices can be marked for removal which can later be reconsidered during the reclassification phase.

As our analysis has shown, one of the major bottlenecks of our approach is the lack of removal candidates. Improving the initial classification to reduce the reliance on the reclassification step and providing a better set of removal candidates can be used to increase parallelism. Vertices that are reclassified during the execution in the current algorithm may provide additional removal candidates at the start of the simplification when an improved classification scheme is applied.

Another factor limiting the parallelism is the restriction of only executing half edge collapses between vertices in R and S. Allowing vertices with no neighbours in S to be subjected to a half edge collapse could be used to reduce the number of necessary iterations and therefore increase the parallelism of the approach.

8 Conclusion

The parallel half edge collapse has proven to allow fast, view-dependant simplification that can make use on the parallel processing power of modern GPUs by relying on isolated per-vertex operations. While our analysis has shown good results in terms of overall quality and execution time, it has also uncovered some limiting factors, namely the reduced parallelism that may be caused by the topology or a lack of removal candidates. Another limiting factor of the parallel half edge collapse lies in the execution of the simplification operator. Given that a vertex is chosen for removal and one half edge collapse selected for each removal candidate, it is not possible to select an “optimal” edge that is collapsed. While this causes iterative approaches to achieve a better overall quality, it is considered as a trade-off for the parallel execution and the performance gain of the parallel half edge collapse.