Probabilistic Seismic Assessment of Existing Buildings: The CNR-DT212 Italian Provisions

Abstract

This chapter briefly illustrates a document recently issued by the Italian National Research Council (CNR), dealing with probabilistic seismic performance assessment of existing buildings. The document, which is aligned with the present international state of the art, is intended to serve the double purpose of providing firmer theoretical bases for the revision of the current European norms on seismic assessment of existing structures and to be practically applicable for cases worth of more rigorous analysis. After a concise overview, this chapter focuses on the specific aspects of limit state quantitative evaluation and of response and capacity modeling.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Seismic assessment of an existing building, designed and built in the absence or with inadequate consideration of the seismic threat, is recognised as a much more challenging problem than designing a new building according to any modern seismic code. The difficulties inherent in the former task are reflected in the current international absence of normative documents possessing the necessary degree of rigour and accuracy.

In the USA, a large multi-annual project funded by FEMA and carried out by the Applied Technology Council has led to the release in 2012 of a comprehensive document: the FEMA-P58 (ATC 2012). Its ambition goes as far as to enabling a probabilistic evaluation of the performances of a structure in terms of the mean annual rate of the occurrence of collapse, of the exceedance of a threshold in terms of direct repair/replacement cost as well as of the indirect cost due to interruption of use. An introductory notice is included in the document, however, stating that “data and […] procedures are not necessarily appropriate for use in actual projects at this time, and should not be used for that purpose. The information contained […] will be subject to further revision and enhancement as the methodology is completed”.

In Europe, the issue of the seismic assessment of buildings is covered in the Eurocode 8 Part 3 (EC8-3): Assessment and Retrofit of Buildings, issued in 2005. It is based on the customary limit state (LS) approach, with the LSs referring to the state of both structural and nonstructural components. Reliability aspects are limited to the choice of the mean return period of the seismic action to be associated with each of LSs and to a global reduction factor to be applied to the material strengths. This factor is a function of the so-called knowledge level acquired on all the geometrical/structural aspects of the building. Only the general methodology of EC8-3 is mandatory, the expressions giving the capacities of the elements to the different LSs having only the status of informative material. This document has been extensively used in European seismic-prone countries since its release, and applications have exposed its insufficient “resolving power”, meaning that, depending on the choices that are left to the user, results that are quite distant apart can be obtained. The sources of this observed dispersion of the results have been identified, and efforts are currently under way to arrive at an improved version of the document.

To help in the above direction, the Italian National Research Council (CNR) has taken the initiative of producing a higher-level, fully probabilistic document, DT212 (CNR 2014), for the seismic assessment of buildings, intended to serve the double purpose of providing firmer theoretical bases for the revision of EC8-3, and of being of direct practical applicability for cases worth of a more rigorous analysis. The DT212 has been presented in some detail in Pinto and Franchin (2014). This paper provides a brief overview before focusing on the characterising aspects of the LS quantification and modelling.

2 Overview of DT212 Provisions

The DT212 provides the conceptual and operational tools to evaluate the seismic performance of a building in terms of λ _LS, the mean annual frequency (MAF) of exceeding an LS of interest (three are defined; see later). The DT212 adopts what is called nowadays the “IM-based approach”, which employs the total probability theorem to express λ _LS as the integral of the product of the probability of exceedance of the LS conditional to the value S = s of the seismic intensity (denominated as “fragility”), times the probability of the intensity being in the neighbourhood of s. This latter is given by the absolute value of the differential of the hazard function at S = s:

$$ {\lambda}_{\mathrm{LS}}={\displaystyle {\int}_0^{\infty }{p}_{\mathrm{LS}}(s)\left|d{\lambda}_S(S)\right|} $$

(7.1)

This approach dates back at least to the early 1980s, e.g. Veneziano et al. (1983), and has been the subject of intensive research since then, the central issue being the optimal related choices of the intensity measure (IM) S and of the ground motions required to compute p _LS. Acceleration in the research and dissemination efforts started in the second half of the 1990s when the PEER framework was formulated (Cornell 1996; Cornell and Krawinkler 2000). It can be said that the approach has now attained maturity for practical application, with the main issue identified above being solved through effective ground motion selection procedures (Bradley 2012; Lin et al. 2013).

The evaluation of the MAF in Eq. (7.1) can be carried out in closed form if the hazard curve is fit with a linear or quadratic function in the log-log plane, e.g. Vamvatsikos (2013), and the fragility function is assumed to have a lognormal (LN) shape. Hazard is obtained by standard PSHA: in Italy, one can take advantage of the availability of response spectra for nine different return periods (both median and 16–84 % fractiles), from which the hazard λ _S can be retrieved (Pinto and Franchin 2014). Thus, the task of engineers consists of the selection of ground motions and performance of nonlinear response analyses to evaluate the fragility:

$$ {p}_{\mathrm{LS}}(s)=p\left({Y}_{\mathrm{LS}}\ge 1\left|S=s\right.\right)=p\left({S}_{Y_{\mathrm{LS}}=1}\le S\right)=\varPhi \left(\frac{ \ln\;S-{\mu}_{\ln {S}_{Y=1}}}{\sigma_{\ln {S}_{Y=1}}}\right) $$

(7.2)

Equation (7.2) states that the fragility can be regarded equivalently as the probability that a global LS indicator function Y _LS (see later) reaches or exceeds the unit value, given S = s, or that the intensity leading to Y _LS = 1 is lower than the current intensity s. The two parameters of the LN fragility function are evaluated in different ways depending on the strategy employed to perform numerical response analyses. The alternatives are the multiple stripe analysis (MSA) (Jalayer and Cornell 2009) and the incremental dynamic analysis (IDA) (Vamvatsikos and Cornell 2002). In the former case, maximum likelihood estimation can be used to fit the LN fragility to the collected s-p _LS pairs. In the latter, which is the main approach put forward in DT212, ${\mu}_{\ln {S}_{y=1}}$ and ${\sigma}_{\ln {S}_{y=1}}$ are simply obtained from the sample of S _Y=1 values collected from IDA.

DT212 provides three methods to produce IDA curves, all requiring a 3D model of the structure: (a) full dynamic, (b) static-dynamic hybrid and (c) static. In all three methods, the engineer must select a suite of recorded ground motion records, each with two orthogonal components, with an indicated minimum of 30 time series. Motions can be selected based on PSHA disaggregation results (M, R, ε), but more advanced methods are also considered (Bradley 2012; Lin et al. 2013). The time series are used in inelastic response-history analysis (IRHA) with the full dynamic (complete 3D model) and the hybrid method. In the latter, IRHAs are carried out on equivalent SDOF oscillators obtained from nonlinear static analysis, e.g. with modal patterns, as in Han and Chopra (2006). The two orthogonal components are applied simultaneously in both the full and the hybrid method. In the latter case, the SDOF is subjected to a weighted excitation (Pinto and Franchin 2014). The difference in the static method consists in the fact that the response of the equivalent SDOFs is obtained with the response spectra (median and fractiles) of the selected ground motion records, rather than with a code or other uniform-hazard spectrum.

Given that a fully exhaustive (i.e. deterministic) knowledge of an existing building in terms of geometry, detailing and properties of the materials is realistically impossible to achieve, it is required that every type of incomplete information be explicitly recognised and quantified, for introduction in the assessment process in the form of additional random variables or of alternative assumptions. Uncertainties on structure and site are lumped in two classes:

• 1. Those describing variations of parameters within a single model, described in terms of random variables, with their associated distribution function (mainly material properties, such as concrete and steel strength, or internal friction angle and shear wave velocity, and model error terms). These are usually modelled as LN variables and are approximately accounted for in the evaluation of λ _LS by associating one-to-one their samples to the selected motions, with the exception of method c, where response surface is used instead (Pinto and Franchin 2014).

• 2. Those whose description requires consideration of multiple models.

Type 2 uncertainties include, among others, factors related to the geometry of the structure in areas of difficult inspection, the reinforcement details in important places, the alternative models for the capacity of the elements or the behaviour of the components. These uncertainties are treated with the logic tree technique, where mass probabilities are assigned to the alternative assumptions for each of uncertain factors (Fig. 7.1) and the MAFs obtained with any particular sequence of assumptions (a tree branch) are unconditioned with the branch probabilities, which are simple products of the probabilities in the sequence, due to the assumed independence of the factors (X and Y in the figure).

Fig. 7.1

Logic tree on two factors X and Y: x _i and y _i are the considered alternatives and p _xi and p _yi the associated probabilities

The search for a balance between the cost for additional information and the potential saving in the intervention is the guiding criterion in the knowledge acquisition process according to DT212. Thus, quantitative minima for the number of elements to be inspected or material samples to be taken are not prescribed. Rather, a sensitivity analysis is required on a preliminary model of the building (a first approximation of the final one). For RC structures, this analysis is of the linear dynamic type (modal with full elastic response spectrum), while for masonry structures, it is nonlinear static with nominal parameter values. In both cases, the results are adequate to expose global modes of response (regular or less regular) and to provide estimates of the member demands, providing guidance on where to concentrate tests and inspections. Further details can be found in Pinto and Franchin (2014).

3 Highlights

3.1 Limit State Quantification Rules

3.1.1 Definition of Limit States

Limit states are defined with reference to the performance of the building in its entirety including, in addition to the structural part, also nonstructural ones like partitions, electrical and hydraulic systems, etc. The following three LSs are considered in DT212:

• Damage limit state (SLD): negligible damages (no repair necessary) to the structural parts and light, economically repairable damages to the nonstructural ones.

• Severe damage limit state (SLS): the loss of use of nonstructural systems and a residual capacity to resist horizontal actions. State of damage is uneconomic to repair.

• Collapse limit state (SLC): the building is still standing but would not survive an aftershock.

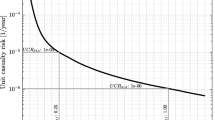
Verification of the first and second LS, as well as the corresponding thresholds, is left to the choice of the stakeholder, since they relate to functionality and economic value of damage. On the other hand, verification of the collapse LS, related to the safety of life and content, is mandatory, and the minimum safety level is prescribed by DT212. Adoption of Eq. (7.1) as a measure of seismic performance required the establishment of the safety level in terms of acceptable values for the collapse MAF. Values, depending on building importance class, have been set within DT212 in continuity with the implied safety level in the current Italian code (aligned with the Eurocodes).

As already noted in the Introduction, the above verbal definitions are qualitative and refer to the global performance of the building. The need thus arises for effective quantitative measures of performance that are truly consistent with these LSs’ definitions. This has led to the formulation of three scalar LS indicators Y _LS described in the following sections, Sects. 7.3.1.2–7.3.1.4.

3.1.2 Light Damage

For the purpose of the identification of the light damage LS, the building is considered as composed by N _st structural members and N _nst nonstructural components:

$$ {Y}_{\mathrm{SLD}}=\frac{1}{\tau_{\mathrm{SLD}}} \max \left[{\displaystyle {\sum}_{i=1}^{N_{\mathrm{st}}}{w}_iI\left(\frac{D_i}{C_{i,\mathrm{S}\mathrm{L}\mathrm{D}}}\right)};\kern1em {\displaystyle {\sum}_{j=1}^{N_{\mathrm{nst}}}{w}_jI\left(\frac{D_j}{C_{j,\mathrm{S}\mathrm{L}\mathrm{D}}}\right)}\right] $$

(7.3)

In the above expression, D and C indicate the appropriate demand and capacity values; demand can be, for example, interstorey drift for partitions and piping, or chord rotation for beams and columns, or floor spectral acceleration for heavy pieces of equipment; the associated capacity must correspond to a light damage threshold, e.g. the yield chord rotation θ _y for structural members, or a drift close to 0.3 % for common hollow-brick partitions (the thresholds associated with nonstructural components must be established based on the specific technology adopted); I is an indicator function taking the value of one when D ≥ C and zero otherwise (see Fig. 7.2a), and the w’s are weights summing up to one, accounting for the importance of different members/components. Typically, since structural damage must be low, not requiring repair action, while light repair is tolerated for nonstructural components, the weights w _i are simply set to 1/N _st, while the weights w _j may be set proportional to the ratio of the component extension (e.g. for partitions) to the total extension of like components.

Fig. 7.2

Indicator function (a), realistic conventional cost function (b) and alternative approximate conventional cost functions (c)

The indicator Y attains unity when the max function equals τ _SLD, a user-defined tolerable maximum cumulated damage (e.g. something in the range 3–5 %).

3.1.3 Severe Damage

For the purpose of the identification of the severe damage LS, the indicator Y is formulated in terms of a conventional total cost of damage to structural and nonstructural elements as

$$ {Y}_{\mathrm{SLD}}=\left\{\begin{array}{c}\hfill \frac{1}{\tau_{\mathrm{SLD}}}\left[{\alpha}_{\mathrm{st}}{\displaystyle {\sum}_{i=1}^{N_{\mathrm{st}}}{w}_ic\left(\frac{D_i}{C_{i,\mathrm{S}\mathrm{L}\mathrm{D}}}\right)}+\left(1-{\alpha}_{\mathrm{st}}\right){\displaystyle {\sum}_{j=1}^{N_{\mathrm{nst}}}{w}_jc\left(\frac{D_j}{C_{j,\mathrm{S}\mathrm{L}\mathrm{D}}}\right)}\right]\ \hbox{If}\ {Y}_{\mathrm{SLC}}<1\hfill \\ {}\hfill 1\ \hbox{If}\ {Y}_{\mathrm{SLC}}\ge 1\hfill \end{array}\right. $$

(7.4)

where α _st is the economic “weight” of the structural part (i.e. about 20 % in a low- to mid-rise residential building) and c(D/C) is a conventional member/component cost function. The choice of employing a conventional cost rather than attempting the evaluation of an actual economic value of damage, as done, for example, in ATC 2012, is regarded as a convenient compromise in view of the difficulty of establishing reliable cost estimates even at the component level. The reasons for this difficulty are that the repair cost for a component depends on many factors beyond its own damage state, such as the number and location of the damaged components, as well as the modified post-earthquake market conditions. Indeed, demand and supply for repair may be such as to increase the actual cost, in case the number of damaged buildings exceeds the capacity of construction firms.

A conventional cost function can be established in a realistic manner, such as that shown in Fig. 7.2b, which varies stepwise to reflect the fact that the same repair action is needed for an interval of damage, irrespective of the actual damage within the interval. Alternatively, simpler approximate cost functions can be adopted (Fig. 7.2c), as simple as a linear one that starts from zero for D = 0 and reaches unity, i.e. the replacement cost for the element, for D = C _SLS (with C _SLS usually a fraction of the ultimate capacity of the element).

As for the light damage LS, the indicator function attains unity when the quantity within square brackets equals τ _SLS, a user-defined fraction of the total building value over which repair is considered economically not competitive with demolition and replacement. Obviously, if collapse occurs, Y _SLS is set to 1. Finally, the same considerations on the weights w _i and w _j already made with reference to light damage apply here to severe damage.

3.1.4 Collapse

Modelling choices, which determine the numerical response, influence the quantification of the collapse LS (see, e.g. Goulet et al. 2007; Baradaran Shoraka et al. 2013). DT212 prescribes exclusive recourse to nonlinear methods of analysis, accounting for material and geometric nonlinear phenomena. Models of the inelastic response of structural members under cyclic loading of increasing amplitude can be distinguished in two classes, as shown in Fig. 7.3:

Fig. 7.3

Inelastic response models: non-degrading (a) vs degrading (b)

• Non-degrading, i.e. stable hysteretic behaviour without degradation of strength but overall degradation of stiffness (Takeda-type models), Fig. 7.3a

• Degrading, where both stiffness and strength degrade with increasing cyclic amplitude down to negligible values, Fig. 7.3b

In the more common case, when non-degrading inelastic response models are adopted, according to DT212, the structural system is described as a serial arrangement of a number of elements in parallel, according to the so-called cut-set formulation, so that the Y variable takes the expression (Jalayer et al. 2007)

$$ {Y}_{\mathrm{SLC}}={\displaystyle \underset{i=1,{N}_s}{ \max }}{\displaystyle \underset{j\in {I}_i}{ \min }}\frac{D_j}{C_{j,\mathrm{S}\mathrm{L}\mathrm{C}}} $$

(7.5)

where N _S is the number of parallel subsystems (cut-sets) in series and I _i is the sets of indices identifying the members in the ith subsystem. This formulation requires the a priori identification of all the cut-sets, i.e. sets of members whose joint failure induces system failure, in order to find the critical one with certainty. Carrying out this task is in general not immediate and actually quite onerous, even for static problems, the more so in dynamics, since the critical cut-set depends on the dynamic response and changes from record to record, with failure modes that can involve one storey (i.e. weak or soft storey, commonly for existing nonconforming buildings) or multiple adjacent storeys (e.g. Goulet et al. 2007).

This said, the widespread use of the peak interstorey drift ratio θ _max, as an indicator of global structural damage, can be regarded as an approximate application of the formulation in Eq. (7.5), with the storeys being the subsystems in series. This baseline choice is appropriate to detect even multistorey failure modes, since one storey will always necessarily be more strained than the others involved in the failure mode. However, since the non-degrading model does not account for all member failure modes, premature shear failures would not be detected by just monitoring θ _max. Thus, the demand-to-capacity ratios in shear, at least for all columns, must be included in the evaluation of Eq. (7.5) by post-processing the response.

This demand-to-capacity ratio can be formulated either in terms of deformation or force. The latter choice is more common (member acting shear V over ductility-reduced shear strength V _R ), since, as discussed later, most available deformation capacity models are established based on data sets that include a smaller proportion of shear failure modes, especially of the brittle type (Fig. 7.4).

Fig. 7.4

The three failure modes of an RC member

At the other end of the modelling spectrum lies the category of ideal “fully degrading” response models, able to simulate all types of failure; accounting, for instance, for the interaction of bending and shear; etc. With these models, the collapse state Y = 1 is identified with the occurrence of the so-called dynamic instability, that is, when the curve intensity-response becomes almost flat. Operatively, in order to identify the point on the curve corresponding to Y = 1, one can use the expression

$$ {Y}_{\mathrm{SLC}}=\left(1+\varDelta \right)-\frac{S^{\prime }}{S_0^{\prime }}\kern1em \mathrm{with}\kern1em 0<{S}^{\prime }<{S}_0^{\prime } $$

(7.6)

with values for Δ in the interval 0.05–0.10, corresponding to a small residual positive stiffness, in order to avoid numerical problems.

Finally, if the response models are of the degrading type but their formulation cannot account for all possible failure modes, the indicator variable can be expressed as

$$ {Y}_{\mathrm{SLC}}= \max \left[\left(1+\varDelta \right)-\frac{S^{\prime }}{S_0^{\prime }};\kern1em {\displaystyle \underset{\mathrm{nsm}}{ \max }}\left(\frac{D}{C}\right)\right] $$

(7.7)

which simply indicates that the collapse condition is attained for the most unfavourable between dynamic instability and the series of the “non-simulated (collapse) modes”. Typically, this set includes the axial failure of columns. Care should be taken in selecting the columns to be included in the evaluation of Eq. (7.7), limiting it only to those that can really be associated with a partial/global collapse. It can be observed that axial failure of columns and the ensuing loss of vertical load-bearing capacity, associated with concomitant loss of shear capacity, are not included in Eq. (7.5) since this failure occurs at larger deformation than that corresponding to the peak shear strength (see Fig. 7.4).

Figure 7.5 shows an idealised intensity-response relation S vs θ _max, with marks on the points corresponding to the attainment of the LSs according to the above definitions. The solid line corresponds to the response of a degrading model while the dashed one to the response of a non-degrading one. The two coincide until the first member in the structural model starts degrading. From this point on, the non-degrading response cannot be relied upon. Collapse is thus identified by post-processing the response to evaluate Eq. (7.5). The point where this equation yields the value of one is below the corresponding point given by Eq. (7.6) or (7.7), for the reasons discussed above. In other words, the failure criterion adopted with non-degrading response models is characterised by more conservatism.

Fig. 7.5

IDA curves as a function of modelling choices

3.2 Modelling Response and Capacity

As mentioned before, DT212 classifies inelastic response models into degrading and non-degrading ones. In general, they all require specification of the monotonic backbone and of a hysteretic rule. Degrading ones, which provide a closer description of reality, intend to follow the cyclic member response up to collapse due to complete exhaustion of its resistance, either in terms of deformation capacity (for monotonic response) or of energy dissipation capacity (for cyclic response). This class of models is schematically represented in Fig. 7.6, which highlights the characterising difference with non-degrading models, i.e. the negative stiffness branch in the backbone and cyclic degradation in strength encoded in the hysteretic rule.

Fig. 7.6

Cyclic and in-cycle components of degradation (response shown is from Ibarra et al. model)

Non-degrading response models are a lower-level representation of member behaviour and thus provide a poorer approximation of the actual response (e.g. the difference in the intensities corresponding to global dynamic instability—plateau—in Fig. 7.5). Their use poses the problem of how to reintroduce the neglected degradation in the assessment of the member. “Capacity models”, which are empirically derived deformation or force thresholds corresponding to state transitions of the member, are conventionally used for this purpose. These are conceptually the same thresholds that mark transition in a degrading response model, e.g. the yield, peak or axial failure chord rotations in Fig. 7.6, but intend to provide the lower cyclic values for these thresholds (Fig. 7.7). In conclusion, if non-degrading models are chosen, one should use Eq. (7.5) for collapse identification, with peak deformation thresholds θ _u,cyclic that account on the capacity side for the degradation disregarded on the response side. The latter is presently the default route in most cases, since degrading models are still not in the average technical background of engineers and, also, they are still evolving towards a more mature and consolidated state. If degrading models are used, Eq. (7.6) or (7.7) is employed, and the monotonic deformation thresholds, θ _u,mono, θ _a,mono, etc., are used as input parameters for the response model (together with degradation parameters). In the following, the term capacity model is used to denote in general analytical formulas predicting deformation or force values marking state transitions in the member response, irrespective of whether they are used as thresholds in conjunction with non-degrading response models or as parameters of degrading ones.

Fig. 7.7

Deformation limits for monotonic and cyclic loading

3.2.1 Response Models

In order to facilitate practical application, DT212 provides a reasoned summary of response models for beam-columns, joints and masonry infills.

In particular, focusing on RC columns, their failure modes have been already schematically shown in Fig. 7.4. The figure illustrates the possible modes of collapse in a monotonic loading condition, in terms of shear force-chord rotation of the member. The plot shows the monotonic response in a pure flexural mode, in green, with the usual I, II and III stages up to ultimate/peak strength, followed by a fourth descending branch to actual collapse, and the shear strength envelope in dashed grey. The latter starts with V _R,0 and decreases as a function of deformation, measured in terms of ductility μ. Depending on whether the two curves cross before flexural yield, after, or do not cross at all, the member fails in brittle shear, ductile shear or flexure. In all cases, collapse occurs due to loss of vertical load-bearing capacity (V _R  = N _R  = 0) at the end of the degrading branch. In cyclic loading at large amplitude, the response presents a second contribution to degradation, which is cyclic degradation, as shown in Fig. 7.6.

Available models can be classified into mechanical and phenomenological. The state of the art of purely mechanical models is not yet capable of describing the full range of behaviour of RC members illustrated in Figs. 7.4 and 7.6 (especially for brittle and ductile shear collapse). Models of this type are all based on the fibre section discretisation and a beam-column element formulation (stiffness, flexibility or mixed field based). The main advantage of the fibre section model is that biaxial flexure and axial force interaction are correctly described within the range of response where the model is applicable. Problems arise when the member is shear sensitive, since fibre models rely almost exclusively on the plane section assumption, and the behaviour of an RC member failing in brittle or ductile shear is not beam-like. Approximate solutions to overcome this difficulty have been proposed in the last two decades, a relatively recent summary of which can be found in Ceresa et al. (2007). Even if the member is not shear sensitive, the plane section assumption is compromised at the largest response levels, closer to flexural collapse, due to bar buckling and slippage, as well as concrete expulsion from the core. Solutions to model these degradation phenomena within the context of fibre models are available (e.g. among many others Monti and Nuti 1992; Gomes and Appleton 1997; Spacone and Limkatanyu 2000), but their increased complexity is usually paid in terms of computational robustness.

Regarding the use of degrading models, currently, the only viable option is to use phenomenological (e.g. Ibarra et al. 2005) or hybrid models (Elwood 2004; Marini and Spacone 2006). These models, however, also have their limitations and, for instance, rely heavily on the experimental base used to develop them, which is often not large enough (e.g. for the Ibarra et al. model, the proportion of ductile shear and flexural failures dominate the experimental base, resulting in limited confidence on the model capability to describe brittle failures). Further, computational robustness is an issue also with these models.

3.2.2 Capacity Models

In parallel with the survey of response models, DT212 provides detailed information on capacity models. Requirements for an ideal set of models are stated explicitly:

• Consistency of derivation of thresholds of increasing amplitude (i.e. yield, peak and axial deformation models derived based on the same experimental tests, accounting also for correlations)

• Support by an experimental base covering the full range of behaviours (different types of collapse, different reinforcement layouts, etc.) in a balanced manner

Such a set of models is currently not available. One set of predictive equations that comes closer to the above requirements and is used for the parameters of the degrading response model by Ibarra et al. (2005) is that by Haselton et al. (2008). As already anticipated, one problem with this model is that brittle shear failures are not represented in the experimental base. Further, the predictive equations provide only mean and standard deviation of the logarithm of each parameter, disregarding pairwise correlation, in spite of the fact that they were established on the same experimental basis (the authors state explicitly that they did not judge the available experiments enough to support the estimation of a full joint distribution). The latter problem requires caution in the use of the equations to establish the member constitutive laws, avoiding non-physical situations. To illustrate this fact, Fig. 7.8 shows the trilinear moment-rotation monotonic envelope according to the Ibarra model, with (marginal) probability density functions for its parameters, as supplied by Haselton et al. (2008). Not all the parameters can be independently predicted at the same time, to maintain physical consistency of the moment-rotation law. For instance, in applications, the rotation increment Δθ _f and Δθ _a can be used (darker PDFs in the figure) in place of θ _f and θ _a, to ensure that situations with θ _f > θ _a cannot occur. Care must be taken also in ensuring that K _y is always larger than K _40% (used as an intermediate value between I and II stage stiffness, since the model is trilinear), by assuming, e.g. that they are perfectly correlated.

Fig. 7.8

Deformation limits for monotonic loading with schematic indication of the marginal PDF of each parameter

The document provides also equations meant to provide cyclic values of the deformation thresholds, for use in conjunction with non-degrading models, such as those by Biskinis and Fardis (2010a, b), adopted since 2005 in earlier form in Eurocode 8 Part 3 (CNR 2015) and in the latest fib Model Code (fib 2013), and those by Zhu et al. (2007).

4 Conclusions

The chapter introduces the latest Italian provisions, issued by the National Research Council as Technical Document 212/2013, for the probabilistic seismic assessment of existing RC and masonry buildings. The characterising traits of the document are:

• (a) The systematic treatment of the problem of identification of global LS exceedance, in a manner consistent with the verbal description of the LSs, with the introduction of LS indicator variables differentiated as a function of LS and modelling option.

• (b) The explicit probabilistic treatment of all uncertainties, related to ground motion, material properties, modelling, geometry and detailing. In particular, the distinction of uncertainties that can be described within a single structural model via random variables and uncertainties that require the use of multiple models (logic tree) is introduced.

• (c) The mandatory use of ground motion time series (preferably recorded) for the description of the seismic motion variability, irrespective of the analysis method (dynamic or static).

It is of course recognised that DT212 does not represent an accomplished final stage of development for such a document, since there are several areas where progress is needed and research is still active. In particular, the most notable research gap is on the inelastic response models and capacity models for collapse. Nonetheless, it is believed that the available analytical tools and models, as well as the theoretical framework, are mature enough for practical application to real buildings, as it is demonstrated by the case studies included in DT212.