Investment Equilibria

Abstract

Investment equilibrium analysis constitutes a useful framework for regulators to gain insights into the behavior of strategic producers and the evolution of generation investment in an electricity market. Such a perspective enables regulators to design better market rules, which in turn may contribute to increasing the competitiveness of the market and to stimulating investment in generation capacity. This chapter provides a methodology based on optimization and complementarity modeling for identifying generation investment equilibria in a network-constrained electricity market.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Investment equilibrium analysis constitutes a useful framework for regulators to gain insights into the behavior of strategic producers and the evolution of generation investment in an electricity market. Such a perspective enables regulators to design better market rules, which in turn may contribute to increasing the competitiveness of the market and to stimulating investment in generation capacity. This chapter provides a methodology based on optimization and complementarity modeling for identifying generation investment equilibria in a network-constrained electricity market.

6.1 Introduction

The objective of a producer competing in an electricity market is to maximize its profit. To this purpose, such a producer makes its own decisions through its investment strategies (long-term decisions) and operational strategies (short-term decisions). However, the strategic decisions of each producer are related to those of other producers (rivals) due to market interactions. In fact, decisions made by each producer may influence the strategies of other producers. Within this framework, a number of investment equilibria generally exist, whereby each producer cannot increase its profit by changing its strategies unilaterally [7, 8, 10, 11, 23, 25]. The objective of this chapter is to identify such investment equilibria mathematically.

Investment equilibrium analysis is particularly useful for a regulator to gain insights into the investment behavior of producers and the evolution of the total production capacity. As a result, the regulator may be able to design better market rules, which in turn may enhance the competitiveness of the market and stimulate investment in production capacity.

In contrast to Chap. 5, in which a single strategic producer is considered, all producers considered in this chapter are strategic, thereby creating an oligopoly. This means that all producers can alter the market outcomes, i.e., market-clearing prices and production quantities, through their strategies. One important observation is that the feasibility region for the investment decision-making problem of each producer is interrelated with those of other producers. Thus, the production capacity investment equilibria problem is a generalized Nash equilibrium (GNE) problem [2, 4, 12].

Several treatments of operational and investment equilibria in the extant literature address oligopolistic energy markets, e.g., [1, 3, 9–11, 13–15, 19, 21, 23, 24].

The remainder of this chapter is organized as follows. Section 6.2 describes the available approaches for solving an equilibrium problem. Section 6.3 presents modeling features and assumptions. Section 6.4 provides a bilevel model for a single producer to make its investment decisions, which renders to a mathematical program with equilibrium constraint (MPEC). Section 6.5 presents the investment decision-making problem of multiple producers, which results in an equilibrium problem with equilibrium constraints (EPEC). Section 6.6 summarizes the chapter and discusses the main conclusions of the models and results reported in the chapter. Section 6.7 proposes some exercises to enable a deeper understanding of the models and concepts described in the chapter. Finally, Sect. 6.8 includes the GAMS code for an illustrative example.

6.2 Solution Approach

Similar to Chap. 5, in which a bilevel model is considered to represent the investment and offering decisions of a strategic producer, we consider in this chapter such a model for each strategic producer. Within the bilevel model of each strategic producer, the upper-level problem determines its optimal investment and strategic offer prices with the aim of maximizing its profit. In addition, a number of lower-level problems represent the clearing of the market under different operating conditions. As in Chap. 5, each lower-level problem is replaced by its optimality conditions, which yields an MPEC. This transformation is schematically illustrated in Fig. 6.1.

Fig. 6.1

Transforming the bilevel models into MPECs in an oligopolistic market with several strategic producers

Note that since several strategic producers are considered in this chapter, several MPECs are obtained, one per strategic producer. The joint consideration of all these MPECs constitutes an EPEC, as depicted in Fig. 6.2. The general mathematical structure of an EPEC is explained in Appendix C. Note that the EPEC solution identifies the market equilibria.

Fig. 6.2

MPECs and EPEC

In general, two solution alternatives are available to solve an EPEC and thus to identify the market equilibria:

• 1. Diagonalization (iterative) approach [18, 22].

• 2. Simultaneous (noniterative) approach [9–11, 19].

The first solution alternative, i.e., the diagonalization approach, is an iterative technique, in which a single MPEC is solved in each iteration, while the strategic decisions of other producers are fixed. For example, consider a duopoly with two strategic producers 1 and 2, whose bilevel models are transformed into two MPECs 1 and 2, respectively. In the first iteration, MPEC 1 is solved, while the strategic decisions of producer 2 are fixed to some initial guesses. Then, in the second iteration, MPEC 2 is solved, while the strategic decisions of producer 1 are fixed to those obtained in the first iteration. This iterative process is continued until no decision is changed in the two subsequent iterations. The solution obtained is a Nash equilibrium since no producer desires to deviate from its decisions. Note that this approach is generally inefficient since it is iterative and provides, if convergence is achieved, at most a single equilibrium point. In addition, it may require a large number of iterations in the case of markets with many producers. Besides, it is not straightforward to find appropriate initial guesses, and suboptimal guesses may greatly affect the functioning of this approach.

The second solution alternative, i.e., the simultaneous approach, is a noniterative technique, in which all producers’ MPECs are solved together. Therefore, it generally yields a complex mathematical problem. In this approach, each MPEC is replaced by its Karush–Kuhn–Tucker (KKT) conditions, which provide its strong stationary conditions. A collection of all those conditions for all producers results in the strong stationary conditions of the EPEC, whose solutions identify the market equilibria. This latter approach is the focus of this chapter.

6.3 Modeling Features and Assumptions

The technical features and assumptions of the investment equilibria model presented in this chapter are stated below:

• 1. An electricity pool is considered in which the market operator clears the pool once a day, one day ahead, and on an hourly basis.

• 2. A dc transmission network representation is considered.

• 3. Pursuing simplicity, a static investment model is used, i.e., a single target year is considered. The target year represents the final stage of the planning horizon, and the model uses annualized costs for this target year. Further details on investment models are available in Chap. 5. Note that a dynamic (multistage) model can also be considered within the investment equilibria problem [23] but at the cost of increased computational complexity.

• 4. A set of operating conditions is considered to represent the potential levels of the consumers’ demands and the production of stochastic units during the target year. Accordingly, we define a set of demand and power capacity factors. Further details on operating conditions are available in Chap. 5.

• 5. For the sake of simplicity, uncertainties are not considered in this chapter. However, note that the investment equilibria problem is generally subject to several uncertainties, e.g., demand growth, investment costs for different technologies, and regulatory changes, which may be modeled through a set of plausible scenarios [3, 8, 21].

The notation used in this chapter is defined below:

Indices

 

g :

Index for producers.

n, m :

Indices for nodes.

o :

Index for operating conditions.

 

Sets

 

$\varOmega _{n}$ :

Set of nodes connected to node n.

Parameters

 

$B_{nm}$ :

Susceptance of the transmission line connecting nodes n and m [S].

$C^\mathrm{{C}}_{gn}$ :

Production cost of the candidate conventional unit of producer g located at node n [$/MWh].

$C^\mathrm{{E}}_{gn}$ :

Production cost of the existing conventional unit of producer g located at node n [$/MWh].

$F^{\mathrm{{max}}}_{nm}$ :

Transmission capacity of the line connecting nodes n and m [MW].

$K^\mathrm{{C}}_{gn}$ :

Annualized investment cost of the candidate conventional unit of producer g located at node n [$/MW].

$K^\mathrm{{S}}_{gn}$ :

Annualized investment cost of the candidate stochastic unit of producer g located at node n [$/MW].

$K_{g}^\mathrm{{max}}$ :

Available annualized investment budget of producer g [$].

$P^{\mathrm{{E}}^\mathrm{{max}}}_{gn}$ :

Capacity of the existing conventional unit of producer g located at node n [MW].

$P^{\mathrm{{D}}^\mathrm{{max}}}_{n}$ :

Maximum load of the consumer located at node n [MW].

$Q^\mathrm{{S}}_{no}$ :

Power capacity factor of the candidate stochastic unit located at node n in operating condition o [p.u.].

$Q^\mathrm{{D}}_{no}$ :

Demand factor of the consumer located at node n in operating condition o [p.u.].

$U^\mathrm{{D}}_{no}$ :

Bid price of the consumer located at node n in operating condition o [$/MWh].

$X^{\mathrm{{C}}^\mathrm{{max}}}_{n}$ :

Maximum production capacity of the candidate conventional unit located at node n [MW].

$X^{\mathrm{{S}}^\mathrm{{max}}}_{n}$ :

Maximum production capacity of the candidate stochastic unit located at node n [MW].

$\rho _{o}$ :

Number of hours (weight) corresponding to operating condition o [h].

 

Variables

 

$p^\mathrm{{C}}_{gno}$ :

Power produced by the candidate conventional unit of producer g located at node n in operating condition o [MW].

$p^\mathrm{{D}}_{no}$ :

Power consumed by the consumer located at node n in operating condition o [MW].

$p^\mathrm{{E}}_{gno}$ :

Power produced by the existing conventional unit of producer g located at node n in operating condition o [MW].

$p^\mathrm{{S}}_{gno}$ :

Power produced by the candidate stochastic unit of producer g located at node n in operating condition o [MW].

$x^\mathrm{{C}}_{gn}$ :

Capacity of the candidate conventional unit of producer g located at node n [MW].

$x^\mathrm{{S}}_{gn}$ :

Capacity of the candidate stochastic unit of producer g located at node n [MW].

$\alpha ^\mathrm{{C}}_{gno}$ :

Offer price by the candidate conventional unit of producer g located at node n in operating condition o [$/MWh].

$\alpha ^\mathrm{{E}}_{gno}$ :

Offer price by the existing conventional unit of producer g located at node n in operating condition o [$/MWh].

$\lambda _{no}$ :

Market-clearing price at node n in operating condition o [$/MWh].

$\theta _{no}$ :

Voltage angle at node n in operating condition o [rad].

 

6.4 Single-Producer Problem

The bilevel model for each single strategic producer is similar to one presented in Chap. 5. We consider two types of generating units: candidate (conventional and stochastic) and existing (conventional) units. These units belong to different strategic producers (i.e., producers $g=1,\ldots ,G$) and offer at strategic prices, except the candidate stochastic units, which always offer at zero. It is also assumed that all existing units (available at the initial year) are conventional, i.e., there is no stochastic production unit within the initial production portfolio of the producers.

The formulation of the bilevel model for a particular strategic producer, e.g., producer G, is given by (6.1). Note that (6.1a)–(6.1f) refer to the upper-level problem of producer G, whereas (6.1g) pertains to the lower-level problems, one per operating condition o. Note that a similar bilevel problem can be considered for any other producers, i.e., producers $g=1,\ldots ,G-1$. The bilevel problem for producer G is formulated below:

$$\begin{aligned}&\ \Biggl .\Biggr \{ \text {min}_{\varXi ^\mathrm{{UL}}_{g} \ \cup \ \varXi ^\mathrm{{Primal}}_{o} \ \cup \ \varXi ^\mathrm{{Dual}}_{o}} \ \ \ \ \sum _{n}\bigg \{ K^\mathrm{{C}}_{gn} \ x^\mathrm{{C}}_{gn} + K^\mathrm{{S}}_{gn} \ x^\mathrm{{S}}_{gn} \nonumber \\&\qquad \quad -\sum _{o}\rho _{o}\bigg [\lambda _{no}\left( p^\mathrm{{C}}_{gno}+p^\mathrm{{S}}_{gno}+p^\mathrm{{E}}_{gno}\right) \bigg . - \bigg . p^\mathrm{{C}}_{gno} \ C^\mathrm{{C}}_{gn}-p^\mathrm{{E}}_{gno} \ C^\mathrm{{E}}_{gn} \bigg ] \bigg \} \end{aligned}$$

(6.1a)

$$\begin{aligned}&\text {subject to}\nonumber \ \\&0 \le x^\mathrm{{C}}_{gn} \le X^{\mathrm{{C}}^\mathrm{{max}}}_{n}\ \ \ \forall {n} \end{aligned}$$

(6.1b)

$$\begin{aligned}&0 \le x^\mathrm{{S}}_{gn} \le X^{\mathrm{{S}}^\mathrm{{max}}}_{n}\ \ \ \forall {n}\end{aligned}$$

(6.1c)

$$\begin{aligned}&\sum _{n}\left( K^\mathrm{{C}}_{gn} \ x^\mathrm{{C}}_{gn} + K^\mathrm{{S}}_{gn} \ x^\mathrm{{S}}_{gn}\right) \le K_{g}^\mathrm{{max}} \ \ \ \ \ \end{aligned}$$

(6.1d)

$$\begin{aligned}&\alpha ^\mathrm{{C}}_{gno} \ge 0\ \ \ \forall {o},\forall {n}\end{aligned}$$

(6.1e)

$$\begin{aligned}&\alpha ^\mathrm{{E}}_{gno} \ge 0\ \ \ \forall {o},\forall {n} \end{aligned}$$

(6.1f)

$$\begin{aligned}&{\text {Lower-level problems }} (6.1\mathrm{h}){-}(6.1\mathrm{p}) \ \ \ \forall {o} \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \ \Biggl .\Biggr \}\ g=G. \nonumber \end{aligned}$$

(6.1g)

The primal variables of the upper-level problem (6.1a)–(6.1f) are those in set $\varXi ^\mathrm{{UL}}_{g}=\{\alpha ^\mathrm{{C}}_{gno}, \alpha ^\mathrm{{E}}_{gno}, x^\mathrm{{C}}_{gn}, x^\mathrm{{S}}_{gn}\}$ plus all primal and dual variables of the lower-level problems (6.1g), which are defined after their formulation through sets $\varXi ^\mathrm{{Primal}}_{o}$ and $\varXi ^\mathrm{{Dual}}_{o}$.

The objective function (6.1a) refers to minus the expected annual profit of the considered producer, i.e., annualized investment cost minus expected annual operational profit. Note that the market-clearing price $\lambda _{no}$ is the dual variable of the power balance constraint at node n and operating condition o obtained endogenously from the corresponding lower-level problem. The objective function (6.1a) comprises the following terms:

• $\displaystyle \sum _{n}K^\mathrm{{C}}_{gn} \ x^\mathrm{{C}}_{gn}$ is the annualized investment cost of candidate conventional units of producer g.

• $\displaystyle \sum _{n}K^\mathrm{{S}}_{gn} \ x^\mathrm{{S}}_{gn}$ is the annualized investment cost of candidate stochastic units of producer g.

• $\displaystyle \sum _{n}\sum _{o}\rho _{o} \ p^\mathrm{{C}}_{gno} \ \lambda _{no}$ is the annualized revenue of producer g obtained from selling the production of candidate conventional units (production quantity multiplied by market-clearing price).

• $\displaystyle \sum _{n}\sum _{o}\rho _{o} \ p^\mathrm{{E}}_{gno} \ \lambda _{no}$ is the annualized revenue of producer g obtained from selling the production of existing conventional units (production quantity multiplied by market-clearing price).

• $\displaystyle \sum _{n}\sum _{o}\rho _{o} \ p^\mathrm{{S}}_{gno} \ \lambda _{no}$ is the annualized revenue of producer g obtained from selling the production of candidate stochastic units (production quantity multiplied by market-clearing price).

• $\displaystyle \sum _{n}\sum _{o}\rho _{o} \ p^\mathrm{{C}}_{gno} \ C^\mathrm{{C}}_{gn}$ is the annualized production cost of candidate conventional units of producer g (production quantity multiplied by marginal cost).

• $\displaystyle \sum _{n}\sum _{o}\rho _{o} \ p^\mathrm{{E}}_{gno} \ C^\mathrm{{E}}_{gn}$ is the annualized production cost of existing conventional units of producer g (production quantity multiplied by marginal cost).

The production cost of stochastic units is assumed to be zero. Note that the market-clearing prices ($\lambda _{no}$) and the production quantities ($p^\mathrm{{C}}_{gno}$, $p^\mathrm{{E}}_{gno}$, and $p^\mathrm{{S}}_{gno}$) belong to the feasible region defined by lower-level problems (6.1g).

For the sake of simplicity, the capacity options for investing in both conventional and stochastic units are assumed continuous. The capacity bounds for such options are enforced by (6.1b) and (6.1c). In addition, a cap on the available annualized investment budget of producer g is enforced by (6.1d). Finally, the upper-level constraints (6.1e)–(6.1f) enforce the nonnegativity of the offer prices associated with the candidate and existing conventional units, respectively, of producer G.

Each lower-level problem, one per operating condition o, is formulated below. The dual variable of each lower-level constraint is indicated following a colon:

$$\begin{aligned}&\Biggl .\Biggr \{\text {min}_{\varXi ^\mathrm{{Primal}}_{o}}\ \ \ \ \sum _{n}\bigg [\sum _{g}\left( \alpha ^\mathrm{{C}}_{gno} \ p^\mathrm{{C}}_{gno}\ +\alpha ^\mathrm{{E}}_{gno} \ p^\mathrm{{E}}_{gno}\right) -U^\mathrm{{D}}_{no} \ p^\mathrm{{D}}_{no}\bigg ]\end{aligned}$$

(6.1h)

$$\begin{aligned}&\text {subject to}\nonumber \ \\&p^\mathrm{{D}}_{no} +\sum _{m\in \varOmega _{n}}B_{nm}\left( \theta _{no}-\theta _{mo}\right) -\sum _{g}p^\mathrm{{C}}_{gno}-\sum _{g}p^\mathrm{{S}}_{gno}\nonumber \\&\qquad \quad -\sum _{g}p^\mathrm{{E}}_{gno}=0 \ \ \ \ :\lambda _{no} \ \ \ \ \ \ \ \ \ \forall {n}\end{aligned}$$

(6.1i)

$$\begin{aligned}&0 \le p^\mathrm{{C}}_{gno}\le x^\mathrm{{C}}_{gn} \ \ \ \ :\mu ^{\mathrm{{C}}^\mathrm{{min}}}_{gno},\mu ^{\mathrm{{C}}^\mathrm{{max}}}_{gno} \ \ \ \ \ \ \ \ \ \forall {g},\forall {n}\end{aligned}$$

(6.1j)

$$\begin{aligned}&0 \le p^\mathrm{{S}}_{gno}\le Q^\mathrm{{S}}_{no} \ x^\mathrm{{S}}_{gn} \ \ \ \ :\mu ^{\mathrm{{S}}^\mathrm{{min}}}_{gno},\mu ^{\mathrm{{S}}^\mathrm{{max}}}_{gno} \ \ \ \ \ \ \ \ \ \forall {g},\forall {n}\end{aligned}$$

(6.1k)

$$\begin{aligned}&0 \le p^\mathrm{{E}}_{gno}\le P^{\mathrm{{E}}^\mathrm{{max}}}_{gn} \ \ \ \ :\mu ^{\mathrm{{E}}^\mathrm{{min}}}_{gno},\mu ^{\mathrm{{E}}^\mathrm{{max}}}_{gno} \ \ \ \ \ \ \ \ \ \forall {g},\forall {n}\end{aligned}$$

(6.1l)

$$\begin{aligned}&0 \le p^\mathrm{{D}}_{no}\le Q^\mathrm{{D}}_{no} \ P^{\mathrm{{D}}^\mathrm{{max}}}_{n} \ \ \ \ :\mu ^{\mathrm{{D}}^\mathrm{{min}}}_{no},\mu ^{\mathrm{{D}}^\mathrm{{max}}}_{no} \ \ \ \ \ \ \ \ \ \forall {n}\end{aligned}$$

(6.1m)

$$\begin{aligned}&B_{nm}\left( \theta _{no}-\theta _{mo}\right) \le F^{\mathrm{{max}}}_{nm} \ \ \ \ :\mu ^{\mathrm{{F}}}_{nmo} \ \ \ \ \ \ \ \ \ \forall {n},\forall {m\in \varOmega _{n}}\end{aligned}$$

(6.1n)

$$\begin{aligned}&-\pi \le \theta _{no}\le \pi \ \ \ \ :\mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{no},\mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{no} \ \ \ \ \ \ \ \ \ \forall {n}\end{aligned}$$

(6.1o)

$$\begin{aligned}&\theta _{no}=0 \ \ \ \ :\mu ^{\mathrm{{\theta }}^\mathrm{{ref}}}_{o} \ \ \ \ \ \ \ \ \ n=\mathrm{{ref.}} \\&\Biggl .\Biggr \}\ \forall {o}.\nonumber \end{aligned}$$

(6.1p)

The primal optimization variables of each lower-level problem (6.1h)–(6.1p) are included in set $\varXi ^\mathrm{{Primal}}_{o}=$ $\{p^\mathrm{{C}}_{gno}, p^\mathrm{{S}}_{gno}, p^\mathrm{{E}}_{gno}, p^\mathrm{{D}}_{no}, \theta _{no}\}$. Additionally, the dual optimization variables of each lower-level problem (6.1h)–(6.1p) are those included in set $\varXi ^\mathrm{{Dual}}_{o}=\{\lambda _{no}, \mu ^{\mathrm{{C}}^\mathrm{{min}}}_{gno}, \mu ^{\mathrm{{C}}^\mathrm{{max}}}_{gno}, \mu ^{\mathrm{{S}}^\mathrm{{min}}}_{gno}, \mu ^{\mathrm{{S}}^\mathrm{{max}}}_{gno}, \mu ^{\mathrm{{E}}^\mathrm{{min}}}_{gno}, \mu ^{\mathrm{{E}}^\mathrm{{max}}}_{gno}, \mu ^{\mathrm{{D}}^\mathrm{{min}}}_{no}, \mu ^{\mathrm{{D}}^\mathrm{{max}}}_{no}, \mu ^{\mathrm{{F}}}_{nmo}, \mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{no}, \mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{no}, \mu ^{\mathrm{{\theta }}^\mathrm{{ref}}}_{o}\}$.

Lower-level problems (6.1h)–(6.1p) represent the clearing of the market for each operating condition and for given investment and offering decisions made in the upper-level problems by different producers. Accordingly, $x^\mathrm{{C}}_{gn}$, $x^\mathrm{{S}}_{gn}$, $\alpha ^\mathrm{{C}}_{gno}$, and $\alpha ^\mathrm{{E}}_{gno}$ are variables in the upper-level problem (6.1a)–(6.1f), but they are fixed values (parameters) in the lower-level problems (6.1h)–(6.1p). This makes the lower-level problems (6.1h)–(6.1p) linear and convex since there is no term containing the product of variables within the lower-level problems. The objective function (6.1h) minimizes minus the social welfare considering the offer prices of all strategic producers $g=1,\ldots ,G$, and bid prices of all demands. The power balance at every node is enforced by (6.1i), and its dual variable provides the market-clearing price at that node under operating condition o. Equations (6.1j), (6.1k), and (6.1l) impose production capacity limits for candidate conventional, candidate stochastic, and existing units, respectively. In addition, Eqs. (6.1m) bounds the power consumption of each demand. Equations (6.1n) enforce the transmission capacity limits of each line. Finally, Eqs. (6.1o) enforce voltage angle bounds for each node, and constraints (6.1p) fix the voltage angle to zero at the reference node.

Note that the market-clearing problems, i.e., the lower-level problems (6.1h)–(6.1p), are common to all producers $g= 1,\ldots ,G$. Thus, the investment equilibria model presented in this chapter is in fact a GNE problem with shared constraints.

Illustrative Example 6.1

A two-node electricity market with two strategic producers (duopoly)

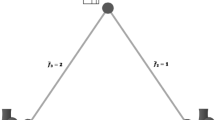
A power system with two nodes ($n_{1}$ and $n_{2}$) is considered as illustrated in Fig. 6.3. The capacity of transmission line $n_1-n_{2}$ is 400 MW, and its susceptance is 1000 S. Node $n_{1}$ is the reference node. Two strategic producers ($g_{1}$ and $g_{2}$) compete together, creating a duopoly. Producer $g_{1}$ owns an existing unit located at node $n_{1}$ with capacity of 150 MW and production cost of $10/MWh. On the other hand, producer $g_{2}$ owns an existing unit located at node $n_{2}$ with capacity of 100 MW and production cost of $15/MWh.

Fig. 6.3

Illustrative Example 6.1: two-node network

Both producers $g_{1}$ and $g_{2}$ desire to build new production units. The available annualized investment budget for each producer is $20 million. In addition, the investment options for each producer are identical and stated below:

• A conventional unit to be built at node $n_{1}$. The maximum capacity of this candidate unit is 200 MW, and its annualized investment cost is $55,000/MW. The production cost of this candidate conventional unit is $12/MWh.

• A stochastic (wind-power) unit to be built at node $n_{2}$. The maximum capacity of this candidate stochastic unit is 200 MW, and its annualized investment cost is $66,000/MW.

As depicted in Fig. 6.3, a single consumer is considered at node $n_{1}$, whose maximum load is equal to 400 MW.

In addition, two operating conditions ($o_{1}$ and $o_{2}$) are considered, whose characteristics are stated below:

• $o_{1}$: Demand factor equals 1.00 p.u. and wind power capacity factor equals 0.35 p.u.

• $o_{2}$: Demand factor equals 0.80 p.u. and wind power capacity factor equals 0.70 p.u.

The weight of condition $o_{1}$ is 3530 h and that of condition $o_{2}$ is 5230 h. The consumer bids in conditions $o_{1}$ and $o_{2}$ at $35/MWh and $32/MWh, respectively.

According to the data above, two bilevel problems, one per producer, are formulated. The bilevel problem for producer $g_{1}$ is given by (6.2) including upper-level problem (6.2a)–(6.2e) and lower-level problems (6.2f):

$$\begin{aligned}&\text {min}_{\varXi ^\mathrm{{UL,Ex}}_{g_{1}} \ \cup \ \varXi ^\mathrm{{P,Ex}}_{o_{1}} \ \cup \ \varXi ^\mathrm{{D,Ex}}_{o_{1}} \ \cup \ \varXi ^\mathrm{{P,Ex}}_{o_{2}} \ \cup \ \varXi ^\mathrm{{D,Ex}}_{o_{2}}} \ \ \ \ 55000 \ x^\mathrm{{C}}_{g_{1} n_{1}} + 66000 \ x^\mathrm{{S}}_{g_{1} n_{2}} \nonumber \\&\qquad \quad - 3530 \ \bigg [ \lambda _{n_{1} o_{1}}\ \left( p^\mathrm{{C}}_{g_{1} n_{1} o_{1}}+p^\mathrm{{E}}_{g_{1} n_{1} o_{1}}\right) + \lambda _{n_{2} o_{1}}\ p^\mathrm{{S}}_{g_{1} n_{2} o_{1}} \nonumber \\&\qquad \quad - 12 \ p^\mathrm{{C}}_{g_{1} n_{1} o_{1}} - 10 \ p^\mathrm{{E}}_{g_{1} n_{1} o_{1}} \bigg ] \nonumber \\&\qquad \quad - 5230 \ \bigg [ \lambda _{n_{1} o_{2}}\ \left( p^\mathrm{{C}}_{g_{1} n_{1} o_{2}}+p^\mathrm{{E}}_{g_{1} n_{1} o_{2}}\right) + \lambda _{n_{2} o_{2}}\ p^\mathrm{{S}}_{g_{1} n_{2} o_{2}} \nonumber \\&\qquad \quad - 12 \ p^\mathrm{{C}}_{g_{1} n_{1} o_{2}} - 10 \ p^\mathrm{{E}}_{g_{1} n_{1} o_{2}} \bigg ] \ \end{aligned}$$

(6.2a)

$$\begin{aligned}&\text {subject to}\nonumber \ \\&0 \le x^\mathrm{{C}}_{g_{1} n_{1}} \le 200\ \ \ \end{aligned}$$

(6.2b)

$$\begin{aligned}&0 \le x^\mathrm{{S}}_{g_{1} n_{2}} \le 200\ \ \ \ \end{aligned}$$

(6.2c)

$$\begin{aligned}&55000 \ x^\mathrm{{C}}_{g_{1} n_{1}} + 66000 \ x^\mathrm{{S}}_{g_{1} n_{2}} \le 2 \times 10^{7} \ \ \ \end{aligned}$$

(6.2d)

$$\begin{aligned}&\alpha ^\mathrm{{C}}_{g_{1} n_{1} o_{1}}, \ \alpha ^\mathrm{{E}}_{g_{1} n_{1} o_{1}}, \ \alpha ^\mathrm{{C}}_{g_{1} n_{1} o_{2}}, \ \alpha ^\mathrm{{E}}_{g_{1} n_{1} o_{2}} \ge 0 \ \ \end{aligned}$$

(6.2e)

$$\begin{aligned}&\text {Lower-level problems } (6.4){-}(6.5). \ \ \ \end{aligned}$$

(6.2f)

Similarly, the bilevel problem for producer $g_{2}$ is given by (6.3) including upper-level problem (6.3a)–(6.3e) and lower-level problems (6.3f):

$$\begin{aligned}&\text {min}_{\varXi ^\mathrm{{UL,Ex}}_{g_{2}}\ \cup \ \varXi ^\mathrm{{P,Ex}}_{o_{1}} \ \cup \ \varXi ^\mathrm{{D,Ex}}_{o_{1}} \ \cup \ \varXi ^\mathrm{{P,Ex}}_{o_{2}} \ \cup \ \varXi ^\mathrm{{D,Ex}}_{o_{2}}} \ \ \ \ 55000 \ x^\mathrm{{C}}_{g_{2} n_{1}} + 66000 \ x^\mathrm{{S}}_{g_{2} n_{2}} \nonumber \\&\qquad \quad - 3530 \ \bigg [ \lambda _{n_{1} o_{1}}\ p^\mathrm{{C}}_{g_{2} n_{1} o_{1}} + \lambda _{n_{2} o_{1}}\ \left( p^\mathrm{{S}}_{g_{2} n_{2} o_{1}}+p^\mathrm{{E}}_{g_{2} n_{2} o_{1}}\right) \nonumber \\&\qquad \quad - 12 \ p^\mathrm{{C}}_{g_{2} n_{1} o_{1}} - 15 \ p^\mathrm{{E}}_{g_{2} n_{2} o_{1}} \bigg ] \nonumber \\&\qquad \quad - 5230 \ \bigg [ \lambda _{n_{1} o_{2}}\ p^\mathrm{{C}}_{g_{2} n_{1} o_{2}} + \lambda _{n_{2} o_{2}}\ \left( p^\mathrm{{S}}_{g_{2} n_{2} o_{2}}+p^\mathrm{{E}}_{g_{2} n_{2} o_{2}}\right) \nonumber \\&\qquad \quad - 12 \ p^\mathrm{{C}}_{g_{2} n_{1} o_{2}} - 15 \ p^\mathrm{{E}}_{g_{2} n_{2} o_{2}} \bigg ] \ \end{aligned}$$

(6.3a)

$$\begin{aligned}&\text {subject to}\nonumber \ \\&0 \le x^\mathrm{{C}}_{g_{2} n_{1}} \le 200\ \ \ \end{aligned}$$

(6.3b)

$$\begin{aligned}&0 \le x^\mathrm{{S}}_{g_{2} n_{2}} \le 200\ \ \ \end{aligned}$$

(6.3c)

$$\begin{aligned}&55000 \ x^\mathrm{{C}}_{g_{2} n_{1}} + 66000 \ x^\mathrm{{S}}_{g_{2} n_{2}} \le 2 \times 10^{7} \ \ \ \ \end{aligned}$$

(6.3d)

$$\begin{aligned}&\alpha ^\mathrm{{C}}_{g_{2} n_{1} o_{1}}, \ \alpha ^\mathrm{{E}}_{g_{2} n_{2} o_{1}}, \ \alpha ^\mathrm{{C}}_{g_{2} n_{1} o_{2}}, \ \alpha ^\mathrm{{E}}_{g_{2} n_{2} o_{2}} \ge 0 \ \end{aligned}$$

(6.3e)

$$\begin{aligned}&\text { Lower-level problems } (6.4){-}(6.5). \ \ \ \end{aligned}$$

(6.3f)

Within bilevel problems (6.2) and (6.3) associated with producers $g_{1}$ and $g_{2}$, lower-level problems (one per operating condition) are common. The lower-level problem referring to the operating condition $o_{1}$ is given by (6.4) below:

$$\begin{aligned} \text {min}_{\varXi ^\mathrm{{P,Ex}}_{o_{1}}} \ \ \ \,&\alpha ^\mathrm{{C}}_{g_{1} n_{1} o_{1}} \ p^\mathrm{{C}}_{g_{1} n_{1} o_{1}}\ +\alpha ^\mathrm{{E}}_{g_{1} n_{1} o_{1}} \ p^\mathrm{{E}}_{g_{1} n_{1} o_{1}}\nonumber \\&\qquad \quad +\alpha ^\mathrm{{C}}_{g_{2} n_{1} o_{1}} \ p^\mathrm{{C}}_{g_{2} n_{1} o_{1}}\ +\alpha ^\mathrm{{E}}_{g_{2} n_{2} o_{1}} \ p^\mathrm{{E}}_{g_{2} n_{2} o_{1}} -35 \ p^\mathrm{{D}}_{n_{1} o_{1}} \ \end{aligned}$$

(6.4a)

$$\begin{aligned}&\text {subject to}\nonumber \ \\&p^\mathrm{{D}}_{n_{1} o_{1}} +1000 \left( \theta _{n_{1} o_{1}}-\theta _{n_{2} o_{1}}\right) - p^\mathrm{{E}}_{g_{1} n_{1} o_{1}} -p^\mathrm{{C}}_{g_{1} n_{1} o_{1}}\nonumber \\&\qquad \quad - p^\mathrm{{C}}_{g_{2} n_{1} o_{1}}=0 \ \ \ \ :\lambda _{n_{1} o_{1}} \end{aligned}$$

(6.4b)

$$\begin{aligned}&1000 \left( \theta _{n_{2} o_{1}}-\theta _{n_{1} o_{1}}\right) - p^\mathrm{{E}}_{g_{2} n_{2} o_{1}} -p^\mathrm{{S}}_{g_{1} n_{2} o_{1}} - p^\mathrm{{S}}_{g_{2} n_{2} o_{1}} =0 \ \ \ \ :\lambda _{n_{2} o_{1}} \ \ \end{aligned}$$

(6.4c)

$$\begin{aligned}&0 \le p^\mathrm{{C}}_{g_{1} n_{1} o_{1}}\le x^\mathrm{{C}}_{g_{1} n_{1}} \ \ \ \ :\mu ^{\mathrm{{C}}^\mathrm{{min}}}_{g_{1} n_{1} o_{1}},\mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{1} n_{1} o_{1}}\ \ \ \end{aligned}$$

(6.4d)

$$\begin{aligned}&0 \le p^\mathrm{{C}}_{g_{2} n_{1} o_{1}}\le x^\mathrm{{C}}_{g_{2} n_{1}} \ \ \ \ :\mu ^{\mathrm{{C}}^\mathrm{{min}}}_{g_{2} n_{1} o_{1}},\mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{2} n_{1} o_{1}}\ \ \ \end{aligned}$$

(6.4e)

$$\begin{aligned}&0 \le p^\mathrm{{S}}_{g_{1} n_{2} o_{1}}\le 0.35 \ x^\mathrm{{S}}_{g_{1} n_{2}} \ \ \ \ :\mu ^{\mathrm{{S}}^\mathrm{{min}}}_{g_{1} n_{2} o_{1}},\mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{1} n_{2} o_{1}}\ \ \end{aligned}$$

(6.4f)

$$\begin{aligned}&0 \le p^\mathrm{{S}}_{g_{2} n_{2} o_{1}}\le 0.35 \ x^\mathrm{{S}}_{g_{2} n_{2}} \ \ \ \ :\mu ^{\mathrm{{S}}^\mathrm{{min}}}_{g_{2} n_{2} o_{1}},\mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{2} n_{2} o_{1}}\ \ \end{aligned}$$

(6.4g)

$$\begin{aligned}&0 \le p^\mathrm{{E}}_{g_{1} n_{1} o_{1}}\le 150 \ \ \ \ :\mu ^{\mathrm{{E}}^\mathrm{{min}}}_{g_{1} n_{1} o_{1}},\mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{1} n_{1} o_{1}}\ \ \end{aligned}$$

(6.4h)

$$\begin{aligned}&0 \le p^\mathrm{{E}}_{g_{2} n_{2} o_{1}}\le 100 \ \ \ \ :\mu ^{\mathrm{{E}}^\mathrm{{min}}}_{g_{2} n_{2} o_{1}},\mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{2} n_{2} o_{1}}\ \ \end{aligned}$$

(6.4i)

$$\begin{aligned}&0 \le p^\mathrm{{D}}_{n_{1} o_{1}}\le 1 \times 400 \ \ \ \ :\mu ^{\mathrm{{D}}^\mathrm{{min}}}_{n_{1} o_{1}},\mu ^{\mathrm{{D}}^\mathrm{{max}}}_{n_{1} o_{1}} \ \ \ \ \end{aligned}$$

(6.4j)

$$\begin{aligned}&1000 \left( \theta _{n_{1} o_{1}}-\theta _{n_{2} o_{1}}\right) \le 400 \ \ \ \ :\mu ^{\mathrm{{F}}}_{n_{1} n_{2} o_{1}} \ \ \ \end{aligned}$$

(6.4k)

$$\begin{aligned}&1000 \left( \theta _{n_{2} o_{1}}-\theta _{n_{1} o_{1}}\right) \le 400 \ \ \ \ :\mu ^{\mathrm{{F}}}_{n_{2} n_{1} o_{1}} \ \ \ \end{aligned}$$

(6.4l)

$$\begin{aligned}&-\pi \le \theta _{n_{1} o_{1}}\le \pi \ \ \ \ :\mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{1} o_{1}}, \mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{1} o_{1}} \ \ \end{aligned}$$

(6.4m)

$$\begin{aligned}&-\pi \le \theta _{n_{2} o_{1}}\le \pi \ \ \ \ :\mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{2} o_{1}}, \mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{2} o_{1}} \ \ \end{aligned}$$

(6.4n)

$$\begin{aligned}&\theta _{n_{1} o_{1}}=0 \ \ \ \ :\mu ^{\mathrm{{\theta }}^\mathrm{{ref}}}_{o_{1}}. \ \ \end{aligned}$$

(6.4o)

In addition, the lower-level problem referring to the operating condition $o_{2}$ (common to both producers) is given by (6.5) below:

$$\begin{aligned} \text {min}_{\varXi ^\mathrm{{P,Ex}}_{o_{2}}} \ \ \ \,&\alpha ^\mathrm{{C}}_{g_{1} n_{1} o_{2}} \ p^\mathrm{{C}}_{g_{1} n_{1} o_{2}}\ +\alpha ^\mathrm{{E}}_{g_{1} n_{1} o_{2}} \ p^\mathrm{{E}}_{g_{1} n_{1} o_{2}}\nonumber \\&\qquad \quad +\alpha ^\mathrm{{C}}_{g_{2} n_{1} o_{2}} \ p^\mathrm{{C}}_{g_{2} n_{1} o_{2}}\ +\alpha ^\mathrm{{E}}_{g_{2} n_{2} o_{2}} \ p^\mathrm{{E}}_{g_{2} n_{2} o_{2}} -32 \ p^\mathrm{{D}}_{n_{1} o_{2}} \ \end{aligned}$$

(6.5a)

$$\begin{aligned}&\text {subject to}\nonumber \ \\&p^\mathrm{{D}}_{n_{1} o_{2}} +1000 \left( \theta _{n_{1} o_{2}}-\theta _{n_{2} o_{2}}\right) - p^\mathrm{{E}}_{g_{1} n_{1} o_{2}} -p^\mathrm{{C}}_{g_{1} n_{1} o_{2}}\nonumber \\&\qquad \quad - p^\mathrm{{C}}_{g_{2} n_{1} o_{2}}=0 \ \ \ \ :\lambda _{n_{1} o_{2}} \end{aligned}$$

(6.5b)

$$\begin{aligned}&1000 \left( \theta _{n_{2} o_{2}}-\theta _{n_{1} o_{2}}\right) - p^\mathrm{{E}}_{g_{2} n_{2} o_{2}} -p^\mathrm{{S}}_{g_{1} n_{2} o_{2}} - p^\mathrm{{S}}_{g_{2} n_{2} o_{2}} =0 \ \ \ \ :\lambda _{n_{2} o_{2}} \ \ \end{aligned}$$

(6.5c)

$$\begin{aligned}&0 \le p^\mathrm{{C}}_{g_{1} n_{1} o_{2}}\le x^\mathrm{{C}}_{g_{1} n_{1}} \ \ \ \ :\mu ^{\mathrm{{C}}^\mathrm{{min}}}_{g_{1} n_{1} o_{2}},\mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{1} n_{1} o_{2}}\ \ \ \end{aligned}$$

(6.5d)

$$\begin{aligned}&0 \le p^\mathrm{{C}}_{g_{2} n_{1} o_{2}}\le x^\mathrm{{C}}_{g_{2} n_{1}} \ \ \ \ :\mu ^{\mathrm{{C}}^\mathrm{{min}}}_{g_{2} n_{1} o_{2}},\mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{2} n_{1} o_{2}}\ \ \end{aligned}$$

(6.5e)

$$\begin{aligned}&0 \le p^\mathrm{{S}}_{g_{1} n_{2} o_{2}}\le 0.70 \ x^\mathrm{{S}}_{g_{1} n_{2}} \ \ \ \ :\mu ^{\mathrm{{S}}^\mathrm{{min}}}_{g_{1} n_{2} o_{2}},\mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{1} n_{2} o_{2}}\ \ \end{aligned}$$

(6.5f)

$$\begin{aligned}&0 \le p^\mathrm{{S}}_{g_{2} n_{2} o_{2}}\le 0.70 \ x^\mathrm{{S}}_{g_{2} n_{2}} \ \ \ \ :\mu ^{\mathrm{{S}}^\mathrm{{min}}}_{g_{2} n_{2} o_{2}},\mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{2} n_{2} o_{2}}\ \ \end{aligned}$$

(6.5g)

$$\begin{aligned}&0 \le p^\mathrm{{E}}_{g_{1} n_{1} o_{2}}\le 150 \ \ \ \ :\mu ^{\mathrm{{E}}^\mathrm{{min}}}_{g_{1} n_{1} o_{2}},\mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{1} n_{1} o_{2}}\ \ \end{aligned}$$

(6.5h)

$$\begin{aligned}&0 \le p^\mathrm{{E}}_{g_{2} n_{2} o_{2}}\le 100 \ \ \ \ :\mu ^{\mathrm{{E}}^\mathrm{{min}}}_{g_{2} n_{2} o_{2}},\mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{2} n_{2} o_{2}}\ \ \end{aligned}$$

(6.5i)

$$\begin{aligned}&0 \le p^\mathrm{{D}}_{n_{1} o_{2}}\le 0.8 \times 400 \ \ \ \ :\mu ^{\mathrm{{D}}^\mathrm{{min}}}_{n_{1} o_{2}},\mu ^{\mathrm{{D}}^\mathrm{{max}}}_{n_{1} o_{2}} \ \ \ \ \end{aligned}$$

(6.5j)

$$\begin{aligned}&1000 \left( \theta _{n_{1} o_{2}}-\theta _{n_{2} o_{2}}\right) \le 400 \ \ \ \ :\mu ^{\mathrm{{F}}}_{n_{1} n_{2} o_{2}} \ \ \ \end{aligned}$$

(6.5k)

$$\begin{aligned}&1000 \left( \theta _{n_{2} o_{2}}-\theta _{n_{1} o_{2}}\right) \le 400 \ \ \ \ :\mu ^{\mathrm{{F}}}_{n_{2} n_{1} o_{2}} \ \ \ \end{aligned}$$

(6.5l)

$$\begin{aligned}&-\pi \le \theta _{n_{1} o_{2}}\le \pi \ \ \ \ :\mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{1} o_{2}}, \mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{1} o_{2}} \ \ \end{aligned}$$

(6.5m)

$$\begin{aligned}&-\pi \le \theta _{n_{2} o_{2}}\le \pi \ \ \ \ :\mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{2} o_{2}}, \mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{2} o_{2}} \ \ \end{aligned}$$

(6.5n)

$$\begin{aligned}&\theta _{n_{1} o_{2}}=0 \ \ \ \ :\mu ^{\mathrm{{\theta }}^\mathrm{{ref.}}}_{o_{2}}. \ \ \ \ \end{aligned}$$

(6.5o)

The primal optimization variables of lower-level problem (6.4) associated with operating condition $o_{1}$ are included in set $\varXi ^\mathrm{{P,Ex}}_{o_{1}}=$ $\{p^\mathrm{{C}}_{g_{1} n_{1} o_{1}}, p^\mathrm{{E}}_{g_{1} n_{1} o_{1}}, p^\mathrm{{S}}_{g_{1} n_{2} o_{1}}, p^\mathrm{{C}}_{g_{2} n_{1} o_{1}}, p^\mathrm{{E}}_{g_{2} n_{2} o_{1}}, p^\mathrm{{S}}_{g_{2} n_{2} o_{1}}, p^\mathrm{{D}}_{n_{1} o_{1}}, \theta _{n_{1} o_{1}}, \theta _{n_{2} o_{1}}\}$. Additionally, its dual variables are those included in set $\varXi ^\mathrm{{D,Ex}}_{o_{1}}=$ $\{\lambda _{n_{1} o_{1}}, \lambda _{n_{2} o_{1}}, \mu ^{\mathrm{{C}}^\mathrm{{min}}}_{g_{1} n_{1} o_{1}}, \mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{1} n_{1} o_{1}}, \mu ^{\mathrm{{C}}^\mathrm{{min}}}_{g_{2} n_{1} o_{1}}, \mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{2} n_{1} o_{1}}, \mu ^{\mathrm{{S}}^\mathrm{{min}}}_{g_{1} n_{2} o_{1}}, \mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{1} n_{2} o_{1}}, \mu ^{\mathrm{{S}}^\mathrm{{min}}}_{g_{2} n_{2} o_{1}}, \mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{2} n_{2} o_{1}}, \mu ^{\mathrm{{E}}^\mathrm{{min}}}_{g_{1} n_{1} o_{1}}, \mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{1} n_{1} o_{1}}, \mu ^{\mathrm{{E}}^\mathrm{{min}}}_{g_{2} n_{2} o_{1}}, \mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{2} n_{2} o_{1}}, \mu ^{\mathrm{{D}}^\mathrm{{min}}}_{n_{1} o_{1}}, \mu ^{\mathrm{{D}}^\mathrm{{max}}}_{n_{1} o_{1}}, \mu ^{\mathrm{{F}}}_{n_{1} n_{2} o_{1}}, \mu ^{\mathrm{{F}}}_{n_{2} n_{1} o_{1}}, \mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{1} o_{1}}, \mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{1} o_{1}}, \mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{2} o_{1}}, \mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{2} o_{1}}, \mu ^{\mathrm{{\theta }}^\mathrm{{ref}}}_{o_{1}}\}$. In addition, the primal optimization variables of lower-level problem (6.5) associated with operating condition $o_{2}$ are included in set $\varXi ^\mathrm{{P,Ex}}_{o_{2}}=$ $\{p^\mathrm{{C}}_{g_{1} n_{1} o_{2}}, p^\mathrm{{E}}_{g_{1} n_{1} o_{2}}, p^\mathrm{{S}}_{g_{1} n_{2} o_{2}}, p^\mathrm{{C}}_{g_{2} n_{1} o_{2}}, p^\mathrm{{E}}_{g_{2} n_{2} o_{2}}, p^\mathrm{{S}}_{g_{2} n_{2} o_{2}}, p^\mathrm{{D}}_{n_{1} o_{2}}, \theta _{n_{1} o_{2}}, \theta _{n_{2} o_{2}}\}$. Likewise, its dual variables are those included in set $\varXi ^\mathrm{{D,Ex}}_{o_{2}}=$ $\{\lambda _{n_{1} o_{2}}, \lambda _{n_{2} o_{2}}, \mu ^{\mathrm{{C}}^\mathrm{{min}}}_{g_{1} n_{1} o_{2}}, \mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{1} n_{1} o_{2}}, \mu ^{\mathrm{{C}}^\mathrm{{min}}}_{g_{2} n_{1} o_{2}}, \mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{2} n_{1} o_{2}}, \mu ^{\mathrm{{S}}^\mathrm{{min}}}_{g_{1} n_{2} o_{2}}, \mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{1} n_{2} o_{2}}, \mu ^{\mathrm{{S}}^\mathrm{{min}}}_{g_{2} n_{2} o_{2}}, \mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{2} n_{2} o_{2}}, \mu ^{\mathrm{{E}}^\mathrm{{min}}}_{g_{1} n_{1} o_{2}}, \mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{1} n_{1} o_{2}}, \mu ^{\mathrm{{E}}^\mathrm{{min}}}_{g_{2} n_{2} o_{2}}, \mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{2} n_{2} o_{2}}, \mu ^{\mathrm{{D}}^\mathrm{{min}}}_{n_{1} o_{2}}, \mu ^{\mathrm{{D}}^\mathrm{{max}}}_{n_{1} o_{2}}, \mu ^{\mathrm{{F}}}_{n_{1} n_{2} o_{2}}, \mu ^{\mathrm{{F}}}_{n_{2} n_{1} o_{2}}, \mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{1} o_{2}}, \mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{1} o_{2}}, \mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{2} o_{2}}, \mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{2} o_{2}}, \mu ^{\mathrm{{\theta }}^\mathrm{{ref}}}_{o_{2}}\}$. The primal optimization variables of upper-level problem (6.2a)–(6.2e) pertaining to producer $g_{1}$ are included in set $\varXi ^\mathrm{{UL,Ex}}_{g_{1}}=$ $\{x^\mathrm{{C}}_{g_{1} n_{1}}, x^\mathrm{{S}}_{g_{1} n_{2}}, \alpha ^\mathrm{{C}}_{g_{1} n_{1} o_{1}}, \alpha ^\mathrm{{E}}_{g_{1} n_{1} o_{1}}, \alpha ^\mathrm{{C}}_{g_{1} n_{1} o_{2}}, \alpha ^\mathrm{{E}}_{g_{1} n_{1} o_{2}} \}$ plus $\varXi ^\mathrm{{P,Ex}}_{o_{1}}$, $\varXi ^\mathrm{{D,Ex}}_{o_{1}}$, $\varXi ^\mathrm{{P,Ex}}_{o_{2}}$, and $\varXi ^\mathrm{{D,Ex}}_{o_{2}}$. Finally, the primal optimization variables of upper-level problem (6.3a)–(6.3e) pertaining to producer $g_{2}$ are included in set $\varXi ^\mathrm{{UL,Ex}}_{g_{2}}=$ $\{x^\mathrm{{C}}_{g_{2} n_{1}}, x^\mathrm{{S}}_{g_{2} n_{2}}, \alpha ^\mathrm{{C}}_{g_{2} n_{1} o_{1}}, \alpha ^\mathrm{{E}}_{g_{2} n_{2} o_{1}}, \alpha ^\mathrm{{C}}_{g_{2} n_{1} o_{2}}, \alpha ^\mathrm{{E}}_{g_{2} n_{2} o_{2}} \}$ plus $\varXi ^\mathrm{{P,Ex}}_{o_{1}}$, $\varXi ^\mathrm{{D,Ex}}_{o_{1}}$, $\varXi ^\mathrm{{P,Ex}}_{o_{2}}$, and $\varXi ^\mathrm{{D,Ex}}_{o_{2}}$. $\square$

6.4.1 MPEC

As stated in the previous section, each strategic producer solves its own bilevel model to derive the most beneficial investment and offering decisions. To this end, each lower-level problem within the bilevel model of each producer needs to be replaced by its equivalent optimality conditions. In general, two alternative approaches are available to derive those conditions for a continuous and linear problem: (i) the KKT conditions and (ii) the primal–dual transformation [7].

In contrast to Chap. 5, in which the first approach, i.e., KKT conditions, is used, we use in this chapter the second approach, i.e., primal–dual transformation, which includes the strong duality equality instead of all complementarity conditions. However, the primal–dual transformation introduces some nonlinearities due to bilinear terms within the strong duality equality.

Pursuing further clarity, we derive the MPECs corresponding to the strategic producers $g_{1}$ and $g_{2}$ in Illustrative Example 6.1 presented in the previous section. Recall that lower-level problems (market-clearing problems for different operating conditions) are common within the bilevel models of both producers. Thus, we derive the optimality conditions corresponding to the lower-level problems (6.4) and (6.5) using the primal–dual transformation. Figure 6.4 schematically illustrates this transformation.

Fig. 6.4

Illustrative Example 6.1: transformation of the bilevel models of strategic producers $g_{1}$ and $g_{2}$ into their corresponding MPECs (primal–dual transformation)

First, we derive the optimality conditions corresponding to the lower-level problem (6.4), which include the primal constraints (6.6), the dual constraints (6.7), and the strong duality equality (6.8). The primal constraints of lower-level problem (6.4) are given by (6.6) below:

$$\begin{aligned}&p^\mathrm{{D}}_{n_{1} o_{1}} +1000 \left( \theta _{n_{1} o_{1}}-\theta _{n_{2} o_{1}}\right) - p^\mathrm{{E}}_{g_{1} n_{1} o_{1}} -p^\mathrm{{C}}_{g_{1} n_{1} o_{1}} - p^\mathrm{{C}}_{g_{2} n_{1} o_{1}}=0 \ \ \ \ \end{aligned}$$

(6.6a)

$$\begin{aligned}&1000 \left( \theta _{n_{2} o_{1}}-\theta _{n_{1} o_{1}}\right) - p^\mathrm{{E}}_{g_{2} n_{2} o_{1}} -p^\mathrm{{S}}_{g_{1} n_{2} o_{1}} - p^\mathrm{{S}}_{g_{2} n_{2} o_{1}} =0 \ \ \ \end{aligned}$$

(6.6b)

$$\begin{aligned}&0 \le p^\mathrm{{C}}_{g_{1} n_{1} o_{1}}\le x^\mathrm{{C}}_{g_{1} n_{1}} \ \ \end{aligned}$$

(6.6c)

$$\begin{aligned}&0 \le p^\mathrm{{C}}_{g_{2} n_{1} o_{1}}\le x^\mathrm{{C}}_{g_{2} n_{1}} \ \ \end{aligned}$$

(6.6d)

$$\begin{aligned}&0 \le p^\mathrm{{S}}_{g_{1} n_{2} o_{1}}\le 0.35 \ x^\mathrm{{S}}_{g_{1} n_{2}} \ \end{aligned}$$

(6.6e)

$$\begin{aligned}&0 \le p^\mathrm{{S}}_{g_{2} n_{2} o_{1}}\le 0.35 \ x^\mathrm{{S}}_{g_{2} n_{2}} \ \ \end{aligned}$$

(6.6f)

$$\begin{aligned}&0 \le p^\mathrm{{E}}_{g_{1} n_{1} o_{1}}\le 150 \ \end{aligned}$$

(6.6g)

$$\begin{aligned}&0 \le p^\mathrm{{E}}_{g_{2} n_{2} o_{1}}\le 100\ \end{aligned}$$

(6.6h)

$$\begin{aligned}&0 \le p^\mathrm{{D}}_{n_{1} o_{1}}\le 1 \times 400 \ \ \ \ \ \end{aligned}$$

(6.6i)

$$\begin{aligned}&1000 \left( \theta _{n_{1} o_{1}}-\theta _{n_{2} o_{1}}\right) \le 400\ \ \ \ \ \end{aligned}$$

(6.6j)

$$\begin{aligned}&1000 \left( \theta _{n_{2} o_{1}}-\theta _{n_{1} o_{1}}\right) \le 400\ \ \ \ \end{aligned}$$

(6.6k)

$$\begin{aligned}&-\pi \le \theta _{n_{1} o_{1}}\le \pi \ \ \end{aligned}$$

(6.6l)

$$\begin{aligned}&-\pi \le \theta _{n_{2} o_{1}}\le \pi \ \ \end{aligned}$$

(6.6m)

$$\begin{aligned}&\theta _{n_{1} o_{1}}=0 . \end{aligned}$$

(6.6n)

The dual constraints of lower-level problem (6.4) are given by (6.7) below:

$$\begin{aligned}&\alpha ^\mathrm{{C}}_{g_{1} n_{1} o_{1}}-\lambda _{n_{1} o_{1}} +\mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{1} n_{1} o_{1}}-\mu ^{\mathrm{{C}}^\mathrm{{min}}}_{g_{1} n_{1} o_{1}}=0 \end{aligned}$$

(6.7a)

$$\begin{aligned}&\alpha ^\mathrm{{E}}_{g_{1} n_{1} o_{1}}-\lambda _{n_{1} o_{1}} +\mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{1} n_{1} o_{1}}-\mu ^{\mathrm{{E}}^\mathrm{{min}}}_{g_{1} n_{1} o_{1}}=0\end{aligned}$$

(6.7b)

$$\begin{aligned}&\alpha ^\mathrm{{C}}_{g_{2} n_{1} o_{1}}-\lambda _{n_{1} o_{1}} +\mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{2} n_{1} o_{1}}-\mu ^{\mathrm{{C}}^\mathrm{{min}}}_{g_{2} n_{1} o_{1}}=0\end{aligned}$$

(6.7c)

$$\begin{aligned}&\alpha ^\mathrm{{E}}_{g_{2} n_{2} o_{1}}-\lambda _{n_{2} o_{1}} +\mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{2} n_{2} o_{1}}-\mu ^{\mathrm{{E}}^\mathrm{{min}}}_{g_{2} n_{2} o_{1}}=0\end{aligned}$$

(6.7d)

$$\begin{aligned}&-\lambda _{n_{2} o_{1}} +\mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{1} n_{2} o_{1}}-\mu ^{\mathrm{{S}}^\mathrm{{min}}}_{g_{1} n_{2} o_{1}}=0\end{aligned}$$

(6.7e)

$$\begin{aligned}&-\lambda _{n_{2} o_{1}} +\mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{2} n_{2} o_{1}}-\mu ^{\mathrm{{S}}^\mathrm{{min}}}_{g_{2} n_{2} o_{1}}=0 \ \end{aligned}$$

(6.7f)

$$\begin{aligned}&-35+\lambda _{n_{1} o_{1}} +\mu ^{\mathrm{{D}}^\mathrm{{max}}}_{n_{1} o_{1}}-\mu ^{\mathrm{{D}}^\mathrm{{min}}}_{n_{1} o_{1}}=0 \end{aligned}$$

(6.7g)

$$\begin{aligned}&1000 \left( \lambda _{n_{1} o_{1}}-\lambda _{n_{2} o_{1}}+\mu ^{\mathrm{{F}}}_{n_{1} n_{2} o_{1}}-\mu ^{\mathrm{{F}}}_{n_{2} n_{1} o_{1}}\right) +\mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{1} o_{1}}-\mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{1} o_{1}} +\mu ^{\mathrm{{\theta }}^\mathrm{{ref}}}_{o_{1}}=0\end{aligned}$$

(6.7h)

$$\begin{aligned}&1000 \left( \lambda _{n_{2} o_{1}}-\lambda _{n_{1} o_{1}}+\mu ^{\mathrm{{F}}}_{n_{2} n_{1} o_{1}}-\mu ^{\mathrm{{F}}}_{n_{1} n_{2} o_{1}}\right) +\mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{2} o_{1}}-\mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{2} o_{1}}=0 \end{aligned}$$

(6.7i)

$$\begin{aligned}&\mu ^{\mathrm{{C}}^\mathrm{{min}}}_{g_{1} n_{1} o_{1}}, \ \mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{1} n_{1} o_{1}} \ge 0 \end{aligned}$$

(6.7j)

$$\begin{aligned}&\mu ^{\mathrm{{C}}^\mathrm{{min}}}_{g_{2} n_{1} o_{1}}, \ \mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{2} n_{1} o_{1}} \ge 0 \end{aligned}$$

(6.7k)

$$\begin{aligned}&\mu ^{\mathrm{{E}}^\mathrm{{min}}}_{g_{1} n_{1} o_{1}}, \ \mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{1} n_{1} o_{1}} \ge 0 \end{aligned}$$

(6.7l)

$$\begin{aligned}&\mu ^{\mathrm{{E}}^\mathrm{{min}}}_{g_{2} n_{2} o_{1}}, \ \mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{2} n_{2} o_{1}} \ge 0 \end{aligned}$$

(6.7m)

$$\begin{aligned}&\mu ^{\mathrm{{S}}^\mathrm{{min}}}_{g_{1} n_{2} o_{1}}, \ \mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{1} n_{2} o_{1}} \ge 0 \end{aligned}$$

(6.7n)

$$\begin{aligned}&\mu ^{\mathrm{{S}}^\mathrm{{min}}}_{g_{2} n_{2} o_{1}}, \ \mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{2} n_{2} o_{1}} \ge 0 \ \end{aligned}$$

(6.7o)

$$\begin{aligned}&\mu ^{\mathrm{{D}}^\mathrm{{min}}}_{n_{1} o_{1}} \ge 0, \ \mu ^{\mathrm{{D}}^\mathrm{{max}}}_{n_{1} o_{1}} \ge 0 \end{aligned}$$

(6.7p)

$$\begin{aligned}&\mu ^{\mathrm{{F}}}_{n_{1} n_{2} o_{1}}, \ \mu ^{\mathrm{{F}}}_{n_{2} n_{1} o_{1}} \ge 0 \end{aligned}$$

(6.7q)

$$\begin{aligned}&\mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{1} o_{1}}, \ \mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{1} o_{1}} \ge 0 \end{aligned}$$

(6.7r)

$$\begin{aligned}&\mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{2} o_{1}}, \ \mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{2} o_{1}} \ge 0. \end{aligned}$$

(6.7s)

Finally, the strong duality equality corresponding to lower-level problem (6.4) is (6.8), which enforces the equality of its primal and dual objective function values at the optimal solution:

$$\begin{aligned}&\alpha ^\mathrm{{C}}_{g_{1} n_{1} o_{1}} \ p^\mathrm{{C}}_{g_{1} n_{1} o_{1}}\ +\alpha ^\mathrm{{E}}_{g_{1} n_{1} o_{1}} \ p^\mathrm{{E}}_{g_{1} n_{1} o_{1}} +\alpha ^\mathrm{{C}}_{g_{2} n_{1} o_{1}} \ p^\mathrm{{C}}_{g_{2} n_{1} o_{1}}\ +\alpha ^\mathrm{{E}}_{g_{2} n_{2} o_{1}} \ p^\mathrm{{E}}_{g_{2} n_{2} o_{1}} \nonumber \\ {}&\qquad \quad -35 \ p^\mathrm{{D}}_{n_{1} o_{1}} = -x^\mathrm{{C}}_{g_{1} n_{1}} \ \mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{1} n_{1} o_{1}} -x^\mathrm{{C}}_{g_{2} n_{1}} \ \mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{2} n_{1} o_{1}} -0.35 \ x^\mathrm{{S}}_{g_{1} n_{2}} \ \mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{1} n_{2} o_{1}}\nonumber \\ {}&\qquad \quad -0.35 \ x^\mathrm{{S}}_{g_{2} n_{2}} \ \mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{2} n_{2} o_{1}} -150 \ \mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{1} n_{1} o_{1}} -100 \ \mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{2} n_{2} o_{1}} -400 \ \mu ^{\mathrm{{D}}^\mathrm{{max}}}_{n_{1} o_{1}}\nonumber \\ {}&\qquad \quad -400 \left( \mu ^{\mathrm{{F}}}_{n_{1} n_{2} o_{1}}+\mu ^{\mathrm{{F}}}_{n_{2} n_{1} o_{1}}\right) -\pi \left( \mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{1} o_{1}}+\mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{1} o_{1}}+\mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{2} o_{1}}+\mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{2} o_{1}}\right) . \end{aligned}$$

(6.8)

Next, we derive the optimality conditions corresponding to lower-level problem (6.5), which consist of primal constraints (6.9), dual constraints (6.10), and strong duality equality (6.11). The primal constraints of lower-level problem (6.5) are given by (6.9) below:

$$\begin{aligned}&p^\mathrm{{D}}_{n_{1} o_{2}} +1000 \left( \theta _{n_{1} o_{2}}-\theta _{n_{2} o_{2}}\right) - p^\mathrm{{E}}_{g_{1} n_{1} o_{2}} -p^\mathrm{{C}}_{g_{1} n_{1} o_{2}} - p^\mathrm{{C}}_{g_{2} n_{1} o_{2}}=0 \ \ \ \ \end{aligned}$$

(6.9a)

$$\begin{aligned}&1000 \left( \theta _{n_{2} o_{2}}-\theta _{n_{1} o_{2}}\right) - p^\mathrm{{E}}_{g_{2} n_{2} o_{2}} -p^\mathrm{{S}}_{g_{1} n_{2} o_{2}} - p^\mathrm{{S}}_{g_{2} n_{2} o_{2}} =0 \ \ \ \ \ \ \end{aligned}$$

(6.9b)

$$\begin{aligned}&0 \le p^\mathrm{{C}}_{g_{1} n_{1} o_{2}}\le x^\mathrm{{C}}_{g_{1} n_{1}} \ \end{aligned}$$

(6.9c)

$$\begin{aligned}&0 \le p^\mathrm{{C}}_{g_{2} n_{1} o_{2}}\le x^\mathrm{{C}}_{g_{2} n_{1}} \ \ \ \end{aligned}$$

(6.9d)

$$\begin{aligned}&0 \le p^\mathrm{{S}}_{g_{1} n_{2} o_{2}}\le 0.70 \ x^\mathrm{{S}}_{g_{1} n_{2}} \ \end{aligned}$$

(6.9e)

$$\begin{aligned}&0 \le p^\mathrm{{S}}_{g_{2} n_{2} o_{2}}\le 0.70 \ x^\mathrm{{S}}_{g_{2} n_{2}}\ \ \end{aligned}$$

(6.9f)

$$\begin{aligned}&0 \le p^\mathrm{{E}}_{g_{1} n_{1} o_{2}}\le 150 \ \end{aligned}$$

(6.9g)

$$\begin{aligned}&0 \le p^\mathrm{{E}}_{g_{2} n_{2} o_{2}}\le 100 \ \end{aligned}$$

(6.9h)

$$\begin{aligned}&0 \le p^\mathrm{{D}}_{n_{1} o_{2}}\le 0.8 \times 400 \ \ \ \ \end{aligned}$$

(6.9i)

$$\begin{aligned}&1000 \left( \theta _{n_{1} o_{2}}-\theta _{n_{2} o_{2}}\right) \le 400\ \ \ \ \ \end{aligned}$$

(6.9j)

$$\begin{aligned}&1000 \left( \theta _{n_{2} o_{2}}-\theta _{n_{1} o_{2}}\right) \le 400\ \ \ \ \ \end{aligned}$$

(6.9k)

$$\begin{aligned}&-\pi \le \theta _{n_{1} o_{2}}\le \pi \ \ \end{aligned}$$

(6.9l)

$$\begin{aligned}&-\pi \le \theta _{n_{2} o_{2}}\le \pi \ \ \end{aligned}$$

(6.9m)

$$\begin{aligned}&\theta _{n_{1} o_{2}}=0. \end{aligned}$$

(6.9n)

The dual constraints of lower-level problem (6.5) are given by (6.10) below:

$$\begin{aligned}&\alpha ^\mathrm{{C}}_{g_{1} n_{1} o_{2}}-\lambda _{n_{1} o_{2}} +\mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{1} n_{1} o_{2}}-\mu ^{\mathrm{{C}}^\mathrm{{min}}}_{g_{1} n_{1} o_{2}}=0 \end{aligned}$$

(6.10a)

$$\begin{aligned}&\alpha ^\mathrm{{E}}_{g_{1} n_{1} o_{2}}-\lambda _{n_{1} o_{2}} +\mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{1} n_{1} o_{2}}-\mu ^{\mathrm{{E}}^\mathrm{{min}}}_{g_{1} n_{1} o_{2}}=0\end{aligned}$$

(6.10b)

$$\begin{aligned}&\alpha ^\mathrm{{C}}_{g_{2} n_{1} o_{2}}-\lambda _{n_{1} o_{2}} +\mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{2} n_{1} o_{2}}-\mu ^{\mathrm{{C}}^\mathrm{{min}}}_{g_{2} n_{1} o_{2}}=0\end{aligned}$$

(6.10c)

$$\begin{aligned}&\alpha ^\mathrm{{E}}_{g_{2} n_{2} o_{2}}-\lambda _{n_{2} o_{2}} +\mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{2} n_{2} o_{2}}-\mu ^{\mathrm{{E}}^\mathrm{{min}}}_{g_{2} n_{2} o_{2}}=0\end{aligned}$$

(6.10d)

$$\begin{aligned}&-\lambda _{n_{2} o_{2}} +\mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{1} n_{2} o_{2}}-\mu ^{\mathrm{{S}}^\mathrm{{min}}}_{g_{1} n_{2} o_{2}}=0\end{aligned}$$

(6.10e)

$$\begin{aligned}&-\lambda _{n_{2} o_{2}} +\mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{2} n_{2} o_{2}}-\mu ^{\mathrm{{S}}^\mathrm{{min}}}_{g_{2} n_{2} o_{2}}=0\end{aligned}$$

(6.10f)

$$\begin{aligned}&-32+\lambda _{n_{1} o_{2}} +\mu ^{\mathrm{{D}}^\mathrm{{max}}}_{n_{1} o_{2}}-\mu ^{\mathrm{{D}}^\mathrm{{min}}}_{n_{1} o_{2}}=0\end{aligned}$$

(6.10g)

$$\begin{aligned}&1000 \left( \lambda _{n_{1} o_{2}}-\lambda _{n_{2} o_{2}}+\mu ^{\mathrm{{F}}}_{n_{1} n_{2} o_{2}}-\mu ^{\mathrm{{F}}}_{n_{2} n_{1} o_{2}}\right) +\mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{1} o_{2}}-\mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{1} o_{2}} +\mu ^{\mathrm{{\theta }}^\mathrm{{ref}}}_{o_{2}}=0\end{aligned}$$

(6.10h)

$$\begin{aligned}&1000 \left( \lambda _{n_{2} o_{2}}-\lambda _{n_{1} o_{2}}+\mu ^{\mathrm{{F}}}_{n_{2} n_{1} o_{2}}-\mu ^{\mathrm{{F}}}_{n_{1} n_{2} o_{2}}\right) +\mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{2} o_{2}}-\mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{2} o_{2}}=0 \end{aligned}$$

(6.10i)

$$\begin{aligned}&\mu ^{\mathrm{{C}}^\mathrm{{min}}}_{g_{1} n_{1} o_{2}}, \ \mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{1} n_{1} o_{2}} \ge 0 \ \end{aligned}$$

(6.10j)

$$\begin{aligned}&\mu ^{\mathrm{{C}}^\mathrm{{min}}}_{g_{2} n_{1} o_{2}}, \ \mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{2} n_{1} o_{2}} \ge 0 \end{aligned}$$

(6.10k)

$$\begin{aligned}&\mu ^{\mathrm{{E}}^\mathrm{{min}}}_{g_{1} n_{1} o_{2}}, \ \mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{1} n_{1} o_{2}} \ge 0 \end{aligned}$$

(6.10l)

$$\begin{aligned}&\mu ^{\mathrm{{E}}^\mathrm{{min}}}_{g_{2} n_{2} o_{2}}, \ \mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{2} n_{2} o_{2}} \ge 0 \end{aligned}$$

(6.10m)

$$\begin{aligned}&\mu ^{\mathrm{{S}}^\mathrm{{min}}}_{g_{1} n_{2} o_{2}}, \ \mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{1} n_{2} o_{2}} \ge 0 \end{aligned}$$

(6.10n)

$$\begin{aligned}&\mu ^{\mathrm{{S}}^\mathrm{{min}}}_{g_{2} n_{2} o_{2}}, \ \mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{2} n_{2} o_{2}} \ge 0 \end{aligned}$$

(6.10o)

$$\begin{aligned}&\mu ^{\mathrm{{D}}^\mathrm{{min}}}_{n_{1} o_{2}}, \ \mu ^{\mathrm{{D}}^\mathrm{{max}}}_{n_{1} o_{2}} \ge 0 \end{aligned}$$

(6.10p)

$$\begin{aligned}&\mu ^{\mathrm{{F}}}_{n_{1} n_{2} o_{2}}, \ \mu ^{\mathrm{{F}}}_{n_{2} n_{1} o_{2}} \ge 0 \end{aligned}$$

(6.10q)

$$\begin{aligned}&\mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{1} o_{2}}, \ \mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{1} o_{2}} \ge 0 \end{aligned}$$

(6.10r)

$$\begin{aligned}&\mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{2} o_{2}}, \ \mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{2} o_{2}} \ge 0. \end{aligned}$$

(6.10s)

Finally, the strong duality equality corresponding to lower-level problem (6.5) is (6.11) below:

$$\begin{aligned}&\alpha ^\mathrm{{C}}_{g_{1} n_{1} o_{2}} \ p^\mathrm{{C}}_{g_{1} n_{1} o_{2}}\ +\alpha ^\mathrm{{E}}_{g_{1} n_{1} o_{2}} \ p^\mathrm{{E}}_{g_{1} n_{1} o_{2}}\ +\alpha ^\mathrm{{C}}_{g_{2} n_{1} o_{2}} \ p^\mathrm{{C}}_{g_{2} n_{1} o_{2}}\ +\alpha ^\mathrm{{E}}_{g_{2} n_{2} o_{2}} \ p^\mathrm{{E}}_{g_{2} n_{2} o_{2}} \nonumber \\ {}&\qquad \quad -32 \ p^\mathrm{{D}}_{n_{1} o_{2}} = -x^\mathrm{{C}}_{g_{1} n_{1}} \ \mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{1} n_{1} o_{2}} -x^\mathrm{{C}}_{g_{2} n_{1}} \ \mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{2} n_{1} o_{2}} -0.70 \ x^\mathrm{{S}}_{g_{1} n_{2}} \ \mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{1} n_{2} o_{2}}\nonumber \\ {}&\qquad \quad -0.70 \ x^\mathrm{{S}}_{g_{2} n_{2}} \ \mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{2} n_{2} o_{2}} -150 \ \mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{1} n_{1} o_{2}} -100 \ \mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{2} n_{2} o_{2}} -320 \ \mu ^{\mathrm{{D}}^\mathrm{{max}}}_{n_{1} o_{2}} \nonumber \\ {}&\qquad \quad -400 \left( \mu ^{\mathrm{{F}}}_{n_{1} n_{2} o_{2}}+\mu ^{\mathrm{{F}}}_{n_{2} n_{1} o_{2}}\right) -\pi \left( \mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{1} o_{2}}+\mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{1} o_{2}}+\mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{2} o_{2}}+\mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{2} o_{2}}\right) . \end{aligned}$$

(6.11)

Accordingly, the MPEC corresponding to the strategic producer $g_{1}$ includes the upper-level problem (6.2a)–(6.2e) and the optimality conditions (6.6)–(6.11). Hereinafter, this MPEC will be called MPEC 1. Similarly, the MPEC corresponding to the strategic producer $g_{2}$ comprises the upper-level problem (6.3a)–(6.3e) and the optimality conditions (6.6)–(6.11). Hereinafter, this MPEC will be called MPEC 2.

One important observation is that both MPECs 1 and 2 are continuous, but nonlinear. The reason for nonlinearities is the existence of bilinear terms within objective functions (6.2a) and (6.3a) and strong duality equalities (6.8) and (6.11).

Note that the dual variables associated with the constraints of MPECs 1 and 2 are needed in the next section. Pursuing notational clarity, we use the equation numbers to indicate the dual variables of the MPECs. The following notional examples are provided:

• 1. In MPEC 1 corresponding to producer $g_{1}$, the dual variable associated with strong duality equality (6.8) is $\eta ^{(6.8)}_{g_{1}}$. However, the dual variable of that equality within MPEC 2 corresponding to producer $g_{2}$ is $\eta ^{(6.8)}_{g_{2}}$.

• 2. In MPEC 1 corresponding to producer $g_{1}$, the dual variables associated with lower and upper bounds in inequality (6.9c) are $\underline{\eta }^{(6.9\mathrm{c})}_{g_{1}}$ and $\overline{\eta }^{(6.9\mathrm{c})}_{g_{1}}$, respectively.

• 3. In MPEC 2 corresponding to producer $g_{2}$, the dual variables associated with nonnegativity conditions (6.10j) are $\underline{\eta }^{(6.10\mathrm{j})}_{g_{2}}$ and $\overline{\eta }^{(6.10\mathrm{j})}_{g_{2}}$, respectively.

6.5 Multiple-Producer Problem: EPEC

The joint consideration of all MPECs, one per producer, constitutes an EPEC. Figure 6.5 illustrates the EPEC corresponding to Illustrative Example 6.1 presented in Sect. 6.4. Accordingly, this EPEC includes both MPECs 1 and 2 corresponding to the strategic producers $g_{1}$ and $g_{2}$, respectively. Note that the EPEC solution identifies the market equilibria.

Fig. 6.5

Illustrative Example 6.1: EPEC

6.5.1 EPEC Solution

To obtain the EPEC solution, we first need to derive the KKT conditions associated with each MPEC. However, it is important to recall that MPECs are continuous, nonlinear, and thus nonconvex. Therefore, the KKT conditions associated with each MPEC provide its strong stationarity conditions. A collection of all those conditions corresponding to all MPECs constitutes the strong stationarity conditions associated with the EPEC, whose solution identifies the equilibria. For Illustrative Example 6.1 of Sect. 6.4, this transformation is depicted in Fig. 6.6.

It is important to note that the solutions obtained from this procedure can be Nash equilibria, local equilibria, and saddle points. To detect the Nash equilibria among the solutions obtained, an ex-post algorithm is provided in Sect. 6.5.3. The next two sections present the KKT conditions of both MPECs.

Fig. 6.6

Illustrative Example 6.1: strong stationarity conditions of the EPEC

6.5.1.1 KKT Conditions of MPEC 1

The KKT conditions of MPEC 1 corresponding to producer $g_{1}$ include the constraints below:  

• 1. Primal equality constraints of MPEC 1 including (6.6a)–(6.6b), (6.6n), (6.7a)–(6.7i), (6.8), (6.9a)–(6.9b), (6.9n), (6.10a)–(6.10i), and (6.11). We refer to these equality constraints as the set $\varGamma _{1}$.

• 2. Equality constraints obtained from differentiating the corresponding Lagrangian associated with MPEC 1 with respect to its variables. We refer to these equality constraints as the set $\varGamma _{2}$. Four examples of the members of this set are stated below. Note that ${\mathscr {L}}_{g_{1}}^\mathrm{{MPEC1}}$ is the Lagrangian function of the MPEC 1 pertaining to the strategic producer $g_{1}$:

  $$\begin{aligned} \frac{\partial {\mathscr {L}}_{g_{1}}^\mathrm{{MPEC1}}}{\partial x^\mathrm{{C}}_{g_{1} n_{1}}}&= 55000 + \overline{\eta }^{(6.2\mathrm{b})}_{g_{1}} - \underline{\eta }^{(6.2\mathrm{b})}_{g_{1}} +55000\ \eta ^{(6.2\mathrm{d})}_{g_{1}}-\overline{\eta }^{(6.6\mathrm{c})}_{g_{1}}\nonumber \\&\quad +\mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{1} n_{1} o_{1}} \ \eta ^{(6.8)}_{g_{1}} -\overline{\eta }^{(6.9\mathrm{c})}_{g_{1}} +\mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{1} n_{1} o_{2}} \ \eta ^{(6.11)}_{g_{1}}=0 \ \ \end{aligned}$$

  (6.12a)
  $$\begin{aligned} \frac{\partial {\mathscr {L}}_{g_{1}}^\mathrm{{MPEC1}}}{\partial x^\mathrm{{C}}_{g_{2} n_{1}}}&=-\overline{\eta }^{(6.6\mathrm{d})}_{g_{1}}+\mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{2} n_{1} o_{1}} \ \eta ^{(6.8)}_{g_{1}} -\overline{\eta }^{(6.9\mathrm{d})}_{g_{1}}\nonumber \\&\quad +\mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{2} n_{1} o_{2}} \ \eta ^{(6.11)}_{g_{1}}=0 \ \ \ \end{aligned}$$

  (6.12b)
  $$\begin{aligned} \frac{\partial {\mathscr {L}}_{g_{1}}^\mathrm{{MPEC1}}}{\partial \alpha ^\mathrm{{E}}_{g_{1} n_{1} o_{2}}}=&-\eta ^{(6.2\mathrm{e})}_{g_{1}}+\eta ^{(6.10\mathrm{b})}_{g_{1}} +p^\mathrm{{E}}_{g_{1} n_{1} o_{2}} \ \eta ^{(6.11)}_{g_{1}}=0 \ \ \ \end{aligned}$$

  (6.12c)
  $$\begin{aligned} \frac{\partial {\mathscr {L}}_{g_{1}}^\mathrm{{MPEC1}}}{\partial \mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{2} n_{2} o_{1}}}=\,&\eta ^{(6.7\mathrm{f})}_{g_{1}}-\overline{\eta }^{(6.7\mathrm{o})}_{g_{1}} + 0.35 \ x^\mathrm{{S}}_{g_{2} n_{2}} \ \eta ^{(6.8)}_{g_{1}}=0. \ \end{aligned}$$

  (6.12d)

• 3. Complementarity conditions related to the inequality constraints of MPEC 1. We refer to these inequality constraints as the $\varGamma _{3}$. Four examples of the members of this set are as follows:

$$\begin{aligned}&0 \le x^\mathrm{{C}}_{g_{1} n_{1}} \perp \underline{\eta }^{(6.2\mathrm{b})}_{g_{1}} \ge 0 \end{aligned}$$

(6.13a)

$$\begin{aligned}&0 \le \left[ 200-x^\mathrm{{C}}_{g_{1} n_{1}}\right] \perp \overline{\eta }^{(6.2\mathrm{b})}_{g_{1}} \ge 0 \end{aligned}$$

(6.13b)

$$\begin{aligned}&0 \le p^\mathrm{{C}}_{g_{2} n_{1} o_{2}} \perp \underline{\eta }^{(6.9\mathrm{d})}_{g_{1}} \ge 0 \end{aligned}$$

(6.13c)

$$\begin{aligned}&0 \le \left[ x^\mathrm{{C}}_{g_{2} n_{1}}-p^\mathrm{{C}}_{g_{2} n_{1} o_{2}}\right] \perp \overline{\eta }^{(6.9\mathrm{d})}_{g_{1}} \ge 0. \ \end{aligned}$$

(6.13d)

6.5.1.2 KKT Conditions of MPEC 2

The KKT conditions of MPEC 2 corresponding to producer $g_{2}$ consist of the following three sets of constraints:

• 1. Primal equality constraints of MPEC 2 that are identical to those included in the constraint set $\varGamma _{1}$.

• 2. Equality constraints resulting from differentiating the corresponding Lagrangian of MPEC 2 with respect to its variables. These equality constraints are referred to as the set $\varGamma _{4}$. Four examples of the members of this set are stated below, in which ${\mathscr {L}}_{g_{2}}^\mathrm{{MPEC2}}$ is the Lagrangian function of the MPEC 2 pertaining to the strategic producer $g_{2}$:

  $$\begin{aligned} \frac{\partial {\mathscr {L}}_{g_{2}}^\mathrm{{MPEC2}}}{\partial x^\mathrm{{S}}_{g_{2} n_{2}}}&= 66000 + \overline{\eta }^{(6.3\mathrm{c})}_{g_{2}} - \underline{\eta }^{(6.3\mathrm{c})}_{g_{2}} +66000\ \eta ^{(6.3\mathrm{d})}_{g_{2}}-0.35 \ \overline{\eta }^{(6.6\mathrm{f})}_{g_{2}}\nonumber \\&\quad +0.35 \ \mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{2} n_{2} o_{1}} \ \eta ^{(6.8)}_{g_{2}} -0.70 \ \overline{\eta }^{(6.9\mathrm{f})}_{g_{2}} \nonumber \\&\quad +0.70 \ \mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{2} n_{2} o_{2}} \ \eta ^{(6.11)}_{g_{2}}=0 \ \ \ \end{aligned}$$

  (6.14a)
  $$\begin{aligned} \frac{\partial {\mathscr {L}}_{g_{2}}^\mathrm{{MPEC2}}}{\partial x^\mathrm{{S}}_{g_{1} n_{2}}}=&-0.35 \ \overline{\eta }^{(6.6\mathrm{e})}_{g_{2}} +0.35 \ \mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{1} n_{2} o_{1}} \ \eta ^{(6.8)}_{g_{2}} \nonumber \\&\quad -0.70 \ \overline{\eta }^{(6.9\mathrm{e})}_{g_{2}} +0.70 \ \mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{1} n_{2} o_{2}} \ \eta ^{(6.11)}_{g_{2}}=0 \ \ \ \end{aligned}$$

  (6.14b)
  $$\begin{aligned} \frac{\partial {\mathscr {L}}_{g_{2}}^\mathrm{{MPEC2}}}{\partial p^\mathrm{{E}}_{g_{2} n_{2} o_{2}}}=&-5230 \ \lambda _{n_{2} o_{2}} - \eta ^{(6.9\mathrm{b})}_{g_{2}} +\overline{\eta }^{(6.9\mathrm{h})}_{g_{2}}-\underline{\eta }^{(6.9\mathrm{h})}_{g_{2}}\nonumber \\&\quad +\alpha ^\mathrm{{E}}_{g_{2} n_{2} o_{2}} \ \eta ^{(6.11)}_{g_{2}}=0 \ \ \ \end{aligned}$$

  (6.14c)
  $$\begin{aligned} \frac{\partial {\mathscr {L}}_{g_{2}}^\mathrm{{MPEC2}}}{\partial \mu ^{\mathrm{{D}}^\mathrm{{max}}}_{n_{1} o_{1}}}&= \eta ^{(6.7\mathrm{g})}_{g_{2}}-\overline{\eta }^{(6.7\mathrm{p})}_{g_{2}} + 400 \ \eta ^{(6.8)}_{g_{2}}=0. \ \end{aligned}$$

  (6.14d)

• 3. Complementarity conditions related to the inequality constraints of MPEC 2. We refer to these inequality constraints as the set $\varGamma _{5}$. Four examples of the members of this set are as follows:

$$\begin{aligned}&0 \le x^\mathrm{{S}}_{g_{2} n_{2}} \perp \underline{\eta }^{(6.3\mathrm{c})}_{g_{2}} \ge 0 \end{aligned}$$

(6.15a)

$$\begin{aligned}&0 \le \left[ 200-x^\mathrm{{S}}_{g_{2} n_{2}}\right] \perp \overline{\eta }^{(6.3\mathrm{c})}_{g_{2}} \ge 0 \end{aligned}$$

(6.15b)

$$\begin{aligned}&0 \le p^\mathrm{{E}}_{g_{2} n_{2} o_{2}} \perp \underline{\eta }^{(6.9\mathrm{h})}_{g_{2}} \ge 0 \end{aligned}$$

(6.15c)

$$\begin{aligned}&0 \le \left[ 100-p^\mathrm{{E}}_{g_{2} n_{2} o_{2}}\right] \perp \overline{\eta }^{(6.9\mathrm{h})}_{g_{2}} \ge 0. \ \end{aligned}$$

(6.15d)

6.5.1.3 Strong Stationarity Conditions of the EPEC: Linearization

The strong stationarity conditions of the EPEC (the right-hand box of Fig. 6.6) is a system of equalities and inequalities included in $\varGamma _{1}$–$\varGamma _{5}$. Although the solution to this system identifies the investment equilibria, this system includes the following three nonlinearities:

• 1. The complementarity conditions included in $\varGamma _{3}$ and $\varGamma _{5}$. Such conditions can be exactly linearized through the approach explained in Chap. 5 using auxiliary binary variables and large enough positive constants [6]. For example, the mixed-integer linear equivalent of complementarity condition (6.15a) is provided by (6.16) below:

  $$\begin{aligned}&x^\mathrm{{S}}_{g_{2} n_{2}} \ge 0 \end{aligned}$$

  (6.16a)
  $$\begin{aligned}&\underline{\eta }^{(6.3\mathrm{c})}_{g_{2}} \ge 0 \end{aligned}$$

  (6.16b)
  $$\begin{aligned}&x^\mathrm{{S}}_{g_{2} n_{2}} \le \psi \ M^{x} \end{aligned}$$

  (6.16c)
  $$\begin{aligned}&\underline{\eta }^{(6.3\mathrm{c})}_{g_{2}} \le \left( 1-\psi \right) M^{\eta } \end{aligned}$$

  (6.16d)
  $$\begin{aligned}&\psi \in \{0,1\}, \ \end{aligned}$$

  (6.16e)

  where $M^{x}$ and $M^{\eta }$ are large enough positive constants. A method for appropriate value selection for those constants is provided in Chap. 5.

• 2. The products of variables involved in the strong duality equalities (6.8) and (6.11) included in $\varGamma _{1}$. Unlike the complementarity conditions included in $\varGamma _{3}$ and $\varGamma _{5}$, which can be exactly linearized through auxiliary binary variables, the strong duality equalities (6.8) and (6.11) included in $\varGamma _{1}$ cannot be linearized straightforwardly due to the nature of the nonlinearities, i.e., the product of continuous variables. However, we take advantage of the fact that the strong duality equality resulting from the primal–dual transformation is equivalent to the set of complementarity conditions obtained from the KKT conditions [7]. Hence, pursuing linearity, the strong duality equality (6.8) is replaced by its equivalent complementarity conditions (6.17) below:

  $$\begin{aligned}&0 \le p^\mathrm{{C}}_{g_{1} n_{1} o_{1}} \perp \mu ^{\mathrm{{C}}^\mathrm{{min}}}_{g_{1} n_{1} o_{1}}\ \ge 0 \ \ \end{aligned}$$

  (6.17a)
  $$\begin{aligned}&0 \le \left( x^\mathrm{{C}}_{g_{1} n_{1}}-p^\mathrm{{C}}_{g_{1} n_{1} o_{1}}\right) \perp \mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{1} n_{1} o_{1}}\ \ge 0 \ \ \ \end{aligned}$$

  (6.17b)
  $$\begin{aligned}&0 \le p^\mathrm{{C}}_{g_{2} n_{1} o_{1}}\perp \mu ^{\mathrm{{C}}^\mathrm{{min}}}_{g_{2} n_{1} o_{1}}\ge 0 \ \ \ \end{aligned}$$

  (6.17c)
  $$\begin{aligned}&0 \le \left( x^\mathrm{{C}}_{g_{2} n_{1}}-p^\mathrm{{C}}_{g_{2} n_{1} o_{1}}\right) \perp \mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{2} n_{1} o_{1}}\ge 0\ \ \ \end{aligned}$$

  (6.17d)
  $$\begin{aligned}&0 \le p^\mathrm{{S}}_{g_{1} n_{2} o_{1}} \perp \mu ^{\mathrm{{S}}^\mathrm{{min}}}_{g_{1} n_{2} o_{1}}\ge 0\ \ \end{aligned}$$

  (6.17e)
  $$\begin{aligned}&0 \le \left( 0.35 \ x^\mathrm{{S}}_{g_{1} n_{2}} - p^\mathrm{{S}}_{g_{1} n_{2} o_{1}}\right) \perp \mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{1} n_{2} o_{1}}\ge 0\ \ \end{aligned}$$

  (6.17f)
  $$\begin{aligned}&0 \le p^\mathrm{{S}}_{g_{2} n_{2} o_{1}} \perp \mu ^{\mathrm{{S}}^\mathrm{{min}}}_{g_{2} n_{2} o_{1}}\ge 0\ \ \end{aligned}$$

  (6.17g)
  $$\begin{aligned}&0 \le \left( 0.35 \ x^\mathrm{{S}}_{g_{2} n_{2}}- p^\mathrm{{S}}_{g_{2} n_{2} o_{1}}\right) \perp \mu ^{\mathrm{{S}}^\mathrm{{max}}}_{g_{2} n_{2} o_{1}}\ge 0\ \ \end{aligned}$$

  (6.17h)
  $$\begin{aligned}&0 \le p^\mathrm{{E}}_{g_{1} n_{1} o_{1}} \perp \mu ^{\mathrm{{E}}^\mathrm{{min}}}_{g_{1} n_{1} o_{1}} \ge 0\ \ \end{aligned}$$

  (6.17i)
  $$\begin{aligned}&0 \le \left( 150-p^\mathrm{{E}}_{g_{1} n_{1} o_{1}}\right) \perp \mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{1} n_{1} o_{1}}\ge 0\ \ \end{aligned}$$

  (6.17j)
  $$\begin{aligned}&0 \le p^\mathrm{{E}}_{g_{2} n_{2} o_{1}} \perp \mu ^{\mathrm{{E}}^\mathrm{{min}}}_{g_{2} n_{2} o_{1}}\ge 0\ \ \end{aligned}$$

  (6.17k)
  $$\begin{aligned}&0 \le \left( 100-p^\mathrm{{E}}_{g_{2} n_{2} o_{1}}\right) \perp \mu ^{\mathrm{{E}}^\mathrm{{max}}}_{g_{2} n_{2} o_{1}}\ge 0\ \ \end{aligned}$$

  (6.17l)
  $$\begin{aligned}&0 \le p^\mathrm{{D}}_{n_{1} o_{1}} \perp \mu ^{\mathrm{{D}}^\mathrm{{min}}}_{n_{1} o_{1}}\ge 0 \ \ \ \ \end{aligned}$$

  (6.17m)
  $$\begin{aligned}&0 \le \left( 400-p^\mathrm{{D}}_{n_{1} o_{1}}\right) \perp \mu ^{\mathrm{{D}}^\mathrm{{max}}}_{n_{1} o_{1}}\ge 0 \ \ \ \ \end{aligned}$$

  (6.17n)
  $$\begin{aligned}&0 \le \left[ 400-1000 \left( \theta _{n_{1} o_{1}}-\theta _{n_{2} o_{1}}\right) \right] \perp \mu ^{\mathrm{{F}}}_{n_{1} n_{2} o_{1}}\ge 0 \ \ \ \end{aligned}$$

  (6.17o)
  $$\begin{aligned}&0 \le \left[ 400-1000 \left( \theta _{n_{2} o_{1}}-\theta _{n_{1} o_{1}}\right) \right] \perp \mu ^{\mathrm{{F}}}_{n_{2} n_{1} o_{1}} \ge 0\ \ \ \ \end{aligned}$$

  (6.17p)
  $$\begin{aligned}&0 \le \left( \pi +\theta _{n_{1} o_{1}}\right) \perp \mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{1} o_{1}} \ge 0\ \ \end{aligned}$$

  (6.17q)
  $$\begin{aligned}&0 \le \left( \pi -\theta _{n_{1} o_{1}}\right) \perp \mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{1} o_{1}} \ge 0\ \ \end{aligned}$$

  (6.17r)
  $$\begin{aligned}&0 \le \left( \pi +\theta _{n_{2} o_{1}}\right) \perp \mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{2} o_{1}} \ge 0\ \ \end{aligned}$$

  (6.17s)
  $$\begin{aligned}&0 \le \left( \pi -\theta _{n_{2} o_{1}}\right) \perp \mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{2} o_{1}} \ge 0.\ \ \ \end{aligned}$$

  (6.17t)

  Similarly, the strong duality equality (6.11) can be replaced by its equivalent complementarity conditions. Recall that these complementarity conditions can be linearized using the auxiliary binary variables and large enough positive constants.

• 3. The ones arising from the product of variables in $\varGamma _{2}$ and $\varGamma _{4}$, e.g., the bilinear term $\mu ^{\mathrm{{C}}^\mathrm{{max}}}_{g_{1} n_{1} o_{1}}$ $\eta ^{(6.8)}_{g_{1}}$ in condition (6.12a). Observe that the common variables of such nonlinear terms are either dual variables $\eta ^{(6.8)}_{g_{1}}$ and $\eta ^{(6.8)}_{g_{2}}$ or dual variables $\eta ^{(6.11)}_{g_{1}}$ and $\eta ^{(6.11)}_{g_{2}}$. From a mathematical point of view, the nonconvex nature of the MPECs 1 and 2 implies that the Mangasarian–Fromovitz constraint qualification (MFCQ) [5] does not hold at any feasible solution, i.e., the set of dual variables associated with the MPECs (all dual variables denoted by $\eta$) is unbounded. In other words, the values of these dual variables are not unique, and thus there are some degrees of freedom in the choice of values for those dual variables at any solution [5, 19, 20]. This redundancy allows the parameterization of dual variables $\eta ^{(6.8)}_{g_{1}}$, $\eta ^{(6.8)}_{g_{2}}$, $\eta ^{(6.11)}_{g_{1}}$, and $\eta ^{(6.11)}_{g_{2}}$. Hence, the bilinear terms in $\varGamma _{2}$ and $\varGamma _{4}$ become linear if the strong stationarity conditions of the EPEC are parameterized in dual variables $\eta ^{(6.8)}_{g_{1}}$, $\eta ^{(6.8)}_{g_{2}}$, $\eta ^{(6.11)}_{g_{1}}$, and $\eta ^{(6.11)}_{g_{2}}$.

6.5.2 Searching for Multiple Solutions

The mixed-integer linear form of the strong stationarity conditions of the EPEC, i.e., condition sets $\varGamma _{1}$–$\varGamma _{5}$, constitutes a system of mixed-integer linear equalities and inequalities that involves continuous and binary variables. This system generally has multiple solutions; however, recall that these solutions can be Nash equilibria, local equilibria, and saddle points. To detect the Nash equilibria among the solutions obtained, an ex-post algorithm is provided in Sect. 6.5.3.

To explore multiple solutions, it is straightforward to formulate an auxiliary optimization problem considering the mixed-integer linear condition sets $\varGamma _{1}$–$\varGamma _{5}$ as constraints. In addition, several auxiliary objective functions can be considered to identify different solutions [19]. For example, the following objectives can be maximized:

• 1. Total profit (TP).

• 2. Annual true social welfare (ATSW) considering the actual production costs of the generation units.

• 3. Annual social welfare considering the strategic offer prices of the generation units.

• 4. Minus the payment of the demands.

• 5. Profit of a given producer.

• 6. Minus the payment of a given demand.

In this chapter, the first two objectives are selected because (i) they can be formulated linearly and (ii) they refer to general market measures. Thus, the auxiliary optimization problem to find multiple solutions is formulated as follows:

$$\begin{aligned}&\text {max TP or ATSW}\end{aligned}$$

(6.18a)

$$\begin{aligned}&\text {subject to the mixed-integer linear system} \ \varGamma _{1}-\varGamma _{5}.\ \end{aligned}$$

(6.18b)

The two linear objective functions selected, i.e., TP and ATSW, to be included in (6.18a) are described in the following two sections.

6.5.2.1 Objective Function (6.18a): TP Maximization

The summation of the MPEC’s objective function for all producers provides minus the total profit of all producers, but this expression is nonlinear due to the products of continuous variables (i.e., production quantities and clearing prices). An identical linearization approach to one presented in Chap. 5 is used to linearize these bilinear terms. For Illustrative Example 6.1 presented in Sect. 6.4, the following exact linear expression can be obtained as an equivalent for the total profit of strategic producers $g_{1}$ and $g_{2}$:

$$\begin{aligned} \mathrm{{TP}}&= 3530 \ \bigg .\bigg [ 35 \ p^\mathrm{{D}}_{n_{1} o_{1}} - 400 \ \mu ^{\mathrm{{D}}^\mathrm{{max}}}_{n_{1} o_{1}} - 400 \left( \mu ^{\mathrm{{F}}}_{n_{1} n_{2} o_{1}}+\mu ^{\mathrm{{F}}}_{n_{2} n_{1} o_{1}}\right) \nonumber \\&\quad -\pi \left( \mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{1} o_{1}}+\mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{1} o_{1}} +\mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{2} o_{1}}+\mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{2} o_{1}}\right) \nonumber \\&\quad - 12 \ p^\mathrm{{C}}_{g_{1} n_{1} o_{1}} - 10 \ p^\mathrm{{E}}_{g_{1} n_{1} o_{1}} -12 \ p^\mathrm{{C}}_{g_{2} n_{1} o_{1}} - 15 \ p^\mathrm{{E}}_{g_{2} n_{2} o_{1}}\bigg .\bigg ] \nonumber \\&\quad +5230 \ \bigg .\bigg [ 32 \ p^\mathrm{{D}}_{n_{1} o_{2}} - 320 \ \mu ^{\mathrm{{D}}^\mathrm{{max}}}_{n_{1} o_{2}} - 400 \left( \mu ^{\mathrm{{F}}}_{n_{1} n_{2} o_{2}}+\mu ^{\mathrm{{F}}}_{n_{2} n_{1} o_{2}}\right) \nonumber \\&\quad -\pi \left( \mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{1} o_{2}}+\mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{1} o_{2}} +\mu ^{\mathrm{{\theta }}^\mathrm{{min}}}_{n_{2} o_{2}}+\mu ^{\mathrm{{\theta }}^\mathrm{{max}}}_{n_{2} o_{2}}\right) \nonumber \\&\quad - 12 \ p^\mathrm{{C}}_{g_{1} n_{1} o_{2}} - 10 \ p^\mathrm{{E}}_{g_{1} n_{1} o_{2}} -12 \ p^\mathrm{{C}}_{g_{2} n_{1} o_{2}} - 15 \ p^\mathrm{{E}}_{g_{2} n_{2} o_{2}}\bigg .\bigg ] \nonumber \\&\quad -55000 \ x^\mathrm{{C}}_{g_{1} n_{1}} - 66000 \ x^\mathrm{{S}}_{g_{1} n_{2}} \ -55000 \ x^\mathrm{{C}}_{g_{2} n_{1}} - 66000 \ x^\mathrm{{S}}_{g_{2} n_{2}}. \ \end{aligned}$$

(6.19)

6.5.2.2 Objective Function (6.18a): ATSW Maximization

For Illustrative Example 6.1 presented in Sect. 6.4, the linear formulation of the ATSW to be included in (6.18a) is given by (6.20) below:

$$\begin{aligned} \mathrm{{ATSW}}&= 3530 \ \bigg [ 35 \ p^\mathrm{{D}}_{n_{1} o_{1}} -12 \ p^\mathrm{{C}}_{g_{1} n_{1} o_{1}}\ -10 \ p^\mathrm{{E}}_{g_{1} n_{1} o_{1}} -12 \ p^\mathrm{{C}}_{g_{2} n_{1} o_{1}}\ -15 \ p^\mathrm{{E}}_{g_{2} n_{2} o_{1}}\bigg ] \nonumber \\&\quad +5230 \ \bigg [ 32 \ p^\mathrm{{D}}_{n_{1} o_{2}} -12 \ p^\mathrm{{C}}_{g_{1} n_{1} o_{2}}\ -10 \ p^\mathrm{{E}}_{g_{1} n_{1} o_{2}} -12 \ p^\mathrm{{C}}_{g_{2} n_{1} o_{2}}\ -15 \ p^\mathrm{{E}}_{g_{2} n_{2} o_{2}}\bigg ]. \end{aligned}$$

(6.20)

Note that to formulate the ATSW in (6.20), instead of the strategic offers of the generating units, their true production costs are considered.

6.5.3 Ex-Post Algorithm for Detecting Nash Equilibria

In this section, we provide an ex-post algorithm [10] based on a single-iteration diagonalization approach, which is the next step after solving problem (6.18). This algorithm allows us to check whether each solution of problem (6.18) obtained is, in fact, a Nash equilibrium. Note that if under the diagonalization framework, no producer desires to deviate from its actual strategy, then the set of strategies of all producers satisfies the definition of a Nash equilibrium [16, 17].

Let us consider the duopoly introduced in Illustrative Example 6.1 in Sect. 6.4 with two strategic producers $g_{1}$ and $g_{2}$. The strategic decisions of producer $g_{1}$ include its investment decisions, i.e., $x^\mathrm{{C}}_{g_{1} n_{1}}$ and $x^\mathrm{{S}}_{g_{1} n_{2}}$, and its offering decisions, i.e., $\alpha ^\mathrm{{C}}_{g_{1} n_{1} o_{1}}$, $\alpha ^\mathrm{{E}}_{g_{1} n_{1} o_{1}}$, $\alpha ^\mathrm{{C}}_{g_{1} n_{1} o_{2}}$, and $\alpha ^\mathrm{{E}}_{g_{1} n_{1} o_{2}}$. We refer to these strategic decisions of producer $g_{1}$ as decision set $S_{g_{1}}$. A similar set can be defined including the strategic decisions of producer $g_{2}$, denoted by $S_{g_{2}}$. In order to verify that each solution obtained for problem (6.18) constitutes a Nash equilibrium, the following four steps are carried out:

• 1. Consider the mixed-integer linear form of MPEC 1 pertaining to producer $g_{1}$.

• 2. Set the investment decisions of producer $g_{2}$, i.e., $S_{g_{2}}$, to those obtained by the equilibrium model through solving problem (6.18). Then, solve MPEC 1. Note that its solution provides the strategic decisions of producer $g_{1}$, which we denote by $\widehat{S}_{g_{1}}$.

• 3. Repeat the two steps above for producer $g_{2}$ through solving MPEC 2, while strategic decisions $S_{g_{1}}$ are fixed to those values obtained from the equilibrium model. This step results in deriving the strategic decisions $\widehat{S}_{g_{2}}$ pertaining to producer $g_{2}$.

• 4. Compare the results obtained from the previous steps of the diagonalization algorithm, i.e., $\widehat{S}_{g_{1}}$ and $\widehat{S}_{g_{2}}$, with those achieved from the equilibrium model, i.e., $S_{g_{1}}$ and $S_{g_{2}}$. If the investment results of each strategic producer obtained from the single-iteration diagonalization algorithm are identical to those attained by the equilibrium model, i.e., $\widehat{S}_{g_{1}}$=$S_{g_{1}}$ and $\widehat{S}_{g_{2}}$=$S_{g_{2}}$, then such a solution is a Nash equilibrium because each producer cannot increase its profit by changing its strategy unilaterally.

6.5.4 Numerical Results

This section provides the numerical results corresponding to Illustrative Example 6.1 presented in Sect. 6.4. Table 6.1 presents the investment equilibrium results. Note that these results are obtained by solving the auxiliary optimization problem (6.18) considering two different terms as objective function (6.18a), i.e., (i) maximizing TP and (ii) maximizing ATSW. The GAMS code for solving this MILP problem maximizing TP is provided in Sect. 6.8. Note that all results reported in Table 6.1 are verified to be Nash equilibria through the ex-post algorithm provided in Sect. 6.5.3.

As described in Sect. 6.5.1.3, the equilibrium model is parameterized in dual variables $\eta ^{(6.8)}_{g_{1}}$, $\eta ^{(6.8)}_{g_{2}}$, $\eta ^{(6.11)}_{g_{1}}$, and $\eta ^{(6.11)}_{g_{2}}$, which makes it a linear problem. The value considered for those parameterized variables, i.e., $\eta ^{(6.8)}_{g_{1}}$, $\eta ^{(6.8)}_{g_{2}}$, $\eta ^{(6.11)}_{g_{1}}$, and $\eta ^{(6.11)}_{g_{2}}$, are equal to the weights of the corresponding operating conditions, that is, 3530, 3530, 5230, and 5230, respectively. We have checked a variety of values for those parameterized dual variables, e.g., half of those values considered, but the numerical results obtained do not change.

Table 6.1 Illustrative Example 6.1: production capacity investment equilibrium results

According to the results presented in Table 6.1, several observations can be made, as stated below:

• 1. In the TP maximization case, the strategic producers $g_{1}$ and $g_{2}$ invest in both conventional and stochastic units. However, the total capacity of newly built units (280 MW) is comparatively lower than that in the ATSW maximization case (400 MW).

• 2. As expected, the TP of producers $g_{1}$ and $g_{2}$ in the TP maximization case ($61.67 million) is comparatively higher than that in the ATSW maximization case ($58.06 million). However, the ATSW in the TP maximization case ($79.27 million) is comparatively lower than that in the ATSW maximization case ($84.46 million).

• 3. Since the stochastic units with zero offer prices lead to a higher ATSW, only those units are built in the ATSW maximization case.

Regarding the investment results for each producer in the TP maximization case, the new units can be built by each of the two producers. In other words, all new units (280 MW) may be built by producer $g_{1}$ or producer $g_{2}$. In addition, those units may be built by both producers, e.g., 80 MW conventional unit by producer $g_{1}$ and 200 MW stochastic unit by producer $g_{2}$. Therefore, several equilibrium points can be found in this case.

Regarding the investment results for each producer in the ATSW maximization case, the only possible equilibrium point is to invest in a 200-MW stochastic unit by each producer (i.e., 400 MW all together) since producers $g_{1}$ and $g_{2}$ cannot invest in such a unit with a capacity greater than 200 MW.

Regarding the LMPs obtained, as expected, at least one of the producers strategically offers at a price identical to the bid price of the demand. Therefore, the LMPs obtained in operation conditions $o_{1}$ and $o_{2}$ are $35 and $32/MWh, respectively. Note that in each condition, the LMPs at both nodes are the same since the transmission line is not congested.

6.6 Summary

This chapter provides a methodology to characterize generation investment equilibria in a pool-based network-constrained electricity market in which all producers behave strategically. To this end, the following steps are carried out:

 

Step (1):

The investment problem of each strategic producer is represented using a bilevel model, whose upper-level problem determines the optimal production investment (capacity and location) and the offer prices to maximize its profit, and whose several lower-level problems represent the clearing of the market for different operating conditions.

Step (2):

The single-producer bilevel models formulated in Step 1 are transformed into single-level MPECs by replacing the lower-level problems with their optimality conditions resulting from the primal–dual transformation. The resulting MPECs are continuous but nonlinear, due to the product of variables in the objective function and strong duality equalities.

Step (3):

The joint consideration of all producer MPECs, one per producer, constitutes an EPEC, whose solution identifies the market equilibria.

Step (4):

To identify EPEC solutions, the strong stationarity conditions associated with the EPEC, i.e., the strong stationarity conditions of all producer MPECs, are derived. To this end, each MPEC obtained in Step 2 is replaced by its KKT conditions. The set of resulting strong stationarity conditions of all MPECs, which are the strong stationarity conditions of the EPEC, is a collection of nonlinear systems of equalities and inequalities.

Step (5):

The strong stationarity conditions associated with the EPEC obtained in Step 4 are linearized without approximation through three procedures: (i) linearizing the complementarity conditions, (ii) parameterizing the resulting conditions in the dual variables corresponding to the strong duality equalities, and (iii) replacing the strong duality equalities with their equivalent complementarity conditions. This linearization results in a mixed-integer and linear system of equalities and inequalities characterizing the EPEC.

Step (6):

To explore multiple solutions, an auxiliary mixed-integer linear optimization problem is formulated, whose constraints are the mixed-integer linear conditions obtained in Step 5 and whose objective function is either a linear form of the total profit of all producers or a linear form of the annual true social welfare.

Step (7):

The auxiliary mixed-integer linear optimization problem formulated in Step 6 is solved and a number of solutions are obtained.

Step (8):

To detect Nash equilibria among the solutions achieved in Step 7, an ex-post algorithm based on a single-iteration diagonalization approach is provided. This algorithm checks whether each solution achieved in Step 7 is, in fact, a Nash equilibrium.

 

To validate numerically the methodology provided in this chapter, a two-node illustrative example with two strategic producers is examined and the equilibrium results obtained are reported and discussed.

6.7 End-of-Chapter Exercises

6.1

Reformulate the production capacity investment equilibrium model (6.1) to include several units per node and piecewise linear production costs.

6.2

Reformulate the production capacity investment equilibrium model (6.1) considering a multistage investment model instead of a static one.

6.3

Reformulate the production capacity investment equilibrium model (6.1) considering uncertainty in demand bid prices and investment costs of different technologies.

6.4

Solve Illustrative Example 6.1 presented in Sect. 6.4 considering the capacity of transmission line to be 200 MW (congested case) and then interpret the investment equilibrium results obtained.

6.5

Solve Illustrative Example 6.1 presented in Sect. 6.4 considering a single producer owning the entire production capacity portfolio (monopoly case) and then interpret the investment equilibrium results obtained.

6.6

Solve Illustrative Example 6.1 presented in Sect. 6.4 considering three strategic producers $f_{1}$, $f_{2}$, and $f_{3}$ (triopoly case), in which the capacity portfolio of each producer $f_{1}$ and $f_{3}$ is equal to half that of producer $g_{1}$ in the original example, while the capacity portfolio of producer $f_{2}$ is identical to that of producer $g_{2}$ is the original example. Then interpret the investment equilibrium results obtained.

6.7

Compare the investment equilibrium results obtained from the monopoly case (Exercise 6.5), the duopoly case (Illustrative Example 6.1 in Sect. 6.4), and the triopoly case (Exercise 6.6).

6.8 GAMS Code

This section provides the GAMS code for solving the MILP problem maximizing TP corresponding to Illustrative Example 6.1. Note that this code is written in a general form, and thus it is straightforward to adapt it to any investment equilibrium example.