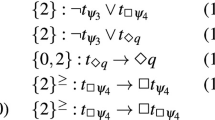Machine-Checked Proof-Theory for Propositional Modal Logics

Abstract

We describe how we machine-checked the admissibility of the standard structural rules of weakening, contraction and cut for multiset-based sequent calculi for the unimodal logics S4, S4.3 and K4De, as well as for the bimodal logic $\mathrm {S4C}$ recently investigated by Mints. Our proofs for both S4 and S4.3 appear to be new while our proof for $\mathrm {S4C}$ is different from that originally presented by Mints, and appears to avoid the complications he encountered. The paper is intended to be an overview of how to machine-check proof theory for readers with a good understanding of proof theory.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Sequent calculi provide a rigorous basis for meta-theoretic studies of various logics. The central theorem is cut-elimination/admissibility, which states that detours through lemmata can be avoided, since it can help to show many important logical properties like consistency, interpolation, and Beth definability. Cut-free sequent calculi are also used for automated deduction, for nonclassical extensions of logic programming, and for studying the connection between normalising lambda calculi and functional programming. Sequent calculi, and their extensions, therefore play an important role in logic and computation.

Meta-theoretic reasoning about sequent calculi is error-prone because it involves checking many combinatorial cases, with some being very difficult, but many being very similar. Invariably, authors resort to expressions like “the other cases are similar”, or “we omit details”. The literature contains many examples of meta-theoretic proofs with serious and subtle errors in the original pencil-and-paper proofs. For example, the cut-elimination theorem for the modal “provability logic” GL, where $\Box \varphi$ can be read as “$\varphi$ is provable in Peano Arithmetic”, has a long and chequered history which has only recently been resolved [11].

Here, we describe how we formalised cut-elimination for traditional, propositional, multiset-based sequent calculi without explicit structural rules for the propositional modal logics S4, S4.3, K4De and $\mathrm {S4C}$ using the interactive proof-assistant Isabelle/HOL. As far as we know, the proofs for S4 and S4.3 are new, and avoid the complexities of previous proofs for these logics. Our results also confirm the recent claim of cut-elimination for $\mathrm {S4C}$ due to Mints, although our proof is different, and avoids the complications he encountered in his proofs.

In Sect. 2.1, we briefly describe traditional sequent calculi, discuss the need for multisets, and describe the general form of our main theorems. In Sect. 2.2 we describe the modal logics we study. In Sect. 2.3 we give a brief overview of how interactive proof assistants work. In Sect. 3 we show how we encode formulae, sequents and rules, showing a sequent rule as an example. In Sect. 4 we describe how we encoded the notion of derivability, giving rise to what we call “implicit derivations”. In Sect. 4.4 we show how we encoded “explicit derivations” as concrete tree data structures, and the functions used to reason about them. In Sect. 5 we describe how we generalised the forms of our sequent rules to easily capture rule skeletons extended with arbitrary contexts which are essential to make weakening admissible. In Sect. 6 we describe how we encoded the properties of weakening, invertible of some rules, and contraction in Isabelle. In Sect. 7 we describe how we generalised our previous work on explicit derivations to facilitate inductive proof of properties (such as the admissibility of contraction or cut), and in Sect. 8 we describe this further specifically for cut-admissibility. In Sects. 9–12 we describe the cut-admissibility proofs for the specific logics S4, S4.3, K4De and S4C. The remaining sections discuss related work and conclude.

We assume the reader is familiar with basic proof-theory and higher-order logic, but assume that the reader is a novice in interactive proof assistants. Our Isabelle code can be found at http://users.cecs.anu.edu.au/~jeremy/isabelle/2005/seqms/. Some of this work was reported informally in [13] and also, more formally, in [6].

2 Preliminaries

2.1 Sequents Built from Multisets Versus Sets

Proof-theorists typically work with sequents $\Gamma \vdash \Delta$ where $\Gamma$ and $\Delta$ are “collections” of formulae. The “collections” found in the literature increase in complexity from simple sets for classical logic [8], to multisets for linear logic [9], to ordered lists for substructural logics [7], to complex tree structures for display logics [1]. A sequent rule typically has a rule name, a (finite) number of premises, a side-condition and a conclusion. Rules are read top-down as “if all the premises hold then the conclusion holds”. A derivation of the judgement $\Gamma \vdash \Delta$ is typically a finite tree of judgements with root $\Gamma \vdash \Delta$ where parents are obtained from children by “applying a rule”. We use “derivation” to refer to a proof within a calculus, reserving “proof” for a meta-theoretic proof of a theorem about the calculus.

Sequent calculi typically contain three structural rules called weakening, contraction and cut. These rules are bad for automated reasoning using backward proof-search since they can be applied at any time. Thus for backward proof-search, we are interested in sequent calculi which do not contain explicit rules for weakening, contraction and cut. The traditional way to design such calculi is to assume that sequents are built out of multisets, omit these rules from the calculus itself, and prove that each of these rules is admissible. That is, for each rule, we have to prove that the conclusion sequent is derivable if each of its premises are derivable. For example, our work does not regard the cut rules shown below as being part of the system:

Thus our results will be lemmata of the form: if $\Gamma \vdash A, \Delta$ is (cut-free) derivable and $\Gamma , A \vdash \Delta$ is (cut-free) derivable then $\Gamma \vdash \Delta$ is (cut-free) derivable.

2.2 Our Modal Logics

The sequent calculi we study are designed to reason about the meta-theory of the basic modal logics S4, S4.3, K4De (called GTD by Mints) and $\mathrm {S4C}$. Semantically, the first three are mono-modal logics characterised, respectively, by Kripke frames having: reflexive and transitive frames; reflexive, transitive and linear frames; and transitive and dense frames. The logic $\mathrm {S4C}$, called dynamic topological logic, is a bimodal logic where $\Box$ is captured by a reflexive and transitive binary relation $R_\Box$ and where $\circ$ is captured by a serial and discrete linear relation $R_\circ$ with an interaction between them of “confluency”:

$$ \begin{aligned} \forall x \forall y \forall z \exists u. R_\Box (x,y) \; \& \; R_\circ (x, z) \Rightarrow R_\circ (y,u) \; \& \; R_\Box (z, u). \end{aligned}$$

(1)

The Hilbert-calculi for these logics are obtained by extending a traditional Hilbert-calculus for classical propositional logic with the axioms and inference rules as shown below using the naming conventions given in Fig. 1:

Fig. 1

Various axioms and inference rules

 

Logic	Axioms	Rules
S4	K,$\Box \bot$,4,T	RN$\Box$
S4.3	K,$\Box \bot$,4,T,.3	RN$\Box$
K4De (GTD)	K,$\Box \bot$,4,De	RN$\Box$
$\mathrm {S4C}$	K,$\Box \bot$,K$_{\circ }$,T,4,C,$\circ \bot$	RN$\Box$, RN$\circ$

 

The modal logic $\mathrm {S4C}$ is designed to capture the basic logic for hybrid systems [4] where Eq. (1) captures the lower semi-continuity of the linear discrete relation with respect to the topological interpretation of the $\Box$-connective.

2.3 Interactive Proof Assistants

Interactive proof-assistants are now a mature technology for “formalising mathematics” [23]. They come in many different flavours as indicated by the names of some of the most popular ones Mizar, HOL, Coq, LEGO, NuPrl, NqThm, Isabelle, $\lambda$ -Prolog, HOL-Light, LF, ELF, Twelf, with apologies to those whose favourite proof-assistant we have omitted.

Most of the modern proof-assistants are implemented using a modern functional programming language such as ML, which was specifically designed for the implementation of, and interaction with, such proof-assistants.

The lowest levels typically implement a typed $\lambda$-calculus with hooks provided to allow the encoding of further logical notions such as equality of terms on top of this base implementation. The base implementation is usually very small, comprising of a few hundred lines of code, so that this code can be scrutinised by experts to ensure its correctness.

Almost all aspects of proof-checking eventually compile down to a type-checking problem using this small core, so that trust rests on strong typing and a well-scrutinised small core of (ML) code.

Most proof-assistants also allow the user to create a proof-transcript which can be cross-checked using other proof-assistants to guarantee correctness.

Fig. 2

Backward chaining in logical frameworks

Figure 2 shows how these logical frameworks typically work. Thus given some goal $\beta$ and an expression which claims that $\alpha$ is implied by the conjunction of $\beta _1$ up to $\beta _n$, the Isabelle engine pattern-matches $\alpha$ and $\beta$ to find a substitution $\theta$ such that $\alpha \theta = \beta$, and then reduces the original goal $\beta$ to the n subgoals $\beta _1\theta , \ldots , \beta _n\theta$ (note that n may be 0). We can then repeat this procedure on each $\beta _i \theta$ until all subgoals are proved (which requires that each final step produces no new subgoals, i.e., has $n = 0$). The pattern matching required is usually higher order unification. The important point is that the logical framework keeps track of sub-goals and the current proof state.

The syntax of the “basic propositions” such as $\alpha$, $\beta$ is defined via an “object logic”, which is a parameter. Different “object logics” can be invoked using the same logical-framework for the task at hand.

The logical properties of “;” such as associativity or commutativity, and properties of the “$\Longrightarrow$” such as classicality or linearity are determined by the “meta-logic”, which is usually fixed for the logical framework in question.

For example, the meta-logic of Isabelle [20] is higher-order typed intuitionistic logic with connectives $\Longrightarrow$ (implication), !! ($\forall$), $==$ (equality), and no negation, while the object-logic is classical higher-order logic (HOL) using $\longrightarrow$, ALL ($\forall$), $=$, EX ($\exists$), and $\sim$ (not) [10]. Unlike in classical first-order logic, which has terms and formulae, functions and predicates, in Isabelle’s meta-logic and in HOL we just have terms (where a formula is a term of type boolean), and functions (where a predicate is a function whose return type is boolean). Further, functions are themselves terms, of a function type, and “higher order” simply means that functions can accept other functions as arguments and can produce functions as results. This allows a uniform treatment of all these entities.

As noted, the meta-logic allows propositions such as $[\beta _1 ; \beta _2] \Longrightarrow \alpha$, which in fact is the pretty-printer’s rendering of $\beta _1 \Longrightarrow (\beta _2 \Longrightarrow \alpha )$. Think of this as meaning “from $\beta _1$ and $\beta _2$ one may infer $\alpha$”. Since the object-logic (HOL) contains the connectives & and $\longrightarrow$ with their usual classical semantics, we find that $\beta _1 \& \beta _2 \longrightarrow \alpha$ means the same (but in a classical rather than intuitionistic setting) as $\beta _1 \Longrightarrow (\beta _2 \Longrightarrow \alpha )$. But to direct Isabelle to actually use an inference to reduce $\alpha$ to $\beta _1 \theta , \ldots , \beta _n \theta$ as explained above, we need the first (meta-logical) form. Thus we shall see two logical syntaxes: $\Longrightarrow$, !! (and ; as explained above) for the Isabelle intuitionistic meta-level, and $\longrightarrow$, ALL, &, EX and $\sim$ for the classical HOL object-level. Together they are referred to as Isabelle/HOL [26].

3 A Deep Embedding of Formulae, Sequents and Rules

Recall that the meta-logic provides us with a method for backward chaining via expressions of the form (see Fig. 2):

$$[ \beta _1 \ ; \cdots \ ; \ \beta _n ] \Longrightarrow \alpha .$$

The usual method for obtaining the power for reasoning about sequent derivations is to use the full power of higher-order classical logic (HOL) to build the basic object-level propositions $\beta _i$.

Isabelle’s incarnation of HOL provides the usual connectives of logic such as conjunction, disjunction, implication, negation and the higher order quantifiers. But it also provides many powerful facilities allowing us to define new types, define functions which accept and return other functions as arguments, and even define infinite sets using inductive definitions [26].

For example, the following HOL expressions would capture the usual inductive definition of the set even_nat of even natural numbers by encoding the facts that “zero is even, and if n is even then so is $n + 2$”, where : stands for set membership $\in$:

Most proof-assistants will automatically generate an induction principle from a given inductive definition. For example, Isabelle will automatically generate the usual induction principle which states that we can prove a property P holds of all even naturals if we can show that P(0) holds and we can show that P(n) implies $P(n+2)$. An implicit assumption which facilitates such induction principles is that the inductive definitions are the only way to construct its members. Thus, if m is an even natural, then it is either 0, or is of the form $n + 2$ for some (“smaller”) even natural n. Together, they form the base case and the inductive step of an inductive definition that defines the set even_nat as the smallest set of terms $0, 0 + 2, 0 + 2 + 2, \ldots$. It is implicit in these definitions that an inference step such as $\mathtt {n : even\_nat} \Longrightarrow \mathtt {n + 2 : even\_nat}$ may be applied only finitely many times.

We previously said that we shall see two syntaxes: a meta-level intuitionistic logic and an object-level classical HOL syntax. Since we wish to reason about sequent calculi for modal logics, we now need to encode a third logical syntax: namely the syntax of modal sequents.

To encode sequent calculus into HOL we first encode terms for capturing the grammar for recognising formulae as below where comments are enclosed in (* and *):

We use three type constructors FC, FV and PP which encode, respectively, formula connectives, formula variables, and atomic formulae (primitive propositions) as HOL terms. Each of them takes one string argument which is simply the string we want to use for that construction. The formula connective constructor FC also accepts a list of formulae, which constitute its subformulae. For example, the term FC “&&” [FV “A”, PP “q”] encodes $A\; \wedge \; q$ where we use “&&” as the string for conjunction of classical logic. Since we want to encode modal logics, we require only the classical connectives, plus three unary modalities FC “Box” [.] for $\Box .$ and FC “Dia” [.] for $\lozenge .$ and FC “Circ” [.] for $\circ$.

Isabelle’s HOL allows us to form sets and multisets of objects of an arbitrary type, so the HOL expressions formula set and formula multiset capture the types of modal formula sets and modal formula multisets.

Using these types we can build a sequent type using a constructor Sequent:

Here ’a is a type variable and the datatype ’a sequent demands that the constructor Sequent is followed by two multisets of items of type ’a. For example, the datatype formula sequent would require our sequents to be constructed out of multisets of formulae (of type formula). An alternative infix notation for the constructor Sequent is $\vdash$ or |-.

We define the type for our sequent rules by the type definition:

Such a sequent rule is a pair (ps, c) of a list of items ps (the premises) and a single item c (the conclusion): the items are of some type ’a which is a parameter. We shall instantiate the type variable ’a with the type formula sequent to obtain sequents built from two multisets of modal formulae.

Note that in common parlance we may say that (ps, c) is a rule meaning that ps and c may be instantiated in any way. Such a “rule” is a schema which can be instantiated to give infinitely many rule instances. When describing the Isabelle implementation we may refer to a specific pair (ps, c) as a “rule”, although in the context of logical rules, this could be better described as a specific instance of a rule schema; where we describe our Isabelle theorems involving “sets of rules”, these will usually be the infinite sets of instances of a finite set of rule schemata.

Thus, we can use the HOL type-declaration below to declare that rls is a set of sequent rules, where each element of rls is a pair (ps, c) whose first component ps is a list of its premise sequents, and whose second component c is its conclusion sequent:

Each sequent consists of two multisets of items of type formula, and inductively define the set rls by giving a finite collection of rule schemata, each denoting an infinite set of instances, which belong to this set. For example, the traditional rule $(\vdash \wedge )$ for introducing a conjunction into the right hand side of a sequent, as shown below, can be given by the encoding below it where we use the string && to encode $\wedge$, “+” for multiset union, and {#A#} to denote a singleton multiset:

$$ \mathtt {(\;[\; G \vdash \texttt {\{}\texttt {\#}A \texttt {\#}\texttt {\}}+ D \ , \ G \vdash \texttt {\{}\texttt {\#}B \texttt {\#}\texttt {\}}+ D \;], \ \ G \vdash \texttt {\{}\texttt {\#}A \; \& \& \; B\texttt {\#}\texttt {\}}+ D \;\; ) \in rls} $$

When this clause appears in the definition of rls, it means that this sequent rule is in rls for each possible value of A, B, G, D of the appropriate type.

Having encoded the notions of formulae and sequents into HOL, we are now in a position to encode the notion of derivability and derivations. As we shall explain shortly, the notion of derivability and derivations are subtly different in the following senses:

Derivability :

we write inductively defined predicates in HOL to capture the set of sequents derivable from a given, possibly empty, set of potential leaf sequents, using a given set of rules defined using the encoding of formulae and sequents described above. The base case will capture that every given leaf is vacuously derivable, and the inductive case will capture that a sequent c is derivable if the rule set contains a rule (ps, c) where each of the premises in ps is itself derivable. We do not construct an actual derivation, as such, but just ensure that there exists a sequence of sequent rule applications which can take us from the given leaf sequents to the given end-sequent. We therefore use the word “implicit” to describe such derivations.

Derivation (trees):

we create a new object type called dertree which will allow us to encode an explicit tree as a HOL term to represent an actual derivation of the given sequent from the given leaves using the given set of rules. We therefore use the word “explicit” to describe such derivations.

4 Implicit and Explicit Derivations

In Sect. 4.1, we give an inductively defined predicate derrec for capturing the set of all recursively derivable sequents. In Sect. 4.2, we describe the principle of induction that is automatically generated by Isabelle/HOL from derrec and describe how it can be used to prove an arbitrary property P of such sequents. In Sect. 4.3, we describe our other implicit derivability predicates in less detail. In Sect. 4.4 we describe how we encoded explicit derivation trees. In Sect. 4.5 we describe how we can move to and fro between these two notions.

4.1 Defining Derivability (Implicitly) in Isabelle

We are now in a position to encode the set $\texttt {derrec}$ of “recursively derivable sequents” given a set plvs of (potential) leaf sequents and a given set rls of sequent rules. The set derrec rls plvs is defined inductively as shown below (the Isabelle code is precisely as it appears in the Isabelle theory file). It defines simultaneously the predicates derrec (that a single sequent is derivable) and dersrec (that all sequents in a list are derivable).

Definition 4.1

(derrec, dersrec) derrec rls plvs is the set of end-sequents which are derivable from the set plvs of potential leaves using the set rls of sequent rules.

dersrec rls plvs is the set of lists of endsequents which are all derivable from potential leaves plvs using sequent rules rls:

We now explain the Isabelle code and why it achieves the meanings for derrec and dersrec given in the definition. These are two mutually inductively defined sets each of which depends on the other. The type declarations mean that where plvs is a set of (potential) leaf sequents and rls is a set of “rules”, instances of (premise list, conclusion) pairs, then derrec rls plvs is a set of sequents. A sequent is in derrec rls plvs if and only if finite repeated application of the clauses of the definition require it to be, and likewise dersrec rls plvs. We now describe the four clauses, each of which is preceded by its name:

 

dpI :

The base case of the inductive definition of $\texttt {derrec}$ captures that each initial sequent eseq from $\mathtt {\mathtt {plvs}}$ is itself (vacuously) derivable from the initial leaf set $\mathtt {\mathtt {plvs}}$ using the rules $\mathtt {}\texttt {rls}$. The : stands for set membership $\in$.

derI :

If (ps, eseq) is the list of premises and the conclusion of a rule, and the premise list ps satisfies dersrec rls plvs, meaning that the premises ps are all derivable (see below), then the conclusion eseq is derivable.

dlNil :

An empty list of sequents satisfies dersrec rls plvs

dlCons :

If seq satisfies derrec rls plvs and the list seqs satisfies dersrec rls plvs then the list seq # seqs satisfies dersrec rls plvs. The symbol # denotes appending an item seq to the front of a list seqs to form a longer list.

Note that the clauses dlNil and dlCons give us that a list is in dersrec rls plvs if all its members are in derrec rls plvs; and since these clauses give all members of dersrec rls plvs, this “if” is in fact “if and only if”.

In fact the actual Isabelle/HOL code is more general, in that the things being derived are of a parametric type ’a and need not be sequents, but could be formulae or other constructs, and a “rule” merely consists of a list of “premises” and a “conclusion”. We describe it in terms of sequents, here, merely to place it in the context of our cut-admissibility proofs.

4.2 Inductive Proofs via Automated Inductive Principles

We use inductive definitions because correct induction principles are generated automatically by Isabelle from the inductive definition of $\texttt {derrec}$. A heavily simplified version of the induction principle automatically generated for proving an arbitrary property $\mathtt {P}$ by the definition of the inductive set derrec is shown below using meta-level intuitionistic connectives (==> , !!, ;) and object-level classical HOL connectives (ALL, - -> , :).

An explanation is:

• 1 for all sequents x and all properties P

• 2 if x is derivable from (potential) leaves $\mathtt {plvs}$ using rules $\mathtt {rls}$, and

• 3 P holds for every sequent c in $\mathtt {plvs}$, and

• 4 for each rule (ps, c), P of each premise in ps implies P of its conclusion c,

• 5 then P holds of x

We can visualise this induction principle as below where we replace the meta-level ==> by a horizontal line and replace the meta-level ; with juxtaposition of premises and replace : by set membership $\in$:

$$ \frac{x \in derrec\ rls\ plvs \quad \forall c \in plvs. P\ c \quad \forall (ps, c) \in rls. (\forall p\ in\ ps. P\ p) \Rightarrow P\ c}{P\ x} $$

This is an induction principle which we use often in proof-theory: prove that some property holds of the leaves of a derivation, and prove that the property is preserved from the premises to the conclusion of each rule. For example, consider the standard translation from sequents of LK to formulae given by $\tau (A_1, \ldots , A_n \vdash B_1, \ldots , B_m) = A_1 \wedge \cdots \wedge A_n \rightarrow B_1 \vee \cdots \vee B_m$. We typically use this translation to argue that all derivable sequents are valid in the semantics of first-order logic. The proof proceeds by showing that the translation of the leaves of a derivation are all valid, and showing that if the translations of the premises are valid then the translations of the conclusion are valid, for every rule. Note that no explicit derivation is created by this induction principle since it uses derivability (implicit derivations).

Thus this induction principle is really a lemma, but our formal encoding of it requires one more definition.

Definition 4.2

For all sets A and all unary predicates P, the property Ball A P holds iff every member x of A satisfies P:

The following is the formal inductive principle described informally above which is generated by Isabelle/HOL, automatically, using “?” to show arguments that are implicitly universally quantified.

Lemma 4.1

(derrec-induction) For every sequent x, every rule set rls, every list of leaves plvs, and every property P, if

• (a) x is derivable from potential leaves plvs using the rules in rls, and

• (b) every sequent c in plvs obeys P, and

• (c) for every sequent c and premise list ps if (ps, c) is a rule in rls, and each premise in ps is derivable from potential leaves plvs using rules in rls and every premise from ps obeys P then c obeys P

then x obeys P:

Proof

Isabelle automatically generates an induction principle (not shown) from the definition of derrec. Since the definition also involves defining dersrec (which expresses that a list of items are all derivable), the automatically generated principle involves a property $P_1$ of derivable sequents and a property $P_2$ of lists of derivable sequents. Naturally we choose property $P_2$ of a list to be that all members of the list satisfy $P_1$. That instantiation gives us the lemma.    $\blacksquare$

Intuitively, Isabelle converts object-level classical implications $(\longrightarrow )$ into meta-level intuitionistic implications (==> ), allowing us to use the lemma itself for sub-goaling.

Using these inductive principles we proved the following lemma about derivability using Isabelle, where the question marks indicate free-variables which are implicitly universally quantified:

Lemma 4.2

If each premise in ps is derivable from leaves $\mathtt {plvs}$ using rules $\mathtt {rls}$, and eseq is derivable from ps using $\mathtt {rls}$, then eseq is derivable from $\mathtt {plvs}$ using $\mathtt {rls}$:

$$\begin{aligned} \nonumber [| \mathtt {?ps \subseteq derrec~?\mathtt {rls}~?\mathtt {plvs}\ ; \ ?eseq}\,&\mathtt {\in derrec~?\mathtt {rls}~?ps} |] \\&\Longrightarrow \mathtt { ?eseq \in derrec~?\mathtt {rls}~?\mathtt {plvs}} \end{aligned}$$

4.3 Further Implicit Derivability Predicates

We briefly describe the remaining functions we used to describe derivability.

Definition 4.3

(derivable rule) For a list of sequents lvs and a sequent eseq, (lvs, eseq) is a derivable rule with respect to the rule set rls if we can construct an implicit derivation using rules in rls whose leaves are exactly the sequents lvs (in the same order), and whose endsequent is eseq.

We formalise this notion using functions derl (for the derivable rules) and dersl (an auxiliary function).

Definition 4.4

(derl, dersl) For a list of sequents lvs and a sequent eseq, the pair (lvs, eseq) is in derl rls if it is a derivable rule with respect to rls.

For lists of sequents lvs and eseqs, the pair (lvs, eseqs) is in dersl rls if there is a sequence of rule instances from rls which take us from (exactly) the list of leaf sequents lvs to the list of endsequents eseqs. We envisage a number of implicit derivations drawn side-by-side, whose endsequents are the members of the list eseqs.

This formalises the notion of a derivable rule: derl rls is the set of derivable rules with respect to rls.

Where an inference rule ’a psc is a list of premises ps and a conclusion c, a “derived rule” is of the same type. We define derl rls to be the set of rules derivable from the rule set rls. This, like derrec, was defined as an inductive set. So $\mathtt {(lvs, eseq) \in \texttt {derl}\ \texttt {rls}}$ reflects the shape of an implicit derivation tree: lvs is a list of exactly the leaves used, in the correct order, whereas $\mathtt {eseq \in \texttt {derrec}\ \texttt {rls}\ plvs}$ holds even if the set of (potential) leaves plvs contains extra sequents.

We note that the definition means that $([c], c) \in$ derl rls: that is, the “trivial” derived rules are included. To define derl rls to exclude the “trivial” derived rules would complicate results such as Theorem 4.1.

The formal Isabelle definitions of derl used also the function dersl, which represents several implicit derivation trees side-by-side:

$\mathtt {(lvss, eseqs) \in dersl~rls}$ when the list lvss is the concatenation of their lists of leaves, and eseqs is the list of their endsequents.

Theorem 4.1

With respect to some given set of rules rls:

• (a) the items derivable from a set plvs of leaves are the items derivable from the set of sequents derivable from plvs:

  

• (b) derivability (whether defined using derrec or derl) using the set of derived rules is equivalent to derivability using the original set of rules:

  

Finally, we can define the notion of an admissible rule.

Definition 4.5

(admissible, adm) A rule (ps, c) is admissible with respect to a rule set rls if, assuming its premises (leaves) ps are derivable from the empty set $\{\}$ of leaves using rules from rls, then so is its conclusion (endsequent) c:

Using Definition 4.5 we obtained the following four results, which were surprisingly tricky since adm is not monotonic in its argument rls, where <= encodes $\subseteq$.

Theorem 4.2

With respect to some given set of rules rls:

• (a) every derivable rule is admissible;

• (b) the admissible rules are closed under admissibility;

• (c) the admissible rules are closed under admissibility after derivability;

• (d) the admissible rules are closed under derivability.

4.4 Explicit Derivation Trees: A Deep Embedding of Derivations

The main advantage of the method outlined in the previous section was that there was no concrete representation of a derivation. That is, we relied on the proof-assistant to perform pattern-matching and rule instantiations in an appropriate way, so that all we needed was to capture the idea that derivations began with leaves and ended with a single end-sequent.

When we reason about cut-elimination, often we are required to perform transformations on explicit derivations. We therefore need a representation of such trees inside our encoding. In previous work [6], we described such an encoding using the following datatype:

The declaration states that a derivation tree can either be an Unfinished (unproved) leaf sequent built using the constructor Unf, or it can be a pair (seq, dts) consisting of a conclusion sequent seq and a list dts of (sub-)derivation trees bound together using the constructor Der.

Definition 4.6

Given an object dt of type dertree, conclDT dt returns the first argument of the constructors Der and Unf as the conclusion (endsequent) of dt.

For a tree dt which is not an Unfinished leaf, nextUp dt returns the list of trees whose conclusions are the premises of the last rule of dt, and botRule dt returns the bottom rule (premise list and conclusion) of dt.

Here, map conclDT dts applies conclDT to each member of the list dts of derivation trees and hence returns the premises of the bottom rule.

Our use of dertee can be seen as an even deeper embedding of proof-theory into Isabelle/HOL since it utilises the proof-assistant to describe an explicit derivation rather than the implicit existence of such a derivation as encoded by our derivability predicates from the previous section.

4.5 To and Fro Between Explicit and Implicit Derivations

Omitting details now, suppose we define valid rls dt to hold when derivation tree dt correctly uses rules from rls only and has no Unfinished leaves: that is, the leaves of dt are all instances of the conclusions of rules which have no premises (i.e., such as $\Gamma , A \vdash A, \Delta$). We linked our two approaches for specifying the derivable sequents by proving:

Lemma 4.3

If derivation tree dt is valid w.r.t. the rules $\mathtt {rls}$ then its endsequent is (implicitly) derivable from the empty set of leaves using $\mathtt {rls}$:

Lemma 4.4

If the end-sequent eseq is (implicitly) derivable from the empty set $\{\}$ of leaves using rules $\mathtt {rls}$ then there exists an explicit derivation tree dt which is valid w.r.t. $\mathtt {rls}$, whose end-sequent is eseq:

Thus we now know that the implicit derivations captured by our derivability predicate $\texttt {derrec}$ can be faithfully captured using the deeper embedding using explicit dertree derivation trees. Indeed, the lemmas allow us to move freely between the two embeddings at will to omit or include details as required [6].

5 Subformula Relation, Rule Skeletons and Extensions with Contexts

Our generalised definition of formulae allows a single definition of the immediate (proper) subformula relation, ipsubfml, which will not need to be changed when new connectives are added.

Definition 5.1

If a formula P is in the set obtained from the list of formulae Ps then P is a proper subformula of any larger formula FC conn Ps created using a formula-connective conn and Ps:

For example, (f, Box f) : ipsubfml because Box f is the abbreviation Box f == FC “Box” [f] where conn is the string “Box” and Ps is the formula-list [f].

In Sect. 3 we showed that the traditional $\wedge R$ rule from LK could be encoded as below using a sequent consisting of a pair $(\Gamma ,\Delta )$ of multisets of formulae, written $\Gamma \vdash \Delta$, where multiset braces are written as {# and #} and multiset union is written as +:

$$ \mathtt {(\;[\; G \vdash \texttt {\{}\texttt {\#}A \texttt {\#}\texttt {\}}+ D \ , \ G \vdash \texttt {\{}\texttt {\#}B \texttt {\#}\texttt {\}}+ D \;], \ \ G \vdash \texttt {\{}\texttt {\#}A \; \& \& \; B\texttt {\#}\texttt {\}}+ D \;\; ) \in \mathtt {rls}} $$

The essence of the rule is more succinctly described by the rule skeleton $\mathcal R_s$ shown below left. We now describe how we can uniformly extend $\mathcal R_s$ with the context $X \vdash Y$ to obtain the extended rule $\mathcal R_e$ shown below at right:

$$ \mathcal R_s = \frac{\vdash A \quad \vdash B}{\vdash A \wedge B} \qquad \qquad \mathcal R_e = \frac{X \vdash Y, A \quad X \vdash Y, B}{X \vdash Y, A \wedge B} $$

Definition 5.2

If the sequent seqXY is the pair (X, Y), representing the sequent $X \vdash Y$, and the sequent seqUV is the pair (U, V), representing the sequent $U \vdash V$, then extend seqUV seqXY is the sequent (X+U, Y+V), representing the sequent $X, U \vdash Y, V$ since seqXY + seqUV is (X+U, Y+V) by the pointwise extension of + to pairs of multisets and the function pscmap allows us to modify a rule (ps, c) by applying an arbitrary function f to each of its components:

We can now take a set rules of rule skeletons and produce their uniform extension with arbitrary context flr (for “formulae left and right”) representing $X \vdash Y$.

Definition 5.3

(extrs) Given a rule set rules, the inductively defined set extrs rules is the set of rules consisting of all uniform extensions of all rules in rules:

For example, we can now use functions extend and pscmap so that

$$\begin{aligned}&\texttt {extend}\ (X \vdash Y)\ (U \vdash V) = (X + U) \vdash (Y + V) \\&\qquad \mathcal R_e = \texttt {pscmap}\ (\texttt {extend}\ (X \vdash Y))\ \mathcal R_s \end{aligned}$$

Thus pscmap uniformly extends the skeleton provided by $\mathcal R_s$ with arbitrary contexts X and Y on respective sides to encode $\mathcal R_e$ using multiset addition $+$. So extrs S means the set of all such extensions of all rules in the set S.

Then we define lksss, the set of rules for Gentzen’s LK; we show just a selection. The rules below are the (skeletons of some of the) traditional invertible logical introduction rules from LK (without any context):

$$ ~ \frac{\vdash A \quad \vdash B}{\vdash A \wedge B } \quad ~ \frac{\vdash A, B}{\vdash A \vee B } \quad ~ \frac{B \vdash \quad \vdash A}{A \rightarrow B \vdash } \quad ~ \frac{A, B \vdash }{A \wedge B \vdash } \quad ~ \frac{A \vdash \quad B \vdash }{A \vee B \vdash } \quad ~ \frac{A \vdash B}{\vdash A \rightarrow B } ~ $$

Using && for $\wedge$, v for $\vee$ and - - for $\lnot$, we can encode the logical introduction rules as shown below, to obtain the set lksir of LK right introduction rule skeletons, where {#} rather than {##} is the empty-multiset:

Definition 5.4

(lksir) lksir is the set of right logical introduction rules, in the form without any context and using the form which is invertible, as shown above.

Similar rules lksil (not shown) give the skeletons of the traditional invertible rules for left-introduction. By adding the initial sequent “axiom” $A \vdash A$ with an empty list [] of premises below we obtain the set of “unextended” rules lksne for LK:

Definition 5.5

(lksne) lksne is the set of rules, not extended by any arbitrary context, without structural rules, for LK.

We can now form the full extended set lksss of rules for LK, by extending each rule skeleton psc from lksne by an arbitrary pair (X, Y) of contexts flr (for formulae left and right) regarded as a sequent $X \vdash Y$:

Definition 5.6

(lksss) lksss is the set of rules, extended by arbitrary contexts, without structural rules, for LK.

Now, we can encode the skeleton shown below right of the traditional K-rule shown below left:

Definition 5.7

(SK) SK is the set of instances of the skeleton of the K rule of modal logic

Note that X is a multiset, and $\Box X$ is informal notation for applying $\Box$ to each member of X; this is implemented using mset_map, used in the encoded SK rule. Using a similar notation we write $\Box B^k$ for $(\Box B)^k$, the multiset containing n copies of $\Box B$. Development of mset_map and relevant lemmas is in the source files Multiset_no_le.{thy,ML}.

By extending the skeletons of the LK rules and extending only the conclusion of the skeleton (SK) of the K rule above, we could obtain an encoding of the traditional sequent calculus for the modal logic K:

Since we actually handle more complex logics, but not K as such, we have not made this a formal definition.

Note that most of these definitions use the Isabelle feature for inductively defined sets, even though many of them are not actually inductive (i.e., recursive). We do this because Isabelle automatically generates useful theorems for them, including rules which help us prove or use an expression such as rl : lksne.

6 The Weakening, Inversion and Contraction Properties

We now encode the weakening, inversion and contraction as properties.

Definition 6.1

A set rls of rules satisfies the weakening admissibility property if, whenever a sequent $X \vdash Y$ is derivable, any larger sequent $(X \vdash Y) + (U \vdash V) = (X, U \vdash Y, V)$ is derivable:

Here, the variable rls is forced to be a set of sequent rules by the type of wk_adm, and thence the variables XY and UV will be forced to be of type sequent by the typing restrictions on the inputs to derrec.

Definition 6.2

(inv_rl) A rule (ps, c) is invertible with respect to a set rls of rules if, whenever c is derivable using rls, so is every member of ps:

Here, the definition of dersrec hides a universal quantifier over the members of the list ps: see Definition 4.1.

To encode contraction, we utilise an axiomatic type class for sequents, described in more detail elsewhere [6]. Thus we can write $(A \vdash 0) + (A \vdash 0) \le (X \vdash Y)$ to mean that the multiset X contains at least two copies of A and write $(X \vdash Y) - (A \vdash 0)$ for the sequent obtained by deleting one of these copies from X. Similarly we can write $(0 \vdash A) + (0 \vdash A) \le (X \vdash Y)$ to mean that the multiset Y contains at least two copies of A and write $(X \vdash Y) - (0 \vdash A)$ for the sequent obtained by deleting one of these copies from Y. More generally, we can write $UV + UV \le XY$ to assert that the sequent $XY - UV$ can be obtained from XY by contracting the contents of the sequent UV. Thus, if the multiset of all formulae in UV (on both sides) is the singleton multiset {#A#} we know that the skeleton of the relevant contraction rule is one of:

$$\frac{A,A \vdash }{A \vdash } \quad \quad \frac{\vdash A,A}{\vdash A}$$

Definition 6.3

A set rls of rules satisfies the contraction admissibility property for the formula A if, whenever a derivable sequent $X \vdash Y$ satisfies $(A \vdash 0) + (A \vdash 0) \le (X \vdash Y)$, the sequent $(X \vdash Y) - (A \vdash 0)$ is derivable, and likewise for $0 \vdash A$.

The first condition ms_of_seq As = {#?A#}, asserts that the formulae on both sides of the sequent As form the singleton multiset {#?A#}, thus capturing that the contraction can happen on either side of the turnstile.

7 Generalising Cut-Admissibility Proofs

We now show how our previous work [6] on multicut admissibility for LK can be formulated to make it as general as possible. We first give details of induction principles and lemmata for “structural” induction over implicit derivations obtained via our derivability predicates and then describe their analogues for explicit derivation trees.

7.1 A General Framework for Reasoning About Implicit Derivations

The initial sequents of our sequent calculi will be allowed to apply to arbitrary formulae, not only atoms, and this excludes the possibility of proving height-preserving invertibility. This, and also the form of our contraction rule, which allows just one contraction per derivation step, prevents us from proving a height-preserving contraction-admissibility result. For proofs of contraction-admissibility, without height-preservation, an induction principle which also involves the size or structure of the relevant formula is required. Furthermore, proving cut-admissibility requires induction on both size of formula and derivation height (or a proxy for it). We therefore require a double induction on height (or proxy) and formula size (as measured by any well-founded subformula relation).

Our first induction principle could be seen as using a lexicographic ordering (n, m) where n is the sub-formula relation and m is the (inverse of the) distance from the end-sequent in the original derivation.

We use a relation sub on formulae: it could be any relation on formulae, but we use the (immediate) sub-formula relation. To put our general results in context, we may refer to sub as a “sub-formula relation”. In general we want sub to be well-founded; more generally our theorems will apply to the “well-founded part” of sub.

In regard to the height measure, or distance from the original end-sequent, our first induction principle, instead of assuming that a property holds for all derivations of lesser height, merely assumes that it holds for sub-derivations.

Definition 7.1

(wfp) For a binary relation sub, a formula A is in wfp sub, the “well-founded part” of sub, iff there is not any infinite descending chain $\ldots , A_2, A_1, A$ such that $(A_1, A), (A_2, A_1), \ldots$ are all in sub.

Definition 7.2

(gen_step) For a formula A, a property P, a subformula relation sub, a set of sequents derivs, and a particular rule r = (ps, c), where ps is a list of premises and c is the conclusion of r:  

gen_step P A sub derivs r :

means

If:

(a):

forall A’ such that (A’, A) $\in$ sub and all sequents s $\in$ derivs the property P A’ s holds, and

(b):

for every premise p $\in$ ps both p $\in$ derivs and P A p holds, and

(c):

c $\in$ derivs

then:

P A c holds.

In this text, ALL p : set ps means $\forall p \in ps$. Typically derivs will be the set of sequents derivable using a given set rls of rules, and a given set of leaves plvs, so derivs = derrec rls plvs.

Intuitively, given a fixed rule r = (ps, c), a fixed formula A, a fixed property P and a fixed relation sub, Definition 7.2(a) formalises for any derivable sequent s that (A, c) is “less than” (A’, s) if (A’, A) $\in$ sub. Definition 7.2(b) formalises for any premise p from ps that (A, p) is “less than” (A, c) if p is a premise of c in the rule r. Thus, it can be seen as a particular instance of a lexicographic ordering on formula-sequent pairs where $(A_1, s_1)$ is “less than” $(A_2, s_2)$ if $(A_1, A_2) \in \mathtt {sub}$ or, if $A_1 = A_2$ and $s_2$ is a premise of c via the particular rule (instance) $r = (ps, c)$.

Alternatively, by Definition 7.2, gen_step describes the situation where if a property P is true generally for sub-formulae $A'$, and for the premises of a particular rule then the property holds for the conclusion of that rule.

The main theorem, named gen_step_lem and given as Theorem 7.1 below, states that if this step case can be proved for all possible rule instances then P holds for all cases.

Theorem 7.1

(gen_step_lem)  For a formula A, a property P, a subformula relation sub, a sequent S and a set of rules rls: If

• (a) A is in the well-founded part of the subformula relation sub, and

• (b) for all formulae A’ and all rules r in rls, the induction step condition gen_step P A’ sub (derrec rls {}) r holds, and

• (c) sequent S is rls-derivable

then P A S holds.

Proof

We combine the principle of well-founded induction, applied to the formula A and the well-founded subfomula relation sub, with the induction principle derrec-induction for derrec shown as Lemma 4.1, which is provided by Isabelle as a consequence of the inductive definition of derrec.   $\blacksquare$

7.2 Induction for Two-Premise Subtrees

We now turn to the induction principle used for deriving cut-admissibility, or indeed any property P of two-premise implicit derivations. In the diagram below, to prove P (c l, c r), for example, to prove that a cut between c l and c r is admissible, the induction assumption is that $P (psl_i, c{r})$ and $P (c{l}, psr_j)$ hold for all i and j:

A proof of P (cl, cr) using this induction assumption inevitably proceeds according to what the rules $\rho _l$ and $\rho _r$ are, and further, for a cut-formula A, whether it is principal in either or both of $\rho _l$ and $\rho _r$. But our proofs also use induction on the size of the cut-formula, or, more generally, on some well-founded relation on formulae. So we actually consider a property $P\ A\ (cl, cr)$ where A is the cut-formula, psl are the premises $psl_{1} \ldots psl_{n}$ of rule $\rho _l$, and cl is its conclusion, and analogously for $\rho _r$ and cr. In proving $P\ A\ (cl, cr)$, in addition to the inductive assumption above, we assume that $P\ A' \ (da, db)$ holds generally for $(A', A) \in \mathtt {sub}$ and all sequents da and db which are “rls-derivable”, i.e., derivable from the empty set of leaves using rules from rls. These intuitions give the following definition gen_step2sr of a condition which permits one step of the inductive proof:

Definition 7.3

(gen_step2sr) For a formula A, a property P, a subformula relation sub, a set of rules rls, sequent rules (psl, cl), and (psr, cr): gen_step2sr P A sub rls ((psl, cl), (psr, cr)) means:

If

• (a) P A’ (da, db) holds for all subformulae A’ of A and all rls-derivable sequents da and db, and

• (b) for each premise pa in psl, pa is rls-derivable and P A (pa, cr) holds, and

• (c) for each premise pb in psr, pb is rls-derivable and P A (cl, pb) holds, and

• (d) cl and cr are rls-derivable,

then P A (cl, cr) holds.

The main theorem gen_step2sr_lem below for proving an arbitrary property P states that if the step of the inductive proof goes through in all cases, i.e., for all possible final rule instances $\rho _l = (psl, cl)$ on the left and $\rho _r = (psr, cr)$ on the right, then P holds for all formulae A and sequents cl and cr on the left and right respectively.

Theorem 7.2

(gen_step2sr_lem) If A is in the well-founded part of the subformula relation; sequents seql and seqr are rls-derivable ; and for all formulae A’, and all rules (psl, cl) and (psr, cr), our induction step condition gen_step2sr P A’ sub rls ((psl, cl), (psr, cr)) holds, then P A (seql, seqr) also holds.

Proof

As with Lemma 7.1, the proof of this involves combining induction principles available to us. It is more complex than Lemma 7.1 because we had to deal with the well-founded induction on the sub-formula relation and derrec-induction (Lemma 4.1) on the two implicit derivations which provide the two premises of the cut.   $\blacksquare$

This enables us to split up an inductive proof, by showing, separately, that gen_step2sr holds for particular cases of the final rules (psl, cl) and (psr, cr) on each side. In some cases these results apply generally to different calculi.

For example, the inductive step for the case where the cut-formula A is parametric, not principal, on the left is encapsulated in the following theorem where prop2 car ?erls ?A (?cl, ?cr), which is equivalent to (?cl, ?cr) : car ?erls ?A, means that the conclusion of a cut on A with premises cl and cr is derivable using rules erls. Below, :# stands for membership of a multiset, and ˜ stands for classical negation, and wk_adm refers to weakening admissibility for a system of rules, defined formally in Definition 6.1.

Theorem 7.3

If weakening is admissible for the rule set erls, all extensions of some rule (ps, U |- V) are in the rule set erls, and the final rule instance pscl of the left hand (implicit) subtree is an extension of (ps, c) where the cut-formula A is not in V (meaning that A is parametric on the left), then gen_step2sr (prop2 car ?erls) ?A ?sub ?rls (?pscl, ?pscr) holds.

Notice that so far we have dealt with a shallow embedding of derivations; it does not apply to proofs which require derivation trees to be represented explicitly. As noted in Sect. 4.4, the derivability of a sequent is equivalent to the existence of a valid derivation tree for it, and so now we describe the similar approach for explicit derivation trees.

7.3 Induction Principles for Explicit Derivation Trees

Sometimes we need to proceed by induction on (for example) the length of a derivation by which a sequent can be obtained, rather than by the fact of a sequent having been obtained earlier in the same derivation. At other times, we not only need to do induction on height, but we may also have to transform the immediate premises in some way, for example, by utilising the admissibility of weakening or contraction.

We could change our (notion of implicit derivations) derivability predicate derrec rls plvs with a third argument ht, say, so that derrec rls plvs ht captured the set of sequents derivable from the leaves in plvs using rules from rls with height ht. But then it becomes much harder to incorporate the transformations of the immediate premises of an end-sequent using the weakening and contraction lemmata since we have no explicit access to the derivation itself. So to compare (say) the heights of derivations, we must be able to define them and for this we need to look at explicit derivation trees.

We can use explicit derivation trees to perform a proof equivalent to one using Theorem 7.1, by using the following definitions and lemmata.

Definition 7.4

(gen_step_tr) For all properties P, all formulae B, all “sub-formula” relations sub and all (explicit) derivation trees dta:

gen_step_tr P B sub dta means:

if

• (a) P C dtb holds for all subformulae C of B and all derivation trees dtb, and

• (b) P B dtsub holds for all the immediate subtrees dtsub of dta

then P B dta holds.

Lemma 7.1

(gen_step_tr_lem) For all properties P, for all formulae A, for all relations sub, for all derivations dt, if A is in the well-founded part of sub, and gen_step_tr P B sub dtb holds for all formulae B and all derivations dtb, then P A dt holds.

Definition 7.5

(gen_step2_tr) For all properties P, for all formulae B, for all “sub-formula” relations sub, for all pairs (dta, dtb) of derivation trees:

gen_step2_tr P B sub (dta, dtb) means:

if

• (a) P C (dtaa, dtbb) holds for every sub-formula C of B and all derivation trees dtaa and dtbb, and

• (b) P B (dtp, dtb) holds for all immediate subtrees dtp of dta, and

• (c) P B (dta, dtq) holds for all immediate subtrees dtq of dtb

then P B (dta, dtb) holds:

Lemma 7.2

(gen_step2_tr_lem) For all properties P, for all formulae A, for all relations sub, for all derivation trees dta and dtb, if A is in the well-founded part of sub, and gen_step2_tr P B sub (dtaa, dtbb) holds for all formulae B and all derivations dtaa and dtbb, then P A (dta, dtb) holds:

These properties are exact analogues, for explicit derivation trees, of the properties gen_step and gen_step2sr and Theorems 7.1 and 7.2, with (for example) Lemma 8.2 linking them.

However, the purpose of using explicit derivation trees is to define different induction patterns. For example, we defined an induction pattern which depends on the inductive assumption that the property P holds for the given tree on one side, and any smaller tree on the other side.

Definition 7.6

(measure) For all a, all b, and all functions f : : ’a => nat, the pair (a, b) is in measure f iff f a < f b:

Definition 7.7

(height_step2_tr) For all properties P, for all formulae A, for all subformula relations sub, for all pairs (dta, dtb) of derivations,

height_step2_tr P A sub (dta, dtb) means:

if

• (a) P B (a, b) holds for all subformulae B of A and for all derivation trees A and B, and

• (b) P A (tp, dtb) holds for all derivation trees tp of smaller height than dta, and

• (c) P A (dta, tq) holds for all derivation trees tq of smaller height than dtb

then P A (dta, dtb) holds.

In some cases we found that this wasn’t enough, and defined a more general pattern, in which the inductive assumption applies where the sum of the heights of the two trees is smaller.

Definition 7.8

(sumh_step2_tr) For a property P, a formula A, a subformula relation sub, and a pair of derivations (dta, dtb),

sumh_step2_tr P A sub (dta, dtb) means:

if

• (a) P B (a, b) holds for all subformulae B of A and all derivation trees a and b, and

• (b) for all derivation trees dtaa and dtbb, we have

  $\texttt {heightDT dtaa} + \texttt {heightDT dtbb}< \texttt {heightDT dta} + \texttt {heightDT} \texttt {dtb}$ implies P A (dtaa, dtbb)

then P A (dta, dtb) holds

We could of course generalise this by replacing heightDT by any natural number function, which may be different for trees on the left and right sides. Indeed it could be further generalised to any well-founded relation on pairs of derivation trees.

Each of these properties is successively weaker since the corresponding inductive assumption is stronger, hence P applies to correspondingly wider classes of derivations: as formalised next.

Lemma 7.3

For a property P, a formula A, a relation sub, and for a pair (dta, dtb) of derivations:

• (a) gen_step2_tr implies height_step2_tr

• (b) height_step2_tr implies sumh_step2_tr

Accordingly we need the lemma that proving these step results is sufficient for only the weakest of them.

Lemma 7.4

(sumh_step2_tr_lem) For a property P and a formula A in the well-founded part of a relation sub, if sumh_step2_tr P A sub (dta, dtb) holds for all derivations dta and dtb then P A (dtaa, dtbb) holds for all derivations dtaa and dtbb:

We are now in a position to define the statement of cut-admissibility in Isabelle, and to apply all of these results.

8 Statement of Cut-Admissibility in Isabelle

Definition 8.1

(cas,car) For all formulae A, and all pair of sequents:  

car rls A :

holds if the sequent obtained by applying the cut rule on formula A to them is derivable: that is, $(X_l \vdash Y_l, X_r \vdash Y_r) \in \texttt {car}\ \texttt {rls}\ A$ iff $(X_l, (X_r - A) \vdash (Y_l - A), Y_r)$ is rls-derivable;

cas rls A :

holds if cut-admissibility on A is available for that pair of sequents: that is, $(X_l \vdash Y_l, X_r \vdash Y_r) \in \texttt {cas}\ \texttt {rls}\ A$ means that if $X_l \vdash Y_l$ and $X_r \vdash Y_r$ are rls-derivable, then $(X_l \vdash Y_l, X_r \vdash Y_r) \in \texttt {car}\ \texttt {rls}\ A$.

 

When we are talking about proving cas or car by induction on the (implicit) derivation of the two sequents, that is, we are talking about two sequents which are derivable, then these two concepts become equivalent. This is because the definition of gen_step2sr only involves the property of the pair of sequents in the cases where those two sequents are derivable. Recall that prop2 simply gives an equivalent concept with a different type.

Lemma 8.1

The induction steps for proving cas and car are equivalent:

Definition 8.2

(casdt) For any set rls of rules and any formula A, two valid (ie. no unproved leaves, and all steps are rules of rls) derivation trees dtl and dtr satisfy casdt rls A iff their conclusions satisfy car:

Here is the lemma linking the induction step for cut-admissibility in terms of implicit derivability with the corresponding induction step for explicit derivation trees.

Lemma 8.2

(gs2_tr_casdt_sr) Given two derivation trees dta and dtb, a cut-formula A, a sub-formula relation sub, and a rule set rls, if the bottom rules of those trees satisfy the step condition gen_step2sr for cut-admissibility, then the two trees satisfy the step condition gen_step2_tr for cut-admissibility:

In fact the two concepts are essentially equivalent:

Theorem 8.1

(gs2_casdt_equiv) Given a set of derivation rules rls, a formula A, a sub-formula relation ipsubfml and two bottom rules pscl and pscr, then the following are equivalent:

• (a) if pscl and pscr are in rls, then they satisfy the step condition gen_ step2sr for cut-admissibility (for implicit derivations)

• (b) all trees dta and dtb whose bottom rules are pscl and pscr respectively, satisfy the step condition gen_step2_tr for cut-admissibility (for explicit derivations)

We are now ready to apply our formalisation work to particular calculi.

9 Weakening, Contraction and Cut Admissibility for S4

There exist both pen and paper [19, 25] and a formalised proof [5] of mix-elimination for sequent calculi for S4 containing explicit weakening and contraction rules. As stated previously, explicit structural rules are detrimental for automated reasoning, giving a practical motivation for proving that such rules are admissible. This is our goal.

Troelstra and Schwichtenberg also state cut-elimination for a sequent calculus G3s [25] for S4 that contains no explicit structural rules. Unfortunately, their “proof” only discusses one actual transformation, and in particular overlooks one non-trivial case—when Cut is applied on a formula $\Box A$, with both premises being an instance of the G3s R$\Box$ rule (shown below). In this case, the deduction cannot be transformed by simply permuting the Cut, or introducing a new Cut of smaller rank, on the sequents in the original deduction. Greater detail is given later in this section.

Goubault [14] acknowledges the problem posed by absorbing Weakening into the R$\Box$ rule. However, his solutions are given in the context of typed $\lambda$-calculi for a minimal version of S4, interpreted as a sequent calculus through a version of the Curry-Howard correspondence. Based on a proposal from [2], Goubault-Larrecq replaces the R$\Box$ rule by a different rule with multiple premises (for subformulae within the principal formula), along with both re-write and garbage collection rules for the $\lambda$ terms involved. While this solution could possibly be extended to sequent calculi, the creation of new premises and hence branching is detrimental to backward proof search. Our solution presented in this section also has the advantage of being significantly simpler.

Negri [18] proves various admissibility theorems for S4, but the calculus involved is labelled. These labels include elements of the Kripke semantics within the calculus, and so the resulting theorems are thus not entirely syntactical proofs. Furthermore, there are rules in the calculus which deal only with reachability between worlds. While perhaps not as inefficient as the standard structural rules, these rules nevertheless do not operate on logical connectives. In particular to S4, from the perspective of automated reasoning, applying all possible instances of the transitivity rule (shown below) or checking whether the transitivity rule has been saturated can be a very time-consuming process.

9.1 Calculus for S4

The sequent calculus we use for S4 is based on the calculus G3cp [25], with the addition of two modal rules. Note that the initial sequents $\Gamma , \varphi \vdash \varphi , \Delta$ do not require that $\varphi$ be atomic, and that there are only rules for $\Box$ formulae since $\lozenge \varphi$ is interpreted as $\lnot \Box \lnot \varphi$. The rules of the calculus are shown in Figs. 3 and 4. Note that the clause boxI in the inductive definition for gs4_rls applies extend only to the conclusion, corresponding to the appearance of the two sets $\Sigma$ and $\Delta$ in the conclusion of the rule $S4\Box$.

Fig. 3

Sequent calculus GS4 for S4

The Isabelle encoding of the calculus is modular, with the overall calculus, gs4_rls, built up from separate declarations of the id rule, the classical rules acting on antecedents and succedents, and the two modal rules.

9.2 Weakening for S4

Intuitively, weakening is admissible for a system of rules if, whenever the conclusion c of a rule (ps, c) is weakened to $c'$, there is a rule with conclusion $c'$ and premises $ps'$ which are (optionally) weakened counterparts of ps.

Fig. 4

Isabelle rules for GS4

The following definition seeks to formalise this condition.

Definition 9.1

A set of rules rls satisfies ext_concl iff: for every list of premises ps and conclusion c that form a rule ($\rho _1$ say) in rls, and for all possible sequents UV, there exists a list of premises ps’ such that the premises ps’ and the extended conclusion c + UV also form an instance of some rule ($\rho _1'$ say) in rls and for every premise P from ps there is a corresponding premise p’ in ps’ such that p’ is either P itself or is an extension of P:

In the Isabelle text (ps, ps’) : allrel r means that ps and ps’ are lists of the same length where each corresponding pair of their members is in r. The relation $\le$ for sequents is defined in terms of $\le$ for multisets, that is, $X \vdash Y \le X' \vdash Y'$ means $X \le X'$ and $Y \le Y'$.

Lemma 9.1

If rule set rls obeys ext_concl then rls admits weakening:

The lemma wk_adm_ext_concl is so simple it can be proved directly by the induction principle for derrec Lemma 4.1 (without using gen_step_lem). Use of lemmas like gen_step_lem is really only for the purpose of breaking up the proofs, so that various different cases of gen_step (ie various final rules of the derivation) can be put into separate lemmata, some of which may be able to be reused for different calculi.

Lemma 9.2

The set of rule gs4_rls satisfies ext_concl.

Corollary 9.1

The rules of S4 satisfy weakening admissibility.

9.3 Invertibility and Contraction for S4

We now describe how we captured the traditional proof of invertibility.

Suppose that we are given a calculus consisting of the rule set drls and suppose that we want to reason about the derivability predicate derrec defined earlier. Let derivs be the set derrec drls of all sequents that are derivable from the empty set of leaves using the rules of drls. Suppose that we wish to prove that every rule in irls is invertible w.r.t. drls (where irls is usually a subset of drls).

Omitting details, the function invs_of irls c returns the set of sequents obtainable by applying each rule of irls to the sequent c backwards once. That is, a sequent seq is in invs_of irls c if applying some rule $\rho$ of irls to c backwards, once, will give seq as one of the premises of $\rho$.

To prove that a rule (ps, concl) is invertible w.r.t. drls requires us to prove that each sequent seq from the list ps of premises is in derivs if concl is in derivs. To prove that each rule in a set of rules irls is invertible w.r.t. drls requires us to prove that the above property holds for each rule (ps, concl) from irls: that is, invs_of irls concl <= derivs where <= encodes the subset relation.

Traditional proofs of invertibility proceed by an induction on the structure of a given derivation of a sequent concl $\in$ derivs. Assuming that the final rule in this derivation is (ps, concl), the induction hypothesis is to assume that the invertibility lemma holds for each premise in ps. That is, we assume that every sequent seq obtained by applying any rule from irls backwards, once, to any premise P in ps is itself in derivs:

Use of the induction hypothesis stated above can then be encoded in inv_step as follows. Let an “irls-inverse” of a sequent s be a sequent $s'$ obtained from s by applying any rule from irls backwards once.

Definition 9.2

(inv_step) For a given set derivs of derivable sequents, for a rule set irls, and for every rule instance (ps, concl), the property:

inv_step derivs irls (ps, concl) means:  

If:

every premise in ps being in derivs implies that every “irls-invert” of premises in ps is in derivs,

then:

every “irls-invert” of the conclusion concl is in derivs.

 

This is the key result for doing invertibility by stating various cases of the induction step as separate lemmata.

The expression UNION (set ?ps) (invs_of ?irls) represents the set X of all sequents obtained by applying some rule from irls backwards once to every sequent P from a list of sequents ps viewed as a set:

$$ X := \bigcup _{\texttt {P}~\in ~\texttt {set ps}} \texttt {(invs\_of ?irls}\,\texttt {p)} $$

Then, (set ?ps Un UNION (set ?ps) (invs_of ?irls)) represents the union of X and the list of sequents ps treated as a set, ie $\texttt {(set ps)} \cup X$.

The property inv_stepm is weaker than inv_step but is monotonic in its first argument, which makes reusing lemmata such as lks_inv_stepm possible as follows.

Definition 9.3

(inv_stepm) For all rule sets drls, for all rule sets irls, for all rules (ps, concl), the expression inv_stepm drls irls (ps, concl) means: the irls-inverses of concl are derivable using derrec drls from (set ps) and the irls-inverses of every P $\in$ set ps:

Lemma 9.3

(inv_step_mono) inv_stepm is monotonic in its first argument:

Lemma 9.4

(inv_step_m) For every set drls of rules and every set plvs of sequents, the function derrec drls plvs returns the set of sequents derivable from plvs using the rules of drls. Let us call this set of sequents derivs. For every set drls of rules used for derivations, for every rule set irls, for every rule psc, if inv_stepm drls irls psc holds then so does inv_step derivs irls psc for any set of leaf sequents plvs:

Lemma 9.5

(gen_inv_by_step) For every rule set rls which is used to construct a set derrec rls of derivations from the empty set of leaves, for every rule set irls, every rule psc from irls is invertible w.r.t. rls if every rule instance (ps, concl) from rls obeys

inv_step (derrec rls ) irls (ps, concl):

Lemma 9.6

Every instance of the rule Refl, extended with arbitrary contexts, is invertible in the rule set gs4_rls:

Proof

Suppose that $\Gamma , \Box \varphi \vdash \Delta$ is derivable. We can show that the premise $\Gamma , \varphi , \Box \varphi \vdash \Delta$ is derivable by applying weakening, which has already been shown to be admissible in gs4_rls.   $\blacksquare$

Lemma 9.7

Every instance of the rule set lksss (of classical propositional logic) is invertible in the rule set gs4_rls:

Proof

By Lemma 9.5, it suffices to prove (inv_step (derrec gs4_rls {}) lksss) psc for every rule psc from gs4_rls. By Lemma 9.4, it suffices to prove inv_stepm gs4_rls lksss psc for every rule psc from gs4_rls. Here, lksss == extrs lksne, the rule set lksne extended with arbitrary contexts. We proceed by cases on each rule psc in gs4_rls:

 

psc = Refl.:

Immediate, the inverse of rule Refl is an instance of weakening.

psc is from LK.:

Where the rule psc is a classical rule, we first prove that the set of classical rules is invertible w.r.t. itself:

Since the rules lksss are a subset of the rules gs4_rls, we can use (the monotonicity) Lemma 9.3 to obtain:

psc = $S4\Box$.:

When the last rule is $S4\Box$ (with arbitrary contexts in conclusion only to make weakening admissible) we prove a general result.

If the rule set rls contains exactly one rule extcs (ps, c) which is the rule (skeleton) (ps, c) with only the conclusion extended by an arbitrary context, and rl is any member (instance) of rls, then inv_stepm rls (extrs (ips, ic)) rl holds for any rule (ips, ic) extended with arbitrary contexts if the (skeleton of the) conclusion ic and the (skeleton of the) conclusion c are disjoint:

In particular, we can put extcs (?ps, ?c) to be the rule $S4\Box$ and put (extrs (?ips, ?ic)) to be any rule from lksss since the skeletons of the conclusions of the lksss rules contain only the principal formula of the respective rule and none of these is a $\Box$-formula.    $\blacksquare$

 

Theorem 9.1

(inv_rl_gs4_refl and inv_rl_gs4_lks) The Refl (lkrefl) rule and all Classical (lksss) rules are invertible within gs4_rls.

Proof

The theorem is simply the conjunction of Lemmas 9.6 and 9.7. We explain some of the cases in English to highlight the new aspects.

Consider invertibility for the R$\vee$ rule. We proceed by an induction on height, and use the induction principle gen_inv_by_step from Lemma 9.5.

 

Case 1 Axiom:

If $\Gamma \vdash \varphi \vee \psi , \Delta$ is an axiom, and $\varphi \vee \psi$ is principal, then $\Gamma = \Gamma ', \varphi \vee \psi$. The derivation for $\Gamma \vdash \varphi , \psi , \Delta$ is then:

If $\varphi \vee \psi$ is parametric in (id), then $\Gamma \vdash \Delta$ is (id), and so is $\Gamma \vdash \varphi , \psi , \Delta$.

Case 2 Principal:

If $\Gamma \vdash \varphi \vee \psi , \Delta$ is not an axiom, but $\varphi \vee \psi$ is principal, then R$\vee$ must have been the last rule applied. Invertibility follows immediately from the premises of the R$\vee$ rule.

Case 3 Parametric:

If $\Gamma \vdash \varphi \vee \psi , \Delta$ is not an axiom, and $\varphi \vee \psi$ is parametric, then an application of a new instance of that last rule (perhaps using the induction hypothesis) obtains the necessary endsequent. This is because all rules allow arbitrary contexts in their conclusion (and premises when the premises contain context). To illustrate, consider the two cases when the last rule used to originally derive $\Gamma \vdash \varphi \vee \psi , \Delta$ is either the Refl or the S4$\Box$ rule:

 

• If the last rule was Refl then $\Gamma = \Gamma ', \Box A$ and the original derivation is:

  

  Applying the inductive hypothesis on the premises gives a derivation of $\Gamma ', A, \Box A \vdash \Delta , \varphi , \psi$. Applying Refl to this gives the required $\Gamma ', \Box A \vdash \varphi , \psi , \Delta$.

• If the last rule was S4$\Box$ then $\Gamma = \Sigma , \Box \Gamma '$ and $\Delta = \Box A, \Delta '$ and the original derivation looks like:

  

  To derive $\Gamma \vdash \varphi , \psi , \Delta$, simply apply a new instance of S4$\Box$ to the original premise, this time with $\varphi , \psi$ as the context instead of $\varphi \vee \psi$:

  

   $\blacksquare$

Theorem 9.2

(gs4_ctr_adm) Contraction is admissible for gs4_rls.

Proof

The cases for the G3cp and Refl rules are handled in the standard manner as in the literature (see [25] and [17]) using the invertibility results above. The formalisation performs the necessary transformations using a simple instantiation gen_ctr_adm_step (not shown) of the induction principle gen_step_lem of Theorem 7.1.

When the rule above the contraction is an instance of the S4$\Box$ rule, there are two possible cases. Either one or both copies of the contraction-formula exist within the context of the S4$\Box$ rule, or both copies are principal.

In the first case, deleting one copy still leaves an instance of the rule. That is, if the contraction-formula is A, with A in the succedent, then the original rule instance is as shown below where either $\Box \varphi = A$ or $A \in \Delta$:

Applying the S4$\Box$ rule without introducing the shown second copy of A in the conclusion above gives a proof of $\Sigma , \Box \Gamma \vdash \Box \varphi , \Delta$ as required since an occurrence of A is still in the succedent as $\Box \varphi = A$ or $A \in \Delta$. Similarly, if A is in the context $\Sigma$ the new S4$\Box$ rule instance is then:

The harder case occurs when both instances of the contraction-formula A are principal. Due to the nature of the S4$\Box$ rule this requires A to occur in the antecedent only, as there cannot be two principal formulae in the succedent. As only boxed formulae are principal, A has form $\Box B$. The original rule instance is thus represented by:

The copies of $\Box B$ and B can be contracted upon, first using the induction hypothesis that the result applies to preceding sequents in the derivation, and then on the rank of the contraction-formula. The S4$\Box$ rule can then be applied to give the required conclusion.

In the Isabelle proof, this step is unfortunately rather more tedious. A significant number of proof steps in the formalisation are dedicated to manipulating the ordering of formulae to convince the proof assistant that the S4$\Box$ rule can be applied after applying the induction hypotheses, and that the resulting sequent is indeed what is required.   $\blacksquare$

9.4 Cut-Admissibility for S4

We first state a lemma used several times in the proof of cut-admissibility.

Lemma 9.8

Given two (explicit) derivation trees dta and dtb, a cut-formula A, a sub-formula relation sub, and a rule set rls, if the bottom rules of those trees satisfy the step condition gen_step2sr for cut-admissibility, then the two trees satisfy the step condition sumh_step2_tr for cut-admissibility:

Proof

By combining Lemmas 7.3, 8.2 and 8.1.   $\blacksquare$

Theorem 9.3

(gs4_cas) Cut is admissible in the calculus gs4_rls.

Proof

Our proof essentially uses a double induction on level and rank, where level measures the sum of the heights of the derivation trees for the left and right premises of the cut, and rank measures the complexity of the cut-formula. It uses Lemma 7.4, in which ?sub is instantiated to the immediate subformula relation.

The two most difficult cases to consider correspond to when the cut-formula is principal below an application of the S4$\Box$ rule on the left, and also principal in either the Refl or the S4$\Box$ rule on the right. As these are all modal rules, the Cut in question must be on a boxed formula, $\Box A$.

In the former case, the original Cut has form:

This is transformed as follows:

Here Refl$^*$ means multiple uses of Refl, once for each member of $\Gamma _L$. Importantly, the new Cut on $\Box A$ has lower level, and the Cut on A is of smaller rank. Thus both can be eliminated by the induction hypotheses.

For the latter case, when S4$\Box$ is principal on both sides, the original Cut has form:

The normal process of reducing Cut level would apply Cut on the left cut-sequent and the premise of the right cut-sequent, as follows:

Unfortunately, this results in a deduction where we can no longer recover the $\Box B$ present in the conclusion of the original Cut. The nature of the calculus and the S4$\Box$ rule means that new box formulae cannot be introduced in any succedent which contains some context $\Delta$ (or where there are additional formula $\Sigma$ in the antecedent). As stated earlier, this case is omitted in the cut-elimination theorem of Troesltra and Schwichtenberg [25].

To overcome this issue without introducing the complications and new branching rule in the solution of Goubault [14], we modify the original derivation of the left premise to produce one of equal height upon which we can still apply the induction hypothesis on level. The new application of the S4$\Box$ rule differs from the original by simply not adding any context in the conclusion. Formally, the $\Sigma$ and $\Delta$ of the generic S4$\Box$ rule in Fig. 3 are $\emptyset$ in the new S4$\Box$ instance below:

In the formalised proof, this instance is the only case where the inductive principle of Lemma 7.4 is actually required. As the combined height of the derivations leading to $\Box \Gamma _L \vdash \Box A$ and $A, \Box A, \Gamma _R, \Box \Gamma _R \vdash B$ is lower than the level of the original Cut, the induction hypothesis on level can be applied. In all the other cases Theorem 7.2 would have sufficed. So in fact in all the other cases the property we prove is gen_step2sr ... and we use Lemma 9.8 to link it to the required property sumh_step2_tr ... where the ellipses indicate arguments to each function as appropriate.   $\blacksquare$

10 Weakening, Contraction and Cut Admissibility for S4.3

There exists a syntactic pen and paper proof of cut-admissibility for S4.3 in the literature [22], however the calculus involved contains Weakening and Contraction as explicit rules, and mix-elimination is proved rather than cut. There also exist published semantic proofs of closure under Cut for both sequent and hypersequent calculi for S4.3 [12, 15]. To our knowledge, there are no published papers for S4.3 providing a sequent calculus devoid of structural rules and proving cut-elimination per se.

Labelled calculi [3, 18] are perhaps the closest representatives in the literature. As noted previously, while these calculi do not use Weakening or Contraction, they explicitly include the semantics of the logic in the calculi, along with corresponding operations on world accessibility rather than logical operators, thus they are not purely syntactic.

10.1 Calculus for S4.3

The rules of the sequent calculus for S4.3 are listed in Fig. 5. The calculus is based on the version of Goré [12], but with Weakening absorbed into the modal rules. Note, in the S4.3$\Box$ rule of Fig. 5, that $\vec {\Phi }= \{\varphi _1, \dots , \varphi _n \}$ and $\vec {\Phi }_{-i} = \{\varphi _1, \dots , \varphi _{i-1}, \varphi _{i+1}, \dots , \varphi _n \}$ for $1 \le i \le n$.

Fig. 5

Sequent calculus for S4.3 where $\dagger$ is $\forall \psi . \Box \psi \not \in \Sigma \cup \Delta$

For backward proof search, the S4.3$\Box$ rule can be thought of as producing a new premise for all boxed formula in its conclusion, each of these formula being un-boxed separately in its own premise. Thus the general statement of the rule contains an indeterminate number of premises, one is necessary for each $\varphi _i \in \vec {\Phi }$. For the sake of simplicity and clarity, at times only one of these premises will be shown as a representative for all n premises. That is, the rule will be represented in the following form shown below at left:

There are two different versions of the S4.3$\Box$ rule: either the context ($\Sigma \cup \Delta$) can contain any formulae, as shown above left, or they cannot include top-level boxed-formulae, as shown above right. In the latter case, the $\Box \Gamma$ and $\Box \vec {\Phi }$ in the conclusion of the S4.3$\Box$ rule must correspond to exactly all the top-level boxed formulae within that sequent. The two versions of the calculus are in fact equivalent, following a proof of the admissibility of Weakening for the latter, however, for efficient backward proof search, the version above right is preferred as it is invertible and hence does not require backtracking during proof search.

Henceforth, $\Sigma$ and $\Delta$ within the S4.3$\Box$ rule will be restricted from containing the $\Box$ operator at the top-level. In Isabelle, this is implemented by creating a new type of formula, based on the default formula type. HOL’s typedef allows a concise method of declaring new types as a subset of an existing type, where $^\sim$= stands for inequality:

The Isabelle formalisation of the overall calculus is based on the calculus for S4 given in Fig. 3. The only change is in the S4.3$\Box$ rule, which requires the mapping function nboxseq to create a new premise for each individual boxed formula in the succedent. The code for this is given in Fig. 6.

Fig. 6

S4.3 calculus as encoded in Isabelle

10.2 Weakening for S4.3

As the S4.3$\Box$ rule does not allow arbitrary contexts, weakening-admissibility must be proved by induction, in this case on both height and rank (of the implicit derivation tree, i.e., using Lemma 7.1). To simplify the case for the S4.3$\Box$ rule and its multiple premises, we prove weakening-admissibility for the antecedent and succedent separately, and only considering a single formula at a time. The Isabelle encodings for these properties are given below. The induction itself proceeds on the height of the derivation, with a sub-induction on the rank of the formula A being inserted into the conclusion.

Definition 10.1

 

wk_adm_single_antec rls :

means:

For any rls-derivable sequent S, and any single formulae A,

if $S \in$ derrec rls {} then $S +$ ({#A#} |- {#}) $\in$ derrec rls {}.

wk_adm_single_succ rls :

means:

For any rls-derivable sequent S, and any single formulae A,

if $S \in$ derrec rls {} then $S +$ ({#} |- {#A#}) $\in$ derrec rls {}.

 

Lemma 10.1

(wk_adm_sides) For a set of rules rls, if wk_adm_single_ antec and wk_adm_single_succ both hold then so does wk_adm.

Proof

By multiset induction, repeatedly applying the results for single formulae.   $\blacksquare$

Theorem 10.1

(gs43_wk_adm) Weakening is admissible for the calculus consisting of the set of rule gs43_rls.

Proof

In the case of the S4.3$\Box$ rule, if A is not boxed, then it is allowed to be contained in the context of the rule’s conclusion. The derivability of the original premises, followed by an application of a new S4.3$\Box$ rule including A as part of its context, then gives the required sequent. The difficulty arises when A is a boxed formula, say $A = \Box B$. For the sake of clarity, the representation of the original sequent can be split into its boxed and non-boxed components, so the original derivation is:

When A is to be added to the antecedent, the induction on height can be used to add $A = \Box B$ to each of the original premises. Following this by an application of the sub-induction on formula rank, allows the addition of B, giving the derivability of $B, \Box B, \Gamma , \Box \Gamma \vdash \varphi _i, \Box \vec {\Phi }_{-i}$. An application of the S4.3$\Box$ rule then completes the case:

The final case to consider is that of adding $A = \Box B$ to the succedent. The goal once again is to use the S4.3$\Box$ rule to give the desired conclusion. From the original premises $\Gamma , \Box \Gamma \vdash \varphi _i, \Box \vec {\Phi }_{-i}$, the induction hypothesis on height (inserting $\Box B$) gives the derivability of $\Gamma , \Box \Gamma \vdash \varphi _i, \Box \vec {\Phi }_{-i}, \Box B$. A different application of the S4.3$\Box$ rule, bringing in empty contexts, on the original premises also gives the derivability of $\Box \Gamma \vdash \Box \vec {\Phi }$. Applying the induction on formula rank then shows that $\Box \Gamma \vdash B, \Box \vec {\Phi }$ is derivable.

At this point, the derivability of all necessary premises for a new S4.3$\Box$ rule instance has been proven. These are sequents of the form $\Gamma , \Box \Gamma \vdash \varphi '_i, \Box \vec {\Phi }_{-i}'$ where $\vec {\Phi }' = \vec {\Phi }, B$ and $\varphi '$ is from the multiset $\vec {\Phi }\cup \{B\}$ as appropriate. The final rule application is then:

   $\blacksquare$

10.3 Invertibility and Contraction for S4.3

As for S4, we prove inversion lemmata for the G3cp and Refl rules within the overall calculus.

Theorem 10.2

(inv_rl_gs43_refl and inv_rl_gs43_lks) Refl (lkrefl) and all Classical rules (lksss) are invertible within the calculus gs43_rls.

Proof

Since the inverse of the Refl rule is an instance of weakening, which we have shown is admissible, the only notable case occurs for the G3cp rules, where the last rule applied in the original derivation is S4.3$\Box$. The proof uses the induction principle of Lemma 9.5.

If the original derivation is as shown below left then proving invertibility for G3cp requires showing the derivability of all premises after applying a G3cp rule backwards from the endsequent of the S4.3$\Box$ rule. The classical rules do not operate on boxed formulae, so this rule can only modify $\Sigma$ or $\Delta$ upwards into $\Sigma '$ and $\Delta '$ respectively as shown below right:

Clarifying again, invertibility of the G3cp rule requires deriving $\Sigma ', \Box \Gamma \vdash \Box \vec {\Phi }, \Delta '$. The usual tactic would apply another instance of the S4.3$\Box$ rule to the original premises, but bringing in a different context. However, this does not admit a proof if there are boxed formula in $\Sigma '$ or $\Delta '$. For example, if the G3cp rule is L$\wedge$ and the principal formula is $A \wedge \Box B$ then $\Sigma '$ contains a boxed formula, $\Box B$, which cannot be introduced within the (box-free) context of a new S4.3$\Box$ rule application.

To accommodate this case, the premises of the modal rule are used to derive the conclusion without any context. Then weakening-admissibility is used to bring the remaining formulae in the premise of the G3cp rule:

   $\blacksquare$

For S4, proving invertibility is sufficient to lead to a contraction admissibility proof. However, using invertibility alone does not allow an obvious transformation when dealing with the S4.3$\Box$ rule. In order to prove contraction-admissibility, we first require the following lemma:

Lemma 10.2

(gs43_refl) The rule R-refl is admissible in gs43_rls.

The corresponding statement of the lemma in Isabelle (not shown) states that if a sequent seq is derivable in gs43_rls and the sequent is equivalent to $X \vdash Y, \Box A$ for any X and Y, then $X \vdash Y, A$ is also derivable.

Proof

By an induction on the structure of the (implicit) derivation tree, using the derrec-induction principle, Lemma 4.1. The analysis is on the last rule applied in deriving $\Gamma \vdash \Delta , \Box A$.

 

Case 1:

The last rule applied was id. If $\Box A$ is parametric then $\Gamma \vdash \Delta$ is an axiom, and the conclusion will be also. If $\Box A$ is principal, then $\Gamma = \{\Box A\} \cup \Gamma '$ and the following transformation is applied:

Case 2:

The last rule applied was from G3cp. No rules in G3cp operate on a boxed formula, so $\Box A$ must be parametric. The induction hypothesis on height is thus applicable to the premise of the G3cp rule. Applying the original G3cp on the resulting sequent gives the desired conclusion.

Case 3:

The last rule applied was Refl. As in Case 2, $\Box A$ must be parametric, as Refl only operates on boxed formula in the antecedent.

Case 4:

The last rule applied was S4.3$\Box$. Then one premise of the original deduction un-boxes $\Box A$. Using Refl for each member of $\Gamma '$ (denoted by Refl$^*$) followed by weakening admissibility on this premise is enough to produce the conclusion. For clarity, here we express $\Gamma = \Sigma \cup \Box \Gamma '$ and $\Delta = \Box \vec {\Phi }\cup \Delta '$. The original derivation is:

This is transformed into:

 

   $\blacksquare$

Theorem 10.3

(gs43_ctr_adm) Contraction is admissible in gs43_rls.

Proof

We use the induction principle Lemma 7.1, for implicit derivation trees. If the last rule used in the derivation was the S4.3$\Box$ rule, there are two cases to consider. The case where the contraction-formula is parametric is handled by simply re-applying another instance of the S4.3$\Box$ rule as in the S4 case. Similarly, when the contraction-formula is principal in the antecedent, then the proof proceeds as for S4. Specifically, one copy of $\Box A$ from $\Sigma , \Box A, \Box A, \Box \Gamma \vdash \Box \vec {\Phi }, \Delta$ must be removed. The original derivation is:

By contracting twice using first the induction hypothesis on height, then the induction hypothesis on rank, on all premises followed by an application of the S4.3$\Box$ rule, the desired endsequent is obtained:

When the contraction-formula is principal in the succedent, there are two possible premises to consider. Either a premise “un-boxes” one of the contraction-formulae,¹ or it leaves both boxed. The original deduction is:

In the latter case, the induction hypothesis can be directly applied, removing one copy of the boxed formulae:

In the former case, we use Lemma 10.2 to produce the following:

   $\blacksquare$

10.4 Cut-Admissibility for S4.3

Theorem 10.4

(gs43_cas) Cut is admissible in the calculus gs43_rls.

Proof

As with Theorem 9.3, we use the induction principle of Lemma 7.4, involving induction on the sums of heights of two explicit trees, although for the majority of cases the simpler principle Theorem 7.2 would suffice. So again, in those cases, we prove gen_step2sr $\ldots$ and we use Lemma 9.8 to link it to the required property sumh_step2_tr $\ldots$, where the ellipses indicate arguments to each function as appropriate.

When S4.3$\Box$ leads to the left cut-sequent, and the Refl rule is used on the right, the transformation mimics the corresponding case for S4. However, for the case where S4.3$\Box$ is principal on both sides we require a new transformation. For clarity, the premises above the S4.3$\Box$ rule on the left are given as two cases, depending on whether the cut-formula is un-boxed or not. The boxed formula in the succedents of the premises are also distinguished by the superscripts L and R for left and right cut premises respectively. Explicitly, these are $\vec {\Phi }^L = \{\varphi _1^L, \ldots , \varphi _i^L, \ldots , \varphi _n^L\}$ and $\vec {\Phi }^R = \{\psi _1^R, \ldots , \psi _k^R, \ldots , \psi _m^R\}$. The original cut thus has the form:

To remove this cut, the derivation is transformed into one where the principal rule (S4.3$\Box$) is applied last to produce the desired endsequent. The problem is then proving that the premises of the following S4.3$\Box$ rule application are derivable. This in itself requires two different transformations of the original derivation, depending on the two forms that the premises can take; either the un-boxed formula in the succedent originated from the left cut premise, that is from $\Box \vec {\Phi }^L$, or from the right, within $\Box \vec {\Phi }^R$. These cases are named $\mathcal {P}_L$ and $\mathcal {P}_R$ respectively. The final S4.3$\Box$ rule used in our new transformation is then:

For both transformations, the same idea behind the principal S4$\Box$ rule case is used. We first derive the original cut-sequents but without their original contexts. These new sequents will be called $\mathcal {D}_L$ and $\mathcal {D}_R$ respectively, that is, $\mathcal {D}_L = \Box \Gamma _L \vdash \Box \vec {\Phi }^L, \Box A$ and $\mathcal {D}_R = \Box A, \Box \Gamma _R \vdash \Box \vec {\Phi }^R$. These are derived using the derivations in the original cut, but applying new instances of the S4.3$\Box$ rule. Importantly, the derivations of the new sequents $\mathcal {D}_L$ and $\mathcal {D}_R$ have the same height as the original cut-sequents. This is the case where the induction principle of Lemma 7.4 is required.

Having introduced all the necessary notation and pre-requisites, the first actual case to consider is deriving $\mathcal {P}_L$. The induction on level allows $\mathcal {D}_R$ to be cut, on cut-formula $\Box A$, with all of the sequents given by the derivation $\Pi _L^a$ above the original left S4.3$\Box$ rule. The transformation performs n cuts, for all premises corresponding to the formulae in $\vec {\Phi }^L$. The results of this cut then match exactly with $\mathcal {P}_L$ after using the admissibility of Weakening to introduce the formulae of $\Gamma _R$ in the antecedent.

To derive the sequents in $\mathcal {P}_R$, the induction hypothesis on level is used to cut $\mathcal {D}_L$ with all of the premises above the right S4.3$\Box$ in the original cut, with cut-formula $\Box A$. The induction on formula rank on A is then used to cut the sequent resulting from $\Pi _L^b$ with all these new sequents. Finally, contraction-admissibility allows the removal of the extra copies of $\Box \Gamma$ and $\Box \vec {\Phi }^L$, and concludes the case.

To conclude, the transformations above derive $\mathcal {P}_L$ and $\mathcal {P}_R$ while reducing cut-level or cut-rank. These are the premises of an instance of the S4.3$\Box$ rule which results in the conclusion of the original cut. This completes the cut-admissibility proof.   $\blacksquare$

11 Weakening, Contraction and Cut Admissibility for GTD

We now describe Isabelle proofs of cut admissibility for a sequent calculus for the logic GTD described in [16]. Axiomatically, GTD is K with the additional axiom $\Box A \Leftrightarrow \Box \Box A$. The sequent inference rules involving $\Box$, allowing arbitrary context in the conclusion so as to make weakening admissible, are shown below:

$$ \frac{\Box \Gamma , \Gamma \vdash A}{\Sigma , \Box \Gamma \vdash \Box A, \Delta } (\vdash \Box ) \qquad \qquad \frac{\Box \Gamma , \Gamma \vdash \Box A}{\Sigma , \Box \Gamma \vdash \Box A, \Delta } (\Box \vdash ) $$

The skeletons of the above two rules are encoded as GTD shown below by factoring out the form of A as either B or as $\Box B$:

11.1 Calculus for GTD

We now look at proving cut admissibility for a version of GTD without structural rules, where the box rules have their conclusions (only) extended with an arbitrary context, which permits weakening to be admissible.

We define the rules of the sequent calculus as follows. The rules used for classical logic (before extending them with a context) form the set lksne where the rule sets idrls, lksil and lksir are the axioms and the left and right logical introduction rules: see Fig. 3.

Definition 11.1

(lkssx) Given, a rule set xrls, every rule of xrls is in the rule set lkssx xrls, and every rule psc in rule set lknse gives a rule in lkssx xrls obtained by uniformly extending both the premise and conclusion of psc with an arbitrary context (sequent) flr:

Definition 11.2

(extcs) Given a rule set rules, the rule set extcs rules is obtained by extending only the conclusion c of each rule (ps, c) in rules by an arbitrary context (sequent) flr (while leaving the premises unchanged):

The rule set lkssx (extcs GTD) for GTD is obtained by extending only the conclusion of the rule GTD and by extending every rule of lknse.

11.2 Weakening-Admissibility for GTD

First we prove weakening admissibility, using a lemma which allows us to apply Lemma 9.1.

Lemma 11.1

For any rule sets rls and rlsa

• (a) extrs rlsa $\cup$ extcs rls satisfies ext_concl

• (b) extrs rlsa $\cup$ extcs rls satisfies weakening admissibility

extrs_cs_ext_concl: "ext_concl (extrs ?rlsa Un extcs ?rls)"

wk_adm_extrs_cs: "wk_adm (extrs ?rlsa Un extcs ?rls)"

Proof

The first is easy. The second follows using Lemma 9.1.   $\blacksquare$

Corollary 11.1

GTD satisfies weakening admissibility.

Proof

Since the rule set lkssx (extcs GTD) for GTD is also equal to extrs lksne $\cup$ extcs GTD, the result follows from Lemma 11.1.   $\blacksquare$

11.3 Inversion and Contraction-Admissibility for GTD

For contraction admissibility, first we need to prove invertibility of the classical logical rules. The general method for doing so was described in Sect. 9.3.

Recall the predicate inv_stepm, which is used in an inductive proof of invertibility. Its three arguments are:  

drls :

first, the set of derivation rules with respect to which the invertibility (a case of admissibility) is defined,

irls :

second, the set of rules whose invertibility is being considered (the inversion rules)

(ps, c) :

third, the final rule of a derivation—since we are talking about proving the invertibility result by induction on the derivation, the inductive hypothesis is that the invertibility result applies to the premises ps of this final rule.

 

By Lemma 9.3, inv_stepm (although not inv_step) is monotonic in the derivation rules argument. For its second argument the following holds.

Lemma 11.2

For a given set drls of derivation rules and a given final rule psc, if inv_stepm applies for inversion rule sets irlsa and irlsb, then it applies for irlsa $\cup$ irlsb.

So far as the third argument is concerned, the requirement to prove a rule is invertible is simply that inv_stepm $\ldots$ applies for all cases of the third argument (see Lemmas 9.4 and 9.5): thus the lemmata we use are expressed to apply to single cases of the third argument.

We now describe the lemmata used as building-blocks for the required invertibility result.

Lemma 11.3

• (a) inv_stepm ... applies where the derivation rules and the set of rules to be inverted are the classical logical rules extrs lksne, and the final rule is any one of those rules

  

• (b) where the set of inversion rules is the set of extensions of a single skeleton whose conclusion is ic, and the set of derivation rules is the set of extensions of a single skeleton rule whose conclusion is c, and these skeleton conclusions ic and c are disjoint (i.e., have no formula in common on the same side of the turnstile), and the final rule is one of those derivation rules, then inv_stepm...applies

  

• (c) as for (b), except that the set of derivation rules is the set of extensions in the conclusion only (using extcs) of the single skeleton

  

• (d) where the set of inversion rules and the set of derivation rules are each the set of extensions of a single skeleton rule whose conclusion has a single formula, and if those two skeletons’ conclusions are equal then the two skeletons are equal, then inv_stepm ... applies

  

Parts (b) and (c) (inv_stepm_disj and inv_stepm_disj_cs) are for the case where the principal formula of the rule to be inverted is in the context of the conclusion of the last rule of the derivation: the first premise gives us that the formula to be inverted is not the principal formula of the rule, though it is expressed in a way which is relevant to a case where the rules in question have more than just one principal formula.

Part (d) (inv_stepm_scrls), whose proof uses part (b), uses the fact that for each formula involved there are unique introduction rules for the left and right sides of $\vdash$, so an inversion step is either parametric or gives us the premise(s) of the last rule applied.

Lemma 11.4

Every rule of lksss is invertible in the calculus for GTD.

Proof

This uses Lemmas 9.4, 9.5 and 11.3.   $\blacksquare$

Then, to prove contraction admissibility, we follow an approach very similar to Sect. 9.3. For the rules ($\Box \vdash$) and ($\vdash \Box$), the proof for the cases where either of these is the final rule is just the same as for the S4$\Box$ rule in Sect. 9.3.

Lemma 11.5

Contraction is admissible in GTD.

11.4 Cut-Admissibility for GTD

Now, for cut admissibility, the difficult cases are where the last rule on both sides is one of the two box rules ($\vdash \Box$) and ($\Box \vdash$):

$$ \frac{\Box \Gamma , \Gamma \vdash B}{\Sigma , \Box \Gamma \vdash \Box B, \Delta } (\vdash \Box ) \qquad \qquad \qquad \frac{\Box \Gamma , \Gamma \vdash \Box B}{\Sigma , \Box \Gamma \vdash \Box B, \Delta } (\Box \vdash ) $$

Since the proof is effectively the same whichever of these two rules is on the right, we define a unary function s4g . such that

• s4g $(\lambda B.\ \{B, \Box B\})$ is all instances of either $(\vdash \Box )$ or $(\Box \vdash )$,

• s4g $(\lambda B.\ \{B\})$ is all instances of $(\vdash \Box )$, and

• s4g $(\lambda B.\ \{\Box B\})$ is all instances of $(\Box \vdash )$

where the function prs B encapsulates the choices of B and/or $\Box B$, as required and where s4g prs below encodes only the skeletons of the rules above: see the definition of GTD at the start of Sect. 11. Formally,

Definition 11.3

(s4g) s4g prs is the set of instances of the following rule where $A \in \texttt {prs} B$:

$$ \frac{\Box \Gamma , \Gamma \vdash A}{\Box \Gamma \vdash \Box B} $$

The case of the ($\vdash \Box$) rule on the left is dealt with in Sect. 9.4: depending on whether we have the rule ($\vdash \Box$) or ($\Box \vdash$) on the right, we may need to change B to $\Box B$ in the diagrams there.

For the case where we have the ($\Box \vdash$) rule on the left, the original derivation is as in the following diagram, where $B'$ is B or $\Box B$.

As in Sect. 9.4, we modify the original derivation of a premise, in this case the right premise, by simply not adding any context in the conclusion. This produces a derivation of equal height upon which we can still apply the induction hypothesis on level. Formally, the $\Sigma$ and $\Delta$ of the generic box rule ($\vdash \Box$) or ($\Box \vdash$) are $\emptyset$ in the new instance below:

For the cut-elimination proof we also use results for the parametric cases, that is, where the cut-formula appears in the context of the last rule on either side above the cut. This includes cases where that rule is in extrs ... (where the rule has a context which appears in premises and conclusion) and where that rule is in extcs ... (where the rule has a context which appears only in the conclusion).

The following lemma is used for the common situation of a cut which is parametric with respect to the last rule of the left-hand derivation.

Lemma 11.6

(lcg_gen_step) Consider a set erls of derivation rules, for which weakening is admissible, and which contains all extensions of a skeleton rule $\rho$ with premises ps and conclusion $U \vdash V$. Consider two derivations of which the final rule of the left side is an extension of $\rho$. Then for a cut-formula A which is not contained in V, and any subformula relation sub, the inductive step condition gen_step2_sr ... holds for the admissibility of a cut on A.

A similar lemma lcg_gen_steps_extcs holds for the case where only extensions in the conclusion of $\rho$ are contained in erls.

Finally we need to deal with the cases of matching instances of the usual logical introduction rules. Here we use a general result giving requirements for certain cases of the final rules on either side of a putative cut to satisfy the step condition for cut-admissibility.

It uses a property c8_ercas_prop, which encodes the property that a cut which is principal (i.e., the cut formula is introduced by a logical introduction rule in the final step) on both sides is reducible to cuts on sub-formulae. It is loosely defined as follows:

Definition 11.4

(c8_ercas_prop) Given a set of derivation rules prls, a cut-formula A, a subformula relation psubfml, and a set of skeleton rules (typically logical introduction rules) rls,

c8_ercas_prop psubfml prls A rls means:

assuming that we have cut-admissibility for cut-formulae which are smaller than A according to psubfml, where two derivations have as their final sequents $X_l \vdash A, Y_l$ and $X_r, A \vdash Y_r$, and on both sides the final rule introduces A using logical introduction rules in rls, then $X_l, X_r \vdash Y_l, Y_r$ is derivable, that is, the cut on A is admissible.

Of course, whether c8_ercas_prop holds depends on the specific set of logical rules. Beyond that, however, the following lemma is quite general.

Lemma 11.7

Given a set of derivation rules drls, a cut-formula A, and a subformula relation psubfml, if

• drls satisfy weakening admissibility

• there is a set rls of skeleton rules all of whose extensions are contained in drls

• all rules in rls, other than axiom rules $B \vdash B$, have a single formula in their conclusion

• the axiom rules are also in drls

• drls and rls satisfy c8_ercas_prop

• the final rules of two derivations are extensions of rules in rls

then the step condition gen_step2sr for cut-admissibility for the two derivations is satisfied.

We apply this result to the logic GTD using first another general result.

Lemma 11.8

(gen_lksne_c8) If a set of derivation rules drls satisfies weakening admissibility and contraction admissibility, and contains the extensions of the logical introduction rule skeletons lksne then the condition c8_ercas_prop is satisfied (for the usual immediate proper subformula relation and for any cut-formula).

Corollary 11.2

[gtdns_lksne_c8] GTD satisfies c8_ercas_prop in relation to the logical introduction rule skeletons lksne.

Finally we get the cut admissibility result. Here, mins $A\ M$ means multiset M with one additional copy of A inserted.

Theorem 11.1

(gtdns_casdt, gtdns_cas) GTD satisfies cut-admissibility.

12 Weakening, Contraction and Cut Admissibility for Dynamic Topological Logic S4C

We now describe Isabelle proofs of the cut admissibility of the logic S4C described by Mints [16]. This system has two “modal” operators, $\Box$ and $\circ$. The S4-axioms hold for $\Box$, $\circ$ commutes with the boolean operators, and the following are given:

$$\begin{aligned} \circ (A \rightarrow B)&\leftrightarrow (\circ A \rightarrow \circ B) \\ \circ \bot&\leftrightarrow \bot \\ \circ \Box A&\rightarrow \Box \circ A \end{aligned}$$

The following sequent rules are given for S4C by Mints [16]

$$ \frac{\circ ^k A, \Gamma \vdash \Delta , \circ ^k B}{\Gamma \vdash \Delta , \circ ^k (A \rightarrow B)}(\vdash \rightarrow ) \qquad \frac{\Gamma \vdash \Delta , \circ ^k A \quad \circ ^k B, \Gamma \vdash \Delta }{\circ ^k (A \rightarrow B), \Gamma \vdash \Delta }(\rightarrow \vdash ) $$

$$ \frac{\circ ^k A, \Gamma \vdash \Delta }{\circ ^k \Box A, \Gamma \vdash \Delta }(\Box \vdash ) \qquad \frac{\Gamma \vdash \Delta }{\circ \Gamma \vdash \circ \Delta }(\circ ) \qquad \frac{\mathcal B \vdash A}{\mathcal B \vdash \Box A}(\vdash \Box ) $$

In the $(\vdash \Box )$ rule, $\mathcal B$ must consist of “$\Box$-formulae”, that is, formulae of the form $\circ ^k \Box A$.

As Mints omits the other logical operators, we include, for them, the usual logical introduction rules with the principal and side formulae preceded by $\circ ^k$ just as with the $(\vdash \rightarrow )$ and $(\rightarrow \vdash )$ rules shown above.

Our version of the calculus contains no explicit structural rules, so we prove invertibility of the logical rules and contraction admissibility. The presence of the $(\circ )$ rule makes the proof more complicated and is handled similarly to our handling of contraction in proving cut admissibility for GTD.

As we have no structural rules, we use a presentation of the system which

• allows an arbitrary context to be added to the conclusion (only) of the $(\vdash \Box )$ and $(\circ )$ rules

• uses a version of the $(\Box \vdash )$ rule which includes the principal formula in the premise

$$ \frac{\Gamma \vdash \Delta }{\Sigma , \circ \Gamma \vdash \circ \Delta , \Pi }(\circ ) \qquad \frac{\mathcal B \vdash A}{\Gamma , \mathcal B \vdash \Box A, \Delta } (\vdash \Box ) \qquad \frac{\circ ^k \Box A, \circ ^k A, \Gamma \vdash \Delta }{\circ ^k \Box A, \Gamma \vdash \Delta }(\Box \vdash ) $$

12.1 Calculus for S4C

We now describe how we encoded the sequent calculus. First we define the rules which can be extended by an arbitrary context in their premises and conclusion. Without the context, these rules form the set s4cnsne.

Applying nkmap k to a rule applies $\circ ^k$ to each formula appearing in that rule, and funpow $f\ x$ means applying f to x, n times, i.e., $f^n(x)$.

We first prove the admissibility of weakening and contraction.

12.2 Weakening for S4C

Weakening admissibility was straightforward using Lemma 9.1.

12.3 Inversion and Contraction-Admissibility for S4C

Invertibility of the logical introduction rules was dealt with using multiple lemmata showing various cases of inv_stepm, as described in Sect. 9.3: as noted there, a proof of invertibility can be split up into

• the invertibility of various different rules

• cases of what the last rule in the derivation, from whose conclusion we wish to apply one of the inverted rules

As in Sect. 9.3, we make significant use of Lemma 9.3.

We then prove contraction admissibility. This uses predicates and results which are essentially Definition 7.2 and Lemma 7.1, but instantiated to apply to the property of contraction admissibility, giving the property ctr_adm_step and a lemma gen_ctr_adm_step.

We now look at proving ctr_adm_step for each possible case for the last rule of a derivation.

Lemma 12.1

If

• rule set lrls consists of rules which are the identity (axiom) rules $A \vdash A$, or are rules with a single formula in their conclusion,

• all rules in lrls have the “subformula” property (which here means that for every premise other than a premise which contains the conclusion, every formula in that premise is a subformula of a formula in the conclusion

• the rule set drls (derivation rules) contains the extensions of lrls

• in regard to the derivation rules drls, the inverses of extensions of lrls are admissible

• rule (ps, c) is an extension of a rule of lrls

then the contraction admissibility step ctr_adm_step holds for the final rule (ps, c) and the derivation rule set drls.

So the conclusion of this lemma means: assuming that

• contraction on formulae $A'$ smaller than A is admissible, and

• contraction on A is admissible in the sequents ps

then contraction on A in sequent c is admissible.

Then the other cases of ctr_adm_step were proved separately:

Lemma 12.2

In S4C, for derivations with final rules $(\vdash \Box )$ and $(\circ )$ (extended in their conclusions), the inductive contraction admissibility step ctr_adm_step holds.

Consequently, we get contraction admissibilty. The only case not covered above is for the reflexivity rule $(\Box \vdash )$, in its form where the principal formula is copied to the premise. This is required for contraction admissibility, which becomes simple with the rule in this form.

Lemma 12.3

(s4cns_ctr_adm) Contraction is admissible in GTD.

12.4 Cut-Admissibility for S4C

To prove cut admissibility for a sequent calculus containing an explicit contraction rule, two methods are

• to prove mix-elimination directly, where the property proved by induction on the derivation is that any instance of the mix rule is admissible; in effect this was done in [6] for the more complex logic GLS,

• in respect of the derivations on either side of the cut, to look up the derivation skipping over consecutive instances of contraction on the cut-formula, and consider the various cases of the next rule on either side above those contractions.

We do something similar to the second approach here, but we look up the derivations on either side to find the last rule before a consecutive sequence of $(\circ )$ rules. For this we use the theorem top_circ_ns. In some cases we also need the fact that if the bottom rule is not $(\circ )$, then the tree asserted to exist is actually the original one. The function forget exists simply to prevent automatic case splitting of its argument: logically it does nothing.

Lemma 12.4

(top_circ_ns) Given a valid (explicit) derivation tree dt, then there is a valid (explicit) tree dtn and an integer k such that

• the bottom rule of dtn is not $(\circ )$,

• the conclusions c and $c'$ of dt and dtn are related by $c = \circ ^k c'$

• height of dt = height of dtn $+ k$

• dt and dtn iff $k = 0$ iff the bottom rule of dt is not $(\circ )$

But one easy case is where the last rule on both sides is the $(\circ )$ rule: then we can apply cut (on a smaller formula) to the premises of the $(\circ )$ rules, and then apply the $(\circ )$ rule. So when we look at the $(\circ )$ rules on both sides immediately preceding the cut, we need only bother about the case where the number of those $(\circ )$ rules is zero on one side.

First, the case where both rules are the $(\vdash \Box )$ rule. The fact that the conclusions of both the $(\circ )$ rule and the $(\vdash \Box )$ rule may be extended by an arbitrary context complicates matters. Consider the following diagram of a number of $(\circ )$ rules followed by the $(\vdash \Box )$ rule.

In this case we can instead construct the following derivation tree, which is of the same height.

Thus we can use, in proving an inductive step, the fact that $\circ ^k \mathcal M\vdash \circ ^k \Box A$ is derivable, and with a derivation of the same height as that of $\Gamma ', \circ ^k \Gamma , \circ ^k \mathcal M\vdash \circ ^k \Box A, \circ ^k \Delta , \Delta '$. This will be used in our proofs without further comment.

Now, where the cut-formula is within $\circ ^k \Delta , \Delta '$ (where this is the derivation tree on the left of a desired cut), or within $\Gamma ', \circ ^k \Gamma$ (where this tree is on the right), the cut is admissible because we can start from the derivable sequent $\mathcal M\vdash A$ and apply $(\vdash \Box )$ and $\circ$ rule without any extra formulae in the conclusions, as discussed above. In this case we just use weakening admissibility to obtain the result of the cut.

These situations are covered by Lemma 12.5 (s4cns_cs_param_l”) below and the symmetric result s4cns_cs_param_r”.

Lemma 12.5

Let the left premise subtree of a desired cut be dt, with dtn and k as in Lemma 12.4, let the bottom rule of dtn be an extension (of the conclusion) of a rule in s4cns whose conclusion is $cl \vdash cr$, and let C not be in $\circ ^k cr$. Then the inductive step sumh_step2_tr for proving cut-admissibility with cut-formula C holds (where list and lista are names automatically generated by Isabelle for the lists of premises of final rules).

A similar pair of results, discussed later (see Lemma 12.6), covers the case where the rule above the $(\circ )$ rules is a skeleton rule which is extended by an arbitrary context in its conclusion and its premises.

Now we can assume that the cut-formula is within the principal part of the rule before the $(\circ )$ rules (noting that for the $(\vdash \Box )$ rule the “principal part” means the entire $\mathcal M\vdash \Box A$). Then there must be zero $(\circ )$ rules on the right side: because if there are zero $\circ$ rules on the left, then the cut-formula must be $\Box A$, whence there would also be zero $(\circ )$ rules on the right.

In the diagrams, (cut ?) represents the instance of the cut rule which we are aiming to show is admissible.

Here we do the cut, by induction, before the $(\vdash \Box )$ rule on the right, using a derivation similar to that on the left, but without any context, then we apply the $(\vdash \Box )$ rule, introducing the required context.

For the other cases, we first consider the “parametric” cases, where the last rule above the $(\circ )$ rules is an extension $\rho '$ of a rule $\rho$ in s4cnsne, and the principal formula of $\rho$ is not the “de-circled” cut-formula A. Recall that s4cnsne consists of the axiom, logical introduction rules and the $(\Box \vdash )$ rule, as skeletons (i.e., not extended with context), but with $\circ ^k$ applied to their formulae.

Here we must apply the $\circ$ rule the requisite number of times to the premise(s) of $\rho '$, then apply (using the inductive hypothesis) cut on $\circ ^k A$ to each of them, and finally apply $\rho ''$ which we get by applying $\circ ^k$ to $\rho$, and then extending it appropriately.

This uses the result that if a rule is in s4cnsne then so is the result of applying $\circ ^k$ to all formulae in its premises and conclusion.

Lemma 12.6 (s4cns_param_l’) and the symmetric result s4cns_ param_r’ cover this case.

Lemma 12.6

Let the left premise subtree of a desired cut be dt, with dtn and k as in Lemma 12.4, let the bottom rule of dtn be an extension of a rule in s4cnsne whose conclusion is $cl \vdash cr$, and let C not be in $\circ ^k cr$. Then the inductive step sumh_step2_tr for proving cut-admissibility with cut-formula C holds.

It is similar for the parametric case on the right. The axiom rule is trivial in all cases.

For the $(\vdash \Box )$ rule on the left, where the rule on the right is an extension of rule $\rho$ whose principal formula is the “de-circled” cut-formula, the only case remaining is where $\rho$ is $(\Box \vdash )$.

Here $k' + k'' = k$, but since we also have that $k = 0$ or $k' = 0$, this means that $k' = 0$ and $k'' = k$. The following diagram omits a final use of the admissibility of weakening.

Next we look at the case of the $(\vdash \Box )$ rule on the right, but for this, since the cut-formula must be a $\Box$-formula, all cases have already been dealt with.

Finally, there is the case where the last rules (above the final sequence of $\circ$-rules) on both sides are extensions of rules in s4cnsne. Most of these cases have been covered, i.e., the axiom rules, and the “parametric” cases, where the “de-circled” cut-formula is not the principal formula of the rule.

So there remain the cases where the rules on either side are the logical introduction rules. For these, the proofs are essentially the same as for other logics generally, except that we need to allow for a number of circles. Conceptually it is easiest to imagine that in each case the final $\circ$ rules are moved upwards to precede the final logical introduction rules, although we didn’t actually prove it this way.

We proved that the usual logical introduction rules, with $\circ ^k$ applied to principal and side formulae (as used in S4C), satisfy c8_ercas_prop (Definition 11.4). Recall that this means that assuming cut admissibility on smaller formulae, us have cut admissibility of a more complex formula where the last rule on either side is a logical introduction rule.

Lemma 12.7

[s4cns_c8_ercas] S4C satisfies c8_ercas_prop in relation to the logical introduction rule skeletons lksil cup lksir, with $\circ ^k$ applied to all formulae.

The following diagrams show an example. We let $t = k + k' = l + l'$. In this case we do not make use of the fact that either k or l must be zero.

The diagram above is simplified by not including the extra context which may be introduced in the conclusion of the $(\circ )$ rules. This is replaced by

Again, we can use weakening admissibility to get the extra context which was introduced by the $(\circ )$ rules, but omitted from the first diagram.

Finally we combine these results to get the cut admissibility result, in terms of explicit derivation trees, and then in terms of derivability.

Theorem 12.1

(s4cns_casdt, s4cns_cas) S4C satisfies cut-admissibility.

12.5 Comparing Our Proofs and the Proofs of Mints

The slides for the presentation of Mints [16] contains a very abbreviated treatment of cut-admissibility for S4C. We attempted to follow the proof shown there, but were unable to. The slides state a lemma (“Substitution Lemma”), that the following rule is admissible

$$ \frac{\mathcal B \vdash \Box C \quad \Box C, \Gamma \vdash \Delta }{\mathcal B, \Gamma \vdash \Delta } $$

As a lemma it is undoubtedly correct (it is a particular case of cut admissibility). However, as part of the proof of cut-admissibility we were unable to prove it as it stands—it appears to need (at least) an assumption that cuts on C are admissible.

13 Related Work

We may compare this approach with that of Pfenning [21]. Pfenning uses the propositions-as-types paradigm, where a type represents (partially) a sequent. More precisely, for intuitionistic logic, a type hyp A -> hyp B -> conc C represents a sequent containing A and B in its antecedent, and C in its succedent. For classical logic, neg A -> neg B -> pos C -> pos D -> # represents a sequent containing A and B in its antecedent, and C and D in its succedent. A term of a given type represents a derivation of the corresponding sequent.

Pfenning’s proof of cut-admissibility proceeds by a triple induction, using structural induction on the formula and the two terms representing the derivations. It therefore most closely resembles our proofs involving explicit derivations, as described in Sect. 7.3.

However in Sect. 7.3 we go on to measure properties (such as the height) of an explicit derivation. It seems as though Pfenning’s approach does not allow the possibility of doing that.

Tews [24] describes the use of Coq to prove cut-elimination for propositional multi-modal logics. In Coq, types are identified with terms, and each term has a type: a type has the type Type . A proposition is a type whose inhabitants are its proofs, so $A \rightarrow B$ means both the type of proofs of the proposition $A \rightarrow B$ and the type of functions which take proofs of A to proofs of B. Since types can depend on terms, this gives a dependently typed system, which can provide a way of capturing side-conditions in the type system. For example, the type counted_list A n is the type of lists of items of type A and whose length is n.

Tews uses a (single) list of formulae as a sequent, where formulae which would appear on the other side of a two-sided sequent are negated. He proves that for the rule sets he uses, for any reordering $s'$ of the conclusion s of a rule, there is a corresponding rule whose conclusion is $s'$, and, assuming sets of rules and hypotheses closed under reordering, that provability is also closed under reordering. He defines an (object-logic) proof as the type proof, similar to our definition of the type dertree, but the type definition also incorporates the requirement that each “node” of the tree must be in the given set of rules. This is an example of a dependent type, where the type proof depends on the term rules.

He proves cut-elimination both semantically (by proving soundness and cut-free completeness) and syntactically (where the proof implements a cut-elimination procedure). Thus his work includes extensive formalisation of the semantics of the logics. His proofs use the modal ranks of formulae, and involve formalising substitution, which we did not find necessary, and in some cases require proving depth-preserving admissibility of rules.

14 Further Work and Conclusion

We have proved cut-admissibility for several different sequent calculi, ranging from the well-known logics S4 and S4.3 to GTD and S4C described recently in [16]. In other work not described here we also proved cut-admissibility for GTD, for a calculus containing explicit contraction and weakening rules, in both the ways described at the start of Sect. 12.4.

We have shown how the proofs can be split up into components some of which were expressed in lemmata which can be reused in similar proofs for other calculi. This was of significant value, as was the use of the type classes described in [6]. It remains to generalise our framework so that these results follow simply by instantiating these general concepts.