Surrogate Scalar Functions and Scalarizing Techniques

Abstract

The most common procedure to compute efficient/nondominated solutions in MOP is using a scalarizing technique, which consists in transforming the original multiobjective problem into a single objective problem that may be solved repeatedly with different parameters. The functions employed in scalarizing techniques are called surrogate scalar functions or scalarizing functions. The optimal solution to these functions should be anon dominated solution to the multiobjective problem. These functions temporarily aggregate in a single dimension the p objective functions of the original model and include parameters derived from the elicitation of the DM’s preference information. Surrogate scalar functions should be able to generate nondominated solutions only, obtain any nondominated solution and be independent of dominated solutions. In addition, the computational effort involved in the optimization of surrogate scalar functions should not be too demanding (e.g., increasing too much the dimension of the surrogate problem or resorting to nonlinear scalarizing functions when all original objective functions are linear) and the preference information parameters should have a simple interpretation (i.e., not imposing an excessive cognitive burden on the DM). Surrogate scalar functions should not be understood as “true” analytical representations of the DM’s preferences but rather as an operational means to transitorily aggregate the multiple objective functions and generate nondominated solutions to be proposed to the DM, which expectedly are in accordance with his/her (evolving) preferences.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

The most common procedure to compute efficient/nondominated solutions in MOP is using a scalarizing technique, which consists in transforming the original multiobjective problem into a single objective problem that may be solved repeatedly with different parameters. The functions employed in scalarizing techniques are called surrogate scalar functions or scalarizing functions. The optimal solution to these functions should be a nondominated solution to the multiobjective problem. These functions temporarily aggregate in a single dimension the p objective functions of the original model and include parameters derived from the elicitation of the DM’s preference information. Surrogate scalar functions should be able to generate nondominated solutions only, obtain any nondominated solution and be independent of dominated solutions. In addition, the computational effort involved in the optimization of surrogate scalar functions should not be too demanding (e.g., increasing too much the dimension of the surrogate problem or resorting to nonlinear scalarizing functions when all original objective functions are linear) and the preference information parameters should have a simple interpretation (i.e., not imposing an excessive cognitive burden on the DM). Surrogate scalar functions should not be understood as “true” analytical representations of the DM’s preferences but rather as an operational means to transitorily aggregate the multiple objective functions and generate nondominated solutions to be proposed to the DM, which expectedly are in accordance with his/her (evolving) preferences.

Three main scalarizing techniques are generally used to compute nondominated solutions:

• 1. Selecting one of the p objective functions to be optimized considering the other p-1 objectives as constraints by specifying the inferior (reservation) levels that the DM is willing to accept. This scalarization is usually called e-constraint technique.

• 2. Optimizing a weighted-sum of the p objective functions by assigning weighting coefficients to them—weighted-sum technique.

• 3. Minimizing a distance function to a reference point (e.g., the ideal solution), the components of which are aspiration levels the DM would like to attain for each objective function. If the reference point is not reachable the closest solution according to a given metric is computed, usually the Manhattan metric (i.e., minimizing the sum of the differences in all objectives) or the Chebyshev metric (i.e., minimizing the maximum difference in all objectives) possibly considering weights, i.e., the differences are not equally valued for all objectives. However, the reference point may also be a point representing attainable outcomes. In this case, the surrogate scalar function is referred to as an achievement scalarizing function, as it aims to reach or surpass the reference point. These approaches are commonly referred to as reference point techniques.

The techniques will be presented for MOLP problems (cf. formulation (2.1) in Chap. 2) and then extended to integer and nonlinear cases. The theorems underlying the techniques for computing nondominated solutions are just sufficient conditions for efficiency. When these conditions are also necessary, then the corresponding technique guarantees the possibility to compute all nondominated solutions. Although this section pays special attention to sufficient conditions, necessary conditions shall not be forgotten since it is important to know the conditions in which all the nondominated solutions can be obtained using a given scalarizing technique.

3.1 Optimizing One of the Objective Functions and Transforming the Remaining p−1 into Constraints

Proposition 1

If x ¹ is the single optimal solution, for some i, to the problem

$$ \begin{array}{l} \max\;{f}_i\left(\mathbf{x}\right)\\ {}\mathrm{s}.\mathrm{t}. \mathbf{x}\in X\\ {} {f}_k\left(\mathbf{x}\right)\ge\ {\mathrm{e}}_k k=1, \dots, i-1,i+1, \dots p\end{array} $$

(3.1)

then x ¹ is an efficient solution to the multiobjective problem.

If, in Proposition 1, the condition of a single optimal solution had not been imposed, weakly efficient solutions could be obtained. This issue could be overcome by replacing the function f _i (x) by ${f}_i\left(\mathbf{x}\right)+{\displaystyle \sum_{k\ne i}{\uprho}_k}{f}_k\left(\mathbf{x}\right)$, with ρ _k  > 0 small positive scalars.

The validity of this proposition assumes that the reduced feasible region is not empty, which may occur whenever the lower bounds e _k set on the p-1 objective functions that are transformed into constraints are too stringent.

The truthfulness of Proposition 1 is easily shown. Suppose that x ¹ is not efficient. Then, by definition of efficient solution, there is an x ²∈X such that f _k (x ²) ≥ f _k (x ¹) for all k (k = 1, …, p), and the inequality f _k (x ²) > f _k (x ¹) holds for at least one k. In these circumstances, f _k (x ²) ≥ e_k, for k = 1, …, i−1, i + 1, …, p. Hence, f _i (x ²) ≥ f _i (x ¹) in problem (3.1) which contradicts the hypothesis of x ¹ being the single optimal solution. Thus, x ¹ must be efficient.

This computation procedure is illustrated in a bi-objective LP model (Fig. 3.1), where f ₁(x) and f ₂(x) are maximized. The efficient frontier of the feasible region X is composed by the solutions on edges [AB] and [BC]. Imposing the additional constraint f ₁(x) ≥ e₁ and optimizing f ₂(x) then the efficient solution E is obtained. Note that E is not a vertex of the feasible region to the original problem.

Fig. 3.1

Computing an efficient solution by optimizing one of the objective functions and transforming the remaining p−1 into constraints

The condition established in Proposition 1 is not a necessary condition for obtaining efficient solutions. In fact, efficient solutions can be obtained without having a single optimum to the scalarizing problem (3.1). In this case, not all solutions obtained are guaranteed to be efficient. If the optimum is not imposed to be unique, then a necessary and sufficient condition for obtaining at least weakly efficient solutions is achieved.

Figure 3.2 illustrates this issue: imposing f ₁(x) ≥ e₁ and optimizing f ₂(x) then the edge [CF] is optimal but only point C is (strictly) efficient. Solutions on the edge [CF], except C, are just weakly efficient solutions.

Fig. 3.2

Computation of weakly efficient solutions

An additional interest of this scalarizing technique is that the dual variable associated with the constraint corresponding to objective function f _k (x) can be interpreted as a local trade-off rate between objectives f _i (x) and f _k (x) at the optimal solution of the scalar problem (3.1). The interpretation and use of this information should be done with care whenever this optimal solution is a degenerate one, since it this case the trade-off rates are not unique (i.e., alternative optima to the dual problem exist).

Although this scalarizing technique is simple to be understood by the DM, capturing the attitude of giving more importance to an objective function and accepting lower bounds on the other objective function values, the choice of the objective function to be optimized may reveal to be difficult in several problems. Also, in the operational framework of a particular method, setting the objective function to be optimized throughout the solution computation process may render the method less flexible and the results too dependent on the function selected.

Solving problem (3.1) enables to obtain all nondominated solutions, i.e., solutions lying on edges or faces (of any dimension) and vertices of the feasible region of the original multiobjective problem.

The preference information associated with this scalarizing technique consists in:

• inter-objective information: the selection of the objective function to be optimized;

• intra-objective information: establishing lower bounds on the other objective functions that are transformed into constraints.

This scalarizing technique can also be used in multiobjective integer, mixed-integer or nonlinear optimization, thus enabling to obtain any type of efficient/nondominated solution to these problems.

Figure 3.3 illustrates examples of bi-objective (a) integer and (b) nonlinear problems, in which f ₁(x) is optimized and f ₂(x) is considered as an additional constraint. In (a) unsupported nondominated solution C is obtained, and in (b) improper solution B is obtained.

Fig. 3.3

Optimization of an objective function considering the other as an additional constraint in the cases of (a) integer and (b) nonlinear bi-objective problems

3.2 Optimizing a Weighted-Sum of the Objective Functions

The process of computation of efficient/nondominated solutions more utilized consists in solving a scalar problem in which the objective function is a weighted-sum of the p original objective functions with positive weights λ _k :

$$ \begin{array}{l} \max\ {z}_{\uplambda}={\displaystyle \sum_{k=1}^p{\uplambda}_k{f}_k\left(\mathbf{x}\right)}\\ {}\mathrm{s}.\mathrm{t}. \mathbf{x}\in X\end{array} $$

(3.2)

Proposition 2

If x ¹ ∈ X is a solution to the problem $\underset{\mathbf{x}\in X}{ \max}\sum_{k=1}^p{\uplambda}_k{f}_k\left(\mathbf{x}\right)$ for $\boldsymbol{\uplambda} =\left({\uplambda}_1,\cdots, {\uplambda}_p\right)$, where λ _k >0, k = 1, …, p, and ${\displaystyle \sum_{k=1}^p{\uplambda}_k=1}$, then x ¹ is an efficient solution to the multiobjective problem.

The truthfulness of Proposition 2 can be shown as follows. Suppose that x ¹ is not efficient. Then, there is an x ² ∈ X such that f _k (x ²) ≥ f _k (x ¹), k = 1, …, p, and the inequality is strict for at least one k. But x ¹ was obtained by optimizing a weighted-sum objective function with strictly positive weights; then ${\displaystyle \sum_{k=1}^p{\uplambda}_k}{f}_k\left({\mathbf{x}}^2\right)>{\displaystyle \sum_{k=1}^p{\uplambda}_k}{f}_k\left({\mathbf{x}}^1\right)$, which contradicts the hypothesis that x ¹ maximizes the weighted-sum objective function.

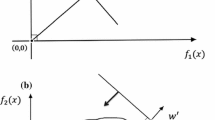
This computation procedure in MOLP is illustrated in Fig. 3.4. This figure also shows two weighted-sum objective functions, considering very different weight vectors (whose gradients are given by f _λ′ and f _λ″), can lead to the computation of the same efficient solution (point A).

Fig. 3.4

Optimizing weighted-sums of the objective functions

The weight normalization used in Proposition 2, ${\displaystyle \sum_{k=1}^p{\uplambda}_k=1}$, can be replaced by λ _i =1, for a given i, 1 ≤ i ≤ p, and λ _k  > 0 and bounded (for k = 1, …, p, and k ≠ i). Nothing is substantially changed since only the weighted-sum vector direction is important. Both weight normalization procedures are illustrated in Fig. 3.5 for the bi-objective case.

Fig. 3.5

Weight normalization

This scalarizing technique can also be applied to integer, mixed-integer and nonlinear programming problems, but it does not allow to obtain unsupported nondominated solutions. Figure 3.6 illustrates the case of integer programming. Solutions B and D are alternative optimal solutions to the weighted-sum objective function with the gradient f _λ. A slight increase of the weight assigned to f ₁(x) leads to solution D only and a slight increase of the weight assigned to f ₂ (x) leads to solution B only; there is no weight vector allowing to reach nondominated solution C, which is unsupported.

Fig. 3.6

Optimization of a weighted-sum of the objective functions in integer programming

In the example of Fig. 3.7, the feasible region Z in the space of the objective functions is convex.

Fig. 3.7

Nonlinear convex problem

Solutions A′ and B′ are nondominated and it is not possible to obtain them by optimizing $\underset{\mathbf{x}\in X}{ \max}\left\{{\uplambda}_1\;{f}_1\left(\mathbf{x}\right)+{\uplambda}_2\;{f}_2\left(\mathbf{x}\right)\right\}$, with both weights strictly positive. In this problem the solutions A′ and B′ are improper, since $\frac{\partial {f}_2}{\partial {f}_1}$(A′) = 0 and $\frac{\partial {f}_2}{\partial {f}_1}$(B′) = −∞, that is, the variation rate of f ₂(x) regarding f ₁(x) is zero and infinite, respectively (the concept of proper/improper nondominated solution is presented in Chap. 2).

In a (nonlinear) problem in which the feasible region is convex and the objective functions are concave it is possible to compute all proper nondominated solutions using strictly positive weights. If the problem has improper nondominated solutions then these can also be obtained by optimizing a weighted-sum allowing weights equal to zero.

Therefore, since all nondominated solutions in MOLP are proper and supported this scalarizing technique can provide the basis for methods to find the entire set of nondominated solutions (the so-called generating methods).

3.2.1 Indifference Regions on the Weight Space in MOLP

The graphical representation of the weight set that leads to the same basic feasible solution (note that each vertex may correspond to more than one basic solution if degeneracy occurs), is called indifference region and can be obtained through the decomposition of the parametric (weight) space λ ∈ Λ = {λ∈ℝ^p: λ _k  > 0, k = 1, …, p, ${\displaystyle {\sum}_{k=1}^p{\uplambda}_k=1\Big\}.}$ The DM can be “indifferent” to all combinations of weights within this region because they lead to the same efficient solution.

The indifference regions depend on the objective function coefficients and the geometry of the feasible region. The analysis of the parametric (weight) space can be used as a valuable tool to learn about the geometry of the efficient/nondominated region in MOLP, since it gives the weight vectors leading to each efficient basic solution.

Let us start by exemplifying the computation of indifference regions for a problem with two objective functions:

$$ \begin{array}{l} \max\ {\mathrm{z}}_1={f}_1\left(\mathbf{x}\right) = 5{x}_1 + 3{x}_2\\ {} \max\ {\mathrm{z}}_2={f}_2\left(\mathbf{x}\right) = 2{x}_1 + 8{x}_2\end{array} $$

s. t.

$$ \left.\begin{array}{l}{x}_1+4{x}_2\le 100\\ {}3{x}_1+2{x}_2\le 150\\ {}5{x}_1+3{x}_2\ge 200\\ {}{x}_1,{x}_2\ge 0\end{array}\right\}\left(\mathrm{feasible}\ \mathrm{region}X\right) $$

In Fig. 3.8, [AC] represents the set of efficient solutions and [A′C′] represents the corresponding set of nondominated solutions. The slope of [A′C′] is −20. The slope of the level lines of the weighted-sum objective functions, ${\uplambda}_1 {f}_1\left(\mathbf{x}\right)+{\uplambda}_2 {f}_2\left(\mathbf{x}\right)$, in the objective function space, is given by $-\frac{\uplambda_1}{\uplambda_2}$. We consider the weights are normalized: ${\displaystyle \sum_{k=1}^2{\uplambda}_k=1}$, i.e., λ₂ = 1–λ₁. Then, the indifference regions associated with vertex A and vertex C, i.e., the sets of weights for which solving the problem $\underset{\mathbf{x}\in X}{ \max}\left\{{\uplambda}_1\;{f}_1\left(\mathbf{x}\right)+{\uplambda}_2\;{f}_2\left(\mathbf{x}\right)\right\}$ leads to A and C, respectively, are obtained with ${\uplambda}_1\in (0, \frac{20}{21}\;]$ and ${\uplambda}_2\in [\frac{1}{21}, 1\;)$ for vertex A, and ${\uplambda}_1\in [\frac{20}{21}, 1\;)$ and ${\uplambda}_2\in (0, \frac{1}{21}\;]$ for vertex C.

Fig. 3.8

Efficient/nondominated basic solutions and indifference regions

For the weight values ${\uplambda}_1=\frac{20}{21}$ and ${\uplambda}_2=\frac{1}{21}$, points A and C are obtained simultaneously, since $\underset{\mathbf{x}\in X}{ \max}\left\{{\uplambda}_1\;{f}_1\left(\mathbf{x}\right)+{\uplambda}_2\;{f}_2\left(\mathbf{x}\right)\right\}$ leads to edge [AC] as alternative optima.

The determination of the indifference regions in the parametric (weight) diagram for this bi-objective problem was carried out just using the information derived from the geometry of the problem. However, the computation of indifference regions can be done using the multiobjective simplex tableau (i.e., with one reduced cost row for each objective function). In particular, the study of problems with three-objective functions allows a meaningful graphical representation of indifference regions using the information available in the simplex tableau corresponding to a basic (vertex) solution as a result of optimizing a weighted-sum scalarizing function $\underset{\mathbf{x}\in X}{ \max}\left\{{\uplambda}_1\;{f}_1\left(\mathbf{x}\right)+{\uplambda}_2\;{f}_2\left(\mathbf{x}\right)+{\uplambda}_3\;{f}_3\left(\mathbf{x}\right)\right\}$ with a given weight vector.

The simplex tableau associated with an efficient basic solution offers the information needed to compute the locus of the weights λ _k (k = 1, …, p) for which the solution to the weighted-sum problem

$$ \begin{array}{l} \max {\displaystyle \sum_{k=1}^p{\uplambda}_k{f}_k\left(\mathbf{x}\right)}\\ {}\mathrm{s}.\mathrm{t}. \mathbf{x}\in X\end{array} $$

with λ∈Λ = {λ∈ℝ^p: λ _k  > 0, k =1,…,p, ${\displaystyle {\sum}_{k=1}^p{\uplambda}_k=1\Big\}}$ leads to the same efficient basic solution.

For a single objective LP a basic feasible solution to

$$ \begin{array}{l} \max\ \mathrm{z} = \mathbf{c}\mathbf{x}\\ {}\mathrm{s}.\ \mathrm{t}.\mathbf{x}\ \mathrm{\in X}=\left\{\mathbf{x}\in {\mathbb{R}}^n:\mathbf{Ax}=\mathbf{b},\mathbf{x}\ge \mathbf{0}\right\}\end{array} $$

is optimal if and only if uA−c ≥ 0, where the elements of the vector (uA−c) are called reduced costs (in general, the last row of the simplex tableau). u = c _B B ⁻¹ is a row vector (of dimension m), whose elements are the dual variables, B is the basis matrix corresponding to the current tableau (a sub-matrix m × m of A, with rank m) and c _B is a sub-vector of c, with dimension 1 × m, corresponding to the basic variables.

In MOLP the multiobjective simplex tableau includes a reduced cost row associated with each objective function:

A	b
−C	0

With respect to basis B this tableau can be transformed as:

x N	x B
B −1 N	I	B −1 b
C B B −1 N−C N	0	C B B −1 b

where B and N, C _B and C _N are the sub-matrices of A and C corresponding to the basic (x _B) and nonbasic (x _N) variables, respectively. W = C _B B ⁻¹ N−C _N is the reduced cost matrix associated with basis B.

In MOLP the set of weights λ for which the basic solution associated with the multiobjective simplex tableau is optimal to the weighted-sum problem is then given by {λW ≥ 0, λ∈Λ}.

Definition of efficient basis

B is an efficient basis if and only if it is an optimal basis to the weighted-sum problem (3.2) for some weight vector λ∈Λ, that is, B is an efficient basis if and only if the system{λW ≥ 0, λ∈Λ} is consistent.

Definition of efficient nonbasic variable

The nonbasic variable x _j is efficient with respect to basis B if and only if λ∈Λ exists such that

$$ \begin{array}{l}\boldsymbol{\uplambda} \mathbf{W}\ \ge \mathbf{0}\\ {}\boldsymbol{\uplambda} \mathbf{W}{.}_j=0\end{array} $$

where W. _j is the column vector of W corresponding to x _j (that is, the reduced cost of the weighted-sum function associated with x _j can be zero).

The definition of efficient nonbasic variable means that, for a given efficient basis, if x _j is an efficient nonbasic variable then any feasible pivot operation associated with x _j as entering variable leads to an adjacent efficient basis (i.e., obtained from the previous basis through the pivot operation). If the pivot operation leading from one basis B ₁ to an adjacent basis B ₂ is non-degenerate then the vertices of the feasible region associated with those bases are different and the edge that connects them is composed by efficient solutions. As the bases (vertices) are connected, then it is possible to develop a multiobjective simplex method as an extension of the (single objective) simplex method (Steuer 1986), using sub-problems to test the efficiency of nonbasic variables. This multiobjective simplex method is aimed at computing all efficient bases (vertices). Using this information it is also able to characterize efficient edges and efficient faces (of different dimensions).

The element w _kj of the reduced cost matrix W represents the rate of change of objective function f _k (x) due to a unit change of the nonbasic variable x _j that becomes basic. Each column of W associated with an efficient nonbasic variable represents the rate of change of the objective functions along the corresponding efficient edge emanating from the current vertex.

From the multiobjective simplex tableau corresponding to an efficient basic solution to the MOLP problem, the set of corresponding weights is defined by {λW ≥ 0, λ∈Λ} thus defining the indifference region. A common frontier to two indifference regions means that the corresponding efficient basic solutions are connected by an efficient edge, which is associated with an efficient nonbasic variable becoming a basic variable. If a point λ∈Λ belongs to several indifference regions, this means that these regions are associated with efficient solutions located on the same efficient face (this face is only weakly efficient if that point is located on the frontier of the parametric diagram, i.e., some weight λ _κ  = 0, k = 1, …, p).

The decomposition of the parametric (weight) diagram into indifference regions, i.e., the graphical representation of the set of weights λ leading to the same efficient basic solution is especially interesting in problems with three objective functions. Note that due to the normalization condition λ₁ + λ₂ + … + λ _p  = 1, Λ can be represented in a diagram of dimension p−1. For the three objective case, the weight diagram Λ = {λ∈ℝ³: λ _k  > 0, k = 1, 2, 3, and ${\displaystyle \sum_{k=1}^3{\uplambda}_k=1}\Big\}$ can be displayed using the equilateral triangle in Fig. 3.9a. Since ${\displaystyle \sum_{k=1}^3{\uplambda}_k=1}$ the diagram corresponding to the equilateral triangle, defined by the points λ = (1, 0, 0), λ = (0, 1, 0) and λ = (0, 0, 1), can be projected, for example, onto the plane (0, λ₁, λ₂), without loss of information (Fig. 3.9b).

Fig. 3.9

Parametric (weight) diagram

Example 1

$$ \max \mathbf{C}\ \mathbf{x}=\left[\begin{array}{cccc}\hfill 3\hfill & \hfill 1\hfill & \hfill 2\hfill & \hfill 1\hfill \\ {}\hfill 1\hfill & \hfill -1\hfill & \hfill 2\hfill & \hfill 4\hfill \\ {}\hfill -1\hfill & \hfill 5\hfill & \hfill 1\hfill & \hfill 2\hfill \end{array}\right] \left[\begin{array}{c}\hfill {x}_1\hfill \\ {}\hfill {x}_2\hfill \\ {}\hfill {x}_3\hfill \\ {}\hfill {x}_4\hfill \end{array}\right] $$

s. t.

$$ X\equiv \left\{\begin{array}{c}\hfill 2{x}_1+{x}_2+4{x}_3+3{x}_4\le 60\hfill \\ {}\hfill 3{x}_1+4{x}_2+{x}_3+2{x}_4\le 60\hfill \\ {}\hfill {x}_1\ge 0,{x}_2\ge 0,{x}_3\ge 0,{x}_4\ge 0\hfill \end{array}\right. $$

Let us compute the indifference region associated with the efficient basic solution that optimizes the weighted-sum problem with equal weights: $\underset{\mathbf{x}\in X}{ \max}\left\{\frac{1}{3}{f}_1\left(\mathbf{x}\right)+\frac{1}{3}{f}_2\left(\mathbf{x}\right)+\frac{1}{3}{f}_3\left(\mathbf{x}\right)\right\}$:

$$ \begin{array}{l}\underset{\mathbf{x}\in X}{ \max} \left\{\frac{1}{3}\left(3{x}_1+{x}_2+2{x}_3+{x}_4\right) + \frac{1}{3}\left({x}_1-{x}_2+2{x}_3+4{x}_4\right) + \frac{1}{3}\left(-{x}_1+5{x}_2+{x}_3+2{x}_4\right)\right\}\hfill \\ {}\underset{\mathbf{x}\in X}{ \max} \left\{{x}_1+\frac{5}{3}{x}_2+\frac{5}{3}{x}_3+\frac{7}{3}{x}_4\right\}\hfill \end{array} $$

To build the multiobjective simplex tableau a reduced cost row for each objective function is added.

The problem $\underset{\mathbf{x}\in X}{ \max} \left\{\frac{1}{3}{f}_1\left(\mathbf{x}\right)+\frac{1}{3}{f}_2\left(\mathbf{x}\right)+\frac{1}{3}{f}_3\left(\mathbf{x}\right)\right\}$ is solved and the reduced cost rows corresponding to the objective functions of the original problem are updated in each pivot operation. s ₁ and s ₂ denote the slack variables associated with the constraints.

${z}_j^{\uplambda}-{c}_j^{\uplambda}$ denotes the reduced cost row of the weighted-sum objective function while ${z}_j^k-{c}_j^k$ denotes the reduced cost row of each objective function f _k (x). Note that ${z}_j^{\uplambda}-{c}_j^{\uplambda}$ is the weighted-sum of ${z}_j^k-{c}_j^k$ (k = 1, 2, 3), i.e., ${z}_j^{\uplambda}-{c}_j^{\uplambda}={\displaystyle \sum_{k=1}^3{\uplambda}_k\left({z}_j^k-{c}_j^k\right)}$ for all nonbasic variables x _j .

The initial tableau is:

		x 1	x 2	x 3	x 4	s 1	s 2
	s 1	2	1	4	3	1	0	60
	s 2	3	4	1	2	0	1	60
Reduced cost row of the weighted−sum objective function	${z}_j^{\uplambda}-{c}_j^{\uplambda}$	−1	$-\frac{5}{3}$	$-\frac{5}{3}$	$-\frac{7}{3}$	0	0	0
Reduced cost matrix	z 1−c 1	−3	−1	−2	−1	0	0	0
	z 2−c 2	−1	1	−2	−4	0	0	0
	z 3−c 3	1	−5	−1	−2	0	0	0

The optimal tableau associated with the basic solution that solves $\underset{\mathbf{x}\in X}{ \max}\left\{\frac{1}{3}{f}_1\left(\mathbf{x}\right)+\frac{1}{3}{f}_2\left(\mathbf{x}\right)+\frac{1}{3}{f}_3\left(\mathbf{x}\right)\right\}$ is

	x 1	x 2	x 3	x 4	s 1	s 2
x 4	$\frac{1}{2}$	0	$\frac{3}{2}$	1	$\frac{2}{5}$	$-\frac{1}{10}$	18
x 2	$\frac{1}{2}$	1	$-\frac{1}{2}$	0	$-\frac{1}{5}$	$\frac{3}{10}$	6
${z}_j^{\uplambda}-{c}_j^{\uplambda}$	1	0	1	0	$\frac{3}{5}$	$\frac{4}{15}$	52
z 1−c 1	−2	0	−1	0	$\frac{1}{5}$	$-\frac{1}{5}$	24
z 2−c 2	$\frac{1}{2}$	0	$\frac{9}{2}$	0	$\frac{9}{5}$	$\frac{7}{10}$	66
z 3−c 3	$\frac{9}{2}$	0	$-\frac{1}{2}$	0	$-\frac{1}{5}$	$\frac{13}{10}$	66

The set of weights (λ₁, λ₂, λ₃) > 0, with λ₃ = 1 − λ₁ − λ₂, for which this basic solution is optimal to the weighted-sum scalar problem and therefore efficient to the MOLP problem is given by

$$ \left\{\begin{array}{l}-2{\uplambda}_1+\frac{1}{2}{\uplambda}_2+\frac{9}{2} \left(1-{\uplambda}_1-{\uplambda}_2\right)\ge 0 \left(\mathrm{a}\right)\hfill \\ {}-{\uplambda}_1+\frac{9}{2}{\uplambda}_2-\frac{1}{2} \left(1-{\uplambda}_1-{\uplambda}_2\right)\ge 0 \left(\mathrm{b}\right)\hfill \\ {}\frac{1}{5}{\uplambda}_1+\frac{9}{5}{\uplambda}_2-\frac{1}{5} \left(1-{\uplambda}_1-{\uplambda}_2\right)\ge 0 \left(\mathrm{c}\right)\hfill \\ {}\frac{1}{5}{\uplambda}_1-\frac{7}{10}{\uplambda}_2+\frac{13}{10} \left(1-{\uplambda}_1-{\uplambda}_2\right)\ge 0 \left(\mathrm{d}\right)\hfill \end{array}\right. $$

Each of these constraints in (λ₁, λ₂, λ₃) is associated with a nonbasic variable w. r. t. the present basis. This set of constraints can be written as a function of (λ₁, λ₂):

$$ \left\{\begin{array}{ll}\frac{13}{2}{\uplambda}_1+4{\uplambda}_2\le \frac{9}{2}\hfill & \left(\mathrm{a}\right)\hfill \\ {}-\frac{1}{2}{\uplambda}_1+5{\uplambda}_2\ge \frac{1}{2}\hfill & \left(\mathrm{b}\right)\hfill \\ {}\frac{2}{5}{\uplambda}_1+2{\uplambda}_2\ge \frac{1}{5}\hfill & \left(\mathrm{c}\right)\hfill \\ {}\frac{11}{10}{\uplambda}_1+2{\uplambda}_2\le \frac{13}{10}\hfill & \left(\mathrm{d}\right)\hfill \end{array}\right. $$

Constraints (a), (b) and (d) delimit the indifference region D (Fig. 3.10). Therefore, the corresponding nonbasic variables x ₁, x ₃ and s ₂ are efficient. Any weight vector λ∈Λ satisfying these constraints leads to a weighted-sum problem $\underset{\mathbf{x}\in X}{ \max}\left\{{\uplambda}_1\;{f}_1\left(\mathbf{x}\right)+{\uplambda}_2\;{f}_2\left(\mathbf{x}\right)+{\uplambda}_3\;{f}_3\left(\mathbf{x}\right)\right\}$ whose optimal solution is the same efficient basis, i.e., the one determined by optimizing the problem $\underset{\mathbf{x}\in X}{ \max} \left\{\frac{1}{3}{f}_1\left(\mathbf{x}\right)+\frac{1}{3}{f}_2\left(\mathbf{x}\right)+\frac{1}{3}{f}_3\left(\mathbf{x}\right)\right\}$. Constraint (c) is redundant, i.e., it does not contribute to define the indifference region associated with the efficient solution (x ₄, x ₂) = (18, 6), (z ₁, z ₂, z ₃) = (24, 66, 66). Therefore, the corresponding nonbasic variable s₁ is not efficient.

Fig. 3.10

Indifference region associated with efficient basic solution D

Constraints (a), (b) and (d) correspond to edges of the efficient region emanating from the current vertex, solution D. “Crossing” these constraints leads to efficient vertices adjacent to D. For instance, making x ₁ a basic variable leads to an adjacent efficient basic solution (vertex) whose indifference region is contiguous to D and delimited by constraint $\frac{13}{2}{\uplambda}_1+4{\uplambda}_2\ge \frac{9}{2}$ (opposite to (a) above). Therefore, x ₁, as well as x ₃ and s ₂ (but not s ₁), are efficient nonbasic variables because, when becoming basic variables, each one leads to an adjacent efficient vertex solution (with the corresponding indifference region) through an efficient edge, i.e., an edge composed of efficient solutions only. Note that there may exist an edge connecting two efficient vertex solutions that is not composed of efficient solutions.

Efficient nonbasic variables can be identified in the multiobjective simplex tableau. In problems with two or three objective functions, efficient nonbasic variables can also be recognized from the display of indifference regions in the parametric (weight) diagram.

3.3 Minimizing a Distance/Achievement Function to a Reference Point

The minimization of the distance, according to a certain metric, of the feasible region to a reference point defined in the objective function space can be used to compute nondominated solutions.

The ideal solution z* is often used as reference point. The rationale is that it offers the best value for each evaluation dimension reachable in the feasible region, since its components result from optimizing individually each objective function. If the reference point represents an attainable outcome, the scalarizing function is called an achievement scalarizing function, as it aims to reach or surpass the reference point.

3.3.1 A Brief Review of Metrics

A metric is a distance function that assigns a scalar $\left\Vert {\mathbf{z}}^1-{\mathbf{z}}^2\right\Vert$ ∈ℝ to each pair of points z ¹, z ² ∈ℝⁿ (where n is the dimension of the space).

For the L _q metric the distance between two points in ℝⁿ is given by:

$$ \begin{array}{l}{\left\Vert {\mathbf{z}}^1-{\mathbf{z}}^2\right\Vert}_q={\left[{\displaystyle \sum_{i=1}^n{\left|\;{z}_i^1-{z}_i^2\right|}^q}\right]}^{\frac{1}{q}}q\in \left\{1,2,\dots \right\}{\left\Vert\;{\mathbf{z}}^1-{\mathbf{z}}^2\right\Vert}_{\infty }=\underset{i=1,\dots, n}{ \max\;}\;\left|\;{z}_i^1-{z}_i^2\right|\end{array} $$

The loci of the points at the same distance from z* (isodistance contour), according to the metrics L ₁, L ₂ and ${L}_{\infty }$ are displayed in Fig. 3.11.

Fig. 3.11

Loci of equidistant points from z* for L ₁, L ₂ and ${L}_{\infty }$ metrics

In Fig. 3.12 a, b and c, points A, B and C minimize the distance of region Z to z*, using the metrics L ₁, L ₂ and ${L}_{\infty }$, respectively.

Fig. 3.12

Nondominated solutions that minimize the distance to the ideal solution according to L ₁, L ₂ and ${L}_{\infty }$ metrics. (a) Point A minimizes the distance to z* according to the L ₁ metric. (b) Point B minimizes the distance to z* according to the L ₂ metric. (c) Point C minimizes the distance to z* according to the ${L}_{\infty }$ metric

The metrics L ₁, L ₂ and ${L}_{\infty }$ are especially important. L ₁ is the sum of all components of $\left|{\mathbf{z}}^1-{\mathbf{z}}^2\right|$, i.e., the city block distance in a “rectangular city” as Manhattan. L ₂ is the Euclidean distance. ${L}_{\infty }$ is the Chebyshev distance in which only the worst case is considered, i.e., the largest difference component in $\left| {\mathbf{z}}^1-{\mathbf{z}}^2 \right|$.

A weighted family of L ^λ _q metrics can also be defined, where the vector λ ≥ 0 is used to assign a different scale (or “importance”) factor to the multiple components:

$$ \begin{array}{l}{\left\Vert\;{\mathbf{z}}^1-{\mathbf{z}}^2\right\Vert}_q^{\uplambda}={\left[{\displaystyle \sum_{i=1}^n{\left({\uplambda}_i\left|\;{z}_i^1-{z}_i^2\right|\right)}^q}\right]}^{\frac{1}{q}}q\in \left\{1,2,\dots \right\}{\left\Vert\;{\mathbf{z}}^1-{\mathbf{z}}^2\right\Vert}_{{}_{\infty}}^{\uplambda}=\underset{i=1,\dots, n}{ \max} {\uplambda}_i\left|\;{z}_i^1-{z}_i^2\right|\end{array} $$

The loci of points at the same distance of z*, according to the weighted L ^λ₁ , L ^λ₂ , and ${L}_{\infty}^{\uplambda}$ metrics are illustrated in Fig. 3.13, representing the isodistance contour for each metric with λ₁ < λ₂.

Fig. 3.13

Loci of points equidistant from z*, for L ^λ₁ , L ^λ₂ and ${L}_{\infty}^{\lambda }$ metrics

The external isodistance contour ${L}_{\infty}^{\uplambda, \uprho}$ presented in Fig. 3.14 regards to ${\left\Vert {\mathbf{z}}^1-{\mathbf{z}}^2\right\Vert}_{{}_{\infty}}^{\uplambda}$ + ${\displaystyle \sum_{i=1}^2 {\uprho}_i}\left|\;{z}_i^1-{z}_i^2\right|$, with a small positive ρ _i , which can be seen as a combination of ${L}_{\infty}^{\uplambda}$ and L ^λ₁ metrics. This is generally called the augmented weighted Chebyshev metric, ${L}_{\infty}^{\uplambda, \rho }$.

Fig. 3.14

Loci of points equidistant from z*, for ${L}_{\infty}^{\lambda }$ and ${L}_{\infty}^{\lambda, \rho }$

Although L ^λ _q , for $q\in \left\{1,2,\dots \right\}$, can be used to determine nondominated solutions by solving scalar problems involving the minimization of a distance to a reference point, we will formally present only the case using the Chebyshev metric (${L}_{\infty}^{\uplambda}$). This metric is important since it captures the attitude of minimizing the largest difference, i.e., the worst deviation, to the value that is desired in all evaluation dimensions. In general, the ${L}_{\infty}^{\uplambda, \rho }$ metric is used to guarantee that the solutions obtained are nondominated and not just weakly nondominated.

Proposition 3

If x ¹∈X is a solution to the problem (3.3)

$$ \underset{\mathbf{x}\in X}{ \min} \left\{ \underset{k=1,\dots, p}{ \max} {\uplambda}_k\left[{z}_k^{*}-{f}_k\left(\mathbf{x}\right)\right] - {\displaystyle \sum_{k=1}^p{\uprho}_{k\;}}{f}_k\left(\mathbf{x}\right)\right\},\ \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{some}\;\boldsymbol{\uplambda} \ge \mathbf{0} $$

(3.3)

where the ρ _k are small positive scalars, then x ¹ is an efficient solution to the multiobjective problem.

This surrogate problem entails determining the feasible solution that minimizes the distance based on an augmented weighted Chebyshev metric to the ideal solution.

The truthfulness of Proposition 3 can be shown as follows. Let us suppose that x ¹ is not an efficient solution and is optimal to problem (3.3), with $\underset{k=1,\dots, p}{max} {\uplambda}_k\left[{z}_k^{*}-{f}_k\left(\mathbf{x}\right)\;\right]={v}_1$. Therefore, there is a solution x ² such that ${f}_k\left({\mathbf{x}}^2\right)\ge {f}_k\left({\mathbf{x}}^1\right)$, k = 1,…, p, and the inequality is strict for at least one k. In these circumstances, ${\uplambda}_k \left({z}_k^{*}-{f}_k\;\left({\mathbf{x}}^2\right)\right)\le {v}_1$, k = 1, …, p, and ${\displaystyle \sum_{k=1}^p{\uprho}_{k\;}}{f}_k\left({\mathbf{x}}^2\right)>{\displaystyle \sum_{k=1}^p{\uprho}_{k\;}}{f}_k\left({\mathbf{x}}^1\right)$. Hence, x ¹ would not be optimal to (3.3), which contradicts the hypothesis. Therefore, x ¹ has to be efficient.

Proposition 3 also establishes a necessary condition for efficiency in MOLP, for sufficiently small ρ _k . Therefore, this scalarizing technique enables to obtain the entire set of efficient/nondominated solutions to a MOLP problem.

The computation process is illustrated in Fig. 3.15. Point D is the solution that minimizes the distance to z ^*according to ${L}_{\infty}^{\uplambda, \rho }$ (3.3) or ${L}_{\infty}^{\uplambda}$ ((3.3) without the term ${\displaystyle \sum_{k=1}^p{\uprho}_k\;{f}_k\Big(\mathbf{x}}\Big)$), considering a particular weight vector λ, where λ₁ < λ₂. Note that $\frac{d_v}{d_h}$ = $\frac{\uplambda_1}{\uplambda_2}$.

Fig. 3.15

Minimizing the augmented weighted Chebyshev distance

The term ${\displaystyle \sum_{k=1}^p{\uprho}_k\;{f}_k\Big(\mathbf{x}}\Big)$ is used to avoid solutions that are only weakly efficient when the scalarizing problem (3.3) has alternative optimal solutions (Fig. 3.16). Considering λ₁ = 0, all solutions on the horizontal line passing through z ^* are equidistant from z ^* according to ${L}_{\infty}^{\uplambda}$. The consideration of ${L}_{\infty}^{\uplambda, \rho }$ enables to obtain the strictly nondominated solution A.

Fig. 3.16

Illustration of the weighted Chebyshev metric and the augmented weighted Chebyshev metric

Problem (3.3) is equivalent to the programming problem (3.4):

$$ \min \left\{ v-{\displaystyle \sum_{k=1}^p{\uprho}_k\ {f}_k\Big(\mathbf{x}}\Big) \right\} $$

s.t.

$$ \begin{array}{l}{\uplambda}_k\left( {z}_k^{*}-f\left(\mathbf{x}\right) \right)\ \le\ v k=1,\dots, p\\ {}\mathbf{x}\in X\\ {}v\ge 0\end{array} $$

(3.4)

Other reference points can be used. The components of the reference point represent the values that the DM would like to attain for each objective function. For this purpose the ideal solution z* is interesting because its components are the best values that can be reached for each objective function in the feasible region.

Figure 3.17 displays the computation of nondominated solutions by minimizing an augmented weighted Chebyshev distance to the unattainable reference point q. In the example of Fig. 3.17, minimizing a (non-augmented) Chebyshev distance would enable to compute all solutions on segment [AB]; however, these solutions are just weakly nondominated except solution B, which is strictly nondominated.

Fig. 3.17

Minimizing an augmented weighted Chebyshev distance to a reference point

If the reference point is in the interior of the feasible region, i.e., it is dominated, it is no longer possible to consider a Chebyshev metric, but this technique for computing nondominated solutions is still valid considering the auxiliary variable v unrestricted in sign in problem (3.4). In these circumstances, this is an achievement scalarizing program. Figure 3.18 shows the projection of a reference point q located in the interior of the feasible region onto the nondominated frontier. z ¹ is the nondominated solution that is obtained through the resolution of problem (3.4), with q replacing z* and considering variable v unrestricted in sign. In the case illustrated in Fig. 3.18, λ₁ < λ₂.

Fig. 3.18

Projection of a dominated reference point located in the interior of the feasible region onto the nondominated frontier

This technique for computing nondominated solutions is valid for more general cases than MOLP.

Figure 3.19 illustrates a nonlinear problem: the point that minimizes the distance to the reference point q, using the augmented weighted Chebyshev metric, is a nondominated solution (point X′). Changing the weights, all nondominated solutions can be computed, i.e., solutions on the arcs B′A′, except B′ (which is weakly nondominated) and C′D′. Note that q > z* is necessary to guarantee that D′ and A′ are obtained.

Fig. 3.19

Finding nondominated solutions in a nonlinear problem using the augmented weighted Chebyshev metric

Figure 3.20 illustrates the integer programming case. Using the (augmented) weighted Chebyshev metric it is possible to reach all nondominated solutions including unsupported solution C. Note that C was unreachable by optimizing weighted sums of the objective functions (Fig. 3.6).

Fig. 3.20

The augmented Chebyshev metric in integer programming

3.4 Classification of Methods to Compute Nondominated Solutions

Different classifications of MOP methods have been proposed according to several parameters, such as the degree of intervention of the DM, the type of modeling of the DM’s preferences, the number of decision makers, the inputs required and the outputs generated, etc. (Cohon 1978; Hwang and Masud 1979; Chankong and Haimes 1983; Steuer 1986).

The classification based on the degree of intervention of the DM establishes, in general, the following categories:

• (a) A priori articulation of the DM’s preferences. Once the method is chosen (and possibly some parameters are fixed), the preference aggregation is established.

• (b) Progressive articulation of the DM’s preferences. This occurs in interactive methods, which comprise a sequence of computation phases (of nondominated solutions) and dialogue phases. The DM’s input in the dialogue phase in face of one solution (or a set of solutions in some cases) generated in the computation phase is used to prepare the next computation phase with the aim to obtain another nondominated solution more in accordance with his/her expressed preferences. The characteristics of the dialogue and computation phases, as well as the stopping conditions of the interactive process, depend on the method. Chap. 4 is entirely devoted to interactive methods.

• (c) A posteriori articulation of the DM’s preferences. This deals with methods for characterizing the entire set of nondominated solutions, and the aggregation of the DM’s preferences is made in face of the nondominated solutions obtained.

The classification based on the modeling of the DM’s preferences generally considers the establishment of a global utility function, priorities between the objective functions, aspiration levels or targets for the objective functions, pairwise comparisons (either of solutions or objective functions) or marginal rates of substitution.

The classification based on the number of decision makers encompasses the situations where a single or several DM are at stake.

The classification based on the type of inputs required and outputs generated consider the type and reliability of data, the participation of the DM in the modeling phase, either the search for the best compromise nondominated solution or a satisfactory solution, selecting, ranking or clustering the solutions.

Other classifications of MOP methods are used according to the fields of application (e.g., systems engineering, project evaluation, etc.).

3.5 Methods Based on the Optimization of an Utility Function

In this type of approach, an utility function U[f ₁(x), f ₂(x), …, f _p (x)] is built. If (concave) function U satisfies certain properties, the optimum of U[f(x)] belongs to the set of nondominated solutions (Steuer 1986). In Fig. 3.21 an illustrative example is presented.

Fig. 3.21

Example of the use of utility functions

The curves U[f ₁(x), f ₂(x), …, f _p (x)] = κⁱ, with κⁱ constant, are called indifference curves, and the point belonging to the nondominated solution set which is tangent to one indifference curve is called compromise point (Fig. 3.21).

The utility functions may have the following structure:

$$ \mathrm{U}\left[{f}_1\left(\mathbf{x}\right),{f}_2\left(\mathbf{x}\right), \dots, {f}_p\left(\mathbf{x}\right)\right] = {\mathrm{U}}_1\left[{f}_1\left(\mathbf{x}\right)\right] + \dots + {\mathrm{U}}_p\left[{f}_p\left(\mathbf{x}\right)\right] $$

The weighted-sum of the objective functions may be faced as a particular case of this utility function structure. The “relative importance” of the objective functions may be taken into account through the assignment of a weight vector. If the problem under study is linear and U[f(x)] is linear then the problem to be solved is also a single objective LP problem.

3.6 The Lexicographic Method

In this method the objective functions are ranked according to the DM’s preferences and then they are sequentially optimized. In each step, an objective function f _k (x) is optimized and an equality constraint is added to the next optimization problems taken into account the optimal value obtained (${f}_k\left(\mathbf{x}\right)={z}_k^{*}$). In some cases the constraint is not an equality, i.e., deviations w. r. t. the obtained optima are allowed. Note that by adopting the first option, if the optimum of the first ranked objective function is unique, then the procedure stops. This method may be considered an a priori method just requiring ordinal information.

3.7 Goal Programming

Goal programming may be viewed as the “bridge” between single objective and MOP, namely concerning reference point approaches. The aim is to minimize a function of the deviations regarding targets (O ₁, …, O _p ) established by the DM for the objective functions. A possible formulation consists in the minimization of a weighted sum of the deviations, with non-negative weights α_k and β_k:

$$ \min {\displaystyle \sum_{k=1}^p\Big({\alpha}_k{d}_k^{-}}+{\beta}_k{d}_k^{+}\Big) $$

s. t.

$$ \begin{array}{l}{f}_k\left(\mathbf{x}\right)+{d}_k^{-}-{d}_k^{+}={O}_k k=1,\dots, p\\ {}\mathbf{x}\in X\\ {}{d}_k^{-}\ge 0,{d}_k^{+}\ge 0 k=1,\dots, p\end{array} $$

where ${d}_k^{-}$ and ${d}_k^{+}$ are negative and positive deviations regarding goal k, respectively.

The targets established by the DM may lead to a dominated solution to the problem under study if the DM is not sufficiently ambitious in specifying his/her goals. In this case, the goal programming model leads to a satisfactory solution, but it may not belong to the nondominated solution set. For further details about different versions of goal programming see, for example, Steuer (1986) or Romero (1991).

3.8 The Multiobjective Simplex Method for MOLP

The algorithms based on the extension of the simplex method for computing the set of efficient vertices (basic solutions) in MOLP can be structured as follows:

• (a) Computation of an efficient vertex. For instance, this can be done by optimizing a weighted-sum of the objective functions as explained above.

• (b) Computation of the remaining efficient vertices by

  • 1. computing the adjacent efficient bases (Zeleny 1974; Yu and Zeleny 1975; Steuer 1986);

  • 2. computing the adjacent efficient vertices (Evans and Steuer 1973; Steuer 1986).

  • 3. using a parametric technique.

In (b1) and (b2) a theorem presented, for instance, in Yu and Zeleny (1975) is used, which establishes the proof that the set of efficient basic solutions is connected¹. This means that the entire set of efficient bases (or vertices) can be obtained, by exhaustively examining the adjacent bases of the set of efficient bases that are progressively obtained starting from the initial one, computed in (b).

Steuer (1986) and Zeleny (1974) use an efficiency test to verify whether each basis (or each vertex) under analysis is efficient or not.

Zeleny (1974) establishes several propositions aimed at exploring the maximum information contained in the multiobjective simplex tableau. This is an extension of the simplex method considering one additional row for each objective function and avoiding, whenever possible, unnecessary pivoting operations and the application of the efficiency test.

3.9 Proposed Exercises

• 1. Consider proposed exercise 1, Chap. 2.

  • (a) Formulate the problem to determine the solution that minimizes the distance to the ideal solution, according to the L _∞ metric. Obtain graphically and analytically (using an LP solver) the solution to this problem.

  • (b) Obtain graphically the solution that minimizes the distance to the ideal solution according to the L ₁ metric. Identify the efficient nonbasic variables for this solution

• 2. Consider proposed exercise 2, Chap. 2.

  • (a) Find the indifference regions in the parametric (weight) diagram corresponding to the efficient basic solutions that optimize each objective function individually.

  • (b) For each solution determined in (a), identify the efficient nonbasic variables

• 3. Consider proposed exercise 3, Chap. 2.

  • (a) Formulate the problem to determine the efficient solution that minimizes the distance to the ideal solution, according to the L ₁ metric. Solve this problem graphically.

  • (b) Represent qualitatively the parametric (weight) diagram decomposition, considering all the indifference regions.

  • (c) Determine graphically the nondominated solution obtained by the e-constraint technique when f ₁(x) is optimized and f ₂(x) ≥ 3.

• 4. Consider the MOLP model with three objective functions:

  $$ \begin{array}{l} \max {f}_1\left(\mathbf{x}\right)=2{x}_1+{x}_2+3{x}_3+{x}_4 \max {f}_2\left(\mathbf{x}\right)=2{x}_1+4{x}_2+{x}_3-{x}_4 \max {f}_3\left(\mathbf{x}\right) = {x}_1+2{x}_2-{x}_3+5{x}_4\mathrm{s}.\ \mathrm{t}. {x}_1+2{x}_2+3{x}_3+4{x}_4 \le 404{x}_1+4{x}_2+2{x}_3+{x}_4 \le 40{x}_1\ge 0,\ {x}_2\ge 0,\ {x}_3\ge 0,\ {x}_4\ge 0\hfill \end{array} $$

  • (a) Find the indifference region corresponding to the efficient solution that optimizes objective function f ₂ (x).

  • (b) What are the efficient nonbasic variables for that solution? Support your analysis on the weight space.

  • (c) Consider the following auxiliary problem:

    $$ \begin{array}{l} \min \mathrm{v}\mathrm{s}.\ \mathrm{t}. \mathbf{x}\in X\left(\mathrm{original}\ \mathrm{feasible}\ \mathrm{region}\right)\mathrm{v}+2{x}_1+4{x}_2+{x}_3-{x}_4\ge 35\mathrm{v}+2{x}_1+{x}_2+3{x}_3+{x}_4\ \ge\ 5\mathrm{v}+{x}_1+2{x}_2-{x}_3+5{x}_4\ \ge\ 15\mathrm{v}\ \ge\ 0\hfill \end{array} $$

  Is the solution to this auxiliary problem a (strictly) nondominated solution to the multiobjective problem? If not, what changes should be made in the formulation of this auxiliary problem in order to guarantee obtaining a (strictly) nondominated solution?

• 5. Discuss the following statements, stating whether they are true or false, and presenting a counter example if they are false. Use graphical examples if that facilitates the analysis.

  • (a) It is always possible to define x ^* (in the decision space), such that z ^* = f(x ^*), where f(x) = [f ₁(x),f ₂(x),…,f _p (x)].

  • (b) In a MOLP problem, the solution obtained by minimizing the distance to a reference point according to the L_∞ metric is always a vertex of the original feasible region.

  • (c) In a MOLP problem, the solution obtained by minimizing the distance to a reference point according to the L₁ metric is always a vertex of the original feasible region.

  • (d) When an additional constraint is introduced into a MOLP problem, it is possible to obtain nondominated solutions to the modified problem that are dominated in the original problem.

  • (e) In a MOLP problem with p objective functions it is possible that the whole feasible region is efficient.

  • (f) The solutions located on an edge that connects two nondominated vertices are also nondominated.

  • (g) Consider a MOLP problem with three objective functions, where three nondominated basic solutions are known. The optimization of a scalarizing function whose gradient is normal to the plane that includes these three solutions always guarantees obtaining a nondominated solution.

  • (h) Consider the MOLP problem:

    $$ \begin{array}{l} \max {f}_1\left(\mathbf{x}\right) = {\mathbf{c}}_1\mathbf{x}\\ {} \max {f}_2\left(\mathbf{x}\right) = {\mathbf{c}}_2\mathbf{x} \\ {} \max {f}_3\left(\mathbf{x}\right) = {\mathbf{c}}_3\mathbf{x} \\ {}\mathrm{s}.\ \mathrm{t}. \mathbf{x}\in X\equiv \left\{\mathbf{Ax}=\mathbf{b},\mathbf{x}\ge \mathbf{0}\right\},\end{array} $$

    where x (n × 1), c _k (1 × n), A (m × n) and b (m × 1)

    • (h.1) Is it possible to obtain a nondominated solution that maximizes f ₃(x) with λ₃ = 0, by solving the weighted-sum problem

      $$ \begin{array}{l} \max {\uplambda}_1{\mathbf{c}}_1\mathbf{x}+{\uplambda}_2{\mathbf{c}}_2\mathbf{x}+{\uplambda}_3{\mathbf{c}}_3\mathbf{x}\\ {}\mathrm{s}.\ \mathrm{t}. \mathbf{x}\in X\end{array} $$

      with (λ₁, λ₂, λ₃) ∈Λ ≡ {λ _k  ≥ 0, k = 1, 2, 3, and λ₁ + λ₂ + λ₃ = 1}?

      If this assertion is true, then represent one possible parametric (weight) diagram decomposition in this condition.

    • (h.2) In what conditions is it possible to guarantee that the optimal solution to

      $$ \begin{array}{l} \max {\uplambda}_1{\mathbf{c}}_1\mathbf{x}+{\uplambda}_2{\mathbf{c}}_2\mathbf{x}+{\uplambda}_3{\mathbf{c}}_3\mathbf{x}\\ {}\mathrm{s}.\ \mathrm{t}. \mathbf{x}\in X\end{array} $$

      is a nondominated solution to the three objective original problem?

• 6. Consider the following MOLP problem:

  $$ \begin{array}{l} \max\ {f}_1\left(\mathbf{x}\right)=1.5\ {x}_1+{x}_2\\ {} \max\ {f}_2\left(\mathbf{x}\right)= {x}_2+2{x}_3\\ {} \max\ {f}_3\left(\mathbf{x}\right)= {x}_1+{x}_2+{x}_3\\ {}\mathrm{s}.\mathrm{t}. {x}_1+{x}_2+{x}_3 \le\ 8\\ {} {x}_1 +2{x}_3\le\ 2\\ {} {x}_1\ge 0,{x}_2\ge 0,{x}_3\ge 0\end{array} $$

  • (a) Compute the nondominated solution that maximizes a weighted-sum of the objective functions assigning equal weight to all objectives.

  • (b) Represent the corresponding indifference region in the parametric (weight) diagram.

  • (c) Compute a nondominated solution which is adjacent to the one computed in (a) improving objective function f ₁(x).

  • (d) Specify the values of the objective functions of a nondominated nonbasic solution, whose value for f ₁(x) is an intermediate value between the ones of the solutions obtained in (a) and in (c).

• 7. Consider the following MOLP problem:

  $$ \begin{array}{l} \max {f}_1\left(\mathbf{x}\right)={x}_2 \max {f}_2\left(\mathbf{x}\right)={x}_1+3{x}_2 \max {f}_3\left(\mathbf{x}\right)=2{x}_1\hbox{--} {x}_2\mathrm{s}.\mathrm{t}. 3{x}_1 + {x}_2 \le\ 30{x}_1+{x}_2 \le\ 20{x}_1 \le\ 8{x}_1\ge\ 0,{x}_2\ge\ 0\hfill \end{array} $$

  The decomposition of the parametric (weight) diagram associated with the efficient vertices of the problem is displayed in the triangle.

  What conclusions about the problem can be drawn from this decomposition?

  

• 8. Consider the following MOLP problem:

  $$ \begin{array}{l} \max\ {f}_1\left(\mathbf{x}\right)= 3{x}_1+{x}_2\\ {} \max\ {f}_2\left(\mathbf{x}\right)= {x}_1+2{x}_2\\ {} \max\ {f}_3\left(\mathbf{x}\right)=-{x}_1+2{x}_2\\ {}\mathrm{s}.\mathrm{t}. -{x}_1+{x}_2 \le 2\\ {} {x}_1+{x}_2\ \le\ 7 \\ {} 0.5{x}_1+{x}_2 \le\ 5 \\ {} {x}_1,{x}_2 \ge\ 0\end{array} $$

  • (a) Represent graphically the set of efficient solutions.

  • (b) Suppose one wants to find the nondominated solution that minimizes the distance to the ideal solution by using a weighted Chebyshev metric. Formulate this problem, knowing that the ideal solution is z* = (21, 10, 6) and considering the following (non-normalized) weights: λ₁ = 1, λ₂ = 2, λ₃ = 1.

  • (c) Consider the following reference point in the objective space, q = (14, 8, 0), belonging to the interior of the feasible region. Solution (x ^a, z ^a), with x ^a = (4.2, 2.8) and z ^a = (15.4, 9.8, 1.4), is optimal to the following problem:

    $$ \begin{array}{l} \min\ v\\ {}\mathrm{s}.\ \mathrm{t}. {\uplambda}_1\left(14\hbox{--} 3{x}_1\hbox{--} {x}_2\right)\le v\\ {} {\uplambda}_2\left(8\hbox{--} {x}_1\hbox{--} 2{x}_2\right)\le v\\ {} {\uplambda}_3\left(0+{x}_1\hbox{--} 2{x}_2\right)\le v\\ {} \mathbf{x}\in X\left(X\;\mathrm{is}\ \mathrm{t}\mathrm{he}\ \mathrm{feasible}\ \mathrm{region}\ \mathrm{defined}\ \mathrm{above}\right)\mathrm{with}\;\uplambda = \left(1,\;1,\;1\right).\end{array} $$

    Identify how the variation trends of the objective function values evolve, regarding z ^a, when the previous problem is solved, but considering λ = (2, 1, 1).

• 9. Ten vertex nondominated solutions to a three objective LP with f _k (x), k = 1,2,3, were calculated using the weighted-sum scalarization, for which the corresponding indifference regions on the weight space are displayed.

  

  • (a) Characterize all nondominated edges and faces using the vertices.

  • (b) Are there nondominated solutions that are alternative optima of any objective function?

  • (c) What are the nondominated vertices that can still be obtained with the weight constraints λ₃ ≥ λ₂ ≥ λ₁?

  • (d) What are the vertices of this three objective problem that are dominated in all 3 bi-objective problems that can be formed (i.e., f ₁(x) and f ₂(x), f ₁(x) and f ₃(x), f ₂(x) and f ₃(x))?

  • (e) Sketch the decomposition of the weight space for the problem with the objective functions f ₂(x) and f ₃(x). How do you classify solution 10 in this problem?