Learning Bayesian Networks with Non-Decomposable Scores

Abstract

Modern approaches for optimally learning Bayesian network structures require decomposable scores. Such approaches include those based on dynamic programming and heuristic search methods. These approaches operate in a search space called the order graph, which has been investigated extensively in recent years. In this paper, we break from this tradition, and show that one can effectively learn structures using non-decomposable scores by exploring a more complex search space that leverages state-of-the-art learning systems based on order graphs. We show how the new search space can be used to learn with priors that are not structure-modular (a particular class of non-decomposable scores). We also show that it can be used to efficiently enumerate the $k$-best structures, in time that can be up to three orders of magnitude faster, compared to existing approaches.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Modern approaches for learning Bayesian network structures are typically formulated as a (combinatorial) optimization problem, where one wants to find the best network structure (i.e., best DAG) that has the highest score, for some given scoring metric [10, 19, 23]. Typically, one seeks a Bayesian network that explains the data well, without overfitting the data, and ideally, also accommodating any prior knowledge that may be available.

Some of the earliest procedures for learning Bayesian network structures used scoring metrics with a certain desirable property, called score decomposability. For example, consider the K2 algorithm which exploited decomposable scores, in combination with an assumption on the topological ordering of the variables [6]. Under these assumptions, the structure learning problem itself decomposes into local sub-problems, where we find the optimal set of parents for each variable, independently. Local search methods exploited decomposability in a similar way [5]. Such methods navigated the space of Bayesian network structures, using operators on edges such as addition, deletion, and reversal. Score decomposability allowed these operators to be evaluated locally and efficiently. Indeed, almost all scoring metrics used for Bayesian network structure learning are decomposable. Such scores include the K2 score, [6], the BDeu score [4], the BDe score [16], and the MDL score [2, 20, 29], among many others.

Modern approaches to structure learning continue to exploit the decomposable nature of such scoring metrics. In particular, the past decade has seen significant developments in optimal Bayesian network structure learning. These recent advances were due in large part to dynamic programming (DP) algorithms, for finding optimal Bayesian network structures [18, 27, 28]. Subsequently, approaches have been proposed based on heuristic search, such as A* search [34, 35], as well as approaches based on integer linear programming (ILP), and their relaxations [7, 17].

By exploiting the nature of decomposable scores, these advances have significantly increased the scalability of optimal Bayesian network structure learning. There is, however, a notable void in the structure learning landscape due to the relative lack of support for non-decomposable scores. This includes a general lack of support for non-decomposable priors, or more broadly, the ability to incorporate more expressive, but non-decomposable forms of prior knowledge (e.g., biases or constraints on ancestral relations). In this paper, we take a step towards a more general framework for Bayesian network structure learning that targets this void.

The modern approaches for optimal structure learning, mentioned earlier, are based on a search space called the order graph [18, 35]. The key property of the order graph is its size, which is only exponential in the number of variables of the Bayesian network that we want to learn. Our proposed framework however is based on navigating the significantly larger space of all network structures (i.e., all DAGs). Moreover, to facilitate the efficient navigation of this larger space, we employ state-of-the-art learning systems based on order graphs as a (nearly) omniscient oracle. In addition to defining this new search space, we instantiate it to yield a concrete system for finding optimal Bayesian networks under order-modular priors, which we evaluate empirically. We further demonstrate the utility of this new search space by showing how it lends itself to enumerating the $k$-best structures, resulting an algorithm that can be three orders of magnitude more efficient than existing approaches based on DP and ILP [9, 32].

This paper is organized, as follows. In Sect. 2, we review Bayesian network structure learning. In Sect. 3, we propose our new search space for learning Bayesian networks. In Sect. 4, we show how our search space can be leveraged to find optimal Bayesian networks under a class of non-decomposable priors. In Sect. 5, we show how our search space can be further used to efficiently enumerate the $k$-best network structures. Finally, we conclude in Sect. 6. Proofs of theorems are provided in the Appendix.

2 Technical Preliminaries and Related Work

In this section, we first review score-based Bayesian network structure learning. We then review a formulation of score-based structure learning as a shortest-path problem in a graph called the order graph. Shortest-path problems can subsequently be solved with heuristic search methods such as A* search.

First, we use upper case letters ($X$) to denote variables and bold-face upper case letters ($\mathbf{X}$) to denote sets of variables. Generally, we will use $X$ to denote a variable in a Bayesian network and $\mathbf{U}$ to denote its parents.

2.1 Score-Based Structure Learning

Given a dataset $\mathcal {D}$, we first consider the problem of finding a DAG $G$ of a Bayesian network which minimizes a decomposable score. Such a score decomposes into a sum of local scores, over the families $X\mathbf{U}$ of the DAG:

$$\begin{aligned} \mathsf {score}(G \mid \mathcal {D}) = \sum _{X\mathbf{U}} \mathsf {score}(X\mathbf{U}\mid \mathcal {D}). \end{aligned}$$

(1)

For example, MDL and BDeu scores are decomposable; see, e.g., [10, 19, 23]. In this paper, we will generally assume that scores (costs) are to be minimized (hence, we negate scores that should otherwise be maximized).

There are a variety of approaches for finding a DAG $G$ that minimizes the score of Eq. 1. One class of approaches is based on integer linear programming (ILP), where 0/1 variables represent the selection of parent sets (families) in a graph. Our goal is to optimize the (linear) objective function of Eq. 1, subject to (linear) constraints that ensure that the resulting graph is acyclic [17]. In some cases, an LP relaxation can guarantee an optimal solution to the original ILP; otherwise, cutting planes and branch-and-bound algorithms can be used to obtain an optimal structure [7, 17].

In this paper, we are interested in another class of approaches to optimizing Eq. 1, which is based on a formulating the score, in a particular way, as a recurrence. This recurrence underlies a number of recent approaches to structure learning, based on dynamic programming [18, 22, 27, 28], as well as more efficient approaches based on A* search [34, 35]. In particular, to find the optimal DAG over variables $\mathbf{X}$, we have the following recurrence:

$$\begin{aligned} \mathsf {score}^\star (\mathbf{X}\mid \mathcal {D}) = \min _{X \in \mathbf{X}} \Big ( \min _{\mathbf{U}\subseteq \mathbf{X}\setminus X} \mathsf {score}(X\mathbf{U}\mid \mathcal {D}) + \mathsf {score}^\star (\mathbf{X}\setminus X \mid \mathcal {D}) \Big ) \end{aligned}$$

(2)

where $\mathsf {score}^\star (\mathbf{X}\mid \mathcal {D})$ denotes the score of the optimal DAG over variables $\mathbf{X}$ given dataset $\mathcal {D}$. According to this recurrence, we evaluate each variable $X$ as a candidate leaf node, and find its optimal family $X\mathbf{U}$. Moreover, independently, we find the optimal structure over the remaining variables $\mathbf{X}\setminus X$. The best structure then corresponds to the candidate leaf node $X$ with the best score.

Fig. 1.

An order graph for variables $\mathbf{X}= \{X_1, X_2, X_3\}$

2.2 Shortest-Paths on Order Graphs

Yuan & Malone [34] formulate the structure learning problem as a shortest-path problem on a graph called the order graph. Figure 1 illustrates an order graph over 3 variables $\mathbf{X}$. In an order graph, each node represents a subset $\mathbf{Y}$ of the variables $\mathbf{X}$. There is a directed edge from $\mathbf{Y}$ to $\mathbf{Z}$ in the order graph iff we add a new variable $X$ to the set $\mathbf{Y},$ to obtain the set $\mathbf{Z}$; we denote such an edge by $\mathbf{Y}\xrightarrow {X} \mathbf{Z}$. The order graph is thus a layered graph where each new layer adds, in total, one new variable to the nodes of the previous layer. Hence, we have a unique root node $\{\}$, and a unique leaf node $\mathbf{X}$. Any path

$$\begin{aligned} \{\} \xrightarrow {X_1} \cdots \xrightarrow {X_n} \mathbf{X}\end{aligned}$$

from the root to the leaf will then correspond to a unique ordering $\langle X_1,\ldots ,X_n \rangle$ of the variables. Suppose that we associate each edge $\mathbf{Y}\xrightarrow {X} \mathbf{Z}$ with a cost

$$\begin{aligned} \min _{\mathbf{U}\subseteq \mathbf{Y}} \mathsf {score}(X\mathbf{U}\mid \mathcal {D}) \end{aligned}$$

where, for the variable $X$ added on the edge, we find the optimal set of parents $\mathbf{U}$ from the set of variables $\mathbf{Y}$. A path from the root node $\{\}$ to the leaf node $\mathbf{X}$ will then correspond to a DAG $G$ since each edge $\mathbf{Y}\xrightarrow {X} \mathbf{Z}$ adds a new leaf node $X$ with parents $\mathbf{U}$ to the DAG, i.e., the $\mathbf{U}$ that minimized $\mathsf {score}(X\mathbf{U}\mid \mathcal {D})$. The cost of the path (the sum of the scores of its edges) gives us the score of the DAG, $\mathsf {score}(G \mid \mathcal {D})$, as in Eqs. 1 and 2. Hence, the shortest path from the root $\{\}$ to the leaf $\mathbf{X}$ corresponds to the DAG with minimum score.

3 A New Search Space for Learning Bayesian Networks

We now describe our A* framework, for learning the structure of Bayesian networks. We first describe the search space that we use, and then propose a heuristic function to navigate that space, which is based on using existing, state-of-the-art structure learning systems as a black-box. Later in this paper, we discuss two learning tasks that are enabled by our framework: (1) learning an optimal Bayesian network structure using a class of non-decomposable scores, and (2) enumerating the $k$-best Bayesian network structures.

Fig. 2.

A BN graph for variables $\mathbf{X}= \{X_1, X_2, X_3\}$

3.1 A New Search Space: BN Graphs

Following Yuan & Malone [34], we formulate structure learning as a shortest-path problem, but on a different graph, which we call the Bayesian network graph (BN graph). The BN graph is a graph where each node represents a BN, but more specifically, each node represents a BN structure, i.e., a DAG. Figure 2 illustrates a BN graph over 3 variables. In this graph, which we denote by $\mathcal {G}_{\mathrm {bn}}$, nodes represent Bayesian network structures over different subsets of the variables $\mathbf{X}$. A directed edge $G_i \xrightarrow {X\mathbf{U}} G_j$ from a DAG $G_i$ to a DAG $G_j$ exists in $\mathcal {G}_{\mathrm {bn}}$ iff $G_j$ can be obtained from $G_i$ by introducing variable $X$ as a leaf node with parents $\mathbf{U}$. Hence, the BN graph, like the order graph, is a layered graph, but where each layer adds one more leaf to an explicit (and not just an implicit) DAG when we walk an edge to the next layer. Correspondingly, when we refer to a DAG $G_i,$ we assume it is on the $i$-th layer, i.e., $G_i$ has $i$ nodes. The top ($0$-th) layer contains the root of the BN graph, a DAG with no nodes, which we denote by $G_0$. The bottom ($n$-th) layer contains DAGs $G_n$ over our $n$ variables $\mathbf{X}$. Any path

$$\begin{aligned} G_0 \xrightarrow {X_1\mathbf{U}_1} \cdots \xrightarrow {X_n\mathbf{U}_n} G_n \end{aligned}$$

from the root to a DAG $G_n$ on the bottom layer, is a construction of the DAG $G_n$, where each edge $G_{i-1} \xrightarrow {X_i\mathbf{U}_i} G_{i}$ adds a new leaf $X_i$ with parents $\mathbf{U}_i$. Moreover, each path corresponds to a unique ordering $\langle X_1,\ldots ,X_n \rangle$ of the variables. Each edge $G_{i-1} \xrightarrow {X_i\mathbf{U}_i} G_{i}$ is associated with a cost, $\mathsf {score}(X_i\mathbf{U}_i \mid \mathcal {D})$, and thus the cost of a path from the empty DAG $G_0$ to a DAG $G_n$ gives us the score of the DAG, $\mathsf {score}(G_n \mid \mathcal {D})$, as in Eq. 1.

For example, consider the BN graph of Fig. 2 and the following path, corresponding to a sequence of DAGs:

Starting with the empty DAG $G_0$, we add a leaf $X_1$ (with no parents), then a leaf $X_2$ (with parent $X_1$), then a leaf $X_3$ (with no parents), giving us a DAG $G_3$ over all $3$ variables.

Both the order graph and the BN graph formulate the structure learning problem as a shortest path problem. The BN graph is however much larger than the order graph: an order graph has $2^n$ nodes, whereas the BN graph has $O(n! \cdot 2^{\left( {\begin{array}{c}n\\ 2\end{array}}\right) })$ nodes. Despite this significant difference in search space size, we are still able to efficiently find shortest-paths in the BN graph, which we shall illustrate empirically, in the remainder of this paper. The efficient navigation of the BN graph depends significantly on the heuristic function, which we discuss next.

3.2 On Heuristic Functions for BN Graphs

A* search is a best-first search that uses an evaluation function $f$ to guide the search process, where we expand first those nodes with the lowest $f$ cost [15]. The evaluation function for A* takes the form:

$$\begin{aligned} f(G) = g(G) + h(G) \end{aligned}$$

where $G$ is a given DAG, function $g$ is the path cost (the cost of the path to reach $G$ from $G_0$), and function $h$ is the heuristic function, which estimates the cost to reach a goal, starting from $G$. If our heuristic function $h$ is admissible, i.e., it never over-estimates the cost to reach a goal, then A* search is optimal. That is, the first goal node $G_n$ that A* expands is the one that has the shortest path from the root $G_0$. Ideally, we want a good heuristic function $h$, since an accurate estimate of the cost to a goal state will lead to a more efficient search. For more on A* search, see, e.g., [26].

Consider the special but extreme case, where we have access to a perfect heuristic $h(G)$, which could predict the optimal path from $G$ to a goal node $G_n$. In this case, search becomes trivial: A* search marches straight to a goal node (with appropriate tie-breaking, where we expand the deepest node first). Having access to a perfect heuristic by itself is not useful, if we are just interested in an optimal DAG. Such a heuristic, however, becomes useful when we are interested in solving more challenging learning tasks. Consider, for example, learning an optimal DAG, subject to a set of structural constraints. In this case, a perfect heuristic is no longer perfect—it will under-estimate the cost to reach a goal. However, in this case, it remains an admissible heuristic, which we can use in A* search to find an optimal DAG, when we subject the learning problem to constraints.

We do, in fact, have access to a perfect heuristic—any learning system could be used as such, provided that it can accept a (partial) DAG $G$, and find an optimal DAG $G_n$ that extends it. Systems such as URLearning meet this criterion [34], which we use in our subsequent experiments. Such a system is treated as a black-box, and used to evaluate our heuristic function in A* search, to potentially solve a learning problem that the black-box was not originally designed for. We shall later highlight two such learning tasks, that are enabled by using existing structure learning systems as black-boxes for A* search.

We also remark that using such a black-box to evaluate a heuristic function, as described above, is also a departure from the standard practice of heuristic search. Conventionally, in heuristic search, one seeks heuristic functions that are cheap to evaluate, allowing more nodes to be evaluated, and hence more of the search space to be explored. Our black-box (which finds an optimal extension of a DAG), in contrast, will be relatively expensive to evaluate. However, for the particular learning tasks that we consider, a strong heuristic can outweigh the expense to compute it, by more efficiently navigating the search space (i.e., by expanding fewer nodes to find a goal). We shall demonstrate this empirically after introducing each of the learning tasks that we consider.

Implementation of A* Search. Finally, we describe two further design decisions, that are critical to the efficiency of A* search on the BN graph. First, if two given DAGs G and $G^\prime$ are defined over the same set of variables, then they have the same heuristic value, i.e. $h(G) = h(G^\prime )$. Hence, we can cache the heuristic value h(G) for a DAG $G$, and simply fetch this value for another DAG $G^\prime$ (instead of re-invoking our black-box), when it has the same set of variables. As a result, the heuristic function is invoked at most once for each subset $\mathbf{Y}$ of the variables $\mathbf{X}$. In addition, when we invoke our black-box on a DAG G, we can infer and then prime other entries of the cache. In particular, when our black-box returns an optimal completion $G^\prime$ of a DAG G, then we know the optimal completion (and heuristic values) of any DAG in between G and $G^\prime$ in the BN graph—their optimal completion is also $G^\prime$ (from which we can infer the corresponding heuristic value). Based on this caching scheme, a single call to our black-box heuristic function suffices, to recover a single best network using A* search in the BN graph (i.e., it is no worse than using the black-box directly).

Next, the branching factor of the BN graph is large, and hence, we can quickly run out of memory if we expand each node and insert all of its children into A*’s priority queue (i.e., open list). We thus use partial-expansion A* in our implementation, i.e., when we expand a node, we only insert the b-best children into the priority queue. We can re-expand this node, as many times as needed, when we want the next b-best children. While we may spend extra work re-expanding nodes, this form of partial-expansion can save a significant amount of memory, without sacrificing the optimality of A* search; see, e.g., [13, 33].

3.3 Experimental Setup

In the subsequent sections, we shall highlight two different tasks that are enabled by performing A* search on the BN graph. After discussing each task, we report empirical results on real-world datasets, which were taken from the UCI machine learning repository [1], and the National Long Term Care Survey (NLTCS). For learning, we assumed BDeu scores, with an equivalent sample size of 1. We adapted the URLearning structure learning package of [34] to serve as our black-box heuristic function.¹ Our experiments were run on a 2.67GHz Intel Xeon X5650 CPU, with access to 144 GB RAM. For our partial-expansion A* search, each time a node is expanded or re-expanded, children are inserted into the priority queue in blocks of 10. We further pre-compute the BDeu scores, which are fed as input into each system evaluated. Finally, all timing results are averages over 10 runs.

4 Structure Learning with Non-Decomposable Scores

Now that we have described our framework for learning Bayesian networks using BN graphs, we will show how we can use it to learn BN structures using for a class of non-decomposable scores.² In particular, we consider a class of non-decomposable priors on network structures, which we discuss next. Subsequently, we propose a heuristic that can be used in A* search, to optimize this class of non-decomposable scores. We then describe our A* search algorithm, and then provide some experimental results.

4.1 Order-Modular Priors

One prevalent non-decomposable prior is the order-modular prior [14, 18]. The uniform order-modular prior ${ Pr}(G)$, in particular, is proportional to the number of topological orderings consistent with a DAG $G$, i.e., the number of its linear extensions, which we denote by $\#G$. Hence,

$$\begin{aligned} \log { Pr}(G) = \log \#G - \log C, \end{aligned}$$

where $C$ is a normalizing constant. More generally, order-modular priors can be viewed in terms of a weighted count of linear extensions [18]. In general, counting the number of linear extensions is itself a challenging problem (let alone optimizing with it); it is a #P-complete problem [3]. We shall revisit this issue, shortly.

Order-modular priors are notable, as they enable MCMC methods for the purposes of (approximate) Bayesian model averaging [14]. They also enable some DP-based methods for exact Bayesian model averaging, when there are a moderate number of network variables [18]. However, to our knowledge, only approximate approaches had been previously considered for this prior, when one wants a single optimal DAG; see Koivisto & Sood [18, Sect. 5], for a discussion on some of the difficulties.

4.2 A Heuristic for Order-Modular Priors

Consider the probability of a DAG $G$ given a dataset $\mathcal {D}$:

$$\begin{aligned} { Pr}(G \mid \mathcal {D}) = \frac{{ Pr}(\mathcal {D}\mid G) { Pr}(G)}{{ Pr}(\mathcal {D})} \end{aligned}$$

where ${ Pr}(\mathcal {D}\mid G)$ is the marginal likelihood, and ${ Pr}(G)$ is a prior on the DAG $G$. Further, the quantity ${ Pr}(\mathcal {D})$ is a normalizing constant, which is independent of the given DAG $G$. To maximize the probability of a graph, it suffices to maximize the log probability:

$$\begin{aligned} \mathop {\text {argmax}}\limits _G \log { Pr}(G \mid \mathcal {D}) = \mathop {\text {argmax}}\limits _G \log { Pr}(\mathcal {D}\mid G) + \log { Pr}(G). \end{aligned}$$

When using the BDeu score, the marginal likelihood decomposes as in Eq. 1. We assume the BDeu score for the remainder of this section.

First, we consider how to update the weights on the edges of a BN graph, to handle a prior on the structure, decomposable or otherwise.

Theorem 1

Let ${ Pr}_i(.)$ denote a distribution over DAGs having $i$ nodes (i.e., our structure prior).³ If we label each edge $G_i \xrightarrow {X\mathbf{U}} G_j$ in graph $\mathcal {G}_{\mathrm {bn}}$ with the cost:

$$\begin{aligned} \mathsf {score}(X\mathbf{U}\mid \mathcal {D}) - \log \frac{{ Pr}_j(G_j)}{{ Pr}_i(G_i)}, \end{aligned}$$

then the total cost of a path from the root $G_0$ to a leaf $G_n$ is

$$\begin{aligned} \mathsf {score}(G \mid \mathcal {D}) - \log { Pr}_n(G_n). \end{aligned}$$

Hence, assuming a structure prior, the DAG with an optimal score corresponds to a shortest path in the BN graph $\mathcal {G}_{\mathrm {bn}},$ from the root $G_0$ (top layer) to a leaf $G_n$ (bottom layer). In what follows, we shall assume that our structure prior is a uniform order-modular prior, although general (weighted) order-modular priors can also be accommodated.

We now propose a simple heuristic function for learning an optimal DAG with a uniform order-modular prior. Let $G_i \leadsto G_n$ indicate that a DAG $G_n$ is reachable from DAG $G_i$ in $\mathcal {G}_{\mathrm {bn}}$. We propose to use the heuristic function $h(G_i) = h_1(G_i) + h_2(G_i)$, which has two components. The first component is:

$$\begin{aligned} h_1(G_i) = \min _{G_n: G_i \leadsto G_n} \sum _{X\mathbf{U}\in G_n-G_i} \mathsf {score}(X\mathbf{U}\mid \mathcal {D}) \end{aligned}$$

(3)

where we sum over families $X\mathbf{U}$ that appear in $G_n$ but not in $G_i$. This component is looking for the shortest path to the goal, based on the decomposable part of the score, ignoring the prior (i.e., maximizing the marginal likelihood). The second component is:

$$\begin{aligned} h_2(G_i) = \min _{G_n: G_i \leadsto G_n} {- \log \frac{{ Pr}_n(G_n)}{{ Pr}_i(G_i)}} \end{aligned}$$

(4)

This component is looking for the shortest path to the goal, based on the prior part of the score, but ignoring the data (i.e., maximizing the prior).

Theorem 2

The heuristic function $h(G_i) = h_1(G_i) + h_2(G_i)$ of Eqs. 3 and 4 is admissible.

To use this heuristic function, we must perform two independent optimization problems (for $h_1$ and $h_2$). The first is the familiar optimization of a decomposable score; we can employ most any existing structure learning algorithm for decomposable scores, as an oracle, as discussed in the previous section. The second is an optimization of the prior, independently of the data. Next, we show how to both optimize and evaluate this component, for order-modular priors.

Optimizing the Prior. Here, we briefly describe how to solve the component $h_2$ for a uniform order-modular prior. Again, we want to identify the most likely goal node $G_n$ reachable from $G_i$, i.e., the DAG $G_n$ with the largest linear extension count. Remember that DAG $G_i$ has $i$ nodes. Since adding any edge to the DAG constrains its possible linear extensions, then the DAG $G_n$ with the largest linear extension count simply adds the remaining $n-i$ nodes independently to DAG $G_i$. If ${\mathrm {\#}G_i}$ is the linear extension count of DAG $G_i$, then

$$\begin{aligned} {\mathrm {\#}G_n}= {\mathrm {\#}G_i}\cdot (i+1) \cdots n \end{aligned}$$

is the linear extension count of DAG $G_n$.⁴ Next, we have that:

$$\begin{aligned} { Pr}_i(G_i) = \frac{1}{C_i} \cdot {\mathrm {\#}G_i}\quad \text{ and } \quad { Pr}_n(G_n) = \frac{1}{C_n} \cdot {\mathrm {\#}G_n}\end{aligned}$$

where $C_k$ is a normalizing constant:

$$\begin{aligned} C_k = \sum _{G_k} \#G_k = \sum _{G_k} \sum _{\pi \sim G_k} 1 = \sum _{\pi } \sum _{\pi \sim G_k} 1 = \sum _{\pi } 2^{\left( {\begin{array}{c}k\\ 2\end{array}}\right) } = k! \cdot 2^{\left( {\begin{array}{c}k\\ 2\end{array}}\right) } \end{aligned}$$

and where $\pi \sim G_k$ denotes compatibility with an ordering $\pi$ and a DAG $G_k$. Thus,

$$\begin{aligned} \frac{{ Pr}_n(G_n)}{{ Pr}_i(G_i)} = \frac{C_i}{C_n} \frac{\#G_n}{\#G_i} = \frac{C_i}{C_n} \cdot (i+1)\cdots n = 2^{\left( {\begin{array}{c}i\\ 2\end{array}}\right) - \left( {\begin{array}{c}n\\ 2\end{array}}\right) } \end{aligned}$$

Hence, $h_2(G_i) = [\left( {\begin{array}{c}n\\ 2\end{array}}\right) - \left( {\begin{array}{c}i\\ 2\end{array}}\right) ] \cdot \log 2$. We note that for all DAGs $G_i$ in the same layer, the heuristic function $h_2(G_i)$ evaluates to the same value, although this value differs for DAGs in different layers.

Note, that we also need to be able to compute the linear-extension counts $\#G_i$ themselves, which is itself a non-trivial problem (it is #P-complete). We discuss this next.

Counting Linear Extensions. In Sect. 4.1, we highlighted the relationship between uniform order-modular priors and counting linear extensions. We now show that the BN graph itself facilitates the counting of linear extensions, for many DAGs at once. Subsequently, we shall show that this computation can be embedded in the A* search itself.

Recall that any path in the BN graph $\mathcal {G}_{\mathrm {bn}}$, from $G_0$ to $G_i$, corresponds to an ordering of variables $\langle X_1,\ldots ,X_i \rangle$. In fact, this ordering is a linear extension of the DAG $G_i$ (by construction). Hence, the linear extension count $\mathrm {\#}G_i$ of a graph $G_i$ is the number of paths from the root $G_0$ to $G_i$, in the BN graph $\mathcal {G}_{\mathrm {bn}}.$ For example, consider the DAG:

There are 3 distinct paths in $\mathcal {G}_{\mathrm {bn}}$ from the root $G_0$ to the DAG above, one path for each topological order that the DAG is consistent with. Next, observe that the number of linear extensions of a DAG $G_i$, (or equivalently, the number of paths that reach $G_i$), is simply the sum of the linear extensions of the parents of $G_i$, in the BN graph $\mathcal {G}_{\mathrm {bn}}$. For example, our DAG above has 3 linear extensions, and 2 parents in $\mathcal {G}_{\mathrm {bn}}$:

the first with one linear extension, and the second with two. In this way, we can count the linear extensions of DAGs in a BN graph $\mathcal {G}_{\mathrm {bn}}$, from top-to-bottom, sharing computations across the different DAGs. A similar algorithm for counting linear extensions is described in, e.g., [24].

Consider how A* navigates the BN graph $\mathcal {G}_{\mathrm {bn}}$ during search. If A* expands a node only when all of its parents are expanded, then as described above, we can count the number of linear extensions of a DAG, when it gets expanded.⁵ Thus, we can evaluate its prior, and in turn, the function $f$. It so happens that, we can moderately weaken the heuristic function that we just described, so that A* will in fact expand a node only when all of its parents are expanded.

Theorem 3

Assuming a uniform order-modular prior, the heuristic function

$$\begin{aligned} h(G_i) = h_1(G_i) + h^\prime _2(G_i) \end{aligned}$$

allows A* to count the linear extensions of any DAG it expands, where $h^\prime _2(G_i) = - \sum _{k=i+1}^n \log k \le h_2(G_i)$ with components $h_1$ and $h_2$ coming from Eqs. 3 and 4.

A proof appears in the Appendix.

4.3 A* Search

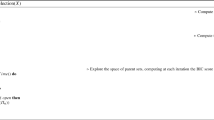
Algorithm 1 provides pseudo-code for A* search using a uniform order-modular prior. Note that this pseudo-code deviates slightly from the standard A* search, as the linear extension counts ${\mathrm {\#}G}$ are computed incrementally during the search.

Theorem 4

Algorithm 1 learns an optimal Bayesian network with a uniform order-modular prior.

A proof appears in the Appendix.

Finally, we note that Theorem 1 and the heuristic functions of Eq. 3 and 4 were proposed for order-modular priors. In principle, the shortest-path formulation, and the heuristic function that we proposed, can support a much broader class of non-decomposable priors. However, one must be able to optimize the probability of a graph, as in the component $h_2$ of the heuristic function that we proposed, in Eq. 4. If we had access to some oracle that can solve this component, then we would in principle have the pieces that are sufficient to perform A* search over the DAG graph $\mathcal {G}_{\mathrm {bn}}$, using the corresponding prior.

4.4 Experiments

Table 1. The performance of A* search on the BN graph when learning with the uniform order-modular prior: (1) The time $T_h$ to compute the heuristic function. (2) The time $T_{{A*}}$ to traverse the BN graph with A* (in seconds) (3) The total time $t = T_h + T_{{A*}}$ spent in A* (4) The number of generated nodes. (5) The number of expanded nodes. (6) The number of re-expanded nodes (in partial-expansion A*). An $\times _m$ corresponds to an out-of-memory (64 GB).

We evaluate our A* search approach to learning optimal Bayesian networks with real-world datasets, assuming a uniform order-modular prior. In Table 1, we find that our approach can scale up to 17 variables on real-world datasets (i.e., the $\mathsf {letter}$ and $\mathsf {voting}$ datasets). We also note that with more data, and with more of the probability mass concentrated on fewer DAGs, traversing the BN graph with A* search appears to become more efficient. In particular, consider the time spent in A* search ($T_{A*}$), and the number of nodes generated (gen.), in the datasets $\mathsf {adult}$ and $\mathsf {wine}$, which both have 14 variables. Similarly, consider the datasets $\mathsf {letter}$ and $\mathsf {voting}$, which both have 17 variables. Moreover, consider dataset $\mathsf {zoo}$, also over 17 variables, which was a very small dataset, containing only 101 instances. Here, A* search exhausted the 64 GB of memory that it was allowed. We remark that, to our knowledge, ours is the first system for finding optimal DAGs using order-modular priors.⁶

In Fig. 3, we consider a simple example, highlighting the effect that a uniform order-modular prior can have on the structure we learn. In Fig. 3(a), we have the classical asia network, which we used to simulate datasets of different sizes. First, we simulated a small dataset of size $2^{7}$ and learned two networks, one with a prior, Fig. 3(b), and one without a prior, Fig. 3(c). Ignoring node $A$, the two networks are Markov equivalent. However, including node $A$, their linear extension counts are very different: 96 for network Fig. 3(b) but only 3 for network Fig. 3(c). This difference can explain why variable $A$ is disconnected in Fig. 3(b), as a disconnected node non-trivially increases the linear extension count (and hence, the weight of the prior). In Fig. 3(d), both cases (with and without the prior) learned precisely the same network when we raised the size of the dataset to $2^{14}$ (this DAG has 150 linear extensions). This network is Markov equivalent to the ground truth network that generated the data.

Fig. 3.

A network asia (a), and networks learned with dataset size $2^7$ with a prior (b), without a prior (c), and a network learned with dataset size $2^{14}$ (d).

5 Enumerating the k-Best Structures

We will next show how we can use our proposed framework for learning Bayesian networks, using BN graphs, to enumerate the k-best Bayesian network structures.

Enumerating the k-best Bayesian network structures is particularly simple to do when we perform A* search on the BN graph $\mathcal {G}_{\mathrm {bn}}$. In particular, the k-th best DAG can be obtained by finding the goal node $G_n$ that is the k-th closest to the root $G_0$. We can thus enumerate the k-best DAGs by simply continuing the A* search, rather than stopping when we reach the first goal node; see [12], for more on using A* search for k-best enumeration.⁷ $^{,}$ ⁸

We also note that if our heuristic is perfect, then we can enumerate all DAGs with an optimal score, relatively efficiently. In particular, A* will only expand nodes that lead to an optimal DAG, as long as a DAG with an optimal score remains (typically, they are all Markov equivalent). However, once we have exhausted all optimal DAGs, our heuristic is no longer perfect; cf. [12]. Given a DAG $G$, our heuristic is still admissible, as it still lower-bounds the cost of the possible extensions to a goal node $G_n$. That is, it may just report a cost for a goal node that was already enumerated (and hence has a lower cost). We can thus continue to employ the same heuristic in A* search, to enumerate the remaining $k$-best DAGs.

We further note a distinction between the BN graph and the order graph. In the BN graph, DAGs are represented explicitly, whereas in an order graph, DAGs are implicit. In particular, each node $\mathbf{Y}$ in the order graph represents just a single optimal DAG over the variables $\mathbf{Y}$. Hence, the $k$-th best DAG may not be immediately recoverable. That is, we may not be able to obtain the $k$-th best DAG starting from an optimal sub-DAG—we can only guarantee that we obtain a single optimal DAG. While it is possible to augment the order graph to find the $k$-th best DAG, as in [32], this is not as effective as searching the BN graph, as we shall soon see.

Finally, we consider another approach to enumerating the $k$-best DAGs in our experiments, based on integer linear programming (ILP) [9]. Basically, once an optimal DAG is obtained from an ILP, a new ILP can be obtained, whose optimal solution corresponds to the next-best DAG. In particular, we assert additional constraints that exclude the optimal DAG that we found originally. This process can be repeated to enumerate the $k$-best DAGs.

Next, we empirically compare the DP and ILP approaches, with our proposal, based on A* search in the BN graph.

5.1 Experiments

We compare our approach, which is based on A* search, with two other recently proposed k-best structure learning algorithms: (1) KBest,⁹ which is based on dynamic programming (DP) [32], and (2) Gobnilp,¹⁰ which is based on integer linear programming (ILP) [7].

For each approach, we enumerate the 10-best, 100-best and 1, 000-best BNs, over a variety of real-world datasets. We impose a 7,200 second limit on running time. To analyze memory usage, we incrementally increased the amount of memory available to each system (from 1 GB, 2 GB, 4 GB, 8 GB, 16 GB, and up to 64 GB), and recorded the smallest limit that allowed each system to finish.

Table 2. A comparison of the time t (in seconds) and memory m (in GBs) used by BN graph and KBest. An $\times _m$ corresponds to an out-of-memory (64 GB), and an $\times _t$ corresponds to an out-of-time (7,200 s). n denotes the number of variables in the dataset, and N denotes the size of the dataset.

Table 2 summarizes our results for A* search on the BN graph, and for the DP-based approach of KBest. We omit the results for the ILP-based approach of Gobnilp, which ran out-of-memory (given 64 GB) for all instances, except for the case of 10-best networks on the $\mathsf {wine}$ dataset, which took 2,707.13 s and under 8 GB of memory.¹¹

We observe a few trends. First, A* search on the BN graph can be over three orders of magnitude more efficient than KBest, at enumerating the $k$-best BNs. For example, when we enumerate the $100$-best BNs on the $\mathsf {voting}$ dataset, A* search is over 4,323 times faster. Next, we observe that A* search is consistently more efficient than KBest at enumerating the $k$-best networks (except for dataset $\mathsf {imports}$ for $k=10$). In general, our approach scales to larger networks (with more variables), and to larger values of $k$. In fact, KBest appears to scale super-linearly with $k$, but A* search appears to scale sub-linearly with respect to $k$. These differences are due in part to: (1) the more exhaustive nature of dynamic programming (DP) (we need to maintain all of the partial solutions that can potentially be completed to a $k$-th best solution), and (2) the more incremental nature of A* (the next best solutions are likely to be in the priority queue already). Finally, we see that the memory usage of these two approaches is comparable, although memory usage by A* search appears to be more memory efficient as we increase the number $k$ of networks that we enumerate.

Table 3. The time $T_h$ to compute the heuristic function and the time $T_{{A*}}$ to traverse the BN graph with A* (in seconds).

Table 4. (1) The number of generated nodes. (2) The number of expanded nodes. (3) The number of re-expanded nodes (in partial-expansion A*).

Table 5. The number of times the black-box is invoked to evaluate the heuristic function.

To gain more insight about the computational nature (and bottlenecks) of A* search on the BN graph, consider Table 3, which looks at how much time $T_h$ that was spent on evaluating the heuristic function, versus the time $T_{{A*}}$ that was spent in navigating the BN graph (where $t = T_h + T_{{A*}}$, with the total time $t$ corresponding to those reported in Table 2). Table 4 further reports the number of nodes generated (the number of nodes inserted into the open list) and expanded by A* search. First, we observe that the vast majority of the time spent in search is spent in evaluating the heuristic function. This is expected, as evaluating our black-box heuristic function is relatively expensive. Next, we observe that the number of nodes expanded is relatively small, which suggests that our black-box heuristic is indeed powerful enough to efficiently navigate the large search space of the BN graph. We also remark again that due to the caching of heuristic values (which we discussed earlier), the number of times that our black-box is invoked, can be much smaller than the number of times that a node is generated. This is illustrated in Table 5.

6 Conclusion

Underlying nearly all score-based methods for learning Bayesian networks from data, is the property of score decomposability. This has been true, since the first Bayesian network learning algorithms were proposed, over two decades ago. While the property of score decomposability has been fruitfully exploited over this time, there is a notable void in the structure learning landscape, in the support of learning with non-decomposable scores. This includes a general lack of support for the integration of more expressive, but non-decomposable forms of prior knowledge.

In this paper, we take a step towards a more general framework for Bayesian network structure learning that targets this void. We proposed a new search space, called the BN graph, which explicates all Bayesian network structures. We proposed to navigate this tremendously large search space, with the assistance of a (nearly) omniscient oracle—any state-of-the-art system for Bayesian network structure learning can be used as this oracle. Using heuristic search methods, such as A* search, we showed how this framework can be used to find optimal Bayesian network structures, using non-decomposable scores (even when our oracle relies on decomposable scores). To our knowledge, ours is the first system for finding optimal DAGs using order-modular priors, in particular. Further, we showed that enumerating the $k$-best DAGs is very simple on the BN graph, where empirically, we observed three orders of magnitude improvement, compared to existing approaches.

A Proofs for Sect. 4.2

Proof

(Theorem 1 ). The total cost of a path from the root $G_0$ to a leaf $G_n$ is:

$$\begin{aligned}&\sum _{G_i \rightarrow G_j} \mathsf {score}(X_j\mathbf{U}_j \mid \mathcal {D}) - \log \frac{{ Pr}_j(G_j)}{{ Pr}_i(G_i)}\\&=\sum _{G_i \rightarrow G_j} \mathsf {score}(X_j\mathbf{U}_j \mid \mathcal {D}) - \log { Pr}_j(G_j) + \log { Pr}_i(G_i)\\&= \mathsf {score}(X_1 \mathbf{U}_1 \mid \mathcal {D}) - \log { Pr}_1(G_1) + \log { Pr}_0(G_0) {} \\&\quad + \mathsf {score}(X_2\mathbf{U}_2 \mid \mathcal {D}) - \log { Pr}_2(G_2) + \log { Pr}_1(G_1) + \ldots {} \\&\quad + \mathsf {score}(X_n\mathbf{U}_n \mid \mathcal {D}) - \log { Pr}_{n}(G_{n}) + \log { Pr}_{n-1}(G_{n-1})\\&= \mathsf {score}(G \mid \mathcal {D}) - \log { Pr}_n(G_n) \end{aligned}$$

as desired.    $\square$

Proof

(Theorem 2 ).

$$\begin{aligned} h(G_i)&= \min _{G_n: G_i \leadsto G_n} \sum _{X\mathbf{U}\in G_n - G_i} \mathsf {score}(X\mathbf{U}\mid \mathcal {D}) + \min _{G_n: G_i \leadsto G_n} - \log \frac{{ Pr}_n(G_n)}{{ Pr}_i(G_i)}\\&\le \min _{G_n: G_i \leadsto G_n} \Big ( \sum _{X\mathbf{U}\in G_n - G_i} \mathsf {score}(X\mathbf{U}\mid \mathcal {D}) - \log \frac{{ Pr}_n(G_n)}{{ Pr}_i(G_i)} \Big )\\&= \min _{G_n: G_i \leadsto G_n} g(G_n) - g(G_i) \end{aligned}$$

Since heuristic function h lower-bounds the true cost of to a goal node, it is admissible.    $\square$

Below we consider the correctness of Algorithm 1.

Lemma 1

In Algorithm 1:

• 1. all $G_i$ that generate $G_{i + 1}$ are extracted from H before $G_{i + 1}$ is extracted;

• 2. when $(G_{i + 1}, f_{i + 1}, l_{i + 1})$ is extracted from H,

  $$\begin{aligned} f_{i + 1} = \mathsf {score}(G_{i + 1} | \mathcal {D}) - \log \#G_{i + 1} + h(G_{i + 1}), \end{aligned}$$

  and $l_{i + 1}$ is the number of linear extensions of $G_{i + 1}$, i.e., $\#G_{i+1}$.

where $h(G_i) = h_1(G_i) - \sum _{j=i+1}^n \log j$.

Proof

Consider a minimum item $(G_{i + 1}, f_{i + 1}, l_{i + 1})$ extracted from H. Below we show by induction that (1) all $G_i$ such that $G_i$ generates $G_{i + 1}$ are extracted from H before $G_{i + 1}$ (2) $f_{i + 1} = \mathsf {score}(G_{i + 1} | \mathcal {D}) - \log \#G_{i + 1} + h(G_{i + 1})$, and $l_{i + 1}$ is the number of linear extensions of $G_{i + 1}$, which is also the number of paths from $G_0$ to $G_{i + 1}$.

For $i = 0$, clearly (1) and (2) are true. Assume (1) and (2) are true for all $(G_i, f_i, l_i)$. Then when $(G_{i + 1}, f_{i + 1}, l_{i + 1})$ is extracted, $l_{i + 1}$ is the number of paths from $G_0$ to $G_{i + 1}$ that pass the $G_i$ extracted from H before $G_{i + 1}$. To see this, note that l is the number of path from $G_0$ to $G_i$. Moreover, since $l_{i + 1}$ is the number paths from $G_0$ to $G_{i + 1}$ that pass the $G_i$ extracted from H before $G_{i + 1}$, when $(G_{i + 1}, f_{i + 1}, l_{i + 1})$ is in H,

$$\begin{aligned} f_{i + 1} = \mathsf {score}(G_{i + 1} | \mathcal {D}) - \log \sum _{G_i \prec G_{i + 1}} N(G_0 \rightarrow \ldots \rightarrow G_i \rightarrow G_{i + 1}) + h (G_{i + 1}), \end{aligned}$$

where $G_i \prec G_{i + 1}$ denotes that $G_i$ is extracted before $G_{i + 1}$, and $N(G_0 \rightarrow \ldots \rightarrow G_i \rightarrow G_{i + 1})$ denotes the number of paths $G_0 \rightarrow \ldots \rightarrow G_i \rightarrow G_{i + 1}$. Note that $f_{i + 1}$ decreases as more $G_i$ are extracted.

Consider when $(G_i, f_i, l_i)$ and $(G_{i + 1}, f_{i + 1}, l_{i + 1})$ are both in H. Below we show that all $G_i$ that generates $G_{i + 1}$ are extracted from H before $G_{i + 1}$. Consider

$$\begin{aligned} f_i&= \mathsf {score}(G_i | \mathcal {D}) \\&\quad - \log \sum _{G_{i - 1} \prec G_i} N(G_0 \rightarrow \ldots \rightarrow G_{i - 1} \rightarrow G_i) + h_1(G_i) - \sum _{j = i + 1}^n \log j\\ f_{i + 1}&= \mathsf {score}(G_{i + 1} | \mathcal {D}) \\&\quad - \log \sum _{G^\prime _i \prec G_{i + 1}} N(G_0 \rightarrow \ldots \rightarrow G^\prime _i \rightarrow G_{i + 1})+ h_1 (G_{i + 1}) - \sum _{j = i + 2}^n \log j\\ \end{aligned}$$

We simply need to show $f_{i + 1} > f_i$. Since $h_1$ is a consistent heuristic function for learning with $\mathsf {score}$, $\mathsf {score}(G_{i + 1} | \mathcal {D}) + h_1(G_{i + 1}) \ge \mathsf {score}(G_i | \mathcal {D}) + h_1 (G_i)$. Then we only need to show

$$\begin{aligned}&(i + 1) \sum _{G_{i - 1} \prec G_i} N(G_0 \rightarrow \ldots \rightarrow G_{i - 1} \rightarrow G_i) \\&> \sum _{G^\prime _i \prec G_{i + 1}} N(G_0 \rightarrow \ldots \rightarrow G^\prime _i \rightarrow G_{i + 1}) \end{aligned}$$

First, for any pair of DAGs $G_i$ and $G^\prime _i$ that can generate a DAG $G_{i+1}$, there exists a unique DAG $G_{i-1}$ that can generate both $G_i$ and $G^\prime _i$. For each $G^\prime _i$ on the right-hand side, there thus exists a corresponding (and unique) $G_{i-1}$ on the left-hand side that can generate both $G^\prime _i$ and $G_i$. Further, since $G^\prime _i$ was expanded, $G_{i-1}$ must also have been expanded (by induction). For each such $G_{i-1}$, if $G^\prime _i$ has a linear extension count of $L$, then $G_{i-1}$ must have at least a linear extension count of $L/i$, and hence the corresponding $N(G_0 \rightarrow \ldots \rightarrow G_{i-1} \rightarrow G_i)$ is at least $L/i$. On the left-hand side, we the corresponding term is thus at least $(i+1)\cdot L/i > L$. Since this holds for each element of the summation on the right-hand side, the above inequality holds.

Since all $G_i$ that generates $G_{i + 1}$ are extracted from H before $G_{i + 1}$, as a result, $f_{i + 1} = \mathsf {score}(G_{i + 1} | \mathcal {D}) - \log \#G_{i + 1} + h(G_{i + 1})$, and $l_{i + 1}$ is the number of all paths from $G_0$ to $G_{i + 1}$.

Proof

(of Theorem 4 ). To see the correctness of the algorithm, simply note that by Lemma 1, when $(G_{i + 1}, f_{i + 1}, l_{i + 1})$ is extracted from H, i.e. the open list, $f_{i + 1} = f(G_{i + 1})$.

Proof

(of Theorem 3 ). By Lemma 1, Algorithm 1 can count the number of linear extensions.