Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

This chapter describes basic properties and modeling of resonators using acoustic waves propagating in a solid body. This type of waves is called the bulk acoustic wave (BAW), which can be excited and detected efficiently using piezoelectricity. The resonators are widely used in various applications such as clock generation, frequency filtering, and sensing. The most popular ones are crystal quartz resonators [1] for relatively low frequency applications (<100 MHz). Recently BAW resonators fabricated by thin film and micromachining technologies, i.e., film bulk acoustic resonators (FBARs) [2], are getting popular for relatively high frequency applications (>1–3 GHz) such as duplexers used in mobile and smart phones.

BAWs can be also excited and detected electrostatically, and some devices have already been mass produced and applied to various frequency control applications [3]. However, owing to the very weak electromechanical coupling, electrostatically driven BAW devices are not feasible for low-loss and wideband applications.

First basic device operation is discussed using a very simple phenomenological model, and a one-dimensional model based on the wave theory is introduced for detailed discussions. Then typical device structures and fabrication steps are explained, and choice of piezoelectric and electrode materials are also discussed. Finally, wave propagation in three-dimensional structures is explained, and possible spurious and loss mechanisms including their countermeasures are discussed.

2 BVD Model

Let us consider acoustic wave propagation in a plate with thickness h. It is known that the plate causes a mechanical resonance (thickness resonance) at frequencies satisfying the condition of

$$ {f}_{\mathrm{r}}=\frac{nV}{2h}, $$
(8.1)

where V is the acoustic wave velocity, and n is an integer called the order of resonance modes. Equation (8.1) indicates that in addition to a lowest order resonance (n = 1) called the fundamental resonance, a series of higher-order (n ≠ 1) ones exist. Since f r for n ≠ 1 will be an integer times f r for n = 1, higher-order resonances are often called harmonic resonances or overtones. When the longitudinal BAW is responsible for the thickness resonance, it is called the thickness extensional (TE) resonance while it is called the thickness shear (TS) resonance when the shear BAW is responsible. In general, V of the longitudinal BAW is faster than that of the shear BAW for the identical propagation direction in the identical material.

When the plate is piezoelectric and sandwiched in between two parallel electrodes (see Fig. 8.1a), we can excite and detect the resonances electrically. This device can be used as an impedance element in electronic circuits. This type of electronic components is called BAW resonators.

Fig. 8.1
figure 1

Simplified model for BAW resonators. (a) Physical model. (b) Electromechanical equivalent circuit

Full size image

In the structure shown in Fig. 8.1a, when a sinusoidal voltage v with the frequency f is applied to two electrodes, a mechanical force v m is generated through piezoelectricity, and the displacement u is generated in the plate as a reaction. The relation might be written as

$$ v\propto {v}_{\mathrm{m}}=M\frac{d^2u}{d{t}^2}+\eta \frac{du}{dt}+Ku, $$
(8.2)

where M, η, and K are an effective mass, effective viscosity, and effective spring constant of the plate, respectively. In the right hand side of the equation, first to third terms correspond to inertia, friction, and elasticity, respectively.

Due to the reciprocity of piezoelectricity, electrical charges q m proportional to u will be induced on the electrodes.

From these relations, we may derive an electromechanical equivalent circuit shown in Fig. 8.1b. In the figure, i m = du/dt is a mechanical current, and C 0 is called the clamped capacitance which expresses the electrostatic coupling between two electrodes.

Since we are only interested in electrical characteristics, the equivalent circuit can be simplified as shown in Fig. 8.2, where C m, L m, and R m are called the motional capacitance, inductance, and resistance, respectively. This circuit is called the Butterworth–Van Dyke (BVD) model [4], and is quite often used as the simplest model for one-port acoustic resonators.

Fig. 8.2
figure 2

Electrical equivalent circuit model (BVD model)

Full size image

Case A in Fig. 8.3 shows a typical frequency dependence of the input admittance Y calculated from the BVD model. In the figure, R r is an impedance used for the normalization. A series resonance where |Y| takes a maximum is seen at 1 GHz while a parallel resonance where |Y| takes a minimum is seen at 1.025 GHz.

Fig. 8.3
figure 3

Frequency dependence of input admittance |Y| derived from the BVD model. Case A: calculated by the original BVD model, Case B: calculated by the modified BVD model (see Fig. 8.5) with R e ≠ 0, and Case C: calculated by the modified BVD model with R 0 ≠ 0

Full size image

From the BVD model, we can express Y in a form of

$$ Y=2\pi jf{C}_0\frac{1-{\left(f/{f}_{\mathrm{a}}\right)}^2+j\left(f/{f}_{\mathrm{a}}\right){Q}_{\mathrm{a}}^{-1}}{1-{\left(f/{f}_{\mathrm{r}}\right)}^2+j\left(f/{f}_{\mathrm{r}}\right){Q}_{\mathrm{r}}^{-1}}. $$
(8.3)

In the equation, f r is the resonance frequency where the series resonance occurs, and f a is the anti-resonance frequency where the parallel resonance occurs. From the equivalent circuit, these frequencies are given by

$$ {f}_{\mathrm{r}}=\frac{1}{2\pi \sqrt{L_{\mathrm{m}}{C}_{\mathrm{m}}}} $$
(8.4)

and

$$ {f}_{\mathrm{a}}=\frac{1}{2\pi \sqrt{L_{\mathrm{m}}{\left({C}_{\mathrm{m}}^{-1}+{C}_0^{-1}\right)}^{-1}}}, $$
(8.5)

respectively. In Eq. (8.3), Q r and Q a are called the resonance and anti-resonance quality factors, respectively, and are given by

$$ {Q}_{\mathrm{r}}=\frac{2\pi {f}_{\mathrm{r}}{L}_{\mathrm{m}}}{R_{\mathrm{m}}} $$
(8.6)

and

$$ {Q}_{\mathrm{a}}=\frac{2\pi {f}_{\mathrm{a}}{L}_{\mathrm{m}}}{R_{\mathrm{m}}}. $$
(8.7)

They give steepness of the resonance peaks, and influence the minimum insertion loss and steepness of the passband edges for filter applications [5].

Here we define the capacitance ratio γ, which is defined as

$$ \gamma =\frac{C_0}{C_{\mathrm{m}}}=\frac{1}{{\left({f}_{\mathrm{a}}/{f}_{\mathrm{r}}\right)}^2-1}. $$
(8.8)

Figure 8.2 implies that γ gives the weakness of piezoelectricity. For filter applications, it influences the minimum insertion loss and determines the maximum passband width [5].

When multiple resonances exist, their influences can be taken into account by increasing the number of LCR branches as shown in Fig. 8.4, where the nth branch expresses the nth order mechanical resonance [4].

Fig. 8.4
figure 4

BVD model taking multiple resonances into account

Full size image

It is important to note that Eqs. (8.6) and (8.7) imply that Q r is almost equal to Q a. This is not true in general. This is because only the viscous loss is considered in the original BVD model shown in Fig. 8.2.

Figure 8.5 shows the modified BVD model taking the difference in Q r and Q a into account [6]. In the figure, R e stands for the ohmic resistance of electrodes, and R 0 considers the dielectric loss in the piezoelectric film. Other loss mechanisms such as the acoustic leakage discussed in Eq. (8.6) may be also included in R e and/or R 0.

Fig. 8.5
figure 5

Modified BVD model

Full size image

Figure 8.2 also shows influence of these resistances on the resonance characteristics. In the figure, R e is considered for case B while R 0 is included for case C. It is seen that R e influences only the response at f ∼ f r while R 0 influences only the response at f ∼ f a. Traces for cases B and C are mostly overlapped with that for case A at the remaining frequency ranges.

Existence of these resistances modifies Eqs. (8.6) and (8.7) as

$$ {Q}_{\mathrm{r}}=\frac{2\pi {f}_{\mathrm{r}}{L}_{\mathrm{m}}}{R_{\mathrm{m}}+{R}_{\mathrm{e}}} $$
(8.9)

and

$$ {Q}_{\mathrm{a}}=\frac{2\pi {f}_{\mathrm{a}}{L}_{\mathrm{m}}}{R_{\mathrm{m}}+{R}_0}. $$
(8.10)

These equations indicate that Q r > Q a when R e < R 0 while Q r < Q a when R e > R 0.

Equation (8.3) indicates that

$$ {Y}_{\max}\equiv {\left.Y\right|}_{f={f}_{\mathrm{r}}}\sim 2\pi {f}_{\mathrm{r}}{C}_0{Q}_{\mathrm{r}}\left\{1-{\left({f}_{\mathrm{r}}/{f}_{\mathrm{a}}\right)}^2\right\}\sim 2\pi {f}_{\mathrm{r}}{C}_0{M}_{\mathrm{r}}, $$
(8.11)

and

$$ {Y}_{\min}\equiv {\left.Y\right|}_{f={f}_{\mathrm{a}}}\sim -2\pi {f}_{\mathrm{a}}{C}_0\frac{Q_{\mathrm{a}}^{-1}}{1-{\left({f}_{\mathrm{a}}/{f}_{\mathrm{r}}\right)}^2}\sim 2\pi {f}_{\mathrm{a}}{C}_0{M}_{\mathrm{a}}^{-1}, $$
(8.12)

where M r = Q r/γ and M a = Q a/γ are the figure of merit for BAW resonators at the resonance and anti-resonance, respectively. Equations (8.11) and (8.12) indicate that when R r is chosen as 2πf r C 0 or 2πf a C 0, M r and M a are approximately given by Y max R r and (Y min R r)−1, respectively, and thus we can estimate them graphically from the |Y|R r curve shown in Fig. 8.3. Since γ are estimated from f r and f a, we can calculate Q r and Q a from estimated M r and M a.

For better understanding of device behavior, we often want to know how the Q factor changes with the frequency. For the purpose, Feld et~al. proposed the following frequency dependent Q factor for device characterization [7];

$$ Q(f)=2\pi f\tau (f)\frac{\left|{S}_{11}\right|}{1-\left|{S}_{11}\right|{}^2},\vspace*{-3pt} $$
(8.13)

where S 11 is the electrical reflection coefficient measured by a vector network analyzer and τ is the group delay estimated by

$$ \tau (f)=-\frac{\partial \angle {S}_{11}}{2\pi \partial f}.\vspace*{-3pt} $$
(8.14)

Variation of f r with temperature T is one of the most important characteristics of acoustic resonators. Equation (8.1) indicates that the temperature coefficient of frequency (TCF) of the acoustic resonator is given by

$$ \mathrm{T}\mathrm{C}\mathrm{F}={f}_{\mathrm{r}}^{-1}\frac{\partial {f}_{\mathrm{r}}}{\partial T}={V}^{-1}\frac{\partial V}{\partial T}-{h}^{-1}\frac{\partial h}{\partial T}.\vspace*{-3pt} $$
(8.15)

In the right hand side of the equation, the first and second terms correspond to the temperature coefficient of the BAW velocity (TCV) and the thermal expansion coefficient of the plate toward the thickness direction, respectively. Equation (8.15) indicates that choice of the plate medium and propagation mode is determinative for the TCF.

It is known that TCF can be very small for a wide temperature range when single-crystal quartz is chosen as a plate material and its crystallographic orientation is set properly [1]. This is the main reason why quartz resonators are widely used for frequency control applications. However, materials with good TCF possess weak piezoelectricity in general, and this is also true for quartz. Thus we must choose an appropriate piezoelectric material under a compromise between TCF and k t 2 (or γ) as we will discuss in Sect. 8.5.

It should be noted that the TCF at f = f r (TCFr) is different from that at f = f a (TCFa). Equation (8.8) indicates that TCFr and TCFa are related to each other by the temperature coefficient of γ (TCF γ ) as

$$ {\mathrm{TCF}}_{\mathrm{a}}={\mathrm{TCF}}_{\mathrm{r}}-\frac{1}{2\left(1+\gamma \right)}{\mathrm{TCF}}_{\gamma }.\vspace*{-3pt} $$
(8.16)

This equation indicates that difference between TCFr and TCFa becomes large when γ is small.

3 Mason’s Equivalent Circuit Model

As for one-dimensional case, the rigorous analysis is possible by using the Mason equivalent circuit [8, 9]. Figure 8.6 shows the equivalent circuit of the resonator structure shown in Fig. 8.1a for the TE vibration. In the figure,

Fig. 8.6
figure 6

Mason equivalent circuit model of the BAW resonator

Full size image
$$ \begin{array}{l}{n}^2={k}_t^2{C}_0{Z}_{\mathrm{p}}{V}_{\mathrm{p}}S/h,\kern0.5em {Z}_{\mathrm{ap}}=-j{Z}_{\mathrm{p}}S \csc \left({\beta}_{\mathrm{p}}h\right),\kern0.5em {Z}_{\mathrm{bp}}=j{Z}_{\mathrm{p}}S \tan \left({\beta}_{\mathrm{p}}h/2\right)\\ {}{Z}_{\mathrm{ae}}=-j{Z}_{\mathrm{e}}S \csc \left({\beta}_{\mathrm{e}}{h}_{\mathrm{e}}\right),\kern0.5em {Z}_{\mathrm{be}}=j{Z}_{\mathrm{e}}S \tan \left({\beta}_{\mathrm{e}}{h}_{\mathrm{e}}/2\right),\end{array} $$

Z p and Ze are the acoustic impedance [9] (mass density × BAW velocity) of the piezoelectric layer and electrodes, β p and β e are the wavenumbers (2πf/BAW velocity) in the piezoelectric layer and electrodes, and h e and S are the thickness and surface area of the electrodes, and k t 2 is the “intrinsic” electromechanical coupling factor of the piezoelectric layer for the TE vibration [9]. In the figure, both ends of acoustic ports are short-circuited because the mechanical voltage (stress) is zero at the top and bottom surfaces.

We can derive the input admittance Y (=i/v) from this circuit as

$$ \begin{array}{l}\begin{array}{ll}Y\hfill & =\frac{2\pi jf{C}_0}{1+j{n}^2{\left(\omega {C}_0\right)}^{-1}{\left[{Z}_{\mathrm{ap}}+{Z}_{\mathrm{bp}}/2+\left\{{Z}_{\mathrm{be}}+{\left({Z}_{\mathrm{be}}^{-1}+{Z}_{\mathrm{ae}}^{-1}\right)}^{-1}\right\}/2\right]}^{-1}}\hfill \\ {}\hfill & =\frac{2\pi jf{C}_0}{1-{k}_t^2{\left({\beta}_{\mathrm{p}}h/2\right)}^{-1}{\left\{ \cot \left({\beta}_{\mathrm{p}}h/2\right)-R\right\}}^{-1}}\hfill \end{array},\\ {}\kern1em \end{array} $$
(8.17)

where R = Z e Z p −1tan(β e h e) is a factor giving influence of the electrodes on the resonance characteristics. It should be noted that when β e h e ≪ 1, R ∼ 2πfZ p −1(ρ e h e), where ρ e is the mass density of the electrode material.

From Eq. (8.17), the resonance frequency f r is given as a solution of

$$ \cot \left({\beta}_{\mathrm{p}}h/2\right)=R $$
(8.18)

while the anti-resonance frequency f a is given as a solution of

$$ \cot \left({\beta}_{\mathrm{p}}h/2\right)-{k}_{\mathrm{t}}^2{\left({\beta}_{\mathrm{p}}h/2\right)}^{-1}=R. $$
(8.19)

Figure 8.7 shows calculated variation of f r and f a of the fundamental resonance with R at f = f a. In the figure, the calculated frequencies are normalized by f a when h e = 0, and k t 2 was set at 0.05. In the calculation, we assume R is proportional tof. It is seen that f r and f a decrease monotonically with R at f = f a. The frequency decrease is due to an increase in the total mass of the resonator structure.

Fig. 8.7
figure 7

Variation of resonance and anti-resonance frequencies, and k e 2 with the electrode related parameter R at f = f a

Full size image

When h e = 0, Eq. (8.17) reduces to

$$ Y=\frac{2\pi jf{C}_0}{1-{k}_{\mathrm{t}}^2 \tan \left({\beta}_{\mathrm{p}}h/2\right)/\left({\beta}_{\mathrm{p}}h/2\right)}. $$
(8.20)

This equation relates f r/f a with k t 2 as

$$ {k}_{\mathrm{t}}^2=\frac{\left(n\pi {f}_{\mathrm{r}}/2{f}_{\mathrm{a}}\right)}{ \tan \left(n\pi {f}_{\mathrm{r}}/2{f}_{\mathrm{a}}\right)}, $$
(8.21)

where n is the resonance order appeared in Eq. (8.1). When f r ∼ f a, we can derive the following relation from Eqs. (8.8) and (8.21);

$$ 2\left({f}_{\mathrm{a}}-{f}_{\mathrm{r}}\right)/{f}_{\mathrm{a}}\sim {\gamma}^{-1}\sim \left\{\begin{array}{cc}\hfill 8{k}_{\mathrm{t}}^2/{n}^2{\pi}^2\hfill & \hfill n:\ \mathrm{odd}\hfill \\ {}\hfill 0\hfill & \hfill n:\ \mathrm{even}\hfill \end{array}\right.. $$
(8.22)

Equation (8.22) indicates that three important facts: (a) achievable γ −1 is limited by k t 2 of the employed piezoelectric material, (b) even-order overtones cannot be excited electrically, and (c) γ −1 decreases rapidly with an increase in n.

Figure 8.8 shows the standing wave pattern of resonances with different n. Because of stress free on the top and bottom surfaces, the displacement takes a maximum there. When n is even, the displacement polarity at the top surface is in-phase with that on the bottom surface. Then the resonance cannot be excited and detected electrically, and γ −1 is zero for the case. Even when n is odd, periodicity of the distribution causes cancellation of excited electric fields, and thus γ −1 becomes very small when n is large.

Fig. 8.8
figure 8

Vertical standing wave pattern

Full size image

It should be noted that Eqs. (8.21)–(8.22) hold only when h e = 0. Since influence of electrodes is not negligible in general, we often characterize piezoelectric strength of the resonator by the “effective” electromechanical coupling factor k e 2 defined by

$$ {k}_{\mathrm{e}}^2=\frac{\left(\pi {f}_{\mathrm{r}}/2{f}_{\mathrm{a}}\right)}{ \tan \left(\pi {f}_{\mathrm{r}}/2{f}_{\mathrm{a}}\right)}. $$
(8.23)

or its approximated forms of

$$ {k}_{\mathrm{e}}^2=\frac{\pi^2}{4}\frac{f_{\mathrm{a}}-{f}_{\mathrm{r}}}{f_{\mathrm{a}}}. $$
(8.24)

Figure 8.7 also shows k e 2 calculated by Eq. (8.23) as a function of R at f = f a. It is seen that k e 2 increases with an increase in R at f = f a, and is going to converge to π 2/8 = 1.234. This value is the coefficient appearing in Eq. (8.22), and originates from unmatching of the excitation electric field with the acoustic wave field. When R is large, the electrodes can be regarded as the mass and the piezoelectric plate behaves like a spring. Then the stress field in the plate becomes uniform, and is matched with the excitation electric field. This positive effect of the electrode mass loading was first reported by Lakin et~al. [10].

It should be noted that the figure of merit are often evaluated by M r = Q r k e 2 and M a = Q a k e 2 instead of M r = Q r/γ and M a = Q a/γ defined in Eqs. (8.9) and (8.10).

4 Resonator Structures

For many years, piezoelectric thin plates required for BAW resonators have been manufactured by mechanical thinning and polishing of piezoelectric plates of quartz and ceramics. Due to difficulty in mechanical processes, practical limit of h was circa a few tens of micrometers, and thus the fundamental resonance frequency was limited in the high frequency (HF) range (<30 MHz). Although use of harmonic resonances with n ≠ 1 extends this limit, it results in significant increase in γ or decrease in k e 2.

Smythe and Angove applied anisotropic chemical etching for thinning quartz plates, and this extended applicability of quartz resonators close to the GHz range[11].

In 1980–1981, three groups independently proposed high frequency BAW resonators fabricated by the thin film and micromachining technologies [12–14]. This technology extended applicability of BAW resonators to the ultra high frequency (UHF) and super high frequency (SHF) ranges.

Figure 8.9a shows the proposed device structure called the film bulk acoustic resonator (FBAR). Bottom electrode, piezoelectric film, and top electrode are sequentially deposited and patterned on a supporting substrate (Si). Then the substrate is partially removed from the back side by chemical etching [12–14] or deep reactive ion etching [15], and the free standing diaphragm is realized.

Fig. 8.9
figure 9

FBAR structures. (a) Back-side etched. (b) Sacrificial-layer etched. (c) Front-side etched

Full size image

Satoh et~al. proposed to use the sacrificial layer technique for the air gap fabrication (see Fig. 8.9b) [16]. First, two additional layers are deposited and patterned, and then bottom electrode, piezoelectric film, and top electrode are successively deposited and patterned. Finally, first additional (bottom) layer is etched away chemically and the air gap is created under the composite diaphragm.

In this process, sticking of the diaphragm to the base substrate is troublesome. The second additional layer is aimed at keeping the distance large and avoiding this problem.

Taniguchi et~al. proposed use of bending of the composite diaphragm caused by the internal stress to keep the air gap height [17]. This can eliminate the second additional layer.

Ruby et~al. proposed to use the surface micromachining for the same purpose (see Fig. 8.9c) [2]. First, the top surface of the supporting substrate is partially etched, and the etched portion is filled with another material such as phosphosilicate glass, which is used as a sacrificial layer. Remaining fabrication steps are identical with those described above.

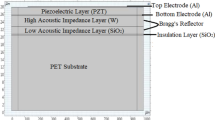
Lakin et~al. proposed to use the Bragg reflection instead of the air cavity to isolate the composite membrane acoustically from the base substrate [18]. Figure 8.10 shows this type of proposed device structure called the solidly mounted resonator (SMR). Thin films of low and high acoustic impedance Z a with quarter wavelength layer are stacked alternately, and they act as the Bragg reflector. SiO2 is used for low Z a layers while W or Ta is chosen for high Z a layers. Due to penetration of acoustic energy into the Bragg reflector, achievable k e 2 is a little smaller than that in the FBAR structure [19].

Fig. 8.10
figure 10

SMR structure

Full size image

It should be noted that the layer thicknesses are slightly modified from quarter wavelengths so that strong reflection occurs not only for the longitudinal vibration but also for shear ones [20]. This modification gives significant enhancement of the Q factors.

5 Material Choice

Choice of the piezoelectric material is determinative for designing high performance RF BAW resonators. That is, k t 2 limits achievable fractional frequency bandwidth for filter applications.

Aluminum nitride (AlN) is widely used for the purpose because of its several distinct features: low propagation loss, high electrical resistivity, and compatibility with CMOS fabrication processes and equipment [21, 22]. Although various materials such as zinc oxide (ZnO) [12–14, 16] and lead zirconate titanate (PZT) [23, 24] have been investigated extensively for the use, realized performances are much worse than those attained by AlN and far from practical use.

In general, piezoelectric films used in these resonators are polycrystalline, and resonator performances are significantly dependent on various film properties such as crystallinity, orientation, grain size, and binding strength among grains, and they must be uniform through the wafer and/or batches for mass production. Thus appropriate techniques and/or apparatus must be selected for the film deposition [22,25].

Recently, Sc doping in AlN films is paid much attention owing to its drastic enhancement of the electromechanical coupling [26–28]. When the Sc content is 43 at.%, k t 2 takes a maximum value about five times larger than non-doped AlN films. Yokoyama et~al., proposed co-doping of Mg and Zr for the same purpose[29].

In general, stiff materials have small acoustic attenuation. With an increase in the doping amount, BAW velocities in these films decrease and the acoustic attenuation becomes large.

Molybdenum (Mo) [2], tungsten (W) [19], and ruthenium (Ru) [30] are often used for the electrodes because their large acoustic impedance offers increase in k e 2 described in Sect. 8.3, and they act as a good seed layer for the AlN growth.

Another important merit of these materials is compensation of the internal stress generated during the AlN deposition. This property is crucial for realization of the free standing membrane in the FBAR structures. In many cases, AlN films with good crystal quality possess large internal stress.

Amorphous silicon dioxide (SiO2) possesses a quite unique feature in acoustics. Namely, SiO2 becomes stiff with temperature T. In contrast, most of all materials including AlN, Mo, and Ru become soft with T. Thus the temperature coefficient of the resonance frequency (TCF) can be improved by inclusion of SiO2 in the resonator structure [31, 32].

It should be noted that SiO2 is non-piezoelectric and relatively lossy. Thus the TCF compensation by SiO2 is only possible at an expense of the k e 2 and Q reduction. In general, SMRs offer better TCF but worse Q than FBARs because SiO2 is used in the Bragg reflector [19].

There is another aspect to be paid much attention when fabricating a BAW resonator with SiO2 layers. That is, properties of SiO2 are very dependent on the deposition technique, apparatus, and conditions, and thus appropriate deposition environments must be endeavored for the current purpose [33].

6 Lateral Wave Propagation

Since real BAW resonators possess three-dimensional structures, we must take their influences into account.

Let us consider, as an example, the FBAR structure shown in Fig. 8.11. When the center portion of the resonator vibrates, excited acoustic waves may also propagate laterally in the diaphragm. Acoustic waves guided in a plate are called Lamb waves. Since leakage of excited Lamb waves causes deterioration of the resonator Q, its suppression is necessary.

Fig. 8.11
figure 11

FBAR structure and Lamb wave propagation and leakage

Full size image

The energy leakage can be suppressed by designing side edges to cause the total reflection for all Lamb modes and confine wave energy in the resonator area. However, this strategy causes another problem. That is, due to phase lag with propagation, trapped Lamb modes cause unnecessary spurious resonances close to the main resonance. They are called the transverse mode resonances or inharmonic overtones. The most important but never ending design theme is their suppression without badly affecting the Q factor of the main mode.

The resonance condition of the transverse modes is given by

$$ {\beta}_yW-\angle {\varGamma}_y={n}_y\pi, $$
(8.25)

where β y is the wavenumber of Lamb modes along the surfaces, W is the electrode width, n is the order of the lateral resonance, and Γ y is the reflection coefficient at the side edges, respectively.

Figure 8.12 shows lateral standing pattern of the Lamb modes when the lateral edges are mechanically free. In this case, the displacement takes a maximum there. It should be noted that, similar to the longitudinal resonances, electrical excitation efficiency will be decreased significantly with an increase in n y (or β y ) because of mutual cancellation of charges induced by the sinusoidal field.

Fig. 8.12
figure 12

Lateral resonance patterns

Full size image

By a simple analogy from electromagnetic waveguides, readers may think the relation between β y and ω, namely, the dispersion relation is given by

$$ {\beta}_y=\sqrt{{\left(\omega /V\right)}^2-{\left(n\pi /h\right)}^2}={V}^{-1}\sqrt{\omega^2-{\omega}_{\mathrm{r}}^2}, $$

where h is the plate thickness and ω r is the thickness resonance frequency. This equation indicates that waveguide modes exhibit cutoff nature and can propagate laterally only when ω > ω r. However, it is more complex for acoustic waveguide cases and cannot be expressed in a closed form even when anisotropy is ignored. This is because the mutual conversion occurs between longitudinal and shear bulk waves at the top and bottom surfaces and its influence to the Lamb wave propagation is significant. Existence of anisotropy and piezoelectricity makes the analysis more complex. Detailed discussions on acoustic waveguides are seen in Ref. [34].

Figure 8.13 shows the horizontal wavenumber β y of Lamb modes propagating in an AlN plate with h e = 0 as a function of f. In the figure, Sn and An indicate the nth order symmetric and anti-symmetric Lamb modes, respectively. A branch of the first-order symmetric (S1) mode intercepts with the vertical axis at f = f S1c (5.55 GHz ∙ μm/h), which corresponds to the resonance frequency f r of the main TE mode. When f S1b < f < f S1c, the S1 mode can propagate laterally, and it may cause spurious lateral resonances after reflections at side edges. On the other hand, when f < f S1b and f > f S1c, the S1 mode is cut off, and the spurious resonances do not occur.

Fig. 8.13
figure 13

Dispersion relation of Lamb modes in the AlN plate

Full size image

Two branches of the S1 mode meet at f = f S1b, and both of them cannot propagate laterally when f < f S1b. This variation of β y with respect to ω, i.e., ∂β y /∂ω < 0, is often called the Type-II dispersion.

In other device structures and materials, ∂β y /∂ω is quite often positive near the cut off frequency corresponding to the fundamental resonance. This type is called the Type-I dispersion, and the transverse resonances occur at frequencies above the fundamental resonance in the case.

Other Lamb modes exist in the structure. When β is large, these modes are hardly excited electrically because sinusoidal variation causes mutual cancellation of excited vibration. A1 and S2 modes correspond to the first and second-order thickness shear resonances, respectively, at the cut off, which are not excitable electrically when c-axis oriented AlN films are used. Thus only the S1 mode close to the cutoff (f = f S1c) is efficiently excitable electrically.

Equation (8.25) indicates that resonance frequencies with n y  ≠ 0 can be set far from the main resonance frequency with n y  = 0 when W is small. But it is not acceptable for filter applications because reduced electrode area results in increased resonator impedance. Furthermore, reduction of the electrode size results in that of the resonator Q factor. Thus it is not practical to connect multiple resonators with small electrode area electrically in parallel.

As a practical solution, electrodes are often shaped into a polygon with nonparallel edges to smear out spurious resonances. This technique is called apodization [35, 36]. It may cause Q deterioration of the main resonance due to relatively large attenuation of Lamb waves with propagation.

One interesting idea is the so called piston mode structure [37], where the resonator side edges are designed to be ∠Γ y  = 0. As shown in Fig. 8.12, charges induced on the electrodes will be cancelled out due to the sinusoidal field variation of higher-order modes (n y  > 0). On the other hand, the fundamental mode (n y  = 0) is excitable and detectable electrically because of uniformity of the displacement field.

This idea seems simple and easy to realize. But it is not true. This is because oblique incidence of longitudinal waves to the boundaries causes conversion to shear waves and vice versa, and Lamb modes incident to side edges will cause additional phase shift and/or conversion to the other modes. Namely, electrode edges cause significant scattering of the TE vibration to Lamb modes.

As shown in Fig. 8.11, top and bottom electrodes and/or the piezoelectric film are often extended to peripherals for the electrical connection. They may cause not only the phase shift and mode conversion but also energy leakage.

It is known that these effects can be reduced by defining boarders for efficient reflection of Lamb modes [38]. An example is the overlay (mass-loading) on the top electrodes shown in Fig. 8.11. Under proper design, the mode conversion is well suppressed and large Γ y is achievable. Furthermore, the piston mode operation is possible by designing the perimeter region so that ∠Γ y  = 0 at its inner edge [39,40].

7 Summary

This chapter described basic properties and modeling of piezoelectric BAW resonators.

Due to the limited space, all rigorous and/or detailed discussions are intentionally omitted. Also, discussions on several important aspects such as history, filter applications, packaging, fabrication, and integration could not be included in this chapter due to the same reason.

Readers who are willing to know them more in detail, please refer to Refs. [41,42].