Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Due to their strong influence on system performance, paging algorithms have been studied extensively since the 1960s. Early studies were based on probabilistic request models [1–3]. In their seminal work, Sleator and Tarjan [4] introduced the notion of competitiveness, which relates the performance of an online algorithm to that of the optimal offline algorithm. By now, the competitiveness of well-known deterministic and randomized paging algorithms is well understood, and various optimal online algorithms [5, 6] have been identified.

In this paper, we study the smoothness of paging algorithms. We seek to answer the following question: How strongly may the performance of a paging algorithm change when the sequence of memory requests is slightly perturbed? This question is relevant in various domains: Can the cache performance of an algorithm suffer significantly due to the occasional execution of interrupt handling code? Can the execution time of a safety-critical real-time application be safely and tightly bounded in the presence of interference on the cache? Can secret-dependent memory requests have a significant influence on the number of cache misses of a cryptographic protocol and thus give rise to a timing side-channel attack?

We formalize the notion of smoothness by identifying the performance of a paging algorithm with the number of page faults and the magnitude of a perturbation with the edit distance between two request sequences.

We show that for any deterministic, demand-paging or competitive algorithm, a single additional memory request may cause \(k+1\) additional faults, where k is the size of the cache. Least-recently-used (LRU) matches this lower bound, indicating that there is no trade-off between competitiveness and smoothness for deterministic algorithms. In contrast, First-in first-out (FIFO) is shown to be least smooth among all strongly-competitive deterministic algorithms.

Randomized algorithms have been shown to be more competitive than deterministic ones. We derive lower bounds for the smoothness of randomized, demand-paging and randomized strongly-competitive algorithms that indicate that randomization might also help with smoothness. However, we show that none of the well-known randomized algorithms Mark, Equitable, and Partition is smooth. The simple randomized algorithm that evicts one of the cached pages uniformly at random is shown to be as smooth as LRU, but not more.

We then introduce a new parameterized randomized algorithm, Smoothed-LRU, that allows to sacrifice competitiveness for smoothness. For some parameter values Smoothed-LRU is smoother than any randomized strongly-competitive algorithm can possibly be, indicating a trade-off between smoothness and competitiveness for randomized algorithms. This leaves the question whether there is a randomized algorithms that is smoother than any deterministic algorithm without sacrificing competitiveness. We answer this question in the affirmative by introducing LRU-Random, a randomized version of LRU that evicts older pages with a higher probability than younger ones. We show that LRU-Random is smoother than any deterministic algorithm for \(k=2\). While we conjecture that this is the case as well for general k, this remains an open problem.

The notion of smoothness we present is not meant to be an alternative to competitive analysis for the evaluation of the performance of a paging algorithm; rather, it is a complementary quantitative measure that provides guarantees about the performance of an algorithm under uncertainty of the input. In general, smoothness is useful in both testing and verification:

  • In testing: if a system is smooth, then a successful test run is indicative of the system’s correct behavior not only on the particular test input, but also in its neighborhood.

  • In verification, systems are shown to behave correctly under some assumption on their environment. Due to incomplete environment specifications, operator errors, faulty implementations, or other causes, the environment assumption may not always hold completely. In such a case, if the system is smooth, “small” violations of the environment assumptions will, in the worst case, result in “small” deviations from correct behavior.

An example of the latter case that motivates our present work appears in safety-critical real-time systems, where static analyses are employed to derive guarantees on the worst-case execution time (WCET) of a program on a particular microarchitecture [7]. While state-of-the-art WCET analyses are able to derive fairly precise bounds on execution times, they usually only hold for the uninterrupted execution of a single program with no interference from the environment whatsoever. These assumptions are increasingly difficult to satisfy with the adoption of preemptive scheduling or even multi-core architectures, which may introduce interference on shared resources such as caches and buses. Given a smooth cache hierarchy, it is possible to separately analyze the effects of interference on the cache, e.g. due to interrupts, preemptions, or even co-running programs on other cores. Our results may thus inform the design and analysis of microarchitectures for real-time systems [8].

Interestingly, our model shows a significant difference between LRU and FIFO, two algorithms whose theoretical performance has proven difficult to separate.

Our results are summarized in Table 1. An algorithm A is \((\alpha , \beta , \delta )\)-smooth, if the number of page faults \(A(\sigma ')\) of A on request sequence \(\sigma '\) is bounded by \(\alpha \cdot A(\sigma ) + \beta \) whenever \(\sigma \) can be transformed into \(\sigma '\) by at most \(\delta \) insertions, deletions, or substitutions of individual requests. Often, our results apply to a generic value of \(\delta \). In such cases, we express the smoothness of a paging algorithm by a pair \((\alpha ,\beta )\), where \(\alpha \) and \(\beta \) are functions of \(\delta \), and A is \((\alpha (\delta ), \beta (\delta ), \delta )\)-smooth for every \(\delta \). Usually, the smoothness of an algorithm depends on the size of the cache, which we denote by k. As an example, under LRU the number of faults may increase by at most \(\delta (k+1)\), where \(\delta \) is the number of changes in the sequence. A precise definition of these notions is given in Sect. 3.

Table 1. Upper and lower bounds on the smoothness of paging algorithms. In the table, k is the size of the cache, \(\delta \) is the distance between input sequences, \(H_k\) denotes the \(k^{th}\) harmonic number, and \(\gamma \) is an arbitrary constant.
Full size table

2 Related Work

2.1 Notions of Smoothness

Robust control is a branch of control theory that explicitly deals with uncertainty in its approach to controller design. Informally, a controller designed for a particular set of parameters is said to be robust if it would also work well under a slightly different set of assumptions. In computer science, the focus has long been on the binary property of correctness, as well as on average- and worst-case performance. Lately, however, various notions of smoothness have received increasing attention: Chaudhuri et al.  [9] develop analysis techniques to determine whether a given program computes a Lipschitz-continuous function. Lipschitz continuity is a special case of our notion of smoothness. Continuity is also strongly related to differential privacy [10], where the result of a query may not depend strongly on the information about any particular individual. Differential privacy proofs with respect to cache side channels [11] may be achievable in a compositional manner for caches employing smooth paging algorithms.

Doyen et al.  [12] consider the robustness of sequential circuits. They determine how long into the future a single disturbance in the inputs of a sequential circuit may affect the circuit’s outputs. Much earlier, but in a similar vein, Kleene [13], Perles, Rabin, Shamir [14], and Liu [15] developed the theory of definite events and definite automata. The outputs of a definite automaton are determined by a fixed-length suffix of its inputs. Definiteness is a sufficient condition for smoothness.

The work of Reineke and Grund [16] is closest to ours: they study the maximal difference in the number of page faults on the same request sequence starting from two different initial states for various deterministic paging algorithms. In contrast, here, we study the effect of differences in the request sequences on the number of faults. Also, in addition to only studying particular deterministic algorithms as in [16], in this paper we determine smoothness properties that apply to classes of algorithms, such as all demand-paging or strongly-competitive ones, as well as to randomized algorithms. One motivation to consider randomized algorithms in this work are recent efforts to employ randomized caches in the context of hard real-time systems [17].

2.2 The Paging Problem

Paging models a two-level memory system with a small fast memory known as cache, and a large but slow memory, usually referred to simply as memory. During a program’s execution, data is transferred between the cache and memory in units of data known as pages. The size of the cache in pages is usually referred to as k. The size of the memory can be assumed to be infinite. The input to the paging problem is a sequence of page requests which must be made available in the cache as they arrive. When a request for a page arrives and this page is already in the cache, then no action is required. This is known as a hit. Otherwise, the page must be brought from memory to the cache, possibly requiring the eviction of another page from the cache. This is known as a page fault or miss. A paging algorithm must decide which pages to keep in the cache in order to minimize the number of faults.

A paging algorithm is said to be demand paging if it only evicts a page from the cache upon a fault with a full cache. Any non-demand paging algorithm can be made to be demand paging without sacrificing performance [18].

In general, paging algorithms must make decisions as requests arrive, with no knowledge of future requests. That is, paging is an online problem. The most prevalent way to analyze online algorithms is competitive analysis [4]. In this framework, the performance of an online algorithm is measured against an algorithm with full knowledge of the input sequence, known as optimal offline or OPT. We denote by \(A(\sigma )\) the number of misses of an algorithm when processing the request sequence \(\sigma \). A paging algorithm A is said to be c-competitive if for all sequences \(\sigma \), \(A(\sigma ) \le c\cdot {\textsc {OPT}} (\sigma ) + \beta \), where \(\beta \) is a constant independent of \(\sigma \). The competitive ratio of an algorithm is the infimum over all possible values of c satisfying the inequality above. An algorithm is called competitive if it has a constant competitive ratio and strongly competitive if its competitive ratio is the best possible [5].

Traditional paging algorithm are Least-recently-used (LRU)—evict the page in the cache that has been requested least recently— and First-in first-out (FIFO)—evict the page in the cache that was brought into cache the earliest. Another simple algorithm often considered is Flush-when-full (FWF)—empty the cache if the cache is full and a fault occurs. These algorithms are k-competitive, which is the best ratio that can be achieved for deterministic online algorithms [4]. An optimal offline algorithm for paging is Furthest-in-the-future, also known as Longest-forward-distance and Belady’s algorithm [1]. This algorithm evicts the page in the cache that will be requested at the latest time in the future.

A competitive ratio less than k can be achieved by the use of randomization. Important randomized paging algorithms are Random—evict a page chosen uniformly at random— and Mark  [19]—mark a page when it is unmarked and requested, and upon a fault evict a page chosen uniformly at random among unmarked pages (unmarking all pages first if no unmarked pages remain). Random achieves a competitive ratio of k, while Mark ’s competitive ratio is \(2H_k-1\), where \(H_k = \sum _{i=1}^k \frac{1}{i}\) is the \(k^{th}\) harmonic number. The strongly-competitive algorithms Partition  [5] and Equitable  [6] achieve the optimal ratio of \(H_k\).

3 Smoothness of Paging Algorithms

We now formalize the notion of smoothness of paging algorithms. We are interested in answering the following question: How does the number of misses of a paging algorithm vary as its inputs vary? We quantify the similarity of two request sequences by their edit distance:

Definition 1

(Distance). Let \(\sigma =x_1,\ldots ,x_n\) and \(\sigma '=x'_1,\ldots ,x'_m\) be two request sequences. Then we denote by \(\varDelta (\sigma ,\sigma ')\) their edit distance, defined as the minimum number of substitutions, insertions, or deletions to transform \(\sigma \) into \(\sigma '\).

This is also referred to as the Levenshtein distance. Based on this notion of distance we define \((\alpha , \beta , \delta )\)-smoothness:

Definition 2

( \((\alpha ,\beta ,\delta )\) -Smoothness). Given a paging algorithm A, we say that A is \((\alpha ,\beta ,\delta )\)-smooth, if for all pairs of sequences \(\sigma ,\sigma '\) with \(\varDelta (\sigma ,\sigma ') \le \delta \),

$$\begin{aligned} A(\sigma ')\le \alpha \cdot A(\sigma )+\beta \end{aligned}$$

For randomized algorithms, \(A(\sigma )\) denotes the algorithm’s expected number of faults when serving \(\sigma \).

An algorithm that is \((\alpha , \beta , \delta )\)-smooth may also be \((\alpha ', \beta ', \delta )\)-smooth for \(\alpha ' > \alpha \) and \(\beta ' < \beta \). As the multiplicative factor \(\alpha \) dominates the additive constant \(\beta \) in the long run, when analyzing the smoothness of an algorithm, we first look for the minimal \(\alpha \) such that the algorithm is \((\alpha , \beta , \delta )\)-smooth for any \(\beta \).

We say that an algorithm is smooth if it is \((1,\beta ,1)\)-smooth for some \(\beta \). In this case, the maximal increase in the number of page faults is proportional to the number of changes in the request sequence. This is called Lipschitz continuity in mathematical analysis. For smooth algorithms, we also analyze the Lipschitz constant, i.e., the additive part \(\beta \) in detail, otherwise we concentrate the analysis on the multiplicative factor \(\alpha \).

We use the above notation when referring to a specific distance \(\delta \). For a generic value of \(\delta \) we omit this parameter and express the smoothness of a paging algorithm with a pair \((\alpha , \beta )\), where both \(\alpha \) and \(\beta \) are functions of \(\delta \).

Definition 3

( \((\alpha ,\beta )\) -Smoothness). Given a paging algorithm A, we say that A is \((\alpha ,\beta )\)-smooth, if for all pairs of sequences \(\sigma ,\sigma '\),

$$\begin{aligned} A(\sigma ')\le \alpha (\delta ) \cdot A(\sigma )+\beta (\delta ), \end{aligned}$$

where \(\alpha \) and \(\beta \) are functions, and \(\delta = \varDelta (\sigma ,\sigma ')\).

Often, it is enough to determine the effects of one change in the inputs to characterize the smoothness of an algorithm A.

Lemma 1

If A is \((\alpha ,\beta ,1)\)-smooth, then A is \((\alpha ^\delta ,\beta \sum _{i=0}^{\delta -1}\alpha ^i)\)-smooth.

All proofs can be found in the full version of this paper [20].

Corollary 1

If A is \((1,\beta ,1)\)-smooth, then A is \((1,\delta \beta )\)-smooth.

4 Smoothness of Deterministic Paging Algorithms

4.1 Bounds on the Smoothness of Deterministic Paging Algorithms

Before considering particular deterministic online algorithms, we determine upper and lower bounds for several important classes of algorithms. Many natural algorithms are demand paging.

Theorem 1

(Lower Bound for Deterministic, Demand-Paging Algorithms). No deterministic,demand-paging algorithm is \((1{,}\delta (k{+}1{-}\epsilon ))\)-smooth for any \(\epsilon \!>\!0\).

The idea of the proof is to first construct a sequence of length \(k+\delta (k+1)\) containing \(k+1\) distinct pages, such that A faults on every request. This sequence can then be transformed into a sequence containing only k distinct pages by removing all requests to the page that occurs least often, which reduces the overall number of misses to k, while requiring at most \(\delta \) changes. While most algorithms are demand paging, it is not a necessary condition for an algorithm to be competitive, as demonstrated by FWF. However, we obtain the same lower bound for competitive algorithms as for demand-paging ones.

Theorem 2

(Lower Bound for Deterministic, Competitive Paging Algorithms). No deterministic, competitive paging algorithm is \((1, \delta (k+1-\epsilon ))\)-smooth for any \(\epsilon > 0\).

By contraposition of Corollary 1, the two previous theorems show that no deterministic, demand-paging or competitive algorithm is \((1, k+1-\epsilon , 1)\)-smooth for any \(\epsilon > 0\).

Intuitively, the optimal offline algorithm should be very smooth, and this is indeed the case as we show next:

Theorem 3

(Smoothness of OPT). OPT is \((1,2\delta )\)-smooth. This is tight.

With Theorem 3 it is easy to show the following upper bound on the smoothness of any competitive algorithm:

Theorem 4

(Smoothness of Competitive Algorithms). Let A be any paging algorithm such that for all sequences \(\sigma \), \(A(\sigma ) \le c\cdot {\textsc {OPT}} (\sigma ) +\beta \). Then A is \((c,2\delta c+\beta )\)-smooth.

Note that the above theorem applies to both deterministic and randomized algorithms. Given that every competitive algorithm is \((\alpha , \beta )\)-smooth for some \(\alpha \) and \(\beta \), the natural question to ask is whether the converse also holds. Below, we answer this question in the affirmative for deterministic bounded-memory, demand-paging algorithms. By bounded memory we mean algorithms that, in addition to the contents of their fast memory, only have a finite amount of additional state. For a more formal definition consult [18, page 93]. Paging algorithms implemented in hardware caches are bounded memory.

Theorem 5

(Competitiveness of Smooth Algorithms). If algorithm A is deterministic bounded-memory, demand-paging, and \((\alpha , \beta )\)-smooth for some \(\alpha \) and \(\beta \), then A is also competitive.

4.2 Smoothness of Particular Deterministic Algorithms

Now let us turn to the analysis of three well-known deterministic algorithms: LRU, FWF, and FIFO. We show that both LRU and FWF are smooth. On the other hand, FIFO is not smooth, as a single change in the request sequence may increase the number of misses by a factor of k.

Theorem 6

(Smoothness of Least-Recently-Used).

\({\textsc {LRU}} \) is \((1,\delta (k+1))\)-smooth. This is tight.

So LRU matches the lower bound for both demand-paging and competitive paging algorithms. We now show that FWF is also smooth, with a factor that is almost twice that of LRU. The smoothness of FWF follows from the fact that it always misses k times per phase, and the number of phases can only change marginally when perturbing a sequence.

Theorem 7

(Smoothness of Flush-When-Full).

\({\textsc {FWF}} \) is \((1,2\delta k)\)-smooth. This is tight.

We now show that FIFO is not smooth. In fact, we show that with only a single difference in the sequences, the number of misses of FIFO can be k times higher than the number of misses in the original sequence. On the other hand, since FIFO is strongly competitive, the multiplicative factor k is also an upper bound for FIFO ’s smoothness.

Theorem 8

(Smoothness of First-in First-Out).

FIFO is \((k, 2\delta k)\)-smooth. FIFO is not \((k-\epsilon ,\gamma ,1)\)-smooth for any \(\epsilon > 0\) and \(\gamma \).

FIFO matches the upper bound for strongly-competitive deterministic paging algorithms. With the result for LRU, this demonstrates that the upper and lower bounds for the smoothness of strongly-competitive algorithms are tight.

5 Smoothness of Randomized Paging Algorithms

5.1 Bounds on the Smoothness of Randomized Paging Algorithms

Similarly to deterministic algorithms, we can show a lower bound on the smoothness of any randomized demand-paging algorithm. The proof is strongly inspired by the proof of a lower bound for the competitiveness of randomized algorithms by Fiat et al.  [19]. The high-level idea is to construct a sequence using \(k+1\) distinct pages on which any randomized algorithm faults at least \(k+H_k + \frac{1}{k}\) times that can be converted into a sequence containing only k distinct pages by deleting a single request.Notice that the lower bound only applies to \(\delta =1\) and so additional disturbances might have a smaller effect than the first one.

Theorem 9

(Lower Bound for Randomized, Demand-Paging Algorithms). No randomized, demand-paging algorithm is \((1, H_k{+}\frac{1}{k}{-}\epsilon , 1)\)-smooth for any \(\epsilon {>}0\).

For strongly-competitive randomized algorithms we can show a similar statement using a similar yet more complex construction:

Theorem 10

(Lower Bound for Strongly-Competitive Randomized Paging Algorithms). No strongly-competitive, randomized paging algorithm is \((1, \delta (H_k-\epsilon ))\)-smooth for any \(\epsilon > 0\).

In contrast to the deterministic case, this lower bound only applies to strongly-competitive algorithms, as opposed to simply competitive. So with randomization there might be a trade-off between competitiveness and smoothness. There might be competitive algorithms that are smoother than all strongly-competitive ones.

5.2 Smoothness of Particular Randomized Algorithms

Two known strongly-competitive randomized paging algorithms are Partition  [5] and Equitable  [6]. We show that neither of the two algorithms is smooth.

Theorem 11

(Smoothness of Partition and Equitable). For any cache size \(k \ge 2\), there is an \(\epsilon > 0\), such that neither Partition nor Equitable is \((1+\epsilon , \gamma , 1)\)-smooth for any \(\gamma \). Also, Partition and Equitable are \((H_k,2\delta H_k)\)-smooth.

The lower bound in the theorem above is not tight, but it shows that neither of the two algorithms matches the lower bound from Theorem 10. This leaves open the question whether the lower bound from Theorem 10 is tight.

Mark  [19] is a simpler randomized algorithm that is \((2H_k-1)\)-competitive. We show that it is not smooth either.

Theorem 12

(Smoothness of Mark). Let \(\alpha =\max _{1< \ell \le k}\left\{ \frac{\ell (1+H_k-H_\ell )}{\ell -1+H_k-H_{\ell -1}}\right\} =\Omega (H_k)\), where k is the cache size. \({\textsc {Mark}} \) is not \((\alpha -\epsilon ,\gamma ,1)\)-smooth for any \(\epsilon >0\) and any \(\gamma \). Also, \({\textsc {Mark}} \) is \((2H_k-1,\delta (4H_k-2))\)-smooth.

We conjecture that the lower bound for Mark is tight, i.e., that Mark is \((\alpha , \beta )\)-smooth for \(\alpha \) as defined in Theorem 12 and some \(\beta \).

We now prove that Random achieves the same bounds for smoothness as LRU and the best possible for any deterministic, demand-paging or competitive algorithm. For simplicity, we prove the theorem for a non-demand-paging definition of Random in which each page gets evicted upon a miss with probability 1 / k even if the cache is not yet full. Intuitively, the additive term \(k+1\) in the smoothness of Random is explained by the fact that a single difference between two sequences can make the caches of both executions differ by one page p. Since \({\textsc {Random}} \) evicts a page with probability 1 / k, the expected number of faults until p is evicted is k.

Theorem 13

(Smoothness of Random).

\({\textsc {Random}} \) is \((1,\delta (k+1))\)-smooth. This is tight.

5.3 Trading Competitiveness for Smoothness

We have seen that none of the well-known randomized algorithms are particularly smooth. Random is the only known randomized algorithm that is \((1, \delta c)\)-smooth for some c. However, it is neither smoother nor more competitive than LRU, the smoothest deterministic algorithm. In this section we show that greater smoothness can be achieved at the expense of competitiveness. First, as an extreme example of this, we show that Evict-on-access (EOA) [17]—the policy that evicts each page with a probability of \(\frac{1}{k}\) upon every request, i.e., not only on faults but also on hits—beats the lower bounds of Theorems 9 and 10 and is strictly smoother than OPT. This policy is non-demand paging and it is obviously not competitive. We then introduce Smoothed-LRU, a parameterized randomized algorithm that trades competitiveness for smoothness.

Theorem 14

(Smoothness of EOA).

\({\textsc {EOA}} \) is \((1,\delta (1+\frac{k}{2k-1}))\)-smooth. This is tight.

Smoothed-LRU. We now describe Smoothed-LRU. The main idea of this algorithm is to smooth out the transition from the hit to the miss case.

The following notion of age is convenient in the analysis of LRU: The age of page p is the number of distinct pages that have been requested since the previous request to p. LRU faults if and only if the requested page’s age is greater than or equal to k, the size of the cache. An additional request may increase the ages of k cached pages by one. At the next request to each of these pages, the page’s age may thus increase from \(k-1\) to k, and turn the request from a hit into a miss, resulting in k additional misses.

By construction, under Smoothed-LRU, the hit probability of a request decreases only gradually with increasing age. The speed of the transition from definite hit to definite miss is controlled by a parameter i, with \(0 \le i < k\). Under Smoothed-LRU, the hit probability \(P(\textit{hit}_{{\textsc {Smoothed-LRU}} _{k,i}}(a))\) of a request to a page with age a is:

$$\begin{aligned} P(\textit{hit}_{{\textsc {Smoothed-LRU}} _{k,i}}(a)) = {\left\{ \begin{array}{ll} 1 &{} : a < k-i\\ \frac{k+i-a}{2i+1} &{} : k-i \le a < k+i\\ 0 &{} : a \ge k+i \end{array}\right. } \end{aligned}$$
(1)

where k is the size of the cache. Figure 1 illustrates this graphically in relation to LRU for cache size \(k=8\) and \(i=4\).

Fig. 1.
figure 1

Hit probabilities of LRU and Smoothed-LRU in terms of the age of the requested page

Full size image

Theorem 15

(Smoothness of Smoothed-LRU).

\({\textsc {Smoothed-LRU}} _{k,i}\) is \((1,\delta (\frac{k+i}{2i+1}+1))\)-smooth. This is tight.

For \(i=0\), \({\textsc {Smoothed-LRU}} \) is identical to \({\textsc {LRU}} \) and \((1,\delta (k+1))\)-smooth. At the other extreme, for \(i=k-1\), \({\textsc {Smoothed-LRU}} \) is \((1, 2\delta )\)-smooth, like the optimal offline algorithm. However, for larger i, Smoothed-LRU is less competitive than LRU:

Lemma 2 (Competitiveness of Smoothed-LRU). For any sequence \(\sigma \) and \(l \le k-i\),

$$\begin{aligned} {\textsc {Smoothed-LRU}} _{k,i}(\sigma ) \le \frac{k-i}{k-i-l+1}\cdot {\textsc {OPT}} _l(\sigma ) + l, \end{aligned}$$

where \({\textsc {OPT}} _l(\sigma )\) denotes the number of faults of the optimal offline algorithm processing \(\sigma \) on a fast memory of size l. For \(l > k-i\) and any \(\alpha \) and \(\beta \) there is a sequence \(\sigma \), such that \({\textsc {Smoothed-LRU}} _{k,i}(\sigma ) > \alpha \cdot {\textsc {OPT}} _l(\sigma ) + \beta .\)

So far we have analyzed Smoothed-LRU based on the hit probabilities given in (1). We have yet to show that a randomized algorithm satisfying (1) can be realized. In the full version of the paper [20], we construct a probability distribution on the set of all deterministic algorithms using a fast memory of size k that satisfies (1). This is commonly referred to as a mixed strategy.

5.4 A Competitive and Smooth Randomized Paging Algorithm: LRU-Random

In this section we introduce and analyze LRU-Random, a competitive randomized algorithm that is smoother than any competitive deterministic algorithm. LRU-Random orders the pages in the fast memory by their recency of use; like LRU. Upon a miss, LRU-Random evicts older pages with a higher probability than younger pages. More precisely, the \(i^{th}\) oldest page in the cache is evicted with probability \(\frac{1}{i\cdot H_k}\). By construction the eviction probabilities sum up to 1: \(\sum _{i=1}^k \frac{1}{i\cdot H_k} = \frac{1}{H_k}\cdot \sum _{i=1}^k \frac{1}{i} = 1\). LRU-Random is not demand paging: if the cache is not yet entirely filled, it may still evict cached pages according to the probabilities mentioned above.

LRU-Random is at least as competitive as strongly-competitive deterministic algorithms:

Theorem 16

(Competitiveness of LRU-Random). For any sequence \(\sigma \),

$$\begin{aligned} {\textsc {LRU-Random}} (\sigma ) \le k \cdot {\textsc {OPT}} (\sigma ). \end{aligned}$$

The proof of Theorem 16 applies to an adaptive online adversary. An analysis for an oblivious adversary might yield a lower competitive ratio.

For \(k=2\), we also show that LRU-Random is \((1,\delta c)\)-smooth, where c is less than \(k+1\), which is the best possible among deterministic, demand-paging or competitive algorithms. Specifically, c is \(1+11/6=2.8\bar{3}\). Although our proof technique does not scale beyond \(k=2\), we conjecture that this algorithm is in fact smoother than \((1, \delta (k+1))\) for all k.

Theorem 17

(Smoothness of LRU-Random).

Let \(k=2\). \({\textsc {LRU-Random}} \) is \((1,\frac{17}{6}\delta )\)-smooth.

Conjecture 1

(Smoothness of LRU-Random).

\({\textsc {LRU-Random}} \) is \((1,\varTheta (H_k^2)\delta )\)-smooth.

Fig. 2.
figure 2

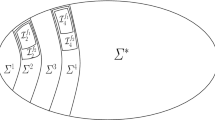
Schematic view of the smoothness and competitiveness landscape. Crosses indicate tight results, whereas ellipses indicate upper bounds. Braces denote upper and lower bounds on the smoothness or competitiveness of classes of algorithms. For simplicity of exposition, \(\gamma _1\) and \(\gamma _2\) are left unspecified; \(\gamma \) can be chosen arbitrarily. More precise statements are provided in the respective theorems.

Full size image

6 Discussion

We have determined fundamental limits on the smoothness of deterministic and randomized paging algorithms. No deterministic competitive algorithm can be smoother than \((1, \delta (k+1))\)-smooth. Under the restriction to bounded-memory algorithms, which is natural for hardware implementations of caches, smoothness implies competitiveness. LRU is strongly competitive, and it matches the lower bound for deterministic competitive algorithms. LRU is strongly competitive, and it matches the lower bound for deterministic competitive algorithms, while FIFO matches the upper bound. There is no trade-off between smoothness and competitiveness for deterministic algorithms.

In contrast, among randomized algorithms, we have identified Smoothed-LRU, an algorithm that is very smooth, but not competitive. In particular, it is smoother than any strongly-competitive randomized algorithm may be. The well-known randomized algorithms Mark, Partition, and Equitable are not smooth. It is an open question, whether there is a randomized “LRU sibling” that is both strongly-competitive and \((1, \delta H_k)\)-smooth. With LRU-Random we introduce a randomized algorithm that is at least as competitive as any deterministic algorithm, yet provably smoother, at least for \(k=2\). Its exact smoothness remains open. Figure 2 schematically illustrates many of our results.