Keywords

1 Introduction

A large number of unsupervised and supervised machine learning techniques are based on the use of distances or dissimilarity measures [4, 5]. Such measures can be employed for pairwise comparison of feature vectors, as for instance in the well-known K-Nearest-Neighbor (KNN) classifier [5, 8, 10]. Prototype-based methods replace the reference data by a number of typical representatives. In unsupervised Vector Quantization (VQ), for instance, they might represent clusters or other structures in the data. In the popular Learning Vector Quantization (LVQ) [12], prototypes serve as characteristic exemplars of the classes and, together with a distance measure, parameterize the classification scheme.

Prototype- and distance-based systems are generally intuitive and straightforward to implement. The selection of appropriate distance measures is a key issue in the design of VQ or LVQ schemes [5]. Frequently, simple Euclidean or other Minkowski measures are employed without taking into account prior knowledge of the problem. Obviously, available insight into the nature of the data should be taken advantage of. So-called relevance learning schemes offer greater flexibility and are particularly suitable for supervised learning due to the use of adaptive distance measures, see [20, 25] for examples in the context of KNN- and LVQ classifiers and [5] for a recent review. In relevance learning, only the basic form of the distance measure is specified in advance. Its parameters are determined in a data-driven training process, which is frequently guided by a suitable cost function, e.g. [18, 20, 25].

Here, we examine the use of prototype-based systems for functional data [17], where feature vectors do not simply comprise a set of more or less independent quantities, but represent a functional relation. This is the case, for instance, in the presence of temporal or other dependencies, which impose a natural ordering of the features. Functional data is found in a large variety of practical application areas [17]. Perhaps, time series and sequences come to mind first in the context of, e.g., bioinformatics, meteorology or economy. Similarly, densities or histograms can be used to represent statistical properties of observations. Another important example is that of spectral data, for instance optical or mass spectra obtained in various fields ranging from remote sensing to chemistry and bioinformatics.

Formally, discretized functional data can be treated by standard prototype-based methods, including relevance learning. However, this naive approach ignores the specific properties of the data, which may result in suboptimal performance due to several problems: Obviously, disregarding the order and intrinsic correlation of neighbored features in functional data can lead to nominally very high-dimensional systems and inappropriately large numbers of adaptive parameters. Thus, the learning problem is rendered unnecessarily complex and may suffer from convergence problems and overfitting effects. In addition, standard measures such as Euclidean metrics are often insensitive to the reordering of features, yielding misleading results when functions are compared [14, 24].

An appropriate functional representation of relevances was proposed and analyzed in [11]. However, there, data samples and prototypes are still considered in the original feature space. Here, we follow a complementary approach and investigate the functional representation of adaptive prototypes and all sample data in terms of appropriate basis functions. We include the implementation of relevance learning in the corresponding space of coefficients, illustrate the method in terms of benchmark datasets and compare with the standard approaches in original feature space.

One previously studied example of this basic idea was considered in [19], where highly specific wavelet representations were employed in the analysis of sharply peaked mass spectra. Here, we discuss the use of supervised LVQ and relevance learning for relatively smooth functional data and restrict the discussion to polynomial expansions. We would like to point out, however, that the framework is quite versatile and can be readily extended to other types of data and basis functions.

In the following section we summarize the mathematical framework and provide details of the classifiers and training prescriptions. In Sect. 3 we introduce benchmark datasets and present the results of computer experiments. We discuss our findings in Sect. 4 before we conclude with a brief Summary and Outlook.

2 The Mathematical Framework

We first review the generic form of the considered supervised learning problem, before detailing the specific approaches for functional data.

2.1 Generalized Matrix Relevance LVQ for Classification

We consider a standard supervised scenario, where d-dimensional feature vectors

$$\begin{aligned} {\varvec{\xi }}^\mu \in \mathbb {R}^d \text { and labels } S^\mu =S({\varvec{\xi }}^\mu ) \in \{1,2,\ldots ,C\} \text { for } \mu =1,2\ldots P, \end{aligned}$$
(1)

serve as examples for the target classification. For simplicity we restrict the following to binary classification schemes with \(C=2\). The extension to multi-class LVQ is conceptually and technically straightforward.

An LVQ system parameterizes the classifier by means of a set of prototypes

$$\begin{aligned} \textstyle \left\{ {\varvec{w}}_\xi ^j \in \mathbb {R}^d \right\} _{j=1}^M \text { with labels } \sigma ^j = \sigma ({\varvec{w}}_\xi ^j) \in \{1,2 \}, \end{aligned}$$
(2)

equipped with an appropriate distance measure \(d({\varvec{w}}_\xi ,{\varvec{\xi }})\). A simple Nearest Prototype Classifier (NPC) assigns a vector \({\varvec{\xi }}\) to the class of the closest prototype, i.e. the \({\varvec{w}}_\xi ^j\) with \(d({\varvec{w}}_\xi ^j,{\varvec{\xi }}) = \min _m \{ d({\varvec{w}}_\xi ^m,{\varvec{\xi }}) \}_{m=1}^M\).

Note that the prototypes are defined in the same space as the considered feature vectors, as indicated by the subscript \(\xi \), here. This fact often facilitates intuitive interpretation of the classifier. Prototypes are usually determined in heuristic iterative procedures like the popular LVQ1 algorithm [12] or by means of cost function based optimization, e.g. [18, 21].

We employ general quadratic distance measures of the form

$$\begin{aligned} d({\varvec{w}}_\xi ,{\varvec{\xi }}) \, = \left( {\varvec{w}}_\xi -{\varvec{\xi }}\right) ^\top \, \varLambda _\xi \, \left( {\varvec{w}}_\xi -{\varvec{\xi }}\right) \, = \left[ \varOmega _\xi \left( {\varvec{w}}_\xi -{\varvec{\xi }}\right) \right] ^2. \end{aligned}$$
(3)

The parameterization \(\varLambda _\xi = \varOmega _\xi ^\top \varOmega _\xi \) ensures that the measure is positive semi-definite [20]. We additionally impose the normalization \(\mathrm{Tr}({\varLambda _\xi })=\sum _{i,j} [\varOmega _\xi ]_{ij}^2 = 1\) in order to avoid numerical problems.

For the sake of clarity, we restrict the formalism to one global distance given by a single square matrix \(\varOmega _\xi \in \mathbb {R}^{d\times d}\). Extensions of this basic framework in terms of local or rectangular matrices are technically straightforward, see [7]. Note that the general form, Eq. (3), reduces to standard (squared) Euclidean distance for \(\varLambda _\xi =I/d\) with the d-dim. identity I.

Generalized Matrix Relevance LVQ (GMLVQ) [20] optimizes the prototype positions and the distance measure, i.e. the matrix \(\varOmega _\xi \), in one and the same data driven training process. It is guided by a cost function of the form

$$\begin{aligned} \textstyle E\, = \, \sum _{\mu =1}^P \, \varPhi \left( \frac{d({\varvec{w}}_\xi ^{J},\xi ^\mu ) - d({\varvec{w}}_\xi ^{K},\xi ^\mu )}{d({\varvec{w}}_\xi ^{J},\xi ^\mu ) + d({\varvec{w}}_\xi ^{K},\xi ^\mu )} \right) , \end{aligned}$$
(4)

which was introduced in [18]. Given a particular feature vector \(\mathbf {\xi }^\mu \), \({\varvec{w}}_\xi ^J\) denotes the correct winner, i.e. the closest prototype representing the class \(S^\mu = S({\varvec{\xi }}^\mu )\), while \({\varvec{w}}_\xi ^K\) denotes the closest of all prototypes with a class label different from \(S^\mu \). Frequently, the function \(\varPhi (\ldots )\) in Eq. (4) is taken to be a sigmoidal [18]. Here, for simplicity and in order to avoid the introduction of additional hyper-parameters we resort to the simplest setting with \(\varPhi (x)=x\).

Training can be done in terms of stochastic gradient descent as in [20] or by means of other methods of non-linear optimization; several implemented variants are available online at [6]. Results presented here were obtained by means of a batch gradient descent optimization of E, cf. Eq. (4), equipped with a conceptually simple scheme for automated step size control along the lines of [16].

2.2 Polynomial Expansion of Functional Data

The main idea of this paper is to exploit the characteristics of functional data in terms of representing feature vectors \({\varvec{\xi }}\in \mathbb {R}^d\) in a parameterized functional form. Such representation can be achieved by expanding the data in terms of suitable basis functions. Interpreting the original features as discretized observations of an underlying continuous function f(x), i.e. \( \xi _j= f(x_j)\) for \(j=1,\ldots ,d\), we consider expansions of the basic form

$$\begin{aligned} \textstyle f_{{\varvec{c}}} (x) = \sum _{i=0}^{n} { c_i g_i(x) }. \end{aligned}$$
(5)

For a given set of basis functions \(\left\{ g_i \right\} _{i=0}^n\), each \({\varvec{\xi }}\) in original d-dim. feature space can be represented by an \((n+1)\)-dim. vector of coefficients denoted as \({\varvec{c}}=(c_0,c_1,\ldots c_n)^\top \) in the following. In practice, \({\varvec{c}}\) is determined according to a suitable approximation criterion. A popular choice would be the minimization of the quadratic deviation \( \sum _{j=1}^d \left( f_{{\varvec{c}}}(x_j) - \xi _j \right) ^2\).

In order to illustrate the basic approach, we consider Chebyshev polynomials of the first kind as a particular functional basis. Hence, the functional representation (5) of the data is given by truncated Chebyshev series, which provide an efficient way to represent smooth non-periodic functions [9]. Specifically, we employed the open source Matlab™ library chebfun [22], which includes a variety of mathematical tools in this context. Here, we make use only of its efficient implementation of Chebyshev approximation of discrete functional data.

2.3 Comparison of Workflows

In Sect. 3 we present results for the application of GMLVQ to a number of benchmark problems. In each of these, d-dimensional spectra—denoted by vectors \({\varvec{\xi }}\)—are assigned to one of two possible classes. We explicitly study and compare the following alternative scenarios:

(A) :

Training in original feature space

As an obvious baseline, we consider the conventional interpretation of the components of \({\varvec{\xi }}\) as d individual features, disregarding their functional nature. Hence, the spectra are taken to directly define the feature vectors \({\varvec{\xi }}\) in Eqs. (1–4) without further processing.

(B) :

Polynomial representation of data and prototypes

For a given degree n of the approximative expansion (5), each data point \({\varvec{\xi }}^\mu \) in the dataset can be represented by the vector of coefficients \({\varvec{c}}^\mu \in \mathbb {R}^{(n+1)}\). Correspondingly, prototypes \({\varvec{w}}^k_c \in \mathbb {R}^{(n+1)}\) and matrices \(\varLambda _c,\varOmega _c \in \mathbb {R}^{(n+1)\times (n+1)}\) can be introduced. The GMLVQ formalism outlined above is readily applied in complete formal analogy to Eqs. (1–4). However, data and prototypes are now represented in \((n+1)\)-dim. coefficient space. Moreover, the distance measure \( d({\varvec{w}}_c, {\varvec{c}}) = ({\varvec{w}}_c-{\varvec{c}})^\top \varLambda _c \, ({\varvec{w}}_c-{\varvec{c}}) \) cannot be interpreted as a simple generalized Euclidean distance in original feature space anymore.

(C) :

Polynomial smoothing of the data

In addition to the suggested functional representations (B), we consider the smoothing of d-dim. spectra by applying a Chebyshev expansion with \(n<d\) and transforming back to original feature space. After replacing original feature vectors by the resulting smoothed versions \({\varvec{\tilde{\xi }}}\), the standard GMLVQ approach is applied. As a result we obtain a classifier which is parameterized in terms of prototypes \({\varvec{w}}^k_{\tilde{\xi }} \in \mathbb {R}^d\) and relevance matrix \(\varLambda _{\tilde{\xi }}= \varOmega _{\tilde{\xi }}^\top \varOmega _{\tilde{\xi }} \in \mathbb {R}^{d\times d}.\)

 

3 Application to Example Datasets

The proposed method is applied and tested in several spectral and, therefore, functional datasets of different sizes and spectral bandwidths.

The wine dataset, available from [15], contains 123 (one outlier removed) samples of wine infrared absorption spectra with 256 values in the range between 4000 and 400 \(\text {cm}^{-1}\). The data should be classified according to two assigned alcohol levels (low/high) as specified in [13].

The Tecator dataset comprises 215 reflectance spectra with 100 values each, representing wavelengths from 850 to 1050 nm. The spectra were acquired from meat probes and labeled according to fat content (low/high), see [23] for details.

The orange juice (OJ) dataset is a collection of 218 near infrared spectra with 700 values each. For each spectrum the level of saccharose contained in the orange juice is given. In order to define a two class problem similar to the above mentioned ones, the level is thresholded at its median in the set, defining two classes (low/high saccharose content). The dataset is publicly available at [15].

The fourth example, the coffee dataset, was made available in the context of a machine learning challenge by the Fraunhofer Institute for Factory Operation and Automation, Magdeburg/Germany, in 2012 [1]. The full set contains 20000 short wave infrared spectra of coffee beans with 256 values in the range of wavelengths between 970 and 2500 nm. The classification task is to discriminate immature and healthy coffee beans. Since the dataset is only used for further benchmark of the presented approach it is reduced in size to keep computation time in easy to handle ranges. For this reason 100 samples were selected randomly from each of the two classes.

For each dataset three strategies were evaluated: First, a GMLVQ system is adapted to the labeled set of original spectra, cf. scenario (A). A second set of experiments is guided by (B) in the previous section: Spectra are approximated by polynomials of a certain degree resulting in \(5, 10, 15, \ldots , 100\) polynomial coefficients as described above. Subsequently, a GMLVQ classifier is trained in terms of the resulting \((n+1)\)-dim. coefficient vectors \(\mathbf {c}^\mu \). Scenario (C) is considered in order to clarify whether the potential benefit of using a polynomial representation could be only an effect of the smoothing achieved by the approximation. To this end, the system is trained on the basis of smoothed versions of the spectra, obtained by equi-distant discretization of the polynomial approximation.

All experiments were done using the same settings and parameters. GMLVQ systems comprised only one prototype per class. A z-score transformation was performed for each individual training process, achieving zero mean and unit variance features in the actual training set. This transformation balances the varying order of magnitudes observed in different feature dimensions and facilitates the interpretation of the emerging relevance matrices [20]. Relevance matrices were initialized as proportional to the identity, prototypes were placed in the class-conditional means in the training set, initially. A batch gradient descent optimization was performed, employing an automated step size control, essentially along the lines of [16]. Matlab™ demonstration code of the precise implementation used here is available from [3], where a more detailed documentation and description of the modification of the step size adaptation scheme is also provided. We used default values of all relevant parameters specified in [3].

A validation scheme was implemented, with each training set containing a random selection of \(90\,\%\) of the available data. Performance was evaluated in terms of the Area under the ROC (AUROC) with respect to the validation set [10]. The latter is obtained by varying a threshold when comparing the distances of a data point from the prototypes, thus deviating from the NPC scheme. All results were obtained as a threshold average over 10 random splits of the data. Figure 1 displays the performance of systems with full polynomial representation (scenario B), with polynomial smoothing of the data (C), and the baseline of GMLVQ in the original space (scenario A), for comparison.

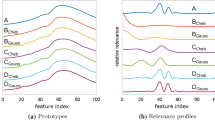
In order to further illustrate the method, we provide more details for the example of the OJ dataset in Fig. 2. The upper panels display the d-dim. prototypes obtained in scenarios (A) and (C). From the vectors \({\varvec{w}}_c^{1,2} \in \mathbb {R}^{(n+1)}\) in scenario (B), we also computed their corresponding functional form in original feature space. Diagonal elements of the relevance matrices \(\varLambda _\xi ,\varLambda _{\tilde{\xi }} \in \mathbf {R}^{d \times d}\) and \(\varLambda _c \in \mathbb {R}^{(n+1)\times (n+1)}\) are depicted in the lower panels. We show results for the example case of 20 coefficients, which yields typical performance, cf. Fig. 1a.

Fig. 1
figure 1

Comparison of the achieved validation performance, i.e. the area under ROC for different datasets in dependence of the degree of the polynomial curve fitting. The solid line represents the value for the classification using the original feature vectors (A). Filled circles represent results achieved using polynomial curve fitting, open squares correspond to polynomial smoothing of the input data only. All results are displayed as a function of the number of coefficients \((n+1)\) in the polynomial expansion. a Wine dataset. b Tecator dataset. c OJ dataset. d Coffee dataset

Full size image

4 Discussion

Our results demonstrate that the proposed approach has potential to improve classification performance with functional data significantly, as verified by the Tecator data (Fig. 1b) and the OJ dataset (Fig. 1c). In both cases, the prediction accuracy as measured by the AUROC is significantly larger when applying GMLVQ in the polynomial representation. For a wide range of degrees n, the AUROC robustly exceeds that of systems trained from the raw datasets. This is not the case for training according to scenario (C), which shows that the improvement in (B) cannot be explained as an effect of the smoothing only.

In the other two datasets, cf. Fig. 1a, d, the accuracy of the system with polynomial representation is comparable or nearly identical to that in original and smoothed feature space. Also for these datasets, the performance is robust with respect to the polynomial degree in a wide range of values n.

Clearly, the positive effect of the functional representation on the performance will depend on the detailed properties of the data and the suitability of the basis functions. However, even if accuracy does not increase, one advantage of the polynomial representation remains: The dimensionality of the problem can be reduced significantly in all considered cases without adverse effects on performance. For approximations with, say, 20 polynomial coefficients, which performs well in all datasets, the number of input dimensions is reduced by 80 % for Tecator, by ca. 92 % for Wine and Coffee data and by 97 % for the OJ dataset. This leads to a drastically reduced number of free parameters, which is quadratic in the number of feature dimensions in GMLVQ, and results in a massive speed-up of the training process. The gain clearly over-compensates the time needed for performing the polynomial approximation, generically. The computational effort of the approximation was evaluated experimentally and appeared to increase linearly with the original dimension d and the polynomial degree n. The observed absolute computation time was on the order of a few seconds for the representation of 50000 feature vectors.

Another point that deserves attention is the question of interpretability of the prototypes and relevances [2, 5]. One important advantage of LVQ and similar methods is the intuitive interpretation of prototypes, since they are determined in original feature space. The proposed polynomial representation seems to void this advantage, by considering data and prototypes in the less intuitive space of coefficients. Note, however, that the transformation can be inverted after training, hence the prototypes can be projected back to the original feature space. Figure 2 shows a comparison of the prototypes achieved from original data, and those achieved in coefficient space, mapped back to original feature space. Although the prototypes for the polynomially approximated data are smoother, the comparison shows that they resemble each other in all three scenarios.

Fig. 2
figure 2

Prototypes (panels a, b, c) representing low and high saccharose content in the Orange Juice dataset, and diagonal elements of the relevance matrices \(\varLambda _\xi , \varLambda _c\) and \(\varLambda _{\tilde{\xi }}\) (d, e, f), respectively. Left panels (a, d) Results for using original features (scenario A). Center panels (b, e) Results for polynomial representation (B) with 20 coefficients, prototypes are shown after back-transformation to original feature space. Right panels (c, f): Scenario (C) with 20 coefficients as in (B). a OJ original. b OJ polynomial fit. c OJ smoothened. d OJ original. e OJ polynomial fit. f OJ smoothened

Full size image

While this provides further evidence for the usefulness of the suggested approach, it is important to be aware of the significant differences in terms of the applied distance measure. Figure 2 (lower panels) displays the corresponding relevance profiles for the OJ dataset as an example. For original (A) and smoothed data (C), the diagonal elements of \(\varLambda _\xi \) and \(\varLambda _{\tilde{\xi }}\) can be directly interpreted heuristically as the relevance of the corresponding components in feature space [5, 20]. The diagonal elements of \(\varLambda _c\), however, assign an accumulated weight \([\varLambda _c]_{ii}=\sum _j [\varOmega _c]_{ij}^2\) to each dimension in coefficient space. In the example case of the OJ dataset, the first three coefficients, corresponding to \(g_o(x)=1, g_1(x)=x, g_2(x)=2x^2-1\), are neglected almost completely in the GMLVQ system. This reflects the fact that constant offset as well as linear and quadratic trend are not discriminative in the sense of the classification task at hand. Note that relevance learning enables the system to disregard these properties without further pre-processing of the data.

5 Summary and Outlook

We presented a framework for the efficient classification of functional data, based on their appropriate representation in terms of basis functions. As a concrete example, we considered polynomial approximations of smooth spectral data. The framework was applied to and evaluated for four real world datasets. The results show, that for a range of degrees n of polynomial approximations, a comparable or even significantly better classification performance can be achieved. In these cases, the improvement is not due to the smoothing effect of the representation only, but reflects the fact that the suggested approach takes into account the functional nature of the data more appropriately.

Besides its potential effect on the accuracy, the functional representation of the data can lead to a massive reduction of the data dimension. Consequently, a much smaller number of adaptive parameters is employed in the classifier, reducing the risk of over-fitting, avoiding potential convergence problems, and resulting in less computational effort.

Our initial study leaves several interesting questions open for further investigation. In future projects we will study more systematically the properties of the distance measure imposed by the polynomial representation. While our example results display great robustness with respect to n, more generally, the choice of a suitable degree for the polynomial approximation could play an important role in practice. Validation schemes should be devised in order to identify optimal choices systematically according to the complementary criteria of best performance and minimal dimensionality.

The considered polynomial approximation appears to be a suitable approach for reasonably smooth spectral data. The degree to which the classification performance can be improved in comparison with the standard approaches clearly depends on the suitability of the functional basis for the particular dataset. The systematic investigation of alternative representations in the context of other application domains will be in the center of forthcoming studies.