Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

There are different types of uncertainty [33] that influence the outcome of large systems that support risk assessment, planning, decision making, validation, etc. Uncertainties can enter the system due to missing knowledge about the physical domain, think of subsurface flow simulations, or there are inherent stochastic processes driving the system, such as Brownian motion. The quantification of the influence of such stochastic components on some quantity of interest is the task of forward propagation of uncertainty in the field of uncertainty quantification (UQ). This is challenging since the statistical characteristics of the uncertainties can be unknown or don’t have an analytic representation. Furthermore, the systems or models we are interested in can be arbitrarily complex (highly nonlinear, discontinuous, etc.). Therefore, we need efficient and reliable algorithms and software that can make expensive statistical analysis feasible.

In this paper we want to focus on data-driven quantification of uncertainties in numerical simulations. There are two main problems we face in that context: First, the uncertainty of the quantity of interest depends strongly on the uncertainty in the input. Therefore, one needs objective measures to get an unbiased representation of the uncertainty of the input. Second, to quantify the uncertainties of some quantity of interest, we need to evaluate the model, which can be very costly and involves to run a whole simulation. However, the accuracy of the quantities we compute should be very high, which means in general that we need to evaluate the model often, and the main challenge is to balance costs and accuracy.

The first problem of obtaining objective measures for the input’s uncertainties has been assessed in various articles in the past. One idea is to use data and estimate the stochastic properties using density estimation techniques. The authors of [7] used kernel density estimators, and [1] proposed to use kernel moment matching methods, for example. A comparison between data-driven approaches and approaches based supervised estimation by experts can be found in [21]. However, often the combination of expert knowledge and data is essential if the reliability in the data is low. A very popular approach to combine them is Bayesian inference [35, 39].

The incorporation of data or estimated densities into a UQ forward problem depends on the method that is required by the application to propagate the uncertainty. For non-intrusive methods, for example, there has been done a lot of work in the field of polynomial chaos expansion (PCE) [37, 38]. The generalized PCE, however, is defined for analytic, independent marginal distributions. It has therefore been extended to the arbitrary PCE [34] that supports also dependent marginal distributions [19] and data [23]. However, global polynomials are not always the best choice to propagate uncertainty [6]. Stochastic collocation methods [2, 36] became popular in the last years, especially due to sparse grids [15, 20]. They are used to obtain a surrogate model of the expensive model function. They can overcome the curse of dimensionality to some extent [3], can handle large gradients [8] or even discontinuities in the response functions [13, 29].

In this paper we present a new approach to incorporate data into the UQ forward propagation pipeline. We propose an integrated data-driven sparse grid method, where we estimate the unknown density of the input using the sparse grid density estimation (SGDE) [24, 26] method and propagate the uncertainty using sparse grid collocation (SGC) with adaptively refined grids. The SGDE method has been widely used for Data Mining problems and can be applied for either small or large data sets. It is highly efficient with respect to learning, evaluating and sampling. It interacts seamlessly with SGC since both are based on the same fundamental principles, which can be exploited to reduce the numerical errors in the forward propagation pipeline.

This paper is structured as follows: First, we give a formal definition of a data-driven UQ forward-propagation problem in Sect. 2. In Sect. 3 we describe the methods we use for density estimation and for uncertainty propagation. Then we compare the performance of our approach with other techniques in Sect. 4. We present a lower-dimensional analytic example and a higher-dimensional subsurface flow problem in porous media. In Sect. 5 we summarize the paper and give an outlook to future work.

2 Problem Formulation

We define \((\Omega,\Sigma,P)\) being a complete probability space with \(\Omega\) being the set of outcomes, \(\Sigma \subset 2^{\Omega }\) the \(\sigma\)-algebra of events and \(P: \Sigma \rightarrow [0,1]\) a probability measure. Let \(\boldsymbol{\xi } = (\xi _{1},\ldots,\xi _{d}) \in \Omega\) be a random sample and let the probability law of \(\boldsymbol{\xi }\) be completely defined by the probability density function \(f: \Omega \rightarrow \mathbb{R}^{+}\) with \(\int _{\Omega }f(\boldsymbol{\xi })\text{d}\boldsymbol{\xi } = 1\). Consider a model \(\mathcal{M}\) defined on a bounded physical domain \(\mathbf{x} \in D \subset \mathbb{R}^{d_{s}}\) with 1 ≤ d s  ≤ 3, a temporal domain \(t \in T \subset \mathbb{R}\) and the probability space \((\Omega,\Sigma,P)\) describing the uncertainty in the model inputs as

$$\displaystyle{ u(\mathbf{x},t,\boldsymbol{\xi }) = \mathcal{M}(\mathbf{x},t,\boldsymbol{\xi }): D \times T \times \Omega \rightarrow \mathbb{R}^{d_{r} }\;, }$$
(1)

with \(0 <d_{r} \in \mathbb{N}\). We restrict ourselves without loss of generality to scalar quantities of u and define an operator Q, which extracts the quantity we are interested in, i.e.

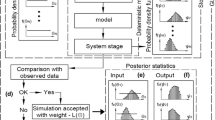
$$\displaystyle{ Q[u(\mathbf{x},t,\boldsymbol{\xi })]: \mathbb{R}^{d_{r} } \rightarrow \mathbb{R}. }$$
(2)

The outcome of u becomes uncertain due to its uncertain inputs \(\boldsymbol{\xi }\). This uncertainty is what we want to quantify. The probability law of \(\boldsymbol{\xi }\), of course, influences heavily the probability law of u. Therefore, in data-driven UQ one assumes to have a set of samples \(\mathcal{D}:=\{ \boldsymbol{\xi }^{(k)}\}_{k=1}^{n}\;,\) with \(\boldsymbol{\xi }^{(k)} = (\xi _{1}^{(k)},\ldots,\xi _{d}^{(k)}) \in \Omega\), which are drawn from the unknown probability density f. \(\mathcal{D}\) is an objective measure describing the uncertainty we want to propagate. A schematic representation of the data-driven UQ pipeline is given in Fig. 1.

Fig. 1
figure 1

Data-driven UQ forward pipeline. The data set \(\mathcal{D}\) describes the stochastic characteristics of the uncertain parameters \(\boldsymbol{\xi }\) for some physical model u. The underlying probability density function f is unknown. The stochastic analysis of the uncertain outcome of u depends strongly on f

Full size image

3 Methodology

In this section we introduce the methods we use to propagate uncertainty. We formally introduce stochastic collocation and the concept of sparse grids based on an interpolation problem. We present the sparse grid density estimation method and describe how it can be used to estimate efficiently moments of some quantity of interest.

3.1 Stochastic Collocation

In stochastic collocation we search for a function g that approximates the unknown model function u. We solve N deterministic problems of u at a set of collocation points \(\Xi _{N}:=\{ \boldsymbol{\xi }^{(k)}\}_{k=1}^{N} \subset \Omega\) and impose

$$\displaystyle{ g^{(i)}(\boldsymbol{\xi }^{(k)}):= Q[u(x_{ i},t_{i},\boldsymbol{\xi }^{(k)})],\;\forall \boldsymbol{\xi }^{(k)} \in \Xi _{ N}\;. }$$
(3)

at a selected point in space x i  ∈ D and time t i  ∈ T. This is, of course, nothing else than an interpolation problem. A common choice for g (i) is to use a sum of ansatz functions on some mesh with either global [17] or local support [8, 12, 15]. The expensive stochastic analysis is then done on the cheap surrogate g (i).

For simplicity in the notation we omit in the following the index i on g and focus on the approximation in \(\Omega\). Without loss of generality, we assume furthermore that there exists a bijective transformation from \(\Omega\) to the unit hypercube and assume the collocation nodes \(\boldsymbol{\xi }^{(k)}\) in the following to stem from [0, 1]d.

3.2 Sparse Grids

We introduce here the most important properties of sparse grids in the context of interpolation problems. The general idea of sparse grids is based on a hierarchical definition of a one-dimensional basis. This means that the basis is inherently incremental. We exploit this property in higher-dimensional settings to overcome the curse of dimensionality to some extent. For details and further reading we recommend [3, 25]. For adaptive sparse grids and efficient implementations of sparse grid methods we refer to [27], for suitable refinement criteria for UQ problems you may read [8, 15, 16].

Suppose we are searching for an interpolant g of an unknown multivariate function \(u(\boldsymbol{\xi }) \in \mathbb{R}\) on the unit hypercube, i.e. \(\boldsymbol{\xi } = (\xi _{1},\xi _{2},\ldots,\xi _{d}) \in [0,1]^{d}\). For g we restrict ourselves to the space of piecewise d-linear functions V ℓ with ℓ being the maximum discretization level in each dimension.

Let \(\mathbf{l} =\{ l_{1},\ldots,l_{d}\}\) and \(\mathbf{i} =\{ i_{1},\ldots,i_{d}\}\) with l k  > 0 and i k  > 0 be multi-indices. We define a nested index set

$$\displaystyle{ \mathcal{I}_{\mathbf{l}}:=\{ (\mathbf{l},\mathbf{i}): 1 \leq i_{k} <2^{l_{k} },i_{k}\text{ odd},k = 1,\ldots,d\} }$$
(4)

of level-index vectors defining the grid points

$$\displaystyle{ \boldsymbol{\xi }_{\mathbf{l},\mathbf{i}}:= (2^{-l_{1} }i_{1},\ldots,2^{-l_{d} }i_{d})\;. }$$
(5)

For each grid point we use the general one-dimensional reference hat function \(\psi (\xi ):=\max (1 -\vert \xi \vert,0)\) to obtain the linear one-dimensional hierarchical hat functions \(\psi _{l,i}(\xi )\) centered at the grid points by scaling and translation according to level l and index i as \(\psi _{l,i}(\xi ):=\psi (2^{l}\xi - i)\), see Fig. 2 (left). We obtain the higher-dimensional basis via a tensor-product approach,

$$\displaystyle{ \psi _{\mathbf{l},\mathbf{i}}(\boldsymbol{\xi }):=\prod _{ k=1}^{d}\psi _{ l_{k},i_{k}}(\xi _{k})\,. }$$
(6)
Fig. 2
figure 2

One-dimensional piecewise linear basis functions up to level 3 (left), polynomial ones (right), and the tableau of hierarchical increments \(W_{\mathbf{l}}\) up to level 3 in two dimensions (center)

Full size image

Note that the level-index vectors \((\mathbf{l},\mathbf{i}) \in \mathcal{I}_{\mathbf{l}}\) define a unique set of hierarchical increment spaces \(W_{\mathbf{l}}:= \mbox{ span}(\{\psi _{\mathbf{l},\mathbf{i}}: (\mathbf{l},\mathbf{i}) \in \mathcal{I}_{\mathbf{l}}\})\), which are shown in the center of Fig. 2. All increment spaces up to \(\vert \mathbf{l}\vert _{\infty } =\max _{i}l_{i} \leq \ell\) span the space of piecewise d-linear functions on a full grid.

Now we take advantage of the hierarchical definition of the basis and reduce the number of grid points by choosing just those spaces \(W_{\mathbf{l}}\) that contribute most to our approximation. An optimal choice is possible a priori if u is sufficiently smooth, i.e. if u is a function of the mixed Sobolev space H mix 2 where the mixed, weak derivatives up to order 2 are bounded. We define the sparse grid space V ℓ (1) as

$$\displaystyle{ V _{\ell}^{(1)}:=\bigoplus _{ \vert \mathbf{l}\vert _{1}\leq \ell+d-1}W_{\mathbf{l}}\;, }$$
(7)

where we select just those subspaces that fulfill \(\vert \mathbf{l}\vert _{1} =\sum _{ k=1}^{d}l_{k} \leq \ell + d - 1\), see the upper triangle in the center of Fig. 2. We define a sparse grid function \(g_{\mathcal{I}_{\mathbf{l}}} \in V _{\ell}^{(1)}\) as

$$\displaystyle{ g_{\mathcal{I}_{\mathbf{l}}}(\boldsymbol{\xi }) =\sum _{(\mathbf{l},\mathbf{i})\in \mathcal{I}_{\mathbf{l}},\vert \mathbf{l}\vert _{1}\leq \ell+d-1}v_{\mathbf{l},\mathbf{i}}\psi _{\mathbf{l},\mathbf{i}}(\boldsymbol{\xi })\;, }$$
(8)

where \(v_{\mathbf{l},\mathbf{i}}\) are the so-called hierarchical coefficients. Note that we omit the index \(\mathbf{l}\) when we refer to \(g_{\mathcal{I}}\) being a sparse grid function defined on an adaptively refined grid.

The sparse grid space V ℓ (1) has one main advantage over the full tensor space V ℓ : The number of grid points is reduced significantly from \(\mathcal{O}((2^{\ell})^{d})\) for a full grid to \(\mathcal{O}(2^{\ell}\ell^{d-1})\) while the interpolation accuracy is of order \(\mathcal{O}((2^{-\ell})^{2}\ell^{d-1})\), which is just slightly worse than the accuracy of a full grid \(\mathcal{O}((2^{-\ell})^{2})\) [3].

If we can impose a higher smoothness for u in a sense that all the weak mixed derivatives up to order p + 1 are bounded, it makes sense to employ a higher-order piecewise polynomial basis \(\psi _{\mathbf{l},\mathbf{i}}^{(\,p)}\) with maximum degree \(1 \leq p \in \mathbb{N}\) in each dimension. Note that these polynomials are defined locally, see Fig. 2 (right). Therefore, we don’t suffer Runge’s phenomenon even though we use equidistant grid spacing in each dimension. For details about the construction of the basis we refer to [3]. The number of grid points, of course, is the same as for the piecewise linear case. However, the interpolation accuracy is now of order \(\mathcal{O}((2^{-\ell})^{p+1}\ell^{d-1})\).

3.3 Sparse Grid Density Estimation Method

The sparse grid density estimation (SGDE) method is based on a variational problem presented in [11], first mentioned in the context of sparse grids in [9] and first developed in [26].

We want to estimate some unknown but existing probability density function f from which a set of observations/samples are available, \(\mathcal{D}:=\{ \boldsymbol{\xi }^{(k)}\}_{k=1}^{n} \subset \Omega\). The SGDE method can be interpreted as a histogram approach with piecewise linear ansatz functions. We search for a sparse grid function \(\hat{f}_{\mathcal{K}} \in V _{\ell}^{(1)}\) with \(\vert \mathcal{K}\vert = M\) grid points that minimizes the following functional [9]

$$\displaystyle{ R(\,\hat{f} _{\mathcal{K}}) = \left \|\hat{f} _{\mathcal{K}}\right \|_{L_{2}}^{2} - \frac{1} {n}\sum _{\boldsymbol{\xi }^{(k)}\in \mathcal{D}}\hat{f} _{\mathcal{K}}(\boldsymbol{\xi }^{(k)}) +\lambda \left \|S\hat{f} _{ \mathcal{K}}\right \|^{2}\;, }$$
(9)

where S is some regularization operator and \(0 \leq \lambda \in \mathbb{R}\) a regularization parameter.

In the unit domain the second term is the discrete version of the first one given a set of observations \(\mathcal{D}\). \(\mathcal{D}\) is a realization of f, so the second term implicitly has larger weights where the probability is larger. This is done explicitly in the first term by the multiplication of the pay-off function with the density \(\hat{f} _{\mathcal{K}}\).

By minimizing \(R(\,\hat{f} _{\mathcal{K}})\) we therefore search for a piecewise continuous density \(\hat{f}_{\mathcal{K}}\) for which the first two terms are equal. Note that the first term is equal to the definition of the expectation value where the pay off function is the probability density function itself.

From the point of view of histograms, we can say that the sparse grid discretization defines the (overlapping) buckets. The first term in R collects the density mass in all the buckets while the second term does the same for the observations available for each hierarchical ansatz function. The penalty term balances fidelity in the data and smoothness of \(\hat{f}_{\mathcal{K}}\) via the regularization parameter \(\lambda\) and the regularization operator S.

Solving \(R(\,\hat{f} _{\mathcal{K}})\) leads to a system of linear equations [11]. The system matrix is the mass matrix of \(\hat{f}_{\mathcal{K}}\), which depends only on the number of grid points and is therefore independent of the number of samples n. We obtain the regularization parameter via cross validation: we split \(\mathcal{D}\) in a training and a test set, solve the optimization problem on the training set and compute the L 2-norm of the residual of the system of linear equations applied on the test set. For details see [26]. The estimated density function has unit integrand if we choose S = ∇ [26].

Algorithm 1: Forcing the sparse grid density to be positive everywhere

Positivity, however, is not guaranteed with this approach. For the numerical examples in this paper we forced \(\hat{f} _{\mathcal{K}}\) to be positive by employing a local full grid search on \(\hat{f}_{\mathcal{K}}\). For piecewise linear ansatz functions there exists a simple algorithm, see Algorithm 1. A sparse grid function can locally be negative if the coefficient of an arbitrary level-index vector \((\mathbf{l},\mathbf{i})\) is negative. If this is the case, then, due to monotony of \(\hat{f}_{\mathcal{K}}\) between grid points, it is sufficient to apply a full grid search on the support of \((\mathbf{l},\mathbf{i})\). We add grid points whenever its function value is negative and obtain the hierarchical coefficients for these grid points by learning the density on the extended grid. We repeat this process until we don’t find any negative function value. This algorithm is, of course, just feasible if the number of local full grid points to be examined is small. Note that for a piecewise polynomial basis the algorithm doesn’t work because the maximum of each ansatz function is not at a grid point.

3.4 Sparse Grid Collocation

The sparse grid collocation method (SGC) is based on the sparse grid discretization scheme (see Sect. 3.2) of the stochastic input space. The level-index vectors \((\mathbf{l},\mathbf{i}) \in \mathcal{I}\) of some sparse grid with \(\vert \mathcal{I}\vert = N\) define our set of collocation nodes as

$$\displaystyle{ \Xi _{N}:=\{ \boldsymbol{\xi }_{\mathbf{l},\mathbf{i}}\}_{(\mathbf{l},\mathbf{i})\in \mathcal{I}}\;\ }$$
(10)

with \(\boldsymbol{\xi }_{\mathbf{l},\mathbf{i}}\) being the grid points, see Eq. (5). We evaluate u at every collocation node of \(\Xi _{N}\) and solve the interpolation problem

$$\displaystyle{ g_{\mathcal{I}}(\boldsymbol{\xi }_{\mathbf{l},\mathbf{i}}):= Q[u(\cdot,\boldsymbol{\xi }_{\mathbf{l},\mathbf{i}})],\forall \boldsymbol{\xi }_{\mathbf{l},\mathbf{i}} \in \Xi _{N}\;, }$$
(11)

by a basis transformation from the nodal basis to the hierarchical basis. Efficient transformation algorithms for both linear and polynomial bases can be found in [3, 27]. We can furthermore employ adaptive refinement to consider local features in u. Suitable refinement criteria can be found in [8, 12, 13, 15, 28].

3.5 Moment Estimation

Let \(\mu = \mathbb{E}_{f}(u)\) and \(\sigma ^{2} = \mathbb{V}_{f}(u)\) be the unknown stochastic quantities of u for the true density f we want to estimate, \(g_{\mathcal{I}}\) be a sparse grid surrogate model for u and therefore \(\mu \approx \mathbb{E}_{f}(g_{\mathcal{I}})\) and \(\sigma ^{2} \approx \mathbb{V}_{f}(g_{\mathcal{I}})\). Let \(\hat{f}\) be an estimated density for the unknown probability density f obtained by a set of samples \(\mathcal{D}:=\{ \boldsymbol{\xi }^{(k)}\}_{k=1}^{n}\) drawn from f.

To estimate the expectation value and the variance we need to solve integrals, which can be higher-dimensional, depending on the correlations of \(\boldsymbol{\xi }\) and the density estimation technique we use. An easy method that can be applied to any estimated density we can sample or evaluate is vanilla Monte Carlo quadrature. We generate a new set of samples \(\hat{\mathcal{D}} =\{ \boldsymbol{\xi }^{(k)}\}_{k=1}^{\hat{n}}\) drawn from \(\hat{f}\) with \(\hat{n} \gg n\). We can now substitute \(\hat{f}\) by the discrete density

$$\displaystyle{ \hat{f} _{\delta } (\xi ) = \frac{1} {\hat{n}}\sum _{\boldsymbol{\xi }^{(k)}\in \hat{\mathcal{D}}}\delta (\boldsymbol{\xi } -\boldsymbol{\xi }^{(k)})\;, }$$
(12)

with δ being the Dirac delta function and estimate the expectation value as

$$\displaystyle{ \mathbb{E}_{\hat{f} } (g_{\mathcal{I}}) =\int _{\Omega }g_{\mathcal{I}}(\boldsymbol{\xi })\hat{f} (\xi )\text{d}\boldsymbol{\xi } \approx \int _{\Omega }g_{\mathcal{I}}(\boldsymbol{\xi })\hat{f} _{\delta } (\xi )\text{d}\boldsymbol{\xi } = \frac{1} {\hat{n}}\sum _{\boldsymbol{\xi }^{(k)}\in \hat{\mathcal{D}}}g_{\mathcal{I}}(\boldsymbol{\xi }^{(k)})\;. }$$
(13)

We obtain the result for the sample variance using the same approach for the numerically stable two-pass algorithm [4]

$$\displaystyle{ \mathbb{V}_{\hat{f} } (g_{\mathcal{I}}) \approx \frac{1} {\hat{n} - 1}\sum _{\boldsymbol{\xi }^{(k)}\in \hat{\mathcal{D}}}(g_{\mathcal{I}}(\boldsymbol{\xi }^{(k)}) - \mathbb{E}_{\hat{ f} } (g_{\mathcal{I}}))^{2}\;. }$$
(14)

Due to the substitution of \(\hat{f}\) by \(\hat{f} _{\delta }\) we can solve the higher-dimensional integrals easily but we introduce a new numerical error, which converges slowly with respect to \(\hat{n}\).

However, this substitution is not necessary if the estimated density \(\hat{f}\) is a sparse grid function \(\hat{f} _{\mathcal{K}}\). Due to the tensor-product approach we can decompose the higher-dimensional integral into one-dimensional ones and solve them separately without a numerical error larger than the machine precision ε. Let us additionally define some arbitrary order on the collocation points so that we can iterate over them in a predefined order. The expectation value of \(g_{\mathcal{I}}\) with respect to \(\hat{f} _{\mathcal{K}}\) can be computed as

$$\displaystyle\begin{array}{rcl} \mathbb{E}_{\hat{f} _{\mathcal{K}}}(g_{\mathcal{I}})& =& \int _{\Omega }g_{\mathcal{I}}(\boldsymbol{\xi })\hat{f} _{\mathcal{K}}(\boldsymbol{\xi })\text{d}\boldsymbol{\xi } \\ & =& \int _{\Omega }\sum _{(\mathbf{l},\mathbf{i})\in \mathcal{I}}v_{\mathbf{l},\mathbf{i}}\psi _{\mathbf{l},\mathbf{i}}^{(\,p)}(\boldsymbol{\xi })\sum _{ (\mathbf{k},\mathbf{j})\in \mathcal{K}}w_{\mathbf{k},\mathbf{j}}\varphi _{\mathbf{k},\mathbf{j}}^{(q)}(\boldsymbol{\xi })\text{d}\boldsymbol{\xi } \\ & =& \sum _{(\mathbf{l},\mathbf{i})\in \mathcal{I}}v_{\mathbf{l},\mathbf{i}}\sum _{(\mathbf{k},\mathbf{j})\in \mathcal{K}}w_{\mathbf{k},\mathbf{j}}\int _{\Omega }\psi _{\mathbf{l},\mathbf{i}}^{(\,p)}(\boldsymbol{\xi })\varphi _{\mathbf{ k},\mathbf{j}}^{(q)}(\boldsymbol{\xi })\text{d}\boldsymbol{\xi } \\ & =& \sum _{(\mathbf{l},\mathbf{i})\in \mathcal{I}}v_{\mathbf{l},\mathbf{i}}\sum _{(\mathbf{k},\mathbf{j})\in \mathcal{K}}w_{\mathbf{k},\mathbf{j}}\mathop{\underbrace{ \int _{\Omega _{1}}\psi _{l_{1},i_{1}}^{(\,p)}\varphi _{k_{1},j_{1}}^{(q)}\text{d}\boldsymbol{\xi }_{1} \cdot \ldots \cdot \int _{\Omega _{d}}\psi _{l_{d},i_{d}}^{(\,p)}\varphi _{k_{d},j_{d}}^{(q)}\text{d}\boldsymbol{\xi }_{d}}}\limits _{=:A_{(\mathbf{l},\mathbf{i}),(\mathbf{k},\mathbf{j})}} \\ & =& \mathbf{v}^{T}A\mathbf{w}\;. {}\end{array}$$
(15)

The same holds for the variance for which we use Steiners translation theorem

$$\displaystyle{ \mathbb{V}_{\hat{f} _{\mathcal{K}}}(g_{\mathcal{I}}) = \mathbb{E}_{\hat{f} _{\mathcal{K}}}(g_{\mathcal{I}}^{2}) - \mathbb{E}_{\hat{ f} _{\mathcal{K}}}(g_{\mathcal{I}})^{2} }$$
(16)

and compute

$$\displaystyle{ \begin{array}{rl} \mathbb{E}_{\hat{f} _{\mathcal{K}}}(g_{\mathcal{I}}^{2})& =\int _{\Omega }g_{\mathcal{I}}^{2}(\boldsymbol{\xi })\hat{f} _{\mathcal{K}}(\boldsymbol{\xi })\text{d}\boldsymbol{\xi } \\ & =\int _{\Omega }\left [\sum _{(\mathbf{l},\mathbf{i})\in \mathcal{I}}v_{\mathbf{l},\mathbf{i}}\psi _{\mathbf{l},\mathbf{i}}^{(\,p)}(\boldsymbol{\xi })\right ]\left [\sum _{({\boldsymbol {\tilde{l}}},{\boldsymbol {\tilde{i}}})\in \mathcal{I}}v_{{\boldsymbol {\tilde{l}}},{\boldsymbol {\tilde{i}}}}\psi _{{\boldsymbol {\tilde{l}}},{\boldsymbol {\tilde{i}}}}^{(\,p)}(\boldsymbol{\xi })\right ]\hat{f} _{\mathcal{K}}(\boldsymbol{\xi })\text{d}\boldsymbol{\xi } \\ & =\sum _{(\mathbf{l},\mathbf{i})\in \mathcal{I}}v_{\mathbf{l},\mathbf{i}}\sum _{({\boldsymbol {\tilde{l}}},{\boldsymbol {\tilde{i}}})\in \mathcal{I}}v_{{\boldsymbol {\tilde{l}}},{\boldsymbol {\tilde{i}}}}\mathop{\underbrace{ \int _{\Omega }\psi _{\mathbf{l},\mathbf{i}}^{(\,p)}(\boldsymbol{\xi })\psi _{{\boldsymbol {\tilde{l}}},{\boldsymbol {\tilde{i}}}}^{(\,p)}(\boldsymbol{\xi })\hat{f} _{\mathcal{K}}(\boldsymbol{\xi })\text{d}\boldsymbol{\xi }}}\limits _{=:B_{(\mathbf{l},\mathbf{i}),({\boldsymbol {\tilde{l}}},{\boldsymbol {\tilde{i}}})}} \\ & = \mathbf{v}^{T}B\mathbf{v}\;, \end{array} }$$
(17)

where the matrix entries \(B_{(\mathbf{l},\mathbf{i}),({\boldsymbol {\tilde{l}}},{\boldsymbol {\tilde{i}}})}\) are

$$\displaystyle{ \begin{array}{rl} B_{(\mathbf{l},\mathbf{i}),({\boldsymbol {\tilde{l}}},{\boldsymbol {\tilde{i}}})} & =\sum _{(\mathbf{k},\mathbf{j})\in \mathcal{K}}w_{\mathbf{k},\mathbf{j}}\int _{\Omega }\psi _{\mathbf{l},\mathbf{i}}^{(\,p)}(\boldsymbol{\xi })\psi _{{\boldsymbol {\tilde{l}}},{\boldsymbol {\tilde{i}}}}^{(\,p)}(\boldsymbol{\xi })\varphi _{\mathbf{k},\mathbf{j}}^{(q)}(\boldsymbol{\xi })\text{d}\boldsymbol{\xi } \\ & =\sum _{(\mathbf{k},\mathbf{j})\in \mathcal{K}}w_{\mathbf{k},\mathbf{j}}\mathop{\underbrace{ \int _{\Omega _{1}}\psi _{l_{1},i_{1}}^{(\,p)}\psi _{\tilde{l}_{1},\tilde{i}_{1}}^{(\,p)}\varphi _{k_{1},j_{1}}^{(q)}\text{d}\boldsymbol{\xi }_{1} \cdot \ldots \cdot \int _{\Omega _{d}}\psi _{l_{d},i_{d}}^{(\,p)}\psi _{\tilde{l}_{d},\tilde{i}_{d}}^{(\,p)}\varphi _{k_{d},j_{d}}^{(q)}\text{d}\boldsymbol{\xi }_{d}}}\limits _{=:b_{(\mathbf{k},\mathbf{j})}} \\ & = \mathbf{w}^{T}\mathbf{b}\;. \end{array} }$$
(18)

The runtime \(\mathcal{O}(N \cdot M)\) for a naive implementation for the expectation value is determined by the matrix vector product. For the variance it holds \(\mathcal{O}(N^{2} \cdot M)\) accordingly. In the inner loop we need to compute the scalar products of the one-dimensional basis functions, which can be done a-priori using Gauss-Legendre quadrature for the corresponding polynomial degree. However, we can reduce the quadratic dependency of the runtime on the number of sparse grid points to just a linear dependency by employing the UpDown-scheme. In the UpDown-scheme we exploit the tree-structure of the grid and apply the uni-directional principle to compute the inner-products [27]. This reduces the quadratic run time for the expectation value to be just linear in the number of grid points, i.e. \(\mathcal{O}(N + M)\).

3.6 The Sparse Grid Data-Driven UQ Forward Pipeline

Here we want to discuss the numerical properties of the sparse grid based data-driven UQ pipeline for forward problems (see Fig. 3).

Fig. 3
figure 3

Data-driven sparse grid UQ forward pipeline

Full size image

It consists of four steps: (1) The data set \(\mathcal{D}\) is a randomly chosen set of n samples drawn from f. The quality of the set, how good it represents the moments of f, can vary significantly depending on it’s size. Furthermore, it makes the estimated density \(\hat{f}_{\mathcal{K}}\) (2) to be a random variable. Peherstorfer et al. [26] showed in this context consistency for the SGDE method, i.e.

$$\displaystyle{ \text{P}\left (\left \|f -\hat{f} _{\mathcal{K}}\right \|_{L_{2}}^{2} = 0\right ) = 1\;, }$$
(19)

for \(\vert \mathcal{K}\vert \rightarrow \infty\) and \(n \rightarrow \infty\). The accuracy of the sparse grid surrogate model \(g_{\mathcal{I}}\) (3) depends on the smoothness of u. Bungartz and Griebel [3] showed that with a piecewise polynomial basis of degree p for regular sparse grids it holds

$$\displaystyle{ \left \|u - g_{\mathcal{I}}\right \|_{L_{2}} \in \mathcal{O}((2^{-\ell})^{p+1} \cdot \ell^{d-1})\;. }$$
(20)

For very specific adaptively refined sparse grids we refer to the results in [15] for a convergence proof. The estimated moments of u in the last step become random variables due to \(\hat{f}_{\mathcal{K}}\) being a random variable. Therefore, when we talk about convergence of the moments of u we need to consider the mean accuracy with respect to density estimations based on different realizations of f. We define the mean relative error for the expectation value as

$$\displaystyle{ \mathbb{E}\vert \vert (\mu -\mathbb{E}_{\hat{f} _{\mathcal{K}}}(g_{\mathcal{I}}))/\mu \vert \vert \;, }$$
(21)

and for the variance as

$$\displaystyle{ \mathbb{E}\vert \vert (\sigma ^{2} - \mathbb{V}_{\hat{ f} _{\mathcal{K}}}(g_{\mathcal{I}}))/\sigma ^{2}\vert \vert \;, }$$
(22)

where μ and \(\sigma ^{2}\) are the true solutions. The quadrature step itself adds numerical errors in the order of the machine precision \(\mathcal{O}(\epsilon )\) per operation since it consists just of computing scalar products of one-dimensional polynomials.

4 Numerical Examples

In this section we discuss an analytic example, consisting of independent marginal Beta-distributions, and a three-dimensional subsurface flow problem with borehole data.

4.1 Analytic Example

In preparation of the subsurface problem we consider a two-dimensional analytic scenario with \(\xi _{1},\xi _{2}\) being two independent Beta-distributed random variables,

$$\displaystyle{ \xi _{1} \sim \mathcal{B}(\alpha _{1},\beta _{1});\xi _{2} \sim \mathcal{B}(\alpha _{2},\beta _{2})\;, }$$
(23)

with shape parameters α 1 = 5, β 1 = 4, α 2 = 3 and β 2 = 2 and sample space \(\Omega _{1} = \Omega _{2} = [0,1]\). The corresponding density functions are defined as

$$\displaystyle{ f_{k}(\xi _{k}) = c_{k}\xi _{k}^{\alpha _{k}-1}(1 -\xi _{ k})^{\beta _{k}-1},\;k \in \{ 1,2\}\;, }$$
(24)

where \(c_{k} = \Gamma (\alpha _{k} +\beta _{k})/(\Gamma (\alpha _{k})\Gamma (\beta _{k}))\) with \(\Gamma\) being the gamma function. Let \(f(\xi _{1},\xi _{2}) = f_{1}(\xi _{1})f_{2}(\xi _{2})\) be the joint probability density function defined on \(\Omega = \Omega _{1} \times \Omega _{2}\). One realization \(\mathcal{D}\) of f of size n was created in two steps: first, we generated n uniformly distributed samples in each dimension. Second, we applied the inverse cumulative distribution function of f k and obtained samples from the beta space \(\Omega\). As a model function u we use a simple parabola with \(u(\partial \Omega ) = 0\) and u(0. 5, 0. 5) = 1

$$\displaystyle{ u(\boldsymbol{\xi }) =\prod _{ k=1}^{2}4\xi _{ k}(1 -\xi _{k})\;. }$$
(25)

This model function has two main advantages: First, we can compute analytic solutions for the expectation value μ and the variance \(\sigma ^{2}\) of u as

$$\displaystyle\begin{array}{rcl} \mu & = \frac{c_{1}c_{2}} {4725} \approx 0.71111&{}\end{array}$$
(26)
$$\displaystyle\begin{array}{rcl} \sigma _{2}& = \frac{c_{1}^{3}c_{ 2}^{3}} {75,014,100,000} - \frac{2c_{1}^{2}c_{ 2}^{2}} {22,325,625} + \frac{4c_{1}c_{2}} {24,255} \approx 0.04843\;,&{}\end{array}$$
(27)

Second, u can be approximated perfectly with a sparse grid function \(g_{\mathcal{I}}\) of level 1 with a piecewise quadratic basis. This means that the numerical error in the surrogate model vanishes. The only two errors remaining are the approximation error estimating the density \(\hat{f}\) and the quadrature error in moment estimation if we use Monte Carlo. The second one can be minimized by increasing the sample size; the first one, however, is limited to the amount of information there is about f, which is encoded in the data \(\mathcal{D}\) we use for density estimation. Due to the randomness in the data we measure the error in the expectation value and the variance according to Eqs. (21) and (22). We compare these two errors for (1) vanilla Monte Carlo (k = 200 realizations of f), omitting the density estimation step, (2) a kernel-density estimator using the libagf library [18] (k = 20 realizations), (3) density trees (dtrees) [30] (k = 50 realizations) and (4) SGDE using the SG\(^{\text{++}}\) library [27] (k = 20 realizations). For the SGDE approach we used regular sparse grids with different levels, estimated the density according to [26] and chose the best approximation with respect to the minimal cross entropy L for a test set \(\mathcal{T}\) of size m = 104.

$$\displaystyle{ L_{\mathcal{T}}(\,\hat{f} ) = -\frac{1} {m}\sum _{\boldsymbol{\xi }^{(k)}\in \mathcal{T}}\log _{2}(\hat{f} (\boldsymbol{\xi }^{(k)}))\;. }$$
(28)

The test set \(\mathcal{T}\) is generated analogous to \(\mathcal{D}\) with a different seed. This measure is known to minimize the Kullback-Leibler-divergence (KL) and is therefore a suitable criterion [32].

Table 1 shows the KL-divergence and the cross entropy for the different density estimation methods and different sizes of training sets.

Table 1 KL-divergence (KL) and cross entropy (L) for different density estimation methods and sizes for the training data sets \(\mathcal{D}\). The test data set \(\mathcal{T}\) to compute the measure had size m = 104
Full size table

We can see three main aspects: First, as expected, the cross entropy minimizes the KL-divergence. Second, the cross entropy decreases monotonically with the sample size for all density estimation methods. This means that the density estimation methods are able to capture the increasing information they get from the larger sample sets. Third, while SGDE and libagf have very similar results for all number of samples, the density trees have a poor performance especially for smaller sample sizes. The KL-divergence of the density trees is 10 times larger for 50–100 training samples than the ones of SGDE and libagf. This is a significant drawback for applications where the real costs lie in obtaining the samples. Think of boreholes that need to be drilled into the ground to obtain information about the physical domain of subsurface flow problems.

If we look at the convergence of the expected error in the expectation value, see Fig. 4 (left), SGDE performs almost one order of magnitude better than libagf. Both methods converge with \(n^{-1/2}\), which is basically the Monte Carlo convergence for the quadrature problem. The convergent phase for density trees starts later at a size of 1000 samples. We see basically the same picture if we look at the variance, see Fig. 4 (right). SGDE performs best compared to the other density estimation methods. However, it seems that the density estimation methods can not outperform Monte Carlo. The reason is that density estimation is based on Monte Carlo estimates for the moments of the distribution, see Eq. (9). It would pay off if there could be gained additional information from the data by extrapolation or regularization. There is no extrapolation in this case due to the definition of the joint probability density function f, which is zero at the boundaries. Neither does regularization, since there is no noise in the data and we measured the mean error over several realizations of f and made it therefore independent of single realizations where regularization could pay off. However, if the number of samples is limited, as it is in the CO2  benchmark problem, the data-driven forward propagation approach with density estimation will reduce the error compared to Monte Carlo.

Fig. 4
figure 4

Decay of the average error in the expectation value (left) and the variance (right) for Monte Carlo (MC), the sparse grid density estimation (SGDE) method, the kernel density estimator (libagf), and the density trees (dtrees)

Full size image

4.2 Multivariate Stochastic Application

In this application we simulate carbon sequestration based on the CO2  benchmark model defined by [5]. We will not introduce here the modeling of this highly non-linear multiphase flow in a porous media problem but rather refer to [5] and focus on the stochastic part. The basic setting however is the following: We inject CO2  through an injection well into a subterranean aquiferous reservoir. The CO2  starts spreading according to the geological characteristics of the reservoir until it reaches a leaky well where the CO2  rises up again to a shallower aquifer. A schematic view on the problem is shown in Fig. 5. The CO2  leakage at the leaky well is the quantity we are interested in. It depends on the plume development in the aquifer and the pressure built up in the aquifer due to injection. While we can control the injection pressure, we cannot control the geological properties of the reservoir like porosity, permeability, etc. This is where the uncertainty comes in and for which we use data to describe it.

Fig. 5
figure 5

Cross-section through the subterranean reservoir [22]

Full size image

4.2.1 Stochastic Formulation

The CO2  benchmark model has three stochastic parameters with respect to the geological properties of the reservoir and the leaky well: (1) the reservoir porosity ϕ, (2) the reservoir permeability K a , and (3) the leaky well permeability K L . For the description of the reservoir, i.e. K a and ϕ, we use a raw data set from the U.S. National Petroleum Council Public Database including 1270 reservoirs, shown in Fig. 6, see also [14]. The data set is assumed to be one realization of the unknown probability density function f that defines the uncertainty of the problem. For the leaky well permeability there is no data available, which makes it necessary to make further assumptions. We make here the same assumptions as in Oladyshkin et al. in [22], see permeability in Table 2. Furthermore, Oladyshkin et al. presented in the same paper an integrative approach to quantify the stochastic outcome of the CO2  benchmark model using analytic densities based on the data at hand, see Table 2. They defined a sample space that is different to the parameter space of the simulation. They substituted \(\text{K}_{a} \in \Omega _{\text{K}_{ a}}\) by a variation parameter \(\nu \in \Omega _{\nu }\) and encoded the correlation in a transformation function from the new sample space to the parameter space, i.e.

$$\displaystyle{ \begin{array}{rl} h: \Omega _{\phi } \times \Omega _{\nu }& \rightarrow \Omega _{\text{K}_{ a}} \\ \phi,\nu &\mapsto c_{1}\phi ^{c_{2}}\left [1 + c_{3}\nu \right ]\;, \end{array} }$$
(29)

with parameters \(c_{1} = 4.0929 \times 10^{-11},c_{2} = 3.6555,c_{3} = -2\). In the new sample space \(\Omega:= \Omega _{\phi } \times \Omega _{\nu } \times \Omega _{\text{K}_{ L}}\) all variables are decorrelated. Therefore we can define analytic independent marginal densities and can propagate the resulting uncertainty directly through the model function using polynomial chaos expansion, for example. We refer to this approach as the analytic approach. To apply stochastic collocation to this problem, we truncated the infinite sample space \(\Omega\) such that in directions of ϕ and K a we collect 99. 99 % of their mass around the corresponding mean, see Table 2. We denote the samples that lie within this truncated space as \(\mathcal{D}:=\{ (\text{K}_{a}^{(k)},\phi ^{(k)})\}_{k=1}^{413}\), see Fig. 7. We use \(\mathcal{D}\) for density estimation to obtain objective measures of the input’s uncertainty.

Fig. 6
figure 6

Raw data for porosity ϕ and permeability K a from the U.S. National Petroleum Council Public Database including 1270 data points. The curves show the upper and the lower bound of the transformed and truncated sample space with respect to the variation ν

Full size image
Table 2 Marginal densities and ranges used in the analytic approach to describe the uncertainty of the CO2  benchmark model. They are fitted to the decorrelated samples according to [22]
Full size table
Fig. 7
figure 7

The plot shows the transformed raw data points h −1(ϕ, K a ) from Fig. 6 that lie within the parameter ranges given in Table 2. They are additionaly linearly scaled to [0, 1]2. The remaining number of samples is 413

Full size image

4.2.2 Results

In this section we want to illustrate the ability of the integrated sparse grid approach to predict accurate expectation values and variances for the CO2  benchmark model with the given input data set. We assume that a surrogate model using adaptive sparse grid collocation is available and approximates the unknown model function so well that the expectation value and the variance can be estimated accurately with respect to the analytic approach (N = 114, refinement according to the variance surplus refinement, see [8] for details). We compare these results of the (1) analytic approach with (2) SGDE, (3) kernel-densities, (4) density trees, and (5) Monte Carlo with bootstrapping on the available data \(\mathcal{D}\).

The results of the density estimations with respect to the cross entropy for a test set \(\mathcal{T}\) with m = 50 are listed in Table 3.

Table 3 Mean cross entropy (L) for different density estimation methods and for 10 randomly chosen training data sets of size 363 and test data sets of size 50
Full size table

The analytic approach has by far the largest cross entropy, which suggests that it doesn’t capture the underlying data as good as the others do. The SGDE method performs best as it has the lowest cross entropy. Note that some samples we use for training are located close to the boundary of the domain (see Fig. 7). This affects the SGDE method since we need to consider the boundary in the discretization of the sample space. For this problem we used trapezoidal boundary sparse grids [27] where each inner grid point has two ancestors in each dimension that lie on the corresponding boundary of the domain.

If we look at the results of the estimation of the expectation value, see Fig. 8 (left), and the variance, see Fig. 8 (right), we obtain surprising results. Let us assume that the results of the Monte Carlo quadrature approach using bootstrapping on the available data is our ground truth. By this we say indirectly that we have large confidence in the available data.

Fig. 8
figure 8

Expectation value (left) and variance (right) over simulation time for the bootstrapping method with the raw data (data), the analytic approach as in [22] (analytic), the sparse grid density estimation (SGDE) method, the kernel density estimator (libagf), and the density trees (dtrees)

Full size image

Compared to this ground truth, the analytic approach overestimates the expectation value and underestimates the variance significantly. We call this difference the “subjective gap”, which has been introduced by expert knowledge. The other density estimation methods lie in between these approaches. The density trees match the expectation value of the data almost exactly. The SGDE method overestimates the expectation value slightly, the kernel density does as well. But if we look at the variance then the SGDE method gives the best results compared to the data, while all others underestimate it.

The overestimation of the expectation value for SGDE with respect to the data can be explained by extrapolation: We used a sparse grid with trapezoidal boundary for SGDE because some samples are located close to the boundary of the domain. Furthermore, we impose smoothness on the unknown density. These two facts let the SGDE method extrapolate towards the boundary resulting in a larger density than there is in the data. This is not even wrong since the boundaries of our transformed and truncated domain \(\Omega\) are located in the middle of the parametric domain in which the raw data lies, see Fig. 6 (left). This leads then to the higher expectation values we see in Fig. 8 (left). In fact, if we use a sparse grid without boundary points for density estimation we match the expectation value of the data as well as the density trees do. However, the cross entropy for this sparse grid density is larger compared to the others (L = 0. 2632) indicating a worse estimation. And indeed, with this estimation we overestimate now the variance significantly.

Due to these arguments, we question the ground truth, which in this application was based on a very limited data set. Of course, this makes the comparison of different methods difficult. But, since the balancing between fidelity in the data and smoothness of the density function is defined clearly for the SGDE approach, we consider it a reliable and robust approach in the context of UQ.

5 Conclusions

In this paper we presented a new integrated sparse grid approach for data-driven uncertainty quantification forward problems. It has two main advantages over common approaches for such problems: First, it is an unsupervised approach that relies on the data at hand. It is not influenced by expert knowledge. Second, the integrated sparse grid approach allows a seamless interaction with the stochastic collocation method with respect to adaptive refinement and quadrature.

Furthermore, the numerical experiments showed that the SGDE method gives good approximations of the unknown probability density function already for small sample sets. It did better than the very popular kernel density. Even newer approaches such as density trees showed worse results compared to SGDE.

However, the SGDE method has drawbacks when it comes to statistical applications for which we need to assure unit integrand and positivity. We presented one way to overcome these problems by suitable discretization and using appropriate regularization. This approach however is limited in terms of the problem’s dimensionality since it implies a local full grid search. There is ongoing work in this field, see [10], to overcome these problems.

In this paper we focused on small sample sets. When it comes to large data sets one can speed up this process significantly using fast algorithms such as SGDE. For example, when one uses Markov chain Monte Carlo to obtain a discrete posterior density in an inverse UQ setting. Such densities are often correlated and pose problems to established forward propagation methods such as the generalized polynomial chaos expansion. The Rosenblatt transformation [31] and the inverse Rosenblatt transformation can play an important role in this context. They can be computed very efficiently without additional numeric errors using sparse grids.