Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Microstructure of a body influences both wave propagation and heat conduction. Microstructure-oriented theories of generalized continua [1–4] are, as a rule, isothermal, whereas the generalization of heat conduction to non-Fourier laws [5–8] is usually restricted by the consideration of homogeneous and even rigid conductors. The main problem is, therefore, to elaborate a conjoint framework for the description of coupled conservative and dissipative processes. As shown recently, such an unification is possible on the basis of the dual internal variables approach [9, 10].

In the conventional thermoelasticity, the free energy density is a function of the deformation gradient and temperature only and cannot depend on the temperature gradient. However, the temperature gradient influence on the thermomechanical response of a microstructured material is expected in the presence of varying temperature fields at the microstructure level [11]. This means that a weakly non-local description should be applied [12]. As a result of the application of the dual internal variables theory, it is possible to obtain a hyperbolic evolution equation for microtemperature keeping the parabolic equation for the macrotemperature [10]. The microtemperature is considered as a macrotemperature fluctuation. Effects of microtemperature gradients exhibit themselves on the macrolevel due to the coupling of equations of macromotion and evolution equations for macro- and microtemperatures. The overall description of thermomechanical processes in microstructured solids includes both direct and indirect couplings of equations of motion and heat conduction at the macrolevel. In addition to the conventional direct coupling, there exists the coupling between macromotion and microtemperature evolution. This means that the macrodeformation induces microtemperature fluctuations due to the heterogeneity in the presence of a microstructure. These fluctuations, propagating with a finite speed, can induce, in turn, corresponding changes in the macrotemperature. Then the appeared changes in the macrotemperature affect macrodeformations again. Numerical simulations demonstrate the formation and propagation of thermoelastic waves in microstructured solids under thermal loading [13].

The purpose of the paper is twofold. First, the difference between the standard single internal variable theory and the dual internal variable approach is emphasized. Next, it is demonstrated how thermal gradients produced by an appropriate microstructure are able to generate fluctuations propagating with a finite speed without introducing a hyperbolic heat conduction equation for the macrotemperature.

2 Internal Variables Formalism

Before the application of the dual internal variable approach to the description of dynamic response of solids with microstructure, it is worth to explain the difference between the single internal variable theory and the dual internal variables approach. We start with the remainder of the single internal variable technique.

2.1 Single Internal Variable in One Dimension

We consider the simplest possible situation, i.e. a “body” or a “system” in one dimension. Suppose that all thermodynamic quantities like temperature, energy, entropy, etc. are defined. Then we assume that the free energy density W is specified as a function of temperature \(\theta \) and an internal variable \(\varphi \) and its space derivative

$$\begin{aligned} W=\overline{W}(\theta ,\varphi ,\varphi _{x}). \end{aligned}$$
(1)

Constitutive assumption (1) allows us to write down so-called “equations of state” (just definition of additional quantities)

$$\begin{aligned} S:=-\frac{\partial \overline{W}}{\partial \theta }, \quad \tau :=-\frac{\partial \overline{W}}{\partial \varphi }, \quad {\eta }:=-\frac{\partial \overline{W}}{\partial \varphi _{x}}, \end{aligned}$$
(2)

where S is the entropy density per unit reference volume.

The balance of internal energy in this case can be represented as

$$\begin{aligned} E_{t}+Q_{x}=0, \end{aligned}$$
(3)

where E is the internal energy density and Q is the heat flux, indices denote time and space derivatives. Remembering the connection between internal energy and free energy, i.e., \(W=E-S\theta \), we arrive at another form of the energy balance

$$\begin{aligned} (S\theta )_{t}+Q_{x}=h^{int}, \quad h^{int}:=-W_{t}, \end{aligned}$$
(4)

where the right-hand side of Eq. (4)\(_1\) is formally an internal heat source [14].

The energy balance should be accompanied by the second law of thermodynamics here written as

$$\begin{aligned} S_{t} + ({Q}/\theta + {K})_{x}\ge 0, \end{aligned}$$
(5)

where K is the “extra” entropy flux that vanishes in most cases, but this is not a basic requirement [14].

Multiplying the second law (5) by \(\theta \)

$$\begin{aligned} \theta S_{t} + \theta ({Q}/\theta +{ K})_{x}\ge 0, \end{aligned}$$
(6)

and taking into account Eq. (4), we obtain

$$\begin{aligned} -\left( W_{t}+S\theta _{ t}\right) + (\theta {K})_{x} -({Q}/{\theta }+{ K})\theta _{x} \ge 0. \end{aligned}$$
(7)

The internal heat source \(h^{int}\) is calculated as follows:

$$\begin{aligned} h^{int}=- W_{t}= -\frac{\partial W}{\partial \theta }\theta _{t} -\frac{\partial W}{\partial \varphi }\varphi _{t} -\frac{\partial W}{\partial \varphi _{x}}\varphi _{xt} =S{\theta }_{t}+\tau {\varphi }_{t}+\eta {\varphi }_{xt}=h^{th}+h^{intr}. \end{aligned}$$
(8)

Accounting for Eq. (8), dissipation inequality (7) can be rewritten as

$$\begin{aligned} \varPhi = \tau {\varphi }_{t}+\eta {\varphi }_{xt}-(Q/\theta +K)\theta _{x} +(\theta {K})_{x}\ge 0. \end{aligned}$$
(9)

To rearrange the dissipation inequality, we add and subtract the same term \(\eta _{x}{\varphi }_{t}\)

$$\begin{aligned} \varPhi = \tau {\varphi }_{t}+\eta \dot{\varphi }_{x} -\eta _{x}{\varphi }_{t}+\eta _{x}{\varphi }_{t} -(Q/\theta +K)\theta _{x} +(\theta {K})_{x}\ge 0, \end{aligned}$$
(10)

which leads to

$$\begin{aligned} \varPhi = (\tau -\eta _{x}){\varphi }_{t} -(Q/\theta +K)\theta _{x} +(\eta {\varphi }_{t}+\theta {K})_{x}\ge 0. \end{aligned}$$
(11)

Following [15], we select the “extra” entropy flux in such a way that the divergence term in Eq. (11) will be eliminated

$$\begin{aligned} {K}=-\theta ^{-1}\eta {\varphi }_{t}. \end{aligned}$$
(12)

Then dissipation inequality (11) reduces to

$$\begin{aligned} \varPhi = (\tau -\eta _{x}){\varphi }_{t} -(Q/\theta +K)\theta _{x} \ge 0. \end{aligned}$$
(13)

It is remarkable that in the isothermal case (\(\theta _{x}=0\)) the dissipation is determined by the internal variable only.

The simplest choice to satisfy the dissipation inequality (13) in the isothermal case

$$\begin{aligned} \varPhi =(\tau -\eta _{x}){\varphi }_{t}\ge 0, \end{aligned}$$
(14)

is the following one:

$$\begin{aligned} {\varphi }_{t}=k (\tau -\eta _{x}), \quad k \ge 0, \end{aligned}$$
(15)

since dissipation inequality (14) is satisfied automatically in this case

$$\begin{aligned} \varPhi =k{\varphi }_{t}^{2}\ge 0, \quad \text{ if } \quad k \ge 0. \end{aligned}$$
(16)

It is easy to see that the dissipation is the product of the thermodynamic flux \({\varphi }_{t}\) and the thermodynamic force \((\tau -\eta _{x})\). The proportionality between the thermodynamic flux and the conjugated force is the standard choice to satisfy the dissipation inequality.

To see how the obtained evolution equation looks like, we specialize free energy dependence (1) in the isothermal case to a quadratic one

$$\begin{aligned} \overline{W} = \frac{1}{2} B \varphi ^{2} + \frac{1}{2} C \varphi ^{2}_{x}, \end{aligned}$$
(17)

where B and C are material parameters. It follows from equations of state (2) that

$$\begin{aligned} \tau :=-\frac{\partial \overline{W}}{\partial \varphi }=-B \varphi , \quad {\eta }:=-\frac{\partial \overline{W}}{\partial \varphi _{x}}=-C \varphi _{x}, \end{aligned}$$
(18)

and evolution equation (15) is an equation of reaction-diffusion type

$$\begin{aligned} {\varphi }_{t}=k (C\varphi _{xx}-B \varphi ), \quad k \ge 0. \end{aligned}$$
(19)

The given standard formalism of internal variables of state is sufficient for many cases [16].

2.2 Dual Internal Variables

The dual internal variables approach is the extension of the technique described above. We suppose that the free energy density depends on internal variables \(\varphi , \psi \) and their space derivatives

$$\begin{aligned} W=\overline{W}(\theta ,\varphi ,\varphi _{x},\psi ,\psi _{x}). \end{aligned}$$
(20)

The equations of state in the case of two internal variables read

$$\begin{aligned} S=-\frac{\partial \overline{W}}{\partial \theta }, \quad \tau :=-\frac{\partial \overline{W}}{\partial \varphi }, \quad {\eta }:=-\frac{\partial \overline{W}}{\partial \varphi _{x}}, \quad \xi :=-\frac{\partial \overline{W}}{\partial \psi }, \quad \zeta :=-\frac{\partial \overline{W}}{\partial \psi _{x}}. \end{aligned}$$
(21)

We introduce the non-zero extra entropy flux following the case of a single internal variable and set

$$\begin{aligned} {K}=-\theta ^{-1}\eta {\varphi }_{t}-\theta ^{-1}\zeta {\psi }_{t}. \end{aligned}$$
(22)

It can be checked that the intrinsic heat source is determined in the considered case as follows

$$\begin{aligned} \widetilde{h}^{intr}:=(\tau -\eta _{x}){\varphi }_{t}+(\xi -\zeta _{x}){\psi }_{t}. \end{aligned}$$
(23)

The latter means that the dissipation inequality in the isothermal case reduces to

$$\begin{aligned} \varPhi =(\tau -\eta _{x}){\varphi }_{t}+(\xi -\zeta _{x}){\psi }_{t}\ge 0. \end{aligned}$$
(24)

The solution of the dissipation inequality can be represented as [17]

$$\begin{aligned} \begin{pmatrix} {\varphi }_{t} \\ {\psi }_{t} \\ \end{pmatrix} = \mathbf {L} \begin{pmatrix} (\tau -\eta _{x}) \\ (\xi -\zeta _{x}) \\ \end{pmatrix}, \quad \text{ or } \quad \begin{pmatrix} {\varphi }_{t} \\ {\psi }_{t} \\ \end{pmatrix} = \begin{pmatrix} L_{11} &{} L_{12} \\ L_{21} &{} L_{22} \\ \end{pmatrix} \begin{pmatrix} (\tau -\eta _{x}) \\ (\xi -\zeta _{x}) \\ \end{pmatrix}. \end{aligned}$$
(25)

The non-negativity of the entropy production (24) results in the positive semidefiniteness of the conductivity matrix \(\mathbf {L}\), which requires

$$\begin{aligned} L_{11}\ge 0,\quad L_{22}\ge 0, \quad L_{11} L_{22} - \frac{(L_{12}+L_{21})^2}{4}\ge 0. \end{aligned}$$
(26)

To be more specific, we keep a quadratic free energy density in the isothermal case

$$\begin{aligned} \overline{W} = \frac{1}{2} B \varphi ^{2} + \frac{1}{2} C \varphi ^{2}_{x}+\frac{1}{2} D \psi ^{2}+\frac{1}{2} F \psi ^{2}_{x}. \end{aligned}$$
(27)

Calculating quantities defined by equations of state

$$\begin{aligned} \tau :=-\frac{\partial \overline{W}}{\partial \varphi } = -B \varphi , \quad {\eta }:=-\frac{\partial \overline{W}}{\partial \varphi _{x}}= -C \varphi _{x}, \end{aligned}$$
(28)
$$\begin{aligned} \xi :=-\frac{\partial \overline{W}}{\partial \psi }=-D \psi , \quad \zeta :=-\frac{\partial \overline{W}}{\partial \psi _{x}}=-F \psi _{x}, \end{aligned}$$
(29)

we can represent system of Eqs. (25) in the form

$$\begin{aligned} {\varphi }_{t} =L_{11}(-B \varphi +C \varphi _{xx}) + L_{12}(-D \psi +F \psi _{xx}), \end{aligned}$$
(30)
$$\begin{aligned} {\psi }_{t}= L_{21}(-B \varphi +C \varphi _{xx}) + L_{22}(-D \psi +F \psi _{xx}). \end{aligned}$$
(31)

Now we will derive a single equation for the internal variable \(\varphi \). For this purpose, Eq. (30) is differentiated with respect to time

$$\begin{aligned} {\varphi }_{tt} =L_{11}(-B \varphi _{t}+C \varphi _{xxt}) + L_{12}(-D \psi _{t}+F \psi _{xxt}). \end{aligned}$$
(32)

Time derivatives of the internal variable \(\psi \) follow from Eq. (31)

$$\begin{aligned} {\psi }_{t}= L_{21}(-B \varphi +C \varphi _{xx}) + L_{22}(-D \psi +F \psi _{xx}), \end{aligned}$$
(33)
$$\begin{aligned} {\psi }_{txx}= L_{21}(-B \varphi _{xx}+C \varphi _{xxxx}) + L_{22}(-D \psi _{xx}+F \psi _{xxxx}). \end{aligned}$$
(34)

At last, the internal variable \(\psi \) can be eliminated using again Eq. (30)

$$\begin{aligned} (-D \psi +F \psi _{xx})=\frac{1}{L_{12}}{\varphi }_{t}-\frac{L_{11}}{L_{12}}(-B \varphi +C \varphi _{xx}), \end{aligned}$$
(35)
$$\begin{aligned} (-D \psi _{xx}+F \psi _{xxxx})=\frac{1}{L_{12}}{\varphi }_{txx}-\frac{L_{11}}{L_{12}}(-B \varphi _{xx}+C \varphi _{xxxx}). \end{aligned}$$
(36)

As a result, time derivatives of the internal variable \(\psi \) can be represented in terms of the internal variable \(\varphi \)

$$\begin{aligned} {\psi }_{t}= & {} L_{21}(-B \varphi +C \varphi _{xx}) + L_{22}\left( \frac{1}{L_{12}}{\varphi }_{t}-\frac{L_{11}}{L_{12}}(-B \varphi +C \varphi _{xx})\right) \nonumber \\= & {} \frac{L_{22}}{L_{12}}{\varphi }_{t}+\frac{L_{12}L_{21}-L_{11}L_{22}}{L_{12}}(-B \varphi +C \varphi _{xx}),\end{aligned}$$
(37)
$$\begin{aligned} {\psi }_{txx}= & {} L_{21}(-B \varphi _{xx}+C \varphi _{xxxx}) + L_{22}\left( \frac{1}{L_{12}}{\varphi }_{txx}-\frac{L_{11}}{L_{12}}(-B \varphi _{xx}+C \varphi _{xxxx})\right) \nonumber \\= & {} \frac{L_{22}}{L_{12}}{\varphi }_{txx}+\frac{L_{12}L_{21}-L_{11}L_{22}}{L_{12}}(-B \varphi _{xx}+C \varphi _{xxxx}), \end{aligned}$$
(38)

and the evolution equation for the internal variable \(\varphi \) has the form

$$\begin{aligned} {\varphi }_{tt}&= L_{11}(-B \varphi _{t}+C \varphi _{xxt}) + L_{12}(-D \psi _{t}+F \psi _{xxt}) \nonumber \\&= L_{11}(-B \varphi _{t}+C \varphi _{xxt}) - D L_{22}{\varphi }_{t}-D (L_{12}L_{21}-L_{11}L_{22})(-B \varphi +C \varphi _{xx}) \nonumber \\&\quad + F L_{22}{\varphi }_{txx} +F (L_{12}L_{21}-L_{11}L_{22})(-B \varphi _{xx}+C \varphi _{xxxx}). \end{aligned}$$
(39)

After rearranging, we have finally

$$\begin{aligned} {\varphi }_{tt}&= (CD + BF)(L_{11}L_{22}-L_{12}L_{21})\varphi _{xx} +(L_{12}L_{21}-L_{11}L_{22})(BD\varphi +CF\varphi _{xxxx}) \nonumber \\&\quad - (BL_{11}+D L_{22}){\varphi }_{t}+(CL_{11}+F L_{22}){\varphi }_{txx}. \end{aligned}$$
(40)

The free energy density W is non-negative by default, which results in non-negativity of material parameters B, C, D, and F. This means that Eq. (40) is the hyperbolic wave equation with dispersion and dissipation.

Thus, extending the state space of our thermodynamic system by an additional internal variable and keeping the quadratic form for the free energy density, we arrive at the hyperbolic evolution equation for the primary internal variable.

3 One-dimensional Thermoelasticity in Solids with Microstructure

Now we are ready to apply the dual internal variables approach to thermoelasticity in solids with microstructure. We will keep the one-dimensional setting to be as simple as possible. The 3D tensorial representation of the application of the dual internal variables approach is given in [18, 19].

3.1 Reminder: Classical Linear Thermoelasticity

The one-dimensional motion of the thermoelastic conductors of heat is governed by local balance laws for linear momentum and energy (no body forces)

$$\begin{aligned} \rho v_{t} -\sigma _{x} =0, \end{aligned}$$
(41)
$$\begin{aligned} E_{t} - \sigma \varepsilon _{t} + Q_{x} = 0, \end{aligned}$$
(42)

and by the second law of thermodynamics

$$\begin{aligned} S_{t} + J_{x} \ge 0. \end{aligned}$$
(43)

Here \(\sigma \) is the one-dimensional stress, v is the particle velocity, J is the entropy flux, subscripts denote derivatives.

The constitutive relations include the Hooke law

$$\begin{aligned} \sigma =(\lambda + 2\mu ) \varepsilon , \end{aligned}$$
(44)

and the Fourier law

$$\begin{aligned} Q= - \kappa ^{2} \theta _{x}, \end{aligned}$$
(45)

where \(\lambda \) and \(\mu \) are Lamé coefficients, \(\kappa ^{2}\) is the thermal conductivity. The entropy flux is proportional to the heat flux

$$\begin{aligned} J = \frac{Q}{\theta }. \end{aligned}$$
(46)

The combined constitutive relation known as the Duhamel-Neumann equation has the form

$$\begin{aligned} W(\varepsilon , \theta )= \frac{1}{2}\left( \lambda + 2\mu \right) u_{x}^{2} -\frac{\rho c_{p}}{2\theta _{0}}\left( \theta -\theta _{0}\right) ^2 +m\left( \theta -\theta _{0}\right) u_{x}, \end{aligned}$$
(47)

where u is the displacement, \(c_{p}\) is the heat capacity, the thermoelastic coefficient m is related to the dilatation coefficient a and the Lamé coefficients \(\lambda \) and \(\mu \) by \(m = -a(3\lambda +2\mu )\), \(\theta _{0}\) is the reference temperature.

Correspondingly, the time derivative of internal energy

$$\begin{aligned} E_{t} = \theta S_{t} +\sigma \varepsilon _{t}, \end{aligned}$$
(48)

and entropy definition

$$\begin{aligned} S=:-\frac{\partial {W}}{\partial \theta }=\frac{\rho c_{p}}{\theta _{0}}\left( \theta -\theta _{0}\right) -m u_{x}, \end{aligned}$$
(49)

yield in the balance of energy

$$\begin{aligned} S_{t}\theta -(k\theta _{x})_{x} =\left( \frac{\rho c_{p}}{\theta _{0}}\theta _{t}-m u_{xt}\right) \theta -(k\theta _{x})_{x}=0, \end{aligned}$$
(50)

which can be reduced for small deviations from the reference temperature to

$$\begin{aligned} \rho c_{p}\theta _{t} -(\kappa ^{2}\theta _{x})_{x}=m \theta _{0}u_{xt}. \end{aligned}$$
(51)

The latter equation together with the balance of linear momentum

$$\begin{aligned} \rho u_{tt}=\left( \lambda + 2\mu \right) u_{xx}+m\theta _{x}, \end{aligned}$$
(52)

form the coupled system of equations for linear thermoelasticity.

3.2 Microstructure Influence: Dual Internal Variables

Now we suppose that the free energy density depends on internal variables \(\varphi , \psi \) and their space derivatives \(W=\overline{W}(u_{x},\theta , \varphi ,\varphi _{x},\psi ,\psi _{x}).\) We use a quadratic free energy function [9]

$$\begin{aligned} {W}&= \frac{1}{2}\left( \lambda + 2\mu \right) u_{x}^{2} -\frac{\rho _{0} c_{p}}{2\theta _{0}}\left( \theta -\theta _{0}\right) ^2+m\left( \theta -\theta _{0}\right) u_{x} \nonumber \\&\quad + A \varphi _{x} u_{x} + \frac{1}{2} C \varphi ^{2}_{x}+\frac{1}{2} D \psi ^{2}. \end{aligned}$$
(53)

Here A, C, and D are material parameters. This means that state variables include strain, temperature, and two internal variables (and their gradients). For simplicity, only a contribution of the second internal variable itself and the gradient of the primary internal variable are included here. The corresponding equations of state determine macrostress \(\sigma \)

$$\begin{aligned} \sigma :=\frac{\partial \overline{W}}{\partial u_{x}} =\left( \lambda + 2\mu \right) u_{x}+m\left( \theta -\theta _{0}\right) +A\varphi _{x}, \end{aligned}$$
(54)

microstress \(\eta \)

$$\begin{aligned} \eta :=-\frac{\partial \overline{W}}{\partial \varphi _{x}}=-C \varphi _{x}-Au_{x}, \end{aligned}$$
(55)

zero interactive internal force \(\tau \)

$$\begin{aligned} \tau :=-\frac{\partial \overline{W}}{\partial \varphi }=0, \end{aligned}$$
(56)

and auxilary quantities related to the second internal variable

$$\begin{aligned} \zeta =-\frac{\partial \overline{W}}{\partial \psi _{x}}=0, \quad \xi =-\frac{\partial \overline{W}}{\partial \psi } =-D\psi . \end{aligned}$$
(57)

Accounting for the time derivative of internal energy

$$\begin{aligned} E_{t} = \theta S_{t} + \sigma \varepsilon _{t}- {\tau \varphi _{t} - \eta \varphi _{xt} - \xi \psi _{t} - \zeta \psi _{xt}}, \end{aligned}$$
(58)

results in the energy balance in the form

$$\begin{aligned} \theta S_{t} - {\tau \varphi _{t} - \eta \varphi _{xt} - \xi \psi _{t} - \zeta \psi _{xt}} + Q_{x} = 0, \end{aligned}$$
(59)

which together with the second law of thermodynamics

$$\begin{aligned} \theta S_{t} +\theta J_{x}\ge 0, \end{aligned}$$
(60)

determines the dissipation inequality

$$\begin{aligned} (\tau -\eta _{x}) \varphi _{t} + {(\xi -\zeta _{x}) \psi _{t}} +(\theta J + \eta {\varphi }_{t}+{\zeta {\psi }_{t}} - Q)_{x}- J \theta _{x} \ge 0. \end{aligned}$$
(61)

Including into consideration the non-zero extra entropy flux according to Eq. (22)

$$\begin{aligned} {K}=-\theta ^{-1}\eta {\varphi }_{t}-\theta ^{-1}\zeta {\psi }_{t}. \end{aligned}$$
(62)

we reduce the dissipation inequality to the sum of intrinsic and thermal parts

$$\begin{aligned} \varPhi =(\tau -\eta _{x}){\varphi }_{t}+(\xi -\zeta _{x}){\psi }_{t}-\left( \frac{{Q}-{\eta }{\varphi }_{t}-\zeta {\psi }_{t}}{\theta }\right) \theta _{x}\ge 0. \end{aligned}$$
(63)

Assuming that the intrinsic dissipation is independent of the temperature gradient, we are forced to modify the Fourier law as follows

$$\begin{aligned} {Q}-{\eta }{\varphi }_{t}-\zeta {\psi }_{t}=-\kappa ^{2} \theta _{x}, \end{aligned}$$
(64)

to satisfy the thermal part of the dissipation inequality.

The remaining intrinsic part of dissipation inequality (63) is satisfied by a choice of evolution equations for internal variables. As it is shown in [9], the thermal influence of a microstructure can be taken into account by the following choice

$$\begin{aligned} {\varphi }_{t}=R (\xi -\zeta _{x}), \quad {\psi }_{t}=-R (\tau -\eta _{x}) + R_{2} (\xi -\zeta _{x}), \end{aligned}$$
(65)

where R and \(R_{2}\) are certain appropriate constants. This choice means that the intrinsic dissipation is partly canceled and its remaining part is the square with a positive coefficient.

It follows from Eqs. (65) and (57) that

$$\begin{aligned} {\varphi }_{t}=-R D\psi , \end{aligned}$$
(66)

i.e., the dual internal variable \(\psi \) is proportional to the time derivative of the primary internal variable \({\varphi }_{t}\). Then the evolution equation for the internal variable \(\psi \)

$$\begin{aligned} {\psi }_{t}=-R (\tau -\eta _{x}) + R_{2} (\xi -\zeta _{x}), \end{aligned}$$
(67)

can be represented as

$$\begin{aligned} -\frac{1}{RD}{\varphi }_{tt}=-R (C \varphi _{xx}+Au_{xx}) + \frac{R_{2}}{R}{\varphi }_{t}, \end{aligned}$$
(68)

or in the following form (\(I=1/R^{2}D\))

$$\begin{aligned} I{\varphi }_{tt} + \frac{R_{2}}{R^{2}}{\varphi }_{t} =C \varphi _{xx}+Au_{xx}, \end{aligned}$$
(69)

which is a Cattaneo-Vernotte-type hyperbolic equation [5] for the internal variable \(\varphi \).

Correspondingly, energy balance (59) in this case has the form

$$\begin{aligned} \rho _{0} c_{p}\, \theta _{t}-\left( \kappa ^{2} \theta _{x}\right) _{x}=m \theta _{0} {u}_{xt}+\frac{R_{2}}{R^{2}}{\varphi }_{t}^{2}. \end{aligned}$$
(70)

Equation for macrotemperature (70) is influenced by a source term which depends on the internal variable \(\varphi \). This equation, as well as evolution equation for the internal variable \(\varphi \) (69) is coupled with the equation of motion [9]

$$\begin{aligned} \rho _{0} u_{tt}=\left( \lambda + 2\mu \right) u_{xx}+m \theta _{x} +{A}\varphi _{xx}, \end{aligned}$$
(71)

which means that the internal variable \(\varphi \) possesses a wave-like behavior induced by the macrodeformation. Identifying the internal variable \(\varphi \) with the microtemperature [9], we see that the microtemperature may induce a wave-like propagation also for the macrotemperature due to the corresponding source term in heat conduction equation (70). Physically, the introduced microtemperature describes fluctuations about the mean temperature due to the presence of a microstructure.

4 Numerical Simulations

Now we will check the influence of microstructure on the thermoelastic wave propagation numerically. The solution of equations (69)–(71) in the case of plane wave motion in a thermoelastic half-space is obtained by means of the wave propagation algorithm explained in detail in [13]. We consider the matrix material as silicon and the microstructure is represented by copper particles embedded randomly in the matrix. Material parameters for silicon are the following [20]: the macroscopic density, \(\rho _{0}\), is equal to 2390 kg/m\(^3\), the Lamé coefficients \(\lambda =\) 48.3 GPa, and \(\mu =\) 61.5 GPa, the heat capacity, \(c_{p}=\) 800 J/(kg K), the reference temperature, \(\theta _{0}=\) 300 K, the thermal conductivity, \(k=\) 149 W/(m K), the thermal expansion coefficient, \(\alpha =2.6 \times 10^{-6}\) 1/K. Correspondingly, material parameters of copper are [21]: the macroscopic density, \(\rho _{0}\), is equal to 8960 kg/m\(^3\), the Lamé coefficients \(\lambda =\) 101.5 GPa, and \(\mu =\) 47.75 GPa, the heat capacity, \(c_{p}=\) 386 J/(kg K), the reference temperature, \(\theta _{0}=\) 300 K, the thermal conductivity, \(k=\) 401 W/(m K), the thermal expansion coefficient, \(\alpha =16.5 \times 10^{-6}\) 1/K.

The problem under consideration is the thermoelastic wave propagation induced by a thermal excitation at the boundary of the half-space. It is assumed that the material is initially at rest. Two consecutive heat pulses are generated at the traction free boundary plane for the first 120 time steps following the rule

$$\begin{aligned} {\theta }(0,t)=\frac{1}{2}\left( 1+\cos \left( \frac{\pi (t-30\varDelta t)}{30}\right) \right) . \end{aligned}$$
(72)

The scale of excitation, \(U_{0}\), is chosen as 6 % of the length of the computational domain, L, so that \(U_0/L=0.06\). The scale of the microstructure, l, is supposed to be even less \(l/L=0.002\). Following [22] coupling parameters used in calculations are chosen as follows:

$$\begin{aligned} \frac{R_{22}}{R_{12}^{2}} = \frac{\rho _{0}c_{0}}{l}, \quad A= 0.02 \rho _{0}c^{2}_{0}, \quad C = \rho _{0}c^{2}_{0}. \end{aligned}$$
(73)

To exclude the direct influence of stress field on the macrotemperature, it was assumed that the velocity gradient in Eq. (70) is negligible.

All calculations were performed by means of the finite-volume numerical scheme [13] using the value of the Courant number 0.98. This scheme is a modification of the previously reported conservative finite-volume algorithm [23, 24] adapted for microstructure modeling. It belongs to a broad class of finite-volume methods for thermomechanical problems [25, 26].

Fig. 1
figure 1

Normalized temperature, stress, and microtemperature distribution at 350 time steps

Full size image

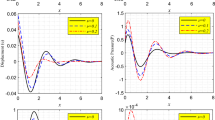
Results of calculations are presented in Fig. 1. This Figure demonstrates explicitly how the coupling in mathematical model (69)–(71) works. In the case of pure silicon we see only thermal diffusion in the vicinity of the boundary. The double pulse thermal excitation generates the corresponding stress pulses propagating through the material. If microstructure is taken into account, this stress pulses induce the microtemperature waves. The microtemperature affects the macrotemperature resulting in the oscillations of the macrotemperature hump with a fading thermal wake.

It should be noted that the scales for all quantities in Fig. 1 are different and chosen artificially to show all quantities in a single picture. The real effect of the microstructure is sufficiently small and can be made visible only by means of a corresponding zooming.

5 Conclusions

The dual internal variables approach leads naturally to a hyperbolic evolution equation for the primary internal variable. In the case of thermoelasticity, this internal variable can be interpreted as a microtemperature or, in other words, as a temperature fluctuation due to the microstructure. Coupling of the governing equations results in the wave-like temperature behavior.

Although the observed effect of the microstructure is small, it exists in the case of realistic values of material parameters. This effect can be amplified by a choice of suitable materials or even by a design of corresponding artificial materials.

It is remarkable that the governing equation for the macrotemperature remains parabolic. The wave-like temperature behavior appears only due to the influence of microstructure.