Some Remarks to Higher Order Frames Occurring in Continuum Mechanics

Abstract

Frame bundles are described with respect to their role in continuum mechanics, the structure jet groups are studied and some expressions in local coordinates are derived. It is introduced the general (r-th order) microstructure configuration and it is suggested what needs to be investigated in subsequent research.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Samuel Forest published in [4] the following nice table representing a hierarchy of higher order continua.

Name	No. of d.o.f.	d.o.f.	References
Cauchy	3	$\mathbf {u}$	Cauchy (1822)
Microdilatation	4	$\mathbf {u}$, $\chi$	Goodman and Cowin (1972); Steeb and Diebels (2003)
Cosserat	6	$\mathbf {u}$, $\mathbf {R}$	Kafadar and Eringen (1971)
Microstretch	7	$\mathbf {u}$, $\chi$, $\mathbf {R}$	Eringen (1990)
Microstrain	9	$\mathbf {u}$, $\mathbf {C}^\sharp$	Forest and Sievert (2006)
Micromorphic	12	$\mathbf {u}$, $\mathbf {\chi }$	Eringen and Suhubi (1964); Mindlin (1964)

The meaning of the symbols is as follows: $\mathbf {u}$ is the displacement field, $\mathbf {\chi }$ is the microdeformation tensor field, $\mathbf {C}^\sharp$ is the right Cauchy-Green tensor, $\mathbf {R}$ is the special microdeformation, namely the rotation.

Certainly, it would be beneficial to have a unified and effective theoretical description of all such cases. In this paper, we show that a very elegant way is to use differential geometry. Using it, a lot of successful and understandable interpretations have already been created, for an example in the book Material Inhomogeneities and their Evolution: A Geometric Approach [3] of authors Marcelo Epstein and Marek Elżanowski, in the lecture notes Introduction to Continuum Mechanics [7] of Panayiotis Papadopoulos or a number of scientific papers as e.g. Continuum dynamics on a vector bundle for a directed medium [8] by Yamaoka and Adachi. Here, we are trying to unify the geometric approach and use a truly modern language of fibered bundles which is systematically developed in the monograph Natural Operations in Differential Geometry [6] of Kolář et al.

Besides this unifying language there are also some of our calculations (principal morphisms between frame bundles with different structure groups, the form of elements of Toupin subgroups) completely new in terms of the explicit expression. We are convinced that local coordinate expressions are necessary to be truly effective in applications. Nevertheless, the paper is much more something else: an outline of the program. The program of an investigation in special higher order principal bundle morphisms—it is shown here that it is a powerful theoretical background.

2 The Configuration

Let B and S be two smooth manifolds ($\dim B=b$, $\dim S=s$, $b\le s$) and

$$ {\kappa } : B \rightarrow S $$

a smooth embedding (i.e. an injective smooth mapping such that $\kappa (B)$ is a submanifold of S and the (co)restricted mapping $B\rightarrow \kappa (B)$ is a diffeomorphism, see [6]). We will call B the body, S the space and $\kappa$ the configuration. As B and S are manifolds, they are endowed with local maps $\varphi ^B_\iota : U_\iota \rightarrow \mathbb R^b$ ($U_\iota \subseteq B$, $\iota \in I$) and $\varphi ^S_{\bar{\iota }}: V_{\bar{\iota }}\rightarrow \mathbb R^s$ ($V_{\bar{\iota }} \subseteq S$, $\bar{\iota }\in \bar{I}$).¹ The maps provide local coordinates: let points $P\in B$ have coordinates $(\xi ^j), j=1,\ldots , b$ and points $p\in S$ have coordinates $(x^i), i=1,\ldots , s$. The local coordinate expression of the configuration $\kappa$ is a map

$$ \bar{\kappa }:\mathbb R^b\rightarrow \mathbb R^s $$

such that

$$ \bar{\kappa }\circ \varphi ^B_\iota =\varphi ^S_{\bar{\iota }}\circ \kappa $$

and it is expressed by

$$ x^i=\kappa ^{i}(\xi ^j). $$

Of course, it is an infinite number of configurations in general. One of them is labeled as significant, so called reference configuration

$$ \kappa _0: B\rightarrow S. $$

We will now assume that different configurations are smoothly parameterized. Let us consider one-dimensional manifold T (with local maps $\varphi ^T_{\tilde{\iota }}: W_{\tilde{\iota }}\rightarrow \mathbb R$, $W_{\tilde{\iota }}\subseteq T$, $\tilde{\iota }\in \tilde{I}$ giving a local coordinate t to a point of T) and a smooth map

$$ \chi : B \times T \rightarrow S $$

endowed with the property that its restrictions to specific t are configurations, in particular

$$ \chi _{|_{t=t_{0}}}=\kappa _0. $$

Usually, t is interpreted as time and the map $\chi$ is called the motion. Its local coordinate expression is

$$ x^i = \chi ^i (\xi ^j, t). $$

The velocity and acceleration vectors are expressed by

$$ v^i = \frac{{\text {d}}\chi ^i}{{\text {d}}t}\quad {\text {and}} \quad a^i = \frac{{\text {d}}^2\chi ^i}{{\text {d}}t^2}. $$

Let us consider the position vector r with respect to the reference configuration $\kappa _0$, as $r: B \times T \rightarrow S$,

$$ r^i(X^j,t)=\chi ^i ({\xi }^j, t) - X^i \quad \text {where}\;\; X^i=\chi ^i ({\xi }^j, t_0); $$

such a position vector is called the deformation of B with respect to the reference configuration $\kappa _0$ in time t. Then the deformation gradient of B is

$$ F^i_{\bar{i}}=\frac{\text {d}\text {r}^i}{{\text {d}}{X^{\bar{i}}}}. $$

Now we will add to the body its microstructure. Classically, the microstructure is expressed by k linearly independent vectors, $k\le s$, called directors (cf. e.g. [8]) assigned to points $p\in \kappa (B)\subseteq S$. Thus, we consider frames over points of $\kappa (B)\subseteq S$, in particular we do not exclude the case $k>b$. It seems well-reasoned, because, for example, two-dimensional plate materials are placed in three-dimensional space, their thickness is neglected, but a rotation of their particles is required three-dimensional. This is illustrated in the Fig. 1. In this situation, we introduce frames by a strictly geometric way in Sect. 2.

Fig. 1

Three directors (blue, red and black) determining rotations of particles of a two-dimensional body in the three-dimensional space

3 Frame Bundles (of the First Order)

Let us consider smooth mappings from $\mathbb R^b$ ($b=\dim B$) to B such that the rank of their tangent maps in $\mathbf 0 = (0, \ldots ,0)$ equals b, i.e. we consider immersions. We define the first order frame bundle $P^1B$ over B as the space of 1-jets of such immersions from $\mathbb R^b$ into B, i.e.

$$ P^1B = \text {imm} \, J^1_{0} \left( {\mathbb R}^b, B \right) . $$

1-jets in question, i.e. elements of $P^1B$, form a principal bundle over the base manifold B. Analogously, we have the bundle $P^1S$ over S. These bundles disposes of right actions by general linear groups $\text {GL} \, (b,\mathbb R)$ and $\text {GL} \, (s,\mathbb R)$, respectively. Now, we take principal bundle morphism (a fiber bundle morphism which interwines with group actions)

$$ K: P^1B\rightarrow P^1S $$

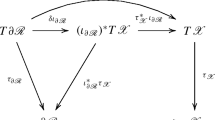
over the base map $\kappa$. This morphism will be called the Cosserat configuration. In local coordinates, $P^1B$ has induced local coordinates $\xi ^j$, $\xi ^j_{\bar{j}}$, $j,\bar{j} = 1,\ldots ,b$, $P^1S$ has induced local coordinates $x^i$, $x^i_{\bar{i}}$, $i,\bar{i} = 1,\ldots ,s$ and the morphism K is expressed by

$$\begin{aligned} x^i= & {} \kappa ^i(\xi ^j) \\ x^i_{\bar{i}}= & {} K^i_{\bar{i}}(\xi ^j,\xi ^j_{\bar{j}}). \end{aligned}$$

Let us express K. First, we take a fixed homomorphism $H_{\varphi }: \text {GL} \, (b,\mathbb R) \rightarrow \text {GL} \, (s,\mathbb R)$ by the following way. The element $\beta \in \text {GL} \, (b,\mathbb R)$ will be embedded to $\text {GL} \, (s,\mathbb R)$ and multiplied by a fixed $\varphi \in \text {GL} \, (s,\mathbb R)$ from right. The result will be denoted by $\sigma \in \text {GL} \, (s,\mathbb R)$. It means $\sigma ^i_{\bar{i}}={H_{\varphi }}^i_{\bar{i}}(\beta )=\beta ^i_k \varphi ^k_{\bar{i}}$ for $i \le b$ and $\sigma ^i_{\bar{i}} ={H_{\varphi }}^i_{\bar{i}}(\beta )=\varphi ^i_{\bar{i}}$ for $b< i \le s$.

Hence K needs to satisfy

$$\begin{aligned} K^i_{\bar{i}}(\xi ^j,\xi ^j_k \beta ^k_{\bar{j}})= & {} K^i_k(\xi ^j,\xi ^j_{\bar{j}})\sigma ^k_{\bar{i}}= K^i_p(\xi ^j,\xi ^j_{\bar{j}})\beta ^p_l\varphi ^l_{\bar{i}}+K^i_q(\xi ^j,\xi ^j_{\bar{j}})\varphi ^q_{\bar{i}}\\&(p\le b, b<q\le s). \end{aligned}$$

If $\varphi$ is the identity, we have $\varphi ^k_{\bar{i}}=\delta ^k_{\bar{i}}$ (Kronecker delta) and the formula transforms into

$$\begin{aligned} K^i_{\bar{i}}(\xi ^j,\xi ^j_k \beta ^k_{\bar{j}})= & {} K^i_p(\xi ^j,\xi ^j_{\bar{j}})\beta ^p_{\bar{i}} \qquad (\bar{i}\le b)\\ K^i_{\bar{i}}(\xi ^j,\xi ^j_k \beta ^k_{\bar{j}})= & {} K^i_{\bar{i}}(\xi ^j,\xi ^j_{\bar{j}}) \qquad (b<\bar{i}\le s). \end{aligned}$$

We recognize $K^i_{\bar{i}}$ as linear in $\xi ^j_{\bar{j}}$ for $\bar{i}\le b$ and as constant in $\xi ^j_{\bar{j}}$ for $b<\bar{i} \le s$.²

4 Jet Groups: Toupin Subgroups

A group G is called a split extension of a group N by a group $\bar{H}$ 1if N is a normal subgroup of G and G contains a subgroup H such that $H \cong \bar{H}$, $N \cap H = \{ e \}$ and $NH = G$. Alternatively one says that G is a semidirect product of N by $\bar{H}$. The notation is $G=N \times | \, \bar{H}$ [2].

Alternatively, given any two arbitrary groups $\bar{N}$ and $\bar{H}$ and a group homomorphism³ $\tau : \bar{H} \rightarrow \text {Aut} \; \bar{N}$, we can construct a new group $G = \bar{N}\times |\, _{\tau }\bar{H}$ through its operation $*$ defined by

$$ (\bar{n}_1,\bar{H}_1)*(\bar{n}_2,\bar{H}_2) = \left( \bar{n}_1 \tau (\bar{H}_1)\left( \bar{n}_2\right) , \bar{H}_1 \bar{H}_2\right) $$

Then pairs $(\bar{n},e_{\bar{H}})$ form a normal subgroup N of G isomorphic to $\bar{N}$, while pairs $(e_{\bar{N}}, \bar{H})$ form a subgroup H of G isomorphic to $\bar{H}$. This semidirect product is consistent with the definition above, namely $\bar{N}\times |\, _{\tau }\bar{H} = N\times |\, \bar{H}$.

r-jets of smooth maps $\mathbb R^n\rightarrow \mathbb R^n$ with non-zero Jacobian determinant in $\mathbf 0 = (0,\ldots ,0)$ and sending $\mathbf 0$ to $\mathbf 0$ together with the jet composition form a group which is called the r-th jet group and denoted by $G^r_n$, for details see [6]. Moreover, for $0\le s<r$, we have a canonical epimorphism $\pi ^{r\rightarrow s}_n: G^r_n\rightarrow G^s_n$. (We consider $G^0_n$ as the trivial group.) Let us write $B^{r\rightarrow s}_n=\text {ker} \; \pi ^{r\rightarrow s}$. Groups $B^{r\rightarrow s}_n$ are normal subgroups of $G^r_n$, see [6], Proposition 13.11.

Thus, in the sense discussed above, we have $G^r_n=B^{r\rightarrow 1}_n \times |\, G^1_n$.

We remark that $G^1_n$ is nothing but the general linear group $\text {GL} \; (n,\mathbb R)$ for which a structure of subgroups is extensively studied for many years and includes i.a. triangular and diagonal subgroups, orthogonal and symplectic subgroups, etc. So, let M be a subgroup of $(e_{B^{r\rightarrow 1}_n},G^1_n)$ (e.g. induced from classical groups just mentioned), $m\in M$ and let $b\in B^{r\rightarrow 1}_n$. Then elements $bmb^{-1}$ generates the conjugate subgroup $T=bMb^{-1}$ of $G^r_n$ which is called the Toupin subgroup of $G^r_n$ associated with M and b.

For a subgroup K of $G^r_n$, let $\pi ^{r\rightarrow 1}_K$ denote the restriction of $\pi ^{r\rightarrow 1}$ to K. Then, for $a\in G^1_n$, we will examine the fiber $\left( \pi ^{r\rightarrow 1}_K\right) ^{-1}(a)$.

First, for a Toupin subgroup T, we observe $\left( \pi ^{r\rightarrow 1}_T\right) ^{-1}(\text {id}_{G^1_n})=\text {id}_T$. This leads to the following definition. We say that a subgroup K of $G^r_n$ is the generalized Toupin subgroup of $G^r_n$ if it has the property that $\left( \pi ^{r\rightarrow 1}_K\right) ^{-1}(\text {id}_{G^1_n})$ is singleton.

In [3], authors proved for $r=2$ that exist

• generalized Toupin subgroups of $G^r_n$ which are not Toupin subgroup;

• one-parameter subgroups in $G^r_n$ which are not generalized Toupin subgroup.

Now, we present the form of Toupin subgroup in local coordinates. First, we recall that for $a=(a^i_j,a^i_{jk}), b=(b^i_j,b^i_{jk}) \in G^2_n$, the composition $c=ba=b\circ a$ is given by $c=(c^i_j,c^i_{jk})=(b^i_k a^k_j, b^i_{lm} a^l_ja^m_k+b^i_la^l_{jk})$. We easily find that for $b=(\delta ^i_j,b^i_{jk})\in B^{2\rightarrow 1}_n$ its inverse $b^{-1} =(\delta ^i_j,-b^i_{jk})$. Then for $h=(h^i_j,0)$, where $(h^i_j)$ represents a subgroup of $G^1_n$,

$$ bhb^{-1}=(h^i_j, b^i_{lm}h^l_jh^m_k-h^i_l b^l_{jk}). $$

We immediately see that for $h^i_j=\delta ^i_j$ we obtain the identity as required.

5 Frame Bundles (of a General Order)

We define the r-th order frame bundle $P^rB$ over B as the space of r-jets of immersions from $\mathbb R^b$ into B, i.e.

$$ P^rB = \text {imm} \, J^r_{0} \left( \mathbb R^b, B \right) . $$

1-jets in question, i.e. elements of $P^1B$, form a principal bundle over the base manifold B. The structure group of $P^rB$ is $G^r_b$ which acts smoothly on $P^rB$ on the right by the jet composition, i.e. $P^rB$ is a principal $G^r_b$-bundle. We generalize the Cosserat configuration by the following way. A principal bundle morphism

$$ \mathscr {K}: P^{r}B \rightarrow P^{r}S $$

over the base map $\kappa$ will be called the general (r-th order) microstructure configuration.

We note that $P^rB$ has induced local coordinates $\xi ^j$, $\xi ^j_{\bar{j}_1}$, ..., $\xi ^j_{\bar{j}_1\ldots \bar{j}_r}$, $j,\bar{j}_1,\ldots ,\bar{j}_r = 1,\ldots ,b$ and $P^1S$ has induced local coordinates $x^i$, $x^i_{\bar{i}_1}$, ..., $x^i_{\bar{i}_1\ldots \bar{i}_r}$ $i,\bar{i}_1,\ldots ,\bar{i}_r = 1,\ldots ,s$.

For the expression of $\mathscr {K}$, we take (analogously as for the Cosserat configuration), a fixed homomorphism $\mathscr {H}_{\varphi }: G^r_b \rightarrow G^r_s$, again, first by the embedding of the element of $G^r_b$ to $G^r_s$ and then by the right multiplying by an element $\varphi$ form $G^r_s$. We are leaving to readers to calculate the coordinate expression of $\mathscr {K}$ now.

6 Higher Order Deformation Bundles and Reductions of Jet Groups—Interesting Challenges

In the Sect. 1, we introduce the deformation gradient for the configuration $\kappa$. Evidently, deformation gradients are 1-jets.

Analogously, deformation gradients for the case of the Cosserat configuration K are represented by nonholonomic 2-jets and the question whether these jets are semiholonomic or even holonomic can be (and is) discussed. In general, deformation gradients of the general microstructure configuration $\mathscr {K}$ form certain nonholonomic ($r+1$)-jets and emerging challenges are similar: what represent jets of special types (semiholonomic, holonomic, but not only), in particular, due to the constitutive equations of the material?

Fig. 2

There are numerous applications of Cosserat theory concerning rectangular structure of blocks; this figure is taken from the paper [1] of Dieter Besdo

Different, but no less important issue is a research of subgroups of jet groups $G^r_n$, similarly as it has been done in the case of Toupin subgroups. Of course, it leads to the phenomenon of material symmetry. Even an uninformed layman anticipates, when he had looked at Fig. 2, that there are situations when a total freedom in all possible ways of the motion is not the best to study; when the whole linear or jet group does not act, but operates only some suitable subgroup. We recall that if we have a principal G-bundle Y and an inclusion of a subgroup H into G, a reduction of the structure group (from G to H) is a principal H-bundle Z such that the pushout $Z \times _H G$ is isomorphic to Y. Note that these do not always exist, nor if they exist are they unique. Despite the complexity of the problem of reductions of jet groups, it is hopeful that it will not just pure mathematics, but also interesting results for continuum mechanics.