BOR$^2$G: Building Optimal Regularised Reconstructions with GPUs (in Cubes)

Abstract

This paper is about dense regularised mapping using a single camera as it moves through large work spaces. Our technique is, as many are, a depth-map fusion approach. However, our desire to work both at large scales and outdoors precludes the use of RGB-D cameras. Instead, we need to work with the notoriously noisy depth maps produced from small sets of sequential camera images with known inter-frame poses. This, in turn, requires the application of a regulariser over the 3D surface induced by the fusion of multiple (of order 100) depth maps. We accomplish this by building and managing a cube of voxels. The combination of issues arising from noisy depth maps and moving through our workspace/voxel cube, so it envelops us, rather than orbiting around it as is common in desktop reconstructions, forces the algorithmic contribution of our work. Namely, we propose a method to execute the optimisation and regularisation in a 3D volume which has been only partially observed and thereby avoiding inappropriate interpolation and extrapolation. We demonstrate our technique indoors and outdoors and offer empirical analysis of the precision of the reconstructions.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction and Prior Work

Building maps and workspace acquisition are established and desired competencies in mobile robotics. Having “better maps” is loosely synonymous with better operation and workspace understanding. An important thread of work in this area is dense mapping in which, in stark contrast to the earliest sparse-point feature maps in mobile robotics, we seek to construct continuous surfaces. This is a well studied and vibrant area of research. In this paper we consider this task in the context of large scale workspace mapping—both indoors (despite depleted texture on drab walls) and outdoors (with a large range of scales) using only a mono-camera.

A precursor to many dense reconstruction techniques, including ours, are 2.5D depth maps. These can be generated using a variety of techniques: directly with RGB-D cameras, indirectly with stereo cameras, or as in our case, from a single camera undergoing known motion.

RGB-D sensor-driven work often uses Microsoft Kinect or Asus Xtion PRO devices for example [11, 17, 19, 23]. Such “RGB-D” systems provide VGA colour and depth images at around 30 Hz, but this is at the cost of range (0.8–3.5 m) and the ability to only reliably operate indoors [20], although outdoor operation is possible at night and with the same range limitation [18]. However, for the indoor environments these structured light sensors can operate in, they produce extremely accurate 3D dense reconstructions even in low-texture environments.

Stereo cameras also enable dense reconstruction but do introduce complexity and concerns around stable extrinsic calibration to the degree that they can be cost-prohibitive for low-end robotics applications [1]. An alternative approach is to leverage a sequence of mono images. In this case we do need an external method to derive, or at least seed, accurate estimates of the inter-frame motion of the camera—perhaps from an IMU-aided Visual Odometry systems or a forward kinematic model of an arm. Note that in this work, because our focus is on the reconstruction component, we assume that this is given and point the reader to [9] for an example system. With the pose estimates between sequential images as a given, the depth of each pixel can be estimated using an identical approach to that taken in creating depth maps from stereo cameras [5, 8].

Full 3D dense reconstruction has only been demonstrated in either indoor environments [14] or small-scale outdoor environments [6, 21]. Interestingly both these methods rely on a fully-observed environment in which the observer orbits the subject. In an important sense and in contrast to what we shall present, these techniques all are object-centred in situ where the camera trajectory is chosen to generate quality depth maps. In many mobile robotics applications—e.g., an autonomous vehicle limited to an on-road trajectory—the environment observations are constrained and suboptimal for these traditional dense reconstruction techniques.

RGB-D based reconstructions can rely on high quality depth maps always being available. In this case, regularisation is not required since an average of measurements in the voxel grid can provide visually appealing results. When using camera-derived depth-maps, a vital and defining point is that the depth maps are almost always noisy and ill formed in places—particularly a problem when operating in regions where there is a dearth of texture. Accordingly, regularisation techniques must be applied to reduce these effects—essentially introducing a prior over the local structure of the workspace (planar, affine, smooth, etc.) [13].

In this paper, we propose a depth map fusion approach to densely reconstruct environments using only a monocular camera as it moves through large work spaces. Given a set of noisy dense depth maps from a sub set of monocular images, we formulate the 3D fusion as a regularised energy minimisation problem acting on the Truncated Signed Distance Function (TSDF) that parametrises the surface induced by the fusion of multiple depth maps. We represent our solution as the zero-crossing level of a regularised cube. Our method can execute the optimisation and regularisation in a 3D volume which has been only partially observed while avoiding inappropriate interpolation and extrapolation.

What follows is a technique that leverages many of the constructs of previous work to achieve 3D dense reconstruction with monocular cameras but with an input range from 1.0 to 75 m in regions of low texture. We do this without requiring privileged camera motion and we do it at a near-interactive rate. We begin in Sect. 2 by describing how we frame the problem in the context of an implicit 3D function, the TSDF. In Sect. 3, we formulate the solution of the depth map fusion problem as a regularised energy minimisation. Section 4 explains the theoretical insights which allow us to set new boundary conditions inside the cube. We present the main steps of algorithmic solution in Sect. 5. Quantitative and qualitative results on a synthetic data set rendering an indoor place, and real experiments on challenging indoors/outdoors are presented in Sect. 6. Finally, we draw our conclusions and future lines of research in Sect. 7.

2 Construction of the Problem Volume: The BOR$^2$G Cube

This paper is about building optimal regularised reconstructions with GPUs. Our fundamental construct is a cube of voxels, which we refer to as the BOR$^2$G Cube, into which data is assimilated.

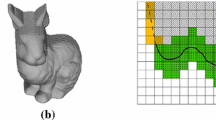
The cube model is a discretised version of a Truncated Signed Distance Function (TSDF) $u: \varOmega \rightarrow \mathbb {R}$ where $\varOmega \subset \mathbb {R}^3$ represents a subset of points in 3D space and u returns the corresponding truncated distance to surfaces in the scene [4]. The TSDF is constructed in such a way that zero is the surface of an object, positive values represent empty space, and negative values correspond to the interior of objects, as shown in Fig. 1. Thus by finding the zero-crossing level-set, $u = 0$, we can arrive at a dense representation of surfaces in the workspace.

Consider first the case of operating with a single depth map D, an image in which each pixel (i, j) represents the depth $d_{i,j}$ of the closest obstacle in space along the z axis. We use the $4\times 4$ homogeneous matrix $\mathbf {T}_{gc}\in \textit{SE}(3)$ to express the depth map’s camera position, c, with respect to the voxel grid’s global frame, g.

Fig. 1

A graphical depiction (a) of how the TSDF values represent the zero-crossing surface in a two-dimensional ‘voxel’ grid. In (b) these TSDF values are discretised into histogram bins ($n_{bins} = 5$). $u \in [-1, 1]$ which directly maps into histogram bins with indices from 1 to $n_{bins}$. There is no u value and no histogram bin when $u \le -\mu$, however the $n_{bins}$ histogram bin includes all $u > \mu$

For each voxel, the steps to obtain u from a single depth map D are as follows:

• 1. Calculate the central point $\mathbf{p}_g =[x_g,y_g,z_g]^T$ of the voxel with respect to the camera coordinate frame as $\mathbf{p}_c = \mathbf {T}_{gc}^{-1} \mathbf{p}_g$

• 2. Compute the pixel (i, j) in D in which the voxel is observed by projecting $\mathbf{p}_c$ into D and rounding each index to the nearest integer.

• 3. If the pixel (i, j) lies within the depth image, evaluate u as the difference between $d_{i,j}$ and the z component of $\mathbf{p}_c$. If $u > 0$, the voxel is between the surface and the camera whereas $u < 0$ indicates the surface occludes the camera’s view of the voxel.

• 4. Finally, linearly scale-and-clamp u such that any voxel for which $u> -\mu$ lies in the interval $[-1, 1]$ whereas voxels for which $u< -\mu$ are left empty. See Fig. 1.

In the next subsection we will explain how to fuse multiple depth images $D_t$ obtained at different moments in time t.

3 Depth Map Fusion

When high-quality depth maps are available, for example depth maps obtained from a Kinect camera, data fusion can be performed by minimising, for each voxel, the following $L_2$ norm energy,

$$\begin{aligned} \mathop {\mathrm {arg\,min}}\limits _{u} \int _{\varOmega } \sum _{t=1}^N ||u - f_t||^2_2 d\varOmega \end{aligned}$$

(1)

where N represents the number of depth maps we want to fuse, $f_t$ is the TSDF that corresponds to depth map $D_t$ and u is the optimised TSDF after fusing all the information available. Using a voxel grid representation for the TSDFs, the solution to this problem can be obtained by calculating the mean of all the ${f_1, \ldots , f_N}$ for each individual voxel. This operation can be performed in real time by sequentially integrating a new $f_t$ when a new depth map is available [11]. The searched TSDF u does not require any additional regularisation due to the high-quality of the depth maps used in the fusion.

However, when cameras are used, the depth maps obtained are of much lower quality due, for example, to poor parallax or incorrect pixel matches. Therefore a more robust method is required. In [21] the authors propose an $L_1$ norm data term, which is able to cope with spurious measurements, and an additional regularisation term, based on Total Variation [16], to smooth the surfaces obtained. The energy minimised is given by,

$$\begin{aligned} \mathop {\mathrm {arg\,min}}\limits _u \int _\varOmega |\nabla u|_1 + \lambda \int _\varOmega \sum _{t=1}^N ||u-f_t||_1 d\varOmega \end{aligned}$$

(2)

The first component is a smoothness term that penalises high-varying surfaces, while the second component, which mirrors Eq. 1, substitutes the $L_2$ norm with a robust $L_1$ energy term. The parameter $\lambda > 0$ is a weight to trade off between the regularisation and the data terms. The main drawback with this approach is that, unlike KinectFusion, we cannot just sequentially update the TSDF u when a new depth map arrives, instead, this method requires to store all previous history of depth values in each voxel. This greatly limits the number of depth maps that can be integrated due to memory requirements.

To overcome this limitation, since by construction the TSDFs $f_t$ integrated are bounded to the interval $[-1, 1]$, [22] proposes to sample this interval by evenly spaced bin centres $c_b$ (see Fig. 1) and approximate the previous data fidelity term $\sum _{t=1}^N |u-f_t|_1$ by $\sum _{b=1}^{n_{bins}} h_b |u-c_b|_1$ where $h_b$ is the number of times the interval has been observed. The corresponding energy for the histogram approach is,

$$\begin{aligned} \mathop {\mathrm {arg\,min}}\limits _u \int _\varOmega |\nabla u|_1 + \lambda \int _\varOmega \sum _{b=1}^{n_{bins}} h_b |u-c_b|_1 d\varOmega \end{aligned}$$

(3)

where the centre of the bins are calculated using,

$$\begin{aligned} c_b = \frac{2b}{n_{bins}}-1 \end{aligned}$$

(4)

The voting process in the histogram is depicted in Fig. 1. While this voting scheme significantly reduces the memory requirements, allowing us to integrate an unlimited number of depth maps, the optimisation process carried out in [22] is not optimal. A mathematically optimal solution to this problem can be found in [10] and has been applied to histogram-based voxel grids by [6]. Before presenting this optimised solution in Sect. 5, we must introduce what we call the $\varOmega$ domain.

4 $\varOmega$ Domain

Since we are moving within the voxel grid and only observe a subset of the overall voxels, we need to develop a new technique to prevent the unobserved voxels from negatively affecting the regularisation results of the observed voxels. In order to achieve this, as illustrated in Fig. 2, we define the complete voxel grid domain as $\varLambda$ and use $\varOmega$ to represent the subset of voxels which have been directly observed and which will be regularised. The remaining subset, $\bar{\varOmega }$, represents voxels which have never been observed. By definition, $\varOmega$ and $\bar{\varOmega }$ form a partition of $\varLambda$ and therefore $\varLambda =\varOmega \cup \bar{\varOmega }$ and $\varOmega \cap \bar{\varOmega } =$ Ø. All works explained in the previous section rely on a fully-observed voxel grid before regularisation and they implicitly assume that $\varLambda = \varOmega$. In our mobile robotics platform, this assumption is not valid. The robot motion results in unobserved regions caused by object occlusion, field-of-view limitations, and trajectory decisions. Therefore, $\varOmega \subset \varLambda$ as Fig. 2b illustrates. In this case Eq. 3 turns into,

Fig. 2

Traditional voxel-grid-based reconstructions focus on object-centred applications as depicted in (a). In this scenario, the objects in the voxel grid are fully observed multiple times from a variety of angles. Even though the internal portion of the object has not been observed, previous regularisation techniques do not make a distinction between $\varOmega$ (observed regions) and $\bar{\varOmega }$ (unobserved regions). This results in spurious interpolation inside the object. However, in mobile robotics applications the world environment is traversed and observed during exploration, requiring large voxel grids (b) which result in significant portions never being observed. For example, at camera capture $t_x$, it is unknown what exists in the camera’s upper field of view. Not accounting for $\bar{\varOmega }$ in regularisation results in incorrect surface generation. Our technique defines $\varLambda$ as the voxel grid domain while $\varOmega$ is the subset we have directly observed and which will be regularised

$$\begin{aligned} \mathop {\mathrm {arg\,min}}\limits _u \int _\varLambda |\nabla u|_1 + \lambda \int _\varOmega \sum _{b=1}^{n_{bins}} h_b |u-c_b|_1 d\varOmega \end{aligned}$$

(5)

Note that $\bar{\varOmega }$ voxels lack the data term. As is explained in [3], this regularisation interpolates the content of voxels in $\bar{\varOmega }$. Extrapolation occurs when we have unobserved voxels surrounding an observed region. To avoid this extrapolation, we use the $\varOmega$ domain boundary conditions to constrain regularisation to observed voxels, thus avoiding the indiscriminate surface creation which would occur when naively applying prior techniques.

5 Optimal Regularisation

In this section we describe the steps required to solve Eq. 3 using our $\varOmega$-domain constraint. Notice that both terms in Eq. 3 are convex but not differentiable since they depend on the $L_1$ norm. To solve this, we can use a Proximal Gradient method [3] which requires us to transform one of the terms into a differentiable form. We transform the Total Variation term using the Legendre-Fenchel Transform [15],

$$\begin{aligned} \min _u \int _\varOmega |\nabla {u}|_1 d\varOmega = \min _u \max _{||\mathbf{p}||_\infty \le 1} \int _\varOmega u\nabla \cdot \mathbf{p}d\varOmega \end{aligned}$$

(6)

where $\nabla \cdot \mathbf{p}$ is the divergence of a vector field $\mathbf{p}$ defined by $\nabla \cdot \mathbf{p}= \nabla {p}_x + \nabla {p}_y + \nabla {p}_z$. Applying this transformation to Eq. 3 the original energy minimisation problem turns into a saddle-point (min-max) problem that involves a new dual variable $\mathbf{p}$ and the original primal variable u,

$$\begin{aligned} \min _u \max _{||\mathbf{p}||_\infty \le 1} \int _\varOmega u \nabla \cdot \mathbf{p}+ \lambda \int _\varOmega \sum _{b=1}^{n_{bins}} h_b |u-c_b|_1 d\varOmega \end{aligned}$$

(7)

The solution to this regularisation problem was demonstrated in [6] with a Primal-Dual optimisation algorithm [3] which we briefly summarise in the following steps:

• 1. $\mathbf{p}$, u, and $\bar{u}$ can be initialised to $\mathbf 0$ since the problem is convex and is guaranteed to converge regardless of the initial seed. $\bar{u}$ is a temporary variable used to reduce the number of optimisation iterations required to converge.

• 2. To solve the maximisation, we update the dual variable $\mathbf{p}$,

  $$\begin{aligned} \begin{aligned} \mathbf{p}&= \mathbf{p}+ \sigma \nabla \bar{u} \\ \mathbf{p}&= \frac{\mathbf{p}}{\max (1,||\mathbf{p}||_2)} \end{aligned} \end{aligned}$$

  (8)

  where $\sigma$ is the dual variable gradient-ascent step size.

• 3. For the minimisation problem, the primal variable u is updated by,

  $$\begin{aligned} \begin{aligned} u&= u - \tau \nabla \cdot \mathbf{p}\\ W_i&= -\sum \limits _{j=1}^i h_j + \sum \limits _{j=i+1}^{n_{bins}} h_j ~~~~~~~~~~~~~~~~ i \in [0,n_{bins}] \\ b_i&= u + \tau \lambda W_i \\ u&= \text {median}(c_1, \ldots , c_{n_{bins}}, b_0, \ldots , b_{n_{bins}}) \end{aligned} \end{aligned}$$

  (9)

  where $\tau$ is the gradient-descent step size, $W_i$ is the optimal weight for histogram bin i, and $b_i$ is the regularisation weight for histogram bin i.

• 4. Finally, to converge in fewer iterations, we apply a “relaxation” step,

  $$\begin{aligned} \bar{u} = u + \theta (u - \bar{u}) \end{aligned}$$

  (10)

  where $\theta$ is a parameter to adjust the relaxation step size.

Equations 8, 9, and 10 are computed for each voxel in each iteration of the optimisation loop. Since each voxel’s computation is independent, we implement this as a GPU kernel which operates within the optimisation loop. The final output, u, represents the regularised TSDF distance.

As discussed in Sect. 4, applying regularisation indiscriminately within the voxel grid produces undesirable results. However, no technique to date, up to the authors’ knowledge, provides a method to perform this regularisation within a voxel grid.

Without loss of generality, we describe for the x component—y and z components can be obtained by changing index i for j and k respectively—of the discrete gradient and divergence operations traditionally used to solve Eqs. 8 and 9 [2],

$$\begin{aligned} \nabla _x{u_{i,j,k}} = {\left\{ \begin{array}{ll} u_{i+1,j,k} - u_{i,j,k} &{} \text {if}~ 1 \le i < V_x\\ 0 &{} \text {if}~ i = V_x\\ \end{array}\right. } \end{aligned}$$

(11)

$$\begin{aligned} \nabla _x\cdot {\mathbf{p}_{i,j,k}} = {\left\{ \begin{array}{ll} \mathbf{p}^x_{i,j,k} - \mathbf{p}^x_{i-1,j,k} &{} \text {if}~ 1 < i < V_x\\ \mathbf{p}^x_{i,j,k} &{} \text {if}~ i = 1\\ -\mathbf{p}^x_{i-1,j,k} &{} \text {if}~ i = V_x\\ \end{array}\right. } \end{aligned}$$

(12)

where $V_x$ is the number of voxels in the x dimension.

We extend the traditional gradient and divergence calculations to account for new conditions which remove the $\bar{\varOmega }$ domain from regularisation. These methods can be intuitively thought of as introducing additional boundary conditions in the cube which previously only existed on the edges of the voxel grid. For an input TSDF voxel grid u, the gradient $\nabla {u} = [\nabla _x{u}, \nabla _y{u}, \nabla _z{u}]^T$ is computed by Eq. 11 with the following additional conditions,

$$\begin{aligned} \nabla _x{u_{i,j,k}} = {\left\{ \begin{array}{ll} 0 &{} \text {if}~ u_{i,j,k} \in \bar{\varOmega }\\ 0 &{} \text {if}~ u_{i+1,j,k} \in \bar{\varOmega }\\ \end{array}\right. } \end{aligned}$$

(13)

Note that the regulariser uses the gradient to diffuse information among neighbouring voxels. Our gradient definition therefore excludes $\bar{\varOmega }$ voxels from regularisation.

Finally, in addition to the conditions in Eq. 12, the divergence operator must be defined such that it mirrors the modified gradient operator

$$\begin{aligned} \nabla _x\cdot {\mathbf{p}_{i,j,k}} = {\left\{ \begin{array}{ll} 0 &{} \text {if}~ u_{i,j,k} \in \bar{\varOmega }\\ \mathbf{p}^x_{i,j,k } &{} \text {if}~ u_{i-1,j,k} \in \bar{\varOmega }\\ -\mathbf{p}^x_{i-1,j,k} &{} \text {if}~ u_{i+1,j,k} \in \bar{\varOmega }\\ \end{array}\right. } \end{aligned}$$

(14)

6 Results

To evaluate the performance of our technique, we performed three experiments comparing our BOR$^2$G method to a KinectFusion implementation. The dense reconstructions are executed on a NVIDIA GeForce GTX TITAN graphics card with 2,880 CUDA Cores and 6 GB of device memory.

Fig. 3

Comparison of KinectFusion (left) and BOR$^2$G regularisation (right) methods for a 3D reconstruction of a synthetic [7] environment by fusing noisy depth maps. As input, we use truth depth maps with added Gaussian noise with standard deviation of $\sigma _n = 10$ cm. The Phong shading demonstrates how our regularisation produces consistent surface normals without unnecessarily adding or removing surfaces

As a proof of concept, we first carried out a qualitative analysis of our algorithm on synthetic data (Fig. 3) before performing more robust tests with real-world environments. The synthetic data set provides high-precision depth maps of indoor scenes taken at 30 Hz [7].¹ $^,$ ² Our chosen scene considers both close and far objects observed from the camera with partial occlusions. The input of our 3D reconstruction pipeline is a set of truth depth maps with added Gaussian noise ($\sigma _n = 10$ cm). As can be seen in Fig. 3, where results are represented using Phong shading, there is a significant improvement in surface normals when the scene is regularised with our BOR$^2$G method compare to KinectFusion. A side-benefit of the regularised normals is that the scene can be represented with fewer vertices. We found that our BOR$^2$G scenes required 2–3 times fewer vertices than the same scene processed by KinectFusion.

Table 1 Timing Results of BOR$^2$G regularisation on an NVIDIA GeForce GTX TITAN graphics card

Fig. 4

Woodstock Data Set: Comparison of the KinectFusion (left) and BOR$^2$G (right) dense reconstruction techniques. The KinectFusion has a larger number spurious outlier segments and requires more than twice the number vertices to represent the structure due to its irregular surfaces. The BOR$^2$G method’s median and standard deviation are approximately half that of the KinectFusion method. a Comparison of Point Clouds. The KinectFusion implementation (left) produced a large range of spurious data points when compared to our BOR$^2$G method (right). The white vertices are truth data and the colour vertices correspond to the histogram bins in b. b Histograms of per-vertex-error when compared to laser-generated point clouds. The KinectFusion (left) has a median error of 373 mm ($\sigma = 571$ mm) while our BOR$^2$G (right) method has a median error of 144 mm ($\sigma = 364$ mm). Note that the BOR$^2$G method requires fewer vertices to represent the same scene

Fig. 5

Acland Data Set: Comparison of the KinectFusion (left) and BOR$^2$G (right) dense reconstruction techniques. Note that the laser truth data was only measured depth data for the lower-half of the hallway. This results in the spurious errors for the upper-half where our depth maps produced estimates but for which there was no truth data. These errors dominate the right tail of the histograms in (b). As with the Woodstock data set, the BOR$^2$G method’s median and standard deviation are approximately half that of the KinectFusion method. a Comparison of Point Clouds. The BOR$^2$G (right) method again outperformed the KinectFusion implementation (left). The white vertices are truth data and the colour vertices correspond to the histogram bins in b. b Histograms of per-vertex-error when compared to laser-generated point clouds. The KinectFusion (left) has a median error of 310 mm ($\sigma = 571$ mm) while our BOR$^2$G (right) method had a median error of 151 mm ($\sigma = 354$ mm). Note that the BOR$^2$G method requires fewer vertices to represent the same scene

Table 2 Error analysis comparing KinectFusion and BOR$^2$G methods

To quantitatively analyse our BOR$^2$G method, we conducted two real-world experiments in large-scale environments. Again, we compare BOR$^2$G and KinectFusion fusion pipelines, but we generate our depth maps from a monocular camera using the techniques described in [12]. The first represents the 3D scene reconstruction of an urban outdoor environment in Woodstock, UK. The second is a long, textureless indoor corridor of the University of Oxford’s Acland building. In both experiments, we used a frontal monocular camera covering a field of view of $65^\circ \times 70^\circ$ and with an image resolution of $512 \times 384$.

For ground truth, we generated metrically consistent local 3D swathes from a 2D push-broom laser using a subset of camera-to-world pose estimates $T_{WC} \in \textit{SE}(3)$ in an active time window as,

Fig. 6

The final 3D reconstruction of the large scale experiments using BOR$^2$G with the Acland building (left) and Woodstock, UK (right)

$$ M_L = f(T_{WC} ,T_{\textit{CL}}, \mathbf{x}_L )$$

where f is a function of the total set of collected laser points $\mathbf{x}_L$ in the same time interval and $T_{\textit{CL}}$ is the extrinsic calibration between camera and laser. The resulting 3D point cloud $M_L$ is used as ground truth for our large scale assessment.

Table 1 summarises the dimensions of the volume used for each of the experiments, the number of primal dual iterations, and the total running time required for our fusion approach. The execution time for regularisation is highly correlated to the size of the $\varOmega$ space because regularisation is only performed on voxels within $\varOmega$. Figures 4 and 5 show a comparison between the ground truth and the 3D reconstructions obtained using the BOR$^2$G and the KinectFusion methods. To calculate our statistics, we perform a “point-cloud-to-model” registration of the ground truth with respect to our model estimate.³ The key statistics comparing the methods are precisely outlined in Table 2. For both scenarios, our BOR$^2$G method was roughly two times more accurate than KinectFusion. Finally, Fig. 6 shows the obtained continuous, dense reconstructions of the indoor and outdoor environments.

7 Conclusions

In this paper we presented a new approach to reconstruct large-scale scenes in 3D with a moving monocular camera. Unlike other approaches, we do not restrict ourselves to object-centred applications or rely upon active sensors. Instead, we fuse a set of consecutive mono-generated depth maps into a voxel grid and apply our $\varOmega$-domain boundary conditions to limit our regularisation to the subset of observed voxels within the voxel grid.

Our BOR$^2$G method results in a median and standard deviation error that is roughly half that produced when using the same depth maps with the KinectFusion method.

In the future, we plan to use the $\varOmega$-domain principles to apply new boundary conditions which select portions of the voxel grid for regularisation. These subsets will be selected based on scene-segmentation heuristics. For example, we can extend the $\varOmega$ domain to include enclosed “holes” which will result in the regulariser interpolating a new surface. Alternatively, we could remove a segment from $\varOmega$ to prevent regularisation of a scene segment which was better estimated in the depth map (e.g., high-texture object).