Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

One of the simplest ways to characterize the animal kingdom is to consider the typically animal ability of voluntarily moving [31, 38]. Animals move in the world to survive, feed, mate, adapt to the environment and adapt the environment to their needs—basically, for everything they do. Mammals, in particular, move and act by activating their muscles, which are an extremely smart product of evolution. Actually, from the point of view of the modern engineer, a muscle is an incredibly energy-efficient, light and versatile actuator.

Such a marvelous set of actuators requires an equally marvelous control system, which however does not resemble much any standard control system as found in Control Theory or on modern robots. Each muscle is in fact composed of up to thousands smaller actuators called Motor Units (MUs), each one producing contractile force on a joint, each one in principle independently controlled [34, 39]; precisely this redundancy, coupled with a smart recruitment mechanism, enables mammals achieve their spectacular performances while running, climbing, swimming, nurturing their offspring, mating, etc. In fact, essentially every action involves most, if not all, the MUs in a certain musculoskeletal region. It therefore seems that MUs are always controlled in large batches altogether at the same time, in a coordinated fashion. Since the total number of MUs in the musculoskeletal system is too large to be directly consciously controlled MU by MU [3], a simplifying paradigm is needed.

In parallel to the concept of kinematic synergies widely discussed in the first part of this book, starting from 1998, the idea of muscle synergies as a solution to this problem was introduced [4, 14–16, 53, 54]. Muscle synergies, as traditionally defined, are basic coordinated muscle activations that can be extracted using, e.g., Principal Component Analysis (PCA) from kinematic or sEMG data. The strong compression factors uniformly obtained by PCA on data gathered from human subjects while performing large sets of everyday-living tasks seem to indicate that only a few synergies (three or four) are required to perform most such actions (see the discussion carried out elsewhere in this book, e.g., in Chaps. 2–4, 6, 8 and 15). The situation becomes less clear when training is involved, for instance when a subject learns to play the piano (see, e.g., [58]). When additional motion finesse is required, it is likely that more and more synergies must consciously be controlled. It is quite possible, anyway, that this paradigm works as a general control schema for the mammalian motion: maybe grabbing a pen, caressing one’s partner, playing the piano, breaking an egg, carrying a 50 kg. weight, all these actions are performed via muscle synergies control [25]. But dealing with this problem is not in the scope of this chapter, and as well, different definitions of this concept exist [16, 32, 52]; in fact, we hereby adopt the simplest possible definition of a muscle synergy: a coordinated, task-directed activation of a set of MUs. In this sense, any voluntary action, for instance the act of flexing one’s index finger to a determined amount of the maximum voluntary contraction, corresponds to a specific synergy.

Now, any specific synergy corresponds to a signal pattern that can be detected by employing an adequate array of sensors and a signal processing system—what we call the Human-Machine Interface or HMI. Such an HMI is the ideal basis of modern, dexterous prosthetic control. A prosthesis is needed whenever a person has lost a limb, be it due to a traumatic event, planned surgery or congenital deficiency; the loss of a limb leads to a severe degradation of the quality of life [37, 44], therefore it is very desirable to restore the lost body functions to the best extent allowed for by the technology. The main idea is that of employing the HMI to let the amputee directly control a robotic prosthesis in the most natural way, that is, “by desiring so” [19, 28]. Our main object of study is, in particular, hand prostheses, given that the human hand is one of the most wonderful tools ever evolved by Nature, and the loss of a hand is a very disabling condition in the modern world.

In Chap. 10, an approach based on minimalistic sEMG mapping has been introduced, showing how such a strategy can be successfully exploited to control the robotic hand described in Chap. 8, under-actuated according to the concept of adaptive synergies. On the other hand, to deal with artificial hands with many DOFs and DOAs, machine learning techniques have been developed and academically tested in hundreds; still, at the time of writing they are essentially not used in the clinics,Footnote 1 the main problem being the unreliability of the HMI [5, 8, 18, 19, 44]. In this case “unreliable” means that the control signals generated by the HMI are not stable with respect to the user’s intent or, equivalently, that the patterns to be recognized are too diverse or change in time. All in all, the prosthetic control system needs to be improved.

We deem necessary a paradigm shift here. In particular, with the advent of multi-fingered hand prostheses, complete arm/hand prosthetic systems and advanced surgery methods such as Targeted Muscle Reinnervation [2, 30, 55], the standard prosthetic control does not suffice any more. Among the several advancements called for by the community [26], we push the incrementality of the control system [20, 57]. Incrementality of a machine learning system is the possibility of updating the model obtained so far whenever required, without recalibrating, without loosing previous information and without waiting for the calibration time; in the context of using a prosthesis, this concept directly leads to interaction between the human subject and the system. We believe that the chance that the subject continually teaches the system new patterns as they arise in real life is paramount to improve the reliability of the prosthetic artifact.

The rest of this chapter is a series of recommendations and ideas on how to pursue this goal. In particular, Sect. 11.2 sets the background, describing the current flaws and limitations of natural prosthetic control and stating a list of requirements for the new kind of control system we are advocating; in Sect. 11.3 we describe our own solution to the problem and show a couple successful applications of a system based upon the ideas described; and lastly Sects. 11.4 and 11.5 contain final remarks.

2 Background

Current prosthetic control systems are in the vast majority based upon machine learning applied to patterns of synergistic muscle activations voluntarily generated by the user. We hereby argue that a specific characteristic of the control system that has been so far neglected might represent a solution to the notorious problem of the unreliability of such kinds of human-machine interfaces, namely incrementality.

2.1 Muscle Activations in Prosthetic Control

Let us concentrate on voluntary muscle activations, that is, movements enacted by a precise, conscious, coordinated muscle contraction—as two typical examples, let us consider playing a C-major chord on a piano, and carrying an egg from A to B in one’s kitchen, for example to prepare an omelet. Each action requires an extremely fine control of the activation of thousands of motor units in the hand, forearm, upper arm and even, in the case of carrying the egg around, of the whole body. Given the right level of granularity of an action (more on this point will be said later on), one can mathematically say that the intent of performing an action generates a dynamic pattern of muscle activation, \(\mathbf {a}(t)\), where the vector \(\mathbf {a}\) denotes the activation level of each motor unit involved in the action. Without loss of generality one can think of \(\mathbf {a}\) being expressed in normalized coordinates, for instance as a fraction of the maximum possible activation of each motor unit; in this case \(\mathbf {a}(t) \in \mathbb {R}^M\) where M is the number of motor units involved. In the above example of the C-major chord, and considering the hand and wrist only, simultaneous activation of the wrist, thumb, middle finger and little finger is required to hit the C, E and G keys at the same time, using the right amount of force to produce the desired volumeFootnote 2; this would correspond to, say, \(\mathbf {a}_1(t)\). In the second example, at least the thumb and index finger (and usually much more) must be activated, again, simultaneously and to the right amount in order to pick up the egg, and carry it without letting it slip and without crushing it. We could denote this action as \(\mathbf {a}_2(t)\). And so on, for each required action.

Notice that an exceptionally fine control over \(\mathbf {a}\) is required along time. The value of \(\mathbf {a}\) must remain as stable as possible in time, notwithstanding any disturbance, external and/or internal to the body. Such disturbances are quintessentially unavoidable, as they include, e.g., other movements required at the same time; for instance, playing a bass line with the other hand on the piano, or walking while carrying the egg. Clearly—and this is the problem of granularity of an action, mentioned above—there is a particular range of values within which \(\mathbf {a}\) must remain in order to achieve the desired goal; for instance, the egg-carrying action can be stably performed across an interval of time \(\varDelta t\) only as long as \(\mathbf {a}_2^{min} < \mathbf {a}_2(t) < \mathbf {a}_2^{max}\) for all \(t \in \varDelta t\). This directly leads to the definition of a muscle activation pattern, which enforces the desired action. From the point of view of the engineer, such a pattern can be represented, in the simplest instance, by the average of the values obtained while the subject repeats the action over and over again: \(\overline{\mathbf {a}_2}\). (More complex representations can include, for instance, a probabilistic description of the distribution of the signal obtained across these repetitions.) Such a pattern is a time-abstracted simultaneous muscle activation, which matches our previous definition of a muscle synergy, precisely the synergy that enables the subject carry the egg in a stable way. Such synergies are also the patterns that a machine-learning based prosthetic control system will try to recognize: as long as the subject keeps her/his activation levels close to that pattern (given a certain distance metric—see also the concept of good variance vs. bad variance in the synergy definition given in [32]), the system will issue the right commands to the prosthesis and enforce stable grasping.

On the other hand, failure by the subject to maintain the synergistic MU activations “close enough” to the reference pattern \(\overline{\mathbf {a}_2}\), or more likely, failure by the system to effectively recognize that pattern, will result in the egg being dropped or crushed; in general, the inability of reliably recognizing a pattern \(\overline{\mathbf {a}_i}\) will lead to unstable grasping of type i, which can have dramatic consequences. Intact human subjects employ a wide array of sensors to close the loop over the MU activations, but this feedback stream of information is precisely what an amputated subject lacks. It is then no wonder that the biggest cause of abandonment of upper-limb prostheses is their unreliability, that is, the inability of the control system to correctly, stably detect the intent of the patient [5, 8, 18].

2.2 Unreliability

Since the 1950s sEMG (surface Electro-Myography), originally a muscle disorder diagnosis technique, has been used to enforce muscle-activation-based control of one-DOF hand prostheses [44]: traditionally, two sites of large residual activity (see also Chap. 10) would be identified on the patient’s stump, usually corresponding to flexion and extension of the wrist; these two sites would be used to determine the speed of opening and closing the prosthesis. With the advancement of prosthetic technology, more sophisticated arrangements of sEMG electrodes have been used (with higher sensitivity, better noise-rejection properties and/or higher spatial resolution) and novel kinds of signals have been explored as potential replacements/augmentations of sEMG. Among these, tactile [47] and pressure sensors [50, 61] detecting the stump surface deformation corresponding to muscle activations; ultrasound imaging [22, 57] detecting the displacement of the remnant anatomical structures in the stump; strain sensors to detect the same kind of deformations; and computer vision [33] to aid the prosthetic control by putting prior information on the decision regarding the action to be performed. Moreover, sophisticated statistical methods belonging to the class of machine learning (ML, also denoted as “pattern matching” or “pattern recognition” in the rehabilitation community) algorithms have been applied to these signals.

In general, once an educated guess has been made about a certain type of bodily signals (sEMG, ultrasound, etc.) to be meaningful of the underlying muscle activity, a ML method works as follows: given a set of pairs \(S = \{(\mathbf {x}_i,y_i)\}\) in which \(\mathbf {x}_i\) is a sample of the signal, and \(y_i\) is an integer (a “label”) abstractly denoting a required action, or a real position/force value directly denoting the required control signals for the DOFs of a prosthesis, a map between signals and actions will be created via some kind of statistical approximation: \(y = f(\mathbf {x})\). The approximant f is usually found by minimization of a cost functional, which makes the operation computationally costly (as is the case, e.g., of Support Vector Machines [6, 56, 59]) and/or unsafe due to the presence of local minima (as with artificial neural networks). Anyway, in the machine-learning lingo, S is called training set, since it is the data set used to “train” the machine to recognize a certain set of patterns in the input signal; similarly, the creation of the map f using S, which an engineer would call “calibration”, is called in this case training phase, as opposed to the prediction phase in which f is actually used to guess y from the signal \(\mathbf {x}\).Footnote 3

Now, the quality of the obtained control function f strictly depends on the “quality” of S (in machine learning, in general, apart from the choice of the basic functions used to compose f, e.g., linear or not, there is little more than S to determine what f looks like); in turn, how to define the quality of a training set is a matter of debate. If the map f, which represents the prosthetic control system, is supposed to stably and reliably recognize a set of patterns (muscle synergies) \(P_i, i=1,\ldots ,N\) corresponding to the required actions \(\overline{\mathbf {a}_i}\), then those patterns

  1. 1.

    must appear in S correctly associated to the required output values;

  2. 2.

    must be repeatable; and

  3. 3.

    they must be stable.

Item (1) is not problematic; as opposed to this, items (2) and (3) can be, and usually are. The gathering of the training set can be long and psychologically challenging for the subject, mainly since (s)he has no control on what (s)he is doing, due to the above-mentioned lack of sensory feedback (this issue is also tackled in Chap. 10). A pattern \(\overline{\mathbf {a}_i}\) can be very different from a pattern \(\overline{\mathbf {a}_i'}\) gathered at some later point in time but representing the same desired action i, due to a number of competing factors such as, e.g., electrical external disturbances; slightly different muscle activations leading to very similar actions; muscular fatigue and sweat, which are well known to significantly alter the sEMG signal [34, 35]; and so on. On top of that, one must notice that in order to guarantee stability of prosthetic control, a pattern \(\overline{\mathbf {a}}\) contained in the training set must represent the corresponding action in all possible conditions subsequently encountered by the subject. This includes all musculoskeletal configurations requiring a different activation for the same action, such as, e.g., all possible weights one might want to carry, all possible pronation/supination configurations of the wrist, all possible activation artifacts due to walking, etc. Often, a prosthetic control system, which was properly trained in the beginning will miserably fail later on, because the subject is standing instead of sitting, or because she is carrying a one-kilogram bottle of water, which was the very purpose of grasping it! (See, e.g., [9] for a study in slightly less lab-controlled conditions.)

To make the situation worse, most ML methods enforce what we call “monolithic learning”: S is gathered at the beginning of the experiment, then f is created (training/calibration), then the prediction starts; there is no chance of updating f once the prediction has begun, unless one stops the prediction, updates S to some new (larger) training set and trains anew. This is unacceptable since S is potentially unlimited in size; as well, particularly whenever it is required that f be non-linear (as is mostly the case in hand prosthetics) training takes a long time and depends on the size of S. This entails that the pattern \(\overline{\mathbf {a}}\) must be gathered correctly once and for all during the training phase.

In other words, the quality of the control strictly depends on S, and S must be gathered optimally since the start. As one might guess, this is an essentially impossible task. We claim that it is mainly for this reason that ML-based prosthetic control is still unreliable nowadays, after 80 years of research, and it is essentially not yet used in the clinics.

2.3 Building a More Detailed Model or Learning More?

Let us call the space of all signals that the prosthetic hardware can gather, the input space I. In practice, only a “useful” subset \(I_U \subseteq I\) is what we are interested in; actually, the task outlined above boils down to building a sensible f restricted to \(I_U\). \(I_U\) can be either defined by the tasks to be correctly carried out, for instance power grasp, pinch grip and stretched hand, or by the prosthetic hand at our disposal, say that we want to control each single motor of the prosthesis. As previously mentioned, this latter idea offers a different perspective to the synergy-inspired simplification strategy discussed in Chaps. 8, 10 and 13. It represents the starting point of the research of the author of the current chapter, see [20] for instance, and stems from the idea of simultaneous and proportional control [27]. Anyway, f should always work correctly on \(I_U\), where “correctly” is defined by the three items in the previous subsection, and may ignore what is outside it. Since S is all we have at our disposal to properly build f, it follows that S must somehow contain \(I_U\), or at least a relevant fraction of it, given the generalization power of f.

Now, if \(I_U\) is too badly structured, or simply too vast to be captured by S, no proper f can be built, and there are two possibilities at hand to improve the situation: either we try and map \(I_U\) onto the space “captured” by S, or we expand S itself.

The first option means that one must have a model of the physical process being approximated via f. A remarkable example of such an attempt is the psycho-physical modeling of muscular fatigue and its effect on the sEMG signal (see, e.g., [36]) which has lead to several systems in which fatigue is detected (e.g., [1]) and somehow “corrected”. We see this as an instance of the first possibility above: given a desired action \(\overline{\mathbf {a}}\), \(I_U\) contains necessarily all of its instances under fatigue, say \(\overline{\mathbf {a}'}\), \(\overline{\mathbf {a}''}\), etc. Since it is impossible to gather an example of each of these instances in S, some kind of preprocessing \(\mathcal {P}\) is applied to I, with the hope that it will project all fatigue-ridden instances \(\overline{\mathbf {a}'},\overline{\mathbf {a}''}\) and so on, onto \(\overline{\mathbf {a}}\) itself. In set-theoretic terms, the operator \(\mathcal {P}\) projects \(I_U\) back onto \(I_U'\), where \(I_U'\) is the reduced portion of \(I_U\), which has originally been captured by S.

Our opinion is that the results achieved by such methods are in practice never guaranteed to make the control system really reliable. The size and extent of the useful input space \(I_U\) is essentially unpredictable, and one is never guaranteed that \(\mathcal {P}\), which must be evaluated a priori, will correctly project the entire \(I_U\) onto \(I_U'\). A model always necessarily represents a limited view of the world, and especially in the case of a prosthesis, in principle actively worn twelve hours a day, the number of situations in which \(\mathcal {P}\) will fail to reduce \(I_U\) to what f already knows is fundamentally unlimited. Think of the action required to carry the egg, namely a precision grip, but performed while the subject is running, doing something else with the other arm or lifting the arm to place the object of interest in a cupboard. Compressing all this information in \(I_U'\) would entail having at our disposal a complete dynamic model of the musculoskeletal system. This is very likely unfeasible.

The second possibility, and in our opinion the only one left, is that of “learning more”, that is, that of expanding S until it induces a useful subset \(I_U'\), which virtually coincides with \(I_U\), that is, it contains all possible instances of each action of interest. This method seems at first as unfeasible as the previous one, for at least two reasons:

  1. 1.

    the size of S is now extremely large—in principle unlimited;

  2. 2.

    again, the initial gathering of S must take into account all possible future situations.

Item 1 can only be solved by using an approach that is bounded in space and time, that is, whose time and space complexity do not depend on the number of samples in S. To solve Item 2 one possibility is that of gathering S piecewise, “on-demand”, only whenever a new situation arises. We propose that incremental learning represents a solution to both problems, having the potential to radically advance the state of the art in prosthetic control.

2.4 Incremental/Interactive Learning

Before we move on to describe our own solution to this problem, that is a working incremental/interactive learning system for hand prosthetics (Sect. 11.3), let us try and enumerate a few characteristics such a system must enjoy. By incremental learning it is hereby meant an adaptive system able to update its own model whenever required. That the system must be adaptive stems from the observations of the previous subsection. In particular we speculate that

  • the range of possible situations in which the control system must be able to reliably work is too large for a monolithic system;

  • a full model of the human arm/hand musculoskeletal system would be too complex to be of any practical usefulness, and anyway unfeasible for miniaturization on a prosthetic device.

Requirement #1 The system must be adaptive. It must be possible to calibrate it specifically for each subject. In other words, it must be possible to build a specific model for each subject.

We believe that machine learning is the way ahead. Potentially, each subject needs a different f to be tailored (“calibrated”, “trained”) for her/him; in particular this is the case, in the literature found so far, for amputees, who present an extremely wide range of stumps and remnant muscle structures to the outside world [8]. As the calibration in this case is represented by the gathering of the training set S, we also require that

Requirement #2 The system must be quickly calibrated. In this case “quickly” means, fast enough not to distract the subject from the task (s)he is performing, without imposing too high a cognitive burden, and without forcing her/him into a potentially distressing or dangerous activity.

Moreover, to take into account the potentially endless range of different situations the subject might want to have the system work correctly, and since no machine can feasibly stand an endless flow of data, we require that

Requirement #3 The system must be bounded in space and time. The model generated by the system must be independent from the size of the training set S and, in general, it must not depend on the time it has been active.

Lastly, whenever a new situation “worth learning” appears, we need the system to be able to update its own model, maintaining the three requirements above. This is our own definition of incrementality:

Requirement #4 The system must be incremental. The model generated by the system must be updatable on-the-fly, whenever required, whenever new information is available and whenever the subject deems that the prediction is no longer reliable (for instance, due to muscular fatigue).

Notice that this last requirement entails the ability to both “correct” previously learned patterns, which change their appearance in time (e.g., because of muscle fatigue), and to learn new patterns the subject deems interesting and that the system has never seen before. Actually, the two cases are completely equivalent from the machine learning point of view, given that the right target values are assigned to each new pattern—old ones in the case of pre-existing patterns found in a new situation, and brand new ones in the case of totally new patterns.

A system which enforced all four requirements above would constitute a new way of coupling a human subject and a complex robotic artifact. Adequate speed and easiness of calibration, united with accuracy of the prediction (a requirement that we assume as already present and do not even list above, of course) and incrementality, leads to the possibility for the subject to stop the prediction whenever required; correct the system’s mistakes or show it a new pattern to be learned; and then go back to prediction.

3 A Practical Method of Incremental Learning

In this section a natural prosthetic control system is described, fulfilling the four requirements set out in Sect. 11.2. The system we describe enforces regression rather than classification, yielding in general approximated values for the activations of each DOF of a prosthesis instead of a label denoting a predefined action. Notice the difference between the two approaches: whereas classification is essentially a decision system, imposing artificial hard boundaries on regions of the input space, regression outputs values in real-valued range, enabling control over an infinite manifold of configurations (of positions, forces and so on).

In each of the following subsections the system is introduced in successive steps. Firstly a simple, monolithic linear method, then its non-linear extension and then its incremental variant. Lastly, a few optimizations are introduced, which improve its practical usability.

3.1 Monolithic Learning in the Linear Case

Machine learning is essentially about building a function approximation starting from a training set S (supervised, non-parametric learning). From this point of view, one of the simplest ML approaches is represented by Least-Squares Regression, which we employ in the regularized form called Ridge Regression (RR from now on, [24]). Given a training set of N (sample, target) pairs, \(S = \{ (\mathbf {x}_i,y_i) \}_{i=1}^N\), RR builds a linear approximation \(\hat{y}_i = \mathbf {w}^T \mathbf {x}_i\) in a numerically stable way, such as to minimize the Mean-Squared Error between \(\hat{y}_i\) and \(y_i\), for all pairs in S. We hereby assume that the input space be represented by d-dimensional feature vectors somehow extracted from the (possibly preprocessed) signals, \(\mathbf {x}\in \mathbb {R}^d\) (this implies that \(\mathbf {w}\in \mathbb {R}^d\), too). We also assume that \(y \in \mathbb {R}\). Notice that this does not restrict the possibility of having many RR machines in parallel, each one yielding a value for a DOF of the prosthesis.

Let X be a matrix representing S, that is, \(X \in \mathbb {R}^{N \times d}\) is the ordered juxtaposition of all signal samples collected so far; similarly, the vector \(\mathbf {y}\in \mathbb {R}^N\) orderly collects all target values. Then the RR model \(\mathbf {w}\) is given by

$$\begin{aligned} \mathbf {w}= (X^T X + \lambda I)^{-1} X^T \mathbf {y}\end{aligned}$$
(11.1)

where I is the identity matrix of order d and \(\lambda > 0\).

RR is a good candidate as a monolithic learning approach, whenever it can be safely assumed that there exists a linear relationship between the samples and the target values. Notice that both the time and space complexity of RR, in turn \(O(d^3+{ {Nd}}^2)\) and \(O(d^2+{ {Nd}})\), depend on the size of the training set N—this is clearly the case since the matrix X must be stored somewhere and used, e.g., to evaluate \(X^T X\). However, this dependency is only linear; the dominating terms, \(d^3\) and \(d^2\), only depend on the dimension of the input space. For instance the \(d^3\) time complexity is due to the matrix inversion in the expression of \(\mathbf {w}\)—but the matrix to be inverted, \((X^T X + \lambda I)\), is only \(d \times d\).

Simple as it is, and limited to the linear case, RR already fulfills Requirement #1 (adaptivity) and partially fulfills Requirement #2 (fast calibration) in the case N is not exceedingly large, since it only depends linearly on it. As opposed to that, it does not not fulfill Requirement #3 (boundedness). Lastly, notice that the model \(\mathbf {w}\) is calculated directly from S (that is from X and \(\mathbf {y}\)) without the need of minimizing a cost functional—actually, the minimum of the regularized Mean-Squared Error cost functional

$$ \text{ arg } \min _\mathbf {w}\sum _{i=1}^N (y_i - \mathbf {w}^T \mathbf {x}_i)^2 $$

is found exactly for the above-mentioned value of \(\mathbf {w}\). Being able to directly evaluate \(\mathbf {w}\) has the non-negligible advantage of getting rid of local minima, guaranteeing that \(\mathbf {w}\) is consistently the optimal model (in the sense of the MSE) given the assumption of linearity and the training set S.

3.2 Extension to the Non-linear Case

In case the assumption of linearity must be lifted, the simplest way of extending RR is that of employing a linear combination of non-linear basis functions to build the approximant f, in other words \(\hat{y}_i = \mathbf {w}^T \phi (\mathbf {x}_i)\). This is essentially a variant of the kernel trick. One very convenient method to build such a theoretically solid extension is given by Random Fourier Features (RFFs, [48, 49]). As opposed to other, more popular and established kernel methods such as, e.g., Support Vector Machines [6, 56], using RFFs one is able to directly compute the mapping \(\phi \), whereas in most kernel-based approaches only the product of two applications of \(\phi \), that is \(k(x,y) = \phi (x)\phi (y)\) can be evaluated. This is a direct consequence of the fact that RFFs represent a finite-dimensional approximation to the Gaussian kernel. The number of RFFs, \(D>0\), which must be decided a priori, controls the accuracy of this approximation and, not incidentally, dominates the computational complexity of RFFs when applied to RR. In the standard case, as D grows the prediction becomes more accurate but the computational requirement grows, too—one must find a trade-off.

Another way to describe RFFs is that they represent a non-linear extension to RR, which can be “plugged into” it. We now give an informal description of the approach, suggesting that the reader interested in the mathematical details should consult the seminal papers [48, 49] as well as [20, 21] for some applications. Here, suffice it to say that according to Bochner’s Theorem (plus some inessential assumptions), any shift-invariant kernel is the expected value of the inner product of two applications of \(\phi _{\varvec{\omega }}\),

$$ k(\mathbf {x},\mathbf {y}) = \mathbb {E}[\phi _{\varvec{\omega }}(\mathbf {x})\phi _{\varvec{\omega }}(\mathbf {y})] \approx \phi _{\varvec{\omega }}(\mathbf {x})\phi _{\varvec{\omega }}(\mathbf {y}) $$

where \({\varvec{\omega }}\), a d-dimensional vector of real numbers, is drawn randomly from a probability distribution corresponding to the kernel being approximated. Intuitively, this means that any kernel can be approximated by a sort-of finite Fourier expansion of its own probability distribution; in the case of the Gaussian kernel, \(k(\mathbf {x},\mathbf {y}) = e^{-\gamma ||\mathbf {x}-\mathbf {y}||^2}\) where \(\gamma >0\), \({\varvec{\omega }}\) can be simply drawn from a normal distribution with zero mean value and covariance \(2\gamma I\), getting to a closed-form expression for \(\phi _{\varvec{\omega }}\),

$$ \phi _{\varvec{\omega }}(\mathbf {x}) = \sqrt{2} \cos ({\varvec{\omega }}^T \mathbf {x}+ \beta ) $$

(additionally, \(\beta \) is drawn from a uniform distribution in \([0,2\pi ]\).) This particular \(\phi _{\varvec{\omega }}\) maps an input vector \(\mathbf {x}\) to a real number, associated to a particular \({\varvec{\omega }}\); it is however standard to create D vectors \({\varvec{\omega }}_i\) rather than just one, in order to reduce the variance associated with a random distribution. In the end (dropping the \({\varvec{\omega }}\) subscript to simplify the notation), the RFF approach works by non-linearly mapping each and every input sample \(\mathbf {x}\in \mathbb {R}^d\) into a D-dimensional vector:

$$ \phi (\mathbf {x}) = \frac{1}{\sqrt{D}} [ \cos ({\varvec{\omega }}_1^T \mathbf {x}+ \beta _1)~\ldots ~\cos ({\varvec{\omega }}_D^T \mathbf {x}+ \beta _D)]^T $$

The operator \(\phi \) induces a D-dimensional space called feature space by projecting \(\mathbf {x}\) onto a manifold of \(\mathbb {R}^D\), namely the surface of the \(\frac{1}{D}\)-radius D-dimensional hypersphere. This particular mapping is guaranteed by Bochner’s theorem to converge to the Gaussian kernel approach as D grows.

Given then \(\phi \), as is standard in kernel-based methods, we hope to be able to linearly solve the originally non-linear problem by pushing all the linear machinery (RR in our case) in the feature space. In order to compute the model \(\mathbf {w}\), which is now D-dimensional, one simply plugs \(\phi \) back into Eq. 11.1, obtaining

$$ \mathbf {w}= (\phi (X)^T \phi (X) + \lambda I)^{-1} \phi (X)^T \mathbf {y}$$

where, with a slight abuse of notation, we denote by \(\phi (X)\) the application of \(\phi \) to each row of X; therefore, \(\phi (X) \in \mathbb {R}^{N \times D}\). This method has several useful properties:

  1. 1.

    it only involves drawing the \({\varvec{\omega }}\)s and \(\beta \)s from two random distributions, once and for all at the beginning. Given a reasonably large value of D, all “runs” of the approach will yield comparable results;

  2. 2.

    its time and space complexities are \(O(D^3+{ {ND}}^2)\) and \(O(D^2+{ {ND}})\) analogously to the linear case; that means that the additional computational burden with respect to RR only depends on the choice of D;

  3. 3.

    as a consequence, the grid search necessary to tune the two additional hyperparameters D and \(\gamma \) is in practice very fast; usually D is set at a “reasonable” value around 500, or anyway to the maximum value that can be afforded, given the computational constraints.

RFFs, coupled with RR, represent a cheap and surprisingly simple non-linear approximant; the computational machinery required is limited to algebraic matrix manipulation plus matrix inversion, provided that in the beginning the \({\varvec{\omega }}_i,\beta _i\) are generated.

3.3 Incrementality

The naive way of making such a method incremental is, of course, to store S and add to it every new (sample, target) pair that is gathered. This is clearly unacceptable since in the long run S will make any finite memory bank overflow, let alone the computational burden required to evaluate \(\mathbf {w}\) every time, a task which depends on N. An alternative approach is that of limiting the size of S, keeping it fixed at some predetermined value \(N_{max}\) entailing a computationally bearable evaluation of \(\mathbf {w}\); this idea has been explored, e.g., in [17, 29, 40]. In our case, a very convenient solution is that of considering the arrival of a new (sample, target) pair as a perturbation to the inverse matrix \((X^T X + \lambda I)^{-1}\). Using a rank-1 update method directly on it, the explicit inversion can be avoided. In practical terms, it is convenient to redefine Eq. 11.1 as the product of a matrix A and a vector \(\mathbf {b}\):

$$\begin{aligned} \mathbf {w}= (X^T X + \lambda I)^{-1} X^T \mathbf {y}:= A\mathbf {b}\end{aligned}$$
(11.2)

where A is \((X^T X + \lambda I)^{-1}\) and \(\mathbf {b}\) is \(X^T \mathbf {y}\)—notice that A already is the inverse of a matrix. Given a new (sample, target) pair \((\mathbf {x}',y')\), the updated model \(\mathbf {w}' = A'\mathbf {b}'\) is given by applying the Sherman-Morrison formula [23]:

$$ A' = A - \frac{A\mathbf {x}'\mathbf {x}'^TA^T}{1+\mathbf {x}'^TA\mathbf {x}'} ~~ \text{ and } ~~ \mathbf {b}' = \mathbf {b}+ \mathbf {x}' y' $$

In practice, one starts by setting \(A = \frac{1}{\lambda } I\) and \(\mathbf {b}= 0\), so that \(\mathbf {w}= 0\); as new \((\mathbf {x}',y')\) pairs arrive, the updated model \(\mathbf {w}'\) is built. It is easy to prove that the model \(\mathbf {w}\) obtained after, say, N such steps is exactly the same that would have been calculated one-shot, having at our disposal the whole training set S containing N (sample, target) pairs. Notice that, as no explicit matrix inversion is required by the above formula, the computational complexity of the update step is only \(O(d^2)\) both in time and space. As a matter of fact, in this case X and \(\mathbf {y}\) need not be explicitly stored anywhere: as soon as \(\mathbf {w}'\) has been evaluated, there is no further need of keeping \((\mathbf {x}',y')\). The Sherman-Morrison formula gives us an effective tool to perform RR incrementally (iRR), without any danger of exhausting the computational resources of the control system.

As a last step, consider the application of RFFs to iRR. Again, the non-linear mapping operator \(\phi \) can be simply applied to \(\mathbf {x}\) wherever it appears in the Sherman-Morrison formula, finally yielding

$$ A' = A - \frac{A{\varvec{\phi }}'{\varvec{\phi }}'^TA^T}{1+{\varvec{\phi }}'^TA{\varvec{\phi }}'} ~~ \text{ and } ~~ \mathbf {b}' = \mathbf {b}+ {\varvec{\phi }}' y' $$

where we denote by \({\varvec{\phi }}'\) the application \(\phi (\mathbf {x}')\) in order to keep the notation light. Again, one can start by setting \(A = \frac{1}{\lambda } I\) (this time I is the identity matrix of order D rather than d) and \(\mathbf {b}= 0\). As one can easily guess, the computational complexity of the model update step is, in this case, \(O(D^2)\) both in time and space.

3.4 Obtaining Ground Truth

Joining RFFs to iRR (call the new approach iRR-RFF) as described in the previous subsection constitutes a practical tool for natural prosthetic control, in the sense outlined by the four Requirements of Sect. 11.2. A detailed summary of this match is given at the end of this section. Before that, as a last remark, let us notice two further factors that potentially limit its applicability, in particular to amputated subjects:

  1. 1.

    amputated subjects cannot operate any position/force sensor, therefore the experimenter has the problem of gathering sensible ground truth, i.e., the target values \(\mathbf {y}\) in S. One partial solution is that of having them use the remaining limb in a bilateral fashion [10, 41], but one is never sure how much the two limbs match each other—bottom line, not even the amputee is!

  2. 2.

    In general, an amputation deprives the subject of sensory feedback (including visual feedback); as a consequence of this, amputated subjects are usually unable to perform finely graded tasks. The experimenter cannot sensibly expect, e.g., that an amputee imagines flexing the middle finger with 50 % of the maximum voluntary contraction.

Additionally, the initial data gathering phase can be tiresome and stressful for the subject—it must be kept as short as possible. To counter these problems, a couple simple strategies can easily be put into place.

Firstly, the usage of goal-directed stimuli in order to have the subject generate sensible ground truth for the system. In practice, rather than relying on data sampled from sensors, the experimenter puts the subject in a maximally comfortable situation and then asks for a specific voluntary muscle contraction. It can either be the activation of a single DOF of the prosthesis, such as, e.g., flexing the index finger or the wrist, as well as enacting a specific type of grasp (power, cylindrical, precision grip, etc.). In order to foster the production of a sensible input signal, a visual stimulus can be presented to the subject, such as a 3D-generated model of the missing limb assuming the required posture; or, the experimenter can vocally instruct the subject while showing the required posture with her/his own limb; or even, the stimulus can be delegated to the prosthesis itself, which can be commanded a specific movement to be imitated by the subject. In some cases, even looking at some graphical representation of the input signal itself (for instance, a radial graph showing the voltages recorded be the sEMG electrodes) can help. As already remarked, there is no assurance that the subject will be doing what (s)he is required to do; not even the subject her/himself can be sure of that. The hope is that the input signal, possibly when stable, faithfully represents the intent of the subject.

Secondly, coherently with the reduction-oriented approach suggested by the notion of synergies as widely discussed throughout the book, it is convenient to only gather minimal and maximal activations and then let the regression machines interpolate the rest. This makes the data gathering phase shorter and more suitable for an amputated subject. These two strategies have been successfully employed together for the first time in [57] in the linear case, where they were collectively termed “realistic approach”. In a further analysis and practical demonstration [20], the approach has been proved successful in the non-linear case, too.

To sum up, here is how iRR-RFF matches the four Requirements outlined at the end of the previous section. As all machine learning approaches, it is adaptive (Requirement #1), meaning that it builds its own model based upon data gathered by a human subject engaged in a goal-oriented task. The significant differences found in the human anatomy of different subjects, as well as the fact that each amputation produces a very different final layout of muscle remnants, suggest that it will be a very hard, if not impossible task, to build such a universal system. The hope is therefore that of making the (machine) adaptation, already called calibration or training phase, as short as possible; possibly, resilient to the daily donning and doffing of the prosthesis—this seems a much more doable task, as the electrode layout in a prosthetic socket never changes along time.

Requirements #2 and #3 are matched by the time complexity of iRR-RFF, as well as by the easiness of the data gathering if one enforces the two last strategies outlined above; and by the fact that iRR-RFF is also bounded in space, the only space requirement being the storage of a \(D \times D\) matrix. Experimental results (see the next subsection for more details) reveal that iRR-RFF can be implemented in practice in a mid-level imperative programming language such as, e.g., C, on standard hardware, achieving a constant update time in the order of magnitude of the tens of milliseconds.

Finally, Requirement #4 is exactly realized by the usage of a rank-1 matrix update technique—in the case outlined above, the Sherman-Morrison formula. It is worth remarking once again that incrementality in this case still yields the theoretically optimal model that would have been achieved using the same data in a batch fashion. iRR-RFF can therefore serve as the basis for a theoretically well-founded, fast, incremental intent gathering system. The next subsection describes two of its practical applications.

3.5 Applications

3.5.1 The Ultrapiano/Ultraharmonium

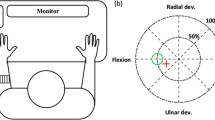
Using an instrumented glove and a commercial ultrasound machine, in [12] it was first proved that first-order spatial averages of the gray levels in ultrasound images of the human forearm are linearly related to the metacarpo-phalangeal angles, i.e., the angles formed by the first phalanx of the fingers with the palm. (A deeper analysis appears in [13].) This unexpected phenomenon was first exploited in [57] to outline and practically show that the above-mentioned averages could be used as the input space to a system enforcing iRR. The update times were found to be on average 16.5 ms, while the prediction without update took only 3.7 ms; these times were ascertained to be independent of the number of samples gathered so far, and compatible with a cinema-quality visualization of a 3D hand model on a screen (30 frames per second). This paved the way to two further applications. The real-time prediction of finger angles and forces, coupled to the detection of the position of the wrist obtained via a standard magnetic tracker, was transmitted to a virtual-reality system showing in turn a piano [51] and a harmonium [11]. The system was tested on several intact subjects revealing a satisfactory level of immersion in the virtual world. The usage of ultrasound imaging as a HMI for the disabled is actually gaining momentum and its perspectives have been widely discussed in [7]. Figure 11.1 shows, and quickly describes, the setup used in [11].

Fig. 11.1
figure 1

The setup used in [11]. A magnetic tracker and an ultrasound transducer are fixed on the subject’s forearm; an HMI based upon iRR converts local spatial features of the ultrasound images to finger forces (screen on the right); lastly, finger forces and wrist position are used in a virtual setup (screen on the left) to play a piano

Full size image

3.5.2 Teleoperated Manipulation with a Prosthesis

In [20] an i-LIMB Ultra hand prosthesis by Touch BionicsFootnote 4 was used to manipulate, pick and place and carry a few everyday-life objects in a teleoperated scenario. Compared to the Pisa/IIT SoftHand described in Chap. 8 and tele-operated leveraging strategies discussed in Chap. 10, the i-LIMB Ultra has more than one DOA, and this justifies the synergy-inspired approach to cope with its control through the techniques described in the current chapter. Teleoperation in this case is used as a proxy for the real-life application of a prosthesis to an amputee: it constitutes a simpler case since all problems related to the weights to be carried can be neglected (as they are taken care of by the slave platform). As in the case outlined above, a magnetic tracker was used to track the position of the human wrist and control the position of the slave’s end-effector using a high-stiffness impedance controller [43] on the humanoid platform TORO. At the same time, 10 standard sEMG electrodes by OttobockFootnote 5 were used to gather the muscle activity of the forearm of the master. Using iRR-RFF, the sEMG signal was converted into torque (current) commands for the five motors of the prosthesis, enforcing one of four predefined grasp schemes. The offline experiment performed in the paper clearly showed that non-linear, incremental regression was required to keep the prediction error at a reasonable level (see Fig. 11.2, reproduced from [20]).

Fig. 11.2
figure 2

Performance obtained by RR (“Linear RR”), Kernel Ridge Regression (“KRR”) and iRR-RFF with \(D=1000\) (“\({\text {iRFFRR}}^{1000}\)”) while predicting five voluntary muscle contractions using sEMG. The possibility of updating the models amidst the prediction (trials 9 and 10 of each session and day) keeps the performance of iRR-RFF well above both RR, which is linear, and KRR, which is non-linear but also not incremental. Reproduced from [20]

Full size image

In the demonstration, a success rate of 75–95 % was obtained while grasping, lifting, picking up and placing objects such as a bottle, a ball, a credit card, independent of wide ranges of hand motion and wrist rotation, and related high speeds.

4 Discussion

Introducing incrementality in a machine-learning-based prosthetic control system represents in our opinion a very beneficial improvement, at least in two senses:

  1. 1.

    it potentially solves the problem of predicting all possible situations in which an action will be performed by introducing on-demand model update;

  2. 2.

    it realizes a virtuous loop between man and machine, exploiting the phenomenon of reciprocal learning.

Notice that, while the first claim is being proved in the academic world in these years, the second is a whole unexplored territory so far. That new muscle synergies (in the broad definition used in this chapter) can be learned, retained over the weeks and then re-used whenever required is the subject of a very exciting line of research (see, e.g., [25, 46]); as well, there are hints that the very usage of a prosthesis induces better signals for its own control [45], which seems to point in the direction of goal-directed stimuli claimed here in Sect. 11.3.

What the best “reciprocal training” strategy is; how to best help the subject use the control system; what kind of games to employ; these questions are still open and indeed fascinating. This research is also motivated by the remarkable fact that improving the embodiment of a prosthesis seems to diminish phantom-limb pain [42] and amend abnormal phantom sensations. In any case, interactive learning would represent a crucial form of help to reach this goal.

4.1 On the Capacity of Incremental Learning

There seems to be a paradox in the claim that a good control system (as defined in the very chapter) must be bounded in space: such a system is limited and it therefore seems that eventually, as \(I_U\) (and accordingly, S) grows, the control function f won’t be able to accommodate all required patterns. This is indeed true and boils down to the question of how “large” the learning machine should be; unfortunately, to the best of our knowledge, so far no machine learning method is known that can change its own capacity (in the sense of the Vapnik-Chervonenkis dimension, see [56, 59]) and there is no substantial way of determining this a priori. To stay with our own example of iRR-RFF: how large a D is required? This is a crucial question since D cannot be sensibly altered after it has been chosen. So far the answer to this question can only be empirical: choose D as large as possible given the hardware at disposal; but a more sensible way to determine the size of a model is a very desirable achievement, and a very interesting research question.

4.2 Relation to Muscle Synergies as Traditionally Defined

At the time of writing we are not sure whether and how the traditional concept of task-based muscle synergy can be used in the control of dexterous prostheses. Early experiments [60] indicate that such a control is indeed possible, but will inevitably be limited to the combinations of a few synergies. If such a control can be extended to more complex control manifolds, such as, e.g., those required to play a keyboard, is unclear; it is as well unclear whether or not even an extended control based upon muscle synergies would not look quite like the one described in this chapter. All in all, in order to improve one’s own dexterity, a subject must learn (think of the painful process required, e.g., to proficiently play tennis!), and that is probably tantamount to using many more synergies than those required for the classical basic set of everyday-life tasks. Here too, the question is open and fascinating.

5 Conclusions

The ideal (hand) prosthesis is like a pair of glasses: you wear it in the morning, it works seamlessly all day long, you take it off in the evening, and then wear it again the morning after.Footnote 6 Clearly, none of the control systems currently available in the academy, let alone in the clinics, can even hope to enforce this. One possible solution is that of simplifying the prosthesis itself: for example, the Pisa/IIT SoftHand (Chap. 8) reduces the complexity of controlling many DOFs through an innovative design with only one DOA—this motivates the minimalistic tele-impedance approach described in Chap. 10. On the other hand, most of the current prosthetic systems have several actuators to be controlled, and in this case right now the control system is the bottleneck. For instance, the i-LIMB Ultra Revolution by Touch Bionics has six independent motors, as well as Vincent System’s Vincent Hand Evolution2; Steeper’s BeBionics has five, while the Michelangelo hand/wrist system has four; and no system so far can control these DOFs independently. That means that there is more dexterity available than what any patient can hope to use. We also believe that machine-learning-based control is the way ahead, but its reliability is still very questionable.

In this chapter we have argued that incremental/interactive learning would make prosthetic control radically more reliable. In one sentence: give the subjects the chance to teach their own control system what is needed. We claim that this idea could in the near future represent a leap forward.