Abstract
In this paper we analyse two variants of SIMON family of light-weight block ciphers against variants of linear cryptanalysis and present the best linear cryptanalytic results on these variants of reduced-round SIMON to date.
We propose a time-memory trade-off method that finds differential/linear trails for any permutation allowing low Hamming weight differential/linear trails. Our method combines low Hamming weight trails found by the correlation matrix representing the target permutation with heavy Hamming weight trails found using a Mixed Integer Programming model representing the target differential/linear trail. Our method enables us to find a 17-round linear approximation for SIMON-48 which is the best current linear approximation for SIMON-48. Using only the correlation matrix method, we are able to find a 14-round linear approximation for SIMON-32 which is also the current best linear approximation for SIMON-32.
The presented linear approximations allow us to mount a 23-round key recovery attack on SIMON-32 and a 24-round Key recovery attack on SIMON-48/96 which are the current best results on SIMON-32 and SIMON-48. In addition we have an attack on 24 rounds of SIMON-32 with marginal complexity.
This work was done while the author was a postdoc at the Technical University of Denmark
Javad Alizadeh, Mohammad Reza Aref and Nasour Bagheri were partially supported by Iran-NSF under grant no. 92.32575.
Praveen Gauravaram is supported by Australian Research Council Discovery Project grant number DP130104304.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Over the past few years, the necessity for limited cryptographic capabilities in resource-constraint computing devices such as RFID tags has led to the design of several lightweight cryptosystems [8, 12, 13, 15, 17–19, 30]. In this direction, Beaulieu et al. of the U.S. National Security Agency (NSA) designed SIMON family of lightweight block ciphers that are targeted towards optimal hardware performance [9]. Meeting hardware requirements of low-power and limited gate devices is the main design criteria of SIMON.
SIMON has plaintext block sizes of 32, 48, 64, 96 and 128 bits, each with up to three key sizes. SIMON-N / K denotes a variant of SIMON with block and key sizes of N and K bits respectively. With the proposed block and key lengths, SIMON is a family of ten lightweight block ciphers. Since the publication of SIMON, each cipher in this family has undergone reduced round cryptanalysis against linear [2–6, 24], differential [3, 4, 11, 28], impossible differential [14], rectangular [3, 4] and integral [29] attacks.
Contributions. In this paper, we analyse the security of SIMON-32 and SIMON-48. First we analyze the security of reduced-round SIMON-32 and SIMON-48 against several variants of linear cryptanalysis and report the best results to date with respect to any form of cryptanalysis in terms of the number of rounds attacked on SIMON-32 / 64 and 48 / 96. Our attacks are described below and results are summarised in Table 1.
-
We propose a time-memory trade-off method that combines low Hamming weight trails found by the correlation matrix (consumes huge memory) with heavy Hamming weight trails found by the Mixed Integer Programming (MIP) method [26] (consumes time depending on the specified number of trails to be found). The method enables us to find a 17-round linear approximation for SIMON-48 which is the best current approximation.
-
We found a 14-round linear hull approximation for SIMON-32 using a squared correlation matrix with input/output masks of Hamming weight \(\le 9\).
-
Using our approximations, we are able to break 23 and 24 rounds of SIMON-32, 23 rounds of SIMON-48 / 72 and 24 rounds of SIMON-48 / 96 with a marginal time complexity \(2^{63.9}\).
Previous Results on SIMON Used in Our Paper. The work in [20] provides an explicit formula for computing the probability of a 1-round differential characteristic of the SIMON’s non-linear function. It also provides an efficient algorithm for computing the squared correlation of a 1-round linear characteristic of the SIMON nonlinear function which we used in our linear cryptanalysis to SIMON-48.
The work in [24] defines a MIP linear model that finds linear trails for SIMON. The solution of the MIP model sometimes yield a false linear trail but most of the time it yields a valid linear trail. When a solution is found whether valid or invalid, we add a new constraint to the MIP model that prevents the current solution from occurring in the next iteration.
Related Work on SIMON. The most improved results in terms of the number of rounds attacked, data and time complexity presented, up-to-date of this publication, are in the scope of differential, linear and integral attacks as reflected in Table 1. Focusing on the different cryptanalysis results of SIMON-32, SIMON-48 / 72 and SIMON-48 / 96, Abed et al. [3, 4] have presented that classical differential results yield attacks on 18 for the smallest variant and 19 rounds for SIMON-48 with data and time stated in Table 1. This was improved to 21 rounds for SIMON-32 and \(22-24\) rounds for SIMON-48 / 72 and SIMON-48 / 96 by Wang et al. [27, 28] using dynamic key guessing and automatic enumeration of differential characteristics through imposing conditions on differential paths to reduce the intended key space searched.
Independent to our work, Ashur [7] described a method for finding linear trails that work only against SIMON-like ciphers. This method finds a multivariate polynomial in GF(2) representing the r-round linear approximation under consideration. Each solution of the multivariate polynomial corresponds to a valid trail that is part of the many linear trails that forms the linear approximation. This suggests that the probability that the r-round linear approximation is satisfied is equivalent to the number of solutions for its corresponding multivariate polynomial divided by the size of the solution space. For \(r=2\), the authors mentioned that the space size is \(2^{10}\). For higher rounds the space gets bigger as many bits will be involved in the corresponding multivariate polynomial. Finding the number of solutions of a multivariate polynomial is a hard problem. To overcome this, the author uses the above method to form what is called a “linear super-trail"which glues two short linear hulls (a short linear hull has a small number of rounds that make it is feasible to find the number of solutions of the corresponding multivariate polynomial) in order to form a super-trail.
In contrast, our time-memory trade-off method which basically combines two different linear trails found using a squared correlation matrix (trails with light Hamming weight) and a mixed integer programming model (trails with heavy Hamming weight) is not SIMON specific, it is very generic and can be used for any permutation allowing low Hamming weight linear/differential trails to find linear/differential trails. As described in Sect. 5.3, we have better attacks on both SIMON-32 (using squared correlation matrix) and SIMON-48 (using time-memory trade-off) compared to the results of [7].
Organization. The paper is structured as follows. In Sect. 2 we describe SIMON. In Sect. 3 concepts and notation required for linear cryptanalysis of SIMON are presented. In Sect. 4 the used Time-Memory Trade-off method is described. In Sect. 5 we used squared correlation matrix to establish a linear hull of SIMON and investigate the data and time complexity for the smallest variant of SIMON. We conclude the paper in Sect. 6.
2 Description of SIMON
SIMON has a classical Feistel structure with the round block size of \(N=2n\) bits where n is the word size representing the left or right branch of the Feistel scheme at each round. The number of rounds is denoted by r and depends on the variant of SIMON.
We denote the right and left halves of plaintext P and ciphertext C by \((P_R, P_L)\) and \((C_R,C_L)\) respectively. The output of round r is denoted by \(X^r=X^r_L\Vert X^r_R\) and the subkey used in a round r is denoted by \(K^r\). Given a string X, \((X)_i\) denotes the \(i^{\mathrm {th}}\) bit of X. Bitwise circular left-rotation of string a by b positions to the left is denoted by \(a\lll b\). Further, \(\oplus \) and&denote bitwise XOR and AND operations respectively.
Each round of SIMON applies a non-linear, non-bijective (and hence non-invertible) function \(F: \mathbb {F}_2^n \rightarrow \mathbb {F}_2^n\) to the left half of the state. The output of F is added using XOR to the right half along with a round key followed by swapping of two halves. The function F is defined as
The subkeys are derived from a master key. Depending on the size K of the master key, the key schedule of SIMON operates on two, three or four n-bit word registers. We refer to [9] for the detailed description of SIMON structure and key scheduling.
3 Preliminaries
Correlation Matrix. Linear cryptanalysis finds a linear relation between some plaintext bits, ciphertext bits and some secret key bits and then exploits the bias or correlation of this linear relation. In other words, the adversary finds an input mask \(\alpha \) and an output mask \(\beta \) which yields a higher absolute bias \(\epsilon _F(\alpha ,\beta )\in [-\frac{1}{2},\frac{1}{2}]\). In other words
deviates from \(\frac{1}{2}\) where \(\langle \cdot ,\cdot \rangle \) denotes an inner product. Let \(a=(a_1,\ldots ,a_n), b=(b_1,\ldots ,b_n)\in \mathbb F_2^n\). Then
denotes the inner product of a and b. The correlation of a linear approximation is defined as
Another definition of the correlation which we will use later is
where n is the block size of F in bits and \(\hat{F}(\alpha ,\beta )\) is the Walsh transform of F which is defined as follows
For a given output mask \(\beta \), the Fast Walsh Transform algorithm computes the Walsh transforms of an n-bit block size function F for all possible input masks \(\alpha \) with output mask \(\beta \) using \(n2^n\) arithmetic operations.
In order to find good linear approximations, one can construct a correlation matrix (or a squared correlation matrix). In the following, we explain what is a correlation matrix and show how the average squared correlation over all keys is estimated.
Given a composite function \(F:\mathbb {F}_2^n \rightarrow \mathbb {F}_2^n\) such that \(F = F_r\circ \dots \circ F_2 \circ F_1,\), we estimate the correlation of an r-round linear approximation \((\alpha _0, \alpha _r)\) by considering the correlation of each linear characteristic between \(\alpha _0\) and \(\alpha _r\). The correlation of \(i^{\mathrm {th}}\) linear characteristic \((\alpha _0 = \alpha _{0i}, \alpha _{1i}, \cdots , \alpha _{(r-1)i}, \alpha _r = \alpha _{ri})\) is
It is well known [16] that the correlation of a linear approximation is the sum of all correlations of linear trails starting with the same input mask \(\alpha \) and ending with the same output mask \(\beta \), i.e. \(C_F(\alpha _0,\alpha _r) = \sum _{i=1}^{N_l}{C_i}\) where \(N_l\) is the number of all possible linear characteristics between \((\alpha _0, \alpha _r)\).
When considering the round keys which affects the sign of the correlation of a linear trail, the correlation of the linear hull \((\alpha ,\beta )\) is
where \(d_i \in \mathbb {F}_2\) refers to the sign of the addition of the subkey bits on the \(i^{\mathrm {th}}\) linear trail. In order to estimate the data complexity of a linear attack, one uses the average squared correlation over all the keys which is equivalent to the sum of the squares of the correlations of all trails, \(\sum _i C^2_i\), assuming independent round keys [16].
Let C denotes the correlation matrix of an n-bit key-alternating cipher. C has size \(2^{n} \times 2^{n}\) and \(C_{i,j}\) corresponds to the correlation of an input mask, say \(\alpha _i\), and output mask, say \(\beta _j\). Now the correlation matrix for the keyed round function is obtained by changing the signs of each row in C according to the round subkey bits or the round constant bits involved. Squaring each entry of the correlation matrix gives us the squared correlation matrix M. Computing \(M^r\) gives us the squared correlations after r number of rounds. This can not be used for real block ciphers that have block sizes of at least 32 bits as in the case of SIMON-32 / 64. Therefore, in order to find linear approximations one can construct a submatrix of the correlation (or the squared correlation) matrix [1, 12]. In Sect. 5, we construct a squared correlation submatrix for SIMON in order to find good linear approximations.
3.1 Mixed Integer Programming Method (MIP)
Mouha et al.’s [21] presented a mixed integer programming model that minimizes the number of active Sboxes involved in a linear or differential trail. Their work was mainly on byte oriented ciphers. Later, Mouha’s framework was extended to accommodate bit oriented ciphers. More recently, at Asiacrypt 2014 [26], the authors described a method for constructing a model that finds the actual linear/differential trail with the specified number of active Sboxes. Of course, there would be many solutions but whenever a solution is found the MIP model is updated by adding a new constraint that discards the current found solution from occurring in the next iteration for finding another solution.
For every input/ouput bit mask or bit difference at some round state, a new binary variable \(x_i\) is introduced such that \(x_i = 1\) iff the corresponding bit mask or bit difference is non-zero. For every Sbox at each round, a new binary variable \(a_j\) is introduced such that \(a_j = 1\) if the input mask or difference of the corresponding Sbox is nonzero. Thus, \(a_j\) indicates the activity of an Sbox. Now, the natural choice of the objective function f of our MIP model is to minimize the number of active Sboxes, i.e., \(f = \sum _{j} a_j\). If our goal from the above integer programming model is to only find the minimum number of active Sboxes existing in a differential/linear trial of a given bit-oriented cipher, then we are only concerned about the binary values which represent the activity of the Sboxes involved in the differential/linear trail \(a_v\). Thus, in order to speed up solving the model, one might consider restricting the activity variables and the dummy variables to be binary and allow the other variables to be any real numbers. This will turn the integer programming model into a Mixed Integer Programming model which is easier to solve than an Integer programming model. However, since we want to find the differential/linear trails which means finding the exact values of all the bit-level inputs and outputs, then all these state variables must be binary which give us an integer programming model rather than a mixed integer programming model.
In order to find the differential/linear trails of a given input/output differential/linear approximation, we set the corresponding binary variables for each input/output to 1 if it is an active bit in the input/output and to 0 otherwise. In this paper, we follow the MIP model for linear cryptanalysis presented in [24] (minimize the number of variables appearing in quadratic terms of the linear approximation of SIMON’s non-linear function) and use the algorithm presented in [20] for computing the squared correlation for the SIMON nonlinear function.
In Sect. 4, we propose a hybrid method that combines the matrix method and the MIP method to amplify the differential probability or the squared correlation of a specified input and output differences or masks. Using this method we are able to find a 17-round linear approximation for SIMON-48.
4 Time-Memory Trade-Off Method
Since the matrix method consumes huge memory and the MIP method takes time to enumerate a certain number of trails. It seems reasonable to trade-off the time and memory by combining both methods to get better differential/correlation estimations. Here we combine the correlation matrix method with the recent technique for finding differentials and linear hulls in order to obtain a better estimation for the correlations or differentials of a linear and differential approximations respectively.
The idea is to find good disjoint approximations through the matrix and the mixed integer programming model. Assume that our target is an r-round linear hull \((\alpha , \beta )\), where \(\alpha \) is the input mask and \(\beta \) is the output mask. The matrix method is used to find the resulting correlation from trails that have Hamming weight at most m for each round, from now on we will call them “light trails”. The MIP method is used to find the resulting correlation from trails that have Hamming weight at least \(m+1\) at one of their rounds, from now on we will call them “heavy trails”.
Now if the target number of rounds is high, then the MIP method might not be effective in finding good estimation for the heavy trails as it will take time to collect all those trails. Therefore, in order to overcome this, we split the cipher into two parts, the first part contains the first \(r_1\) rounds and the second part contains the remaining \(r_2 = r-r_1\) rounds. Assume \(r_1 > r_2\), where \(r_2\) is selected in such a way that the MIP solution is reachable within a reasonable computation time. Now, we show how to find two disjoint classes that contains heavy trails. The first class contains an \(r_1\)-round linear hull \((\alpha , \gamma _i)\) consisting of light trails found through the matrix method at the first \(r_1\) rounds glued together with an \(r_2\)-round linear hulls \((\gamma _i,\beta )\) consisting of heavy trails found through the MIP method. We call this class, the lower-round class. The second class basically reverse the previous process, by having an \(r_1\)-round linear hull of heavy weight trails found through MIP method glued with an \(r_2\)-round linear hull containing light trails found through the matrix method. We call this class the upper-round class. Now, adding the estimations from these two classes (upper-round and lower-round classes) gives us the estimation of the correlation of the heavy trails which will be added to the r-round linear hull of the light trails found through the matrix method. We can also include a middle-round class surrounded by upper lightweight trails and lower lightweight trails found by the matrix method.
Next we describe how to find the heavy trails using MIP with the Big M constraints which is a well known technique in optimization.
4.1 Big M Constraints
Suppose that only one of the following two constraints is to be active in a given MIP model.
The above situation can be formalized by adding a binary variable y as follows:
where M is a big positive integer and the value of y indicates which constraint is active. So y can be seen as an indicator variable. One can see that when \(y=0\), the first constraint is active while the second constraint is inactive due to the positive big value of M. Conversely, when y = 1, the second constraint is active.
The above formulation can be generalized to the case where we have q constraints under the condition that only p out of q constraints are active. The generalization can be represented as follows:
where \(y_i\) is binary for all i. Sometimes, we might be interested on the condition where at least p out of the q constraints are active. This can be achieved by simply changing the last equation in the constraints above, \(\sum _{i=1}^{l}y_i = q-p\) to \(\sum _{i=1}^{l}y_i \le q-p\). This turns out to be useful in our Hybrid method as it will allow us to find r-round trails which have a heavy Hamming weight on at least one of the r rounds.
5 Linear Hull Effect in SIMON-32 and SIMON-48
In this section we will investigate the linear hull effect on SIMON using the correlation matrix method to compute the average squared correlation.
5.1 Correlation of the SIMON F Function
This section provides an analysis on some linear properties of the SIMON F function regarding the squared correlation. This will assist in providing an intuition around the design rationale when it comes to linear properties of SIMON round Function F. A general linear analysis was applied on the F function of SIMON, with regards to limits around the squared correlations for all possible Hamming weights on input masks \(\alpha \) and output masks \(\beta \), for SIMON-32 / 64.
5.2 Constructing Correlation Submatrix for SIMON
To construct a correlation submatrix for SIMON, we make use of the following proposition.
Proposition 1
Correlation of a one-round linear approximation [10]. Let \(\alpha = (\alpha _L,\alpha _R)\) and \(\beta = (\beta _L, \beta _R)\) be the input and output masks of a one-round linear approximation of SIMON. Let \(\alpha _F\) and \(\beta _F\) be the input and output masks of the SIMON F function. Then the correlation of the linear approximation \((\alpha ,\beta )\) is \(C(\alpha , \beta ) = C_F(\alpha _F,\beta _F)\) where \(\alpha _F = \alpha _L \oplus \beta _R\) and \(\beta _F = \beta _L = \alpha _R\).
As our goal is to perform a linear attack on SIMON, we construct a squared correlation matrix in order to compute the average squared correlation (the sum of the squares of the correlations of all trails) in order to estimate the required data complexity. Algorithm 1 constructs a squared correlation submatrix whose input and output masks have Hamming weight less than a certain Hamming weight m, where the correlation matrix is deduced from the algorithm proposed in [20].

The size of the submatrix is \(\sum _{i=0}^{m}\left( {\begin{array}{c}2n\\ i\end{array}}\right) \times \sum _{i=0}^{m}\left( {\begin{array}{c}2n\\ i\end{array}}\right) \) where n is the block size of SIMON’s F function. One can see that the time complexity is in the order of \(2^n\sum _{i=0}^{m}\left( {\begin{array}{c}2n\\ i\end{array}}\right) \) arithmetic operations. The submatrix size is large when \(m > 5\), but most of its elements are zero and therefore it can easily fit in memory using a sparse matrix storage format. The table below shows the number of nonzero elements of the squared correlation submatrices of SIMON-32 / K when \(1 \le m \le 9\). These matrices are very sparse. For instance, based on our experimental results when \(m \le 8\), the density of the correlation matrix is very low, namely \(\frac{133253381}{15033173 \times 15033173} \approx 2^{-20.7}\).
5.3 Improved Linear Approximations
One can see that Algorithm 1 is highly parallelizable. This means the dominating factor is the memory complexity instead of time complexity. We constructed a sparse squared correlation matrix of SIMON-32 / K with input and output masks that have Hamming weight \(\le 8\). Using this matrix, we find a 14-round linear approximations with an average squared correlation \(\le 2^{-32}\) for SIMON-32 / K. We also get better estimations for the previously found linear approximations which were estimated before using only a single linear characteristic rather than considering many linear characteristics with the same input and output masks. For example, in [4], the squared correlation of the 9-round single linear characteristic with input mask \(\mathtt{0x01110004}\) and output mask \(\mathtt{0x00040111}\) is \(2^{-20}\). Using our matrix, we find that this same approximation has a squared correlation \(\approx 2^{-18.4}\) with \(11455 \approx 2^{13.5}\) trails, which gives us an improvement by a factor of \(2^{1.5}\). Note that this approximation can be found using a smaller correlation matrix of Hamming weight \(\le 4\) and we get an estimated squared correlation equal to \(2^{-18.83}\) and only 9 trails. Therefore, the large number of other trails that cover Hamming weights \(\ge 5\) is insignificant as they only cause a factor of \(2^{0.5}\) improvement.
Also, the 10-round linear characteristic in [6] with input mask \(\mathtt{0x01014404}\) and output mask \(\mathtt{0x10004404}\) has squared correlation \(2^{-26}\). Using our correlation matrix, we find that this same approximation has an estimated squared correlation \(2^{-23.2}\) and the number of trails is \(588173 \approx 2^{19.2}\). This gives an improvement by a factor of \(2^3\). Note also that this approximation can be foundusing a smaller correlation matrix with Hamming weight \(\le 5\) and we get an estimated squared correlation equal to \(2^{-23.66}\) and only 83 trails. So the large number of other trails resulting covering Hamming weights \(\ge 5\) is insignificant as they only cause a factor of \(2^{0.4}\) improvement. Both of these approximations give us squared correlations less than \(2^{-32}\) when considering more than 12 rounds.
In the following, we describe our 14-round linear hulls found using a squared correlation matrix with Hamming weight \(\le 8\).
Improved 14-round Linear Hulls on SIMON-32 (Squared Correlation Matrix Only). Consider a squared correlation matrix M whose input and output masks have Hamming weight m. When \(m \ge 6\), raising the matrix to the rth power, in order to estimate the average squared correlation, will not work as the resulting matrix will not be sparse even when r is small. For example, we are able only to compute \(M^6\) where M is a squared correlation matrix whose masks have Hamming weight \(\le 6\). Therefore, we use matrix-vector multiplication or row-vector matrix multiplications in order to estimate the squared correlations for any number of rounds r.
It is obvious that input and output masks with low Hamming weight gives us better estimations for the squared correlation. Hence, we performed row-vector matrix multiplications using row vectors corresponding to Hamming weight one. We found that when the left part of the input mask has Hamming weight one and the right part of input mask is zero, we always get a 14-round squared correlation \(\approx 2^{-30.9}\) for four different output masks.Therefore, in total we get 64 linear approximations with an estimated 14-round squared correlation \(\approx 2^{-30.9}\).
We also constructed a correlation matrix with masks of Hamming weight \(\le 9\) but we have only got a slight improvement for these 14-round approximations by a factor of \(2^{0.3}\). We have found no 15-round approximation with squared correlation more than \(2^{-32}\). Table 2 shows the 14-round approximations with input and output masks written in hexadecimal notation.
Improved 17-Round Linear Hulls on SIMON-48 (Squared Correlation Matrix + MIP). Using a squared correlation matrix of SIMON-48 having input and output masks with Hamming weight \(\le 6\) and size \(83278000 \times 83278000\), we found that a 17-round linear approximation with input mask 0x404044000001 and output mask 0x000001414044 (\(0x404044000001 \xrightarrow {17-round} 0x000001C04044\)) has squared correlation \(2^{-49.3611}\). Also the output masks 0x000001414044 and 0x000001414044 yield a similar squared correlation \(2^{-49.3611}\). Unlike the case for SIMON-32 where we can easily use brute force to compute the squared correlation of a 1-round linear approximation, the squared correlation matrix for SIMON-48 was created using the algorithm proposed in [20]. Again the matrix is sparse and it has \(48295112 \approx 2^{25.53}\) nonzero elements.
However, it seems difficult to build matrices beyond Hamming weight 6 for SIMON-48. Therefore we use our time-memory trade-off method to improve the squared correlation of the linear approximation \(0x404044000001 \xrightarrow {17-round} 0x000001414044\).
To find the lower class where the heavy trails are on the bottom are glued with the light trails on top. The light trails are found using the matrix method for 11 rounds and the heavy trails are found using the MIP method for 6 rounds. Combining them both we get the 17-round lower class trails. In more detail, we fix the input mask to 0x404044000001 and we use the matrix method to find the output masks after 11 rounds with the most significant squared correlation. The best output masks are 0x001000004400, 0x001000004410 and 0x0010000044C0, each give an 11-round linear hull with squared correlation \(2^{-28.6806}\) coming from 268 light trails. We first create a 6-round MIP model with 0x001000004400 as an input mask and with the target output mask 0x000001414044 as the output mask for the 6-round MIP model \(0x001000004400 \xrightarrow {6-round} 0x000001414044\). In order to find heavy trails we added the big M constraints described in Sect. 4.1 and set \(M=200\) and all the \(c_i\)’s to 7 from the end of round 1 to beginning of round 5. So \(q = 5\), setting \(p=1\) and using \(\sum _{i=1}^{l}y_i \le q-p=4\), we guarantee that the trails found will have Hamming weight at least 7 at one of the rounds. The constraints should be set as follows:
where \(y_j\) is a binary variable and \(s_{48.j+i}\) is a binary variable representing the intermediate mask value in the jth round at the ith position.
Limiting our MIP program to find 512 trails for the specified approximation, we find that the estimated squared correlation is \(2^{-22.3426}\). Combining the light trails with the heavy, we get a 17-round sub approximation whose squared correlation is \(2^{-28.6806}\times 2^{-22.3426} = 2^{-51.0232}\). To get a better estimation, we repeated the above procedure for the other output masks 0x001000004410 and 0x0010000044C0 and get an estimated squared correlation equivalent to \(2^{-28.6806} \times 2^{-24.33967} = 2^{-53.02027}\) and \(2^{-28.6806} \times 2^{-24.486272} = 2^{-53.166872}\) respectively. Adding all these three sub linear approximations we get an estimated squared correlation equivalent to \(2^{-51.0232} + 2^{-53.02027} + 2^{-53.166872} \approx 2^{-50.4607}\). Moreover, we repeat the same procedure for the 27 next best 11-round linear approximations and we get \(2^{-49.3729}\) as a total estimated squared correlation for our 17-round lower class trails (\(0x404044000001 \xrightarrow {17-round} 0x000001414044\)). All these computations took less than 20 hrs on a standard laptop (See Table 11 in the Appendix).
Similarly to find the upper class where the heavy trails are on the top, are glued with the light trails on bottom. The light trails are found using the matrix method for 11 rounds and the heavy trails are found using the MIP method for 6 rounds under the same big M constraints described above. Combining them both we get the 17-round upper class trails. In more detail, we fix the output mask to 0x000001414044 and we use the matrix method to find the input masks with the most significant squared correlation after 11 rounds. The best input masks are 0x004400001000, 0x004410001000, 0x004C00001000 and 0x004C10001000, each give an 11-round linear hull with squared correlation \(2^{-28.6806}\) coming from 268 light trails. We first create a 6-round MIP model with 0x004400001000 as an output mask and the target input mask 0x404044000001 as the input mask for the 6-round MIP model \(0x404044000001 \xrightarrow {6-round} 0x004400001000\). Limiting our MIP program to find 512 trails for the specified approximation, we find that the estimated squared correlation is \(2^{-22.3426}\). Combining the light trails with the heavy, we get a 17-round sub approximation whose squared correlation is \(2^{-28.6806}\times 2^{-22.3426} = 2^{-51.0232}\). Repeating the above procedure for the other three input masks 0x04410001000, 0x004C00001000 and 0x004C10001000, we get an estimated squared correlation equivalent to \(2^{-28.6806} \times 2^{-24.33967} = 2^{-53.02027}\), \(2^{-28.6806} \times 2^{-24.486272} = 2^{-53.166872} \) and \(2^{-28.6806} \times 2^{-23.979259} = 2^{-52.659859} \) respectively. Adding all these four sub linear approximations we get an estimated squared correlation equivalent to \(2^{-51.0232} + 2^{-53.02027} + 2^{-53.166872} + 2^{-52.659859} \approx 2^{-50.1765}\). Repeating the same procedure for the 26 next best input masks and adding them up, we get a total squared correlation equivalent to \(2^{-49.3729}\) as a total estimated squared correlation for our 17-round upper class trails (\(0x404044000001 \xrightarrow {17-round} 0x000001414044\)). All these computations took less than 18 hrs on a standard laptop (See Table 12 in the Appendix).
Adding the contributions of the lower and upper classes found through the above procedure to the contribution of the light trails found through the matrix method, we get \(2^{-49.3729} + 2^{-49.3729} + 2^{-49.3611} = 2^{-47.7840} \approx 2^{-47.78}\) as a total estimation for the squared correlation of the 17-round linear hull (\(0x404044000001 \xrightarrow {17-round} 0x000001414044\)).
5.4 Key Recovery Attack on 24 and 23 Rounds of SIMON-32 / K Using 14-Round Linear Hull
We extend the given linear hull for 14 rounds of SIMON-32 / K (highlighted masks in the last row of Table 2) by adding some rounds to the beginning and the end of the cipher. The straight-forward approach is to start with the input mask of the 14-round linear hull (e.g. \((\varGamma _0,-)\)) and go backwards to add some rounds to the beginning. With respect to Fig. 1, we can append an additional round to the beginning of the cipher. Since SIMON injects the subkey at the end of its round function, this work does not have any computational complexity. More precisely, for the current 14-round linear hull, we evaluate \(((X^i_L)_0\oplus (X^{i+14}_R)_6\oplus (X^{i+14}_L)_8)\) to filter wrong guesses. On the other hand, we have \((X^i_L)_0=(F(X^{i-1}_L))_0\oplus ((X^{i-1}_R)_0\oplus (K^i)_0\), where \( (F(X^{i-1}_L))_0=(X^{i-1}_L)_{14}\oplus ((X^{i-1}_L)_{15} \& (X^{i-1}_L)_{8})\). Hence, if we add a round in the backwards direction, i.e. round \(i-1\), we know \(X^{i-1}_R\) and \(X^{i-1}_L\) we can determine \(F(X^{i-1}_L)\). Then it is possible to use the following equation to filter wrong keys, instead of \(((X^i_L)_0\oplus (X^{i+14}_R)_6\oplus (X^{i+14}_L)_8)\), where \((K^i)_0\) is an unknown but a constant bit (in Fig. 1 such bits are marked in  ):
):
We can continue our method to add five rounds to the beginning of linear hull at the cost of guessing some bits of subkeys. To add more rounds in the backwards direction, we must guess the bit
On the other hand, to determine \((F(X^{i-1}_L))_0\) we guess \((X^{i-1}_L)_{14}\) and \((X^{i-1}_L)_{15}\) only if the guessed value for \((X^{i-1}_L)_{8}\) is 1. Therefore, on average we need one bit guess for \((X^{i-1}_L)_{15}\) and \((X^{i-1}_L)_{8}\) (in Fig. 1 such bits are indicated in  ).
).
The same approach can be used to add five rounds to the end of linear hull at the cost of guessing some bits of subkeys. More details are depicted in Fig. 1.
On the other hand, in [29], Wang et al. presented a divide and conquer approach to add extra rounds to their impossible differential trail. We note that it is possible to adapt their approach to extend the key recovery using the exist linear hull over more rounds. Hence, one can use the 14-round linear hull and extend it by adding extra rounds to its beginning and its end. We add five rounds to the beginning and five rounds to the end of the linear hull to attack 24-round variant of SIMON-32 / K. This key recovery attack processes as follows:
-
1.
Let \(T_{max}\) and \(T_{cur}\) be counters (initialized by 0) and \(SK_{can}\) be a temporary register to store the possible candidate of the subkey.
-
2.
Collect \(2^{30.59}\) known plaintext and corresponding ciphertext pairs \((p_{i},c_{i})\) for 24-round SIMON-32 / 64 and store them in a table \(\mathcal {T}\).
-
3.
Guess a value for the subkeys involved in the first five rounds of reduced SIMON-32 / K, i.e.

 and do as follows (note that the
and do as follows (note that the  subkey bits involved in the rounds are the constant bits and do not have to be guessed):
subkey bits involved in the rounds are the constant bits and do not have to be guessed):-
(a)
For any \(p_{j}\in \mathcal {T}\) calculate the partial encryption of the first five rounds of reduced SIMON-32 / K and find
 .
. -
(b)
Guess the bits of subkeys
 ,
, 
 ,
,  , and
, and  , step by step.
, step by step. -
(c)
For any \(c_{j}\in \mathcal {T}\):
-
i.
calculate the partial decryption of the last five rounds of reduced SIMON-32 / K and find
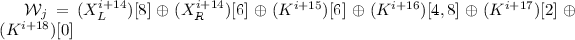 .
. -
ii.
If \(\mathcal {V}_j=\mathcal {W}_j\) then increase \(T_{cur}\).
-
i.
-
(d)
If \(T_{max}<T_{cur}\) (or resp. \(T_{max}<(2^{32}- T_{cur})\)) update \(T_{max}\) and \(SK_{can}\) by \(T_{cur}\) (resp. \(2^{32}- T_{cur}\)) and the current guessed subkey respectively.
-
(a)
-
4.
Return \(SK_{can}\).
Following the approach presented in [29], guessing the bits of subkeys
 ,
, 
 ,
,  , and
, and  , step by step, to find the amount of
, step by step, to find the amount of  , for any \(c_j\), are done as follows:
, for any \(c_j\), are done as follows:
-
1.
Let \(T_2\) be a vector of \(2^{32}\) counters which correspond to all possible values of \(\mathcal {V}_j \Vert (X^{i+19}_L)[0 \ldots 7,\) \( 10 \ldots 14] \Vert (X^{i+19}_R)[0 \ldots 6, 8 \ldots 15] \Vert (X^{i+18}_R)[8,9,15]\) (denoted as \(S^1_2\)). Guess the subkey bit \((K^{i+19}\) )[8, 9, 15] decrypt partially for each possible value of \(S^1_1\) (\(\mathcal {V}_j \Vert (X^{i+19}_L) \Vert (X^{i+19}_R)\)) to obtain the value of \((X^{i+18}_R)[8,9,15]\) (and hence \(S^1_2\)), then increase the corresponding counter \(T_{2,S^1_2}\).
-
2.
Guess the subkey bits
 ,
,  , \((K^{i+19})[12]\), \((K^{i+19})[13]\), and \((K^{i+19})\) [0, 2, 3, 4, 6, 7] step by step (see Table 3), do similarly to the above and finally get the values of the counters corresponding to the state \(\mathcal {V}_j \Vert (X^{i+18}_L)[0 \ldots 6, 8, 10 \ldots 12, 14,15] \Vert (X^{i+18}_R)\) (denoted as \(S_0^{2}\)).
, \((K^{i+19})[12]\), \((K^{i+19})[13]\), and \((K^{i+19})\) [0, 2, 3, 4, 6, 7] step by step (see Table 3), do similarly to the above and finally get the values of the counters corresponding to the state \(\mathcal {V}_j \Vert (X^{i+18}_L)[0 \ldots 6, 8, 10 \ldots 12, 14,15] \Vert (X^{i+18}_R)\) (denoted as \(S_0^{2}\)). -
3.
Let \(X_1\) be a vector of \(2^{29}\) counters which correspond to all possible values of \(\mathcal {V}_j \Vert (X^{i+18}_L)[0 \ldots 5,\) \(8,10\ldots 12,14,15] \Vert (X^{i+18}_R)[0\ldots 4,6\ldots 15] \Vert (X^{i+17}_R)[6]\) (denoted as \(S_1^2\)). Guess the subkey bit
 . For each possible value of \(S^2_0\) (\(\mathcal {V}_j \Vert (X^{i+18}_L)[0 \ldots 6, 8, 10 \ldots 12, 14,15] \Vert (X^{i+18}_R)\)), do partial decryption to derive the value of \((X^{i+17}_R)[6]\) and add \(T_{7,S^1_7}\) to the corresponding counter \(X_{1,S^2_1}\) according to the value of \(S^2_1\). After that, guess the subkey bits
. For each possible value of \(S^2_0\) (\(\mathcal {V}_j \Vert (X^{i+18}_L)[0 \ldots 6, 8, 10 \ldots 12, 14,15] \Vert (X^{i+18}_R)\)), do partial decryption to derive the value of \((X^{i+17}_R)[6]\) and add \(T_{7,S^1_7}\) to the corresponding counter \(X_{1,S^2_1}\) according to the value of \(S^2_1\). After that, guess the subkey bits 
 , and
, and  , step by step (see Table 4). Do similarly to the above and eventually obtain the values of the counters corresponding to the state \(\mathcal {V}_j \Vert (X^{i+17}_L)[0',2\ldots 4,6,7,12,13] \Vert (X^{i+17}_R)[0\ldots 6,8, 10\ldots 12,14,15 ]\) (denoted as \(S_0^3\)) where
, step by step (see Table 4). Do similarly to the above and eventually obtain the values of the counters corresponding to the state \(\mathcal {V}_j \Vert (X^{i+17}_L)[0',2\ldots 4,6,7,12,13] \Vert (X^{i+17}_R)[0\ldots 6,8, 10\ldots 12,14,15 ]\) (denoted as \(S_0^3\)) where  .
. -
4.
Let \(Y_1\) be a vector of \(2^{21}\) counters which correspond to all possible values of \(\mathcal {V}_j \Vert (X^{i+17}_L)[0,2,3,\) \(6,7,12,13] \Vert (X^{i+17}_R)[0\ldots 2, 4 \ldots 6,8, 10\ldots 12,14,15 ]\Vert \) \((X^{i+16}_R)[4]\) (denoted as \(S_1^3\)). Guess the subkey bit
 . For each possible value of \(S^3_0\) (\(\mathcal {V}_j \Vert (X^{i+17}_L)[0,2\ldots 4,6,7,12,13] \Vert (X^{i+17}_R)\) \([0\ldots 6,8, 10\ldots \)12, 14, 15 ]), do partial decryption to derive the value of \((X^{i+16}_R)[4]\) and add \(X_{9,S^2_9}\) to the corresponding counter \(Y_{1,S^3_1}\) according to the value of \(S_1^3\). After that, guess the subkey bits \((K^{i+17})[3]\), \((K^{i+17})[12]\),
. For each possible value of \(S^3_0\) (\(\mathcal {V}_j \Vert (X^{i+17}_L)[0,2\ldots 4,6,7,12,13] \Vert (X^{i+17}_R)\) \([0\ldots 6,8, 10\ldots \)12, 14, 15 ]), do partial decryption to derive the value of \((X^{i+16}_R)[4]\) and add \(X_{9,S^2_9}\) to the corresponding counter \(Y_{1,S^3_1}\) according to the value of \(S_1^3\). After that, guess the subkey bits \((K^{i+17})[3]\), \((K^{i+17})[12]\),  ,
,  , and \((K^{i+17})[{0,6}]\), step by step (see Table 5). Do similarly to the above and eventually obtain the values of the counters corresponding to the state \(\mathcal {V}_j \Vert (X^{i+16}_L)[4,5,8,14] \Vert (X^{i+16}_R)[0,2',3,4,6,7,12,13 ]\) (denoted as \(S_0^4\)) where
, and \((K^{i+17})[{0,6}]\), step by step (see Table 5). Do similarly to the above and eventually obtain the values of the counters corresponding to the state \(\mathcal {V}_j \Vert (X^{i+16}_L)[4,5,8,14] \Vert (X^{i+16}_R)[0,2',3,4,6,7,12,13 ]\) (denoted as \(S_0^4\)) where  .
. -
5.
Let \(Z_1\) be a vector of \(2^{6}\) counters which correspond to all possible values of \(\mathcal {V}_j \Vert (X^{i+15}_L)[6] \Vert \) \( (X^{i+15}_R)[4,5,8,14]\) (denoted as \(S_1^4\)) where
 and
and  . Guess the subkey bits
. Guess the subkey bits  and for each possible value of \(S_0^4\) (\(\mathcal {V}_j \Vert (X^{i+16}_L)[4,5,8,14] \Vert (X^{i+16}_R)[0, 2, 3,4,6,7,12,13 ]\)) do partial decryption to derive the value of \((X^{i+15}_R)[5,14]\) and add \(Y_{6,S^3_6}\) to the corresponding counter \(Z_{1,S^4_1}\) according to the value of \(S_1^4\).
and for each possible value of \(S_0^4\) (\(\mathcal {V}_j \Vert (X^{i+16}_L)[4,5,8,14] \Vert (X^{i+16}_R)[0, 2, 3,4,6,7,12,13 ]\)) do partial decryption to derive the value of \((X^{i+15}_R)[5,14]\) and add \(Y_{6,S^3_6}\) to the corresponding counter \(Z_{1,S^4_1}\) according to the value of \(S_1^4\). -
6.
Let \(W_{1,S^5_1}\) be a vector of \(2^{4}\) counters which correspond to all possible values of \(\mathcal {V}_j \Vert (X^{i+14}_L)[4',8'] \Vert \) \( (X^{i+14}_R)[6']\) (denoted as \(S^5_1\)) where \((X^{i+14}_R)[6']=(X^{i+14}_R)[6] \oplus (K^{i+15})[6]\), \((X^{i+14}_L)[4']=(X^{i+14}_L)[4] \oplus (K^{i+16})[4] \oplus (K^{i+17})[2] \oplus (K^{i+18})[0]\), and \((X^{i+14}_L)[8']=(X^{i+14}_L)[8] \oplus (K^{i+16})[8]\). This state are extracted of \(S_1^4\) and add \(Z_{1,S^4_1}\) to the corresponding counter \(W_{1,S^5_1}\) according to the value of \(S_1^5\) (See Table 7).
-
7.
Let O be a vector of \(2^{2}\) counters which correspond to all possible values of \(\mathcal {V}_j \Vert \mathcal {W}_j\) (Note that
 and can be extracted from \(S^5_1\)). Each possible value of \(S^5_1\) is converted to \(\mathcal {V}_j \Vert \mathcal {W}_j\) and \(W_{1,S^5_1}\) and is added to the relevant counter in O according to the value of \(\mathcal {V}_j \Vert \mathcal {W}_j\). Suppose that \(O_0\) means that \(\mathcal {V}_j=0\) and \( \mathcal {W}_j=0\) and \(O_3\) means that \(\mathcal {V}_j=1\) and \( \mathcal {W}_j=1\). If \(O_0 + O_3 \ge T_{max}\) or \(2^{32}-(O_0 + O_3) \ge T_{max}\) keep the guessed bits of subkey information as a possible subkey candidate, and discard it otherwise.
and can be extracted from \(S^5_1\)). Each possible value of \(S^5_1\) is converted to \(\mathcal {V}_j \Vert \mathcal {W}_j\) and \(W_{1,S^5_1}\) and is added to the relevant counter in O according to the value of \(\mathcal {V}_j \Vert \mathcal {W}_j\). Suppose that \(O_0\) means that \(\mathcal {V}_j=0\) and \( \mathcal {W}_j=0\) and \(O_3\) means that \(\mathcal {V}_j=1\) and \( \mathcal {W}_j=1\). If \(O_0 + O_3 \ge T_{max}\) or \(2^{32}-(O_0 + O_3) \ge T_{max}\) keep the guessed bits of subkey information as a possible subkey candidate, and discard it otherwise.
Attack Complexity. The time complexity of each sub-step was computed as shown in the Tables 3, 4, 5, 6 and 7. The time complexity of the attack is about \(2^{63.9}\). It is clear that, the complexity of this attack is only slightly less than exhaustive search. However, if we reduce the last round and attack 23 round of SIMON-32 / K then the attack complexity reduces to \(2^{50}\) which is yet the best key-recovery attack on SIMON-32 / K for such number of rounds.
5.5 Key Recovery Attack on SIMON-48 / K Using 17-Round Linear Hull
Given the 17-round approximation for SIMON-48, introduced in Sect. 5.3, we apply the approach presented in Sect. 5.4 to extend key recovery over more number of rounds. Our key recovery for SIMON-48/72 and SIMON-48/96 covers 23 and 24 rounds respectively. The data complexity for these attacks is \(2^{-47.78}\) and their time complexities are \(2^{62.10}\) and \(2^{83.10}\) respectively. Since the attack procedure is similar to the approach presented in Sect. 5.4, we do not repeat it. Related tables and complexity of each step of the attack for SIMON-48/96 has been presented in Appendix B (The time complexity of each sub-step was computed as shown in the Tables 8, 9, and 10). To attack SIMON-48/72, we add three rounds in forward direction instead of the current four rounds. Hence, the adversary does not need to guess the average 21 bits of the key in the last round of Fig. 2.
6 Conclusion
In this paper, we propose a time-memory tradeoff that finds better differential/linear approximation. The method benefits from the correlation matrix method and the MIP method to improve the estimated squared correlation or differential probability. Using MIP we can find the trails that are missed by the matrix method. This method enables us to find a 17-round linear hull for SIMON-48. Moreover, we have analyzed the security of some variants of SIMON against different variants of linear cryptanalysis, i.e. classic and linear hull attacks. We have investigated the linear hull effect on SIMON-32 / 64 and SIMON-48 / 96 using the correlation matrix of the average squared correlations and presented best linear attack on this variant.
Regarding SIMON-64, the squared correlation matrix which we are able to build and process holds masks with Hamming weight \(\le 6\). Using only the matrix and going for more than 20 rounds, the best squared correlation we found has very low squared correlation \(< 2^{-70}\) and this is because we are missing good trails with heavy Hamming weights. Applying our time-memory trade-off has not been effective due to the large number of rounds. However, trying to find good trails with heavy Hamming weight in the middle beside the upper and lower classes might yield better results. We note here that we have been looking for fast solutions. It could be that trying to add up many linear trails for some days or weeks can yield better results. Our method seems to be slow due to the slow processing of the huge squared correlation matrix. So it would be very interesting to build a dedicated sparse squared correlation matrix for SIMON-64 in order to speed up the selection of the intermediate masks in our time-memory trade-off method. This will allow us to select many intermediate masks which might yield better results. One interesting target would be also to apply this method to the block cipher PRESENT which also allows low Hamming weight trails and see if we can go beyond the current best 24-round linear approximations [1].
References
Abdelraheem, M.A.: Estimating the probabilities of low-weight differential and linear approximations on PRESENT-like ciphers. In: Kwon, T., Lee, M.-K., Kwon, D. (eds.) ICISC 2012. LNCS, vol. 7839, pp. 368–382. Springer, Heidelberg (2013)
Abdelraheem, M.A., Alizadeh, J., AlKhzaimi, H., Aref, M.R., Bagheri, N., Gauravaram, P., Lauridsen, M.M.: Improved Linear Cryptanalysis of Round Reduced SIMON. IACR Cryptology ePrint Archive, 2014:681 (2014)
Abed, F., List, E., Lucks, S., Wenzel, J.: Differential Cryptanalysis of Reduced-Round Simon. IACR Cryptology ePrint Archive 2013:526 (2013)
Abed, F., List, E., Lucks, S., Wenzel, J.: Differential cryptanalysis of round-reduced simon and speck. In: Cid, C., Rechberger, C. (eds.) FSE 2014. LNCS, vol. 8540, pp. 525–545. Springer, Heidelberg (2015)
Alizadeh, J., Alkhzaimi, H.A., Aref, M.R., Bagheri, N., Gauravaram, P., Kumar, A., Lauridsen, M.M., Sanadhya, S.K.: Cryptanalysis of SIMON variants with connections. In: Sadeghi, A.-R., Saxena, N. (eds.) RFIDSec 2014. LNCS, vol. 8651, pp. 90–107. Springer, Heidelberg (2014)
Alizadeh, J., Bagheri, N., Gauravaram, P., Kumar, A., Sanadhya, S.K.: Linear Cryptanalysis of Round Reduced SIMON. IACR Cryptology ePrint Archive 2013:663 (2013)
Ashur, T.: Improved linear trails for the block cipher simon. Cryptology ePrint Archive, Report 2015/285 (2015). http://eprint.iacr.org/
Aumasson, J.-P., Henzen, L., Meier, W., Naya-Plasencia, M.: Quark: a lightweight hash. In: Mangard, S., Standaert, F.-X. (eds.) CHES 2010. LNCS, vol. 6225, pp. 1–15. Springer, Heidelberg (2010)
Beaulieu, R., Shors, D., Smith, J., Treatman-Clark, S., Weeks, B., Wingers, L.: The SIMON and SPECK Families of lightweight block ciphers. IACR Cryptology ePrint Archive 2013, 404 (2013)
Biham, E.: On matsui’s linear cryptanalysis. In: De Santis, A. (ed.) EUROCRYPT 1994. LNCS, vol. 950, pp. 341–355. Springer, Heidelberg (1995)
Biryukov, Alex, Roy, Arnab, Velichkov, Vesselin: Differential analysis of block ciphers SIMON and SPECK. 8540, 546–570 (2015)
Bogdanov, A., Knezevic, M., Leander, G., Toz, D., Varici, K., Verbauwhede, I.: SPONGENT: A Lightweight Hash Function. In: Preneel and Takagi [22], pp. 312–325
Bogdanov, A.A., Knudsen, L.R., Leander, G., Paar, C., Poschmann, A., Robshaw, M., Seurin, Y., Vikkelsoe, C.: PRESENT: an ultra-lightweight block cipher. In: Paillier, P., Verbauwhede, I. (eds.) CHES 2007. LNCS, vol. 4727, pp. 450–466. Springer, Heidelberg (2007)
Boura, C., Naya-Plasencia, M., Suder, V.: Scrutinizing and improving impossible differential attacks: applications to CLEFIA, Camellia, LBlock and Simon. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8873, pp. 179–199. Springer, Heidelberg (2014)
De Cannière, C., Preneel, B.: Trivium. In: Robshaw and Billet [23], pp. 244–266
Daemen, J., Rijmen, V.: The Design of Rijndael: AES - The Advanced Encryption Standard. Information Security and Cryptography. Springer, Heidelberg (2002)
Guo, J., Peyrin, T., Poschmann, A.: The PHOTON Family of Lightweight Hash Functions. In: Rogaway, P. (ed.) CRYPTO 2011. Lecture Notes in Computer Science, vol. 6841, pp. 222–239. Springer, Heidelberg (2011)
Guo, J., Peyrin, T., Poschmann, A., Robshaw, M.J.B.: The LED Block Cipher. In: Preneel and Takagi [22], pp. 326–341
Hell, M., Johansson, T., Maximov, A., Meier, W.: The grain family of stream ciphers. In: Robshaw and Billet [23], pp. 179–190
Kölbl, S., Leander, G., Tiessen, T.: Observations on the SIMON Block Cipher Family. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 161–185. Springer, Heidelberg (2015)
Mouha, N., Wang, Q., Gu, D., Preneel, B.: Differential and Linear Cryptanalysis Using Mixed-Integer Linear Programming. In: Wu, C.-K., Yung, M., Lin, D. (eds.) Inscrypt 2011. LNCS, vol. 7537, pp. 57–76. Springer, Heidelberg (2012)
Preneel, B., Takagi, T. (eds.): CHES
Robshaw, M.J.B., Billet, O. (eds.): New Stream Cipher Designs - The eSTREAM Finalists. LNCS, vol. 4986. Springer, Heidelberg (2008)
Shi, D., Lei, H., Sun, S. Song, L., Qiao, K., Ma, X.: Improved Linear (hull) Cryptanalysis of Round-reduced Versions of SIMON. IACR Cryptology ePrint Archive 2014: 973 (2014)
Sun, S., Lei, H., Wang, M., Wang, P., Qiao, K., Ma, X., Shi, D., Song, L., Kai, F.: Towards Finding the Best Characteristics of Some Bit-oriented Block Ciphers and Automatic Enumeration of (Related-key) Differential and Linear Characteristics with Predefined Properties. IACR Cryptology ePrint Archive 2014: 747 (2014)
Sun, S., Hu, L., Wang, P., Qiao, K., Ma, X., Song, L.: Automatic security evaluation and (Related-key) differential characteristic search: application to SIMON, PRESENT, LBlock, DES(L) and other bit-oriented block ciphers. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8873, pp. 158–178. Springer, Heidelberg (2014)
Wang, N., Wang, X., Jia, K., Zhao, J.: Differential Attacks on Reduced SIMON Versions with Dynamic Key-guessing Techniques. IACR Cryptology ePrint Archive 2014: 448 (2014)
Wang, N., Wang, X., Jia, K., Zhao, J.: Improved Differential Attacks on Reduced SIMON Versions. IACR Cryptology ePrint Archive 2014: 448 (2014)
Wang, Qingju, Liu, Zhiqiang, Kerem Varici, Yu., Sasaki, Vincent Rijmen, Todo, Yosuke: Cryptanalysis of Reduced-Round SIMON32 and SIMON48. In: Meier, Willi, Mukhopadhyay, Debdeep (eds.) INDOCRYPT 2014. Lecture Notes in Computer Science, vol. 8885, pp. 143–160. Springer, Heidelberg (2014)
Yang, G., Zhu, B., Suder, V., Aagaard, M.D., Gong, G.: The simeck family of lightweight block ciphers. In: Güneysu, T., Handschuh, H. (eds.) CHES 2015. LNCS, vol. 9293, pp. 307–329. Springer, Heidelberg (2015)
Acknowledgments
The authors would like to thank Lars Knudsen, Stefan Kölbl, Martin M. Lauridsen, Arnab Roy and Tyge Tiessen for many useful discussions about linear and differential cryptanalysis of SIMON. Many thanks go to Anne Canteaut and the anonymous reviewers for their valuable comments and suggestions to improve the quality of the paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Steps of the Key Recovery Attack on SIMON-32/64
B Steps of the Key Recovery Attack on SIMON-48/96
C MIP Experiments
Table 11 shows the 30 sub approximations that have been used to estimate the squared correlations of the lower class trails. The experiments where the MIP solutions are limited to 512 trails per approximation took exactly 70125.382718 seconds which is less than 20 hrs using a standard laptop.
Table 12 shows the 30 sub approximations that have been used to estimate the squared correlations of the upper class trails. The experiments where the MIP solutions are limited to 512 trails per approximation took exactly 62520.033249 seconds which is less than 18 hrs using a standard laptop.
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Abdelraheem, M.A., Alizadeh, J., Alkhzaimi, H.A., Aref, M.R., Bagheri, N., Gauravaram, P. (2015). Improved Linear Cryptanalysis of Reduced-Round SIMON-32 and SIMON-48. In: Biryukov, A., Goyal, V. (eds) Progress in Cryptology -- INDOCRYPT 2015. INDOCRYPT 2015. Lecture Notes in Computer Science(), vol 9462. Springer, Cham. https://doi.org/10.1007/978-3-319-26617-6_9
Download citation
DOI: https://doi.org/10.1007/978-3-319-26617-6_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-26616-9
Online ISBN: 978-3-319-26617-6
eBook Packages: Computer ScienceComputer Science (R0)






 and do as follows (note that the
and do as follows (note that the  subkey bits involved in the rounds are the constant bits and do not have to be guessed):
subkey bits involved in the rounds are the constant bits and do not have to be guessed): .
. ,
, 
 ,
,  , and
, and  , step by step.
, step by step.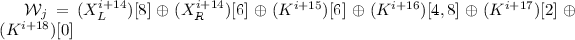 .
. ,
,  ,
,  . For each possible value of
. For each possible value of 
 , and
, and  , step by step (see Table
, step by step (see Table  .
. . For each possible value of
. For each possible value of  ,
,  , and
, and  .
. and
and  . Guess the subkey bits
. Guess the subkey bits  and for each possible value of
and for each possible value of  and can be extracted from
and can be extracted from 
