Denoising Cluster Analysis

Abstract

Clustering or cluster analysis is an important and common task in data mining and analysis, with applications in many fields. However, most existing clustering methods are sensitive in the presence of limited amounts of data per cluster in real-world applications. Here we propose a new method called denoising cluster analysis to improve the accuracy. We first construct base clusterings with artificially corrupted data samples and later learn their ensemble based on mutual information. We develop multiplicative updates for learning the aggregated cluster assignment probabilities. Experiments on real-world data sets show that our method unequivocally improves cluster purity over several other clustering approaches.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Cluster analysis or clustering is an exploratory data analysis tool which aims at dividing data objects into groups such that objects in the same group are more similar than those in other groups. As one of the major tools for modern data mining and analysis, clustering research has found a wide variety of applications in many domains of science and technology.

Most clustering methods are built upon statistical laws, assuming a wealth of samples are available per cluster. With a limited amount of data points, many existing cluster analysis approaches can only achieve mediocre performance. Especially, methods that employ non-convex objectives are prone to yield poor local optima, which demands more complicated pre-training or initialization.

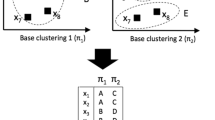
In this paper we propose a new clustering technique called denoising cluster analysis (DECLU). We first manually incorporate a small amount of noise among the data points. This is equivalent to sampling from the underlying smoothed data distribution, which potentially can generate infinite amounts of training data. We first build a base clustering for each noisy version of the data set. Next we aggregate the basal partitions into a single final clustering by using an information theoretic measure based on mutual information.

As an algorithmic contribution, we develop a new clustering ensemble method based on nonnegative learning, without construction of dense and expensive consensus relationship graph. We derive the multiplicative update rule for right stochastic matrices, which result in probabilistic cluster assignments.

We test the new method on various real-world data sets and compare it with several other clustering and ensemble clustering methods. The experimental results indicate that our method is more advantageous in terms of clustering accuracy.

The remaining paper is organized as follows. Section 2 briefly reviews mutual information and its application in comparing clusterings. Next we present our method in Sect. 3, with the base clustering generation, the ensemble clustering objective, and its optimization using multiplicative updates. In Sect. 4, we report the experiment setting and results. Section 5 summarizes the paper and discusses some possibilities for future work.

In what follows, a clustering is represented by a cluster indicator matrix, for example, denoted by U where $U_{ik}=1$ if the ith sample is in the kth cluster, and $U_{ik}=0$ elsewhere.

2 Preliminary: Mutual Information

In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual dependence between variables. The mutual information of two discrete random variables X and Y can be defined as

$$\begin{aligned} I(X;Y) = \sum _{y\in Y}\sum _{x\in X}P(x,y)\log \frac{P(x,y)}{P(x)P(y)}. \end{aligned}$$

(1)

Mutual information measures the information that X and Y share. If X and Y are independent, then knowing X does not give any information about Y and vice versa, so their mutual information is zero. At the other extreme, if X is a deterministic function of Y and Y is a deterministic function of X then all information conveyed by X is shared with Y. In this case the mutual information is the same as the uncertainty (entropy) contained in Y (or X) alone.

Mutual information (MI) can be used to compare two clusterings U and V (see e.g., [12]). Let $n_{ij}$ be the number of objects that are common to the ith cluster in U and the jth cluster in V, $a_i=\sum _jn_{ij}$, $b_j=\sum _in_{ij}$, and $\sum _{ij}n_{ij}=N$. Then

$$\begin{aligned} I(U;V) = \sum _i\sum _j\frac{n_{ij}}{N}\log \frac{n_{ij}/N}{a_ib_j/N^2}. \end{aligned}$$

(2)

A larger MI indicates that the two clusterings are closer up to a certain cluster permutation. Various normalizations can be applied to fix the MI range in [0, 1]. See [12] for a summary.

3 Denoising Clustering

Learning with artificially corrupted data, represented by training samples with manually incorporated noise, is a well-known trick in many machine learning settings, for example, generating additional training examples for Support Vector Machine classifier to improve generalization performance (see e.g., [2, 4]), and reconstructing input data from artificial corruption in Denoising Auto-Encoder for learning useful representations of data (see e.g., [10, 11]). In this work, we apply a similar trick to cluster analysis. This encompasses two steps: we first construct base clusterings for noisy versions of the data, and then aggregate them into a single final clustering.

3.1 Generating Base Clusterings

A good clustering should respect the data distribution that underlies finite amount of sample data points. Kernel smoothing or Parzen window method [6] is a common approach to estimate the distribution that underlies the given data points.

In this work, instead of explicitly run kernel density estimation, which is usually expensive, we employ an implicit way to achieve a similar regularization for the clustering task for better accuracy. In the following, we implicitly use the Parzen window with Gaussian radial kernel, but the same technique can be extended to other kernels in a straightforward manner.

We add white noise to each data point $x_i$:

$$\begin{aligned} \tilde{x}_i = x_i + \epsilon _i, \end{aligned}$$

(3)

where $\epsilon _i\sim \mathcal {N}(0,\sigma )$. Next we apply a relatively simple clustering method to partition the noisy data $\widetilde{X}=\{\tilde{x}_1,\dots ,\tilde{x}_N\}$. We choose Normalized Cut [8] for the base clusterings because it is less sensitive to the initializations and performs better for data in curved manifolds.

3.2 Clustering Ensemble Using Mutual Information

Next we find the consensus clustering of the basal partitions based on noisy versions of the original data. Classical clustering ensemble methods require construction of a pairwise relationship graph, which is quadratic to the number of samples and thus prohibitive for large-scale data sets. Here we propose a new method that directly learns the cluster assignment probabilities of size $N\times r$ for N data points and r clusters. This significantly reduces the computational cost.

Let $U^{(m)}$ denote the mth base clustering indicator matrix, where $m=1,\dots ,M$. We seek a probabilistic cluster ensemble W where $W_{ik}$ is the probability of the kth cluster given the ith sample. The ensemble minimizes the total difference to the base clusterings, measured by the “$D_\text {sum}$” distance based on mutual information [12]:

(4)

(5)

where H is the entropy of cluster assignment. We choose this objective because it is a valid metric, bounded in $[0, M\log N]$, and with relatively simple gradient for optimization.

Writing out the objective, we have

$$\begin{aligned} \nonumber \mathcal {J}(W)=~&~\sum _m\left[ -\sum _k\frac{1}{N}\sum _iW_{ik}\log \frac{1}{N}\sum _iW_{ik}\right. \\ \nonumber ~&~-\sum _k\frac{1}{N}\sum _iU_{ik}^{(m)}\log \frac{1}{N}\sum _iU_{ik}^{(m)}\\ \nonumber ~&~\left. -2\sum _{kl}\frac{1}{N}\sum _iW_{ik}U^{(m)}_{il}\log \frac{\frac{1}{N}\sum _iW_{ik}U^{(m)}_{il}}{\frac{1}{N}\sum _iW_{ik}\frac{1}{N}\sum _iU^{(m)}_{il}}\right] \\ \nonumber =~&~\sum _m\left[ \frac{1}{N}\sum _k\sum _iW_{ik}\log \sum _iW_{ik}\right. \\ \nonumber ~&~-\frac{2}{N}\sum _{kl}\sum _iW_{ik}U^{(m)}_{il}\log \sum _iW_{ik}U^{(m)}_{il}\\ ~&~+\left. \frac{2}{N}\sum _i\left( \sum _kW_{ik}\right) \sum _lU^{(m)}_{il}\log \sum _jU^{(m)}_{jl}\right] +\text {constant}. \end{aligned}$$

(6)

Using Lagrangian multipliers $\lambda =[\lambda _1,\dots ,\lambda _N]$ for the sum-to-one constraints, the relaxed objective function is

$$\begin{aligned} \widetilde{\mathcal {J}}(W,\lambda ) = \mathcal {J}(W) - \sum _i\lambda _i(\sum _k W_{ik}-1). \end{aligned}$$

(7)

Its gradient w.r.t. W is $\displaystyle \frac{\partial \widetilde{\mathcal {J}}(W)}{\partial W_{ik}}=\mathcal {\nabla }^+_{ik}-\mathcal {\nabla }^-_{ik} - \lambda _i$, where $\mathcal {\nabla }^+$ and $\mathcal {\nabla }^-$ are the positive and (unsigned) negative parts of the $\frac{\partial \mathcal {J}(W)}{\partial W}$

$$\begin{aligned} \mathcal {\nabla }^+_{ik}&=-\frac{2}{N}\sum _{m}\sum _t\left( \log \frac{\sum _iW_{ik}U^{(m)}_{it}}{N}\right) U^{(m)}_{it}+\frac{M}{N}(1+\log N)\end{aligned}$$

(8)

$$\begin{aligned} \mathcal {\nabla }^-_{ik}&=-\frac{M}{N}\log \frac{\sum _iW_{ik}}{N}-\frac{2}{N}\sum _m\sum _lU^{(m)}_{il}\log \frac{\sum _jU^{(m)}_{jl}}{N}. \end{aligned}$$

(9)

This suggests the preliminary multiplicative update rule $\displaystyle W'_{ik}= W_{ik}\frac{\mathcal {\nabla }^-_{ik}+\lambda _i}{\mathcal {\nabla }^+_{ik}}$. Imposing the constraints $\sum _kW'_{ik}=1$, we have $\displaystyle \sum _k W_{ik}\frac{\mathcal {\nabla }^-_{ik}}{\mathcal {\nabla }^+_{ik}} + \lambda _i\sum _k\frac{W_{ik}}{\mathcal {\nabla }^+_{ik}} =1$. Solving the equation we obtain

$$\begin{aligned} \lambda _i = \frac{1-\sum _k W_{ik}\mathcal {\nabla }^-_{ik}/\mathcal {\nabla }^+_{ik}}{\sum _k W_{ik}/\mathcal {\nabla }^+_{ik}} \end{aligned}$$

(10)

Putting them back to the preliminary rule, we have $W_{ik}^{'} = W_{ik}\frac{\mathcal {\nabla }^-_{ik}A_{ik} + 1 - B_{ik}}{\mathcal {\nabla }^+_{ik}A_{ik} }$, where

$$\begin{aligned} A_{ik} = \sum _k\frac{W_{ik}}{\mathcal {\nabla }^+_{ik}}\text { and } B_{ik}=\sum _kW_{ik}\frac{\mathcal {\nabla }^-_{ik}}{\mathcal {\nabla }^+_{ik}}. \end{aligned}$$

(11)

There is a negative term $-B_{ik}$ in the numerator, which may cause negative entries in the updated W. To overcome this, we apply the “moving term” trick [15–18, 21] to resettle $B_{ik}$ to the denominator, giving the final update rule

$$\begin{aligned} W_{ik}^\text {new} = W_{ik}\frac{\mathcal {\nabla }^-_{ik}A_{ik} + 1 }{\mathcal {\nabla }^+_{ik}A_{ik} + B_{ik}}. \end{aligned}$$

(12)

Our ensemble algorithm simply iterates the above update rule until W converges. The updates have the following guarantee

Theorem 1

$\widetilde{\mathcal {J}}(W^\text {new},\lambda )\le \widetilde{\mathcal {J}}(W,\lambda )$, with $\lambda$ given in Eq. 10.

The proof is given in the Appendix. The theorem shows that the algorithm jointly reduces $\mathcal {J}(W)$ while steering W rows to the probability simplex. The tradeoff between these two forces is adaptively adjusted by $A_{ik}$.

4 Experiments

We have tested our new method on six real-world data sets from the UCI repository¹. Their statistical characteristics are given in Table 1 and below a brief verbal description of each data set is given:

• ECOLI, the UCI Ecoli data set, containing protein localization sites, originally with 8 attributes.

• WINE, the UCI Wine data set, which is a result of a chemical analysis of wines grown in the same region in Italy but derived from three different cultivars, originally with 13 dimensional features;

• MFEAT, the UCI Multiple Features data set, which consists of features of handwritten numerals; the digits are represented in terms of 649 features from six aspects;

• SEGMENT, the UCI Image Segmentation data set, image patches from 7 outdoor images, originally with 19 high-level features;

• OPTDIGITS, the UCI optical recognition of handwritten digits data set, originally with 64 dimensions;

• PENDIGITS, the UCI pen-based recognition of handwritten digits data set, originally with 16 dimensions.

Table 1. Statistics of the data sets.

Table 2. Clustering purities for the compared methods. Boldface numbers indicate the best for each data set.

We have compared DECLU with five other clustering approaches, three single clustering methods and two clustering ensemble methods:

• Normalized Cut (Ncut) [8], a spectral clustering method that projects the tailing eigenvectors of symmetric normalized Laplacian of the similarity matrix to the closest cluster indicator matrix;

• Probabilistic Latent Semantic Indexing (PLSI) [5] which factorize the similarity matrix $P(x_i,x_j)\approx \sum _kP(x_i|C=k)P(x_j|C=k)P(C=k)$, where C is the cluster variable; the cluster assignment $P(C=k|x_i)$ can then be obtained with $P(x_i|C=k)$ and $P(C=k)$ through Bayes rule;

• Left Stochastic Decomposition (LSD) [1] which factorizes the similarity matrix into two left-stochastic matrices;

• Cluster-based similarity partitioning algorithm (CSPA) [9], the similarity between two data-points is defined to be directly proportional to number of constituent clusterings of the ensemble in which they are clustered together;

• Meta-clustering algorithm (MCLA) [9], which is based on clustering clusters; first, it tries to solve the cluster correspondence problem and then uses voting to place data-points into the final consensus clusters.

We use the default setting in the above methods. The number of clusters is set to the number of known classes in each data set. We followed the convention that uses kmeans for generating base clustering for CSPA and MCLA. For DECLU, we have used $\sigma =0.02$ in noise generation and $K=5$ in K-Nearest-Neighbor similarity graph. For all cluster ensemble methods, we have used $M=10$ base clusterings.

The clustering performance is evaluated by cluster purity, calculated by $\text {purity}=\displaystyle \frac{1}{N}\sum _{k=1}^r\max _{1\le l\le r}n_k^l$, where $n_k^l$ is the number of data samples in the cluster k that belong to ground-truth class l. A larger purity in general corresponds to a better clustering result.

The resulting cluster purities are shown in Table 2. We can see that DECLU yields top performance for all data sets, with a tie with a different method on two (MFEAT and SEGMENT) out of the six data sets in total.

5 Conclusion

In this paper we have proposed a new clustering method which consists of two steps. First, we repeatedly incorporate a small amount of noise to the data to generate multiple base partitions of the data. Next, we have developed a new ensemble method using information theoretic metric and its multiplicative optimization algorithm. Empirical studies on the new method indicate that it outperforms several other existing clustering approaches in terms of clustering accuracy.

In this work we used a fixed amount of Gaussian noise. Other types of noise would be interesting to study in the future. Similarly, it would be valuable to investigate how to automatically adjust the noise level for generating better base clusterings. Moreover, we aim at examining other information divergence (e.g., [3, 20]) or mutual information variants besides $D_\text {sum}$ to improve the ensemble performance (e.g., [7, 12, 19]). Other types of base clustering generation methods (e.g., [13, 14]) could further improve the accuracy. In summary, the consistently satisfactory performance of DECLU and its computational scalability suggest considerable potential for further development of denoising based clustering methods.

Appendix: Proof of Theorem 1

Proof

We use W for current estimate, $\widetilde{W}$ for variable, and $W^\text {new}$ for the new estimate, respectively. The objective function $\widetilde{\mathcal {J}}$ fulfills the theorem conditions in [16]. Therefore, we can construct the majorization function

$$\begin{aligned} \nonumber G(\widetilde{W},W)=&\sum _{ik}\left[ \mathcal {\nabla }^+_{ik}\widetilde{W}_{ik}-\mathcal {\nabla }^-_{ik}W_{ik}\log \widetilde{W}_{ik}+\frac{B_{ik}}{A_{ik}}W_{ik}-\frac{W_{ik}}{A_{ik}}\log \widetilde{W}_{ik}\right] +\text {constant}\end{aligned}$$

such that $G(\widetilde{W},W)\ge \widetilde{\mathcal {J}}(\widetilde{W},\lambda )$ and $G(W,W)=\widetilde{\mathcal {J}}(W,\lambda )$. Let $W^\text {new}$ be the minimum of $G(\widetilde{W},W)$, which is implemented by zeroing $\partial G/\partial \widetilde{W}$ and yields Eq. 12. Therefore $\widetilde{\mathcal {J}}(W^\text {new},\lambda ) \le G(W^\text {new},W) \le G(W,W) =\widetilde{\mathcal {J}}(W,\lambda )$.