Experiments on Data Classification Using Relative Entropy

Abstract

Data classification is one of the basic tasks in data mining. In this paper, we propose a new classifier based on relative entropy, where data to particular class assignment is made by the majority good guess criteria. The presented approach is intended to be used when relations between datasets and assignment classes are rather complex, nonlinear, or with logical inconsistencies; because such datasets can be too complex to be classified by ordinary methods of decision trees or by the tools of logical analysis. The relative entropy evaluation of associative rules can be simple to interpret and offers better comprehensibility in comparison to decision trees and artificial neural networks.

1 Introduction

Data classification and data compression shares several common concepts, first of all they both try to reduce provided data into some smaller unit. In this sense, data classification can be considered as a lossy compression, but in data classification ability to recover former data from resulting class is not our ambition, we are perfectly confident with reduction and recovery is not needed. There are several basic categories of classification algorithms, there are algorithms based on decision trees, learning set of rules, neural networks, naive Bayesian classifiers, instance-based learning, and support vector machines, a review of algorithms can be found in Kotsiantis [1]. Classification algorithms presented in this paper belong to the learning set of rules class, extensive overview of the learning set of rules class of algorithms is provided in [2]. Experiments made in this paper use several concepts from Information Theory [3, 4], especially concept of entropy and relative entropy. The role of entropy in data classification was already studied and several algorithms reducing entropy of training dataset like ID3 [5] and PRISM [6] were developed. The main idea covered in this paper is to use relative entropy to evaluate rules, such evaluation can then be used to sort rules and consequently to select first n of them for classification purposes. Class of classifiers presented in this paper is in the present state able to distinguish only between two classes, so our presented results will deal only with binary classification. We compared our results with the work of Thabtah [7] and Li [8]. The rest of the paper is organized as follows. Section 2 contains description of entropy, relative entropy, and introduces basics of these concepts. Section 3 describes rules, their types, and how can be rules evaluated by relative entropy. Section 4 describes the proposed classifier. Section 5 contains discussion and presents results achieved on the selected datasets. Last Sect. 6 concludes the paper and discusses the future experiments.

2 Entropy

Entropy is the key concept of Information Theory, but the term itself has many interpretations, statisticians would say it is uncertainty in random variable, Information Theory scientist would say it is the amount of information, data compression scientist would say it is the average number of bits needed to describe symbols and we can continue with physicists and so on; in this paper, we will follow Fano’s [9] interpretation of entropy, as in his point of view the entropy is an average number of binary questions that we would put in infinitely many trials to distinguish between different events. When probabilities of classes are given, we can compute entropy by Shannon’s equation:

$$\begin{aligned} H = -\sum _{x}p(x)\log {p(x)} \end{aligned}$$

(1)

Entropy is always nonnegative and is zero only when one item $x_i$ has probability $p(x_i)=1$, since when probability of some event is equal to one, then we do not need to put any questions about incoming event, because we know exactly what the event is. All logarithms in this paper are based two. For the given set of events, the entropy is maximal when distribution of events is uniform: $p(x_i)=p(x_j)$ for all indices i, j of events $x_i,x_j$ in p(x).

2.1 Relative Entropy

Using entropy, we get an amount of information respective number of binary questions about single probability distribution. In Information Theory, the concept of relative entropy D(P||Q) is used to measure distance between two different probability distributions p(x) and q(x).

$$\begin{aligned} D(P||Q) = \sum _{x\in \varSigma }p(x)\log \frac{p(x)}{q(x)} \end{aligned}$$

(2)

Relative entropy defined by (2) measures distance in bits, respectively; in extra binary questions, we have to put if instead of proper distribution p(x) use other distribution q(x). Relative entropy in (2) is nonnegative but it is not a metric function, because symmetry condition fails: $D(P||Q)\ne D(Q||P)$. In the former paper of Kullback and Leibler [10], authors derived symmetric measure later called by their names as Kullback–Leibler divergence $D_{KL}$:

$$\begin{aligned} D_{KL} = D(P||Q) + D(Q||P) \end{aligned}$$

(3)

When computing rules, we analyze individual terms in summations of (2) and (3), the individual term:

$$\begin{aligned} D(x)=p(x)\log \frac{p(x)}{q(x)} \end{aligned}$$

(4)

uncovers several properties about single shared event x from the two distributions p, q when they are compared. Since probabilities are defined on closed interval $p(x)\in <0;1>$, then D(x) is positive when $\log \frac{p(x)}{q(x)}>0$ and so must hold that $p(x)>p(y)$. When both distributions are equal $p(x)=q(x)$ for all x then each term $\log \frac{p(x)}{p(x)}=0$ and also $D(P||Q)=D_{KL}(P||Q)=0$. If we view entropy as an average number of questions to differentiate between classes, then relative entropy can be interpreted as the increase of an average number of question, we have to put, if instead of distribution P distribution Q is used. We hope that concepts of entropy and relative entropy can be more comprehensible for interpretation than, for example, decision tree structure or weight given by artificial neural network.

2.2 Zeros and Infinities in Relative Entropy

By definition $0\log 0 = 0$, even when $\log 0$ is undefined, the factor in front of logarithm will force the term to be zero, but the case when $\log x/0$ is present then it is interpreted as infinity, because $\lim _{x\rightarrow 0^+}\log 1/x = \infty$. Zeros and infinities in relative entropy bring several problems, infinities in comparison of a relative entropy of different probability distributions causes their incomparability. In computational implementation, division by zero problem appears. For comparison purposes, the error into computation of relative entropy is introduced, suppose that in the training data set, the frequency of some particular event x from class $c_1$ is $f_{1}(x)>0$ and for class $c_2$ is $f_{2}(x)=0$, then we set the zero frequency to be equal to one: $f_{2}(x)=1$.

2.3 Relative Entropy of Multiple Attributes

When we need to compute relative entropy over several attributes $a_{1},a_{2},\ldots ,a_{n}$, we simply substitute $p(x_{i})$ for its joint form $p(x_{1},x_{2},\ldots ,x_{n})$:

$$\begin{aligned} D(P||Q) = p(x_{1},x_{2},\ldots ,x_{n})\log \frac{p(x_{1},x_{2},\ldots ,x_{n})}{q(x_{1},x_{2},\ldots ,x_{n})} \end{aligned}$$

(5)

2.4 Example

Suppose a simple dataset given in Table 1 consisting of two attributes and two classes into which we would like to assign individual records. Each class-attribute combination has associated joint probability vector $p(c_i,a_i)$, in our example case, classes $c_1$ and $c_2$ have for attribute $a_1$ corresponding vectors:

$$\begin{aligned} p(c_1,a_1) = (p(c_1,x_1),p(c_1,y_1))=(1,0) \end{aligned}$$

(6)

and

$$\begin{aligned} p(c_2,a_1)=(p(c_2,x_1),p(c_1,y_1))=(0,1) \end{aligned}$$

(7)

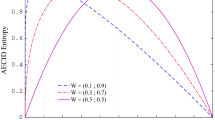
Probabilities are computed only from records belonging to particular class. When the relative entropy is computed over attribute’s $a_1$ probability vectors, we get infinities since: $D(P(c_1,a_1)||Q(c_2,a_1)) = 1\log \frac{1}{0} + 0\log \frac{0}{1}=\infty + 0=\infty$, the same value is achieved when the measuring set is P: $D(Q(c_2,a_1)||P(c_1,a_1))=\infty$. When attribute $a_2$ is considered then its corresponding joint probability vectors are: $p(c_1,a_2) =(1,0)$ and for the second class $p(c_2,a_2) =(0.5,0.5)$. In this case, relative entropies will be $D(P(c_1,a_2)||Q(c_2,a_2)) = 1\log \frac{1}{0.5} + 0\log \frac{0}{0.5}=1 + 0=1$. To get a better understanding of the topic, consider a following situation, let the classifier knowledge of the incoming event be equal to $q=(0.5,0.5)$, but the real distribution of events is given by $p=(1,0)$, in this situation classifier is forced to put one question to reveal the value of attribute, but if classifier would knew the real case, the vector p, then the classifier would not reveal any information about event at all.

Table 1 Description of example dataset

3 Rules

Let $r=\{a_1 = x_1, \ldots , a_n = x_n\}$ is a rule, where $a_i$ is attribute and $x_i$ is a particular value of attribute $a_i$. The number of different attributes in rule r is a length of the rule. Let R be a set of rules $r_i$ over data source S. In the present section, we will describe several classes of rules we distinguish:

• correct rules,

• mostly correct rules,

• neutral rules,

• incorrect rules.

 

Definition 1

Correct rule is a rule, when applied on training data set, which makes only good predictions.

In PRISM algorithm, the author proposed a method that works only with rules of ‘correct’ class, rules of this class make only good predictions over training data. From relative entropy perspective, every time some rule is classified as ‘correct’ then its single relative entropy (4) is infinite.

Definition 2

The mostly correct rule is a rule, that when applied on training data set, makes majority of predictions correct.

The mostly correct rules have single relative entropy positive. In our experiments, we deal primarily with rules, which are correct over majority number of training samples. This class contains as a subclass ‘correct’ rules class.

Definition 3

Neutral rule is a rule, that when applied has equal number of correct and incorrect predictions.

The neutral rule has its corresponding single relative entropy equal to zero. The last class of rules is a class of incorrect rules. The incorrect rule has the single relative entropy negative. We do not use neutral and incorrect rules in our experiments, since these rules contribute mainly to misprediction.

Definition 4

Incorrect rule is a rule, that when applied, makes majority number of predictions incorrect.

3.1 Relative Entropy of Rules

Suppose again individual summation terms from Eq. (3) for some event $x_i$ and suppose that $p(x_{i})>q(x_{i})$, then there are exactly two individual relative entropies that can be computed $D(P=x_{i}||Q=x_{i})$ and $D(Q=x_{i}||P=x_{i})$, meanwhile the former is positive the latter is negative and because the relative entropy is nonnegative func-tion $D(P=x_{i}||Q=x_{i}) > -D(Q=x_{i}||P=x_{i})$. In our experiments we considered two ways of rules comparison:

• the ratio between relative entropies,

• and the sum of relative entropies.

In the case when the ratio between relative entropies is applied, when nominator and denominator are evaluated, and the whole equation is simplified we realize that the ratio between relative entropies is exactly the negative ratio between probabilities:

$$\begin{aligned} r = \frac{p(x_{i})\log \frac{p(x_{i})}{q(x_{i})}}{q(x_{i})\log \frac{q(x_{i})}{p(_{i}x)}} = \frac{p(x_{i})\log \frac{p(x_{i})}{q(x_{i})}}{-q(x_{i})\log \frac{p(x_{i})}{q(x_{i})}}=-\frac{p(x_{i})}{q(x_{i})} \end{aligned}$$

(8)

When rules are being sorted, the absolute value of (8) is taken. The ratio is dimensionless parameter, meanwhile in the second case, when the sum of relative entropies is applied, then we are using one term of Kullback–Leibler divergence from Eq. (3) and the unit of measure is a bit (binary question):

$$\begin{aligned} s = p(x_{i})\log \frac{p(x_{i})}{q(x_{i})} + q(x_{i})\log \frac{q(x_{i})}{p(x_{i})} =(p(x_{i})-q(x_{i}))\log \frac{p(x_{i})}{q(x_{i})} \end{aligned}$$

(9)

Our philosophy is that every rule in binary classification is a rule that must predict at least neutrally, rules that are not neutral are always positive when interpreted as classifying one of the classes.

4 Basic Principles of the Classifier

The most important concept in the present paper is the concept of relative entropy and its applicability to data classification. This section describes training and test phases of the classification algorithm. The training data are prepared in the following way:

• 1. Prepare a set of all accessible rules of length n.

• 2. For each rule from the step 1, compute single relative entropies by Eq. (8) resp. (9).

• 3. Sort rules by values of relative entropies from step 2.

When the training data were processed and n-best rules were produced, we can apply these rules on particular record from the test dataset in the following way:

• 1. Select the currently best rule.

• 2. Check if the record satisfies the rule, i.e., the record has exact pairs of attribute-values like the rule. If the record do not satisfies the rule, then go to step 4.

• 3. Since each rule classifies particular class, then if the rule is present we add one to counter of corresponding class.

• 4. Select the next best rule, if there is one, and repeat step 2, otherwise go to step 5.

• 5. If the sum of predictions of one class is higher than the sum of predictions of the second class, then the record is classified as a class with higher prediction counter, otherwise the record is not classified.

Finally, all predictions of records from the test dataset are merged together and if the predicted class is equal to the class corresponding to the test record, then the classification of the record is considered to be correct. In the step 5, classifier makes the prediction by majority voting, when there is more rules in one class then in the other one, then classifiers selects as a prediction the one with more rules (voters are rules).

Table 2 Description and results on datasets from UCI

Table 3 UCI dataset—Breast

Table 4 UCI dataset—Tic Tac Toe—Endgame

Table 5 UCI dataset—Votes

5 Results and Discussion

Results were produced on datasets from UCI, since in present time our experiments have been prepared for prediction of binary classes from categorical data only, there is a limited number of datasets available to evaluate. We compared our approach with other algorithms dealing with classification by learning set of rules. Accuracies were achieved by performing tenfold cross-validation. In Table 2, the results that were achieved in [7] are summarized. Our experiments were setup to compare two characteristics, the comparison of n-best rules selection by relative entropies based on (8) and (9), and evaluation of the case when all mostly correct rules are applied. We did not setup weights to rules so far as the intention of this paper is an initial study and we focus on basic properties before we introduce more complex classification system. Accuracies of predictions are summarized in Tables 3, 4, and 5 based on two comparison criteria: classifier D-Ratio is a classifier that sorts rules by the ratio between the relative entropies, meanwhile D-Sum is a classifier based on a single Kullback–Leibler relative entropy. Both classifiers are evaluated in two scenarios, in the first scenario, rules consist of only one attribute-value pair(Attrs-1) and in the second scenario, rules consist of two attribute-value pairs(Attrs-2). In the Breast dataset, classifier was able to achieve accuracy comparable of other classifiers. One attribute sized rules performed better than in the case when two attributes were used. The best result on the dataset was achieved by CBA algorithm. To examine if classifier is able to deal with data that are logically structured, Tic Tac Toe—Endgame dataset was used and the results are summarized in Table 4. There are several reasons why classifier is unable to deal with a logically structured data, but the main reason is that the classifier uses mostly correct rules that misclassifies many records and in comparison with classifiers that are building the least set of correct rules cannot succeed. The prediction problems can be solved when we permit only rules of correct class and selects three or more attributes, such rules always leads to good prediction no matter of which subset of training data was used, because these rules are logically correct and they would mispredict only in cases when provided test dataset is logically inconsistent. The last case examined in the experiment was a UCI Votes dataset, in this particular case the accuracies of predictions achieved using four-best rules two attribute classifier were better in comparison with other algorithms. In comparison with techniques that constructs the least size set of rules, we prefer to build as large set as possible and discriminate rules afterward. Let $s_l$ is the size of the set of all rules of length l, then the presented technique selection by n-best rules will discriminate $l-n$ rules. In the presented results, we saw that usage of all rules does not lead to as good prediction as in cases with less rules, so in the future work we will consider application of weights to rules and we will try to make the all (resp. nearly all) rules prediction more accurate.

6 Conclusion

In this paper, we proposed and experimentally examined classification of categorical data using comparison of rules based on their relative entropies and selecting n-best of them. The experiments showed that the classifier has ability to classify data and even on one dataset and particular setup of classifier it was able to exceed accuracies achieved by other algorithms, but it should be also mentioned that the classifier is unable to distribute logically based datasets correctly. In the future work, we would like to prepare a version of classifier that would be able to decide between more than two classes as well as to allow the classifier to process continuous data, as that would allow us to make many more experiments and comparisons.