Cross-Domain Collaborative Recommendation by Transfer Learning of Heterogeneous Feedbacks

Abstract

With the rapid development of information society, the era of big data is coming. Various recommendation systems are developed to make recommendations by mining useful knowledge from massive data. The big data is often multi-source and heterogeneous, which challenges the recommendation seriously. Collaborative filtering is the widely used recommendation method, but the data sparseness is its major bottleneck. Transfer learning can overcome this problem by transferring the learned knowledge from the auxiliary data to the target data for cross-domain recommendation. Many traditional transfer learning models for cross-domain collaborative recommendation assume that multiple domains share a latent common rating pattern which may lead to the negative transfer, and only apply to the homogeneous feedbacks. To address such problems, we propose a new transfer learning model. We do the collective factorization to rating matrices of the target data and its auxiliary data to transfer the rating information among heterogeneous feedbacks, and get the initial latent factors of users and items, based on which we construct the similarity graphs. Further, we predict the missing ratings by the twin bridge transfer learning of latent factors and similarity graphs. Experiments show that our proposed model outperforms the state-of-the-art models for cross-domain recommendation.

1 Introduction

With the rapid development of computer and network technologies, especially the mobile internet, people can easily acquire all kinds of information from the internet. Under the big data environment of web, massive information often makes people dazzling and unable to get valuable information rapidly and effectively. In order to solve this problem of information overload, personalized recommendation systems are developed. For example, the famous personalized recommendation platforms of Amazon, Movielens, Alibaba and so on. They help users obtain the required service quickly and accurately and make huge benefits for the relevant manufacturers. Collaborative Filtering (CF) is an excellent recommendation algorithm which is widely used at present. CF in recommender systems is designed to predict the missing ratings for a user or an item based on the collected ratings from like-minded users or similar items [1, 2]. CF is simple, which doesn’t need the configuration information of users and has no special requirements to the recommendation objects. CF is effective, which can make multiple recommendations. Although CF has such advantageous properties, the recommendation performance would be degraded seriously when the observed data is very sparse.

To address the sparseness problem, many improved CF methods based on the single domain have been proposed. But these methods are subject to the data quality of the target domain. They may be invalid when the target data is extremely sparse. In reality, especially in the current era of big data, we often have many data in the associated domains of the target domain. Why not try to make use of them? So we research the cross-domain recommendation which combines relevant data from different domains with the original target data to improve the recommendation. Transfer learning [3] can be used for cross-domain CF recommendation particularly. During the transfer learning, useful knowledge will be learned from the auxiliary data and transferred to the target data so that the sparseness problem of the target data can be addressed effectively. However, traditional transfer learning models for cross-domain CF recommendation have some issues as follows:

• They are often limited to the transfer of homogeneous user feedbacks. However, the heterogeneous user feedbacks are common in reality, especially in the current big data era.

• They usually suppose that different domains share a common latent rating pattern based on the user-item co-clustering. In fact, however, the associated domains do not necessarily share such a common latent rating pattern, and the diversity among associated domains may outweigh the advantages of this common latent rating pattern [4], which may degrade the recommendation performance.

• Since the target data is extremely sparse, it is expected that more useful common knowledge is transferred from the auxiliary data to the target data. Only using the latent factors extracted from the auxiliary data may result in that the positive information transferred to the target data is insufficient.

To solve these problems, we propose a new model of cross-domain CF recommendation based on the twin bridge transfer learning of heterogeneous user feedbacks. Our contributions are summarized as follows:

• To transfer the rating information of heterogeneous user feedbacks, the initial data are preprocessed to be homogenous. Then we do the collective factorization to rating matrices of the target data and its auxiliary data, and get the initial latent factors of uses and items respectively, when we consider both the common and domain-specific latent rating patterns.

• Based on the initial latent factors, the similarity graphs are constructed. The model can be formulated as an optimization problem based on the graph regularized weighted nonnegative matrix tri-factorization [5]. In the process of optimization, latent factors and similarity graphs are regarded as a implicit bridge and a explicit bridge for transfer respectively to learn more useful knowledge.

• An efficient gradient descent method is executed to optimize the objective function with convergence guarantee. Extensive experiments on several real-world data sets suggest that our proposed model outperforms the state-of-the-art models for the cross-domain recommendation.

2 Related Work

CF is widely used due to its simpleness and high-efficiency. However, since CF method fully depends on the observed rating data, the sparseness issue has become its major bottleneck [6]. In real life, we may easily find some related CF domains with the similar recommendation as the target domain. A question was then asked in [7]: Can we establish a bridge between related CF domains and transfer useful knowledge from one another to improve the performance?, which is an emerging research topic about cross-domain CF [8].

Transfer learning is used for cross-domain CF recommendation in particular. Liu bin [9] gives a brief survey of the pilot studies on cross-domain CF in CF domains and knowledge transfer styles. Chungyi Li et al. [10] try to match users and items across domains for transfer learning to improve the recommendation quality. Weiqing Wang et al. [11] research cross-domain CF by tag transfer learning. Zhongqi Lu et al. [12] explore selective transfer learning for cross-domain recommendation. Pan et al. [13–15] propose the models to transform knowledge from domains which have heterogeneous forms of user feedbacks.

The majority of the existing transfer learning models for cross-domain recommendation assumes that the target domain and its auxiliary domains are related but doesnt suggest ways to compute the relatedness across multiple domains. The usual way of the existing models is to exploit the common latent structure shared among multiple domains as the information bridge to transfer the useful knowledge. For example, Shi, Y. et al. [16] propose a generalized cross domain CF model by tag transfer learning. They use user-generated tags as the common features to connect multiple domains together and perform transfer learning across different domains for knowledge transfer. Traditional cross-domain recommendation models assume that all the domains share the common latent rating pattern, which is inconsistent with the reality and may cause the recommendation performance of a hard decline. Gao et al. [4] propose a cluster-level latent factor model, which can not only learn the common rating pattern shared across domains with the flexibility in controlling the optimal level of sharing, but also learn the domain-specific rating patterns of users in each domain that involve the discriminative information propitious to performance improvement. This model is referred to as GAO model by us.

Liu bin et al. propose Codebook Based Transfer (CBT) model [7] and Rating Matrix Generative model [17] to transfer the cluster-level codebook to the target data, which are novel and influential. However, because the dimension of codebook is limited, the codebook cannot transfer enough useful knowledge when the observed data are quite sparse. To overcome this problem, Transfer by Collective Factorization (TCF) [15, 18], Coordinate System Transfer (CST) [19], and Transfer by Integrative Factorization (TIF) [12] extract both latent tastes of users and latent features of items in forms of latent factor matrices, and transfer the useful knowledge they contain from the auxiliary data to the sparse target data. However, these models do not take full account of the negative transfer. In addition, they only employ a single information bridge to transfer the knowledge. In Graph Regularized Weighted Nonnegative Matrix Factorization (GMF) [5] model, the neighborhood information is integrated into the factorization. The associated information among users or items can be utilized with the help of the similarity of user tastes or item features. But it requires dense ratings to calculate the neighborhood structure. When the data are very sparse, the neighborhood structure may be rather inaccurate so that the recommendation can’t be performed effectively. Different from these methods, Shi et al. [20] explore the twin bridge of latent factors and their similarity graphs for the purpose of transferring more useful knowledge to the target data, which is referred to as SHI model by us. SHI model can enhance efficient transfer by transferring more knowledge, while alleviate negative transfer by regularizing the learning model with latent factors and similarity graphs, which can naturally filter out the negative information contained in the latent factors.

3 Problem Definition

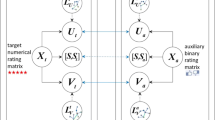
Suppose that multiple domain-related rating matrices are given. Let $\eta$ be the domain index, ${R_\eta } \in {R^{{M_\eta } \times {N_\eta }}}(\eta \in [1,t],t \in {N^ + })$ is the rating matrix of the $\eta$-th domain, where ${M_\eta }$ and ${N_\eta }$ represent the numbers of users and items, respectively. A binary weighting matrix $Z_{\eta }$ with the same size as ${R_\eta }$ is used to mark the missing ratings, where ${[{Z_\eta }]_{ij}} = 1$ if ${[{R_\eta }]_{ij}}$ is observed and ${[{Z_\eta }]_{ij}}=0$ otherwise. The rating matrix in which missing ratings are to be predicted is deemed as the target data, and other rating matrices related to the target data are deemed as the auxiliary data. The goal is to predict missing ratings in the target data by transferring useful knowledge from the auxiliary data.

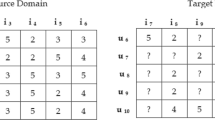
Without loss of generality, we prepare to solve a concrete problem which is the same as SHI model. Suppose that $R \in {R^{M \times N}}$ is the rating matrix of the target data, $Z \in \{ 0,1\}$ is the indicator matrix, ${Z_{ij}} = 1$ if user i has rated item j and ${Z_{ij}} = 0$ otherwise. $R_{1}$ and $R_{2}$ are rating matrices of two auxiliary data sets respectively. $R_{1}$ shares the common set of users with R, while $R_{2}$ shares the common set of items with R. We try to predict the missing ratings of R by transfer learning from $R_{1}$ and $R_{2}$. Of course, when neither the users nor the items in the ratings matrices across multiple domains such as R, $R_{1}$ and $R_{2}$ are overlapping, our proposed model will be still effective.

4 Related Models

4.1 GAO Model [4]

In GAO model, the cluster level structures hidden across domains are extracted to learn the rating pattern of user groups on the item clusters for knowledge transfer, and to clearly demonstrate the co-clusters of users and items. The co-clustering of the data matrix in domain $\eta$ can be performed by the orthogonal non-negative matrix tri-factorization, and the integrated objective function is

$$\begin{aligned} \mathop {\min }\limits _{{U_\eta },{S_0},{S_\eta },{V_\eta } \ge 0} f = \sum \limits _\eta {||[{R_\eta } - {U_\eta }[{S_0},{S_\eta }]V_\eta ^T] \odot {Z_\eta }|{|^2}} \end{aligned}$$

(1)

where $\odot$ is the entry-wise product, ${U_\eta }/{V_\eta }$ denotes the user/item latent factor matrix, ${S_0}$ denotes the share rating pattern matrix, ${S_\eta }$ denotes the specific rating pattern matrix of domain $\eta$. In order to make the factorization more accurate, some prior knowledge can be imposed on the latent factors during the optimization, such as the L1 norm constraint: ${U_\eta }1 = 1$ and ${V_\eta }1 = 1$.

4.2 SHI Model [20]

Shi et al. extract latent factors $U_{0}$ and $V_{0}$ from $R_{1}$ and $R_{2}$ by GMF [5] and construct similarity graphs $W_{U}$ and $W_{V}$ based on $U_{0}$ and $U_{0}$, respectively. $W_{U}$ and $W_{V}$ are defined as follows:

Where $u_{{i_*}}^0$ is the i th row of $U_{0}$ denoting the latent taste of user i,  $v_{{i_*}}^0$ is the i th row of $V_{0}$ denoting the latent feature of item i,  ${N_p}(u_{{j_*}}^0)$ and ${N_p}(v_{{j_*}}^0)$ are the sets of p-nearest neighbors of $u_{{i_*}}^0$ and $v_{{i_*}}^0$ respectively. Latent factors and similarity graphs are integrated into a unified optimization framework for twin bridge transfer learning:

$$\begin{aligned} \begin{aligned} \mathop {\min }\limits _{U,V,B > = 0} O = ||Z \odot (R - UB{V^T})||_F^2 + {\lambda _U}||U - {U_0}||_F^2+\\{\lambda _V}||V - {V_0}||_F^2 + {\gamma _U}{G_U} + {\gamma _V}{G_V} \end{aligned} \end{aligned}$$

(2)

where ${G_U} = tr({U^T}{L_U}U)$, ${G_V} = tr({V^T}{L_V}V)$ (tr refers to the trace of matrix), $L_{U}$ and $L_{V}$ are the graph Laplacian matrices for the similarity graphs $W_{U}$ and $W_{V}$ respectively. $\lambda _{U}$ and $\lambda _{V}$ are regularization parameters indicating the confidence on the latent factors. $\gamma _{U}$ and $\gamma _{V}$ are regularization parameters indicating the confidence on the similarity graphs, U / V denotes the user/item latent factor matrix, B denotes the latent pattern matrix of ratings. ${L_U} = {D_U} - {W_U}$, ${L_V} = {D_V} - {W_V}$, ${D_u} = diag{(\sum \limits _j {({W_U}} )_{ij}}$, ${D_v} = diag{(\sum \limits _j {({W_V}} )_{ij}}$.

5 HFT Model

Inspired from the related models above, we propose a novel model of cross-domain CF recommendation based on twin bridge transfer learning of heterogeneous user feedbacks named HFT. At first the data is preprocessed for our proposed HFT model.

In a user-item rating matrix, the observed ratings such as the 5-star ratings are often extremely sparse, so over-fitting may easily happen when we predict the missing ratings. However, we observe that some auxiliary data in the form of like/dislike may be more easily obtained. For example, we can easily collect the favored/disfavored data in Moviepilot, the love/ban data in Last.fm and the Want to see/Not Interested data in Flixster, which are implicit feedbacks and heterogeneous to the numerical ratings [15]. Moreover, the implicit feedbacks can be collected from the user behaviors and formalized to be binary ratings. For example, if the user browses, forwards or collects some information, we set the rating as 1, and 0 otherwise. It is more frequently for users to express such implicit tastes than to mark numerical ratings. We can make use of implicit feedbacks to alleviate the sparseness problem in explicit feedbacks. For the explicit feedbacks, such as the numerical rating matrix $R = ({R_{ui}}),{R_{ui}} \in \{ 1,2,3,4,5\}$, let ${R^{'}} = (R_{ui}^{'})$, $R_{ui}^{'} = \frac{{{R_{ui}} - 1}}{4}$. $R^{'}$ is the preprocessed rating matrix of R. $R_{ui}$ can be restored by ${R_{ui}} = 4R_{ui}^{'} + 1$ at the end of prediction. To alleviate the data heterogeneity between different kinds of feedbacks, such as $\left\{ {0,1} \right\}$ and $\frac{{\{ 1,2,3,4,5\} - 1}}{4}$ , let $\sigma (x) = \frac{1}{{1 + {e^{ - (x - 0.5)}}}},$ $x \in \{ 0,1\}$ is the implicit feedback, $\sigma (x)$ is a logistic link function to revise the implicit feedbacks. So the heterogeneous rating data are normalized to be homogeneous for the collective factorization. Then HFT model is mainly divided into the following three steps.

5.1 Extraction of Latent Factors

To extract latent factors, we do the flowing two collective factorizations respectively. Each factorization is learning from the GAO model.

$$\begin{aligned} \begin{aligned} \mathop {\min }\limits _{_{{U_0},{S_0},{S_1},S,V,{V_1} \ge 0}} {f_1} = ||[R - {U_0}[{S_0},S]{V^T}] \odot Z|{|^2} + \\ ||[{R_1} - {U_0}[{S_0},{S_1}]{V_1}^T] \odot {Z_1}|{|^2} \end{aligned} \end{aligned}$$

(3)

$$\begin{aligned} \begin{aligned} \mathop {\min }\limits _{{U_2},U,S_0^{'},{S_2},{S^{'}},{V_0} \ge 0} {f_2} = ||[R - U[S_0^{'},{S^{'}}]{V_0}^T] \odot Z|{|^2} +\\ ||[{R_2} - {U_2}[S_0^{'},{S_2}]{V_0}^T] \odot {Z_2}|{|^2} \end{aligned} \end{aligned}$$

(4)

We solve Eqs. (3) and (4) by the gradient descent method, and get the latent factors ${U_0}$ and ${V_0}$, respectively.

Solving Equation ( 3 )

Let $V = [V_{00}^T,V_{01}^T] \in {R^{N \times L}}$, ${V_1} = [V_{10}^T,V_{11}^T] \in {R^{N \times {L_1}}}$, where $V_{00}^{T}=V(:, 1:D)$, $V_{01}^{T}=V(:,(D+1):L)$, $V_{10}^{T}=V_{1}(:, 1:D)$, $V_{11}^{T}=V_{1}(:,(D+1):L_{1})$, D is the dimension of shared common rating pattern. Here $L-D$ is the dimension of domain-specific rating pattern of R, $L_{1}-D$ is the dimension of domain-specific rating pattern of $R_{1}$, ${S_0} \in {R^{K \times D}}$, $S \in {R^{K \times (L - D)}}$, ${S_1} \in {R^{K \times ({L_1} - D)}}$, ${U_0} \in {R^{M \times K}}$, $Z \in {R^{M \times N}}$. $U_{0}^{T}U_{0}=I$, $V_{1}^{T}V_{1}=I$, $V^{T}V=I$.

Taking the learning of latent factor S as an example, we will show how to optimize S by deriving its updating rule while fixing other latent factors. For this purpose we can rewrite the objective function in Eq. (3) as follows:

$$\begin{aligned} \begin{aligned} \mathop {\min }\limits _S {f_1}(S) = ||R - {U_0}{S_0}{V_{00}} - {U_0}S{V_{01}}] \odot Z|{|^2} + \\ ||[{R_1} - {U_0}{S_0}{V_{10}} - {U_0}{S_1}{V_{11}}] \odot {Z_1}|{|^2} \end{aligned} \end{aligned}$$

(5)

The derivative of $f_{1}(S)$ with respect to S is

$$\begin{aligned} \frac{{\partial {f_1}(S)}}{{\partial S}} = 2({U_0}^T([{U_0}{S_0}{V_{00}}] \odot Z)V_{01}^T - {U_0}^T(R \odot Z)V_{01}^T) + 2{U_0}^T([{U_0}{S_1}{V_{01}}] \odot Z)V_{01}^T. \end{aligned}$$

We use the Karush-Kuhn-Tucker complementary condition for the nonnegativity of S and let $\frac{{\partial {f_1}(S)}}{{\partial S}}=0$, then can get the following updating rule for learning S:

$$\begin{aligned} S \leftarrow S\sqrt{\frac{{U_0^T(R \odot Z)V_{01}^T}}{{U_0^T([{U_0}{S_0}{V_{00}}] \odot Z)V_{01}^T + U_0^T([{U_0}S{V_{01}}] \odot Z)V_{01}^T}}} \end{aligned}$$

(6)

Similarly, we can get the updating rules for learning other latent factors as follows:

$$\begin{aligned} {S_1} \leftarrow {S_1}\sqrt{\frac{{U_0^T({R_1} \odot {Z_1})V_{11}^T}}{{U_0^T([{U_0}{S_0}{V_{10}}] \odot {Z_1})V_{11}^T + U_0^T([{U_0}{S_1}{V_{11}}] \odot {Z_1})V_{11}^T}}} \end{aligned}$$

(7)

$$\begin{aligned} {U_0} \leftarrow {U_0}\sqrt{\frac{{(R \odot Z)V{{[{S_0},S]}^T}}}{{([{U_0}[{S_0},S]{V^T} \odot Z) \odot V{{[{S_0},S]}^T}}}} \end{aligned}$$

(8)

$$\begin{aligned} V \leftarrow V\sqrt{\frac{{{{[{S_0},S]}^T}{U_0}^T(R \odot Z)}}{{{{[{S_0},S]}^T}{U_0}^T([{U_0}[{S_0},S]{V^T}] \odot Z)}}} \end{aligned}$$

(9)

$$\begin{aligned} {V_1} \leftarrow {V_1}\sqrt{\frac{{{{[{S_0},{S_1}]}^T}{U_0}^T({R_1} \odot {Z_1})}}{{{{[{S_0},{S_1}]}^T}{U_0}^T([{U_0}[{S_0},{S_1}]{V_1}^T] \odot {Z_1})}}} \end{aligned}$$

(10)

$$\begin{aligned} {S_0} \leftarrow {S_0}\sqrt{\frac{{U_0^T(R \odot Z)V_{00}^T + U_0^T({R_1} \odot {Z_1})V_{10}^T}}{{P + Q}}} \end{aligned}$$

(11)

where

$$\begin{aligned} P&= U_0^T([{U_0}{S_0}{V_{00}}] \odot Z)V_{00}^T + U_0^T([{U_0}S{V_{01}}] \odot Z)V_{00}^T\\ Q&= U_0^T([{U_0}{S_0}{V_{10}}] \odot {Z_1})V_{10}^T + U_0^T([{U_0}{S_1}{V_{11}}] \odot {Z_1})V_{10}^T \end{aligned}$$

Based on the above updating rules for learning different latent factors, it can be proved that the objective function in Eq. (3) will decrease monotonically and the learning algorithm demonstrated above is convergent [4]. At last, we can extract latent factor ${U_0}$ by enough iterations. In the same way, we can extract latent factor $V_{0}$ by solving Eq. (4).

5.2 Similarity Graph Construction

When the observed user-item rating data is very sparse, two users may rate the common item with a fairly low probability though they have the same taste, so the neighborhood information of users or items can not be effectively utilized. To overcome this problem, the similarity graphs from dense auxiliary data are constructed since the auxiliary data is closely related to the target data. Because ${U_0}$ and ${V_0}$ are denser than $R_{1}$ and $R_{2}$, they can better represent the neighborhood information. We construct the user-side similarity graph $W_{U}$ and item-side similarity graph $W_{V}$ based on the extracted ${U_0}$ and ${V_0}$, respectively [20]. In SHI model, the distance is simply defined by the concept of p-nearest neighbors with binary values of 0 and 1, so $W_{U}$ and $W_{V}$ may be inaccurate to be the weight matrices for the similarity graphs. Here we adopt the PCC (Pearson Correlation Coefficient) to measure the similarity:

$$\begin{aligned} {({W_U})_{ij}} = \rho (u_{{i_*},}^0u_{{j_*}}^0) = \frac{{\sum {(u_{{i_*}}^0 - \overline{u_{{i_*}}^0} )(u_{{j_*}}^0 - \overline{u_{{j_*}}^0} )} }}{{\sqrt{\sum {{{(u_{{i_*}}^0 - \overline{u_{{i_*}}^0} )}^2}} } \sqrt{\sum {{{(u_{{j_*}}^0 - \overline{u_{{j_*}}^0} )}^2}}} }} \end{aligned}$$

$$\begin{aligned} {({W_V})_{ij}} = \rho (v_{{i_*},}^0v_{{j_*}}^0) = \frac{{\sum {(v_{{i_*}}^0 - \overline{v_{{i_*}}^0} )(v_{{j_*}}^0 - \overline{v_{{j_*}}^0} )} }}{{\sqrt{\sum {{{(v_{{i_*}}^0 - \overline{v_{{i_*}}^0} )}^2}} } \sqrt{\sum { {{(v_{{j_*}}^0 - \overline{v_{{j_*}}^0} )}^2}}} }} \end{aligned}$$

where $u_{{i_*}}^0$ is the i th row of ${U_0}$ denoting the latent taste of user i,  $v_{{i_*}}^0$ is the i th row of ${V_0}$ denoting the latent feature of item i, $\overline{u_{{i_*}}^0} /\overline{v_{{i_*}}^0}$ is the mean of $u_{{i_*}}^0/v_{{i_*}}^0.$

5.3 Predicting of Missing Ratings

We predict missing ratings by the graph regularized weighted nonnegative matrix tri-factorization. The optimization function is

$$\begin{aligned} \mathop {\min }\limits _{U,V,B > = 0} O = ||Z \odot (R - UB{V^T})||_F^2 + {\gamma _U}{G_U} + {\gamma _V}{G_V} \end{aligned}$$

(12)

where ${G_U} = tr({U^T}{L_U}U),$ ${G_V} = tr({V^T}{L_V}V),$ $L_{U}$ and $L_{V}$ are the graph Laplacian matrices for the similarity graphs $W_{U}$ and $W_{V}$ respectively. $\gamma _{U}$ and $\gamma _{V}$ are regularization parameters indicating our confidence on the similarity graphs.

We solve the optimization problem in Eq. (12) by the gradient descent method [20]. The derivative of O with respect to U is

$$ \frac{{\partial O}}{{\partial U}} = - 2Z \odot RV{B^T} + 2Z \odot (UB{V^T})V{B^T} + 2{\gamma _U}{L_U}U. $$

We use the Karush-Kuhn-Tucker (KKT) complementary condition for the nonnegativity of U and let $\frac{{\partial O}}{{\partial U}} = 0,$ then get

$$\begin{aligned}{}[ - Z \odot RV{B^T} + Z \odot (UB{V^T})V{B^T} + {\gamma _U}{L_U}U] \odot U = 0 \end{aligned}$$

Because $L_{U}$ may take any signs, we decompose it as ${L_U} = L_U^ + - L_U^ -$, where $L_U^ + = \frac{1}{2}(|{L_U}| + {L_U})$, $L_U^ - = \frac{1}{2}(|{L_U}| - {L_U})$. $L_U^+$ and $L_U^-$ are positive-valued matrices. We get the following updating rule for learning U:

$$\begin{aligned} U \leftarrow U \odot \sqrt{\frac{{Z \odot RV{B^T} + {\gamma _U}L_U^ - U}}{{Z \odot (UB{V^T})V{B^T} + {\gamma _U}L_U^ + U}}} \end{aligned}$$

(13)

Similarly, we can obtain the updating rules for learning V and B as follows:

$$\begin{aligned} V \leftarrow V \odot \sqrt{\frac{{{{(Z \odot R)}^T}UB + {\gamma _V}L_V^ - U}}{{{{(Z \odot (UB{V^T}))}^T}UB + {\gamma _V}L_V^ + V}}} \end{aligned}$$

(14)

$$\begin{aligned} B \leftarrow B \odot \sqrt{\frac{{{U^T}(Z \odot R)V}}{{{U^T}(Z \odot (UB{V^T}))V}}} \end{aligned}$$

(15)

According to [5], the objective function in Eq. (12) will monotonically decrease until convergence when updating U, V and B sequentially and iteratively by Eqs. (13–15). R can be calculated by $UB{V^T}$, so the missing ratings can be predicted.

6 Experiments

6.1 Data Sets

MovieLens10M ¹. It contains 10000054 ratings and 95580 tags applied to 10681 movies by 71567 users of the online movie recommender service MovieLens. The preference of the user for a movie is rated on a 5-star scale, with half-star increments. If the movie is not rated by any user, the rating is marked as 0.

Epinions ². It contains 2,372,198 ratings given by 44,157 users to 50,682 products. Users can mark products with integer ratings ranging from 1 to 5.

Book-Crossing ³. It contains 278,858 users providing 1,149,780 ratings expressed on a scale from 0 to 10 about 271,379 books.

6.2 Compared Models

• $\star$ GMF (Graph Regularized Weighted Nonnegative Matrix Factorization) [5]: A good single-domain model which constructs two graphs on user side and item side to exploit the internal and external information. In this model, the missing ratings are predicted by the graph regularized weighted nonnegative matrix tri-factorization.

• $\star$ SHI [20].

• $\star$ CBT (Codebook Based Transfer) [7]: a classical model for cross-domain CF recommendation which can only make use of the common rating pattern via the codebook information among different domains.

• $\star$ HPT:our proposed new model.

6.3 Evaluation Metrics

Mean Absolute Error (MAE) and Root Mean Square Error (RMSE) are the two widely used evaluation metrics for evaluating CF algorithms. We adopt MAE to measure the prediction accuracy of multiple recommendation models. It is defined as follows:

$$\begin{aligned} MAE = \frac{{\sum \limits _{i,j} {|{R_{ij}} - R_{ij}^{p}|} }}{{|{T_E}|}} \end{aligned}$$

where $R_{ij}$ is the rating that user i gives to item j in test set, while $R_{ij}^{p}$ is the predicted value of $R_{ij},$ ${|T_E}|$ is the number of ratings in test set. The smaller the value of MAE is, the better the recommendation model performs.

6.4 Experimental Results

To simulate the heterogeneous feedbacks, we reference to Weike Pan’s method [14]. When the observed ratings range from 1 to 5, we set the ratings to 1 if they are 4 or 5 and set the ratings to 0 otherwise. When the observed ratings range from 1 to 10, we set the ratings to 1 if the ratings are 7, 8, 9 or 10 and set the ratings to 0 otherwise.

The data sets used in our experiments are constructed by the same strategy as [19]. Take the Book-Crossing data set as an example, we first randomly sample a $2N \times 2N(N\in {N^ + })$ dense rating matrix X, then take the submatrix $R = {X_{1\sim N,1\sim N}}$ as the target rating matrix, the submatrix ${R_1} = {X_{1\sim N,(N + 1)\sim 2N}}$ as the user-side auxiliary data matrix and the submatrix ${R_2} = {X_{(N + 1)\sim 2N,1\sim N}}$ as the item-side auxiliary data matrix. In this way, R and $R_{1}$ share common users, while R and $R_{2}$ share common items. And we apply the same construction strategy to Epinions data set and MovieLens10M data set.

The target ratings matrix R is randomly split into a training set and a test set, with the proportion of 60 % and 40 % respectively. Let l be the sparseness level of the data set. To evaluate the performance of each model in different sparse data, we sample the target training set randomly with various sparseness levels ranging from 0.01 % to 1 %. The utilized auxiliary data is always much denser than the target data. Different dimensions of latent factors such as {10, 20, 50, 100, 150, 200, 300, 500, 800} and different values of regularization parameters such as {0.01, 0.1, 0.5, 1, 5, 10, 50, 80} of each model are tried, the best of which are selected for comparisons. Given that the major algorithms in the models are iterative, we run each model 5 repeated times and report the average results of MAE. In different data sets with various sparseness levels l, varies of the values of MAE in different models with respect to N are as follows:

Fig. 1.

MovieLens

Fig. 2.

Epinions

Fig. 3.

Book-Crossing

In each one of Figs. 1, 2 and 3, the data sparseness level l in the left subgraph is smaller than that in the right subgraph, which means the sampled data in the left subgraph are sparser than that in the right subgraph. The above experimental results show that the values of MAE in our proposed HFT model are almost always smaller than those in other models in all cases, which is more significant when the data is sparser in each data set. So it is demonstrated that HFT model is more effective than others, especially when the data is sparser. Also it performs well in the case of heterogeneous user feedbacks.

Let T be the dimension of the share latent rating pattern between MovieLens and Book-Crossing. MovieLens is the target data with the sparse level of 0.5 %, and Book-Crossing is the auxiliary data with the sparse level of 8 %. Varies of the values of MAE in different models with respect to T are as follows:

Fig. 4.

MovieLens and Book-Crossing

From Fig. 4, we can see that the values of MAE in HFT model are almost always smaller than those in other methods, in which the values of MAE are fixed with respect to T. Specially we can get the optimal value of T by adjusting it freely, thereby significantly improve the accuracy of prediction. The results show that the HFT model we proposed is effective and flexible.

6.5 Theoretical Analysis

HFT model considers both the common latent rating pattern and domain-specific latent rating pattern so that it can get more accurate initial latent factors, based on which the similarity graphs are constructed more accurately too. Given this, latent factors can be used as an implicit bridge together with the similarity graphs to perform the twin bridge transfer learning. Since the latent factors are adopted as an implicit bridge for knowledge transfer, the transfer in HFT model is simpler than the explicit twin-bridge transfer in SHI model. Moreover, we adopt the PCC to measure the weight matrices for the similarity graphs, which is time-saving and more accurate than the way based on the p-nearest neighbors in SHI model. So HFT model owns a lower time complexity but higher recommendation accuracy than SHI model. By the twin bridge transfer learning, HFT model can transfer more useful knowledge, while alleviate negative transfer by regularizing the learning model with the similarity graphs, which can effectively filter out the negative information contained in the latent factors. So it is easy to understand that HFT model has higher recommendation accuracy than GMF model and CBT model, which not only are based on the single bridge transfer learning, but also don’t consider the domain-specific latent rating patterns. In addition, HFT model applies to the transfer of heterogeneous user feedbacks across multiple domains by data normalization and the collective factorization, which makes the advantages of it more significant in the multi-source and heterogeneous environment of big data.

7 Conclusions and Future Work

We propose a novel HFT model of transfer learning for cross-domain CF recommendation, which not only performs well in the case of heterogeneous feedbacks, but also improves the recommendation by transferring more useful knowledge considering both the common latent rating pattern and domain-specific latent rating pattern and learning knowledge from the twin bridge of latent factors and similarity graphs. In addition, in HFT model the latent factors of users and items can be extracted by the collective factorization, so HFT model can be flexible to data quality across multiple domains. Extensive experiments show that our proposed HFT model is more efficient in sparse data and more flexible across domains than other three excellent models.

In the future, we try to exploit more auxiliary information for transfer. Social information, topic information and context information can be used for regularization fitting in the process of optimization. Moreover, given that recommendation tasks are often diverse, we intent to research multi-view and multi-task cross-domain transfer learning [21, 22] for the cross-domain recommendation.