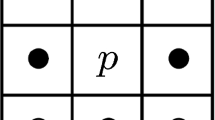Equivalent Sequential and Parallel Subiteration-Based Surface-Thinning Algorithms

Abstract

Thinning is a frequently applied technique for extracting skeletons or medial surfaces from volumetric binary objects. It is an iterative object reduction: border points that satisfy certain topological and geometric constraints are deleted in a thinning phase. Sequential thinning algorithms may alter just one point at a time, while parallel algorithms can delete a set of border points simultaneously. Two thinning algorithms are said to be equivalent if they can produce the same result for each input binary picture. This work shows that it is possible to construct subiteration-based equivalent sequential and parallel surface-thinning algorithms. The proposed four pairs of algorithms can be implemented directly on a conventional sequential computer or on a parallel computing device. All of them preserve topology for (26, 6) pictures.

1 Introduction

A digital binary picture on the digital space ${\mathbb Z}^3$ is a mapping that assigns a color of black or white to each point [6]. Thinning is an iterative object reduction until only some skeleton-like shape features (i.e., medial curves, medial surfaces, or topological kernels) are left [4, 6, 19, 25]. Thinning algorithms use reduction operators that transform binary pictures only by changing some black points to white ones, which is referred to as deletion. Parallel thinning algorithms are comprised of reductions that can delete a set of border points simultaneously [4, 8, 26], while sequential thinning algorithms traverse the boundary of objects and may remove just one point at a time [8, 26].

Two reductions are said to be equivalent if they produce the same result for each input picture. Similarly, a deletion rule is called equivalent if it yields equivalent parallel and sequential reductions. One of the authors established some sufficient conditions for equivalent deletion rules [21]. This concept can be extended to complex algorithms composed of reductions: two surface-thinning algorithms are called equivalent if they produce the same medial surface for each input picture.

Sequential reductions (with the same deletion rule) suffer from the drawback that different visiting orders (raster scans) of border points may yield various results. A deletion rule is called order-independent if it yields equivalent sequential reductions for all the possible visiting orders. In [21] one of the authors gave necessary and sufficient conditions for order-independent deletion rules. By extending this concept: a sequential reduction is said to be order-independent if its deletion rule is order-independent, and a sequential surface-thinning algorithm is called order-independent [22] if it is composed of order-independent sequential reductions.

There are three major strategies for parallel thinning [4]: a fully parallel algorithm applies the same parallel reduction in each iteration step; a subiteration-based algorithm decomposes an iteration step into $k\ge 2$ successive parallel reductions according to k deletion directions, and a subset of border points associated with the actual direction can be deleted by a parallel reduction; and in subfield-based algorithms the digital space is partitioned into $s\ge 2$ subfields which are alternatively activated, at a given iteration step s successive parallel reductions assigned to these subfields are performed, and some black points in the active subfield can be designated for deletion. In this paper, our attention is focussed on the subiteration approach. Since there are six kinds of major directions in 3D, 6-subiteration 3D thinning algorithms are generally proposed [3, 9, 11, 15, 19, 23, 27, 28]. Note that there are some 8-subiteration [16] and 12-subiteration [10, 17] 3D thinning algorithms as well.

In [20] one of the authors proved that the deletion rule of the known 2D fully parallel thinning algorithm proposed by Manzanera et al. [14] is equivalent. Furthermore, he also showed in [21] that a fully parallel thinning algorithm with an equivalent deletion rule yields various subfield-based algorithms that are equivalent to the original fully parallel one. As far as we know, no one showed that there exists a pair of equivalent parallel and sequential 3D subiteration-based thinning algorithms. In this paper we propose four pairs of equivalent parallel and sequential 6-subiteration surface-thinning algorithms that use the same deletion rules, but they apply diverse geometric constraints.

The rest of this paper is organized as follows. Section 2 gives an outline from basic notions and results from digital topology, topology preservation, and equivalent reductions. Then in Sect. 3 the proposed algorithms are presented. In Sect. 4 we show that our parallel algorithms are equivalent to topology-preserving sequential surface-thinning algorithms. Finally, we round off the paper with some concluding remarks.

2 Basic Notions and Results

We use the fundamental concepts of digital topology as reviewed by Kong and Rosenfeld [5, 6]. Note that there are other approaches that are based on cellular/cubical complexes [7]. The most important of them uses critical kernels [2] which constitute a generalization of minimal non-simple sets. Since the topological correctness of the thinning algorithms presented in this paper is based only on the concept of simple points, we can consider the traditional paradigm of digital topology.

Consider the digital space ${\mathbb Z}^3$, the three frequently applied adjacency relations on ${\mathbb Z}^3$ (see Fig. 1), and a point $p\in {\mathbb Z}^3$. Then, we denote by $N_j(p)\subset {\mathbb Z}^3$ the set of points that are j-adjacent to point p and let $N^*_j(p) = N_j(p)\setminus \{p\}$ $(j=6, 18, 26)$.

Fig. 1.

The considered three adjacency relations on ${\mathbb Z}^3$. The set $N_6(p)$ contains p and the six points marked ‘U’, ‘D’, ‘N’, ‘E’, ‘S’, and ‘W’; the set $N_{18}(p)$ contains $N_{6}(p)$ and the twelve points marked ‘$\bullet$’; the set $N_{26}(p)$ contains $N_{18}(p)$ and the eight points marked ‘$\circ$’.

The sequence of distinct points $\langle x_0, x_1, \dots , x_n \rangle$ is called a j-path of length n from $x_0$ to $x_n$ in a non-empty set of points X if each point of the sequence is in X and $x_i$ is j-adjacent to $x_{i-1}$ for each $i = 1, \ldots , n$. Note that a single point is a j-path of length 0. Two points are said to be j-connected in the set X if there is a j-path in X between them. A set of points X is j-connected in the set of points $Y \supseteq X$ if any two points in X are j-connected in Y. A j-component of a set of points X is a maximal j-connected subset of X.

A (26, 6) binary digital picture on ${\mathbb Z}^3$ is a quadruple $({\mathbb Z}^3, 26, 6, B)$, where each point in $B\subseteq {\mathbb Z}^3$ is called a black point; each point in ${\mathbb Z}^3\setminus B$ is said to be a white point. A black component (or object) is a 26-component of B, while a white component is a 6-component of ${\mathbb Z}^3\setminus B$. A black point p is an interior point if all points in $N^*_6(p)$ are black. A black point is said to be a border point if it is not an interior point (i.e., it is 6-adjacent to at least one white point).

Topology preservation [5, 6, 12] is a major concern of thinning algorithms. A black point is called simple point if its deletion is a topology-preserving reduction. A sequential reduction and a sequential thinning algorithm is topology-preserving if their deletion rules delete only simple points. Various authors gave characterizations of simple points in (26, 6) pictures [5, 6, 13, 24]. We make use of the following one:

Theorem 1

[13, 24] A black point p is simple in picture $({\mathbb Z}^3,26,6,B)$ if and only if all of the following conditions hold:

• 1. The set $N^*_{26}(p)\cap B$ contains exactly one 26-component.

• 2. $N^*_6(p)\setminus B\not =\emptyset$.

• 3. Any two points in $N^*_6(p)\setminus B$ are 6-connected in the set $N^*_{18}(p)\setminus B$.

Theorem 1 states that the simplicity of a point p in (26, 6) pictures is a local property (i.e., it can be decided by examining $N^*_{26}(p)$).

Existing sufficient conditions for topology-preserving parallel reductions are generally based on (or derived from) the notion of minimal non-simple sets [5, 12]. One of the authors established a new sufficient condition for arbitrary pictures with the help of equivalent deletion rules [21]. Let us recall and rephrase his results:

Theorem 2

Let R be a deletion rule, let $({\mathbb Z}^3,26,6,B)$ be a picture, and let $p\in B$ be a black point that can be deleted by R from that picture. If deletion rule R deletes only simple points and the deletability of any black point in $q\in B\setminus \{p\}$ by R does not depend on the ‘color’ of p, then the followings hold:

• 1. The parallel reduction with deletion rule R is topology-preserving.

• 2. The sequential reduction with deletion rule R is order-independent and topology-preserving.

• 3. The parallel and the sequential reductions with deletion rule R are equivalent.

Thinning algorithms generally classify the set of black points of the input picture into two (disjoint) subsets: the set of interesting points (i.e., potentially deletable points) for which the deletion rule associated with a thinning phase is evaluated and the constraint set whose black points are not taken into consideration (i.e., safe points that cannot be deleted). Since a phase of a subiteration-based algorithm cannot delete interior points and border points that do not fall into the actual type, these points are certainly in the constraint set.

Conventional thinning algorithms preserve some simple (border) points called endpoints that provide relevant geometrical information with respect to the shape of the object. Here we consider the following characterizations of surface-endpoints.

Definition 1

[19] A black point p in picture $({\mathbb Z}^3,26,6,B)$ is a surface-endpoint of type 1 if there is no interior point in $N^*_6(p)\cap B$ (i.e., p is not 6-adjacent to any interior point).

Definition 2

[17] A black point p in picture $({\mathbb Z}^3,26,6,B)$ is a surface-endpoint of type 2 if at least one of the three pairs of points in $N^*_6(p)\cap B$ (U,D), (N,S), and (E,W) is formed by two white points.

Definition 3

[3] A black point p in picture $({\mathbb Z}^3,26,6,B)$ is not a surface-endpoint of type 3 if $\Vert N^*_{26}(p)\cap B\Vert \ge 8$, or $4\le \Vert N^*_{26}(p)\cap B\Vert \le 7$ and $N^*_6(p)\cap B$ contains three mutually 26-adjacent points. $(\,\Vert S \Vert$ stands for the count of elements in set S).

Definitions 1–3 make us possible to specify three pairs of endpoint-based surface-thinning algorithms (P-6-SI- i, S-6-SI- i) ($i = 1, 2, 3)$, see Algorithms 1 and 2 in Sect. 3.

Some advanced thinning algorithms preserve accumulated isthmuses [1] (i.e., generalization of curve interior points):

Definition 4

[1] A black point p in a (26, 6) picture is a surface-isthmus of type 4 if p is a non-simple border point (i.e., Condition 1 of Theorem 1 or Condition 3 of Theorem 1 is violated).

Definition 4 helps us to give a pair of isthmus-based surface-thinning algorithms (P-6-SI-4, S-6-SI-4), see Algorithms 1 and 2 in Sect. 3.

Note that surface-endpoints of type 4 and surface-isthmuses of type i ($i = 1, 2, 3$) are not defined (i.e., there is neither surface-endpoint of type 4 nor surface-isthmuses of type i ($i = 1, 2, 3$)). Definitions 1–4 make us possible to give a unified description of the proposed endpoint-based and isthmus-based surface-thinning algorithms (see Algorithms 1 and 2 in Sect. 3).

3 Parallel and Sequential 6-Subiteration Surface-Thinning Algorithms

In this section, four pairs of 3D parallel and sequential 6-subiteration surface-thinning algorithms (P-6-SI- i, S-6-SI- i) are presented for (26, 6) pictures $( i = 1, 2, 3, 4 )$. All of these algorithms use the same deletion rule, but diverse pairs of them apply different constraint sets. The proposed parallel thinning algorithms P-6-SI- i and the sequential algorithms S-6-SI- i are given by Algorithms 1 and 2, respectively.

It is easy to see that the first three pairs of algorithms (P-6-SI- i, S-6-SI- i) are endpoint-based $( i = 1, 2, 3 )$, and the fourth pair of algorithms (P-6-SI-4, S-6-SI-4) is isthmus-based (see Definitions 1–4).

By comparing the parallel algorithm P-6-SI- i (see Algorithm 1) and sequential algorithm S-6-SI- i (see Algorithm 2), we can state that in the parallel case the initial set of black points P is considered when the deletability of all the interesting points are investigated. On the contrary, the set of black points S is dynamically altered when a sequential reduction/subiteration is performed; the deletability of the actual point is evaluated in a modified picture (in which some previously visited interesting points are white).

The applied deletion rules that specify d-DELETABLE points ($d =$ U, D, N, E, S, W) are given by $3\times 3\times 3$ matching templates depicted in Fig. 2. Note that the six deletion rules were originally proposed by Gong and Bertrand [3] in their endpoint-based 6-subiteration surface-thinning algorithm with respect to surface-endpoints of type 3 (see Definition 3).

Fig. 2.

Matching template $T_d$ associated with d-DELETABLE points ($d = \mathbf{U}, \mathbf{D}, \mathbf{N}, \mathbf{E}, \mathbf{S}, \mathbf{W}$). Notations: the central position marked p matches an interesting (black) point; the position marked ‘$\blacksquare$’ matches a (black) point in the constraint set; the position marked ‘$\square$’ matches a white point; if the position marked ‘$v_k$’ coincides with a white point, then the position marked ‘$w_k$’ coincides with a white point ($k=0,1,2,3$); if all the three positions marked ‘$v_k$’, ‘$x_{(k+1)\ \mathrm {\tiny mod}\ 4}$’, and ‘$v_{(k+1)\ \mathrm {\tiny mod}\ 4}$’ coincide with white points, then the position marked ‘$y_{(k+1)\ \mathrm {\tiny mod}\ 4}$’ coincides with a white point ($k=0,1,2,3$); each ‘$\cdot$’ (don’t care) matches either a black or a white point.

A period of six subiterations/reductions (i.e., the kernel of the repeat cycle in Algorithms 1 and 2) is decomposed into six successive subiterations according to the six main directions in 3D, and this period is repeated until stability is reached (i.e., no point is deleted within the last six subiterations/reductions). We propose the following ordered list of the deletion directions: $\langle \mathbf{U}, \mathbf{D}, \mathbf{N}, \mathbf{E}, \mathbf{S}, \mathbf{W} \rangle$. Note that a subiteration-based thinning algorithm is sensitive to the order of directions. Hence choosing another order of the deletion directions yields another algorithm.

An interesting black point ($p\in X$) is d-DELETABLE if template $T_d$ matches it ($d = \mathbf{U}, \mathbf{D}, \mathbf{N}, \mathbf{E}, \mathbf{S}, \mathbf{W}$). Note that the templates assigned to the deletion direction d give the condition to delete certain d-border points, and templates associated with the last five deletion directions can be obtained by proper rotations of the templates that give U-DELETABLE points.

In experiments the proposed pairs of equivalent algorithms (P-6-SI- i, S-6-SI- i) were tested on objects of different shapes. Here we have room to present four illustrative examples, see Figs. 3, 4, 5 and 6. The results of our four pairs of algorithms can be compared to the medial surfaces produced by two existing 3D parallel surface thinning algorithms proposed by Manzanera et al. [14] and Palágyi [18]. The numbers refer to the count of black points in the pictures. We can state that the isthmus-based pair of algorithms (P-6-SI-4, S-6-SI-4) result less object points than the other five methods. The authors note that, unfortunately, there is no known method for quantitative comparison of surface-thinning algorithms.

Fig. 3.

The original $45\times 45\times 45$ image of a cube with two tunnels and its six medial surfaces produced by two existing algorithms and the proposed four pairs of equivalent 6-subiteration surface-thinning algorithms.

Fig. 4.

The original $321\times 153\times 227$ image of a bird and its six medial surfaces produced by two existing algorithms and the proposed four pairs of equivalent 6-subiteration surface-thinning algorithms.

Fig. 5.

The original $47\times 193\times 193$ image of a gear and its six medial surfaces produced by two existing algorithms and the proposed four pairs of equivalent 6-subiteration surface-thinning algorithms.

Fig. 6.

The original $350\times 132\times 217$ image of a dolphin and its six medial surfaces produced by two existing algorithms and the proposed four pairs of equivalent 6-subiteration surface-thinning algorithms.

4 Verification

Now we will show that the 6-subiteration parallel surface-thinning algorithm P-6-SI- i and the sequential algorithm S-6-SI- i are equivalent and topology-preserving ($i = 1, 2, 3, 4$). It will also be proved that the sequential algorithms are order-independent. It is sufficient to show that deletion rules of these algorithms (see Sect. 3) satisfy all conditions of Theorem 2.

Since the five templates $T_{\mathbf {D}}$, $T_{\mathbf {N}}$, $T_{\mathbf {E}}$, $T_{\mathbf {S}}$, and $T_{\mathbf {W}}$ assigned to d-DELETABLE points ($d = \mathbf{D}, \mathbf{N}, \mathbf{E}, \mathbf{S}, \mathbf{W}$) are rotated versions of the template $T_{\mathbf {U}}$ (see Fig. 2), it is sufficient to prove that the deletion rule associated with the first subiteration deletes only simple points, and the deletability of a point does not depend on the ‘color’ of a deletable point. It can be carried out for the remaining five deletion rules in the same way.

Let us state some important properties of the U-DELETABLE points:

Lemma 1

All U-DELETABLE points are simple.

It is obvious by a careful examination of the matching template $T_{\mathbf {U}}$ that all conditions of Theorem 1 hold.

Lemma 2

The deletability of a point by template $T_{\mathbf {U}}$ does not depend on the ‘color’ of a U-DELETABLE point.

Proof. Let us assume that the (interesting) black point p is U-DELETABLE. Since U-DELETABLE points are given by a $3\times 3\times 3$ matching template, it is sufficient to investigate the deletability of interesting black points in $N^*_{26}(p)$.

Due to the symmetries that are present in template $T_{\mathbf {U}}$ (see Fig. 2), it is sufficient to check the eight template positions marked ‘$\bigstar$’ in Fig. 7a. Hence it is assumed that the U-DELETABLE point p coincides with these eight positions. Consider the deletability of an interesting black point $q\in N^*_{26}(p)$ with the help of the eight corresponding configurations depicted in Figs. 7b–i.

Fig. 7.

The eight positions marked ‘$\bigstar$’ are checked by Lemma 2 (a), and the eight configurations (b)–(i) are associated with these positions. Points marked ‘$\blacksquare$’ are in the constraint set, and points marked ‘$\square$’ are white.

Let us investigate all that eight cases:

• If the U-DELETABLE point p coincides with a position marked ‘$\bigstar$’ in Fig. 7b, d, e, f, g, and i, then the deletability of q does not depend on the ‘color’ of p.

• If point p coincides with a position marked ‘$\bigstar$’ in Fig. 7c (after its deletion), then the interesting point q is in the constraint set. Hence we arrived at a contradiction.

• If point p coincides with a position marked ‘$\bigstar$’ in Fig. 7h (before its deletion), then the interesting point p is in the constraint set. Hence we arrived at a contradiction.    $\square$

We are now ready to state our main theorem — as an easy consequence of Theorem 2, Lemmas 1 and 2.

Theorem 3

The followings hold for the proposed algorithms:

• 1. The sequential surface-thinning algorithm S-6-SI- i is order-independent $(i = 1, 2, 3, 4)$.

• 2. The sequential surface-thinning algorithm S-6-SI- i is topology-preserving for (26, 6) pictures $(i = 1, 2, 3, 4)$.

• 3. The parallel surface-thinning algorithm P-6-SI- i is topology-preserving for (26, 6) pictures $(i = 1, 2, 3, 4)$.

• 4. Algorithms S-6-SI- i and P-6-SI- i are equivalent, i.e., they produce the same result for each input picture $(i = 1, 2, 3, 4)$.

Note that Lemma 2 is valid for arbitrary constraint sets — not only for the four kinds of sets that are used by algorithms (S-6-SI- i, P-6-SI- i) $(i = 1, 2, 3, 4)$. Other constraint sets coupled with the set of templates depicted in Fig. 2 yield additional pairs of equivalent 6-subiteration parallel and sequential thinning algorithms.

It is important to emphasize that the parallel algorithm P-6-SI-3 coincides with the 6-subiteration 3D parallel surface-thinning algorithm proposed by Gong and Bertrand in 1990 [3]. According to Theorem 3, that existing parallel algorithm is equivalent to the (order-independent) sequential algorithm S-6-SI-3 (with the same deletion rules and constraint set). In addition, the topological correctness of an existing parallel thinning algorithm is also confirmed. Note that Gong and Bertrand sketched a proof in [3] to show that their algorithm does not change the topological properties of the input pictures. At that time (i.e., in 1990) they could not apply the very first sufficient conditions for topology-preserving 3D parallel reductions reported by Ma in 1994 [12].

5 Conclusions

In this paper four pairs of 3D 6-subiteration sequential and parallel surface-thinning algorithms were presented. Each of the proposed algorithm uses the same deletion rules that are given by $3\times 3\times 3$ matching templates, but different pairs of algorithms apply diverse constraint sets. It was shown that the proposed pairs of algorithms are equivalent (i.e., they produce the same medial surfaces for each input picture). It was also proved that all the reported algorithms are topology-preserving for (26, 6) pictures.