Abstract
Ionizing radiation is used in many aspects of modern life: in science, industry, power generation, and medicine. In medicine it is used in diagnosis of disease with x-rays and gamma rays (imaging) as well as in treatment of malignant disease with high energy x-rays, electrons, and heavy charged particles. Measurement of quality and quantity of ionizing radiation, referred to as radiation dosimetry, is the most important area of medical physics, essentially its “raison d’être”. This chapter provides a general introduction to radiation dosimetry starting with a discussion of physical quantities and units used for describing radiation sources and radiation beams. The chapter also introduces the concept of charged particle equilibrium, deals with radiation dosimetry systems and types of dosimeters, and introduces the basic cavity theories of radiation dosimetry. The chapter concludes with a brief discussion of the basic calibration of radiotherapy machine output and radiation dosimetry protocols.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
- Optically Stimulate Luminescence
- Absorb Dose Rate
- Radiation Dosimetry
- Normal Tissue Complication Probability
- Photon Interaction
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
Ionizing radiation is used in many aspects of modern life: in science, industry, power generation, and medicine. In medicine it is used in diagnosis of disease with x-rays and gamma rays (imaging) as well as in treatment of malignant disease with high energy x-rays, electrons, and heavy charged particles.
Measurement of the quantity and quality of ionizing radiation, generally referred to as radiation dosimetry, is the most important aspect of medical physics, essentially its “raison d’être”. It has played a pivotal role in physics since the birth of radiation physics during the last five years of the 19th century. Initially, development of techniques in ionizing radiation measurement was stimulated by the rapid expansion of radiation physics research; later on, however, with the realization of the tremendous potential of x-rays in medicine, and radioactivity in medicine as well as industry and defense, radiation dosimetry became and still is the most important component of radiation physics.
Pioneers in radiation physics research did not pay attention to detrimental effects of ionizing radiations on human tissues and many of them suffered severe consequences as a result of their lack of understanding. The situation today is significantly different and the use of ionizing radiation is strictly controlled, monitored, and regulated.
Wilhelm Conrad | Henri-Antoine | Marie SKŁODOWSKA- |
RÖNTGEN | BECQUEREL | CURIE & Pierre CURIE |
1895 | 1896 | 1898 |
Discovery of | Discovery of | Discovery of |
x-rays | natural radioactivity | radium and polonium |
Nobel Prize: 1901 | Nobel Prize: 1903 | Nobel Prize: 1903 |
 | ||
Use of ionizing radiation in science, industry or medicine requires an ability to measure accurately the quantity and quality of ionizing radiation produced by a radioactive source or radiation-producing machine. Accuracy is especially important in medical use of ionizing radiation for diagnosis (x-ray imaging and nuclear medicine) or treatment (radiotherapy) of disease. In imaging the goal is to obtain optimal image quality with minimal radiation dose; in radiotherapy it is imperative to deliver the prescribed dose to the target volume with optimal numerical and geometrical accuracy.
The principal physical quantity determined in radiation dosimetry is the absorbed dose , i.e., energy per unit mass, imparted to an absorber; however, several other physically relevant quantities, characteristic of the radiation source or the radiation beam, may also be of interest. A few of these are: radiation source activity, beam fluence, air-kerma in air, and effective dose in an animate medium such as the human body.
Radiation dosimetry is divided into two categories: absolute and relative. Absolute radiation dosimetry , discussed in Chap. 16, refers to measurement of radiation dose directly without requiring calibration in a known radiation field. Only three absolute radiation dosimetry systems have been developed to date: (i) calorimetric absolute radiation dosimetry, (ii) chemical (Fricke) absolute radiation dosimetry, and (iii) ionometric radiation dosimetry. Relative radiation dosimetry is based on dosimeters that require calibration of their signal in a known radiation field. Many relative radiation dosimetry systems are known and the most important of them are discussed in Chap. 17.
This chapter presents an introduction to radiation dosimetry, starting with the basic principles of radiation dosimetry in Sect. 15.1 and quantities used for describing a radiation beam in Sect. 15.2. The chapter then introduces the concept of charged particle equilibrium (CPE) in Sect. 15.3 and a comparison between kerma and absorbed dose in Sect. 15.4. The theoretical basis of radiation dosimetry is introduced in Sect. 15.7 through a discussion of three basic cavity theories used in radiation dosimetry. The chapter concludes with a description of basic aspects of radiotherapy machine output calibration in Sect. 15.10 and radiation dosimetry protocols in Sect. 15.10.
15.1 Ionizing Radiation Beams
The term “radiation dosimetry” was originally used to describe the measurement of radiation dose delivered to an absorber by directly or indirectly ionizing radiation, but the meaning of the term has subsequently been expanded to include the determination or calculation of dose distribution in the human body, irradiated either by one or multiple external beams or by an internal radiation beam. An external beam is defined as an ionizing radiation beam originating in a radiation source located outside the patient, while the term internal beam implies that the radiation source is placed inside the patient.
External radiation beams are used in diagnostic radiology imaging and are produced by x-ray equipment. They are also used in standard external beam radiotherapy and are commonly produced by cobalt machines, x-ray tubes, and linear accelerators. Internal radiation beams, on the other hand, are produced either in nuclear medicine imaging with the use of unsealed radiation sources deposited into human tissues or in brachytherapy with the use of sealed radiation sources placed into body cavities or embedded in tissue.
In all applications of ionizing radiation in medicine the absorbed dose delivered to the patient must be known. In radiotherapy this is of utmost importance in order to ensure that the absorbed dose delivered to the patient matches as closely as possible the prescribed dose (see Sect. 1.12.5) to maximize the tumor control probability (TCP) and minimize the normal tissue complication probability (NTCP) . The ICRU has recommended an overall accuracy in tumor dose delivery of ±5%, based on an analysis of dose response data and on an evaluation of errors in dose delivery in a clinical setting. Considering all uncertainties involved in radiation dose delivery to the patient, the ±5% recommendation on accuracy is by no means easy to attain and implies that the accuracy of the basic physical calibration of radiotherapy machine output be of the order of ±2% or better.
In diagnostic and nuclear medicine imaging the knowledge of the accurate dose to the patient is not as critical as it is in radiotherapy. However, even here, in order to optimize image quality and simultaneously minimize the possible deleterious effects of ionizing radiation on human tissues, the radiation dose should be known to better than ±10%. The same requirement must typically be fulfilled with respect to doses determined for radiation protection and health physics purposes.
15.2 Quantities Used for Describing a Radiation Beam
The International Commission on Radiation Units and Measurements (ICRU) in its Report 33 recommends an extensive list of quantities and units for general use in radiation sciences. Special emphasis is given to photon beams that are described with three distinctly different categories of quantities: radiometric quantities, interaction coefficients, and dosimetric quantities.
-
1.
Radiometric quantities describe the radiation beam in terms of the number and energy of particles constituting the radiation beam.
-
2.
Interaction coefficients deal with quantities related to photon interactions with matter (photoelectric effect, Compton scattering, pair production, etc.).
-
3.
Dosimetric quantities describe the amount of energy the radiation beam deposits in a given medium, such as air, water, tissue, etc. For photon beams they are given as a product of radiometric quantities and interaction coefficients.
15.2.1 Important Radiometric Quantities
The definitions in this section are valid for all ionizing radiations:
-
1.
Directly ionizing (charged) particles such as electrons, positrons, protons, etc.
-
2.
Indirectly ionizing (neutral) particles such as photons and neutrons.
Particle fluence \(\varphi \) is defined as the ratio of \({\mathrm{d}}N/{\mathrm{d}}A\), where \(\mathrm{d}N\) is the number of particles that enter a sphere of cross-sectional area \({\mathrm{d}}A\). The SI unit of particle fluence \(\varphi \text { is }\mathrm{m}^{-2}\); the traditional unit, still in common use, is \({\mathrm{cm}}^{-2}\), where 1 m\(^{-2} = 10^{-4}~\mathrm{cm}^{-2}\) or 1 cm\(^{-2} = 10^{4}~\mathrm{m}^{-2}\).
Particle fluence rate \(\dot{\varphi }\) is defined as the ratio \({\mathrm{d}}\varphi /{\mathrm{d}}t\), where \({\mathrm{d}}\varphi \) is the increment of particle fluence in the time interval \({\mathrm{d}}t\). The SI unit of particle fluence rate \(\varphi \) is \(\mathrm{m}^{-2}{\cdot }\mathrm{s}^{-1}\); the traditional unit, still in common use, is \({\mathrm{cm}}^{-2}{\cdot }\mathrm{s}^{-1}\), where
\(1\,\mathrm{m}^{-2}{\cdot }\mathrm{s}^{-1} = 10^{-4}~{\mathrm{cm}}^{-2}{\cdot }\mathrm{s}^{-1}\) or
\(1\,{\mathrm{cm}}^{-2}{\cdot }\mathrm{s}^{-1}={10}^{4}\,\mathrm{m}^{-2}{\cdot }\mathrm{s}^{-1}\)
Energy fluence \(\psi \) is defined as the ratio \({\mathrm{d}}E_{v}/{\mathrm{d}}A\), where \({\mathrm{d}}E_{v}\) is the radiant energy incident on a sphere of cross-sectional area \({\mathrm{d}}A\). The SI unit of energy fluence \(\psi \) is \(\mathrm{J}{\cdot }\mathrm{m}^{-2}\); the traditional unit, still in common use, is \(\mathrm{MeV}{\cdot }{\mathrm{cm}}^{-2}\), where
\(1~\mathrm{J}{\cdot }\mathrm{m}^{-2}= 6.242{\times }10^{8}~\mathrm{MeV}{\cdot }\mathrm{cm}^{-2}\) or
\(1\,\,\mathrm{MeV}{\cdot }{\mathrm{cm}}^{-2} = 1.602{\times }10^{-9}~\mathrm{J}{\cdot }\mathrm{m}^{-2} = 1.602{\times }10^{-13}~\mathrm{J}{\cdot }\mathrm{cm}^{-2}\).
For a monoenergetic photon beam \({\mathrm{d}}E_{v}\) equals the number of photons \({\mathrm{d}}N\) multiplied with their energy \(E_{v}\) to give
Energy fluence rate \(\dot{\psi }\) is defined as the ratio \(\mathrm{d}\psi /{\mathrm{d}}t\), where \({\mathrm{d}}\psi \) is the increment of energy fluence in the time interval \({\mathrm{d}}t\). The SI unit of photon energy fluence rate \(\psi \) is \(\mathrm{W}{\cdot }\mathrm{m}^{-2}\); the traditional unit, still in common use, is \(\mathrm{MeV}{\cdot }\mathrm{cm}^{-2}{\cdot }\mathrm{s}^{-1}\), where
\(1~\mathrm{W}{\cdot }\mathrm{m}^{-2}=6.242{\times }10^{8}~\mathrm{MeV}{\cdot }{\mathrm{cm}}^{-2}{\cdot }\mathrm{s}^{-1}\) or
\(1~\mathrm{MeV}{\cdot }{\mathrm{cm}}^{-2}{\cdot }\mathrm{s}^{-1} = 1.602{\times }10^{-9}~\mathrm{J}{\cdot }\mathrm{m}^{-2}{\cdot }\mathrm{s}^{-1} = 1.602{\times }10^{-13}~\mathrm{J}{\cdot }{\mathrm{cm}}^{-2}{\cdot }\mathrm{s}^{-1}\).
15.2.2 Important Photon Interaction Coefficients
Mass attenuation coefficient \(\mu /\rho \) of an absorber material for photons is defined as the ratio of \({\mathrm{d}}N/N\) over \(\rho {\mathrm{d}}l\), where \({\mathrm{d}}N/N\) is the fraction of photons that undergo interactions in traveling a distance \({\mathrm{d}}l\) in an absorber of mass density \(\rho \) (see Sect. 8.1)
The SI unit of mass attenuation coefficient \(\mu /\rho \) is \(\mathrm{m}^{2}{\cdot }\mathrm{kg}^{-1}\); the traditional unit, still in use, is \({\mathrm{cm}}^{2}{\cdot }{{\mathrm{g}}}^{-1}\), where \(1~\mathrm{m}^{2}{\cdot }\mathrm{kg}^{-1} = 10~{\mathrm{cm}}^{2}{\cdot }{{\mathrm{g}}}^{-1}\) or \(1~\mathrm{cm}^{2}{\cdot }{{\mathrm{g}}}^{-1} =0.1~\mathrm{m}^{2}{\cdot }\mathrm{kg}^{-1}\) (see Sect. 8.1).
Mass energy transfer coefficient \(\mu _{\mathrm{tr}}/\rho \) of an absorber material for photons is given as a product of the mass attenuation coefficient \(\mu /\rho \) and \(\bar{E}_{\mathrm{tr}}/E_{v}\), where \(E_{v}\) is incident photon energy \(hv; \bar{E}_{\mathrm{tr}}\) is the mean energy transferred from incident photon to charged particles (electrons and positrons) averaged over all possible photon interactions; and \(\bar{f}_\mathrm{tr}=\bar{E}_{\mathrm{tr}}/E_{v}\) is the mean energy transfer fraction (Sect. 8.2)
The SI unit of mass energy transfer coefficient \(\mu _{\mathrm{tr}}/\rho \) is \(\mathrm{m}^{2}{\cdot }\mathrm{kg}^{-1}\); the traditional unit, still in use, is \({\mathrm{cm}}^{2}{\cdot }{{\mathrm{g}}}^{-1}\), where \(1\,\,\mathrm{m}^{2}{\cdot } \mathrm{kg}^{-1}=10\,\,{\mathrm{cm}}^{2}{\cdot }{{\mathrm{g}}}^{-1}\) or \(1~\mathrm{cm}^{2}{\cdot }{{\mathrm{g}}}^{-1} = 0.1~\mathrm{m}^{2}{\cdot }\mathrm{kg}^{-1}\).
Mass energy absorption coefficient \(\mu _{\mathrm{{ab}}}/\rho \) of an absorber material for photons is the product of the mass energy transfer coefficient \(\mu _{\mathrm{tr}}/\rho \) and (\(1-\bar{g}\)), where \(\bar{g}\) is the mean radiation fraction , i.e., fraction of energy of secondary charged particles that is lost to bremsstrahlung and/or in-flight positron annihilation in the absorber (Sect. 8.3). We can also write \(\bar{\mu }_{\mathrm{{ab}}}/\rho \) as a product of the mass attenuation coefficient \(\mu /\rho \) and total mean energy absorption fraction \(\bar{f}_{\mathrm{{ab}}}\). Thus, we have the following expressions for \(\bar{\mu }_{\mathrm{{ab}}}/\rho \)
The SI unit of the mass energy absorption coefficient \(\bar{\mu }_{\mathrm{{ab}}}/\rho \) is m\(^{2}{\cdot }\mathrm{kg}^{-1};\) the traditional unit, still in use, is \({\mathrm{cm}}^{2}{\cdot }\mathrm{g}^{-1}\), where \(1~\mathrm{m}^{2}{\cdot }\mathrm{kg}^{-1}=10~{\mathrm{cm}}^{2} {\cdot }{{\mathrm{g}}}^{-1}\) or \(1~{\mathrm{cm}}^{2}{\cdot }{{\mathrm{g}}}^{-1} = 0.1~\mathrm{m}^{2}{\cdot }\mathrm{kg}^{-1}\).
Note: the ICRU uses notations \(\mu _{\mathrm{tr}}/\rho \) and \(\mu _\mathrm{en}/\rho \) for the mass energy transfer coefficient and mass energy absorption coefficient, respectively. We use the notation of Johns and Cunningham: \(\bar{\mu }_{\mathrm{{tr}}}/\rho \) and \(\bar{\mu }_\mathrm{ab}/\rho \) for the two coefficients because they are easier to distinguish from each other; “tr” stands for energy transferred, while “ab” stands for energy absorbed.
15.2.3 Important Dosimetric Quantities
Exposure X is defined as the ratio dQ/dm, where dQ stands for the absolute value of the total charge of the ions of one sign produced in air when all charged particles (electrons and positrons) released by photons in air of mass dm are completely stopped in air. The SI unit of exposure X is C\({\cdot }\)kg\(^{-1}\); however, the old unit of exposure, the röntgen R, is still often used and corresponds to 1 R \(= 2.58{\times }10^{-4}\text { C}{\cdot }\text {kg}^{-1}\) or 1 C/kg \(=\) 3876 R.
The seemingly arbitrary choice of 1 R \(= 2.58{\times }10^{-4}\) C/kg is traced back to the original definition of one röntgen (1 R) as being equal to one “electrostatic unit of electricity” (1 esu) of charge collected in 1 cm\(^3\) of air at STP (standard temperature of \(T=0\) \(^{\circ }\mathrm{C}=273.16\) K and standard pressure of \(p = 760~\mathrm{torr}\,=\,101.3~\mathrm{kPa}\)). Since 1 C \(= 3{\times }10^{9}\) esu or 1 esu \(= \) 3.333\({\times }10^{-10}\) C and mass density of air at STP is \(1.293{\times }10^{-3}\) g/cm\(^{3}\) or 1 cm\(^{3}\) of air at STP contains \(1.293{\times }10^{-6}\) kg of air, we get:
Exposure X is a measure of the ability of photons to ionize air and is of limited value in modern radiation physics because it is only defined for air as absorbing medium and only for photons in a relatively narrow energy hv range of 1 keV \(< hv< 3\) MeV. It cannot be used for neutrons and charged particle beams, but is of some historical significance because: (i) it was the first radiation quantity defined by the ICRU in 1928 to quantify radiation beams and (ii) it was subsequently for several decades used as an intermediate step in the determination of absorbed dose in absorbing medium such as water and tissue.
Kerma \(K_{{\mathrm{med}}}\) (acronym for “kinetic energy released in matter”) is given by the ratio d\(\bar{E}_{\mathrm{tr}}\) over dm, where d\(\bar{E}_{\mathrm{tr}}\) is the mean energy transferred from indirectly ionizing radiation (photon and neutron) to secondary charged particles released by photons and neutrons in absorber medium of mass dm. The SI unit of kerma is \(\text {J}{\cdot }\text {kg}^{-1}\) and the special unit is gray (Gy), with 1 Gy \(=\) 1 \(\text {J}{\cdot }\text {kg}^{-1}\).
For monoenergetic photons kerma may also be expressed as a product of photon energy fluence \(\psi \) and the mass energy transfer coefficient (\(\mu _{\mathrm{tr}}/\rho \))\(_{{\mathrm{med}}}\) of the absorber medium
with \(\psi =E_{v}\varphi \) and \(F_{K}=E_{v}(\mu _{\mathrm{tr}}/\rho )_\mathrm{med}\) the so-called kerma factor . For a beam of photons with energy \(E_{v}\) and photon fluence \(\varphi \), inserting (15.5) into (15.7) and using (7.19) allows us to express kerma as follows
where \(\mathrm{(}\mu /\rho \mathrm{)}_{{\mathrm{med}}}\) is the mass attenuation coefficient of the absorber medium and \(\bar{E}_{\mathrm{tr}}\) is the mean energy transferred to charged particles in the medium at each interaction. The product \(\varphi {\times }(\mu /\rho )\) gives the number of photon interactions per unit mass of absorber medium irradiated by photon fluence \(\varphi \).
Kerma rate \(\dot{K}_{{\mathrm{med}}}\) is defined as the ratio d\(K_{{\mathrm{med}}}/\)dt, where d\(K_{{\mathrm{med}}}\) is the increment of kerma in the time interval dt. The SI unit of kerma rate \(\dot{K}_{{\mathrm{med}}}\) is \(\mathrm{J}{\cdot }\mathrm{kg}^{-1}{\cdot }\mathrm{s}^{-1}\) or \(\text {Gy}{\cdot }\text {s}^{-1}\).
Absorbed dose \(D_{{\mathrm{med}}}\) is the most important quantity in radiation dosimetry. It is defined as the ratio d\(\bar{E}_\mathrm{ab}/\)dm, where d\(\bar{E}_{\mathrm{{ab}}}\) is the mean energy imparted by ionizing radiation to matter of mass dm. The SI unit of absorbed dose is J\(\cdot \)kg\(^{-1}\) and the special unit is gray (Gy), with 1 Gy \(=\) 1\(\,\,\mathrm{J}{\cdot }\mathrm{kg}^{-1}\).
For indirectly ionizing radiations the mean energy \(\bar{E}_\mathrm{ab}\) is imparted to absorbing medium through a two-step process: in the first step, energy is transferred from a neutral particle (photon or neutron) to energetic charged particles (resulting in kerma \(K_{{\mathrm{med}}}\)); in the second step, the liberated charged particles, as they travel through the absorber, gradually impart a portion of their kinetic energy to absorbing medium (resulting in absorbed dose \(D _{{\mathrm{med}}}\)).
Absorbed dose rate \(\dot{D}_{{\mathrm{med}}}\) is defined as the ratio d\(D_{{\mathrm{med}}}/\)dt, where d\(D_{{\mathrm{med}}}\) is the increment of absorbed dose in the time interval dt. The SI unit of absorbed dose rate \(\dot{D}_{{\mathrm{med}}}\) is \(\mathrm{J}{\cdot }\mathrm{kg}^{-1}{\cdot }\mathrm{s}^{-1}\) or \(\text {Gy}{\cdot }\mathrm{s}^{-1}\).
15.3 Concept of Charged Particle Equilibrium
As discussed in detail in Chap. 7, when photons traverse an absorbing medium, they may interact with absorber atoms through various interactions (effects) in which secondary charged particles (electrons and positrons) are released in the medium and the interacting photon either disappears or is scattered.
The concept of charged particle equilibrium (CPE) is an important concept in radiation physics. It states that under CPE each secondary charged particle that leaves volume-of-interest  with kinetic energy \(E_\mathrm{K}\) is replaced by another secondary charged particle that enters
with kinetic energy \(E_\mathrm{K}\) is replaced by another secondary charged particle that enters  with same kinetic energy \(E_\mathrm{K}\) and expends it inside
with same kinetic energy \(E_\mathrm{K}\) and expends it inside  . This means that under CPE a perfect energy balance in volume
. This means that under CPE a perfect energy balance in volume  is maintained and the kinetic energy that charged particles carry out of volume
is maintained and the kinetic energy that charged particles carry out of volume  is replenished by same amount of kinetic energy carried by other charged particles into volume
is replenished by same amount of kinetic energy carried by other charged particles into volume  .
.
Schematic illustration of charged particle equilibrium (CPE). Photons of energy 10 MeV (not shown) are irradiating a block of material (phantom) shown in grey color and containing a volume-of-interest  in yellow color. Secondary charged particles (only electrons are shown) released in photon interactions with absorber atoms are shown with straight arrows, representing electron tracks. There are 9 electron tracks, each starting with a black dot (\(\bullet \)) and the initial electron kinetic energy in MeV is indicated. The tracks end when electron kinetic energy is zero at points indicated with 0. Electron kinetic energy in MeV entering or exiting
in yellow color. Secondary charged particles (only electrons are shown) released in photon interactions with absorber atoms are shown with straight arrows, representing electron tracks. There are 9 electron tracks, each starting with a black dot (\(\bullet \)) and the initial electron kinetic energy in MeV is indicated. The tracks end when electron kinetic energy is zero at points indicated with 0. Electron kinetic energy in MeV entering or exiting  is indicated at the boundary of
is indicated at the boundary of 
The concept of CPE is illustrated schematically in Fig. 15.1 that depicts a block of material irradiated by 10 MeV photons. Secondary charged particles
(only electrons are shown) released in photon interactions with absorber atoms are shown with straight arrows representing electron tracks. The volume-of-interest  is shown in yellow color, the block of absorbing material in grey color. The numbers at track origins (i.e., at points of photon interaction) indicate initial kinetic energy (\(E_\mathrm{K}\))\(_0\) of secondary electrons in MeV. Numbers at track crossing the boundary of
is shown in yellow color, the block of absorbing material in grey color. The numbers at track origins (i.e., at points of photon interaction) indicate initial kinetic energy (\(E_\mathrm{K}\))\(_0\) of secondary electrons in MeV. Numbers at track crossing the boundary of  indicate electron kinetic energy in MeV at specific track crossings. Electron kinetic energy at track-ends is zero.
indicate electron kinetic energy in MeV at specific track crossings. Electron kinetic energy at track-ends is zero.
Nine electron tracks are shown in Fig. 15.1:
-
1.
Three electrons (e\(_{1}\), e\(_{2}\), and e\(_{3})\) originate inside
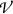 and expend all their kinetic energy through collision losses inside
and expend all their kinetic energy through collision losses inside 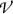 .
. -
2.
Three electrons (e\(_{4}\), e\(_{5}\), and e\(_{6})\) originate in
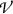 but carry a portion of their kinetic energy out of
but carry a portion of their kinetic energy out of 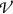 .
. -
3.
Three electrons (e\(_{7}\), e\(_{8}\), and e\(_{9})\) originate outside of
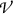 and carry a portion of their kinetic energy into
and carry a portion of their kinetic energy into 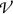 .
. -
4.
Electron e\(_{4 }\) carries kinetic energy of 3 MeV out of
 . Energy loss of 3 MeV is compensated by electron e\(_{9}\) that brings kinetic energy of 3 MeV into
. Energy loss of 3 MeV is compensated by electron e\(_{9}\) that brings kinetic energy of 3 MeV into 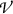 .
. -
5.
Electron e\(_{5}\) carries kinetic energy of 2 MeV out of
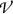 . Energy loss of 2 MeV is compensated by electron e\(_{8}\) that brings kinetic energy of 2 MeV into
. Energy loss of 2 MeV is compensated by electron e\(_{8}\) that brings kinetic energy of 2 MeV into 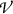 .
. -
6.
Electron e\(_{6}\) carries kinetic energy of 3 MeV out of
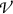 . Energy loss of 3 MeV is compensated by electron e\(_{7}\) that carries kinetic energy of 3 MeV into
. Energy loss of 3 MeV is compensated by electron e\(_{7}\) that carries kinetic energy of 3 MeV into 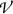 .
.
Since all kinetic energy, lost to volume-of-interest  by electrons released in
by electrons released in  and leaving
and leaving  with kinetic energy \(E_\mathrm{K}\), is compensated by an equal amount of kinetic energy \(E_\mathrm{K}\) entering
with kinetic energy \(E_\mathrm{K}\), is compensated by an equal amount of kinetic energy \(E_\mathrm{K}\) entering  , we can assume that: (i) all energy released in
, we can assume that: (i) all energy released in  is actually absorbed in
is actually absorbed in  and (ii) conditions for charged particle equilibrium (CPE) are satisfied in volume-of-interest
and (ii) conditions for charged particle equilibrium (CPE) are satisfied in volume-of-interest  in Fig. 15.1.
in Fig. 15.1.
For simplicity, in Fig. 15.1 only electron tracks are shown, implying that no pair production photon interactions occur in the absorber. Moreover, an assumption is made that electrons experience only collision losses and no radiation losses occur inside volume-of-interest  . These would be valid assumptions for photons below 1 MeV; at higher photon energies, however, pair production interactions as well as radiation losses (bremsstrahlung and in-flight positron annihilation) would increase in importance with photon energy and would have to be taken into consideration. However, the basic concepts of CPE would still apply.
. These would be valid assumptions for photons below 1 MeV; at higher photon energies, however, pair production interactions as well as radiation losses (bremsstrahlung and in-flight positron annihilation) would increase in importance with photon energy and would have to be taken into consideration. However, the basic concepts of CPE would still apply.
15.4 Kerma Versus Absorbed Dose
Both kerma \(K_{{\mathrm{med}}}\) in absorber medium and absorbed dose \(D_{{\mathrm{med}}}\) in absorber medium are defined by the ratio dE / dm, where, for kerma, dE stands for mean energy transferred from incident particle to liberated charged particle in absorber medium of mass dm and, for absorbed dose, dE stands for mean energy transferred from the liberated charged particle to absorber medium of mass dm.
Kerma \(K_{{\mathrm{med}}}\) occurs at the point of interaction between the incident particle (photon or neutron) and the absorber atom, while absorbed dose \(D_{{\mathrm{med}}}\) is spread over a larger mass element dm. For kerma \(K_{{\mathrm{med}}}\) the choice of mass element dm size is not important; for absorbed dose \(D_{{\mathrm{med}}}\), on the other hand, the choice of dm size is very important for two reasons:
-
(i)
To avoid statistical fluctuations that occur when dm is too small
-
(ii)
To achieve adequate spatial resolution that is less than optimal when dm is too large. For large dm the absorbed dose represents the mean dose \(\bar{D}_{{\mathrm{med}}}\) over the absorber mass dm.
Kerma \(K_{{\mathrm{med}}}\) is conceptually easy to understand, relatively easy to calculate, but difficult to measure. It is defined only for beams of neutral particles (photons and neutrons) that are, because of their two-step dose delivery process, referred to as indirectly ionizing radiations , in contrast to charged particles that fall into the category of directly ionizing radiations (Sect. 1.10).
15.4.1 Absorbed Dose for Photons
For photons the two-step dose delivery process proceeds as follows:
-
1.
In the first step the photon interacts with an absorber atom through one of the following effects: photoelectric effect, Compton scattering, nuclear pair production, and triplet production (see Chap. 7). An energetic secondary electron and/or an electron-positron pair is liberated in the absorber and the mean energy \(\bar{E}_{\mathrm{tr}}\) transferred from the photon to energetic charged particles per unit mass results in kerma \(K_{{\mathrm{med}}}\).
-
2.
In the second step the energetic charged particles (electrons and positrons) travel through the absorber medium and undergo multiple Coulomb interactions with the atoms of the absorber thereby slowly losing their kinetic energy in two possible manners:
-
Coulomb interaction between energetic secondary charged particles (electrons and positrons) and orbital electrons of absorber atoms is described as collision loss and results in energy transfer from secondary charged particle to absorber. This energy per unit mass is called collision kerma \(K_{{\mathrm{med}}}^\mathrm{col}\) and is, under the condition of electronic equilibrium , called absorbed dose \(D_{{\mathrm{med}}}\) in the absorber.
-
Coulomb interaction between the energetic secondary charged particles and nuclei of absorber atoms results in radiation loss in the form of either bremsstrahlung photons (for electrons and positrons) or annihilation photons following in-flight annihilation of a positron of non-zero kinetic energy. This radiation loss per unit mass results in radiation kerma \(K_{{\mathrm{med}}}^\mathrm{rad}\) that is assumed to escape the volume-of-interest and thus does not contribute to radiation absorbed dose \(D_{{\mathrm{med}}}\) in the absorber.
-
For photons, kerma \(K_{{\mathrm{med}}}\) is a sum of two components: the smaller and often negligible component called radiation kerma \(K_{{\mathrm{med}}}^\mathrm{rad}\) that escapes the volume of interest V and the larger component called collision kerma \(K_{{\mathrm{med}}}^\mathrm{col}\) that, under the condition of charged particle equilibrium (CPE) , is equal to absorbed dose \(D_{{\mathrm{med}}}\) in the volume-of-interest V
and
Equations (15.7) for kerma \(K_{{\mathrm{med}}}\) and (15.10) for absorbed dose \(D_\mathrm{med}\) suggest that measuring absorbed dose for indirectly ionizing radiations should be simple. However, both \(K_{{\mathrm{med}}}\) and \(D_\mathrm{med}\) depend on particle (photon or neutron) fluence that is difficult to measure with high accuracy and precision, and this makes radiation dosimetry based on particle fluence difficult in practice; especially so in a clinical setting. Therefore, other more suitable and practical techniques have been developed based on cavity theories, as discussed in Sect. 15.7.
15.4.2 Absorbed Dose for Neutrons
For neutrons the two-step dose delivery process is simpler than that for photons and is characterized as follows:
-
1.
In the first step the neutron interacts with an absorber atom through one of the following interactions (Sect. 9.2): inelastic scattering, neutron capture, spallation, and nuclear fission. In many of these nuclear reactions a proton or heavier charged particle is released and the energy \(E_{\mathrm{tr}}\) transferred from neutron to the secondary charged particles contributes to kerma \(K_{{\mathrm{med}}}\) at a point-of-interest in the absorber.
-
2.
In the second step the energetic secondary charged particles (protons and heavier ions) travel through the absorber and undergo multiple Coulomb interactions with the orbital electrons and nuclei of the absorber atoms. Interactions with orbital electrons result in collision losses (Sect. 6.4) that contribute to collision kerma \(K_{{\mathrm{med}}}^\mathrm{col}\). Two simplifying assumptions can be made:
-
Since radiation loss of heavy charged particles in Coulomb interactions with absorber nuclei is negligible, neutron kerma has only one component
$$\begin{aligned} K_{{\mathrm{med}}} = K_{{\mathrm{med}}}^\mathrm{col} \end{aligned}$$(15.11) -
Since the range of secondary charged particles (protons and heavier ions) in absorber media is generally short, standard CPE conditions apply in most situations of interest in neutron dosimetry and absorbed dose \(D_{{\mathrm{med}}}\) is generally equal to kerma \(K_{{\mathrm{med}}}\)
-
15.4.3 Example of Kerma and Absorbed Dose Calculation
By way of example we now take a closer look at Sect. 8.7.1 in which we examined the interaction of photons of energy \(E_{v}=2\,\,\mathrm{MeV}\) with lead absorber. We established that in a 2 MeV photon interaction with lead absorber on average the following conditions apply:
-
1.
Mean energy transferred to secondary charged particles (electrons and positrons) is \(\bar{E}_{\mathrm{tr}}=1.13\) MeV
-
2.
Energy of scattered photon is \(E_{v}^{'}=0.87\) MeV
Of the \(\bar{E}_{\mathrm{tr}}=1.13\) MeV transferred to secondary charged particles:
-
1.
Mean energy absorbed in lead is \(\bar{E}_{\mathrm{{ab}}}=1.04\,\,\mathrm{MeV}\).
-
2.
Energy emitted in the form of bremsstrahlung photons and in-flight annihilation photons is \({E}_{v}^{''}=0.09\) MeV.
We also determined the mass attenuation coefficient (\(\mu /\rho \))\(_{\mathrm{Pb}}\), mass energy transfer coefficient (\(\mu _{\mathrm{tr}}/\rho \))\(_{\mathrm{Pb}}\), and mass energy absorption coefficient (\(\mu _\mathrm{ab}/\rho \))\(_{\mathrm{Pb}}\) and got the following results:
The mean radiation fraction \(\bar{g}\) (Sect. 8.3.1) was determined as \(\bar{g}=0.08\). It has two components: the predominant bremsstrahlung component \(\bar{g}_\mathrm{B}\) and the smaller, often neglected, in-flight annihilation \(g_\mathrm{A}\) component.
Photon of energy 2 MeV interacts with lead atom at point A. In the interaction the photon is scattered and a secondary charged particle (electron and possibly positron) are released. Volume-of-interest  containing mass of lead dm is shown with yellow circle. Electron track ABC is shown in blue color. Radiation loss in the form of bremsstrahlung photons and annihilation photons produced in in-flight positron annihilation is shown with one bremsstrahlung photon originating at point B
containing mass of lead dm is shown with yellow circle. Electron track ABC is shown in blue color. Radiation loss in the form of bremsstrahlung photons and annihilation photons produced in in-flight positron annihilation is shown with one bremsstrahlung photon originating at point B
To illustrate the difference between kerma
\(K_{\mathrm{Pb}}\) and absorbed dose
\(D_{\mathrm{Pb}}\) we show in Fig. 15.2a schematic diagram of the 2-MeV photon interaction presented in Sect. 8.7.1 with a lead atom at point A. The volume-of-interest  containing mass of lead dm is shown with a circle and dm is indicated in yellow color. The following facts related to Fig. 15.2 are of interest:
containing mass of lead dm is shown with a circle and dm is indicated in yellow color. The following facts related to Fig. 15.2 are of interest:
-
1.
Interaction at point A can be photoelectric effect, Rayleigh scattering, Compton scattering, nuclear pair production or electronic (triplet) production. As shown in Sect. 8.7.1, on the average over a large number of such interactions, mean energy \(\bar{E}_{\mathrm{tr}}\) transferred from 2-MeV photon to charged particles (electrons and positrons) is \(\bar{E}_{\mathrm{tr}}\) = 1.13 MeV, while \(E_{v}^{'} =0.87\) MeV goes to scattered photons (Rayleigh and Compton).
-
2.
The secondary charged particles are represented by a single electron track ABC. Starting with initial kinetic energy \((\bar{E}_\mathrm{K})_{0}\) = 1.13 MeV at point A the secondary charged particle undergoes numerous collision (ionization) losses as well as radiation losses (bremsstrahlung and in-flight positron annihilation) progressing from point A through point B to point C where its kinetic energy is fully expended (\(E_\mathrm{K} =0\)).
-
3.
Bremsstrahlung and in-flight annihilation photons that are produced through radiation losses in track ABC are represented in Fig. 15.2 by a single bremsstrahlung photon of energy \(E_{v}^{''}= 0.09\) MeV originating at point B and escaping volume-of-interest
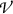 .
. -
4.
Mean energy \(\bar{E}_{\mathrm{tr}}\) = 1.13 MeV, transferred from photon to secondary electron on a single atom at point A, forms part of kerma \(K_{\mathrm{Pb}}\) that has two components: collision kerma \(K_{\mathrm{Pb}}^\mathrm{col}\) and radiation kerma \(K_\mathrm{Pb}^\mathrm{col}\). Under the condition of charged particle equilibrium, collision kerma \(K_{\mathrm{Pb}}^\mathrm{col}\) is equal to absorbed dose \(D_{\mathrm{Pb}}\).
-
5.
The secondary charged particle loses all of its initial kinetic energy (\(E_\mathrm{K}\))\(_{0} = 1.13\) MeV in the volume-of-interest
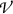 through numerous interactions with lead atoms along the track ABC:
through numerous interactions with lead atoms along the track ABC:-
1.04 MeV of 1.13 MeV is lost through collision (ionization) losses and represents mean energy \(\bar{E}_{\mathrm{{ab}}}\) that is absorbed in
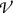 and contributes to absorbed dose \(D_{\mathrm{Pb}}\);
and contributes to absorbed dose \(D_{\mathrm{Pb}}\); -
0.09 MeV of 1.13 MeV is lost through radiation losses \(E_{v}^{''}\) and escapes
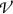 .
.
-
-
6.
To get an idea about the size of the volume-of-interest
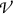 containing mass dm we now estimate the CSDA range
(Sect. 6.8) of a secondary electron with initial kinetic energy of \(\bar{E}_{\mathrm{tr}}=\mathrm{(}E_\mathrm{K} \mathrm{)}_{0} =\) 1.13 MeV. The NIST
gives a range of \({\sim }1\) g/cm\(^{2}\) that corresponds to \({\sim }\)0.9 mm of lead. This is a relatively short distance, yet sufficiently long to allow the electron to expend all of its initial kinetic energy through a large number of ionizations and excitations of lead atoms. Since the ionization energy
IE(Pb) of lead is 7.4 eV, a 1.13 MeV electron can create of the order of \(10^{5}\) ionizations and excitations during its \({\sim }\)0.9 mm travel through lead.
containing mass dm we now estimate the CSDA range
(Sect. 6.8) of a secondary electron with initial kinetic energy of \(\bar{E}_{\mathrm{tr}}=\mathrm{(}E_\mathrm{K} \mathrm{)}_{0} =\) 1.13 MeV. The NIST
gives a range of \({\sim }1\) g/cm\(^{2}\) that corresponds to \({\sim }\)0.9 mm of lead. This is a relatively short distance, yet sufficiently long to allow the electron to expend all of its initial kinetic energy through a large number of ionizations and excitations of lead atoms. Since the ionization energy
IE(Pb) of lead is 7.4 eV, a 1.13 MeV electron can create of the order of \(10^{5}\) ionizations and excitations during its \({\sim }\)0.9 mm travel through lead.
Let us now assume that the photon fluence \(\varphi \) of the 2 MeV photon beam is \(\varphi = 5{\times }10^{10}~{\mathrm{cm}}^{-2}\) and the charged particle equilibrium (CPE) is satisfied in the lead absorber.
Determine the following dosimetric quantities in volume of interest  : 1. Kerma
; 2. Collision kerma
; 3. Radiation kerma
; and 4. Absorbed dose
.
: 1. Kerma
; 2. Collision kerma
; 3. Radiation kerma
; and 4. Absorbed dose
.
The calculation of the dosimetric quantities proceeds as follows:
-
1.
Kerma will be determined using (15.8) to get
$$\begin{aligned} K_{\mathrm {Pb}}&=\varphi \left( \frac{\mu }{\rho }\right) _{\mathrm {Pb}} \bar{E}_{{\mathrm tr}} = (5{\times }10^{10}~{{\mathrm {cm}}}^{-2}){\times } \left( 0.0453\; \frac{{\mathrm {cm}}^{2}}{{\mathrm {g}}} \right) {\times }(1.13~{\mathrm {MeV}}) \nonumber \\&\quad {\times }\!\left( 1.602{\times }10^{-13}~\frac{\mathrm{J}}{\mathrm{eV}}\right) \!{\times }\!\left( \frac{10^{3}~{{\mathrm {g}}}}{\mathrm {kg}}\right) = 0.4100~\frac{{\mathrm J}}{\mathrm {kg}} = 0.4100~{\mathrm {Gy}}=41~{{\mathrm {cGy}}}. \end{aligned}$$(15.14) -
2.
Collision kerma \(K_{\mathrm{Pb}}^\mathrm{col}\) is calculated from kerma \(K_{\mathrm{Pb}}\) and mean radiation fraction \(\bar{g}\)
$$\begin{aligned} K_{\mathrm{Pb}}^{\mathrm{col}} = K_{\mathrm{Pb}}(1-\bar{g})=\mathrm{(0.4100~Gy)} {\times }(1-0.08) = 0.3772~\mathrm{Gy}. \end{aligned}$$(15.15) -
3.
Radiation kerma \(K_{\mathrm{Pb}}^\mathrm{rad}\) is calculated from kerma \(K_{\mathrm{Pb}}\) and mean radiation fraction \(\bar{g}\) as
$$\begin{aligned} K_{\mathrm{Pb}}^\mathrm{rad} = K_{\mathrm{Pb}}(\bar{g}) = \mathrm{(0.4100~Gy)}{\times }0.08=0.0328~\mathrm{Gy}. \end{aligned}$$(15.16) -
4.
Since an assumption is made that the charged particle equilibrium (CPE) is satisfied, we can determine absorbed dose \(D_{\mathrm{Pb}}\) in lead simply by stating that absorbed dose equals collision kerma \(K_{\mathrm{Pb}}^\mathrm{col}\) of (15.15) or else we can use the following expression
$$\begin{aligned} D_{\mathrm{Pb}}&=\varphi \left( \frac{\mu }{\rho }\right) \bar{E}_{\mathrm{{ab}}} = (5{\times }10^{10}~{\mathrm{cm}}^{-2}){\times }\!\left( 0.0453~\frac{{\mathrm{cm}}^{2}}{{\mathrm{g}}} \right) \!{\times }(1.04~\mathrm{MeV}) \nonumber \\&\quad {\times }\!\left( 1.602{\times }10^{-13}\,\frac{\mathrm{J}}{\mathrm{eV}}\right) \! {\times }\!\left( \frac{10^{3} {{\mathrm{g}}}}{\mathrm{kg}}\right) \!= 0.3774 \frac{\mathrm{J}}{\mathrm{kg}}=\! 0.3774~\mathrm{Gy}\!= \!37.74\,\mathrm{cGy}. \nonumber \\ \text {or} \end{aligned}$$(15.17)$$\begin{aligned} D_{\mathrm{Pb}}&=\varphi \left( \frac{\mu }{\rho }\right) \bar{E}_\mathrm{tr}(1-\bar{g}) = (5{\times }10^{10}~{\mathrm{cm}}^{-2}){\times }\left( 0.0453~\frac{{\mathrm{cm}}^{2}}{{\mathrm{g}}} \right) {\times }(1.13~\mathrm{MeV}) \nonumber \\&\quad {\times }(1-0.08){\times }\!\left( 1.602{\times }10^{-13}~\frac{\mathrm{J}}{\mathrm{eV}}\right) \! {\times }\!\left( \frac{10^{3}~{{\mathrm{g}}}}{\mathrm{kg}}\right) \\&= 0.3772~\frac{\mathrm{J}}{\mathrm{kg}} = 0.3772~\mathrm{Gy} = 37.72~\mathrm{cGy}. \end{aligned}$$where \(\bar{E}_{\mathrm{{ab}}}\) is the portion of the mean energy \(\bar{E}_{\mathrm{tr}}\) transferred to charged particles that contributes to energy absorbed in the absorber. The slight discrepancy between (15.17) and (15.15) results from rounding errors.
15.5 Radiation Dosimetry Systems
Radiation-related quantities, such as dose absorbed in medium, are measured with devices referred to as radiation dosimetry system. These devices consist of a radiation dosimeter (detector) and associated electronics (reader). The radiation dosimeter responds to a certain physical characteristic of the ionizing radiation under investigation and produces a suitable physical or chemical signal that is measured by the reader.
Radiation dosimetry generally relies on measurement of a radiation-induced physical signal that is emitted by a radiation dosimeter and measured by a reader of a dosimetry system. Typical physical signals measured in modern radiation dosimetry cover a wide variety of physical quantities, such as, for example:
-
1.
Temperature rise in calorimetric radiation dosimetry (discussed in Sect. 16.1).
-
2.
Ion current in ionization chamber dosimetry (discussed in Sect. 16.3).
-
3.
Emission of ultraviolet or visible light (thermally activated phosphorescence) in thermoluminescence (TL) dosimetry (discussed in Sect. 17.2.4).
-
4.
Emission of ultraviolet or visible light in optically stimulated luminescence (OSL) dosimetry (discussed in Sect. 17.2.5).
-
5.
Transmission of visible light in radiographic and radiochromic film dosimetry (discussed in Sect. 17.4).
15.5.1 Active Versus Passive Radiation Dosimetry System
With respect to the connection between the dosimeter and reader of a dosimetry system two categories of dosimetry system are in use: 1. Active or 2. Passive.
-
1.
A dosimetry system that allows direct measurement of absorbed dose rate as well as the accumulated absorbed dose is referred to as an active or electronic dosimetry system. It is characterized with a direct connection between the dosimeter that responds to ionizing radiation and the reader that measures the dosimeter response during the dosimeter’s exposure to radiation.
-
2.
A dosimetry system in which the dosimeter and reader are not connected during dosimeter exposure to ionizing radiation is called a passive dosimetry system. In this category of dosimetry system the dosimeter and reader are not connected during dosimeter’s exposure to radiation; the dosimeter accumulates a suitable signal proportional to absorbed dose during exposure to radiation and the reader measures the accumulated dose in the dosimeter upon completion of radiation exposure after connection between the dosimeter and reader is established.
15.5.2 Absolute Versus Relative Radiation Dosimetry System
A radiation dosimetry system consists of a detector–reader combination, with the detector (dosimeter) producing a suitable signal M in response to ionizing radiation and the reader measuring the signal M that is related to mean dose \(\bar{D}_\mathrm{cav}\) deposited in the dosimeter’s sensitive volume V by ionizing radiation. With regard to dose determination two major categories of dosimetry system are known: absolute dosimetry systems and relative dosimetry systems.
-
1.
Absolute radiation dosimetry system is based on a dosimeter that produces a signal from which the absorbed dose in its sensitive volume can be determined directly without requiring calibration in a known radiation field. As discussed in Chap. 16, three types of absolute radiation dosimetry system are in use:
-
(i)
Calorimetric radiation dosimetry , based on carbon or water calorimeters.
-
(ii)
Chemical radiation dosimetry , based on ferrous sulfate chemical dosimeters.
-
(iii)
Ionometric radiation dosimetry , based on ionization chambers.
Note that ionization chamber-based systems are used not only in absolute dosimetry, they are also commonly used as relative dosimetry systems.
-
(i)
-
2.
Relative dosimetry systems are based on a dosimeter that requires calibration of its signal in a known radiation field. Many relative dosimetry systems have been developed to date, ranging from systems of significant practical value and usefulness (e.g., ionization chambers, radiographic film, and thermoluminescence dosimetry) down to systems of purely scientific interest and of little practical value in radiation dosimetry (e.g., radioelectret and thermally activated exoelectron emission).
15.5.3 Main Characteristics of Radiation Dosimetry Systems
Many dosimetry systems have been developed since Röntgen and Becquerel discovered ionizing radiation in 1895 and 1896, respectively. The basic requirements that a radiation dosimetry system (detector–reader combination) must satisfy are as follows:
-
(1)
High sensitivity to dose. The signal produced by the radiation detector in response to the radiation beam should be of adequate magnitude to match the reader specifications even at relatively low doses.
-
(2)
Large range of absorbed dose coverage.
-
(3)
Linear response to dose over the large range of the dosimetry system to avoid difficulties with supralinear response in the intermediate dose range and signal saturation of response at high doses. In supralinear response the detector signal exceeds linear response with increasing dose (example: thermoluminescence dosimetry); in saturation at high doses the signal attains a constant level or even diminishes with increasing dose (example: Geiger–Müller counter).
-
(4)
High accuracy and high precision. Accuracy is stipulated by the degree of agreement between the measured value and the true (i.e., expectation) value of a physical quantity, while precision is inferred from the reproducibility of results measured at same conditions. Thus, accuracy is associated with systematic errors , precision with random errors .
-
(5)
Dose rate independence of the detector signal. Ideally, for the same dose the detector signal should be independent of dose rate; however, in practice this is generally not the case and the dose rate effect must be known and accounted for when one is interested in accurate determination of absorbed dose .
-
(6)
Detector signal dependence on beam energy must be known and accounted for when the measured user’s beam quality differs from that of the calibration beam.
-
(7)
Special issues, such as beam direction striking the detector, spatial resolution of the detector, and various spurious effects affecting the detector response, must also be considered when accurate dosimetry is the objective of the dose measurement process.
15.6 Radiation Dosimeters
A radiation dosimeter typically consists of two major components: (1) Dosimeter cavity and (2) Dosimeter wall .
-
1.
“Cavity” is a shorthand term for the radiation sensitive medium producing the radiation-induced dosimeter signal and its volume is called the radiation sensitive volume. The signal that the cavity produces in response to ionizing radiation contains information on the dose imparted to the cavity and is based on a wide variety of physical or chemical quantities that are proportional to the dose imparted to the dosimeter.
-
2.
“Wall” is a shorthand term for the dosimeter component that defines, supports, and contains gaseous and liquid cavities. Solid cavities do not need a wall for containment and are in this context more practical than gaseous and liquid cavities. The wall can be of various sizes and shapes, such as cylinder, vial, pillbox, sphere, etc. and its thickness is made as thin as possible to minimize its effect on the cavity signal, yet thick enough to provide mechanical support for the cavity.
Since direct non-invasive measurements with a radiation dosimeter are difficult to accomplish on a patient, they are normally carried out in a suitable tissue-equivalent medium referred to as a phantom. Water is the most commonly used soft tissue substitute material for absorbed dose measurements in photon and electron beams. However, use of water in dosimetry is not always practical and dosimetric measurements are often carried out in more practical solid phantom materials, such as polystyrene , Lucite , and “Solid Water” that closely approximate water and soft tissue in terms of absorption and scattering properties. Three physical parameters of a given material are important in determining water equivalency: mass density, number of electrons per gram, and effective atomic number .
Determination of absorbed dose at a given point A in a patient is accomplished by measuring the dose at the corresponding point A in a tissue-equivalent phantom. As shown schematically in Fig. 15.3, a radiation dosimeter, consisting of a radiation sensitive cavity and wall, is placed into the tissue-equivalent phantom in such a way that its reference point (typically the center of the cavity volume) corresponds with the point-of-interest A at depth z on the central axis of the radiation beam. The radiation beam is produced by an external radiation source that is characterized by beam type and energy as well as by the source-surface distance (SSD) and field size A at the surface of the water phantom.
Measurement of dose to point A in a tissue-equivalent phantom with a radiation dosimeter consisting of: (i) cavity filled with radiation sensitive medium and (ii) wall to contain the radiation sensitive medium. The reference point of the dosimeter, typically but not necessarily at the center of the cavity volume, is placed into point A in the phantom
The absorbed dose measurement involves many experimental and calculation steps as well as some approximations and corrections. Assuming that an appropriate phantom was chosen and experimental setup was completed, as depicted in Fig. 15.3, the absorbed dose (or absorbed dose rate) determination proceeds as follows:
-
1.
Dosimeter cavity produces a radiation-induced signal that is converted to dose-to-cavity \(D_\mathrm{cav}\) (or dose rate-to-cavity \(\dot{D}_\mathrm{cav}\)) using corrections for influence quantities and parameters appropriate for the dosimetry technique used in \(D_\mathrm{cav}\) measurement. Influence quantities are quantities that affect the dosimeter response and may arise from environmental causes, dosimeter itself, or radiation field. Some influence quantities can be controlled during the measurement, the effect of other influence quantities on measurement result must be accounted for with appropriate correction factors.
-
2.
Dose-to-cavity \(D_\mathrm{cav}\) is converted into dose-to-medium \(D_{{\mathrm{med}}}\) where the subscript “med” refers to the tissue-equivalent phantom into which the dosimeter is introduced and in which the cavity radiation-induced signal is measured. \(D_{{\mathrm{med}}}\) is determined from \(D_\mathrm{cav}\) using a cavity theory appropriate for the conditions in which \(D_\mathrm{cav}\) was measured (see Sect. 15.7).
15.7 Cavity Theories for Radiation Dosimetry
To determine absorbed dose \(D_{{\mathrm{med}}}\) in a medium such as a tissue-equivalent (water) phantom, a radiation dosimeter (cavity) is introduced into the phantom and absorbed dose \(D_\mathrm{cav}\) to the cavity is measured. Generally, the radiation sensitive material of the cavity differs from the medium in which dose \(D_\mathrm{med}\) is to be determined. Therefore, the dosimeter placed into the phantom may perturb the photon fluence as well as the charged particle fluence and, consequently, the measured \(D_\mathrm{cav}\) may not reflect the fluence conditions that prevail in the phantom in the absence of the dosimeter. This makes the relationship between \(D_\mathrm{cav}\) and \(D_{{\mathrm{med}}}\) very complex and involves several computational steps, parameters, corrections, and approximations.
Various theories deal with the \(D_\mathrm{cav}\) to \(D_{{\mathrm{med}}}\) transition. They are referred to as cavity theories of radiation dosimetry and are governed by the cavity size they address. Somewhat vaguely, the cavities used in radiation dosimetry are categorized into small (Bragg–Gray) cavities, intermediate (Burlin) cavities, and large size cavities depending on the relative magnitude of their size d compared to the range R of secondary charged particles released through photon interactions in the phantom and traversing the cavity (dosimeter).
Figure 15.4 shows a schematic representation of the three cavity sizes: small cavity in (b), intermediate cavity in (c), and large cavity in (d). Part (a) shows the phantom with an incident photon undergoing an interaction at point P releasing an energetic secondary electron whose range R in the phantom is indicated by an arrow. Point A represents the point-of-interest at which the absorbed dose is to be determined with a radiation dosimeter. The reference point of the dosimeter is positioned in such a way that it coincides with point A in the phantom.
Schematic representation of absorbed dose measurement at point A in water phantom. Part a shows the phantom with an incident photon undergoing an interaction at point P releasing an energetic secondary electron whose range R in the phantom is indicated by a straight arrow through point A. Parts b, c, and d show the measurement of dose at point A with dosimeters of various cavity sizes: Bragg–Gray (small) cavity in (b); Burlin (intermediate) cavity in (c); and large cavity in (d)
15.7.1 Small Cavity and Bragg–Gray Cavity Theory for Photon Beams
For \(d\ll R\), the cavity size is classified as small (Fig. 15.4b) and called a Bragg–Gray cavity in honor of William H. Bragg and Louis H. Gray who developed the first cavity theory, now referred to as the Bragg–Gray cavity theory. The theory was subsequently refined and expanded into the so-called Spencer-Attix cavity theory , but its basic tenets enunciated a century ago in the format of two specific conditions are still valid today. The two Bragg–Gray conditions for photon beams of energy \(hv>\) 200 keV are as follows:
-
1.
The radiation cavity is small to give a reasonable spatial resolution of the measurement as well as to avoid perturbing the secondary charged particle fluence produced by photon interactions in the phantom. This means that \(\varphi _\mathrm{cav} \approx \varphi _\mathrm{med}\) where \(\varphi _\mathrm{cav}\) and \(\varphi _{{\mathrm{med}}}\) are secondary charged particle fluences in the cavity and in phantom medium surrounding the cavity, respectively.
-
2.
Dose \(D_\mathrm{cav}\) absorbed in the Bragg–Gray cavity is deposited solely by secondary charged particles traversing it; photon interactions in the cavity are rare and therefore ignored.
The following two relationships hold for \(D_\mathrm{cav}\) in the cavity and \(D_{{\mathrm{med}}}\) at the same point A in the phantom in the absence of the cavity, respectively
where \((\bar{S}_\mathrm{col}/\rho )_\mathrm{cav}\) and \((\bar{S}_\mathrm{col}/\rho )_{{\mathrm{med}}}\) are the spectrum averaged mean mass collision stopping powers for cavity (dosimeter) and surrounding medium (phantom), respectively (see Sect. 6.5).
From the first Bragg–Gray condition (\(\varphi _\mathrm{cav} \approx \varphi _{{\mathrm{med}}}\)) and (15.18) we now get the following Bragg–Gray relationship between the cavity dose \(D_\mathrm{cav}\) and phantom dose \(D_{{\mathrm{med}}}\)
or
for a small Bragg–Gray cavity embedded in a tissue-equivalent phantom irradiated by an ionizing photon beam. Note: The Spencer-Attix relationship that currently constitutes the recommended approach to radiation dosimetry is based on the Bragg–Gray theory except that, instead of unrestricted mean mass collision stopping powers \(\bar{{S}}_{\mathrm{col/}\rho } \) of Bragg–Gray equations, it uses mean restricted mass collision stopping powers \(\bar{{L}}\hbox {/}\rho \) and kinetic energy threshold \(\varDelta \) of 10 keV (see Sect. 6.10).
15.7.2 Large Cavity in Photon Beam
For \(d\gg R\), the cavity is classified as a large cavity (Fig. 15.4d) and the dose \(D_\mathrm{cav}\) absorbed in the cavity is attributed to secondary electrons released mainly by photon interactions inside the cavity. The contribution to \(D_\mathrm{cav}\) from electrons that originated in the phantom medium outside the cavity is negligible and therefore ignored.
Absorbed dose-to-cavity \(D_\mathrm{cav}\) and absorbed dose-to-phantom \(D_{{\mathrm{med}}}\), respectively, can be expressed as
where \(\psi _\mathrm{cav}\) and \(\psi _{{\mathrm{med}}}\) are photon energy fluences (in MeV\({\cdot }{\mathrm{cm}}^{-2}\)) in the cavity and phantom in the absence of the cavity, respectively, while (\(\bar{\mu }_\mathrm{ab}/\rho )_\mathrm{cav}\) and \(\mathrm{(}\bar{\mu }_{\mathrm{{ab}}}/\rho )_{{\mathrm{med}}}\) are mass energy absorption coefficients (in cm\(^{2}{\cdot } {{\mathrm{g}}}^{-1}\)) averaged over the photon fluence spectra for the cavity and phantom medium, respectively (see Sect. 8.3).
Assuming that the cavity density \(\rho _\mathrm{cav}\) is similar to the density \(\rho _{{\mathrm{med}}}\) of the tissue-equivalent phantom (\(\rho _\mathrm{cav} \approx \rho _{{\mathrm{med}}}\)), we stipulate that the photon energy fluences \(\psi _\mathrm{cav}\) for the cavity and \(\psi _{{\mathrm{med}}}\) for the phantom are similar (i.e., \(\psi _\mathrm{cav} \approx \psi _{{\mathrm{med}}}\)) to get the following relationship between \(D_\mathrm{cav}\) and \(D_{{\mathrm{med}}}\) from (15.21)
or
for a large cavity embedded in a tissue-equivalent phantom irradiated by ionizing photon beam.
15.7.3 Intermediate Cavity and Burlin Cavity Theory
Radiation dose measurements based on cavity theory are most often carried out with the use of a Bragg–Gray cavity embedded in a tissue-equivalent (water) phantom. The main stipulation of the Bragg–Gray cavity theory is that the cavity dimensions d are small compared to the range R of secondary charged particles traversing the cavity. This means that: (i) cavity is small to prevent perturbation of the secondary charged particle fluence in the phantom and (ii) dose absorbed in the cavity is produced solely by charged particles released by photon interactions in the phantom; photon interactions in the small cavity are negligible.
Meeting the Bragg–Gray conditions in practice is not always possible, such as, for example, for \(d\gg R\) in the case of large cavities and for \(d \approx R\) where the cavity dimensions d are comparable to the range R of secondary charged particles in the cavity. The \(d \approx R\) case deals with the so-called intermediate cavity (Fig. 15.4c) that is also known as Burlin cavity in honor of T. E. Burlin who investigated this problem both experimentally and theoretically in the 1960s.
Burlin proposed a semi-empirical equation for \(D_\mathrm{cav}/D_\mathrm{med}\), the ratio of cavity dose \(D_\mathrm{cav}\) versus phantom dose \(D_{{\mathrm{med}}}\) in the absence of the cavity in the phantom. The Burlin equation is
where \(\varDelta \) is a parameter related to the size d of the cavity and
\((\bar{S}_\mathrm{col}/\rho )_\mathrm{cav}\) and \((\bar{S}_\mathrm{col}/\rho )_{{\mathrm{med}}}\) are the mean mass collision stopping powers of the cavity medium and phantom medium, respectively.
\((\bar{\mu }_{\mathrm{{ab}}}/\rho )_\mathrm{cav}\) and \((\bar{\mu }_\mathrm{ab}/\rho )_{{\mathrm{med}}}\) are the mean mass energy absorption coefficients of the cavity medium and phantom medium, respectively.
Burlin equation in principle covers the whole range of dosimetric cavities from small (Bragg–Gray) cavities where \(d \ll R\) through intermediate (Burlin) cavities where \(d\approx R\) to large size cavities where \(d \gg R\). Parameter \(\varDelta \) in Burlin equation is related to the cavity size, approaching \(\varDelta \rightarrow 0\) for large cavities in agreement with (15.23) and \(\varDelta \rightarrow 1\) for small (Bragg–Gray) cavities in agreement with (15.20).
15.8 Media Used for Cavity, Wall, and Phantom
The dosimeter that is placed into a phantom to determine \(D_{{\mathrm{med}}}\) in phantom consists of two major components: radiation sensitive cavity and wall that contains the cavity. As shown in Fig. 15.3, there are three components of major importance in dose-to-medium (phantom) \(D_{{\mathrm{med}}}\) measurement with a dosimeter at point A in a phantom:
-
(i)
Radiation sensitive cavity C filled with solid, liquid, or gas radiation sensitive medium;
-
(ii)
Wall W of the cavity for liquid and gaseous cavities (Note: solid cavities do not require a wall for containment); and
-
(iii)
Phantom P into which the radiation dosimeter is embedded.
In general, each one of these components is made of its own suitable material that, in its own way, affects the fluence of photons as well as the fluence of secondary charged particles released by photon interactions in the phantom. The dosimeter placed into a phantom to determine \(D_{{\mathrm{med}}}\) in phantom, consists of a cavity filled with a radiation sensitive material and a wall.
The goal of \(D_{{\mathrm{med}}}\) measurement is to determine \(D_{{\mathrm{med}}}\) at point A in phantom in the absence of the dosimeter; however, the dosimeter measures the mean dose-to-cavity \(\bar{D}_\mathrm{cav}\) at point A from which \(D_{{\mathrm{med}}}\) is inferred by applying an appropriate cavity theory , as discussed in Sect. 15.7.
To simplify the transition from \(\bar{D}_\mathrm{cav}\) to \(D_{{\mathrm{med}}}\) one must coordinate the choice of material for each of the three components: phantom, wall, and cavity, accounting for relevant constraints. For example, in most clinical dosimetry situations the phantom must be tissue-equivalent and the wall for containment of liquid or gaseous cavities must be rigid. For simplicity, it is desirable for the wall and cavity to be tissue-equivalent and of same material, i.e., cavity and wall are homogeneous and matched. Obviously, the constraints are stringent, difficult to satisfy, and somewhat contradictory. Therefore, in practice compromises must be made and accounted for in the determination of \(D_{{\mathrm{med}}}\) from \(\bar{D}_\mathrm{cav}\).
Some of the parameters of importance for matching cavity and wall to phantom medium are: atomic composition, effective atomic number , density (solid, liquid, or gas), mass collision stopping power , and mass energy absorption coefficient . The four most obvious media matches are: P = W = C. In an ideal situation, the phantom P, wall W, and cavity C are made of same material. The phantom-dosimeter combination is said to be homogeneous and its three components are perfectly matched. In practice, finding perfect match and tissue equivalency is difficult, essentially impossible, considering that one must match with the water phantom the dosimeter with its radiation sensitive cavity and the wall.
\(\mathbf{P \approx W \approx C}\). In this more realistic approach, the components are not matched perfectly; however, an attempt is made to match most of the pertinent parameters as closely as possible, so that field perturbation that the dosimeter introduces into the phantom are small and can be ignored.
\(\mathbf{P} \ne \mathbf{W} \approx \mathbf{C}\). The wall and cavity of the dosimeter are almost perfectly matched (i.e., they are homogeneous), but the dosimeter is not matched to the phantom. Thus, \(D_\mathrm{wall} \approx \bar{D}_\mathrm{cav}\), and a correction must be applied to \(D_\mathrm{wall}\) in the transition from dose-to-wall \(D_\mathrm{wall}\) to dose-to-medium (phantom) \(D_{{\mathrm{med}}}\).
\(\mathbf{W \ne C}\). In a general case where the wall and cavity media are not matched (i.e., the dosimeter is not homogeneous), one can invoke the Burlin relationship for intermediate cavities see (15.24) and express the relationship between the mean dose-to-cavity \(\bar{D}_\mathrm{cav}\) and dose-to-wall \({D}_\mathrm{wall}\) as
where \(\varDelta \) is a parameter related to cavity size and
- \((\bar{S}_\mathrm{col}/\rho )_\mathrm{cav}\) :
-
and \((\bar{S}_\mathrm{col}/\rho )_\mathrm{wall}\) are the mean mass collision stopping powers of the cavity medium and wall medium, respectively.
- \((\bar{\mu }_{\mathrm{{ab}}}/\rho )_\mathrm{cav}\) :
-
and \((\bar{\mu }_\mathrm{ab}/\rho )_\mathrm{wall}\) are the mean mass energy absorption coefficients of the cavity medium and wall medium, respectively.
Note that irrespective of the value of parameter \(\varDelta \) we get a perfect match between the cavity medium and wall medium when both the mass collision stopping powers \((\bar{S}_\mathrm{col}/\rho )\) and mass energy absorption coefficients \(\bar{\mu }_{\mathrm{{ab}}}/\rho \) for cavity and wall are matched, i.e., \((\bar{S}_\mathrm{col}/\rho )_\mathrm{cav}= (\bar{S}_\mathrm{col}/\rho )_\mathrm{wall}\) and \((\bar{\mu }_\mathrm{ab}/\rho )_\mathrm{cav} = (\bar{\mu }_{\mathrm{{ab}}}/\rho )_\mathrm{wall}\). If the match between the cavity and wall is bad, then a reasonable approximation for parameter \(\varDelta \) must be estimated and (15.25) used to obtain \(D_\mathrm{wall}\) from the measured \(\bar{D}_\mathrm{cav}\) and subsequently \(D_{{\mathrm{med}}}\) from \(D_\mathrm{wall}\). This can become very difficult to manage in practice; finding reasonable matches from an assortment of suitable materials seems to be a more promising approach.
15.9 Basic Calibration of Radiotherapy Machine Output
Output of ionizing radiation beams produced by external beam radiotherapy treatment machines must be determined accurately before the machine is used clinically and, moreover, it must also be verified on a regular basis during clinical use to ensure accurate delivery of the prescribed dose to the patient. Radiotherapy beams that need accurate calibration in modern radiotherapy include photon beams of standard field sizes in the range from \(4{\times }4~\mathrm{cm}^{2}\) to \(40{\times }40~\mathrm{cm}^{2}\), electron beams of standard field sizes of \(4{\times }4~\mathrm{cm}^{2}\) to \(30{\times }30~\mathrm{cm}^{2}\), photon and electron beams of small field sizes (less than \(4{\times }4~\mathrm{cm}^{2})\), as well as heavy charged particle beams such as proton beams and heavier particle beams. Brachytherapy sealed radionuclide sources such as iridium-192 and cesium-137 require their own calibration before clinical use. Each beam type has its own special demands and presents its own special constraints, making accurate absorbed dose determination a very complex undertaking.
The basic output calibration of a radiotherapy beam (to \(\pm 2\)% or better) is but one, albeit the essential one, of the links constituting the chain representing an accurate prescribed dose delivery to the patient during the radiotherapy treatment. The other links deal with:
-
(i)
Procedures for measurement and use of relative dose data, such as percentage depth dose distribution, surface dose, exit dose, depth of dose maximum, etc. (see Sect. 1.12);
-
(ii)
Equipment commissioning and quality assurance ;
-
(iii)
Treatment planning consisting of calculation of dose distribution in tissues of the target volume and tissues surrounding the target volume;
-
(iv)
Actual set up of the patient on the treatment machine .
The basic machine output calibration can in principle be carried out with one of the three known absolute radiation dosimetry systems: (i) calorimetric, (ii) Fricke chemical, and (iii) ionometric. These systems are discussed in detail in Chap. 16; however, they are quite complicated and cumbersome to use, so that, in practice, they are relegated to use in radiation standards laboratories that define primary radiation standards.
Rather than with one of the three absolute radiation dosimetry systems, clinical machines are calibrated with a suitable relative dosimetry system that traces its calibration coefficient to an accredited National or International Standards Laboratory . This hybrid approach to clinical machine output calibration can be regarded as the second tier absolute radiation dosimetry, since it provides absolute machine output combining an absolute radiation dosimetry technique with a suitable relative dosimetry system. The relative dosimetry system so used is most commonly based on an ionization chamber with a calibration coefficient traceable to a national standards laboratory. One should note that when an absolute dosimetry system is used for radiation beam calibration in a standards laboratory , it relies on its own accuracy, in contrast to a hybrid field-calibration with a relative dosimetry system that traces its calibration coefficient to a standard that is common to many other users and originated in a standards laboratory.
Not all National and International Standards Laboratories deal with radiation standards; however, the ones that do so, typically provide absorbed dose calibration coefficients on two distinct levels: clinical level and high dose level.
-
1.
Clinical level. For cobalt-60 gamma beams in the absorbed dose range from \({\sim }1\) Gy to \({\sim }10\) Gy that are used in radiotherapy where the cobalt-60 calibration coefficient of a dosimeter, traceable to a standards laboratory, is used in dosimetry protocols (see Sect. 15.10) for calibration of megavoltage x-ray beams (4 MeV to 25 MV) and megavoltage electron beams (4 MeV to 30 MeV).
-
2.
High dose level. For cobalt-60 gamma beams as well as megavoltage photon and electron beams in the dose range from \({\sim } 0.5\) kGy to \({\sim }1\) MGy used in radiation processing and food irradiation .
15.10 Dosimetry Protocols
The procedures to be followed when carrying out a basic output calibration of a clinical photon or electron beam produced by a radiotherapy machine are prescribed in international, national, or regional radiation dosimetry protocols or dosimetry codes of practice . The choice of the dosimetry protocol to be used is largely left to individual radiotherapy departments or is prescribed by a national governmental agency. Output of radiotherapy equipment is usually quoted as absorbed dose or dose rate under specific reference conditions. Water was chosen as the standard reference medium , because of its absorption and scattering characteristics that are similar to those of tissue.
The best known international radiation dosimetry protocol is the IAEA TRS–398 protocol issued by the Vienna-based International Atomic Energy Agency (IAEA) in 2000 entitled: “Absorbed Dose Determination in External Beam Radiotherapy”; however, many other dosimetry protocols are also available from national or regional organizations, most notably from the American Association of Physicists in Medicine (AAPM) for North America; Institution of Physics and Engineering in Medicine and Biology (IPEMB) for the UK; Deutsches Institut für Normung (DIN) for Germany; Nederlandse Commissie voor Stralingsdosimetrie (NCS) for Holland and Belgium; and Nordic Association of Clinical Physics (NACP) for Scandinavia.
Radiation Dosimetry in Radiation Medicine
Radiation dosimetry, defined as measurement of ionizing radiation dose or some other dose-related physical quantity, is a branch of medical physics that plays a very important role in the use of ionizing radiation in diagnosis and treatment of disease. In addition, radiation dosimetry forms the foundation of radiation protection services that deal with:
-
1.
Recommendations on, and enforcement of, safe practices in the use of ionizing radiation in medicine, science, industry, and power generation.
-
2.
Estimation of absorbed dose to general public resulting from peaceful use of ionizing radiation in medicine, science, industry and power generation.
-
3.
Estimation of absorbed dose to individuals involved in radiation accidents.
Diagnosis of disease (imaging) with ionizing radiation is carried out in two specialties of radiation medicine: diagnostic radiology using x-rays and nuclear medicine (also called molecular imaging) with unsealed radioactive sources. Both of these specialties strive to obtain the optimal image quality with a minimum dose to the patient and staff.
Treatment of disease with ionizing radiation usually implies treatment of cancer with ionizing radiation; a specialty of radiation medicine, commonly called radiotherapy or radiation oncology. It is carried out with a variety of external or internal radiation sources producing x-rays, gamma rays, electrons, protons, or heavier particles. The goal of radiotherapy is to deliver the prescribed tumoricidal (oncolytic) dose to the tumor with a high degree of spatial and numerical accuracy and minimal total body patient dose as well as minimal dose to staff providing the radiotherapy treatment to the patient.
Radiotherapy involves directly a team of four professionals sharing responsibilities as follows:
-
1.
Radiation oncologist diagnoses the patient’s malignant disease, decides on course of treatment, and prescribes the type of radiation, dose fractionation, and treatment dose.
-
2.
Medical physicist : (i) organizes equipment maintenance and servicing, (ii) calibrates the radiation beams produced by radiotherapy equipment, such as x-ray machines, cobalt units, and linear accelerators, and (iii) deals with governmental regulatory agencies and ensures that hospitals and clinics meet regulatory requirements to make the use of ionizing radiation in diagnosis and treatment of disease safe for patients and staff.
-
3.
Medical dosimetrist , in cooperation with medical physicist and radiation oncologist, produces a detailed computerized treatment plan and determines the optimal dose distribution for patient’s treatment.
-
4.
Radiation therapist (radiotherapy technologist) delivers the prescribed radiation dose to the patient on the prescribed radiotherapy machine according to the treatment plan and a prescribed fractionation of typically 20 to 30 daily fractions.
As evident from Chaps. 16 and 17 that deal with absolute and relative radiation dosimetry, respectively, radiation dosimetry is an important, well-developed and sophisticated field of physics, mainly applied to medicine. Professionals who work in this field must carry out their work with utmost accuracy and care to ensure that the patient treatment is safe for the patient as well as staff and that the desired diagnostic or treatment outcome is attained.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Podgoršak, E.B. (2016). Fundamentals of Radiation Dosimetry. In: Radiation Physics for Medical Physicists. Graduate Texts in Physics. Springer, Cham. https://doi.org/10.1007/978-3-319-25382-4_15
Download citation
DOI: https://doi.org/10.1007/978-3-319-25382-4_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-25380-0
Online ISBN: 978-3-319-25382-4
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)






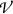 and expend all their kinetic energy through collision losses inside
and expend all their kinetic energy through collision losses inside 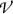 .
.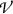 but carry a portion of their kinetic energy out of
but carry a portion of their kinetic energy out of 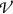 .
.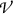 and carry a portion of their kinetic energy into
and carry a portion of their kinetic energy into 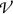 .
. . Energy loss of 3 MeV is compensated by electron e
. Energy loss of 3 MeV is compensated by electron e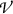 .
.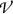 . Energy loss of 2 MeV is compensated by electron e
. Energy loss of 2 MeV is compensated by electron e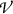 .
.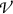 . Energy loss of 3 MeV is compensated by electron e
. Energy loss of 3 MeV is compensated by electron e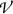 .
.
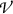 .
.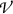 through numerous interactions with lead atoms along the track ABC:
through numerous interactions with lead atoms along the track ABC: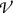 and contributes to absorbed dose
and contributes to absorbed dose 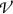 .
.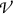 containing mass dm we now estimate the CSDA range
(Sect.
containing mass dm we now estimate the CSDA range
(Sect. 
