Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Numerical methods known as Monte Carlo methods can be loosely defined in general terms to be any methods that rely on random sampling to estimate the solutions. Monte Carlo methods are often applied to problems which are either too complicated to be described by a mathematical model or whose parameter space is too large to be explored systematically.

Recent years have witnessed dramatic increase of data in many fields of science and engineering [1], due to the advancement of sensors, mobile devices, biotechnology, digital communication, and internet applications. These massive, continuously growing, complex, and diverse data sets are often referred to as the “big data.” Analyzing big data demands cost-effective and innovative forms of information processing for enhanced insight and decision making. While many traditional, deterministic data analysis methods have great difficulties to scale to the massive big data sets, Monte Carlo methods, which are based on random sampling techniques, become important and powerful tools for big data applications. Particularly, for certain big data sets beyond the computational capability of the most powerful supercomputers, Monte Carlo data analysis methods using random sampling are the only viable approaches.

This article starts with a basic description of the principles of Monte Carlo methods. It then discusses the variance reduction techniques, including stratified sampling, control variates, antithetic variates, and importance sampling, to design “smart” Monte Carlo. Examples of Monte Carlo methods on estimating sum of a large array, solving linear systems, multiplying matrix products, recovering missing matrix, and approximating low-rank matrices. Although in order to keep the presentation simple, these application examples are presented in a relatively small scale, the underlying Monte Carlo techniques can be effectively extended to big data sets.

2 The Basic of Monte Carlo

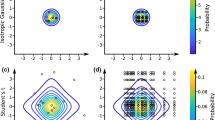
Monte Carlo methods provide approximate solutions to a variety of mathematical problems by random sampling. Let us take the numerical integration as an example, which constitutes a broad family of algorithms in numerical analysis. Suppose we want to calculate a one-dimensional definite numerical integral, \(I =\int _{ a}^{b}f\left (x\right )dx\). A common numerical integral method is to divide the one-dimensional interval into N subintervals and then to sum the area corresponding to each subinterval using either rectangular, trapezoidal, or Simpson’s rules (Fig. 7.1a) [2]. Similarly, for two-dimensional intervals, the number of 2D subintervals becomes N 2 (Fig. 7.1b). In general, for d-dimensional integration problems, the d-dimensional space needs to be divided into N d subintervals. For a not very high dimensional problem with d = 20 and N = 100, the total number of subintervals that need to be evaluated goes up to 1040, which is unapproachable by most numerical integration algorithms. Mathematically, this is referred to as the “curse of dimensionality.”

Fig. 7.1
figure 1

Numerical integration using deterministic methods. (a) 1D integral. (b) 2D integral

Full size image

In contrast, Monte Carlo methods estimate the integral by statistical sampling techniques [3]. Let us consider a one-dimensional integral \(I_{0-1} =\int _{ 0}^{1}f\left (x\right )dx\), which can be easily extended to a more general integral of \(I =\int _{ a}^{b}f\left (x\right )dx\). Suppose that the random variables x 1, x 2, ⋯ , x N are drawn independently from the probability density function p(x). A function F may be defined as

$$\displaystyle{F =\sum _{ i=1}^{N}f\left (x_{ i}\right )p\left (x_{i}\right ).}$$

The expectation value of F becomes

$$\displaystyle{E\left (F\right ) =\int _{ 0}^{1}f\left (x\right )p\left (x\right )dx.}$$

The crude Monte Carlo integration method assumes that the probability density function p(x) is uniform, i.e., the random samples \(f(x_{1}),f(x_{2}),\cdots \,,f(x_{N})\) are equally important, and then

$$\displaystyle{E\left (F\right ) =\int _{ a}^{b}f\left (x\right )dx.}$$

Correspondingly, the variance of F becomes

$$\displaystyle{V ar\left (F\right ) = \dfrac{1} {N}\int _{0}^{1}\left (f(x) - E(F)\right )^{2}dx = \dfrac{1} {N}\sigma ^{2},}$$

where σ 2 is the inherent variance of the integrant function f(x). Clearly, we can find that the standard deviation of the estimator θ is \(\sigma N^{-1/2}\). This means that as N → ∞, the distribution of F narrows around its mean at the rate of \(O\left (N^{-1/2}\right )\).

Now, let us extend the Monte Carlo integration method to a d-dimensional integral \(I_{d} =\int _{ 0}^{1}\cdots \int _{0}^{1}f\left (x\right )dx\), the expectation of \(F_{d} =\sum _{ i=1}^{N}f(x_{i})/N\) on uniformly distributed random variable vectors x 1, x 2, ⋯ , x N becomes

$$\displaystyle{E\left (F_{d}\right ) =\int _{ 0}^{1}\cdots \int _{ 0}^{1}f\left (x\right )dx = I_{ d}.}$$

The variance of the estimator F d is σ d 2∕N, where σ d 2 is the inherent variance of the integrant function f(x). If an integral function f(x) is given, σ d 2 is a constant and therefore, similar to one-dimensional integral, the convergence rate of Monte Carlo is \(O\left (N^{-1/2}\right )\), which is independent of dimensionality.

In summary, compared to the deterministic numerical integration methods, whose convergence rate is \(O(N^{-\alpha /d})\), where α is the algorithm related constant and d is the dimension, Monte Carlo integration method yields a convergence rate of \(O(N^{-1/2})\) [4], which can somehow avoid the “curse of dimensionality.” Moreover, computations on each random samples are independent, which can be carried out in an embarrassingly parallel minor to harness the power of large-scale parallel and distributed computing architectures [5, 6]. On the other hand, the main disadvantage of Monte Carlo is that the convergence of Monte Carlo methods is very slow, roughly for every one digit of accuracy usually requiring 100 times more computations.

3 Variance Reduction

Crude Monte Carlo treats all random samples are equally important. In reality, we can often gain additional knowledge from the application domain, which can be taken advantage to come up with better estimators. Variance reduction is a procedure of deriving an alternative estimator to obtain a smaller variance than the crude Monte Carlo estimator and improve the precision of the Monte Carlo estimates for a given number of samples. In practical applications, a good estimator leading to million times more accurate than a bad one is not rarely seen. In this section, we describe some of the popular variance reduction techniques [3, 4], including stratified sampling, control variates, antithetic variates, and importance sampling. These variance reduction methods, if appropriately used, can significantly improve the efficiency of Monte Carlo methods in processing and analyzing big data sets.

3.1 Stratified Sampling

The inherent variance of the integral function f(x) may vary significantly in different regions. The fundamental idea of stratified sampling is to apply more samples in the region with large variability and vice versa. Using the one-dimensional integral in interval \(\left [0,1\right ]\) as an example, stratified sampling is to partition the interval \(\left [0,1\right ]\) into several disjoint subinterval ranges, i.e., \(\left [0,\alpha _{1}\right ),\left [\alpha _{1},\alpha _{2}\right ),\cdots \,,\left [\alpha _{k-1},\alpha _{k}\right ),\left [\alpha _{k},1\right ]\). Then a Monte Carlo estimator \(F_{\alpha _{i-1},\alpha _{i}}\) is applied to each range \(\left [\alpha _{i-1},\alpha _{i}\right )\) separately so that

$$\displaystyle{F_{\alpha _{i-1},\alpha _{i}} =\sum _{ j=1}^{n_{i} }\left (\alpha _{i} -\alpha _{i-1}\right ) \dfrac{1} {n_{i}}f(x_{j}),}$$

where x j is a random sample in \(\left [\alpha _{i-1},\alpha _{i}\right )\) and n i is the total number of samples. Clearly,

$$\displaystyle{E\left (F_{\alpha _{i-1},\alpha _{i}}\right ) =\int _{ \alpha _{i-1}}^{\alpha _{i} }f(x)dx.}$$

The overall stratified sampling estimator F stratified is the combination of all estimators in different subinterval ranges

$$\displaystyle{F_{stratified} =\sum _{ i=1}^{k+1}F_{\alpha _{ i-1},\alpha _{i}},}$$

which is an unbiased estimator of the integral. The variance of the stratified sampling estimator becomes

$$\displaystyle{V ar\left (F_{stratified}\right ) =\sum _{ i=1}^{k+1}\left (\alpha _{ i} -\alpha _{i-1)}\right ) \dfrac{1} {n_{i}}\sigma _{\alpha _{i-1},\alpha _{i}}^{2},}$$

where \(\sigma _{\alpha _{ i-1},\alpha _{i}}^{2}\) is the variance of the integrant function f(x) in subinterval \(\left [\alpha _{i-1},\alpha _{i}\right )\). This reveals the rationale of stratified sampling, which is to minimize \(\dfrac{1} {n_{i}}\sigma _{\alpha _{ i-1},\alpha _{i}}^{2}\) in each subinterval. If stratification is well carried out, the variance of stratified sampling will be less than that of crude Monte Carlo.

3.2 Control Variates

If there is another estimator which is positively correlated to the one to be evaluated and can be easily calculated with known expectation, it can be used as a control variate. For example, in the Monte Carlo integration example, the original integral \(I_{0-1} =\int _{ 0}^{1}f(x)dx\) can be rewritten into a summation of two parts

$$\displaystyle{I_{0-1} =\int _{ 0}^{1}g(x)dx +\int _{ 0}^{1}\left (f(x) - g(x)\right )dx,}$$

where g(x) is a simple function that can be either integrated theoretically or easily calculated and absorbs most of the variation of f(x) by mimicking f(x) as shown in Fig. 7.2, we only need to estimate the difference between f(x) − g(x), which will result in variance reduction of the estimator.

Fig. 7.2
figure 2

Control variates approach. If g(x) can be estimated theoretically, the sampling errors are limited to the area of f(x) − g(x)

Full size image

3.3 Antithetic Variates

Contrast to the control variates method based on a strongly positively correlated estimator with F, the antithetic variates method takes advantage of an estimator F ′ that is strongly negatively correlated with F. Suppose that F is an unbiased estimator of a quantity, E(F) = E(F ′), and Cov(F, F ′) < 0. Then, the antithetic estimator \(F_{antitheticc} = (F + F^{{\prime}})/2\) is also an unbiased estimator of this quantity. The sampling variance of F antitheticc becomes

$$\displaystyle{V ar\left (F_{antitheticc}\right ) = \dfrac{V ar\left (F\right )} {v} + \dfrac{V ar\left (F^{{\prime}}\right )} {4} + \dfrac{Cov\left (F,F^{{\prime}}\right )} {2}.}$$

Here Cov(F, F ′) < 0 due to negative correlation between F and F ′, which leads to overall smaller variance in F antitheticc than that of F and F ′.

3.4 Importance Sampling

The importance sampling technology is often used in statistical resampling, which reduces variance by emphasizing the sampling on regions of interest. For example, by introducing a new proposal function g(x), the original integral \(I_{0-1} =\int _{ 0}^{1}f(x)dx\) can be rewritten as

$$\displaystyle{I_{0-1} =\int _{ 0}^{1}\dfrac{f(x)} {g(x)}g(x)dx =\int _{ 0}^{1}\dfrac{f(x)} {g(x)}dG(x),}$$

where G(x) is a cumulative density function (CDF). f(x)∕g(x) is called the likelihood ratio. With random samples drawn from a proposal distribution whose CDF is G(x) instead of sampling from a uniform distribution, the variance of the importance sampling estimator F importance sampling becomes

$$\displaystyle{V ar\left (F_{importance\ sampling}\right ) =\int _{ 0}^{1}\left (\dfrac{f(x)} {g(x)} - E(F)\right )^{2}dG(x).}$$

A good likelihood ratio can result in a significant variance reduction.

In practice, assume that we know nothing about the target distribution at the very beginning, we may have to start from uniform sampling. However, after initial sampling, we have a better understanding of the target distribution, which results in a better proposal function. The resampling can be guided by the new proposal function and leads to a better approximation of the target distribution.

4 Examples of Monte Carlo Methods in Data Science

In this section, we present several application examples as case studies of using Monte Carlo methods for data analysis. Variance reduction techniques are applied to build “smart” Monte Carlo estimators to enhance sampling efficiency.

4.1 Case Study 1: Estimation of Sum

In many practical data analysis applications, we are often required to estimate the sum of a large data set. However, due to many reasons, we are not allowed to visit every element in the data set but want to get a good estimation. The following is an application example to estimate the overall salary expense in a company.

Consider a big, global company having 7140 employees falling in the following categories, 78 managers, 4020 engineers, 2008 salesmen, and 1034 technicians. Now we want to estimate the overall expense in employee salaries in this company. Due to cost as technical difficulty, we are only allowed to use 100 samples.

The simplest sampling method is the crude Monte Carlo using uniform sampling without considering different categories. The main problem of uniform sampling is ignoring the differences among categories, which will thus lead to a large estimation variance 460, 871K ± 80, 712K. More importantly, the percentage of managers is around 1 % in all employees. There is a high chance that the selected 100 samples may miss the manager category. Stratified sampling can better address this problem. We can calculate the number of samples falling into each category, specifically, \(78/7140 \times 100 = 1\) sample in managers, \(4020/7140 \times 100 = 56\) samples in engineers, \(2008/7140 \times 100 = 28\) samples in salesmen, and \(1034/7140 \times 100 = 15\) samples in technicians. As a result, stratified sampling yields better estimation (500, 112K ± 30, 147K) than that of uniform sampling.

If we have additional information, we can construct even better stratified sampling estimator. If we happen to know about the salary variation in each employee category (for example, from previous years’ data), i.e., Managers (200K ∼ 500K), Salesmen (40K ∼ 120K), Engineers (60K ∼ 80K), and Technicians (50K ∼ 70K), we can take advantage of this information. We can find that the managers and salesmen have large variances, which deserves more samples while the engineers and technicians categories have small variances, where small number of samples will work. By reassigning the number of samples in different categories, 32 samples for Managers, 7 samples for Engineers, 59 samples for Salesmen, and 2 samples for Technicians, the overall estimated result becomes 520, 066K ± 10, 113K, which provides us more precise estimation than simple stratified sampling.

4.2 Case Study 2: Monte Carlo Linear Solver

Applying Monte Carlo sampling to estimate solutions in linear systems is originally proposed by Ulam and von Neumann and later described by Forsythe and Leibler in [7]. Considering a linear system of

$$\displaystyle{x = Hx + b,}$$

where H is an n × n non-singular matrix, b is the given constant vector, and x is the vector of unknowns. The fundamental idea of the Monte Carlo solver is to construct Markov chains by generating random walks to statistically sample the underlying Neumann series

$$\displaystyle{I + H + H^{2} + H^{3} + \cdots }$$

of the linear system [8]. The transition probabilities of the random walks are defined by a transition matrix P satisfying the following transition conditions:

$$\displaystyle\begin{array}{rcl} P_{ij} \geq 0;& & {}\\ \sum _{j}P_{ij} \leq 1;& & {}\\ H_{ij}\neq 0 \rightarrow P_{ij}\neq 0,& & {}\\ \end{array}$$

and the termination probability T i at row i is defined as

$$\displaystyle{T_{i} = 1 -\sum _{j}P_{ij}.}$$

Then, a random walk starting at i 0 and terminating after k steps is defined as

$$\displaystyle{\gamma _{k}: r_{0} \rightarrow r_{1} \rightarrow r_{2} \rightarrow \cdots \rightarrow r_{k}}$$

where the integers r 0, r 1, r 2, ⋯ , r k are the row indices of matrix H visited during the random walk.

As noted in existing literature [9], if the necessary and sufficient condition for the convergence of Monte Carlo solver holds, a random variable X(γ k ) defined as

$$\displaystyle{X\left (\gamma _{k}\right ) = \frac{H_{r_{0}r_{1}}H_{r_{1}r_{2}}\cdots H_{r_{k-1}r_{k}}} {P_{r_{0}r_{1}}P_{r_{1}r_{2}}\cdots P_{r_{k-1}r_{k}}} b_{r_{k}}/T_{r_{k}}}$$

is an unbiased estimator of component \(x_{r_{0}}\) in the unknown vector x.

Variance reductions have been commonly employed in the Monte Carlo algorithms to improve the sampling efficiency. Let’s consider a simple linear with \(H = \left [\begin{array}{ccc} 0.1 &0.45& 0.225\\ - 0.15 & 0.1 & - 0.3 \\ - 0.18&0.36& 0.1 \end{array} \right ]\) and \(b = \left [\begin{array}{c} 0.225\\ 1.35 \\ 0.72 \end{array} \right ]\). Clearly, the exact solution is \(b = \left [\begin{array}{c} 1\\ 1 \\ 1 \end{array} \right ].\)

Figure 7.3 compares the convergence of Monte Carlo linear solvers using three sampling schemes listed in Table 7.1 with different transition matrices in terms of estimate value x 1. One can find that even though all of these sampling schemes have the same convergence rate of \(O(N^{-1/2})\), the estimator based on Monte Carlo Almost Optimal (MAO) scheme [10], which samples the matrix elements according to their importance, yields significant smaller variance than the other two.

Fig. 7.3
figure 3

Comparison of Monte Carlo linear solver with different transition matrices

Full size image
Table 7.1 Uniform, original, and MAO sampling scheme with different transition matrices
Full size table

4.3 Case Study 3: Image Recovery

In this case study, we investigate the image processing technology of using a small number of pixel samples to recover an incomplete or fuzzy image. The strategy of Monte Carlo sampling plays a critical role for the quality of the recovered image.

We use an aerial image chosen from the USC-SIPI Image Database [11] as an example. The image recovery method is based on a matrix completion algorithm by optimizing the constrained nuclear norm of the matrix [12]. Two sets of pixel samples (12. 19 % samples in each) are used—one is generated by uniform sampling and the other by importance sampling. The importance sampling process consists of two stages:

  1. (1)

    initial uniform sampling is performed with 3. 05 % pixel samples to learn the rough pixel distribution in the image to produce a proposal function; and

  2. (2)

    importance sampling is performed based on the proposal function created in (1) to generate the rest 9. 14 % samples.

As shown in Fig. 7.4, the pixel samples generated by the importance sampling scheme lead to a recovered image in significantly higher quality than the one by using uniform samples.

Fig. 7.4
figure 4

Comparison of image recovery from pixel samples generated by uniform sampling and importance sampling

Full size image

4.4 Case Study 4: Matrix Multiplication

In this case study, we investigate the Monte Carlo methods of approximating the product of large matrices. Let A be an m × n matrix and B be an n × p matrix, where m,n, and p are large. The Monte Carlo sampling algorithm to fast approximate the product matrix C = AB using s samples is described as follows [13]:

  1. (1)

    Generate s random integers i k between 1 and n with probability \(p_{i_{k}}\), for k = 1, ⋯ , s;

  2. (2)

    Set \(M^{(k)} = A^{(i_{k})}/\sqrt{sp_{ i_{k}}}\) and \(N_{(k)} = B_{(i_{k})}/\sqrt{sp_{( } i_{k } )}\), for k = 1, ⋯ , s;

  3. (3)

    Compute the matrix product of MN.

The fundamental idea of the Monte Carlo sampling algorithm is to construct a discrete random variable X with probability \(p\left (X = \dfrac{A^{(k)}B_{(k)}} {p_{k}} \right ) = p_{k}\) for k = 1, ⋯ , n, where A (k) and B (k) represent the kth column of A and the kth row of B, respectively. The expectation of X is

$$\displaystyle{E(X) =\sum _{ k=1}^{n}\dfrac{A^{(k)}B_{ (k)}} {p_{k}} p_{k} =\sum _{ k=1}^{n}A^{(k)}B_{ (k)},}$$

which is identical to matrix C. Therefore, matrix C can be fast approximated from the product of MN, where \(MN = \dfrac{1} {s}\sum _{k=1}^{s}\dfrac{A^{(i_{k})}B_{ (i_{k})}} {p_{i_{k}}}\) is an estimator. The variance on each element in MN is [13]

$$\displaystyle{V ar\left [\left (MN\right )_{ij}\right ] =\sum _{ k=1}^{n}\dfrac{A_{ik}^{2}A_{ kj}^{2}} {s^{2}p_{k}} - \dfrac{1} {s^{2}}\left (AB\right )_{ij}^{2}.}$$

To improve the accuracy of approximating matrix–matrix multiplication, importance sampling can be effectively applied by using the optimal probabilities

$$\displaystyle{p_{k} = \dfrac{\left \vert A^{(k)}\right \vert \left \vert B_{(k)}\right \vert } {\sum _{j=1}^{n}\left \vert A^{(j)}\right \vert \left \vert B_{(j)}\right \vert },}$$

where the expectation of approximation error can be theoretically minimized [13, 14].

Let us consider a simple toy example where

$$\displaystyle{A = \left [\begin{array}{cccccc} 1.6254 & 8.5799 & 8.5596 & 5.4832 & 9.1047 &1.3797\\ 9.8717 & 4.5759 & 7.5434 & 1.1230 & 8.4098 &8.3874 \\ 4.8246 & 3.9563 & 5.1322 & 1.0143 & 8.6938 &7.7045\\ 0.9104 &545.3701 & 4.6611 &769.1278 & 9.1947 &4.4734 \\ 14.9880& 6.4549 &197.7756& 5.2276 &88.9237&7.4417 \end{array} \right ]}$$

and

$$\displaystyle{B = \left [\begin{array}{cccc} 5.5899& 2.6152 &7.8102& 8.2298\\ 5.9020 &666.2519 &2.6396 & 7.7184 \\ 7.3150&143.9785&9.0632& 4.9668\\ 2.1493 &695.7888 &3.2657 &974.7106 \\ 1.3544&758.2126&2.7377& 4.6348\\ 9.1003 & 8.3607 &6.7709 & 27.5470\\ \end{array} \right ]}$$

Figure 7.5 compares the relative approximation error of the resulting product matrix using uniform sampling and the one using important sampling with respect to sample size in 1000 runs. One can clearly find that when optimal selection probabilities are used, importance sampling outperforms uniform sampling with better approximation of the matrix product.

Fig. 7.5
figure 5

Comparison of relative approximation error in matrix–matrix multiplication using uniform sampling and importance sampling with respect to sample size in 1000 Monte Carlo runs

Full size image

4.5 Case Study 5: Low-Rank Approximation

Given a matrix A, it is often desirable to find a good low-rank approximation to A in many data analysis applications. Denote u 1, ⋯ , u n and v 1, ⋯ , v n as the left and right singular vectors, respectively, σ 1, σ 2, ⋯ , σ n , are singular values in non-increasing order, the matrix A can be expressed as

$$\displaystyle{A =\sum _{ i=1}^{n}\sigma _{ i}u_{i}v_{i}^{T}}$$

The best k-rank approximation [15] to a matrix A is formed as \(A_{k} =\sum _{ i=1}^{k}\sigma _{i}u_{i}v_{i}^{T}\) with minor error

$$\displaystyle{\min _{rank(B)=k}\|A - B\|_{2} =\| A - A_{k}\|_{2} =\sigma _{k+1}.}$$

To handle the computational challenges involved in very big matrices, randomized Singular Value Decomposition (SVD) algorithm with Gaussian sampling [16–18] is widely used to approximate top-k singular values and singular vectors. The rationale is to construct a small condensed subspace by sampling A, where the dominant actions of A could be fast estimated from this small subspace with relatively low computation cost and high confidence. The procedure of randomized SVD is described as follows:

  1. (1)

    Sample A with a standard Gaussian matrix Ω so that Y = A Ω;

  2. (2)

    Construct a basis Q for the range of Y;

  3. (3)

    Compute matrix multiplication of B = A T Q;

  4. (4)

    Perform a deterministic SVD decomposition on \(B = U_{B}\varSigma _{B}V _{B}^{T}\);

  5. (5)

    Assign \(u_{j} = Qv_{B_{j}}\), \(\sigma _{j} =\sigma _{B_{j}}\), and \(v_{j} = u_{B_{j}}\), j = 1, ⋯ , k.

We consider an example of applying the randomized SVD algorithm to obtain a low-rank approximation of an image while minimizing the approximation error. The control variates approach is applied. First of all, the whole range space of matrix A is sampled to approximate the largest r singular components and then derive an approximate \(\widetilde{A_{r}}\) such that \(\widetilde{A_{r}} =\sum _{ i=1}^{r}\sigma _{i}u_{i}v_{i}^{T}\). If the approximation error is too high, \(\widetilde{A_{r}}\) is used as the control variate to sample the next dominating singular components. This process is repeated until satisfactory approximation accuracy is achieved.

Figure 7.6 shows the results of applying randomized SVD algorithm and control variate to compute a low-rank approximation of the aerial image with less than 1 % error. Figure 7.6a presents the original image. Figures 7.6b–d illustrate the adaptive reconstructed images with increasing numbers of singular components. Finally with 100 singular components, a low-rank approximation of the original image with 0. 9 % error is obtained.

Fig. 7.6
figure 6

Low-rank approximation using randomized SVD with Gaussian sampling and control variates strategy. (a) The original image. (b) Rank 10 with approximation error 14. 3 %. (c) Rank 40 with approximation error 2. 1 %. (d) Rank 100 with approximation error 0. 9 %

Full size image

5 Summary

Monte Carlo methods are powerful tools to analyze large data sets, particularly in the big data era when the data growth outpaces the computer processing capability. We review the basics of Monte Carlo methods and the popular techniques for variance reduction in this article. Several application examples using Monte Carlo for data analysis are presented. The rule of thumb in Monte Carlo is, the more known knowledge is incorporated into the estimator, the more uncertainty can be reduced and the better data analysis accuracy can be obtained.