Intelligent Quality Function Deployment

Abstract

Quality function deployment (QFD) is commonly used in the product planning stage to define the engineering characteristics and target value settings of new products. However, some QFD processes substantially involve human subjective judgment, thus adversely affecting the usefulness of QFD. In recent years, a few studies have been conducted to introduce various intelligent techniques into QFD to address the problems associated with subjective judgment. These studies contribute to the development of intelligent QFD. This chapter presents our recent research on introducing intelligent techniques into QFD with regard to four aspects, namely, determination of importance weights of customer requirements , modeling of functional relationship s in QFD, determination of importance weights of engineering characteristics and target value setting of engineering characteristics. In our research, a fuzzy analytic hierarchy process with an extent analysis approach is proposed to determine the importance weights for customer requirements to capture the vagueness of human judgment and a chaos-based fuzzy regression approach is proposed to model the relationships between customer satisfaction and engineering characteristics by which fuzziness and nonlinearity of the modeling can be addressed. To determine importance weights of engineering characteristics, we propose a novel fuzzy group decision-making method to address two types of uncertainties which integrates a fuzzy weighted average method with a consensus ordinal ranking technique. Regarding the target value setting of engineering characteristics, an inexact genetic algorithm is proposed to generate a family of inexact optimal solutions instead of determining one set of exact optimal target values. Possible future research on the development of intelligent QFD is provided in the conclusion section.

11.1 Introduction

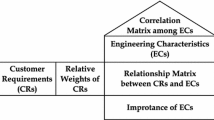
Quality function deployment (QFD) is a systematic method of translating customer requirements (CRs) into engineering characteristics (ECs) in the product planning stage (Terninko 1997). QFD provides a visual relationship to help engineers focus on design requirements instead of design function in the whole development process. QFD uses the voices of the customers from the beginning of product development and deploys it throughout the whole product design process. Customer requirements (CRs) in a new product are collected. Then, product development teams map the CRs to ECs based on their knowledge, experience, and judgement. A QFD system comprises four inter-linked phases: product planning phase, part deployment phase, process planning phase, and production/operation planning phase (Karsak 2004). Figure 11.1 shows the four phases of QFD.

Fig. 11.1

The four phases of QFD

The implementation of QFD is called house of quality (HoQ), which offers a global view of information on a new product and on how CRs can be met at different stages of new product development. A HoQ typically contains information on “what to do” (CRs or voice of customers), importance weights of CRs, “how to do” (ECs) , importance weights of ECs, the relationship matrix (relationships between CRs and ECs), technical correlation matrix , benchmarking data, and the target values settings of the ECs (Govers 1996). QFD was proposed to develop products with higher quality to meet or surpass customer’s needs through collecting and analysing the voice of the customer (Chan and Wu 2002). It has been applied successfully in many industries. New product designs with QFD can enhance organizational learning and improve customer satisfaction. QFD can also decrease product costs, simplify manufacturing processes, and shorten the development time of new products (Vonderembse and Raghunathan 1997).

11.2 Literature Review

Determining the importance weights of CRs is a crucial QFD step because these weights can largely affect the target value setting of ECs in the later stage. Conducting surveys, such as lead user and focus group surveys, is common to determine the importance weights. The weights are then determined by analyzing the survey data. Respondents in surveys are always asked to rate various CRs, such as good quality and user-friendliness (Mochimaru et al. 2012). The product ratings of respondents involve subjective judgments. CRs always contain ambiguity and multiplicity of meaning. The description of CRs is usually linguistic and vague. Thus, conventional methods, which determine the importance weights of CRs on the basis of crisp numerical data, are inadequate. Some intelligent techniques have been introduced in previous studies to determine the importance weights of CRs, such as artificial neural network (Che et al. 1999), fuzzy and entropy methods (Chan et al. 1999), fuzzy AHP (Kwong and Bai 2002), supervised learning with a radial basis function (RBF) neural network (Chen 2003), fuzzy group decision-making approach (Zhang 2009), and fuzzy decision making trial and evaluation laboratory (DEMATAL) method (Shahraki and Paghaleh 2011).

Another important step of QFD is to prioritize ECs to facilitate resource planning. However, the inherent vagueness or impreciseness of QFD makes the prioritization of ECs ineffective. Two types of uncertainties in QFD exist. The first type is human assessment and judgment on qualitative attributes, which are always subjective and imprecise; thus, the input information of human perception can be ambiguous. The second type is the involvement of various stakeholders and/or the number of customers in the assessment of the importance of CRs, as well as the degree of relationships between CRs and ECs in QFD . Uncertainty that is associated with group assessment will exist because of individual heterogeneity. Previous studies have employed intelligent techniques to prioritize ECs, such as fuzzy outranking approach (Wang 1999), fuzzy set theory of axiomatic design review (Huang and Jiang 2002), a combined analytic network process (ANP) and goal programming approach (Karsak et al. 2002), fuzzy ANP (Buyukozkan et al. 2004), an integrated fuzzy weighted average method and fuzzy expected value operator method (Chen et al. 2006), and a methodology of determining aggregated importance of ECs with the considerations of fuzzy relation measures between CRs and ECs as well as fuzzy correlation measures among ECs (Kwong et al. 2007). However, most previous studies only address one of the two types of uncertainties that can affect the robustness of prioritizing ECs .

The success of products is heavily dependent on the associated customer satisfaction level. If customers are satisfied with a new product, the chance of that product being successful in marketplaces would be higher. A product usually is associated with a number of ECs, such as size, weight, and power consumption that could affect customer satisfaction. In this regard, modeling the functional relationships between CRs and ECs for product design is crucial. The developed models can be employed to formulate an optimization model to determine an optimal EC setting that leads to maximum customer satisfaction. Some techniques such as statistical regression (Han et al. 2000) and fuzzy rule-based method (Fung et al. 1998) were adopted to model the functional relationships. However, only a small number of data sets are usually available from the HoQ for modeling. On the other hand, the CRs obtained from market surveys are commonly ambiguous and qualitative in nature, and the relationships between CRs and ECs can be highly nonlinear. The customer satisfaction models developed based on QFD should be able to address nonlinearity and fuzziness. Intelligent techniques such as fuzzy regression (FR) (Chan et al. 2012), fuzzy least squares regression (Kwong et al. 2010) and genetic programming (Chan et al. 2011) have been recently adopted to model nonlinear and fuzzy relationships. However, the modeling methods of nonlinear and fuzzy relationships and the development of explicit customer satisfaction models based on a small number of data sets have not been addressed well in previous studies.

One of the key issues in QFD is how the EC settings of new products can be determined such that a high degree or even maximum customer satisfaction can be obtained. This involves a complex decision-making process with multiple variables. Currently, the setting of target EC values relies heavily on the professional experience and intuition of engineers; thus, the setting of such values is accomplished in a subjective manner. However, determining the optimal setting for target EC values based on this approach is very difficult. Some previous research has attempted to develop systematic procedures and methods for setting optimal target values of ECs in QFD , such as linear programming (Wasserman 1993), integer programming (Kim and Park 1998), mixed integer linear programming (Zhou 1998), fuzzy inference system (Fung et al. 1999), nonlinear mathematical program (Dawson and Askin 1999), and prescriptive fuzzy optimization (Kim et al. 2000).

Few studies have been conducted to introduce intelligence techniques in QFD. The results of previous studies on the introduction of intelligent techniques into QFD undoubtedly contribute to the development of intelligent QFD. In the following sections, our research on the development of intelligent QFD with regard to four aspects, namely, determination of importance weights of CRs, modeling of functional relationships in QFD , determination of importance weights of ECs and target value setting of ECs, is described.

11.3 Determination of Importance Weights of CRs by Using Fuzzy AHP with Extent Analysis

Quite a number of techniques were introduced to determine the importance weights of CRs in QFD. One of them is AHP which is very popular to be used in determining importance weights. AHP was used to determine the importance weights for product planning (Lu et al. 1994; Armacost et al. 1994; Hsiao, 2002) but has been mainly applied in crisp (non-fuzzy) decision applications. However, human judgment on the importance of CRs is always imprecise and vague. To address this deficiency in AHP, a fuzzy AHP with an extent analysis approach is proposed to determine the importance weights for CRs. In this method, the linguistic assessment of CRs is converted to triangular fuzzy numbers . These triangular fuzzy numbers are used to build a pairwise comparison matrix for the AHP. By applying the fuzzy AHP with extent analysis, the importance weights for the CRs can be obtained. Extent analysis refers to the “extent” in which an object can be satisfied for the goal. In this approach, the “satisfied extent” is defined by triangular fuzzy numbers. The use of the extent analysis technique and principles for the comparison of fuzzy numbers allows the calculation of weight vectors for fuzzy AHP. The new approach can improve the imprecise ranking of CRs inherited from studies based on conventional AHP. The fuzzy AHP with extent analysis is simple and easy to implement for prioritizing CRs in the QFD process compared with conventional AHP. The details of the fuzzy AHP are described as follows.

11.3.1 Development of a Hierarchical Structure for CRs

All CRs are initially structured into different hierarchical levels to apply AHP in prioritizing CRs. An affinity diagram, a tree diagram, or a cluster analysis can be used for this purpose. The voices of the customers can be gathered by a variety of methods. All of these approaches aim to ask customers to express their needs of a particular product. Such needs are usually expressed in words that are too general to use as CRs directly. However, by sorting, classifying, and structuring the voices of customers, useful CRs can be obtained.

11.3.2 Construction of Fuzzy Judgment Matrixes for AHP

The hierarchy of attributes is the subject of a pairwise comparison of AHP. After constructing a hierarchy , decision makers are asked to compare the elements at a given level on a pairwise basis to estimate their relative importance in relation to the element at the immediately proceeding level. Figure 11.2 shows an example of a hierarchy of attributes. The total importance weights of CRs can be calculated based on the expression, $W_{{_{CRi} }}^{*} = W_{cj} \cdot W_{sk} \cdot W_{CRi}$, where $W_{{_{CRi} }}^{*}$ is the total importance weight of the $i$ th CR , $W_{cj} ,\,\,W_{sk}$ and $W_{CRi}$ are the importance weights of the $j$th, $k$th and $i$th element in the category level, subcategory level and attributes level, respectively. In conventional AHP, the pairwise comparison is made by using a ratio scale. A nine-point scale is commonly used to show the judgment or preference of participants between options as equally, moderately, strongly, very strongly, or extremely preferred. Even though a discrete scale of one to nine has the advantages of simplicity and ease of use, such a scale does not consider the uncertainty associated with the mapping of one’s perception (or judgment) to a number. The linguistic terms that people use to express their feelings or judgments are vague. The use of this objective is unfeasible for defining the precise numbers to present linguistic assessment. Fuzzy set theory was first advocated to manage ambiguity in a system. The widely adopted triangular fuzzy number technique is employed to represent a pairwise comparison of CRs.

Fig. 11.2

An example of hierarchy of CRs for hair dryer design

A fuzzy number is a special fuzzy set ${\text{F}} = \{ (x,\mu_{F} (x)),x \in R\}$, where $x$ takes its values on the real line $R_{1}$: $- \infty < x < \infty$, and $\mu_{F} (x)$ is a continuous mapping from $R_{1}$ to the close interval $[0,1]$. A triangular fuzzy number can be denoted as $M = (l,m,u)$. The membership function $\mu_{M} (x):R \to [0,1]$ of a triangular fuzzy number is equal to the following:

$$ \mu_{M} (x) = \left\{ {\begin{array}{*{20}l} {\frac{x}{m - l} - \frac{l}{m - l},} & {x \in [l,m]} \\ {\frac{x}{m - u} - \frac{u}{m - u},} & {x \in [m,u]} \\ {0,} & {otherwise,} \\ \end{array} } \right. $$

(11.1)

where $l \le m \le u$; $l$ and $u$ stand for the lower and upper values of the support of $M$, respectively; $m$ is the mid-value of $M$. When $l = m = u$, it is a non-fuzzy number by convention.

The main operational laws for two triangular fuzzy numbers , $M_{1}$ and $M_{2}$, are as follows:

$$ \begin{aligned} M_{1} + M_{2} = &\, (l_{1} + l_{2} ,m_{1} + m_{2} ,u_{1} + u_{2} ) \\ M_{1} \otimes M_{2} \approx &\, (l_{1} l_{2} ,m_{1} m_{2} ,u_{1} u_{2} ) \\ \lambda \otimes M_{1} = &\, (\lambda l_{1} ,\lambda m_{1} ,\lambda u_{1} ),\lambda > 0,\lambda \in R \\ M_{1}^{ - 1} \approx &\, (\frac{1}{{u_{1} }},\frac{1}{{m_{1} }},\frac{1}{{l_{1} }}). \\ \end{aligned} $$

(11.2)

To consider vagueness in an assessment during the pairwise comparison of CRs, triangular numbers $M_{1} ,\,M_{3} ,\,M_{5} ,\,M_{7} ,\,M_{9}$ are used to represent the assessment from “equal to extremely preferred”; $M_{2} ,\,M_{4} ,\,M_{6} ,\,M_{8}$ are middle values. Figure 11.3 shows the triangular fuzzy numbers $M_{t} = (l_{t} ,\,m_{t} ,\,u_{t} )$ and $t = 1,2 \ldots 9$, where $l_{t}$ and $u_{t}$ are the lower and upper values of fuzzy number $M_{t}$, respectively; $m_{t}$ is the middle value of fuzzy number $M_{t}$. $\delta$ represents a fuzzy degree of judgment where $u_{t} - l_{t} = l_{t} - u_{t} = \delta$, which should be larger than or equal to 0.5. A larger $\delta$ value implies a higher fuzzy degree of judgment. When $\delta = 0$, the judgment is a non-fuzzy number.

Fig. 11.3

The membership functions of the triangular numbers

Participants of the survey use triangular numbers ($M_{1} - M_{9}$) to express their preferences between options. For example, a participant may consider that element $i$ is very important compared with element $j$ under certain criteria; he/she may set $a_{ij} = (4,5,6)$. If element $j$ is thought to be less important than element $i$, the pairwise comparison between $j$ and $i$ can be presented by using the fuzzy number , $a_{ij} = (\frac{1}{6},\frac{1}{5},\frac{1}{4})$. On the basis of the results of pairwise comparisons for the CRs obtained from participants, Eq. (11.2) is applied to obtain the fuzzy judgment matrixes, $FCM_{n}$, for the CRs.

The AHP methodology provides a consistency index to measure any inconsistency within the judgments in each comparison matrix and for the entire hierarchy . The index can be used to indicate whether the targets can be arranged in an appropriate order of ranking and the consistency of pairwise comparison matrixes. The defuzzification method of triangular fuzzy numbers was employed to convert fuzzy comparison matrixes into crisp matrixes, which are then used to investigate consistency. The consistency index, $CI$, and the consistency ratio , $CR$, for a comparison matrix can be computed by the following equations:

$$ CI = {\raise0.7ex\hbox{${\left( {\lambda_{\hbox{max} } - n} \right)}$} \!\mathord{\left/ {\vphantom {{\left( {\lambda_{\hbox{max} } - n} \right)} {n - 1}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${n - 1}$}}, $$

(11.3)

$$ CR = \left( {{\raise0.7ex\hbox{${\left( {CI} \right)}$} \!\mathord{\left/ {\vphantom {{\left( {CI} \right)} {RI\left( n \right)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${RI\left( n \right)}$}}} \right)100\,\% $$

(11.4)

where $\lambda_{\hbox{max} }$ is the largest eigenvalue of the comparison matrix, $n$ is the dimension of the matrix, and $RI(n)$ is a random index that depends on $n$.

If the calculated CR of a comparison matrix is less than 10 %, the consistency of the pairwise judgment can be considered acceptable; otherwise, the judgments expressed by the experts are considered inconsistent and the decision maker has to repeat the pairwise comparison matrix.

A triangular fuzzy number , denoted as $M = (l,m,u)$ can be defuzzified to a crisp number:

$$ M\_ crisp = {\raise0.7ex\hbox{${\left( {4m + l + u} \right)}$} \!\mathord{\left/ {\vphantom {{\left( {4m + l + u} \right)} 6}}\right.\kern-0pt} \!\lower0.7ex\hbox{$6$}}. $$

(11.5)

11.3.3 Calculation of Weight Vectors for Individual Levels of a Hierarchy of the CRs

The extent analysis method and the principles for the comparison of fuzzy numbers were employed to obtain estimates for the weight vectors for individual levels of a hierarchy of CRs. The extent analysis method is used to consider the extent of an object to be satisfied for the goal, that is, the satisfied extent. In this method, the “extent” is quantified by a fuzzy number . On the basis of the fuzzy values for the extent analysis of each object, a fuzzy synthetic degree value can be obtained.

Let $X = \{ x_{1} ,x_{2} , \ldots ,x_{n} \}$ be an object set and $U = \{ u_{1} ,u_{2} , \ldots ,u_{m} \}$ be a goal set. According to the extent analysis method, each object can be used to perform extent analysis for each goal. Therefore, $m$ extent analysis values for each object can be obtained as follows:

$$ M_{{g_{i} }}^{1} ,M_{{g_{i} }}^{2} , \ldots ,M_{{g_{i} }}^{m} ,i = 1,2 \ldots n, $$

(11.6)

where all $M_{{g_{i} }}^{j}$ (j = 1, 2,…, m) are triangular fuzzy numbers . The value of fuzzy synthetic degree with respect to the $i$th object is thus defined as follows:

$$ D_{i} = \sum\limits_{j}^{m} {M_{{g_{i} }}^{j} } \otimes \left( {\sum\limits_{i}^{n} {\sum\limits_{j}^{m} {M_{{g_{i} }}^{j} } } } \right)^{ - 1} . $$

(11.7)

According to the above definition, the fuzzy synthetic degree values of all elements in the $k$th level can be calculated by using Eq. (11.7) based on the fuzzy judgment matrix of the $k$th level:

$$ D_{i}^{k} = \sum\limits_{j = 1}^{n} {a_{ij}^{k} } \otimes \left( {\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {a_{ij}^{k} } } } \right)^{ - 1} ,i = 1,2, \ldots ,n, $$

(11.8)

where $D_{i}^{k}$ is the fuzzy synthetic degree values of element $i$ in the $k$th level and $A^{k} = (a_{ij}^{k} )_{nn}$ is the fuzzy judgment matrix of the $k$th level.

The principles for the comparison of fuzzy numbers were introduced to derive the weight vectors of all elements for each level of the hierarchy with the use of fuzzy synthetic values. The principles that allow the comparison of fuzzy numbers are as follows:

Definition 1

$M_{1}$ and $M_{2}$ are two triangular fuzzy numbers . The degree of possibility of $M_{1} \ge M_{2}$ is defined as $V(M_{1} \ge M_{2} ) = \sup_{x \ge y} [\hbox{min} (\mu_{{M_{1} }} (x),\mu_{{M_{2} }} (y))]$.

Theorem 1

If $M_{1}$ and $M_{2}$ are triangular fuzzy numbers denoted by $(l_{1} ,m_{1} ,u_{1} )$ and $(l_{2} ,m_{2} ,u_{2} )$, respectively, then the following holds:

• (1) The necessary and sufficient condition of $V(M_{1} \,\ge\, M_{2} ) = 1$ is $m_{1} \,\ge\, m_{2}$.

• (2) If $m_{1} \le\, m_{2}$, let $V(M_{1}\, \ge\, M_{2} ){\text{ = hgt(}}M_{1} \,\cap\, M_{2} )$. $V(M_{1} \ge M_{2} )\,{ = }\,\mu (d) = \left\{ \begin{aligned} \frac{{l 2 { } - \, u 1}}{(m1 - u1) - (m2 - l2)},l2 \le u1 \hfill \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} otherwise \hfill \\ \end{aligned} \right.$, where $d$ is the crossover point’s abscissa for $M_{1}$ and $M_{2}$.

Definition 2

The degree of possibility for a fuzzy number to be greater than $k$ fuzzy numbers $M_{i} (i = 1,2, \ldots ,k)$ can be defined by $V(M\, \ge\, M_{1} ,M_{2} , \ldots ,M_{k} ){ = }$ ${ \hbox{min} }V(M \,\ge \,M_{i} ),i = 1,2, \ldots ,k.$

Let $d(p_{i}^{k} ) = \hbox{min} V(S_{i}^{k} \,\ge\, S_{j}^{k} )$, where $p_{i}^{k}$ is the $i$th element of the $k$th level, $j = 1,2, \ldots ,n$; $j \ne i$. The number of elements in the $k$th level is $n$. The weight vector of the $k$th level is then obtained as follows:

$$ W_{k}^{\prime} = (d(p_{1}^{k} ),d(p_{2}^{k} ), \ldots ,d(p_{n}^{k} ))^{T} . $$

(11.9)

After normalization, the normalized weight vector, $W_{k}$, is expressed as follows:

$$ W_{k} = (w(p_{1}^{k} ),w(p_{2}^{k} ), \ldots ,w(p_{n}^{k} ))^{T} . $$

(11.10)

Taking the hierarchy of CRs for the hair dryer design (Fig. 11.2) as an example, the pairwise comparisons of C ₁ , C ₂ and C₃ are shown in Table 11.1.

Table 11.1 Pairwise comparison for category level

Equation (11.2) is applied to obtain the fuzzy judgment matrixes, $FCM_{1}$, for the category level.

$$ FCM_{1} {\text{ = }}_{{\begin{array}{*{20}c} {C1} \\ {C2} \\ {C3} \\ \end{array} \left[ {\begin{array}{*{20}l} {(1,1,1)} & {(1.33,2,3)} & {(1.00,1.33,2.33} \\ {(0.33,0.50,0.75)} & {(1,1,1)} & {(1.00,1.33,2.33)} \\ {(0.43,0.75,1.00)} & {(0.43,0.75,1.00)} & {(1,1,1)} \\ \end{array} } \right]}}^{{\begin{array}{*{20}c} {\quad \quad C1} & {\quad \quad \quad \qquad\qquad \qquad C2} & {\quad \quad\qquad \qquad\qquad C3} \\ \end{array} }} $$

The fuzzy synthetic degree values of the element $C_{1}$, $D_{{C_{1} }}$, can be calculated based on (11.8) as follows:

$$ \begin{aligned} D_{{C_{1} }} =& \sum\limits_{j = 1}^{3} {a_{1j} \otimes \left( {\sum\limits_{i = 1}^{3} {\sum\limits_{j = 1}^{3} {a_{ij}^{{}} } } } \right)^{ - 1} } \\ =&\, \left( {(1,1,1) + (1.33,2,3) + (1.00,1.33,2.33)} \right) \otimes \left( {(1,1,1) + (1.33,2,3) + \cdots (1,1,1)} \right)^{ - 1} \\ = &\,(0 . 2 5 , 0. 4 5 , 0. 8 4 )\\ \end{aligned} $$

Following the similar calculation, $D_{{C_{2} }} = (0.17,0.29,0.54)$ and $D_{C3} = (0.14,0.26,0.40)$ can be obtained. The following comparison results are then derived based on Theorem 1.

$$ \begin{aligned} & V(D_{{C_{1} }} \ge D_{{C_{2} }} ) = 1;\,V(D_{{C_{1} }} \ge D_{{C_{3} }} ) = 1; \\ & V(D_{{C_{2} }} \ge D_{{C_{1} }} ) = \frac{(0.25 - 0.54)}{(0.29 - 0.54) - (0.45 - 0.25)} = 0.65; \\ & V(D_{{C_{2} }} \ge D_{{C_{3} }} ) = 1;\,V(D_{{C_{3} }} \ge D_{{C_{1} }} ) = \frac{(0.25 - 0.40)}{(0.26 - 0.40) - (0.45 - 0.25)} = 0.44; \\ & V(D_{{C_{3} }} \ge D_{{C_{2} }} ) = \frac{(0.17 - 0.40)}{(0.26 - 0.40) - (0.29 - 0.17)} = 0.88. \\ \end{aligned} $$

Based on Definitions 1, 2 and Eq. (11.9), the weight vector $W_{C}^{\prime}$ of the category level can be calculated by using the following formula:

$$ \begin{aligned} d(C_{1} ) = &\,\hbox{min} (V(D_{{C_{1} }} \ge D_{{C_{2} }} ,D_{C3} ) = \hbox{min} \{ 1,1\} = 1.00; \\d(C_{2} ) =&\, \hbox{min} (V(D_{{C_{2} }} \ge D_{{C_{1} }} ,D_{C3} ) = \hbox{min} \{ 0.65,1\} = 0.65; \\ d(C_{3} ) = &\,\hbox{min} (V(D_{{C_{3} }} \ge D_{{C_{1} }} ,D_{{C_{2} }} ) = \hbox{min} \{ 0.44,0.88\} = 0.44; \\ W_{C}^{\prime} = &\, (d(C_{1} ),d(C_{2} ),d(C_{3} ))^{T} = (1.00,0.65,0.44). \\ \end{aligned} $$

Based on (11.10), the normalized weight vectors of the category level are obtained as follows:

$$ (W_{{C_{1} }} ,W_{{C_{2} }} ,W_{{C_{3} }} ) = (0.48,0.31,0.21). $$

Following the similar calculation, the weight vectors of the subcategory level, $W_{sk}$, and attributes level, $W_{CRi}$, can be calculated. Hence, the total importance weights of CRs can be calculated based on the expression, $W_{{_{CRi} }}^{*} = W_{cj} \cdot W_{sk} \cdot W_{CRi}$. For example, referring to Fig. 11.2, $W_{{_{CR4} }}^{*} = W_{c1} \cdot W_{s3} \cdot W_{CR4} = \, 0.078.$

11.4 Modeling of Functional Relationships in QFD by Using Chaos-Based FR

As mentioned in Sect. 11.1, the methods of modeling nonlinear and fuzzy relationships in QFD and the development of explicit customer satisfaction models based on a small number of data sets have not been addressed in previous studies. In this section, a novel FR approach, namely chaos-based FR, is described to model the relationships between customer satisfaction and ECs in order to address the limitations of previous studies. This approach employs a chaos optimization algorithm (COA) to generate the polynomial structures of customer satisfaction models with second- and/or higher-order terms and interaction terms. COA employs chaotic dynamics to solve an optimization problem. COA does not rely on learning factors, has fast convergence, and can search for accurate solutions compared with the conventional optimization methods. COA also has better capacity in searching for the global optimal solution of an optimization problem and can escape from a local minimum easier than conventional optimization algorithms. However, COA cannot address the fuzziness of survey data. The FR method of Tanaka et al. (1982) was introduced to determine the fuzzy coefficients of models. FR is effective for modeling problems wherein the degree of fuzziness of the data sets for modeling is high and only a small amount of data sets is available for modeling. However, the FR method can yield only linear type models. The chaos-based FR approach combines the advantages of COA and FR to generate customer satisfaction models wherein the modeling fuzziness can be explicitly addressed and nonlinear models can be developed. The proposed approach to the modeling of functional relationships in QFD mainly involves four processes: development of HoQ , generation of polynomial structures of customer satisfaction models by COA , determination of fuzzy coefficients of customer satisfaction models by Tanaka’s FR, and generation of fuzzy polynomial customer satisfaction models.

11.4.1 Fuzzy Polynomial Models with Second- and/or Higher-Order Terms and Interaction Terms

Kolmogorov–Gabor polynomial has been widely used to evolve general nonlinear models but is incapable of addressing the fuzziness of modeling data. In fuzzy polynomial models developed based on the proposed approach, nonlinear terms and interaction terms between independent variables are represented in a form of a higher-order Kolmogorov–Gabor polynomial. The fuzzy coefficients of the models are determined by using Tanaka’s FR method. The proposed models can overcome the limitation of conventional FR models where only first-order terms are generated. A fuzzy polynomial model based on the chaos-based FR approach can be expressed as follows:

$$ \begin{aligned} \tilde{y} = &\, \tilde{f}_{NR} \left( x \right) \\ {\kern 1pt} = &\, \tilde{A}_{0} + \sum\limits_{{i_{1} = 1}}^{N} {\tilde{A}_{{i_{1} }} x_{{i_{1} }} } + \sum\limits_{{i_{1} = 1}}^{N} {\sum\limits_{{i_{2} = 1}}^{N} {\tilde{A}_{{i_{1} i_{2} }} x_{{i_{1} }} x_{{i_{2} }} } } + \sum\limits_{{i_{1} = 1}}^{N} {\sum\limits_{{i_{2} = 1}}^{N} {\sum\limits_{{i_{3} = 1}}^{N} {\tilde{A}_{{i_{1} i_{2} i_{3} }} x_{{i_{1} }} x_{{i_{2} }} x_{{i_{3} }} } } } + \cdots \sum\limits_{{i_{1} = 1}}^{N} { \ldots \sum\limits_{{i_{d} = 1}}^{N} {\,\tilde{A}_{{i_{1} \ldots i_{d} }} \prod\limits_{j = 1}^{d} {x_{{i_{j} }} } {\kern 1pt} {\kern 1pt} {\kern 1pt} ,} } \\ \end{aligned} $$

(11.11)

where $\tilde{y}$ is the dependent variable, $x_{{i_{j} }}$ is the $i_{j}$th independent variable, $i_{j} = 1, \ldots ,N$ and $j = 1,2, \ldots d$. $N$ and $d$ denote the number of design variables. $\mathop A\limits^{\sim }$ is the fuzzy coefficients of the linear, second order, and/or higher-order terms and the interaction terms of the model.

$$\begin{aligned} \tilde{A}_{0} =&\, \left( {a_{0}^{c} ,a_{0}^{s} } \right),\,\tilde{A}_{1} = \left( {a_{1}^{c} ,a_{1}^{s} } \right),\,\tilde{A}_{2} = \left( {a_{2}^{c} ,a_{2}^{s} } \right),\, \ldots ,\,\tilde{A}_{N} = \left( {a_{N}^{c} ,a_{N}^{s} } \right), \\ \tilde{A}_{11} =& \,\left( {a_{11}^{c} ,a_{11}^{s} } \right),\,\tilde{A}_{12} = \left( {a_{12}^{c} ,a_{12}^{s} } \right),\,\tilde{A}_{13} = \left( {a_{13}^{c} ,a_{13}^{s} } \right),\, \ldots ,\,\tilde{A}_{NN} = \left( {a_{NN}^{c} ,a_{NN}^{s} } \right),\\ \tilde{A}_{111} = &\,\left( {a_{111}^{c} ,a_{111}^{s} } \right),\,\tilde{A}_{112} = \left( {a_{112}^{c} ,a_{112}^{s} } \right),\,\tilde{A}_{113} = \left( {a_{113}^{c} ,a_{113}^{s} } \right),\, \ldots , \\ \tilde{A}_{NNN} = &\,\left( {a_{NNN}^{c} ,a_{NNN}^{s} } \right), \\ &\ldots \ldots \tilde{A}_{N \ldots N} = \left( {a_{N \ldots N}^{c} ,a_{N \ldots N}^{s} } \right),\end{aligned} $$

where $a_{{}}^{c}$ and $a_{{}}^{s}$ are the central value and spread of fuzzy numbers, respectively.

The fuzzy polynomial model (11.11) can be rewritten as follows:

$$ \tilde{y} = \tilde{A}^{\prime}_{0} + \tilde{A}^{\prime}_{1} *{\kern 1pt} {\kern 1pt} x^{\prime}_{1} + \tilde{A}^{\prime}_{2} *{\kern 1pt} {\kern 1pt} x^{\prime}_{2} \ldots + \tilde{A}^{\prime}_{{N_{NR} }} *{\kern 1pt} {\kern 1pt} {\kern 1pt} x^{\prime}_{{N_{NR} }} , $$

(11.12)

or

$$ \tilde{y} = \left( {a_{0}^{c}{'} ,a_{0}^{s}{'} } \right) + \left( {a_{1}^{c}{'} ,a_{0}^{s}{'} } \right) * x_{1}^{\prime} + \left( {a_{2}^{c}{'} ,a_{2}^{s}{'} } \right) * x_{2}^{\prime} + \,\, \ldots \,\, + \left( {a_{{N_{NR} }}^{c}{'} ,a_{{N_{NR} }}^{s}{'} } \right) * x_{{N_{NR} }}^{\prime} , $$

(11.13)

where $\tilde{A}^{\prime}_{0} = \tilde{A}_{0}$, $\tilde{A}^{\prime}_{1} = \tilde{A}_{1}$, $\tilde{A}^{\prime}_{2} = \tilde{A}_{2}$, $\ldots$, $\tilde{A}^{\prime}_{{N_{NR} }} = \tilde{A}_{N \ldots N}$; $\tilde{A}_{0}^{\prime} = \left( {a_{0}^{c^{\prime}} ,a_{0}^{s^{\prime}} } \right)$, $\tilde{A}_{1}^{\prime} = \left( {a_{1}^{c^{\prime}} ,a_{1}^{s^{\prime}} } \right)$, $\ldots$, $\tilde{A}_{{N_{NR} }}^{\prime} = \left( {a_{{N_{NR} }}^{c\,\,\,\,'} ,a_{{N_{NR} }}^{s\,\,\,\,'} } \right)$, and $x^{\prime}_{\,0} = 1$, $x^{\prime}_{\,1} = x_{1}$, $x^{\prime}_{\,2} = x_{1} x_{2}$, $\ldots$, $x^{\prime}_{{N_{NR} }} = x_{1} {\kern 1pt} x_{2} \ldots {\kern 1pt} {\kern 1pt} x_{d}$. $x^{\prime}_{\,\,j}$ and $\tilde{A}^{\prime}_{\,\,j}$ ($j = 0,1,2 \ldots ,N_{NR}$) denote the transformed variables and fuzzy coefficients , respectively.

The vector of the fuzzy coefficients can be defined as follows:

$$ \tilde{A}^{\prime} = \left( {\tilde{A}_{0}^{\prime} ,\tilde{A}_{1}^{\prime} , \ldots \tilde{A}_{{N_{NR} }}^{\prime} } \right) = \left( {\left( {a_{0}^{c}{'} ,a_{0}^{s}{'} } \right),\left( {a_{1}^{c}{'} ,a_{1}^{s}{'}} \right), \ldots ,{\kern 1pt} \left( {a_{{N_{NR} }}^{c}{'} ,a_{{N_{NR} }}^{s}{'} } \right)} \right), $$

(11.14)

$$ a^{c}{'} = (a_{0}^{c}{'} ,a_{1}^{c}{'} , \ldots ,a_{{N_{NR} }}^{c}{'} ), $$

(11.15)

$$ a^{s}{'} = (a_{0}^{s}{'} ,a_{1}^{s}{'} , \ldots ,a_{{N_{NR} }}^{s}{'} ) $$

(11.16)

11.4.2 Determination of Model Structures Utilizing COA

In this approach, COA was introduced to determine the polynomial structure of fuzzy models. COA is a stochastic search algorithm wherein chaos is introduced into the optimization strategy to accelerate the optimum seeking operation and determine the global optimal solution. Two phases exist in searching for an optimal solution in the chaos optimization process. The first phase is called wide search and involves the whole solution space according to an ergodic track. When the end condition is satisfied, the current optimal state becomes close to the optimal solution and the second phase starts. The second phase is based on the results of the first phase and involves a narrow search focused on a local region. The second phase adds a small disturbance term until the final requirement is met. The added disturbance can be a chaos variable, a random variable based on Gaussian distribution/uniform distribution, or a bias generated by the mechanism of gradient descent. Current COAs use the carrier wave method to map chosen chaos variables linearly to the space of optimization variables and then search for optimal solutions on the basis of the ergodicity of chaos variables. COAs focus on chaos variable-based optimization rather than on introducing chaos variables as a small disturbance in search optimization.

The logistic model used in chaos optimization is shown in Eq. (11.17). Logistic mapping can generate chaos variables by iteration:

$$ c_{n + 1} = f(c_{n} ) = \mu c_{n} (1 - c_{n} ), $$

(11.17)

where $\mu = 4$ and $c_{n} \in \left[ {0,1} \right]$ is the $n$th iteration value of the chaos variable $c$.

The optimization process uses the chaos variables generated from logistic mapping to search through its own locomotion law. Chaos has dynamic properties including ergodicity, intrinsic stochastic property, and sensitive dependence on initial conditions. The characteristic of randomness ensures the possibility of large-scale search. Ergodicity allows COA to traverse all possible states without repetition and to overcome the limitations caused by ergodic search in general random methods.

The linear mapping for converting chaos variables into optimization variables is formulated as follows:

$$ q_{n} = a + (b - a) \cdot c_{n} , $$

(11.18)

where $q_{n}$ is the optimization variable; $a$ and $b$ are the lower and upper limits of the optimization variable $q$, respectively.

According to the iteration, the chaos variables traverse in $\left[ {0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1} \right]$ and the corresponding optimization variables traverse in the corresponding range $\left[ {a,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} b} \right]$. Therefore, the optimal solution can be found in the area of feasible solution.

Each optimization variable represents the polynomial structure of a fuzzy model and is described by the input variables $\left[ {x_{1} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} x_{2} ,{\kern 1pt} {\kern 1pt} \ldots {\kern 1pt} and{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x_{m} } \right]$ and arithmetic operations. The two arithmetic operations of addition (“+”) and multiplication (“*”) are employed in the fuzzy polynomial model (Eq. 11.12). The optimization variable at the $n$ th generation is defined as follows:

$$ q_{n} {\kern 1pt} {\kern 1pt} { = }{\kern 1pt} \left[ {q_{n}^{1} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} q_{n}^{2} ,{\kern 1pt} {\kern 1pt} \ldots {\kern 1pt} ,{\kern 1pt} {\kern 1pt} q_{n}^{{N_{c} }} {\kern 1pt} } \right], $$

(11.19)

where $N_{c}$ is an odd number representing the number of elements in a chaos variable. For example, if four variables exist in the model, the value of $N_{c}$ is first set to seven with four elements representing four design variables. Another three elements in the middle of every two adjacent design variables represent the arithmetic operations to guarantee that the optimization variable, $q_{n}$, can include all four variables. If the error requirement is not satisfied, the $N_{c}$ value is adjusted until a satisfactory modeling error that is close to zero and is smaller than the modeling errors based on the previous studies is achieved.

The elements in odd numbers ($q_{n}^{1} {\kern 1pt}$, $q_{n}^{3} {\kern 1pt}$, $\ldots$, $q_{n}^{{N_{c} }} {\kern 1pt}$) are used to represent variables in a nonlinear structure. For the odd number $k$, if ${\raise0.7ex\hbox{${\left( {l - 1} \right)}$} \!\mathord{\left/ {\vphantom {{\left( {l - 1} \right)} m}}\right.\kern-0pt} \!\lower0.7ex\hbox{$m$}} < \,q_{n}^{k}\, \le\, {\raise0.7ex\hbox{$l$} \!\mathord{\left/ {\vphantom {l m}}\right.\kern-0pt} \!\lower0.7ex\hbox{$m$}}$ ($m$ is the number of variables in a nonlinear fuzzy model, $1{\kern 1pt} {\kern 1pt} \le {\kern 1pt} {\kern 1pt} {\kern 1pt} l{\kern 1pt} {\kern 1pt}\, \le\, m$), the position of ${\kern 1pt} q_{n}^{k}$ is represented by the ${\kern 1pt} l$th variable ${\kern 1pt} x_{l}$. The elements in even numbers ($q_{n}^{2} {\kern 1pt}$, $q_{n}^{4} {\kern 1pt}$, $\ldots$, $q_{n}^{{N_{c} - 1}} {\kern 1pt}$) are used to determine the arithmetic operations. For even number $k$, if $0 < \,q_{n}^{k} \, \le {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}$ and ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}} < \,q_{n}^{k} \, \le \,1$, the arithmetic operations are addition (“+”) and multiplication (“*”), respectively. For example, an optimization variable with nine elements is used to represent the structure of a fuzzy polynomial model with four dependent variables. If the optimal variable is obtained as $q = \left[ {x_{2} ,\, + \,,\,x_{3} ,\, * ,\,{\kern 1pt} x_{4} ,{\kern 1pt} \, * ,\,x_{4} ,\, + ,\,x_{1} } \right]$, the polynomial structure can be expressed as $x_{2} + x_{3} x_{4}^{2} + x_{1}$. The transformed variables are $x^{\prime}_{0} {\kern 1pt} \,{ = 1,}{\kern 1pt} {\kern 1pt} x^{\prime}_{1} { = }{\kern 1pt} x_{2} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} x^{\prime}_{2} = x_{3} x_{4}^{2} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x^{\prime}_{3} = x_{1}$. Therefore, the fuzzy polynomial model with fuzzy coefficients can be represented as

$$ \tilde{y} = \tilde{A}^{\prime}_{\,0} + \tilde{A}^{\prime}_{1} x_{2} + \tilde{A}^{\prime}_{2} x_{3} x_{4}^{2} + \tilde{A}^{\prime}_{\,3} x_{1} $$

where $\tilde{A}_{0}^{\prime} = \left( {a_{0}^{c^{\prime}} ,a_{0}^{'s} } \right),\,\tilde{A}_{1}^{\prime} = \left( {a_{1}^{c^{\prime}} ,a_{1}^{s^{\prime}} } \right),\,\tilde{A}_{2}^{\prime} = \left( {a_{2}^{c^{\prime}} ,a_{2}^{s^{\prime}} } \right)\,\,\,{\rm and}\,\,\,\tilde{A}_{3}^{\prime} = \left( {a_{3}^{c^{\prime}} ,a_{3}^{s^{\prime}} } \right)$. The central values $a_{j}^{c} {\kern 1pt}^{\prime}$ and spread values $a_{j}^{s} {\kern 1pt} ^{\prime}$ ($j = 0,1, \ldots ,4$) of the fuzzy coefficients are determined by using Tanaka’s FR analysis.

11.4.3 Determination of Fuzzy Coefficients by Using FR Analysis

Tanaka’s FR aims to use fuzzy functions to describe an imprecise and vague phenomenon. All input and output variables, as well as the coefficients of the relationships, are considered as fuzzy numbers . Two different criteria (i.e., the least absolute deviation and the minimum spread) are used to evaluate the fuzziness of the output. Deviations between observed and estimated values depend on the indefiniteness of system structures and are considered as the fuzziness of system parameters. The fuzzy parameters of FR models indicate the possibility distribution and are obtained as fuzzy sets that represent the fuzziness of models. The objective of FR analysis is to minimize the fuzziness of the model by minimizing the total spread of the fuzzy coefficients, thus leading to the minimum uncertainty of the output.

On the basis of chaos optimization, a fuzzy model containing second- and/or higher-order terms and interaction terms is represented in a polynomial structure. Tanaka’s FR analysis is employed to determine the fuzzy coefficients for each term of the fuzzy polynomial model. Fuzzy coefficients with the central point $a^{c}{'}$ and spread value $a^{s}{'}$ are determined by solving the following linear programming (LP) problem:

$$ Min\,\,J = \sum\limits_{j = 0}^{{N_{NR} }} {\left( {a_{j}^{s}{'} \sum\limits_{i = 1}^{M} {\left| {x_{\,\,\,\,j}^{\prime} \left( i \right)} \right|} } \right)} , $$

(11.20)

where $J$ is the objective function that represents the total fuzziness of the system, $1 + N_{NR}$ is the number of terms of the fuzzy polynomial model, $M$ is the number of data sets, $x^{\prime}_{\,\,\,j} \left( i \right)$ is the $j$th transformed variable of the $i$th data set in the fuzzy polynomial model, and $\left| . \right|$ refers to absolute value of the transformed variable. The constraints can be formulated as follows:

$$ \sum\limits_{j = 0}^{{N_{NR} }} {a_{j}^{c}{'} {\kern 1pt} x^{\prime}_{\,\,j} (i)} + (1 - h)\sum\limits_{j = 0}^{{N_{NR} }} {a_{j}^{s}{'} {\kern 1pt} \left| {x'_{\,\,j} (i)} \right|} \ge y_{i} \;\;\;\;\;i = 1,2, \ldots ,M, $$

(11.21)

$$ \sum\limits_{j = 0}^{{N_{NR} }} {a_{j}^{c}{'}x'_{\,\,j} (i)} - (1 - h)\sum\limits_{j = 0}^{{N_{NR} }} {a_{j}^{s} {'}\left| {x'_{\,\,j} (i)} \right|} \le y_{i} \;\;\;\;i = 1,2, \ldots ,M, $$

(11.22)

$$ a_{j}^{s}{'}{\kern 1pt} \ge\, 0,\,\,a_{j}^{c} {\kern 1pt} '{\kern 1pt} {\kern 1pt} \in R,{\kern 1pt} {\kern 1pt} j = 0,1,2, \ldots N_{NR} , $$

$$ x_{0} {'}(i) = 1 \; {\rm for}\;{\rm all}\; i \;{\rm and} \; 0 \,\le\, h \,\le\, 1.$$

where $h$ refers to the degree of fit of the fuzzy model in a given data (between zero and one), and $y_{i} \;$ is the value of the $i$th dependent variable. Constraints (11.21) and (11.22) ensure that each objective $y_{i}$ has at least $h$ degree of belonging to $\tilde{y}_{i}$ as $\mu_{{\tilde{y}_{i} }} (y_{i} ) \ge h\;,i = 1,\;\;2,\; \ldots ,M$. The last constraints for the variables ensure that $a_{j}^{s} {'}{\kern 1pt}$ and $a_{j}^{c} {'}$ are non-negative. Therefore, the fuzzy parameters $\tilde{A}'_{\,\,j} (j = 0,1,2, \ldots N_{NR} )$ can be determined by solving the LP problem subject to $\mu_{{\tilde{y}_{i} }} (y_{i} )\, \ge\, h.$

11.4.4 Algorithms of Chaos-Based FR

The algorithms of the proposed chaos-based FR method are described as follows:

• (1) The number of iterations and the number of elements $N_{c}$ in a chaos variable are initialized. $N_{c}$ is an odd number, and $N_{c}$ values are chosen randomly in the range of $\left[ {0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1} \right]$ to decide the value of the initialized chaos variable.

• (2) The iteration starts from $n = 1$. The chaos variables $c_{n}$ are generated based on the logistic model in Eq. (11.17) and are transformed into the optimization variables, $q_{n}$, by using Eq. (11.18). The polynomial structure of the fuzzy model is determined based on the value of the optimization variable $q_{n}$. According to the rules described in Sect. 11.4.2, the elements in odd numbers and even numbers are substituted by input variable $x_{k}$ ($k = 1, \ldots ,N$ and $N$ is the number of variables) and arithmetic operations “+” and “*,” respectively. Subsequently, the transformed variable $x'_{\,j}$ with linear, second order, and/or higher-order terms and interaction terms are generated based on arithmetic operations. If the operation is “*,” the second- and/or higher-order terms and interaction terms are determined by multiplying the variables on both sides of “*”. The arithmetic operation “+” is used to add all terms, including linear terms, to generate the final polynomial structure of the fuzzy model.

• (3) According to the generated polynomial structure, the fuzzy coefficients $\tilde{A}_{j}^{'} = \left( {a_{j}^{c}{'} ,a_{j}^{s}{'} } \right)$ are assigned to all transformed variables of the developed structure. The values of the fuzzy coefficients are calculated by solving the LP problem as shown in Eqs. (11.20–11.22).

• (4) Based on the developed fuzzy polynomial model, the predicted variable $\tilde{y}_{i}$ can be calculated. The fitness value $RE$ can then be obtained by calculating the relative error between $\tilde{y}_{i}$ and the actual data $y_{i}$.

• (5) Step (2) is repeated. The algorithms are again executed by another training data set until all training data sets are employed. The mean fitness value $MRE(n)$ for all training data sets is calculated.

• (6) The iteration continues by $n + 1 \to n$ and stops after the number of iterations reaches the predefined value. The values of $MRE(n)$ are recorded for each iteration and the solution with the smallest mean fitness value is selected. The fuzzy polynomial model with the smallest training error is then found. Finally, the chaos-based FR model is generated.

We have applied the proposed approach on modeling the functional relationships in QFD for mobile phone products. The following shows an example of a customer satisfaction model for the CR “comfortable to hold” based on the chaos-based FR approach.

$$ \begin{aligned} \tilde{y} = &\, \left( {{ 14} . 9 9 9 1, 2. 8 4 2 2* 10^{ - 1 4} } \right) + \left( { - 1.5036, 2. 8 4 2 2* 10^{ - 1 4} } \right)x_{3} \\ &{ + }\left( { - 0. 2 8 9 0,0} \right)x_{4} + \left( { - 0.3634, 5. 6 8 4 3* 10^{ - 1 4} } \right)x_{1} \\ {\kern 1pt} &+ (0.0045, 0.0077)x_{1} x_{2} , \\ \end{aligned} $$

(11.23)

where $\tilde{y}$ is the predicted value of “comfortable to hold”; $x_{1} ,x_{2} ,x_{3}$, and $x_{4}$ are four ECs that denote weight, height, width, and thickness, respectively.

11.5 Determination of Importance Weights of ECs by Using Fuzzy Group Decision-Making Method

Regarding the determination of importance weights of ECs in QFD, most previous studies only address one type of uncertainties as described in Sect. 11.1 that would adversely affect the robustness of prioritizing ECs. Thus, it is necessary to consider the two types of uncertainties simultaneously while determining the importance weights of ECs. In this section, a novel fuzzy group decision-making method that integrates a fuzzy weighted average method with a consensus ordinal ranking technique is described to address the two types of uncertainties. The approach consists of two stages. The first stage involves the determination of the importance weights of ECs with respect to each customer by using fuzzy weighted average method with the fuzzy expected operator. The second stage determines a consensus ranking by synthesizing all customer preferences on the ranking of ECs. The flowchart for the proposed methodology is presented in Fig. 11.4.

Fig. 11.4

Flowchart of the fuzzy group decision-making method

11.5.1 Determination of the Importance Weights of ECs Based on the Fuzzy Weighted Average Method with Fuzzy Expected Operator

For the first type of uncertainty in QFD , fuzzy set theory can be an effective tool to deal with uncertain inputs. On the basis of fuzzy set theory, the inputs required for QFD are represented with linguistic terms characterized by fuzzy sets. The two sets of input data should be expressed as fuzzy numbers , namely, the relative weights of CRs and the relationship measures between CRs and ECs, to determine the importance weights of ECs .

Some notations that are used in this section are shown as follows:

$CR_{i}$ :

The $i$th customer requirement where $i = 1,2, \ldots ,m$

$EC_{j}$ :

The $j$th engineering characteristic where $j = 1,2, \ldots ,n$

$C_{l}$ :

The $l$th customer surveyed in a target market where $l = 1,2, \ldots ,K$

$m$ :

The number of CRs

$n$ :

The number of ECs

$K$ :

The number of customers surveyed in a target market

$\tilde{W}_{i}^{l}$ :

The $l$th customer’s individual preference on the $i$th customer need, which is a triangular fuzzy number belonging to certain predefined linguistic terms, such as “very important,” “important,” and “moderately important.”

$\tilde{R}_{ij}$ :

The relationship measure between the $i$ th CR and $j$th EC, which is a triangular fuzzy number belonging to some predefined linguistic terms, such as “strong,” “moderate,” and “weak.”

The relative importance of the $i$th CR with respect to the $l$th customer and relationship measures between CRs and ECs are expressed as triangular fuzzy numbers . Thus, the determination of the importance of ECs falls under the category of fuzzy weighted average. The fuzzy importance of $EC_{j}$ with respect to the $l$th customer, which is denoted by $\tilde{Z}_{j}^{l}$, can be expressed as follows:

$$ \tilde{Z}_{j}^{l} = {{\sum\limits_{i = 1}^{m} {\tilde{W}_{i}^{l} \tilde{R}_{ij} } } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^{m} {\tilde{W}_{i}^{l} \tilde{R}_{ij} } } {\sum\limits_{i = 1}^{m} {\tilde{W}_{i}^{l} } }}} \right. \kern-0pt} {\sum\limits_{i = 1}^{m} {\tilde{W}_{i}^{l} } }}. $$

(11.24)

Several methods can be devised to calculate the fuzzy weighted average. A common method for calculating the fuzzy ECs of Eq. (11.24) was proposed by Kao and Liu (2001):

Let $\left( {W_{i}^{l} } \right)_{\alpha } ,\left( {R_{ij} } \right)_{\alpha }$ denote the $\alpha$-level sets of $\tilde{W}_{i}^{l} ,\tilde{R}_{ij}$, respectively, which can be defined as follows:

$$ \begin{aligned} \left( {W_{i}^{l} } \right)_{\alpha } & = \left[ {\left( {W_{i}^{l} } \right)_{\alpha }^{L} ,\left( {W_{i}^{l} } \right)_{\alpha }^{U} } \right] = \left[ {\mathop {\hbox{min} }\limits_{{w_{i}^{l} }} \left\{ {{{w_{i}^{l} \in W_{i}^{l} } \mathord{\left/ {\vphantom {{w_{i}^{l} \in W_{i}^{l} } {\mu_{{\tilde{W}_{i}^{l} }} \left( {w_{i}^{l} } \right) \ge \alpha }}} \right. \kern-0pt} {\mu_{{\tilde{W}_{i}^{l} }} \left( {w_{i}^{l} } \right) \ge \alpha }}} \right\},\mathop {\hbox{max} }\limits_{{w_{i}^{l} }} \left\{ {{{w_{i}^{l} \in W_{i}^{l} } \mathord{\left/ {\vphantom {{w_{i}^{l} \in W_{i}^{l} } {\mu_{{\tilde{W}_{i}^{l} }} \left( {w_{i}^{l} } \right) \ge \alpha }}} \right. \kern-0pt} {\mu_{{\tilde{W}_{i}^{l} }} \left( {w_{i}^{l} } \right) \ge \alpha }}} \right\}} \right] \\ \left( {R_{ij} } \right)_{\alpha } & = \left[ {\left( {R_{ij} } \right)_{\alpha }^{L} ,\left( {R_{ij} } \right)_{\alpha }^{U} } \right] = \left[ {\mathop {\hbox{min} }\limits_{{r_{ij} }} \left\{ {{{r_{ij} \in R_{ij} } \mathord{\left/ {\vphantom {{r_{ij} \in R_{ij} } {\mu_{{\tilde{R}_{ij} }} \left( {r_{ij} } \right) \ge \alpha }}} \right. \kern-0pt} {\mu_{{\tilde{R}_{ij} }} \left( {r_{ij} } \right) \ge \alpha }}} \right\},\mathop {\hbox{max} }\limits_{{e_{ik} }} \left\{ {{{r_{ij} \in R_{ij} } \mathord{\left/ {\vphantom {{r_{ij} \in R_{ij} } {\mu_{{\tilde{R}_{ij} }} \left( {r_{ij} } \right) \ge \alpha }}} \right. \kern-0pt} {\mu_{{\tilde{R}_{ij} }} \left( {r_{ij} } \right) \ge \alpha }}} \right\}} \right] . \\ \end{aligned} $$

(11.25)

These intervals indicate where the relative weight of customer attributes and the relationship between CRs and ECs are located at possibility level $\alpha$. According to the extension principle of Zadeh (1978), the membership function, $\mu_{{\tilde{Z}_{j}^{l} }}$, can be derived from the following equation:

$$ \mu_{{\tilde{Z}_{j}^{l} }} \left( {z_{j}^{l} } \right) = \begin{array}{*{20}c} {\mathop {\sup }\limits_{r,w} } & {\hbox{min} \left\{ {{{\begin{array}{*{20}c} {\mu_{{\tilde{W}_{i}^{l} }} \left( {w_{i}^{l} } \right),\mu_{{\tilde{R}_{ij} }} \left( {r_{ij} } \right)} & {\forall i,j} \\ \end{array} } \mathord{\left/ {\vphantom {{\begin{array}{*{20}c} {\mu_{{\tilde{W}_{i}^{l} }} \left( {w_{i}^{l} } \right),\mu_{{\tilde{R}_{ij} }} \left( {r_{ij} } \right)} & {\forall i,j} \\ \end{array} } {z_{j}^{l} = {{\sum\limits_{i = 1}^{m} {w_{i}^{l} r_{ij} } } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^{m} {w_{i}^{l} r_{ij} } } {\sum\limits_{i = 1}^{m} {w_{i}^{l} } }}} \right. \kern-0pt} {\sum\limits_{i = 1}^{m} {w_{i}^{l} } }}}}} \right. \kern-0pt} {z_{j}^{l} = {{\sum\limits_{i = 1}^{m} {w_{i}^{l} r_{ij} } } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^{m} {w_{i}^{l} r_{ij} } } {\sum\limits_{i = 1}^{m} {w_{i}^{l} } }}} \right. \kern-0pt} {\sum\limits_{i = 1}^{m} {w_{i}^{l} } }}}}} \right\}} \\ \end{array} . $$

(11.26)

Therefore, the upper and lower bounds of the $\alpha$-level of $\tilde{Z}_{j}^{l}$ can be obtained. The solution of the upper and lower bounds can be attained by solving the following LP model:

$$ \begin{aligned} & \left( {Z_{j}^{l} } \right)_{\alpha }^{U} = \begin{array}{*{20}c} {\hbox{max} } & {{{\sum\limits_{i = 1}^{m} {w_{i}^{l} r_{ij} } } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^{m} {w_{i}^{l} r_{ij} } } {\sum\limits_{i = 1}^{m} {w_{i}^{l} } }}} \right. \kern-0pt} {\sum\limits_{i = 1}^{m} {w_{i}^{l} } }}} \\ \end{array} \\ & s.t. \\ & \left( {W_{i}^{l} } \right)_{\alpha }^{L} \le w_{i}^{l} \le \left( {W_{i}^{l} } \right)_{\alpha }^{U} \\ & \left( {R_{ij} } \right)_{\alpha }^{L} \le r_{ij} \le \left( {R_{ij} } \right)_{\alpha }^{U} \\ & i = 1, \ldots ,m{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} , \\ \end{aligned} $$

(11.27)

and

$$ \begin{aligned} & \left( {Z_{j}^{l} } \right)_{\alpha }^{L} = \begin{array}{*{20}c} {\hbox{min} } & {{{\sum\limits_{i = 1}^{m} {w_{i}^{l} r_{ij} } } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^{m} {w_{i}^{l} r_{ij} } } {\sum\limits_{i = 1}^{m} {w_{i}^{l} } }}} \right. \kern-0pt} {\sum\limits_{i = 1}^{m} {w_{i}^{l} } }}} \\ \end{array} \\ & s.t. \\ & \left( {W_{i}^{l} } \right)_{\alpha }^{L} \le w_{i}^{l} \le \left( {W_{i}^{l} } \right)_{\alpha }^{U} \\ & \left( {R_{ij} } \right)_{\alpha }^{L} \le r_{ij} \le \left( {R_{ij} } \right)_{\alpha }^{U} \\ & i = 1, \ldots ,m{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} . \\ \end{aligned} $$

(11.28)

Assume that $q = {1 \mathord{\left/ {\vphantom {1 {\sum\limits_{i = 1}^{m} {w_{i}^{l} } }}} \right. \kern-0pt} {\sum\limits_{i = 1}^{m} {w_{i}^{l} } }}$ and $\begin{array}{*{20}c} {t_{i} = qw_{i}^{l} } & {i = 1,2, \ldots ,m} \\ \end{array}$, Eqs. (11.27) and (11.28) can be transformed into the following LP model:

$$ \begin{aligned} & \left( {Z_{j}^{l} } \right)_{\alpha }^{U} = \begin{array}{*{20}c} {\hbox{max} } & {\sum\limits_{i = 1}^{m} {t_{i} } \left( {R_{ij} } \right)_{\alpha }^{U} } \\ \end{array} \\ & s.t. \\ & q\left( {W_{i} } \right)_{\alpha }^{L} \le t_{i} \le q\left( {W_{i} } \right)_{\alpha }^{U} \\ & \sum\limits_{i = 1}^{m} {t_{i} } = 1 \\ & i = 1, \ldots ,m;\,q,\,t_{i} \ge 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} , \\ \end{aligned} $$

(11.29)

and

$$ \begin{aligned} & \left( {Z_{j}^{l} } \right)_{\alpha }^{L} = \begin{array}{*{20}c} {\hbox{min} } & {\sum\limits_{i = 1}^{m} {t_{i} } } \\ \end{array} \left( {R_{ij} } \right)_{\alpha }^{L} \\ & s.t. \\ & q\left( {W_{i} } \right)_{\alpha }^{L} \le t_{i} \le q\left( {W_{i} } \right)_{\alpha }^{U} \\ & \sum\limits_{i = 1}^{m} {t_{i} } = 1 \\ & i = 1, \ldots ,m;\,\,q,t_{i} \ge 0. \\ \end{aligned} $$

(11.30)

According to the method of Chen et al. (2006), the expected value of $\tilde{Z}_{j}^{l}$ can be calculated by the following:

$$ E\left[ {\tilde{Z}_{j}^{l} } \right] = \frac{1}{2L}\sum\limits_{f = 1}^{L} {\left( {\left( {\tilde{Z}_{ji}^{l} } \right)_{{\alpha_{f} }}^{\text{U}} + \left( {\tilde{Z}_{Ji}^{l} } \right)_{{\alpha_{f} }}^{\text{L}} } \right)} ,j = 1,2, \ldots ,m. $$

(11.31)

The amount of information is best reflected by a single value derived by using the fuzzy expected value operator. This condition is caused by the fuzzy importance weights of CRs lying in a range, as well as the different $\alpha$-cuts providing different intervals and uncertainly levels of importance weights of CRs. When the importance weights of ECs are calculated, their ordinal rankings can also be derived. Details of the methods to determine importance weights of ECs are given by Chen et al. (2006).

11.5.2 Synthesis of Individual Preferences on the Ranking of ECs

In synthesizing individual preferences on ECs in terms of ordinal rankings to address the second type of uncertainty, a form of consensus can be derived by simply adding up the member preferences and taking their average. However, such an approach does not necessarily lead to a consensus ranking because the ranking derived by taking a simple arithmetic average may not be robust. The ranking of ECs should be viewed in terms of a “distance” measure. Such a measure relative to a pair of rankings will be an indicator of the degree of correlation between rankings. In this research, a method is proposed to deal with the problem of synthesizing ordinal preferences expressed as priority vectors to form a consensus. This method suggests the problem of determining a compromise or consensus ranking that best agrees with all individual rankings through an assignment problem.

In the proposed approach, a metric or distance function for a set of rankings is introduced. The consensus ranking approach can minimize the total absolute distance (disagreement). We begin by examining some conditions where such a distance, $d$, should be satisfied. First, the following axioms are required:

Axiom 1

$d\left( {A,B} \right) \succ 0$ with equality if $A = B$

Axiom 2

$d\left( {A,B} \right) = d\left( {B,A} \right)$

Axiom 3

$d\left( {A,C} \right) \prec d\left( {A,B} \right) + d\left( {B,C} \right)$ with equality if the ranking B is between A and C.

Axiom 4

(Invariance)

(1) If $A^{\prime}$ results from A by a permutation of the objects, and $B^{\prime}$ results from B by the same permutation, then $d\left( {A^{\prime},B^{\prime}} \right) = d\left( {A,B} \right)$

(2) If $\bar{A}$ and $\bar{B}$ result from A and B by reversing the order of the objects, then $d\left( {\bar{A},\bar{B}} \right) = d\left( {A,B} \right)$

Axiom 5

(Lifting-moving from $n$ to $n + 1$ dimensional space)

If $A$ and $B$ are two rankings of $n$ objects and A* and B* are the rankings that result from A and B, then $d\left( {A^{*} ,B^{*} } \right) = d\left( {A,B} \right)$ by listing the same $\left( {n + 1} \right)^{st}$ object last.

Axiom 6

(Scaling)

The minimum positive distance is one.

The axioms are consistent and can characterize a unique distance function. We can consider the problem wherein $K$ customers provide the ordinal rankings $\left\{ {A^{l} } \right\}_{l = 1}^{K}$ of $n$ ECs. Let $A^{l} = \left( {a_{1}^{l} , \ldots ,a_{n}^{l} } \right)$ and $b_{j} \in \left\{ {1,2, \ldots ,n} \right\}$, where $b_{i}$ represents the ordinal ranking of the ECs .

Definition 1

The median or consensus ranking $\hat{B}$ refers to the ranking that minimizes the total absolute distance.

$$ M(B) = \sum\limits_{l = 1}^{K} {d\left( {A^{l} ,B} \right)} = \sum\limits_{l = 1}^{K} {\sum\limits_{j = 1}^{n} {\left| {a_{j}^{l} - b_{j} } \right|} } . $$

(11.32)

The median ranking is in the best agreement with the set of selected rankings, thus providing an objective criterion to arrive at a consensus.

Let $B_{0}$ be the set of all rankings of $n$ objects. Thereafter, the following is obtained:

$$ \mathop {\hbox{min} }\limits_{{B \in B_{0} }} \sum\limits_{l = 1}^{K} {d\left( {A^{l} ,B} \right)} \ge \mathop {\hbox{min} }\limits_{{B \in R^{n} }} \sum\limits_{l = 1}^{K} {d\left( {A^{l} ,B} \right)} = \mathop {\hbox{min} }\limits_{{B \in R^{n} }} \sum\limits_{l = 1}^{K} {\sum\limits_{i = 1}^{n} {\left| {a_{j}^{l} - b_{j} } \right|} } . $$

(11.33)

Equation (11.33) attains its minimum when the following is satisfied:

$$ b_{j} = median\left\{ {a_{j}^{l} } \right\}_{l = 1}^{m} = b^{\prime}_{j} . $$

(11.34)

Let $B^{\prime} = \left( {b^{\prime}_{i} , \ldots ,b^{\prime}_{n} } \right)$. Thereafter, we obtain the following:

$$ M\left( {B^{\prime}} \right) \le M\left( B \right)\,\,{\text{For}}\,\,{\text{all}}\,\,B \in B_{0} . $$

(11.35)

Thus, we have:

Theorem 1

Let $\left\{ {A^{l} } \right\}_{l = 1}^{K}$ be a set of rankings and $B^{\prime}$ be given by (11.34). If $B^{\prime} \in B_{0}$ , then $B^{\prime}$ is the median ranking.

The determination of the median ranking requires a specialized algorithm. However, if consideration is restricted to the set of complete rankings, the problem can be represented by an LP formulation.

The problem can be solved effectively by representing the problem as an assignment problem. $d_{jq}$ is defined as follows:

$$ d_{jq} = \sum\limits_{l = 1}^{K} {\left| {a_{j}^{l} - q} \right|} . $$

(11.36)

Considering the following expression:

$$ \sum\limits_{l = 1}^{K} {d\left( {A^{l} ,B} \right)} = \sum\limits_{l = 1}^{K} {\sum\limits_{j = 1}^{n} {\left| {a_{j}^{l} - b_{j} } \right|} } . $$

(11.37)

Equation (11.36) is the value of the $j$ th sum in Eq. (11.37) if $b_{j}$ is set equal to $q\left( {q \in \left\{ {1,2, \ldots ,n} \right\}} \right).$

If we define the following expression

$$ x_{jq} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & {\begin{array}{*{20}c} {if} & {b_{j} = q} \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & {otherwise{\kern 1pt} {\kern 1pt} ,} \\ \end{array} } \\ \end{array} } \right. $$

(11.38)

then the restricted problem is equivalent to the following assignment problem:

$$ \begin{array}{*{20}c} {\mathop {\hbox{min} }\limits_{{x_{jq} }} } & {\sum\limits_{j = 1}^{n} {\sum\limits_{q = 1}^{n} {d_{jq} x_{jq} } } } & {} & {} & {} \\ {s.t.} & {\sum\limits_{j = 1}^{n} {x_{jq} = 1} } & {for} & {all} & q \\ {} & {\sum\limits_{q = 1}^{n} {x_{jq} = 1} } & {for} & {all} & j \\ {} & {x_{jq} \ge 0} & {for} & {all} & {j,q.} \\ \end{array} $$

(11.39)

The above integer programming model is capable of handling large problems. By solving the model, the consensus rankings of ECs can be obtained.

11.5.3 Evaluation of Robustness

The measurement of robustness depends on the perspective of robustness. Kim and Kim (2009) proposed an index to evaluate the robustness of ordinal ranking, namely, priority relationships among ECs . This approach indicates the relative priority order among two or more ECs. The robustness on the priority relationships among ECs can be measured as the degree in which the relative priority relationships among ECs are maintained despite the presence uncertainty. In this viewpoint, the robustness index on the priority relationships among ECs are expressed as the likelihood that a priority relationship in $V$ is retained. For instance, if $V$ is $\left[ {j_{1} j_{2} } \right]$, $V$ represents a priority relationship wherein $EC_{{j_{1} }}$ has a higher priority than $EC_{{j_{2} }}$. The robustness index on the priority relationship, denoted as $RI\left( V \right)$, can be calculated as follows:

$$ \begin{array}{*{20}c} {RI\left( V \right) = \frac{{\sum\nolimits_{l}^{L} {y(l)} }}{L}} \\ {where\left\{ {\begin{array}{*{20}c} {y(l) = 1,if\,\,\,ranking\left( {EC_{V\left( v \right)} ,l} \right)\, \le\, ranking\left( {EC_{{V\left( {v + 1} \right)}} ,l} \right)\forall v = 1, \ldots ,N\left( V \right) - 1} \\ {y\left( l \right) = 0,\begin{array}{*{20}c} {} & {otherwise} \\ \end{array} } \\ \end{array} {\kern 1pt} {\kern 1pt} ,} \right.} \\ \end{array} $$

(11.40)

where $y\left( l \right)$ is an indicator variable, $EC_{V\left( v \right)}$ denotes the $v$th EC in $V$, and $N\left( V \right)$ denotes the array size of $V$.

Considering that $RI\left( V \right)$ is expressed as a type of likelihood measured by an empirical probability, it has a value between zero and one. The larger value of $RI\left( V \right)$ implies that higher robustness on the absolute ranking of ECs or the priority relationship in $V$ can be obtained. If $RI\left( V \right)$ is equal to one, the priority relationship in $V$ is always retained despite the variability. By using the robustness index, the robustness of the prioritization decision, EC or $V$, can be evaluated.

The design of a flexible manufacturing system (FMS) (Liu 2005; Chen et al. 2006) is used to illustrate the proposed method. Assume that ten customers, denoted as $C_{l} ,l = 1,2, \ldots ,10$, are surveyed in a target market. Seven fuzzy numbers are used to express their individual assessments on the eight CRs, as shown in Table 11.2. $W_{1} \sim W_{7}$ are the importance weights of CRs, which represent very unimportant, quite unimportant, unimportant, slightly important, moderately important, important and very important, respectively. The relationship measures between CRs and ECs are shown in Table 11.3. $R_{1} \sim R_{4}$ denote four relationship linguistic terms, which are very weak, weak, moderate, and strong, respectively.

Table 11.2 The fuzzy importance of eight CRs assessed by ten customers using fuzzy numbers

Table 11.3 The relationship matrix between CRs and ECs

The proposed approach was applied to compute the ranking of ECs and the final ordinal rankings of ECs can be obtained.

$$ EC_{3} \succ EC_{7} \succ EC_{1} \succ EC_{2} \succ EC_{4} \succ EC_{8} \succ EC_{9} \succ EC_{10} \succ EC_{6} \succ EC_{5} $$

Based on the method of Chen et al. (2006), the ordinal ranking of ECs is shown as follows:

$$ EC_{3} \succ EC_{7} \succ EC_{1} \succ EC_{2} \succ EC_{4} \succ EC_{8} \succ EC_{9} \succ EC_{6} \succ EC_{10} \succ EC_{5} $$

From the ranking results of ECs of the two methods, we can find the difference in the order of EC₁₀ and EC₆. Based on the method of Chen et al. (2006), the ordinal ranking of EC₁₀ and EC₆ is EC₆ > EC₁₀. Based on the proposed approach, the result is opposite. Therefore, the robustness index is used to evaluate the ordinal ranking of EC₁₀ and EC₆ between the method of Chen et al. (2006) and the proposed approach. In the prior method, the prioritization relationship $V$ is [6 10]. For the first customer, ECI₆ > ECI₁₀ is consistent with $V$. Hence, $y\left( 1 \right)$ is equal to 1. In the proposed approach, $V$ is [10 6]. For the first customer, ECI₁₀ < ECI₆ is not consistent to $V$. Hence, $y\left( 1 \right)$ is equal to 0. Similarly, the value of $y\left( l \right)$ for the ten customers can be derived, as shown in Table 11.4. Then, $RI\left( V \right)$ value based on the Chen’s method can be calculated as follows:

Table 11.4 An illustration of the robustness index between the two methods

$$ RI\left( V \right) = \frac{1 + 0 + 0 + 1 + 0 + 0 + 1 + 0 + 1 + 0}{10} = 0.4 $$

and $RI\left( V \right)$ value based on the proposed approach can be calculated as shown below.

$$ RI\left( V \right) = \frac{0 + 1 + 1 + 0 + 1 + 1 + 0 + 1 + 0 + 1}{10} = 0.6 $$

Finally, the index values for the ranking based on the prior method and the proposed approach are calculated as 0.4 and 0.6 respectively. Therefore, the proposed approach outperforms the method of Chen et al. (2006) in prioritizing the ECs in terms of robustness.

11.6 Target Value Setting of ECs by Using Fuzzy Optimization and Inexact Genetic Algorithm

In the product design stage, product development teams may need to consider various design scenarios while determining design specifications. However, in previous studies of target value setting of ECs in QFD, only a single solution is obtained and target value setting for different design scenarios cannot be considered. In this section, a fuzzy optimization model is presented to determine the target value setting for ECs in QFD . An inexact genetic algorithm approach is described to solve the model that takes the mutation along the weighted gradient direction as a genetic operator. Instead of obtaining one set of exact optimal target values , the approach can generate a family of inexact optimal target values setting within an acceptable satisfaction degree. Through an interactive approach, a product development team can determine a combination of preferred solution sets from which a set of preferred target values of ECs based on a specific design scenario can be obtained.

11.6.1 Formulation of Fuzzy Optimization Model for Target Values Setting in QFD

The processes of determining the target values for ECs in QFD can be formulated as shown below:

Determine target values $x_{1} ,x_{2} , \ldots ,x_{n}$ by maximizing the overall customer satisfaction:

$$ y_{i} = f_{i} (X),i = 1, \ldots ,m, $$

$$ X_{j} = g_{j} (X^{j} ),j = 1, \ldots ,n, $$

where

$$ X = (x_{1} ,x_{2} , \ldots ,x_{n} )^{T} , $$

$$ X^{j} = (x_{1} , \ldots ,x_{i - 1} ,x_{j + 1} , \ldots ,x_{n} )^{T} , $$

$y_{i}$ :

is the customer perception of the degree of satisfaction of the $i$ th CR $i = 1, \ldots ,m$,

$x_{j}$ :

is the target value of the $j$th EC, $j = 1, \ldots ,n$,

$f_{i}$ :

is the functional relationship between the $i$th CR and ECs, i.e. $y_{i} = f_{i} (x_{1} , \ldots ,x_{n} )$, and

$g_{j}$ :

is the functional relationship between the $j$th EC and other ECs, i.e., $x_{j} = g_{j} (x_{1} , \ldots ,x_{j - 1} ,x_{j + 1} , \ldots x_{n} )$

The above equation is a general model to determine the target values of ECs. Additional constraints can be added to the above formulation as appropriate. In reality, many design tasks are performed in an environment wherein system parameters, objectives, and constraints are not known precisely. Therefore, developing a crisp optimization model to set the target values of ECs in QFD is difficult. For the establishment of an objective function, customers usually cannot provide a precise satisfaction value and instead express their satisfaction in linguistic terms such as “quite satisfied” and “very satisfied.” The relationships between CRs and ECs , as well as among ECs, can be very complicated. Engineers usually do not have full knowledge of the impact of an EC on CRs or on other ECs. Thus, setting the relationship values between a CR and an EC is also imprecise. Regarding the constraints, vagueness also exists. For example, the cost is usually described as a function of CR and should not exceed a predetermined upper limit. The cost constraint can then be formulated as follows:

$$ c_{1} x_{1} + c_{2} x_{2} + \cdots + c_{n} x_{n} \le \tilde{c}, $$

where, $\tilde{c}$ is the upper limit of cost and $c_{1}$,$c_{2}$, … $c_{n}$ are the coefficients. Owing to the imprecise and incomplete design information available in the early design stage, the values of $\tilde{c}$ may be imprecise.

The fuzziness presents a special challenge to model effectively the process of target values setting by using traditional mathematical programming technique. One way to deal with such vagueness quantitatively is to employ fuzzy set theory , which can be used to develop a fuzzy optimization model for the target value setting of ECs in QFD . On the basis of the work of Kim et al. (2000), a general fuzzy optimization model to set target values of ECs in QFD is proposed as follows:

$$ \begin{aligned} & M\tilde{a}x\;\mu (y_{1} ,\,y_{2} , \ldots ,y_{n} ) \\ & s.\,t. \\ & C1:{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} y_{i} \,\tilde{ = }\,f_{i} (X),\,\,\,\,\,i = 1, \ldots ,m \\ & C2:X_{j} \,\tilde{ = }\,g_{j} (X^{j} ),\,\,\,\,j = 1, \ldots ,n \\ & C3:C(X) \le \tilde{c} , \\ \end{aligned} $$

(11.41)

where $\mu$ is the satisfaction degree of customers to CRs; $C1$ and $C2$ are the fuzzy relationship constraints; $C3$ is the cost constraint.

11.6.2 Tolerance Approach to the Determination of an Exact Optimal Solution from the Fuzzy Optimization Model

The symmetric models, which are based on the definition of fuzzy decision, were frequently adopted in fuzzy LP models. They assumed that the objective and constraints in an imprecise situation could be represented by fuzzy sets. A decision could be stated as the union of the fuzzy objective and constraints and defined by a max–min operator. A fuzzy objective set G and a fuzzy constraint set C are assumed to be given in a space X. G and C are then combined to form a decision D, which is a fuzzy set resulting from the intersection of G and C, and the corresponding $\mu_{D}$ is equal $\mu_{G} \,\cap\, \mu_{c}$. Lai and Hwang (1992) mentioned that the approaches of Zimmermann, Werner, Chanas and Verdegay are the most practical approaches among various techniques in fuzzy LP. Transforming a fuzzy optimization model into a crisp model is the common idea of these approaches. In this research, Zimmerman’s tolerance approach (Zimmerman 1996) is adopted to solve the fuzzy optimization model . First, the membership function of fuzzy constraints and the fuzzy objective have to be determined. Customers usually cannot provide a satisfaction value precisely. Customers express satisfaction in fuzzy terms such as “quite satisfactory” and “not very satisfactory.” Let $y_{i}^{\hbox{min} }$ and $y_{i}^{\hbox{max} }$ represent the lower and upper bounds of aspirations, respectively, with respect to $y_{i}^{{}}$. A customer would then express complete dissatisfaction of a design ($X$) in which $y_{i} (X) \,\le\, y_{i}^{\hbox{min} }$; but would express complete satisfaction if $y_{i} (X)\, \ge\, y_{i}^{\hbox{max} }$. A membership function $\mu_{{y_{i} }} (X)$ can be introduced to measure the satisfaction degree of customers to the $i$ th CR at various ECs for design ($X$). The membership function $\mu_{{y_{i} }} (X)$ can be represented as follows:

$$ \mu_{{y_{i} }} (X) = \left\{ {\begin{array}{*{20}l} 0 & {if} & {y_{i} (X) \,\le \,y_{i}^{\hbox{min} } } \\ {\tau (X)} & {if} & {y_{i}^{\hbox{min} } \, \le\, y_{i} (X)\, \le\, y_{i}^{\hbox{max} } } \\ 1 & {if} & {y_{i} (X\,) \ge\, y_{i}^{\hbox{max} } ,} \\ \end{array} } \right. $$

(11.42)

where $\tau (X)$ could be linear or nonlinear.

The membership functions for all CRs $\mu_{{y_{i} }} (X)$, where $i{ = }1,2, \ldots ,m$, form the membership function of a fuzzy objective function. Each fuzzy constraint in the fuzzy optimization model can be represented by a fuzzy set. The membership function of the fuzzy relationship constraints are $\mu_{{f_{i} }} (X,Y)$ and $\mu_{{g_{j} }} (X,Y)$, where $i = 1,2 \ldots ,m$ and $j = 1,2 \ldots ,n$, respectively. The membership functions of a fuzzy constraint “$AX\,\tilde{ = }\,b$” can be represented as follows (Zimmerman 1996):

$$ \mu (X) = \left\{ {\begin{array}{*{20}l} 0 & {if} & {AX \le b - d\,\,or\,\,AX \ge b + d} \\ 1-\frac{|AX-b|}{d} & {if} & {b - d < AX < b + d} \\ 1 & {if} & {AX = b} \\ \end{array} } \right. $$

(11.43)

where $A$ is a row vector, $b$ is a constant, and $d$ is a subjectively chosen constant of the admissible violations of the constraint.

The membership of the cost constraint, $\mu_{c} (X)$, can be represented in the following form:

$$ \mu_{c} (X) = \left\{ \begin{aligned} & 1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}\; \;\; \;if\;CX < \;c \\ & 1 - \tfrac{(CX - c)}{t}\;\;\;\;\;\;if\;c \le CX \le c + t \\ & 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;if\;\;CX > c + t{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} , \\ \end{aligned} \right. $$

where $t$ is a pre-specified non-negative tolerance level to cost $c$. The above membership function denotes the following:

$\mu (X)$ :

is zero if the constraints are strongly violated,

$\mu (X)$ :

is one if the constraints are very satisfied, and

$\mu (X)$ :

increases monotonously from zero to one

With the use of Zimmerman’s tolerance approach, the crisp form of the fuzzy optimization model in Eq. (11.41) can be formulated as follows:

$$ \begin{aligned} & Maximize\,\lambda \\ & subject\,\,to \\ & \lambda \le \mu_{y\,i} (X),\,\,\,\,\,\,\,\,\,\,i = 1,\,2,\, \ldots ,m \\ & \lambda \le \mu_{{f\,_{i} }} (X,Y),\,\,\,\,\,i = 1,\,2,\,. \ldots m \\ & \lambda \le \mu_{{g_{j} }} (X,Y),\,\,\,\,\,\,j = 1,\,2,\, \ldots ,n \\ & \lambda \le \mu_{c} (X){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} , \\ \end{aligned} $$

(11.44)

where $\lambda \,(0 \le \lambda \le 1)$ represents the overall value of membership functions.

A unique optimal solution for the above model can be obtained by using an LP technique, which is a set of optimal target values for ECs $x_{1} ,x_{2} , \ldots ,x_{n}$. The exact setting of optimal target values for ECs obtained by using the LP technique may not be acceptable to a product development team in a new product design. This condition is caused by the inherent or permitted possibility and flexibility in the target values setting of ECs existing in QFD and the obtained solutions allowing a product development team to reconcile tradeoffs among the CRs and ECs under various design scenarios. The provision of a family of inexact satisfactory target values setting for ECs would then be very useful to the product development team. In this chapter, an inexact genetic algorithm is employed to generate a family of inexact satisfactory target values setting for ECs from the fuzzy optimization model . Detailed descriptions are shown below.

11.6.3 Inexact Genetic Algorithm Approach to the Generation of a Family of Inexact Solutions from the Fuzzy Optimization Model

During the last 30 years, interest in problem solving systems based on principles of evolution and hereditary has grown. Even though many different classes of the systems exist, such as genetic algorithms , evolutionary programming, and evolution strategies, they all rely on the same concept of mimicking mechanisms of biological evolution. Admittedly, the gap among them is getting smaller and smaller. They have also been called as some common terms such as evolutionary algorithms and evolution programs. The inexact genetic algorithm is a specially designed one to solve these problems with fuzziness.

The basic idea of the inexact genetic algorithm (Wang 1997) is that the mutation operator moves along a weighted gradient direction. An individual is led by this mutation operator to arrive at inexact solutions within an acceptable range of the fuzzy optimal solution sets. By means of an interactive approach, a set of preferred solutions can be sought by a convex combination of the solutions selected from the family. The basic idea of the method is applied to solve the fuzzy optimization model Eq. (11.44) to obtain a set of preferred solutions corresponding to a particular design scenario.

Generally, two types of genetic operators exist for the genetic algorithm: crossover and mutation. For the linear problem, only the mutation operator is utilized. In the inexact genetic algorithm , the mutation operator moves along a weighted gradient direction. For model Eq. (11.44), the mutation operator can be induced as follows.

Based on the tolerance method, the fuzzy optimal solution set of the fuzzy optimization model Eq. (11.44) is a fuzzy set defined by the following:

$$ \tilde{S} = \{ (X,\mu_{{\tilde{S}}} (X,Y))|X,Y \in R_{ + }^{n} \} , $$

(11.45)

where

$$ \mu_{{\tilde{S}}} (X,Y) = \hbox{min} \{ \mu_{yi} (X),\mu_{{f_{i} }} (X,Y),\mu_{{g_{j} }} (X,Y),\mu_{c} (X)\} \,\,i = 1,2, \ldots ,n;j = 1,2, \ldots ,m, $$

(11.46)

and $R_{ + }^{n}$ is the non-negative $n$-dimensional space. Based on the equivalent unconstrained max-min optimization problem, a weighted gradient of $\mu_{{\tilde{S}}} (X,Y)$ can be defined as follows:

$$ \begin{aligned} G(X,Y)\, \equiv\, & \nabla \mu_{{\tilde{S}}} (X,Y) \\ = & -\Gamma (\mu_{yi} ) \cdot \sum\limits_{i} {\mu_{yi} (X) +\Gamma (\mu_{fi} ) \cdot \sum\limits_{i} {\mu_{fi} (X,Y)} +\Gamma (\mu_{gj} ) \cdot \sum\limits_{j} {\mu_{gj} (X,Y)} } +\Gamma (\mu_{c} ) \cdot \mu_{c} (X){\kern 1pt} {\kern 1pt} , \\ i = & 1,2, \ldots ,n{\kern 1pt} ;j = 1,2, \ldots ,m \\ \end{aligned} $$

(11.47)

where $\Gamma (\mu )$ represents the weight of the corresponding membership, which can be designed as follows:

Let $\mu_{\hbox{min} } = \hbox{min} \{ \mu_{yi} (X),\mu_{{f_{i} }} (X,Y),\mu_{{g_{j} }} (X,Y),\mu_{c} (X),i = 1,2, \ldots ,n;j = 1,2, \ldots ,m\}$; then

$$ \Gamma (\mu ) = \left\{ \begin{aligned} & 1,\,\,\,\,\,\,\,\,\,\,\,\mu = \mu_{\hbox{min} } \\ & \frac{\sigma }{\mu },\,\,\,\,\,\,\mu_{\hbox{min} } < \mu < 1 \\ & 0\,\,,\,\,\,\,\,\,\,\mu = 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} , \\ \end{aligned} \right. $$

(11.48)

where $\sigma$ is a sufficiently small positive number.

If $(x,y)^{k + 1}$ is the child of the individual, $(x,y)^{k}$, the mutation along the weighted gradient direction can be described as follows:

$$ (x,y)^{k + 1} = (x,y)^{k} + \theta G(x,y), $$

(11.49)

where $\theta$ is a random step length of the Erlang distribution, which is generated by a random number generator.

By employing the inexact genetic algorithm to solve the fuzzy optimization model , a family of inexact optimal solutions can be obtained. The interactive approach allows a product development team to select a preferred solution from the fuzzy optimal solutions. First, the team provides an acceptable membership degree level of the fuzzy optimization. They then choose their preference structure utilizing the human-computer interaction. The product development team needs to point out which criteria are of utmost concern to them. The criteria could be the objective, constraints, or decision variables. The solutions in the α-cut of the fuzzy solutions set, $\tilde{S}_{\alpha }$, with the highest and lowest values of these criteria are stored in memory and updated in each interaction. Given the large number of the visited points, the solutions preferred by the product development team can be found with high probability. Considering that in general, more than one criterion of concerns from the product development team exists, more than one solution would be derived. When the iteration terminates, the solutions with their criteria values will be displayed to the product development team. The product development team can then select a couple of preferred solutions each time. By repeating the above procedures, the preferred final solution can be generated.

The proposed approaches have been applied to car door design. Table 11.5 shows the 5 sets of optimal solutions, which correspond to maximum values of the decision variables. In this table, $y_{1}$–$y_{5}$ are the satisfaction values of five CRs, which are “easy to close from outside,” “stays open on a hill,” “rain leakage,” “road noise,” and “cost,” respectively; $x_{1}$ to $x_{6}$ are target values setting of six ECs, which are “energy to close the door,” “check force on level ground,” “check force on 10 % slope,” “door seal resistance,” “road noise reduction,” and “water resistance,” respectively; $\mu (z)$ is the membership function of the fuzzy optimal solution set, which can be calculated based on Eq. (11.46); The last column shows the maximum values of $y_{1}$ to $y_{5}$. For example, the maximum of $y_{1}$ = $ma{\kern 1pt} x\{ 4.9273, 3. 3 5 4 7 , 4. 9 2 7 3 , 4.0 5 1 7 , 3. 1 5 1 5\}$ $\,= 4.9273$.

Table 11.5 A family of satisfactory solutions corresponding to the maximum values of decision variables

From the results, various sets of preferred target values setting ECs can be obtained for different design scenarios rather than the only one exact optimal target values setting. For example, the design team would like to have the maximum satisfaction values of all the CRs. In this case, the design team should select the solutions, Z _max(1), Z _max(2), Z _max(3), Z _max(4) and Z _max(5). The satisfaction values of the individual CRs, Y ^final, and the target values setting of the ECs, X ^final can be calculated using the following linear combination.

$$ Z = Z_{\hbox{max} (1)} *\omega_{1} + Z_{\hbox{max} (2)} *\omega_{2} + Z_{\hbox{max} (3)} *\omega_{3} + Z_{\hbox{max} (4)} *\omega_{4} \,\, + Z_{\hbox{max} (5)} *\omega_{5} $$

where $Z = (Y^{final} ,\;X^{final} )$, and $\omega_{1} \,{ = }\,0.3,\omega_{2} \,{ = }\,0.2,\,\omega_{3}\, { = }\,0.1,\,\omega_{4} { = }0.1\,\,$ and $\omega_{5} { = }0.3$ are the importance weights of the corresponding CRs.

Based on the above linear combination, $Y^{final}$ and $X^{final}$ can be determined as follows:

$$ \begin{aligned} Y^{final} =&\, (y_{1}^{final} ,y_{2}^{final} ,y_{3}^{final} ,y_{4}^{final} ,y_{5}^{final} ) = ( 3. 9 9 2 5 , { 3} . 0 0 2 1 , { 5} . 4 9 6 7 , { 4} . 6 2 4 7 , { 4} . 2 2 1 4 { }) \hfill \\ X^{final} = &\,(x_{1}^{final} ,x_{2}^{final} ,x_{3}^{final} ,x_{4}^{final} ,x_{5}^{final} ,x_{6}^{final} ) = ( 8. 5 0 4 8 , { 14} . 0 9 8 3 , { 7} . 5 7 5 2 , { 4} . 7 0 1 2 , { 6} . 7 9 4 2 , { 74} . 5 9 7 5) \hfill \\ \end{aligned} $$

11.7 Conclusion

In this chapter, our recent research on the development of intelligent QFD is described. First, a fuzzy AHP with extent analysis approach is described to determine the importance weights for CRs. The approach is effective to determine the importance weights as it is capable of capturing the vagueness of human judgment in assessing the importance of CRs. The fuzzy AHP with extent analysis is also easy to implement because the tedious calculation of eigenvectors required by the conventional AHP is no longer necessary. Second, a chaos-based FR approach is described to model the functional relationships between CRs and ECs . This approach can address the issues pertaining to the modeling of the functional relationships based on QFD: (1) only a small number of data sets are available for modeling, (2) relationships between CRs and ECs are nonlinear in nature, (3) data sets for modeling contain a high degree of fuzziness, and (4) explicit customer satisfaction models are preferred. Third, a fuzzy group decision-making method is described to address the two uncertainties simultaneously in prioritizing ECs and to determine the importance weights of ECs. It mainly involves an ordinal ranking of ECs based on a fuzzy weighted average method with fuzzy expected operator and a consensus ranking method. Finally, a fuzzy optimization model is presented and an inexact genetic algorithm approach is described to solve the model to determine the target value setting of ECs. Considering that product development teams may consider product design under various design scenarios, a unique optimal solution obtained from the fuzzy model may not be acceptable to them. The proposed approaches are capable of generating a family of optimal target values setting for ECs , from which various sets of preferred target values setting for ECs can be obtained for different design scenarios rather than the only one exact optimal target values setting.

Future research on developing intelligent QFD can involve the detection and elimination of outliers to improve survey data quality. Outliers may exist in the survey data and can affect the predictive accuracy of the models. Regarding the chaos-based FR approach for modeling functional relationships , minimizing the complexity of the generated fuzzy polynomial models could be considered in future work as an objective together with minimizing errors in the formulation of the fitness function. This approach would help develop fuzzy polynomial models with simpler structures and good modeling accuracy. Future works can also consider cost minimization as an objective in the fuzzy optimization model apart from maximizing customer satisfaction. The optimization problem thus becomes a multi-objective one. Other solving techniques such as multi-objective genetic algorithms and particle swarm optimization need to be introduced to solve the optimization problem.