Data Analytics and Optimisation for Assessing a Ride Sharing System

Abstract

Ride-sharing schemes attempt to reduce road traffic by matching prospective passengers to drivers with spare seats in their cars. To be successful, such schemes require a critical mass of drivers and passengers. In current deployed implementations, the possible matches are based on heuristics, rather than real route times or distances. In some cases, the heuristics propose infeasible matches; in others, feasible matches are omitted. Poor ride matching is likely to deter participants from using the system. We develop a constraint-based model for acceptable ride matches which incorporates route plans and time windows. Through data analytics on a history of advertised schedules and agreed shared trips, we infer parameters for this model that account for 90 % of agreed trips. By applying the inferred model to the advertised schedules, we demonstrate that there is an imbalance between riders and passengers. We assess the potential benefits of persuading existing drivers to switch to becoming passengers if appropriate matches can be found, by solving the inferred model with and without switching. We demonstrate that flexible participation has the potential to reduce the number of unmatched participants by up to 80 %.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Road traffic is one of the main generators of carbon emissions, and traffic congestion is a significant contributor to pollution around major cities and urban areas. Partly motivated by these issues, there has been recent strong growth in ride-sharing schemes (e.g. Blabla car, Carma, BLyft, Sidecar, Uber), where participants post details of intended trips, and the system then proposes possible matches between drivers and prospective passengers. As more matches are agreed, the number of car journeys decreases, and the total driven distance also decreases, helping to reduce congestion, emissions and energy consumption. Increasing participation in such schemes is thus considered both a benefit for society and a commercial objective for the system operators.

Deployed schemes focus on proposing a set of possible matches for each request, leaving the participants to contact each other, negotiate ride details, and to agree the match. In order to generate these offers quickly, the ride sharing systems typically propose matches using heuristics that are fast to compute, based on Euclidean distance between locations and on fixed time windows. This means that the set of proposed matches may include some that are infeasible given the road network, and may omit some that would be a user’s preferred match. However, users who receive few offers, or who are given offers that are a poor match for their travel plans, are unlikely to continue with the system. There is a need to assess the performance of the current matching schemes, identify ways in which performance could be improved, and assess the improvements that could be gained. To do this, we employ data analytics to infer constraints on possible matches, and to assess current performance. We then use the inferred constraints to build optimisation models and to evaluate proposed improvements.

Specifically, (i) we use shortest path routing algorithms to determine the impact of a driver being matched with a passenger; (ii) by mining records of previously agreed matches, we infer constraints on the departure and arrival time windows for drivers, and on deviations from the shortest routes, that capture 90 % of agreed matches; (iii) we compare the inferred constraint model with the heuristic matching algorithm, and assess the discrepancies between the two approaches; (iv) we analyse histories of proposed trip schedules and show an imbalance between drivers and passengers that may be hampering participation in the scheme; and (v) we propose and evaluate the potential of persuading drivers to be flexible in their roles in the scheme, showing a reduction in unmatched participants of up to 80

2 Related Work

The dial-a-ride problem has been long studied in the OR community [6]. Dial-a-ride typically assumes a single vehicle, picking up and dropping off riders at specified locations within time windows, although multiple vehicle problems have also been studied [4, 5]. In [10], the authors compare different scenarios of dial-a-ride problems and show that these scenarios can be solved extending the variable neighborhood search algorithms. The dial-a-ride drivers have no journey requirements of their own. For ride-sharing schemes [7], both the drivers and the riders have their own objectives. Specific schemes vary as to whether the drivers move to the riders locations or the riders move to and from the driver routes, and whether or not drivers take single or multiple riders on a trip. One extension includes participants known as shifters, who may either drive or ride as a rider [1]. Armant et al. [3] also include shifters, but also assume that each pure rider who is not served in the matching has a probability of driving on their own, included as a penalty in the objective function. Computing an optimal matching is hard [2], and the complexity increases as the number of shifters increases. Kamar and Horvitz [8] model the problem as one of collaborative planning, where agents must balance competing goals. Yousaf et al. [13] model the problem as multi source-destination path planning, with a wide range of competing objectives including privacy and incentives. Schilde et al. [11] and Manna and Prestwich [9] consider stochastic problems, in which trip requests arrive during the execution of the solution, using scenario-based methods to minimise expected delays or unserved requests. Simonin and O’Sullivan [12] focus on the matching problem, assuming an input graph of all feasible pairings, and establishes the complexity of a number of two variations, showing that in some cases polynomial time solutions are possible. In this study, from the analysis of agreed rideshare trips advertised by real users, we model the users’ behaviour and infer a Constraint Programming problem. The last problem allows us to assess the quality and the potential improvement of the heuristics used in deployed applications when answering to users’ queries. A comparison of different ride-sharing problem formulations or algorithms to improve the solving time is beyond the scope of the study.

3 Euclidean-Distance Ride Matching

In the basic ride sharing scheme, drivers and riders post their start and end locations, and an expected start time, and the system proposes possible matches to the participants. The participants then select from the possible matches and contact each other to agree the details of the trip, which involves establishing a pick-up and drop-off location, and a time for the pick up. The agreed values might differ from the original values posted by the participants. When the actual ride takes place, both the driver and rider use a smartphone app to inform the system, with the driver informing the system on first departure and final arrival, and each rider notifying the system on pick-up and drop-off. The app reports GPS readings and times, from which payments are computed.

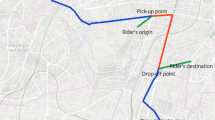
When a driver or rider posts their trip request, the ride sharing system should return in real-time a list of potential users with which the poster can share their journey. To ensure a real-time response $(< 1s)$, a Euclidean distance heuristic is typically used to find the possible matches. First, for each driver, a straight line path is drawn from the driver start location to the driver destination. Secondly, for all possible riders, the euclidean distances between the rider start and destination and the driver line are computed. Only riders with distances to and from the driver line below a threshold are considered as potential matches. These are further filtered by restricting (i) rider start and destination locations to be within a threshold angle of deviation from the driver line, and (ii) rider start times to lie within a fixed threshold of the driver’s start time. This simple heuristic is fast to compute, and can be more or less accurate in large cities having a road network similar to a grid. Without this particular road network configuration the heuristics frequently return infeasible matches, and also omit some high quality potential matches. The main cause of inappropriate matches is the use of straight line paths and distances, since in many circumstances the shortest or fastest route is significantly different from the straight line path. In the Fig. 1, we show an extreme example. T45 denotes the fixed threshold heuristic that we investigate. It fits to regular grid road maps and is similar to some heuristics used by deployed applications for fast computation of the matches. The subfigure on the left shows the standard heuristic, with trips starting and finishing in the grey zone being offered as potential matches. The subfigure on the right shows that fastest path for the driver, and of the two passenger request, the only feasible match is the one which was not previously offered. Secondly, the system requires each user to post a preferred start time, and then applies a fixed time window around start times to match participants. However, individual users may have different flexibility over their start or arrival times, and these are also likely to vary with the expected travel time for the journey. Repeated offering of matches which would require significant deviation from a route, or which are infeasible because of the length of time required for the journey, are liable to act as a disincentive for users to continue with the system. Similarly, if well matched participants are not offered rides, there is a reduced incentive to continue with the system.

Fig. 1.

Example of feasible and infeasible ride matches

4 Ride Sharing Optimisation Model

To describe the trip schedules and the users’ constraints we introduce the following notation. D denotes the set of possible drivers, R is the set of possible riders, and $U = D \cup R$ represents the set of all users. To generate the time and geographical constraints, we use Open Street Map data to deduce minimal path distances and times between two locations. $L= \{ l_{1}, \ldots , l_{n} \}$ denotes the set of road node locations identified by their GPS coordinates. A path $\pi =(l_i, \ldots ,l_j)$ is an ordered list of locations, and $time(\pi )$ (resp. $dist(\pi )$) returns the driving path time (resp distance) for $\pi$. The path $\pi ^{*}_{l_{i},l_{j}}$ (resp. $\pi ^{\diamond }_{l_{i},l_{j}}$) denotes a minimal time (resp. distance) path from $l_{i}$ to $l_{j}$. A trip schedule is a tuple $ts_{u}=( t^{start}_{d}, l^{start}_{d}, l^{dest}_{d} )$ describing user u’s intended start time $t^{start}_{u}$, start location $l^{start}_{u}$, and destination $l^{dest}_{u}$. $TS=\{ts_{u_1}, \ldots , ts_{u_n}\}$ denotes the set of user trip schedules sent to the system. To simplify the notation we consider one trip schedule per user, but the approach remains valid for multiple schedules per user. For a trip schedule $ts_u$, the inferred time window $tw_u=(et^{start}_{u},lt^{dest}_{u})$ describes an earliest start time $et^{start}_{u}$ and a latest arrival time $lt^{dest}_{u}$. Intuitively, the driver trip time window $tw_{d}$ is consistent with a rider trip time window $tw_{r}$ when there exists a time interval intersecting both $tw_{r}$ and $tw_{d}$ in which the rider can be picked-up and dropped-off by the driver. For a driver trip schedule $ts_d$, $\pi ^{*}_{l^{start}_{d},l^{dest}_{d}}$ denotes the inferred minimal time path from $l^{start}_{d}$ to $l^{dest}_{d}$. For a rider trip schedule $ts_r$, $m^{pick}_{r}$ denotes the inferred maximal path distance r is willing to walk from his intended start $l^{start}_{r}$ to a pick-up location $l^{pick}_{r}$ on the driver path $\pi ^{*}_{l^{start}_{d},l^{dest}_{d}}$. Similarly $m^{drop}_{r}$ denotes the inferred maximal path distance the rider is willing to walk from a drop-off location $l^{drop}_{r}$ to his destination $l^{dest}_{r}$.

Given the above we define the feasible matches relaying both on the users’ inferred path constraints and the users’ inferred time constraints.

Definition 1

(inferred feasible ride match). A driver trip schedule and a rider trip schedule, $ts_{d}$ and $ts_{r}$, represent a likely feasible ride match if:

• 1. their inferred time windows $tw_{d}$, $tw_{r}$ are consistent with the rider pick-up and drop-off time:

  • (a) $lt^{dest}_{d}- et^{start}_{r}> \pi ^{*}_{l^{pick},l^{drop}}$, the interval between the driver latest arrival and the rider earliest start is greater than the fastest path from the rider’s inferred pick-up to his inferred drop-off, or,

  • (b) $lt^{dest}_{r}- et^{start}_{d}> \pi ^{*}_{l^{pick\diamond },l^{drop\diamond }}$, the interval between the earliest driver start and the latest rider arrival is greater than the fastest path from the rider inferred pick-up to the inferred drop-off.

• 2. The expected driving path intersects the rider’s possible pick-up and drop-off points.

  • (a) $dist(\pi ^{\diamond }_{l^{start}_{r},\pi _{d}} ) < m^{pick}_{r}$, the shortest path distance between the rider intended start and the expected driver path is lower than the maximal distance for the rider’s pick-up.

  • (b) $dist(\pi ^{\diamond }_{l^{start}_{r},\pi _{d}} ) < m^{drop}_{r}$, the shortest path distance between the rider intended destination and the expected driver path is lower than the maximal distance for the rider’s drop-off.

Given a set of trip schedules, by iteratively checking if each pair of trip schedules are likely feasible, we incrementally discover a bipartite graph of feasible ride matches $G_{} =(TSD_{}, TSR_{}, E_{})$ s.t. $TSD \subseteq TS$ is the set of drivers’ trip schedules, $TSR \subseteq TS$ is the set of riders’ trip schedules, and every edge $(ts_d,ts_r) \in E$ is a feasible ride match. G is the input parameter of the constraint programming model we build to assess the potential of a ride-sharing scheme. For each feasible match between a rider trip schedule $ts_r$ and a driver trip schedule $ts_d$ in $G_{} =(TSD_{}, TSR_{}, E_{})$ is associated to a ride share trip $y_{ts_d,ts_r}$ encoded as a collection of decision variables s.t.:

• $y_{ts_d,ts_r}.start$ represents the pick-up time of r,

• $y_{ts_d,ts_r}.end$ denotes a the drop-off time of r,

• $y_{ts_d,ts_r}.duration$ is the time duration of the rideshare trip,

• $y_{ts_d,ts_r}.presence$ denotes presence of the ride share trip in the optimal solution.

We model a served rider using $x_{,ts_r}$ s.t. $x_{,ts_r}$ equal 1 when the rider is allocated to exactly one of feasible share ride $y_{ts_d,ts_r}$. To assess the potential of a ride-sharing scheme, our objective is to maximize:

$$\begin{aligned} \underset{ (ts_d,ts_r)\in E}{\Sigma } x_{,ts_r} \end{aligned}$$

(1)

 

subject to:

$$\begin{aligned} \begin{array}{lc} y_{ts_d,ts_r}.start \ge max(t^{early}_{d},t^{early}_{r}) \text {, } &{} \forall (ts_d,ts_r) \in E \\ \end{array} \end{aligned}$$

(2)

$$\begin{aligned} \begin{array}{lc} y_{ts_d,ts_r}.end \le min(t^{latest}_{d},t^{latest}_{r}) \text {, } &{} \forall (ts_d,ts_r) \in E \\ \end{array} \end{aligned}$$

(3)

$$\begin{aligned} \begin{array}{lc} y_{ts_d,ts_r}.duration = y_{ts_d,ts_r}.end - y_{ts_d,ts_r}.start \text {, } &{} \forall (ts_d,ts_r) \in E \\ \end{array} \end{aligned}$$

(4)

$$\begin{aligned} \begin{array}{lc} y_{ts_d,ts_r}.duration \ge \pi *_{l^{start},l^{dest}} \text {, }&{} \forall (ts_d,ts_r) \in E \\ \end{array} \end{aligned}$$

(5)

$$\begin{aligned} \begin{array}{lc} CUMULATIVE(\{y_{ts_d,ts_r} \},nbSeats_{d},\le ) \text {, } &{} \forall ts_d \in TSD\\ \end{array} \end{aligned}$$

(6)

$$\begin{aligned} \begin{array}{lc} ALTERNATIVE(x_{ts_r},\{ y_{ts_d,ts_r}| (ts_d,ts_r) \in E \}) \text {, } &{} \forall ts_r \in TSR\\ \end{array} \end{aligned}$$

(7)

$$\begin{aligned} \begin{array}{lc} (x_{ts_c}.presence \Rightarrow y_{tr_c,ts_r}.presence) \text {, } &{} \forall (ts_d,ts_r) \in E \\ \end{array} \end{aligned}$$

(8)

The aim is to maximize the total number of served riders (1). The constraints (2) force each rideshare trip to start after the earliest rider start and the earliest driver start. Similarly, the constraints (3) force each rideshare trip to end before the latest rider arrival and the latest driver arrival. The duration of the rideshare trip is the difference between the end and the start (4) and it is greater than the rider shortest path (5). The cumulative constraints (6) restrict each driver car occupancy to not exceed the number of available seats at any moment of the trip. When a rideshare trip is chosen in a solution, i.e., $y_{ts_d,ts_r}.presence=1$, it corresponds to one occupied seat in a driver’s car, it is equal to 0 otherwise. At any time, the driver’s car occupancy corresponds to the following definition $\underset{ (ts_d,ts_r) \in E}{\Sigma } y_{ts_d,ts_r}.presence \le nbSeats_{d}$, $\forall ts_d \in TSD$. The alternative constraints (7) enforce that at most one $y_{ts_d,ts_r}$ rideshare trip is chosen. In the successful case of the rider rideshare trip $x_{ts_r}$ is equal to the chosen rideshare $y_{ts_d,ts_r}$ otherwise the rider is not chosen. The constraints (8) state that a shifter assigned to be a rider does not drive.

5 Inferring Constraints from Users’ Behaviour

The raw data maintained in the ride-sharing scheme is not enough to establish the parameters of the optimisation model. Participants do not post time windows for their trips, and their advertised locations may be inaccurate (to protect privacy). Similarly, details of actual shared rides are subject to errors and missing data, as they are reliant on participants reporting GPS coordinates at the time of departure and arrival; in particular, drivers have no need to start the system until the first pickup. Finally, although we have records of advertised trips, we only have confirmed data on positive examples of acceptable ride shares; a pair of schedules which did not result in a trip might not have been feasible, but equally might not have been proposed to the participants, or might have been rejected in preference to another trip for either distance or personal factors. To assess the potential of the ride-sharing scheme, we need to infer the parameters of the model from the set of positive examples.

For a trip schedule $ts_u$, inferring the time window $tw_u$ involves inferring the earliest start time $t^{early}_{u}$ and the latest arrival time $t^{latest}_{u}$ in which a user expect the journey to happen. For this purpose, we extract from the trip records three parameters: the maximal positive start time delay, $\delta ^{+}$, the maximal negative start time delay, $\delta ^{-}$, and the estimated travel time $f_{1}$ and, as explained in Fig. 2, we add them together to infer the earliest start and the latest arrival time of the inferred time window $tw_{u}$.

Fig. 2.

Time Window Parameters

Fig. 3.

Positive and negative time delay for riders in region 4

The positive and negative start time delay represents the user’s time flexibility for advancing or delaying the intended start. In Fig. 3 we observe the difference between the riders’ intended start time $t^{start}_{r}$ and their reported pick-ups time $t^{pick}_{r}$ while observing the trip duration between the riders’ pick-ups and drop off. We observe no correlation between the ride share duration and the user’s delayed times. Riders appear to be willing to change their start times by an amount greater than the duration of their journey in order to find a ride. To extract the maximal positive and negative time changes, $\delta ^{+}$ and $\delta ^{-}$, we determine the minimal change which encompasses almost all ($90\,\%$) accepted ride shares. The horizontal lines show the maximal positive start time (left) and negative start time delay (right) observed for the riders in region 4. We compute similarly the maximal positive and negative time delay for the drivers.

The estimated travel time represents the approximate time a user can expect to spend on the road. In Fig. 4 (left) we plot the duration of the riders’ travel time from the reported pick-up $t^{pick}_{r}$ to the reported drop-off $t^{drop}_{r}$ against the minimal path time computed between these locations. There is a clear correlation, with linear regression indicating a factor of approximately 1.5 for the increase in travel time over the minimal path. This increase may be due to many factors, including traffic congestion and the presence of multiple passengers in a single trip, and will be the subject of further study. Moreover, one can notice few points below the diagonal (fastest path time = recorded path time). These represent cases where the driver was faster than the faster path time respecting to the speed limit indicated in OSM map.

Fig. 4.

Observed trip time compared to minimal path time, for region 4 (Colour figure online)

The Riders’ Maximal Meeting Path Distances represent the maximal pick-up path distance, $m^{pick}$, from the rider intended start to the driver path, and the maximal drop off path distance, $m^{drop}$ from the driver path to the rider intended destination. In Fig. 4 (right) we plot the path distance between the riders intended destination and reported drop-off against the minimal path distance between the destination and drop-off. Here there exists no clear correlation between the observed and minimal drop off path distances. Again, our aim is to find the minimal threshold on the meeting path distance within which $90\,\%$ of the users accepted a ride. Based on the inferred path times (which would be used in deciding whether or not to accept a ride), a limit of 4.5km (black line) includes $90\,\%$ of all accepted rides. For comparison, we show (blue line) a similar derived threshold of 5.8 km on the observed times.

We summarize the optimisation model parameters extracted from the trip records in the following table. Times are described in minutes and the distances in kilometers. We recall that given a trip schedule$ts_{u}$, we infer its time-window parameter using the following formulae: the infered earliest start time $t^{early}_{u} = t^{start}_{u} -\delta ^{-}$ while the latest arrival time $t^{latest}_{u} = t^{start}_{u} +\delta ^{-} + f_1(x)$. We notice that in all the regions studied, riders are more flexible than drivers, but both are willing to start early. The estimated travel time varies from 1.4 to twice the minimal path time computed using OSM Street Map, and varies depending on the region.

	drivers $\delta ^{+}$	drivers $\delta ^{-}$	riders $\delta ^{+}$	riders $\delta ^{-}$	$f_1(x)$	riders $m^{pick}$	riders $m^{drop}$
region 1	63	56	74	94	2x+11.2	2.2	1.7
region 2	31	60	57	46	1.15x+13.2	2.0	1.0
region 3	45	45	56	60	1.4x+9.7	11.3	14.3
region 4	45	54	70	56	1.4x+7.5	2.4	4.5

6 Assessing the Ride-Match Models

We now use the inferred model described in previous section to assess the quality of the existing matching heuristics for the 4 regions in the study.

The basic Euclidean heuristic is augmented with a 45 degree sweep angle, and allows up to 2 hours variation in the start times. In the following table we evaluate the precision and the recall of this heuristic with respect to inferred feasible ride match model represented as the graph G. The recall rate (the percentage of feasible matches from G returned by the heuristic) is relatively high, ranging between $90\,\%$ and $95\,\%$, although this still indicates that between 5 and $10\,\%$ of feasible matches are not being considered. The precision rate (percentage of matches returned by the heuristic that are feasible in G) however varies from $58\,\%$ to $90\,\%$, indicating that many infeasible matches are being proposed. The heuristic is most effective on region 3, with poor performance on region 1 and region 2. The appears to be a consequence of the geography of the regions - region 3 is a large urban area with a regular road network, while region 2 has a mix of urban and rural roads, and an irregular road network around harbours and coastal areas. Relatively low precision and recall (regions 1 and 2) indicate many inappropriate match suggestions and missing proposal, which are believe to act as a disincentive for potential users.

T45	nb edges	# feasible	# feasible	# unfeas	# feasible	precision	recall
			found	ible found	not found
region 1	802	647	588	214	59	0.733	0.909
region 2	559	364	326	233	38	0.583	0.896
region 3	1678	1691	1616	62	75	0.963	0.956
region 4	4223	3590	3326	897	264	0.788	0.926

To assess the potential of the ride-sharing scheme, we use the inferred CP model to compute the maximum number of assignments of riders to drivers’ cars. In next table, we compare the number of matched users found in G, with number of matched users found among the feasible matches for the typical heuristic T45FM. Note that T45FM is a filtered version of the typical heuristic, removing those matches considered infeasible in G, since those matches would be rejected by the optimisation model. The first thing to note is the percentage of unmatched participants is higher in each case for the T45FM filtered heuristic compared to the inferred model, although the losses are relatively small. However, perhaps more importantly, the ratio column shows that there is a significant imbalance in the participants in the scheme; a healthy scheme should have a ratio of at least 1, and ideally should be higher, allowing multiple passengers per car. A low ratio means many drivers will be unmatched, and thus will drive with empty seats. In addition, frequent failed attempts to find a match are likely to deter those users from participating. The current optimisation model prioritises riders, and thus some drivers may have multiple passengers. Changing the criterion to balance driver utilisation may encourage drivers to continue with the system, but cannot increase the total number of matched participants, and thus is likely to reduce the society benefits of sharing journeys. Therefore, we consider a different approach, and evaluate the effect of persuading all drivers to become shifters, and to accept an offer to be a passenger rather than remain exclusively as a driver. The results of running these flexible models are shown in the rows FMS and T45FMDS. We note that FMDS is still providing a benefit over the (filtered) heuristic, but more importantly, the increased flexibility allows us to match significantly more participants. The number of unmatched participants drops by a factor of 0.33 in the poorest case (region 2) and by a factor of 5 in the best case (region 3). We conclude that, where there is a participant imbalance, the focus of the ride sharing scheme operators should be to persuade drivers to be flexible in their roles, as this appears to offer the biggest potential for continued participation in the scheme and for removing vehicles from the road network.

region 1	users	ratio	matched	matched	%	region 2	users	ratio	matched	matched	%
		R / D	riders	drivers	unmatch			R / D	riders	drivers	unmatch
FM	992	0.55	246	133	61.79	FM	658	0.7	142	79	66.41
T45FM			223	124	65.02	T45FM			132	81	67.61
FMDS	992	1.55	488	196	31.05	FMDS	658	1.7	258	99	45.74
T45FMDS			446	176	37.30	T45FMDS			248	98	47.42
region 3						region 4
FM	1871	0.67	656	328	47.41	FM	4784	0.82	1592	758	50.88
T45FM			630	332	48.58	T45FM			1521	774	52.03
FMDS	1871	1.67	1392	321	8.44	FMDS	4784	1.82	2876	864	21.82
T45FMDS			1340	316	11.49	T45FMDS			2741	880	24.31

7 Conclusion

Ride-sharing is a rapidly growing practice for reducing the number of cars on the road in urban regions. Successful ride sharing schemes require committed users, and they in turn require the scheme to provide them with feasible ride matches in real-time. In current systems, the emphasis has been on the real-time requirement rather than the feasibility of the matches. We have developed a model which uses route planning and time windows to describe feasible matches as a constraint satisfaction problem, and the ultimate goal of the ride-matching scheme as constraint optimisation. Through analysis of data sets of advertised schedules and agreed trips, we infer the parameters of the these constraint models, chosen to accept 90 % of all agreed matches. By applying the model to the data sets of advertised trips, we identify the errors in the current heuristics, and find an imbalance among participants in the ride sharing schemes. We consider the benefits that might be obtained if drivers can be persuade to switch roles and act as passengers, and by re-running the optimisation model we show that there is potential to reduce the number of unmatched participants by up to 80 %. Such flexible switching would have a societal benefit, of reducing the number of vehicles on the road and reducing the total driven distance, and would also benefit the companies concerned, by allowing more matches and encouraging sustained user participation. Future work will focus on validating the hypothesis through field trial with user in the scheme, and on developing real-time response to the users which respects the constraints on feasible matches.