Tree PCA for Extracting Dominant Substructures from Labeled Rooted Trees

Abstract

We propose novel principal component analysis (PCA) for rooted labeled trees to discover dominant substructures from a collection of trees. The principal components of trees are defined in analogy to the ordinal principal component analysis on numerical vectors. Our methods substantially extend earlier work, in which the input data are restricted to binary trees or rooted unlabeled trees with unique vertex indexing, and the principal components are also restricted to the form of paths. In contrast, our extension allows the input data to accept general rooted labeled trees, and the principal components to have more expressive forms of subtrees instead of paths. For this extension, we can employ the technique of flexible tree matching; various mappings used in tree edit distance algorithms. We design an efficient algorithm using top-down mappings based on our framework, and show the applicability of our algorithm by applying it to extract dominant patterns from a set of glycan structures.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Capturing the characteristic features of a given data set is one of the fundamental problems in data mining. A popular method for high dimensional numerical vector data is Principal Component Analysis (PCA, for short) proposed by Pearson [8]. In PCA, the features are subspaces, and the projected subspaces are extracted so that the amount of information of the original data set is retained as possible. We want to apply PCA also to non-numerical data such as tree structure data for extracting dominant features in a set of data. Since PCA requires a feature space and a distance on the space, we have to tailor a suitable feature space and a distance to capture common patterns in tree structures.

PCA for tree structure data was first formulated by Wang and Marron [11]. They applied it to binary trees representing the brain artery structures obtained from MRA images. Ayding et al. [2] proposed an efficient algorithm to compute principal components for unlabeled rooted binary trees. They further extended the method to unlabeled rooted ordered trees with indexing [1], like a k-way tree indexing [3]. In their methods, the total space of the input data set is defined as the support tree which is the smallest supertree including all members of the data set as subtrees. The support tree is defined as the union of all trees in a given data set on the assumption that all tree structures share the same index schema uniquely. The projected space is defined as a tree-line, which is a sequence of subtrees $\{l_0,\dots , l_k\}$ where $l_0$ is a given subtree and $l_i$ is defined from $l_{i-1}$ by the addition of a single vertex to the same direction. We can treat the tree space like the Euclidean space when we regard $l_0$ as the origin, the tree-space as a two dimensional total space, and the tree-line as a one dimensional axis.

In this paper, we extend the idea due to [1] and introduce PCA for labeled rooted unordered trees without indexing; i.e., our methods do not rely on the strong assumption above. Our idea is to use a mapping, a set of pairs of vertices with some restrictions, to express principal components. In the previous work [1, 2], the expression of principal components is restricted to paths on trees, while our methods allow principal components to have more expressive forms of subtrees by taking advantage of mappings. The notion of mappings was originally introduced for defining the distance between trees [9]. The mapping is regarded as a common substructure between two trees, and many variants of tree edit distance are formulated by the classes of mappings [7]. In this paper, we introduce a general schema for defining PCA for labeled rooted trees and show an algorithm using top-down mappings as an instance of the schema. We apply it to a glycan structure data set, and compute principal components for extracting dominant patterns in the structures. We confirm its validity by classifying the glycan data, and evaluate the accuracy. The comparison of PCA properties among the conventional numerical vector, previous methods and our methods is shown in Table 1.

Table 1. The comparison of PCAs for three types of input data.

2 Preliminary

A rooted tree (tree, for short) is a connected directed acyclic graph in which every vertex is connected from a root vertex. A tree $T=(V,E,r,\alpha )$ is a labeled rooted unordered tree, where V is a set of vertices, E is a set of edges, r is a vertex in V called the root, and $\alpha$ is a label function defined as $\alpha : V\rightarrow \varSigma$, assuming an alphabet to be $\varSigma$. The label of $v\in V$ is denoted by l(v). We write $v\in T$ instead of $v\in V$. A forest $F=\{T_1,\dots ,T_n\}$ is a set of trees. If $|F|=1$, we identify $F=\{T_1\}$ with $F=T_1$. The ancestor-descendant relation is denoted by $<$, and for $v,w\in T$, $v<w$ means that w is an ancestor of v. The depth of a vertex v is defined as $\mathrm {dep}(v)=|\{w\mid v\le w\}|$. The sibling relation is denoted by $\prec$, and for $v,w\in T$, $v\prec w$ means that w is a right sibling vertex of v. The parent vertex of $v\in V\setminus \{r\}$ is denoted by $\text{ parent }(v)$.

For two trees $T_1$ and $T_2$, the following operations are called edit operations : deletion and insertion of a vertex $v\in T_1$, and substitution of the label of $v\in T_1$ for the label of $w\in T_2$. The costs of edit operations, deletion, insertion and substitution, are denoted by $\gamma (v\rightarrow \lambda ), \gamma (\lambda \rightarrow w)$ and $\gamma (v\rightarrow w)$, respectively. An edit distance is the minimum sum of the costs for transforming $T_1$ to $T_2$ if all of the costs of edit operations are the same. When $\gamma (v\rightarrow w)\ge \gamma (v\rightarrow \lambda )+\gamma (\lambda \rightarrow w)$, that is, the edit distance without substitution operations, is called an indel (insertion-deletion) distance.

A mapping $M\subseteq V_1\times V_2$ is a set of pairs of vertices for two trees $T_1=(V_1,E_1)$ and $T_2=(V_2,E_2)$. Various types of mappings have been proposed [7]. They are distinguished by their restrictions such as an ancestor-descendent relation. We show two instances of mappings; i.e., a Tai mapping and a top-down mapping.

Tai Mapping [9]: Let $T_1=(V_1,E_1)$ and $T_2=(V_2,E_2)$ be rooted ordered trees, a set $M\subseteq V_1\times V_2$ is called a Tai mapping on ordered trees if any pairs $(v_1,v_2),(w_1,w_2)\in M$ satisfy all of the following conditions.

$$\begin{aligned} v_1 = w_1&\Longleftrightarrow v_2 = w_2\quad \text{(one-to-one } \text{ relation) },\\ v_1 < w_1&\Longleftrightarrow v_2 < w_2\quad \text{(ancestor-descendant } \text{ preservation) }, \text{ and }\\ v_1 \prec w_1&\Longleftrightarrow v_2 \prec w_2\quad \text{(sibling } \text{ order } \text{ preservation) }. \end{aligned}$$

If $T_1$ and $T_2$ are unordered trees, the third condition is not considered.

Top-Down Mapping [12]: A Tai mapping M between two trees $T_1$ and $T_2$ is a top-down mapping if for any pair of vertices $(v, w)\in M$ such that both of v and w are not root vertices, there exists a pair $(\text{ parent }(v), \text{ parent }(w))\in M$.

The sets of vertices of $V_1$ and $V_2$ including in a mapping M are respectively denoted by $M|^{T_1}$ and $M|^{T_2}$ which are defined as $M|^{T_1}=\{v\in V_1\mid \exists w\in V_2, (v,w)\in M\}$ and $M|^{T_2}=\{w\in V_2\mid \exists v\in V_1, (v,w)\in M\}$. The total cost of edit operations for M is $\gamma (M)=\sum _{(v,w)\in M}\gamma (v\rightarrow w)+\sum _{v\in M|^{T_1}}\gamma (v\rightarrow \lambda )+\sum _{w\in M|^{T_2}}\gamma (\lambda \rightarrow w)$. Calculating the edit distance between $T_1$ and $T_2$ is equivalent to finding a mapping M minimizing the cost $\gamma (M)$ [9]. We call such mappings by optimal mappings. Below, we assume a rule R for selecting an optimal mapping from the set of all optimal mappings. Given a set $FS =\{F_1,\dots ,F_n\}$ of forests, and a mapping M, we define a forest $FS ^M$ recursively as follows:

$$\begin{aligned} FS ^M=\left\{ \begin{array}{ll} F_1&{}\text{ if }\quad | FS |=1,\\ \{F_n, \{F_1,\dots , F_{n-1}\}^M\}=M(F_n,\{F_1,\dots , F_{n-1}\}^M)&{}\text{ otherwise }. \end{array} \right. \end{aligned}$$

where $M(F_1,F_2)$ is the forest induced by an optimal mapping M between $F_1$ and $F_2$ following the rule R.

3 Tree PCA by Top-Down Mappings

3.1 New Schema for Tree PCA

In this section, we introduce new methods for extracting principal components from labeled rooted unordered trees without indexing and we give a new schema for formulating principal components based on the following three contents. The first is a distance metric $d_{M}(\cdot ,\cdot )$ based on a mapping M, and the second is the total space of given data set $\mathcal {T}$, denoted by $TS (\mathcal {T})$. The total space $TS (\mathcal {T})$ is a set of trees. The third is the set of all components, denoted by $AC (\mathcal {E})$, for any elements $\mathcal {E}$ of $TS (\mathcal {T})$. For example, the set of all components of a path is a tree-line.

The projection of the tree T onto the union of $AC (t_1)\uplus \dots \uplus AC (t_k)$ is defined by using the inclusion-exclusion principle as follows:

$$\begin{aligned} P_{\{t_1\dots t_k\}}(T) \equiv \mathop {\text {arg~min}}\limits _{ PS \in AC (t_1)\uplus \dots \uplus AC (t_k)}\sum _{n=1}^{| PS |}(-1)^{n+1}\sum _{ ps \in \{U\subset PS \mid |U|=n\}}d_M(T, ps ^M), \end{aligned}$$

(1)

where $S\uplus T$ denotes the set $\{\{s,t\}\mid s\in S, t\in T\}$. The k-th principal component is defined as

$$\begin{aligned} PC _k\equiv \mathop {\text {arg~min}}\limits _{\mathcal {E}\in TS(\mathcal {T})}\sum _{T\in \mathcal {T}}\sum _{t\in P_{\{ PC _1\dots PC _{k-1},\mathcal {E}\}}(T)}d_{M}(T,t). \end{aligned}$$

(2)

3.2 Path Features by Top-Down Mappings

In this section, we show how to apply the top-down mappings to the new schema. The sequence of labels of the path from the root r to v is defined as $\mathrm {Path}(v)\equiv \langle \alpha (r)\alpha (\mathrm {parent}^\mathrm{{dep}({ v})-2}(v))\dots \alpha (\mathrm {parent}^1(v))\alpha (v)\rangle ,$ where $\mathrm {parent}^n(v)$ is defined as $\underbrace{\mathrm {parent}(\mathrm {parent}(\dots \mathrm {parent}}_{n}(v)))$, and thus $\mathrm {parent}^1(v)=\mathrm {parent}(v)$. The set $\mathrm {Fiber}(T)\equiv \{\mathrm {Path}(v) \mid v\in \mathrm {Leaf}(T)\}$ of paths is called the fiber of T. We define the total space as the support fiber of an input data set $\mathcal {T}$, denoted by $SF (\mathcal {T})$ while the total space is defined as the support tree in the previous section. The support fiber representing the total space is defined as $SF (\mathcal {T})=\bigcup _{T\in \mathcal {T}}\mathrm {Fiber}(T)$.

Given a path P, the tree-line composed of P is $TL(P)=\bigcup _{v\in P} \mathrm {Path}(v),$ where v is a vertex of path P. Given two trees $T_1$ and $T_2$, an indel distance based on a top-down mapping between $T_1$ and $T_2$ is denoted by $d_{\textsc {td}}(T_1,T_2)$. The top-down mapping without substitution operations following the rule R is denoted by $M_{\textsc {td}}^{T_1,T_2}$. In other words, $M_{\textsc {td}}^{T_1,T_2}$ is a set of pairs of vertices corresponding with the both of labels of vertices from the root vertex completely.

Therefore, we can extract principal component paths by adapting M to $M_{\textsc {td}}$, $d_M(\cdot ,\cdot )$ to $d_{\textsc {td}}(\cdot ,\cdot )$, $TS (\mathcal {T})$ to $SF (\mathcal {T})$, and $AC (\mathcal {E})$ to $TL (P)$ where P is a path. Our method extends the previous methods by Alfaro et al. [1] and Aydin et al. [2]. Our method based on the top-down mappings can apply to ordered trees if we just give the label of a vertex to a sibling information.

Fig. 1.

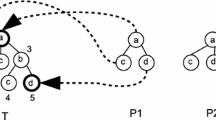
(a) An example of input data set $\mathcal {T}$. The characters, a,b and c, are labels of vertices. (b) The super tree of the input data (Fig. 1a). A label $\epsilon$ represents the terminal and d represents the dummy vertex. An integer which describes the right-hand side of each vertex is the weight of Eq. (4). The heavy line is the first principal component.

Fig. 2.

The accuracy of classification based on a top-down indel distance between cumulative principal components and the given data tree.

3.3 An Algorithm for PCA by Top-Down Mappings

In this subsection, we give an algorithm for extracting principal component based on the top-down mappings. First, we make a super tree from the each path of $SF (\mathcal {T})$ and we show the algorithm for making such super tree in Algorithm 1. The algorithm is similar to making a prefix tree representing an upper common subtree. In Algorithm 1, for a tree T, the maximum depth and maximum number of leaves of T is denoted by $\mathrm {dep}(T)$ and $\mathrm {Leaf}(T)$, respectively. The label meaning the empty is denoted by $\epsilon \not \in \varSigma$. We show an example of the input data set in Fig. 1a and the super tree of the input data set in Fig. 1. We generalize $ST (\mathcal {T})$ in accordance with Algorithm 1 and we regard $ST (\mathcal {T})$ as a set of paths. The k-th principal component derived from Eq. (2) is

$$\begin{aligned}&PC_k=\mathop {\text {arg~max}}\limits _{P\in ST (\mathcal {T})}\sum _{v\in P}\sum _{T\in \mathcal {T}}w_{k}(v,T,P),\end{aligned}$$

(3)

$$\begin{aligned} \text{ where }&w_{k}(v,T,P)=\left\{ \begin{array}{ll} 1&{}\quad \text{ if }\quad v\in M_{\textsc {td}}^{\{P,T\}}|^{P}\text{ and } v\not \in P_1\cup \dots \cup P_{k-1},\\ 0&{}\quad \text{ otherwise. } \end{array} \right. \end{aligned}$$

(4)

Therefore, the k-th principal component is the path whose sum of weights is the maximum. Then, we can extract k principal components, converting $w_k$ on principal components to 0. The time complexity of extracting k principal components is $O((\mathrm {Leaf}( ST (\mathcal {T}))\mathrm {dep}( ST (\mathcal {T}))+k|V|)|\mathcal {T}|)$ where $|V|=\max \{|V_1|,|V_2|\}$.

4 Experiment

In our experiment, we use glycan structure data from the KEGG/GLYCAN database [5] and their annotations are from the CarbBank/CCSD database [4]. We regard a glycan structure as a labeled tree as with [6]. A glycan structure is often regarded as an ordered tree, however, in our experiment, we regard it as a labeled unordered tree because we focus on only paths.

For a glycan structure, many studies have been proposed e.g. [6, 13]. Each glycan structure is assigned to a blood component class among Leukemic, Erythrocyte, Serum, and Plasma, and the number of each class data used in our experiment is 140, 127, 78 and 60, respectively.

Fig. 3.

The super trees of Leukemic and Erythrocyte, respectively, where the each root vertex is a dummy vertex and not including $\epsilon$ vertices. The heaviest and second heaviest lines are 1st and 2nd principal component paths, respectively.

Table 2. Comparing the classification accuracy.

First, we visualize super trees and the first and second principal components of the Leukemic and Erythrocyte in Fig. 3. The heaviest and the second heaviest lines in Fig. 3 are the first and second principal component paths, respectively. Next, we try to classify the input data set into the 4 classes by using principal components. First, we classify a given data set with a top-down indel distance, that is the number of vertices not including the largest common prefix structure. The results are shown in Fig. 2. The accuracy of all class labels is mostly over 0.8. We compare the accuracy of classification by using principal components from 1st to 20th with the one of measuring a global edit distance. The result is shown in Table. 2. The classification of the Erythrocyte and Plasma using principal components is higher while the one of the other classes using the global edit distance is higher. According to the results, we could conclude Leukemic has specific global structures while Erythrocyte and Plasma have specific local structures because principal components are local dominant structures of the given data. Moreover, the classification using principal components runs faster because the time complexity of computing the global edit distance between two trees is $O(|V|^3)$.

5 Concluding Remarks

We introduced a general schema for defining PCA for labeled rooted trees in Sect. 3. Because of lack of space, we gave only one instance of the schema. Another instance can be given with bottom-up mappings [10]. We should select a mapping depending on the given data set.

In [5, 6], glycan data are classified by using kernels, but in this method, we cannot know the similar structures explicitly. By extracting principal components, we can observe the dominant structures and the similar structures and classify the given data by using the principal components. Moreover, the time complexity of classification by using principal components is lower than the one by measuring a global edit distance between two unordered trees, NP-hard problem.